Adaptive Optical Closed-Loop Control Based on the Single-Dimensional Perturbation Descent Algorithm
Abstract
1. Introduction
2. Principles of Algorithm and Convergence Speed Analysis
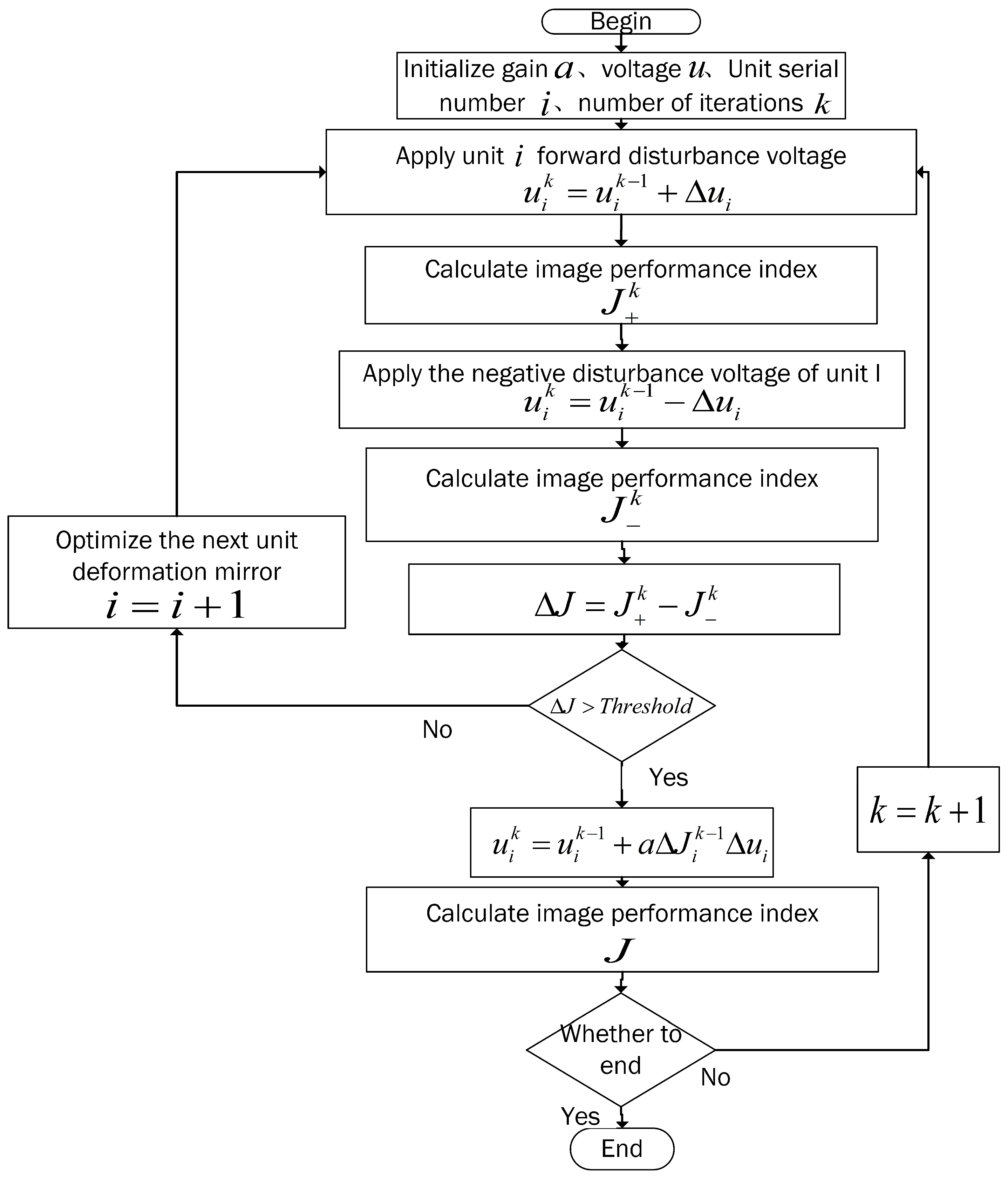
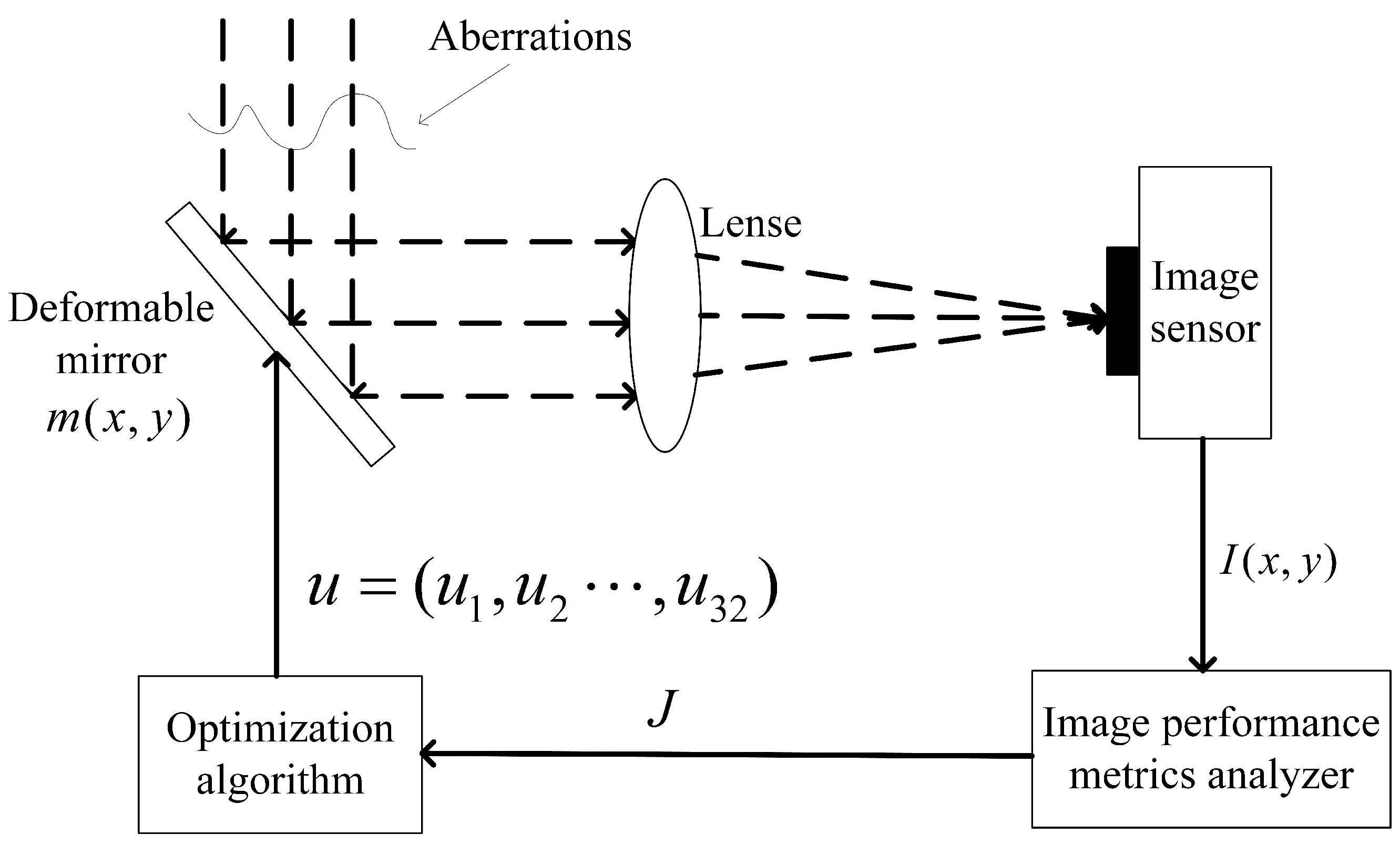
2.1. Algorithm Principle
2.2. Analysis of the Convergence Speed of the Algorithm
3. Experiments and Results Analysis
3.1. Numerical Simulation
3.2. Analysis of Simulation Result
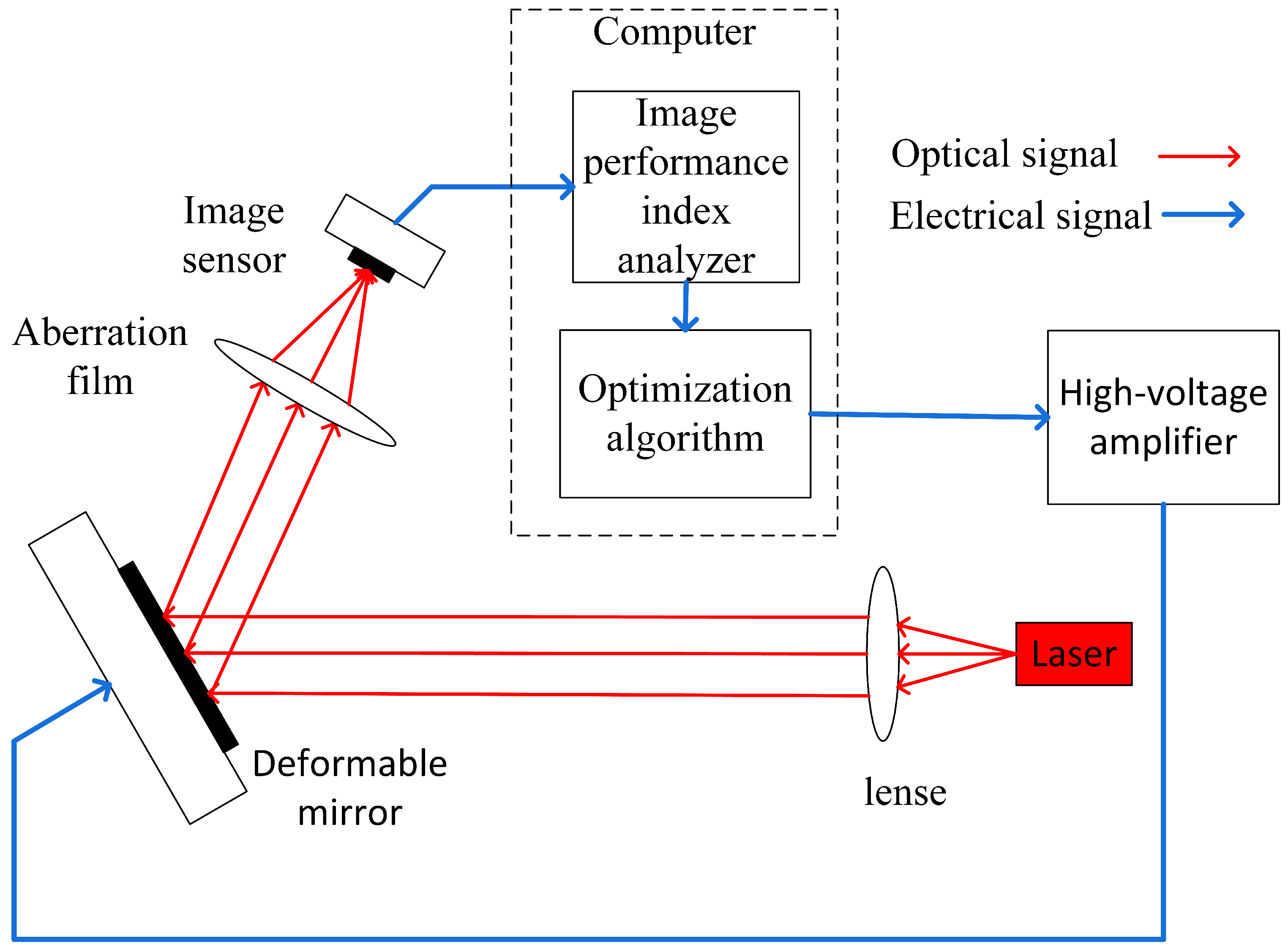
3.3. Experiments and Results Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SDPD | Single-dimensional perturbation descent |
| SPGD | Stochastic parallel gradient descent |
| 2SPGD | Second-order stochastic parallel gradient descent |
| SPSA | Simultaneous perturbation of the stochastic approximation |
| FDSA | Finite difference stochastic approximation |
References
- Cao, J.; Zhao, X.; Li, Z.; Liu, W.; Song, Y. Stochastic parallel gradient descent laser beam control algorithm for atmospheric compensation in free space optical communication. Optik 2014, 125, 6142–6147. [Google Scholar] [CrossRef]
- Li, Y.; Li, L.; Guo, Y.; Zhang, H.; Fu, S.; Gao, C.; Yin, C. Atmospheric turbulence forecasting using two-stage variational mode decomposition and autoregression towards free-space optical data-transmission link. Front. Phys. 2022, 10, 970025. [Google Scholar] [CrossRef]
- Peng, J.; Qi, B.; Li, H.; Mao, Y. AS-SPGD algorithm to improve convergence performance for fiber coupling in free space optical communication. Opt. Commun. 2022, 519, 128397. [Google Scholar] [CrossRef]
- Xie, Z.; Ma, H.; He, X.; Qi, B.; Ren, G.; Dong, L.; Tan, Y. Adaptive piston correction of sparse aperture systems with stochastic parallel gradient descent algorithm. Opt. Express 2018, 26, 9541–9551. [Google Scholar] [CrossRef] [PubMed]
- Azimipour, M.; Migacz, J.V.; Zawadzki, R.J.; Werner, J.S.; Jonnal, R.S. Functional retinal imaging using adaptive optics swept-source OCT at 1.6 MHz. Optica 2019, 6, 300–303. [Google Scholar] [CrossRef]
- Salter, P.S.; Booth, M.J. Adaptive optics in laser processing. Light Sci. Appl. 2019, 8, 1–16. [Google Scholar]
- Chen, J.; Ma, J.; Mao, Y.; Liu, Y.; Li, B.; Chu, J. Experimental evaluation of a positive-voltage-driven unimorph deformable mirror for astronomical applications. Opt. Eng. 2015, 54, 117103. [Google Scholar] [CrossRef]
- Huang, G.; Geng, C.; Li, F.; Yang, Y.; Li, X. Adaptive SMF coupling based on precise-delayed SPGD algorithm and its application in free space optical communication. IEEE Photonics J. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Ren, H.; Dong, B. Fast dynamic correction algorithm for model-based wavefront sensorless adaptive optics in extended objects imaging. Opt. Express 2021, 29, 27951–27960. [Google Scholar] [CrossRef]
- Toselli, I.; Gladysz, S. Improving system performance by using adaptive optics and aperture averaging for laser communications in oceanic turbulence. Opt. Express 2020, 28, 17347–17361. [Google Scholar] [CrossRef]
- Sun, L.; Guo, Y.; Shao, C.; Li, Y.; Zheng, Y.; Sun, C.; Wang, X.; Huang, L. 10.8 kW, 2.6 times diffraction limited laser based on a continuous wave Nd: YAG oscillator and an extra-cavity adaptive optics system. Opt. Lett. 2018, 43, 4160–4163. [Google Scholar] [CrossRef] [PubMed]
- Pomohaci, R.; Oudmaijer, R.D.; Goodwin, S.P. A pilot survey of the binarity of Massive Young Stellar Objects with K-band adaptive optics. Mon. Not. R. Astron. Soc. 2019, 484, 226–238. [Google Scholar] [CrossRef]
- Li, Y.; Lim, Y.J.; Xu, Q.; Beattie, L.; Gardiner, E.E.; Gaus, K.; Heath, W.R.; Lee, W.M. Raster adaptive optics for video rate aberration correction and large FOV multiphoton imaging. Biomed. Opt. Express 2020, 11, 1032–1042. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.; Cheng, T.; Kong, L.; Wang, S.; Xu, B. A Single Far-Field Deep Learning Adaptive Optics System Based on Four-Quadrant Discrete Phase Modulation. Sensors 2020, 20, 5106. [Google Scholar] [CrossRef] [PubMed]
- Xin, Q.; Ju, G.; Zhang, C.; Xu, S. Object-independent image-based wavefront sensing approach using phase diversity images and deep learning. Opt. Express 2019, 27, 26102–26119. [Google Scholar] [CrossRef]
- Liu, W.; Jin, D.; Shi, W.; Cao, J. Performance analysis of coherent optical communication based on hybrid algorithm. Opt. Laser Technol. 2022, 149, 107878. [Google Scholar] [CrossRef]
- Booth, M.J. Wavefront sensorless adaptive optics for large aberrations. Opt. Lett. 2007, 32, 5–7. [Google Scholar] [CrossRef]
- Huang, L.H. Coherent beam combination using a general model-based method. Chin. Phys. Lett. 2014, 31, 094205. [Google Scholar] [CrossRef]
- Liu, M.; Dong, B. Efficient wavefront sensorless adaptive optics based on large dynamic crosstalk-free holographic modal wavefront sensing. Opt. Express 2022, 30, 9088–9102. [Google Scholar] [CrossRef]
- Yang, S.; Ke, X. Experimental study on adaptive optical wavefront correction with dual mirrors in free space optical communication. Optik 2021, 242, 167146. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, T.; Mbemba, D.; Wang, Y.; Wei, X.; Zhang, Z.; Iqbal, A. Wavefront Sensorless Aberration Correction with Magnetic Fluid Deformable Mirror for Laser Focus Control in Optical Tweezer System. IEEE Trans. Magn. 2020, 57, 1–6. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, B.; Liao, J.; Li, X.; Wang, C.; Sun, Y.; Jin, L.; Feng, J.; Cao, C. Calibration of 16× 16 SOI optical phased arrays via improved SPGD algorithm. Opt. Laser Technol. 2023, 157, 108743. [Google Scholar] [CrossRef]
- Wu, J.; Hu, C.; Liu, R.; Wu, S.; Cao, J.; Cheng, Z.; Yu, B.; Zhang, L. Adam SPGD algorithm in freeform surface in-process interferometry. Opt. Express 2022, 30, 32528–32539. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Chen, L.; Chen, Y.; Zhang, W. Accelerating federated learning via momentum gradient descent. IEEE Trans. Parallel Distrib. Syst. 2020, 31, 1754–1766. [Google Scholar] [CrossRef]
- Yang, H.; Li, X. Comparison of several stochastic parallel optimization algorithms for adaptive optics system without a wavefront sensor. Opt. Laser Technol. 2011, 43, 630–635. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, L.; Spall, J.C. Efficient implementation of second-order stochastic approximation algorithms in high-dimensional problems. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3087–3099. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, N.; Bullins, B.; Hazan, E. Second-order stochastic optimization in linear time. Stat 2016, 1050, 15. [Google Scholar]
- Xu, P.; Roosta, F.; Mahoney, M.W. Newton-type methods for non-convex optimization under inexact Hessian information. Math. Program. 2020, 184, 35–70. [Google Scholar] [CrossRef]
- Cauwenberghs, G. A fast stochastic error-descent algorithm for supervised learning and optimization. Adv. Neural Inf. Process. Syst. 1992, 5, 244–251. [Google Scholar]

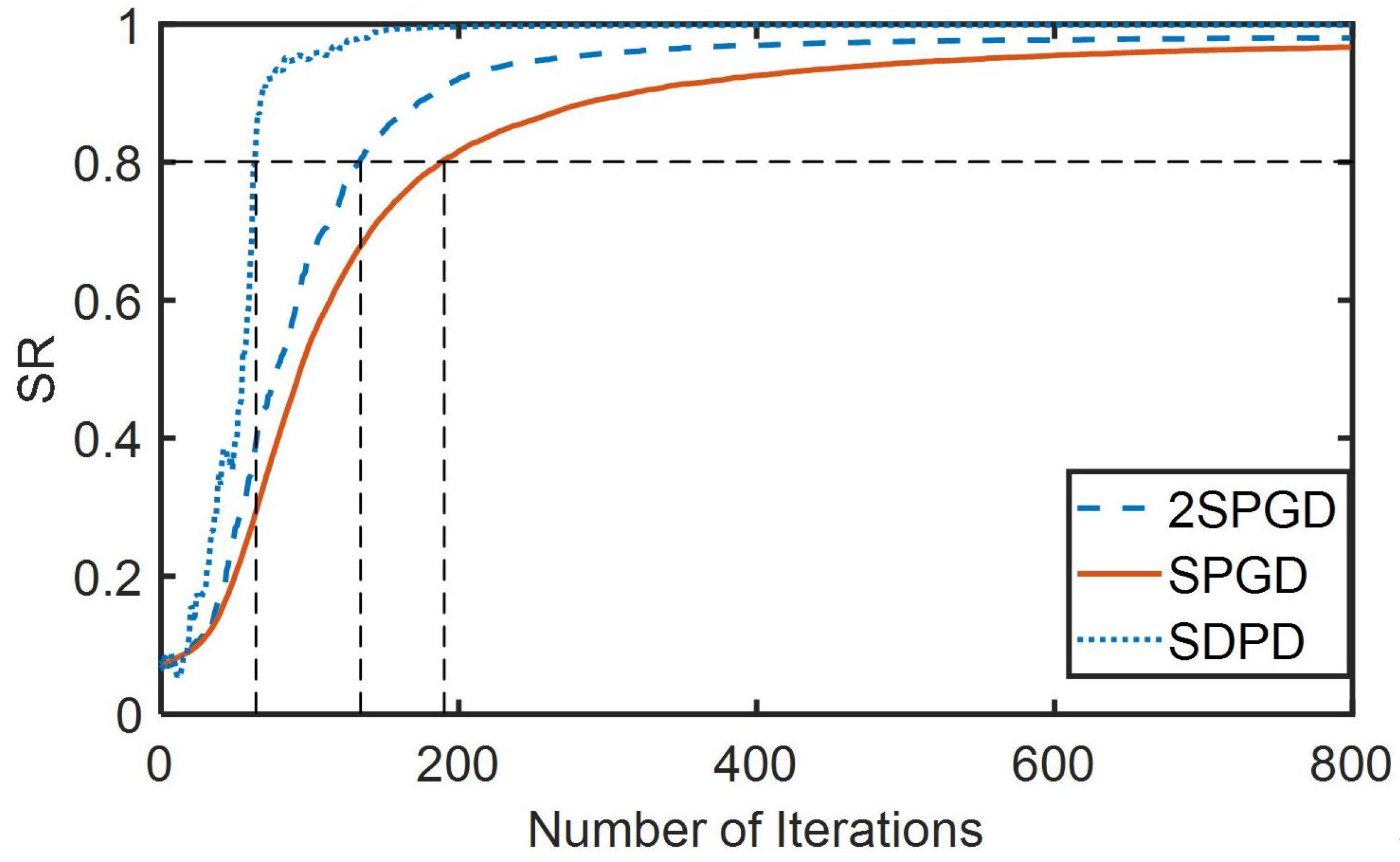
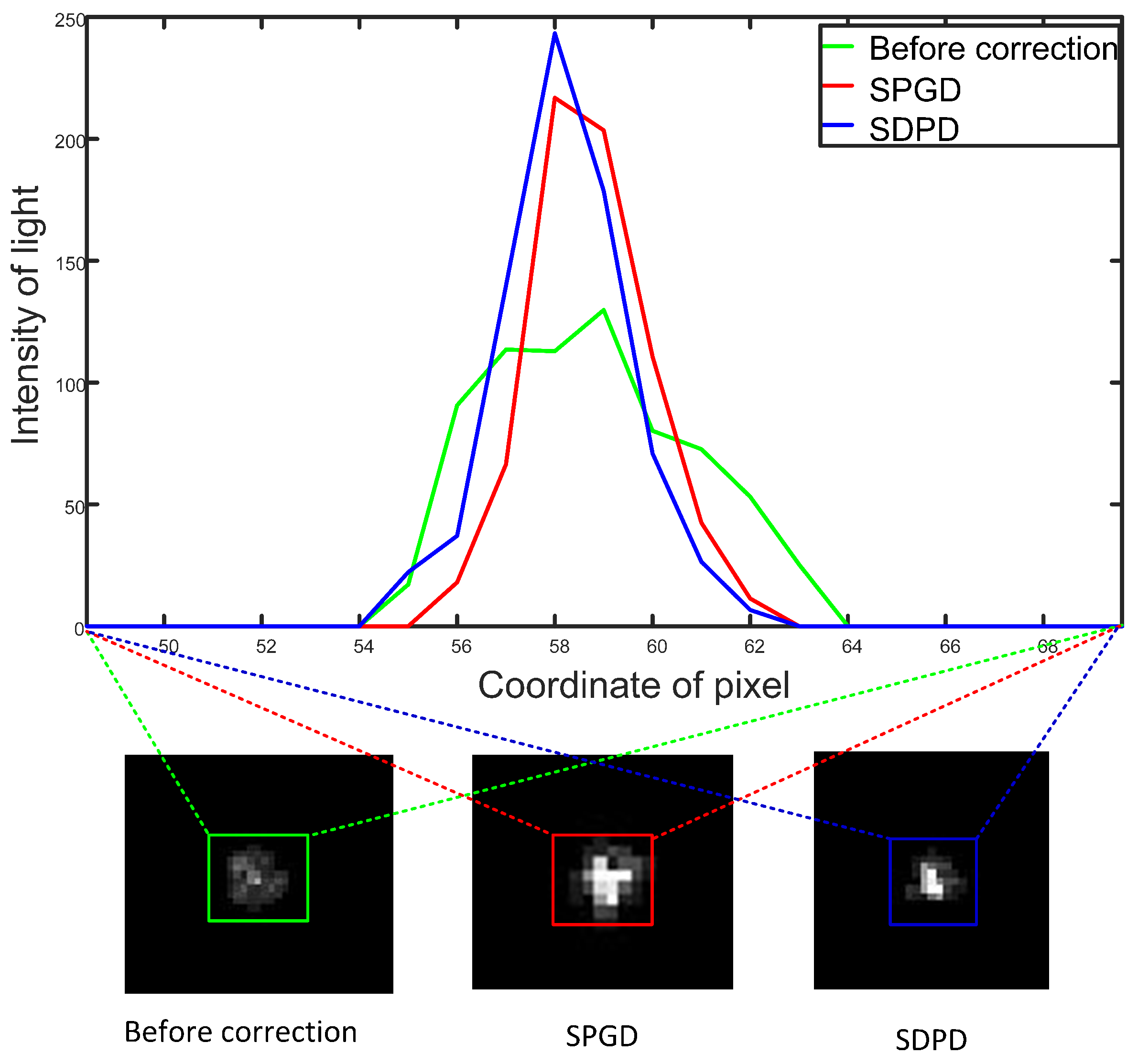
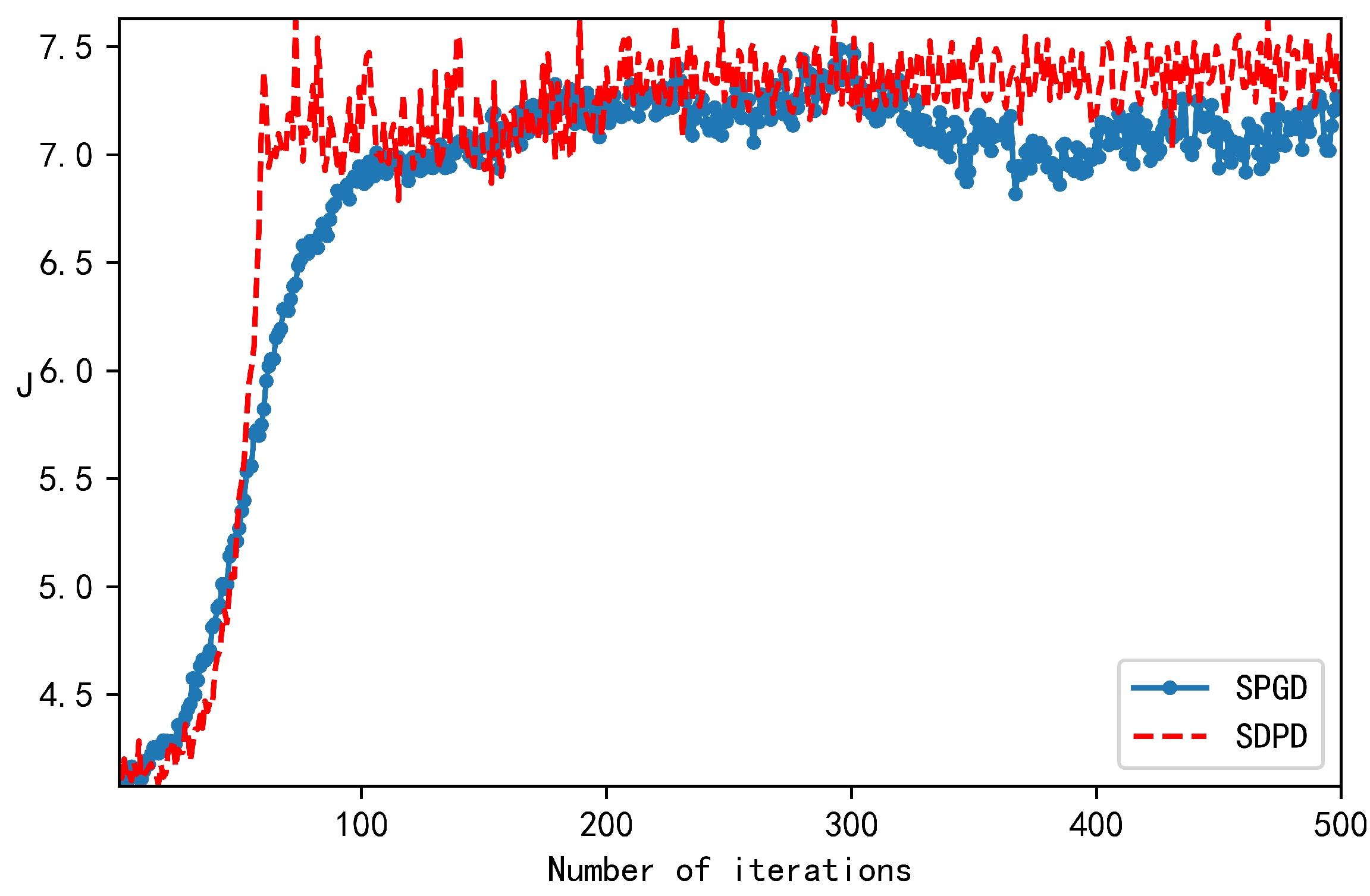
| Types of Algorithms | Number of Iterations | Convergence Times | Final Convergence Value of SR |
|---|---|---|---|
| SDPD | 65 | 0.73 ms | 0.999 |
| 2SPGD | 134 | 4.02 ms | 0.958 |
| SPGD | 182 | 3.185 ms | 0.957 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Zhou, Y.; Li, Z.; Jia, J.; Zhang, Y. Adaptive Optical Closed-Loop Control Based on the Single-Dimensional Perturbation Descent Algorithm. Sensors 2023, 23, 4371. https://doi.org/10.3390/s23094371
Chen B, Zhou Y, Li Z, Jia J, Zhang Y. Adaptive Optical Closed-Loop Control Based on the Single-Dimensional Perturbation Descent Algorithm. Sensors. 2023; 23(9):4371. https://doi.org/10.3390/s23094371
Chicago/Turabian StyleChen, Bo, Yilin Zhou, Zhaoyi Li, Jingjing Jia, and Yirui Zhang. 2023. "Adaptive Optical Closed-Loop Control Based on the Single-Dimensional Perturbation Descent Algorithm" Sensors 23, no. 9: 4371. https://doi.org/10.3390/s23094371
APA StyleChen, B., Zhou, Y., Li, Z., Jia, J., & Zhang, Y. (2023). Adaptive Optical Closed-Loop Control Based on the Single-Dimensional Perturbation Descent Algorithm. Sensors, 23(9), 4371. https://doi.org/10.3390/s23094371







