Yttrium-Iron Garnet Magnetometer in MEG: Advance towards Multi-Channel Arrays
Abstract
1. Introduction
1.1. History
1.2. Motivation
2. Theory
2.1. Governing Equations
2.2. Lead-Field Matrix
3. Methods
3.1. Signal Power and Signal-to-Noise Ratio
3.2. Information Capacity
4. Sensors
4.1. Description of the Sensors
4.2. Output Computation
4.3. Sensor Arrays
4.3.1. SQUID-like Layout
4.3.2. Uniform Layouts
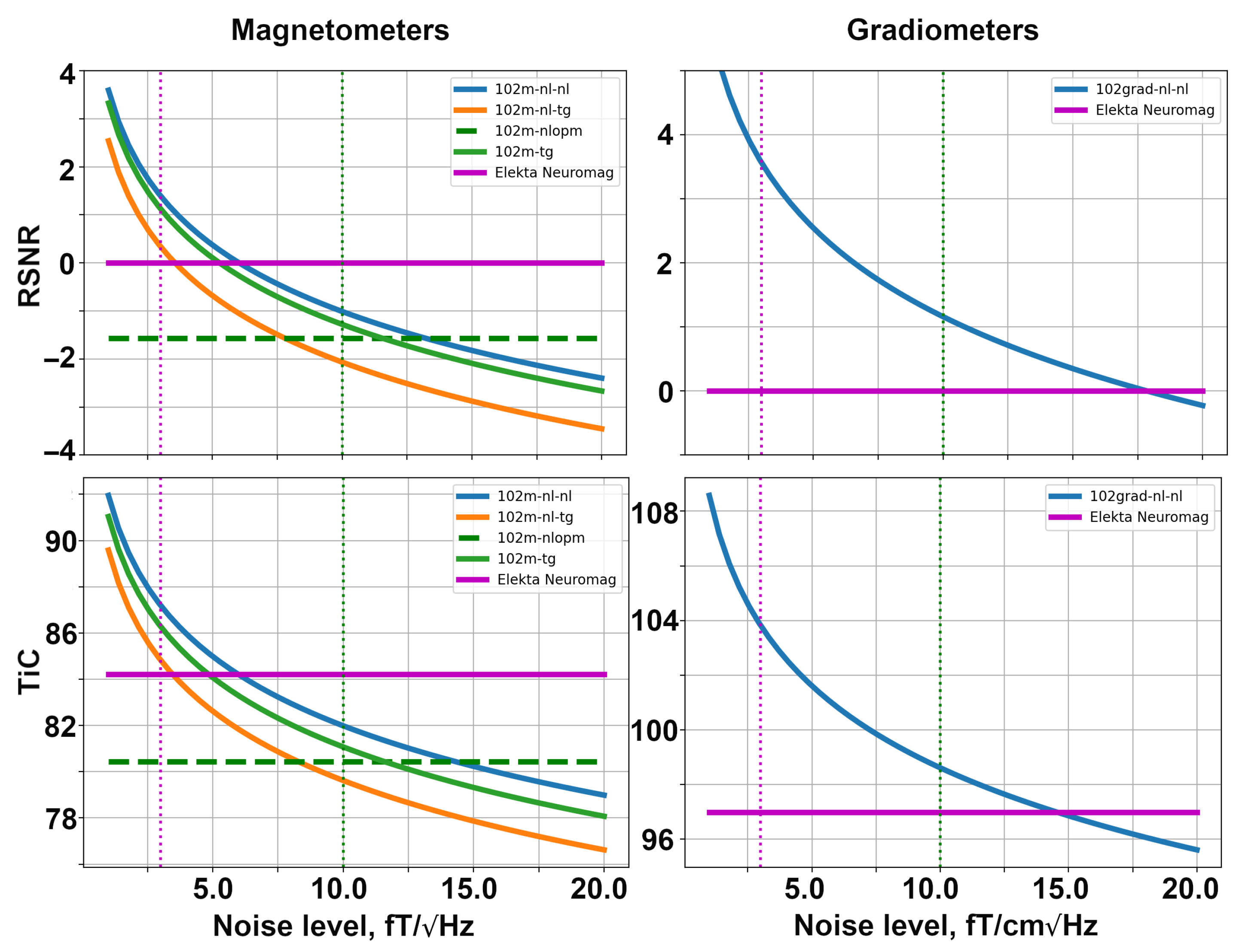
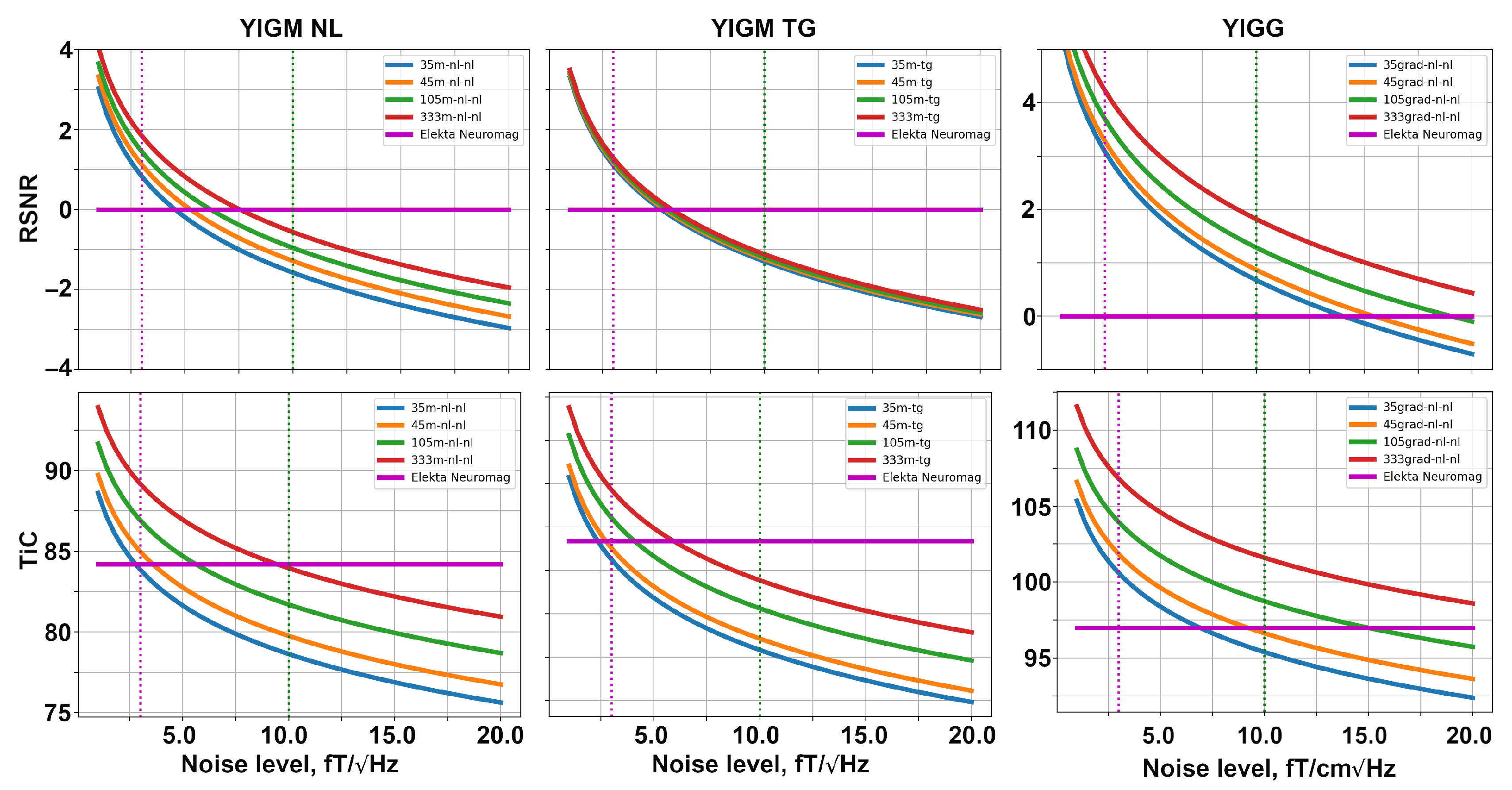
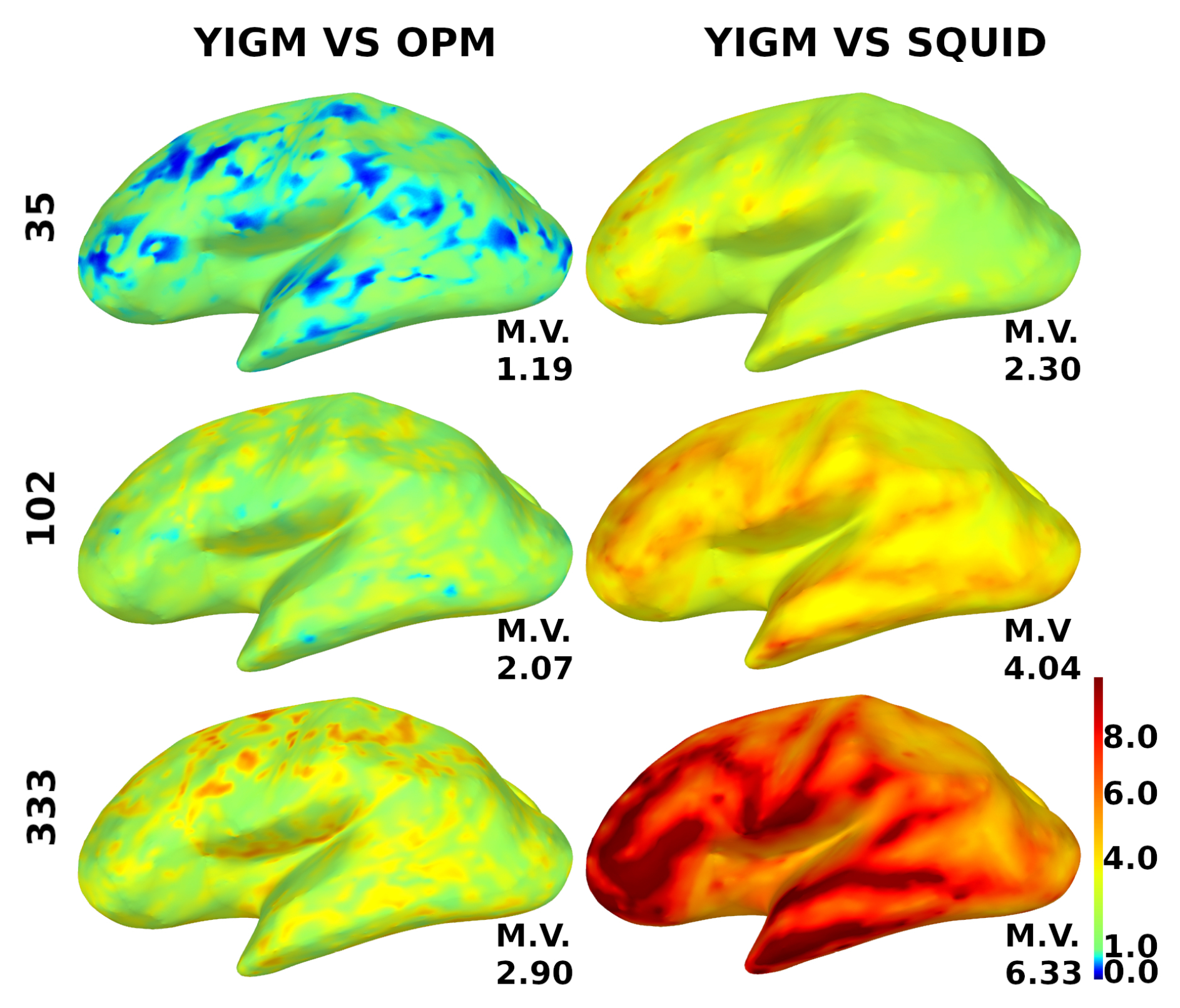
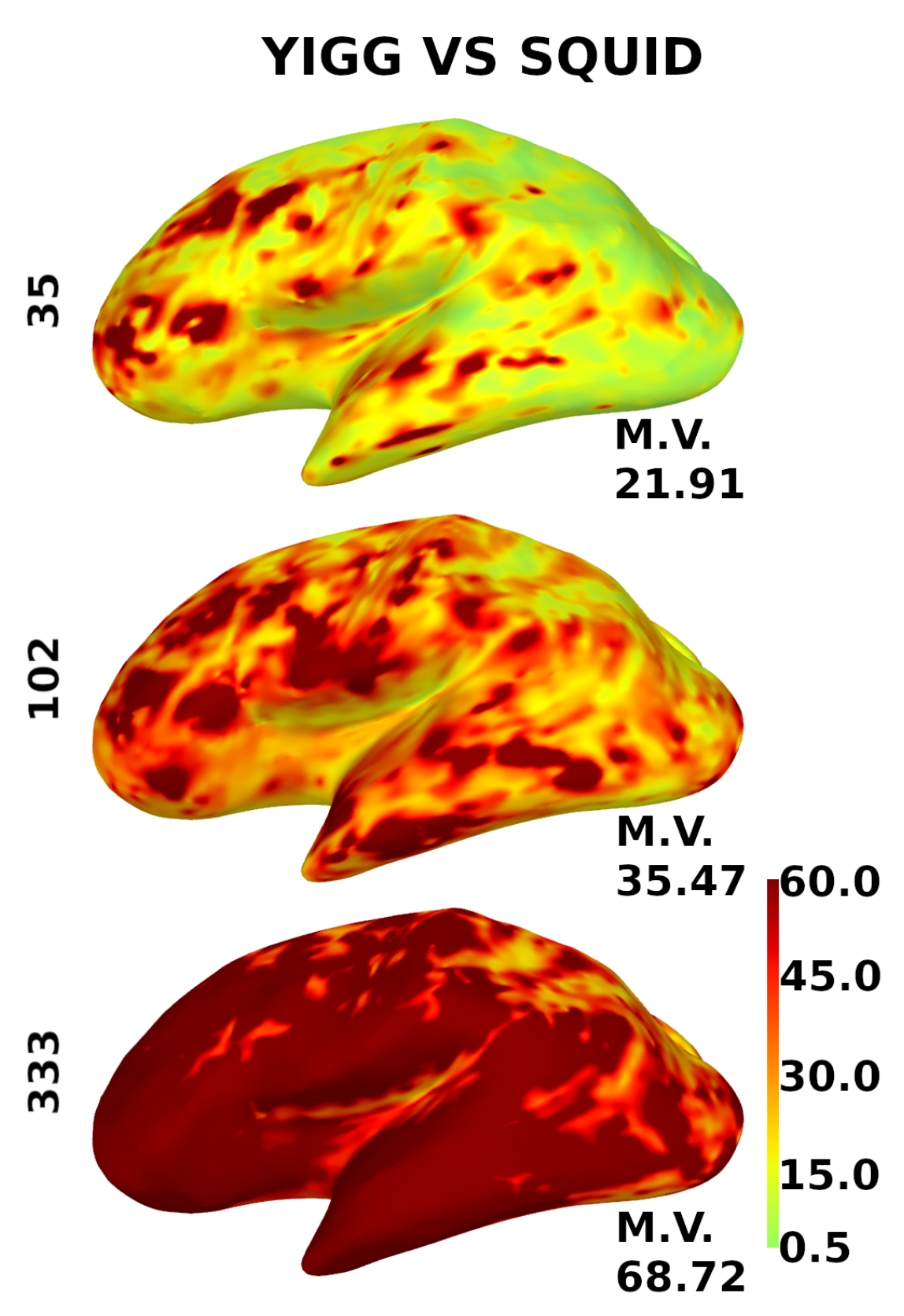
5. Results
5.1. SQUID-like Layouts
5.2. Uniform Layouts
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cohen, D. Magnetoencephalography: Detection of the brain’s electrical activity with a superconducting magnetometer. Science 1972, 175, 664–666. [Google Scholar] [CrossRef] [PubMed]
- Iivanainen, J.; Stenroos, M.; Parkkonen, L. Measuring MEG closer to the brain: Performance of on-scalp sensor arrays. NeuroImage 2017, 147, 542–553. [Google Scholar] [CrossRef] [PubMed]
- Faley, M.; Dammers, J.; Maslennikov, Y.; Schneiderman, J.; Winkler, D.; Koshelets, V.; Shah, N.; Dunin-Borkowski, R. High-tc SQUID biomagnetometers. Supercond. Sci. Technol. 2017, 30, 083001. [Google Scholar] [CrossRef]
- Andersen, L.M.; Oostenveld, R.; Pfeiffer, C.; Ruffieux, S.; Jousmäki, V.; Hämäläinen, M.; Schneiderman, J.F.; Lundqvist, D. Similarities and differences between on-scalp and conventional in-helmet magnetoencephalography recordings. PLoS ONE 2017, 12, e0178602. [Google Scholar] [CrossRef] [PubMed]
- Andersen, L.M.; Pfeiffer, C.; Ruffieux, S.; Riaz, B.; Winkler, D.; Schneiderman, J.F.; Lundqvist, D. On-scalp MEG SQUIDs are sensitive to early somatosensory activity unseen by conventional MEG. NeuroImage 2020, 221, 117157. [Google Scholar] [CrossRef]
- Schwindt, P.D.; Johnson, C.N. Atomic Magnetometer for Human Magnetoencephalography; Sandia Report SAND2010-8443; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 2010.
- Borna, A.; Carter, T.R.; Goldberg, J.D.; Colombo, A.P.; Jau, Y.Y.; Berry, C.; McKay, J.; Stephen, J.; Weisend, M.; Schwindt, P.D. A 20-channel magnetoencephalography system based on optically pumped magnetometers. Phys. Med. Biol. 2017, 62, 8909. [Google Scholar] [CrossRef]
- Boto, E.; Meyer, S.S.; Shah, V.; Alem, O.; Knappe, S.; Kruger, P.; Fromhold, T.M.; Lim, M.; Glover, P.M.; Morris, P.G.; et al. A new generation of magnetoencephalography: Room temperature measurements using optically pumped magnetometers. NeuroImage 2017, 149, 404–414. [Google Scholar] [CrossRef]
- Lin, C.H.; Tierney, T.M.; Holmes, N.; Boto, E.; Leggett, J.; Bestmann, S.; Bowtell, R.; Brookes, M.J.; Barnes, G.R.; Miall, R.C. Using optically pumped magnetometers to measure magnetoencephalographic signals in the human cerebellum. J. Physiol. 2019, 597, 4309–4324. [Google Scholar] [CrossRef]
- Boto, E.; Holmes, N.; Leggett, J.; Roberts, G.; Shah, V.; Meyer, S.S.; Mu noz, L.D.; Mullinger, K.J.; Tierney, T.M.; Bestmann, S.; et al. Moving magnetoencephalography towards real-world applications with a wearable system. Nature 2018, 555, 657–661. [Google Scholar] [CrossRef]
- Borna, A.; Carter, T.R.; Colombo, A.P.; Jau, Y.Y.; McKay, J.; Weisend, M.; Taulu, S.; Stephen, J.M.; Schwindt, P.D. Non-Invasive Functional-Brain-Imaging with an OPM-based Magnetoencephalography System. PLoS ONE 2020, 15, e0227684. [Google Scholar] [CrossRef]
- Zhang, R.; Mhaskar, R.; Smith, K.; Prouty, M. Portable intrinsic gradiometer for ultra-sensitive detection of magnetic gradient in unshielded environment. Appl. Phys. Lett. 2020, 116, 143501. [Google Scholar] [CrossRef]
- Hill, R.M.; Boto, E.; Rea, M.; Holmes, N.; Leggett, J.; Coles, L.A.; Papastavrou, M.; Everton, S.K.; Hunt, B.A.; Sims, D.; et al. Multi-channel whole-head OPM-MEG: Helmet design and a comparison with a conventional system. NeuroImage 2020, 219, 116995. [Google Scholar] [CrossRef] [PubMed]
- Limes, M.; Foley, E.; Kornack, T.; Caliga, S.; McBride, S.; Braun, A.; Lee, W.; Lucivero, V.; Romalis, M. Portable magnetometry for detection of biomagnetism in ambient environments. Phys. Rev. Appl. 2020, 14, 011002. [Google Scholar] [CrossRef]
- Petrenko, M.V.; Dmitriev, S.P.; Pazgalev, A.S.; Ossadtchi, A.E.; Vershovskii, A.K. Towards the non-zero field cesium magnetic sensor array for magnetoencephalography. IEEE Sens. J. 2021, 21, 18626–18632. [Google Scholar] [CrossRef]
- Riaz, B.; Pfeiffer, C.; Schneiderman, J.F. Evaluation of realistic layouts for next generation on-scalp MEG: Spatial information density maps. Sci. Rep. 2017, 7, 6974. [Google Scholar] [CrossRef]
- Iivanainen, J.; Zetter, R.; Grön, M.; Hakkarainen, K.; Parkkonen, L. On-scalp MEG system utilizing an actively shielded array of optically pumped magnetometers. Neuroimage 2019, 194, 244–258. [Google Scholar] [CrossRef]
- Zahran, S.; Mahmoudzadeh, M.; Wallois, F.; Betrouni, N.; Derambure, P.; Le Prado, M.; Palacios-Laloy, A.; Labyt, E. Performance Analysis of Optically Pumped 4He Magnetometers vs. Conventional SQUIDs: From Adult to Infant Head Models. Sensors 2022, 22, 3093. [Google Scholar] [CrossRef]
- Marhl, U.; Sander, T.; Jazbinšek, V. Simulation study of different OPM-MEG measurement components. Sensors 2022, 22, 3184. [Google Scholar] [CrossRef]
- Beltrachini, L.; von Ellenrieder, N.; Eichardt, R.; Haueisen, J. Optimal design of on-scalp electromagnetic sensor arrays for brain source localisation. Hum. Brain Mapp. 2021, 42, 4869–4879. [Google Scholar] [CrossRef]
- Boto, E.; Seedat, Z.A.; Holmes, N.; Leggett, J.; Hill, R.M.; Roberts, G.; Shah, V.; Fromhold, T.M.; Mullinger, K.J.; Tierney, T.M.; et al. Wearable neuroimaging: Combining and contrasting magnetoencephalography and electroencephalography. NeuroImage 2019, 201, 116099. [Google Scholar] [CrossRef]
- Tierney, T.M.; Holmes, N.; Mellor, S.; López, J.D.; Roberts, G.; Hill, R.M.; Boto, E.; Leggett, J.; Shah, V.; Brookes, M.J.; et al. Optically pumped magnetometers: From quantum origins to multi-channel magnetoencephalography. NeuroImage 2019, 199, 598–608. [Google Scholar] [CrossRef] [PubMed]
- QZFM Gen-3. Available online: https://quspin.com/products-qzfm/ (accessed on 11 July 2022).
- Morales, S.; Corsi, M.; Fourcault, W.; Bertrand, F.; Cauffet, G.; Gobbo, C.; Alcouffe, F.; Lenouvel, F.; Le Prado, M.; Berger, F.; et al. Magnetocardiography measurements with 4He vector optically pumped magnetometers at room temperature. Phys. Med. Biol. 2017, 62, 7267. [Google Scholar] [CrossRef] [PubMed]
- Labyt, E.; Corsi, M.C.; Fourcault, W.; Laloy, A.P.; Bertrand, F.; Lenouvel, F.; Cauffet, G.; Le Prado, M.; Berger, F.; Morales, S. Magnetoencephalography with optically pumped 4 He magnetometers at ambient temperature. IEEE Trans. Med. Imaging 2018, 38, 90–98. [Google Scholar] [CrossRef] [PubMed]
- Fourcault, W.; Romain, R.; Le Gal, G.; Bertrand, F.; Josselin, V.; Le Prado, M.; Labyt, E.; Palacios-Laloy, A. Helium-4 magnetometers for room-temperature biomedical imaging: Toward collective operation and photon-noise limited sensitivity. Opt. Express 2021, 29, 14467–14475. [Google Scholar] [CrossRef]
- Koshev, N.; Butorina, A.; Skidchenko, E.; Kuzmichev, A.; Ossadtchi, A.; Ostras, M.; Fedorov, M.; Vetoshko, P. Evolution of MEG: A first MEG-feasible fluxgate magnetometer. Hum. Brain Mapp. 2021, 42, 4844–4856. [Google Scholar] [CrossRef] [PubMed]
- Vetoshko, P. Remagnetization of Iron-Garnet Films by Coherent Rotation for Sensitive Elements of Magnetic Sensors. Ph.D. Thesis, M.N. Mikheev Institute of Metal Physics of the Ural Branch of the Russian Academy of Sciences (IMP UB RAS), Yekaterinburg, Russia, 2017. (In Russian). [Google Scholar]
- Brookes, M.J.; Boto, E.; Rea, M.; Shah, V.; Osborne, J.; Holmes, N.; Hill, R.M.; Leggett, J.; Rhodes, N.; Bowtell, R. Theoretical advantages of a triaxial optically pumped magnetometer magnetoencephalography system. NeuroImage 2021, 236, 118025. [Google Scholar] [CrossRef]
- Hochwald, B.; Nehorai, A. Magnetoencephalography with diversely oriented and multicomponent sensors. IEEE Trans. Biomed. Eng. 1997, 44, 40–50. [Google Scholar] [CrossRef]
- Hamalainen, M.S.; Sarvas, J. Realistic conductivity geometry model of the human head for interpretation of neuromagnetic data. IEEE Trans. Biomed. Eng. 1989, 36, 165–171. [Google Scholar] [CrossRef]
- Ilmoniemi, R. The forward and inverse problems in the spherical model. In Biomagnetism: Applications & Theory; Pergamon: Oxford, UK, 1985. [Google Scholar]
- Schneiderman, J.F. Information content with low-vs. high-Tc SQUID arrays in MEG recordings: The case for high-Tc SQUID-based MEG. J. Neurosci. Methods 2014, 222, 42–46. [Google Scholar] [CrossRef]
- Tierney, T.M.; Mellor, S.; O’Neill, G.C.; Holmes, N.; Boto, E.; Roberts, G.; Hill, R.M.; Leggett, J.; Bowtell, R.; Brookes, M.J.; et al. Pragmatic spatial sampling for wearable MEG arrays. Sci. Rep. 2020, 10, 21609. [Google Scholar] [CrossRef]
- Samuelsson, J.G.; Peled, N.; Mamashli, F.; Ahveninen, J.; Hämäläinen, M.S. Spatial fidelity of MEG/EEG source estimates: A general evaluation approach. Neuroimage 2021, 224, 117430. [Google Scholar] [CrossRef] [PubMed]
- Sarvas, J. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys. Med. Biol. 1987, 32, 11–22. [Google Scholar] [CrossRef] [PubMed]
- Hamalainen, M.; Hari, R.; Ilmoniemi, R.J.; Knuutila, J.; Lounasmaa, O.V. Magnetoencephalography: Theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev. Mod. Phys. 1993, 65, 413. [Google Scholar] [CrossRef]
- Geselowitz, D. On the magnetic field generated outside an inhomogeneous volume conductor by internal current sources. IEEE Trans. Magn. 1970, 6, 346–347. [Google Scholar] [CrossRef]
- Plonsey, R.; Heppner, D.B. Considerations of quasi-stationarity in electrophysiological systems. Bull. Math. Biophys. 1967, 29, 657–664. [Google Scholar] [CrossRef]
- De Munck, J.; Wolters, C.; Clerc, M. EEG and MEG: Forward Modeling; CUP/BRRR; Cambridge University Press: Cambridge, UK, 2012; Chapter 6; pp. 203–272. [Google Scholar]
- Sereno, M. Improved localization of cortical activity by combining EEG and MEG with MRI cortical surface reconstruction: A linear approach. J. Cogn. Neurosci. 1993, 5, 162–176. [Google Scholar]
- Hillebrand, A.; Barnes, G.R. Beamformer analysis of MEG data. Int. Rev. Neurobiol. 2005, 68, 149–171. [Google Scholar]
- Pascual-Marqui, R.D.; Esslen, M.; Kochi, K.; Lehmann, D. Functional imaging with low-resolution brain electromagnetic tomography (LORETA): A review. Methods Find. Exp. Clin. Pharmacol. 2002, 24, 91–95. [Google Scholar]
- Uutela, K.; Hämäläinen, M.; Somersalo, E. Visualization of magnetoencephalographic data using minimum current estimates. NeuroImage 1999, 10, 173–180. [Google Scholar] [CrossRef]
- Lin, F.H.; Belliveau, J.W.; Dale, A.M.; Hämäläinen, M.S. Distributed current estimates using cortical orientation constraints. Hum. Brain Mapp. 2006, 27, 1–13. [Google Scholar] [CrossRef]
- Vetoshko, P.; Gusev, N.; Chepurnova, D.; Samoilova, E.; Syvorotka, I.; Syvorotka, I.; Zvezdin, A.; Korotaeva, A.; Belotelov, V. Flux-gate magnetic field sensor based on yttrium-iron garnet films for magnetocardiography investigations. Tech. Phys. Lett. 2016, 42, 860–864. [Google Scholar] [CrossRef]
- Vetoshko, P.; Gusev, N.; Chepurnova, D.; Samoilova, E.; Zvezdin, A.; Korotaeva, A.; Belotelov, V. Rat Magnetocardiography Using a Flux-Gate Sensor Based on Iron Garnet Films. Biomed. Eng. 2016, 50, 237–240. [Google Scholar] [CrossRef]
- Kemppainen, P.; Ilmoniemi, R. Channel capacity of multichannel magnetometers. In Advances in Biomagnetism; Springer: New York, NY, USA, 1989; pp. 635–638. [Google Scholar]
- Osborne, J.; Orton, J.; Alem, O.; Shah, V. Fully integrated standalone zero field optically pumped magnetometer for biomagnetism. In Proceedings of the Steep Dispersion Engineering and Opto-Atomic Precision Metrology XI. International Society for Optics and Photonics, San Francisco, CA, USA, 29 January–1 February 2018; Volume 10548, p. 105481G. [Google Scholar]
- Elzenheimer, E.; Laufs, H.; Schulte-Mattler, W.; Schmidt, G. Magnetic measurement of electrically evoked muscle responses with optically pumped magnetometers. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 756–765. [Google Scholar] [CrossRef] [PubMed]
- Skidchenko, E.; Butorina, A.; Koshev, N. How to Build OP-MEG: Specific Issues and Challenges. Int. J. Psychophysiol. 2021, 168, S121. [Google Scholar] [CrossRef]
- MNE-Python. Available online: https://mne.tools/stable/index.html (accessed on 11 July 2022).
- Yavich, N.; Koshev, N.; Malovichko, M.; Razorenova, A.; Fedorov, M. Conservative finite element modeling of EEG and MEG on unstructured grids. IEEE Trans. Med. Imaging 2021, 41, 647–656. [Google Scholar] [CrossRef] [PubMed]
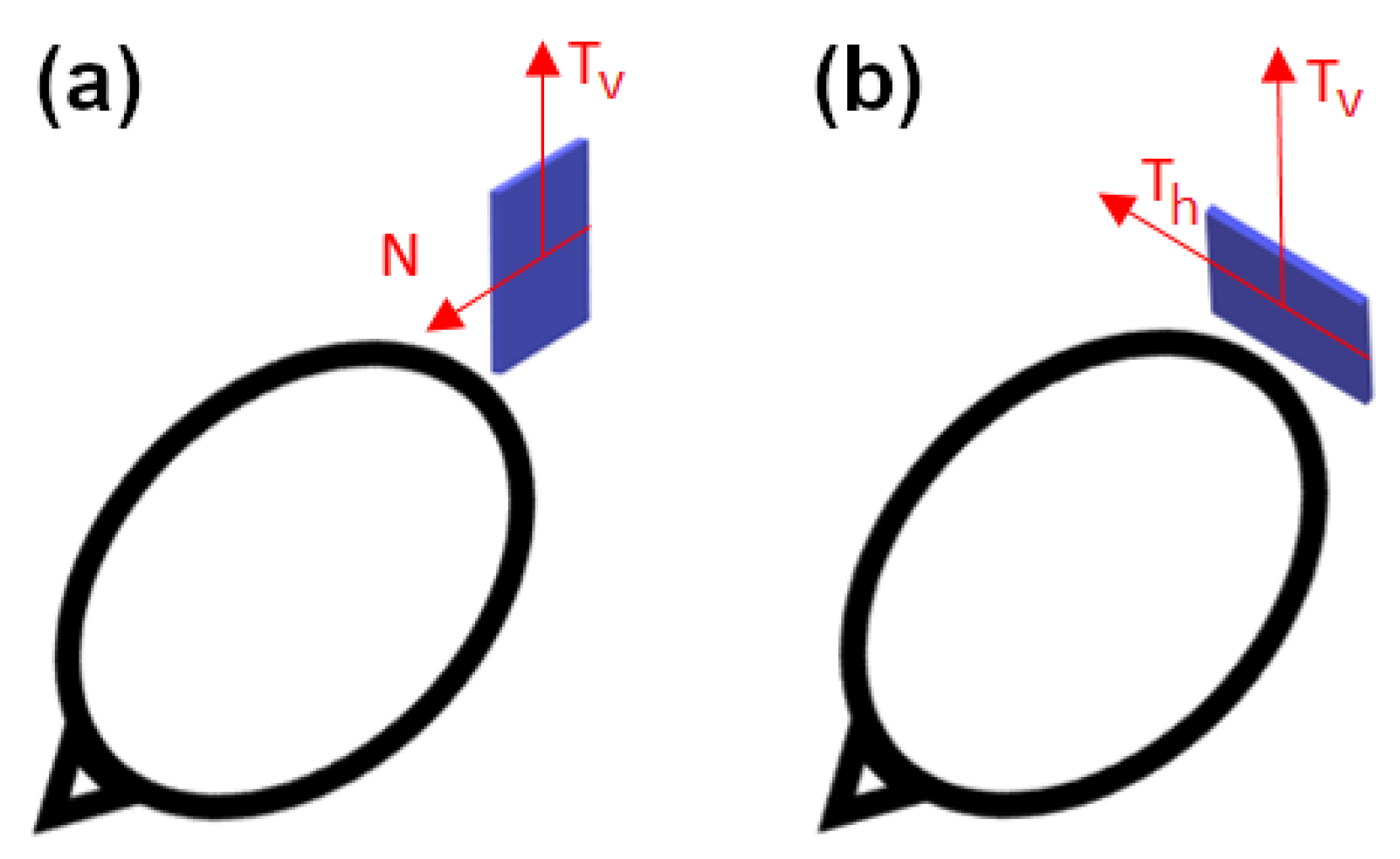
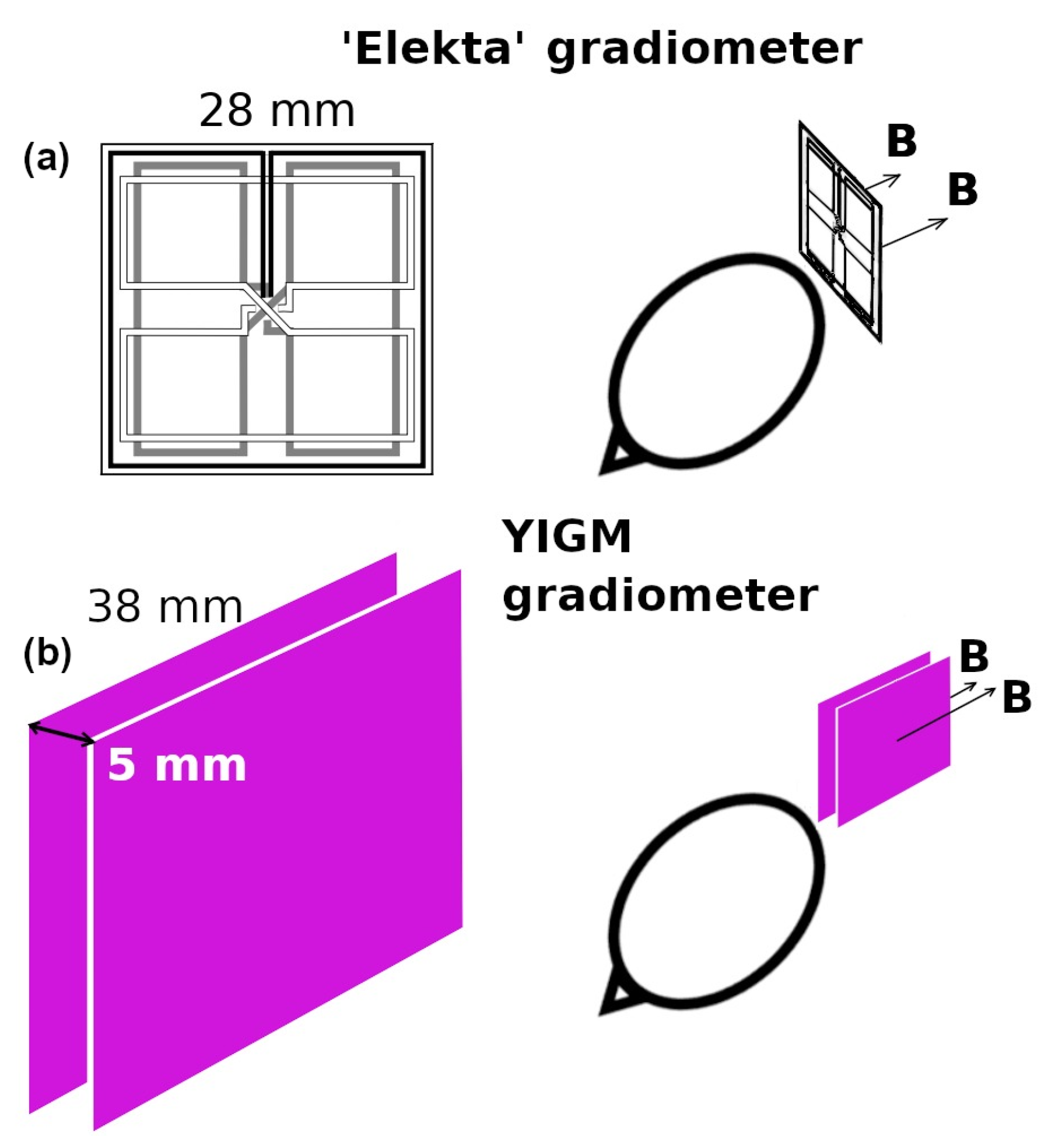



| Sensor Type | d, mm | Base, mm | Size | ||
|---|---|---|---|---|---|
| OPM | 10 [23] | 10.0 | 24 | N/A | mm3 |
| SQUID magnetometer | 3 | 25.0 | 16 | N/A | mm2 |
| YIGM magnetometer (rad.) | 1...35 | 2.0 | 25 | N/A | mm2 |
| YIGM magnetometer (tang.) | 2.0 | 25 | N/A | mm2 | |
| Sensor Type | , mm | Base, mm | Size | ||
| SQUID gradiometer | 3 | 25.0 | 8 | 16.8 | mm2 |
| YIGM gradiometer | 2.0 | 50 | 5.0 | mm3 |
| Size, mm2 | 382 | 302 | 202 | 102 |
| 35 | 45 | 105 | 333 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skidchenko, E.; Butorina, A.; Ostras, M.; Vetoshko, P.; Kuzmichev, A.; Yavich, N.; Malovichko, M.; Koshev, N. Yttrium-Iron Garnet Magnetometer in MEG: Advance towards Multi-Channel Arrays. Sensors 2023, 23, 4256. https://doi.org/10.3390/s23094256
Skidchenko E, Butorina A, Ostras M, Vetoshko P, Kuzmichev A, Yavich N, Malovichko M, Koshev N. Yttrium-Iron Garnet Magnetometer in MEG: Advance towards Multi-Channel Arrays. Sensors. 2023; 23(9):4256. https://doi.org/10.3390/s23094256
Chicago/Turabian StyleSkidchenko, Ekaterina, Anna Butorina, Maxim Ostras, Petr Vetoshko, Alexey Kuzmichev, Nikolay Yavich, Mikhail Malovichko, and Nikolay Koshev. 2023. "Yttrium-Iron Garnet Magnetometer in MEG: Advance towards Multi-Channel Arrays" Sensors 23, no. 9: 4256. https://doi.org/10.3390/s23094256
APA StyleSkidchenko, E., Butorina, A., Ostras, M., Vetoshko, P., Kuzmichev, A., Yavich, N., Malovichko, M., & Koshev, N. (2023). Yttrium-Iron Garnet Magnetometer in MEG: Advance towards Multi-Channel Arrays. Sensors, 23(9), 4256. https://doi.org/10.3390/s23094256









