Virtual Sensor: Simultaneous State and Input Estimation for Nonlinear Interconnected Ground Vehicle System Dynamics
Abstract
1. Introduction
1.1. Related Works on Virtual Sensors
1.2. Proposed Methodology and Contributions
- The main distinction of the proposed LPV estimation approach compared to the existing methods is that no decoupling of the vehicle interconnected dynamics nor nonlinearities considered as non-measurable time-varying external parameters are required for the reconstruction of both vehicle lateral and longitudinal nonlinear dynamics, as well as the unknown inputs. In particular, variations in the forward speed and tire slip velocities of the front and rear wheels are considered as unmeasurable nonlinearities in the interconnected scheme and processed through the boundary domain.
- The proposed interconnection configuration presents an interesting way to reduce the conservatism and give more relaxation for a complete vehicle observer design. This relaxation allows us to derive fewer linear matrix inequality (LMI) conditions for the optimization problem, which can be efficiently solved with numerical solvers.
- Based on the input-to-state stability property, the usual sign definition of the Lyapunov principle can be relaxed. It provides a framework in which we can formulate stability arguments with respect to input disturbances. Thus, it has the advantage of providing further theoretical guarantees of robustness against unknown inputs and disturbances, as well as non-measurable non-linearity terms.
- The effectiveness of the new interconnected configuration of the proposed UI observer algorithm was evaluated in a hardware interactive simulation on the “SHERPA full-scale car driving simulator” and then experimentally using the “Twingo” vehicle prototype platform, with a robustness test performed regarding road friction uncertainties.
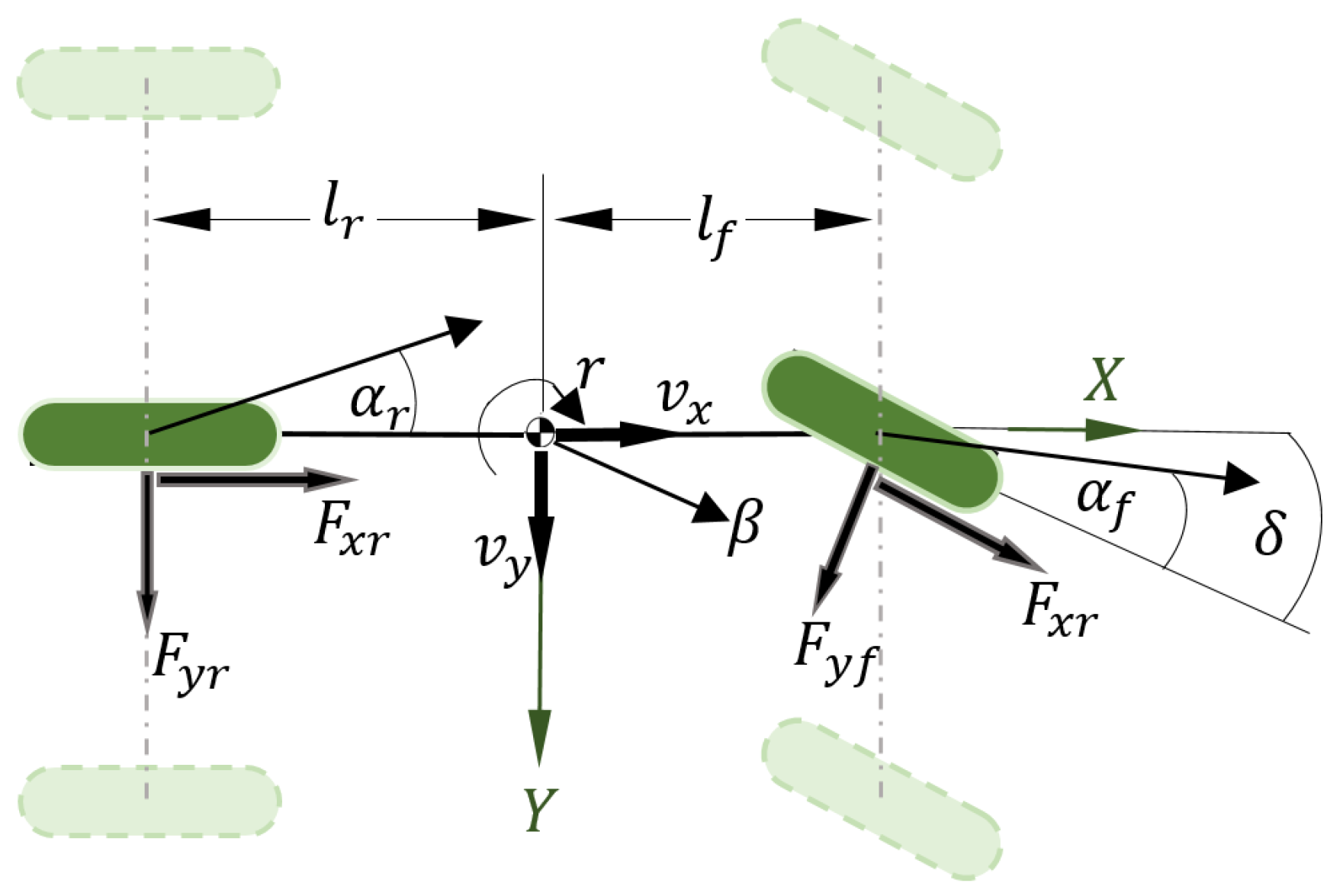
2. Interlinked Road–Vehicle Lateral and Longitudinal Dynamics
- Longitudinal, lateral, and yaw motions:
- Wheels’ rotational movements:
- Vehicle positioning on the road:
- Electronic power steering system dynamics:
3. T-S Structure of the Interlinked Dynamics
4. Observer Design
- (i)
- The state (, ) and the unknown inputs of the system are all bounded.
- (ii)
- The pairs and are observable or detectable in order to guarantee solutions to the LMI problem.
- −
- The polytopic sub-systems (8) are observable, i.e.,
- −
- (iii)
- Each sub-observer exchanges some information through the interconnection scheme.
- (iv)
- The matching condition for the model holds
4.1. NI-UIO Stability and Convergence Analysis
- asymptotically if ;
- Bounded error if .
- (1)
- Condition (21) allows us to compute the Hurwitz gains
- (2)
- (3)
- After computing , we obtain: ; then, from (23), .
4.2. Algebraic Reconstruction of Unknown Inputs
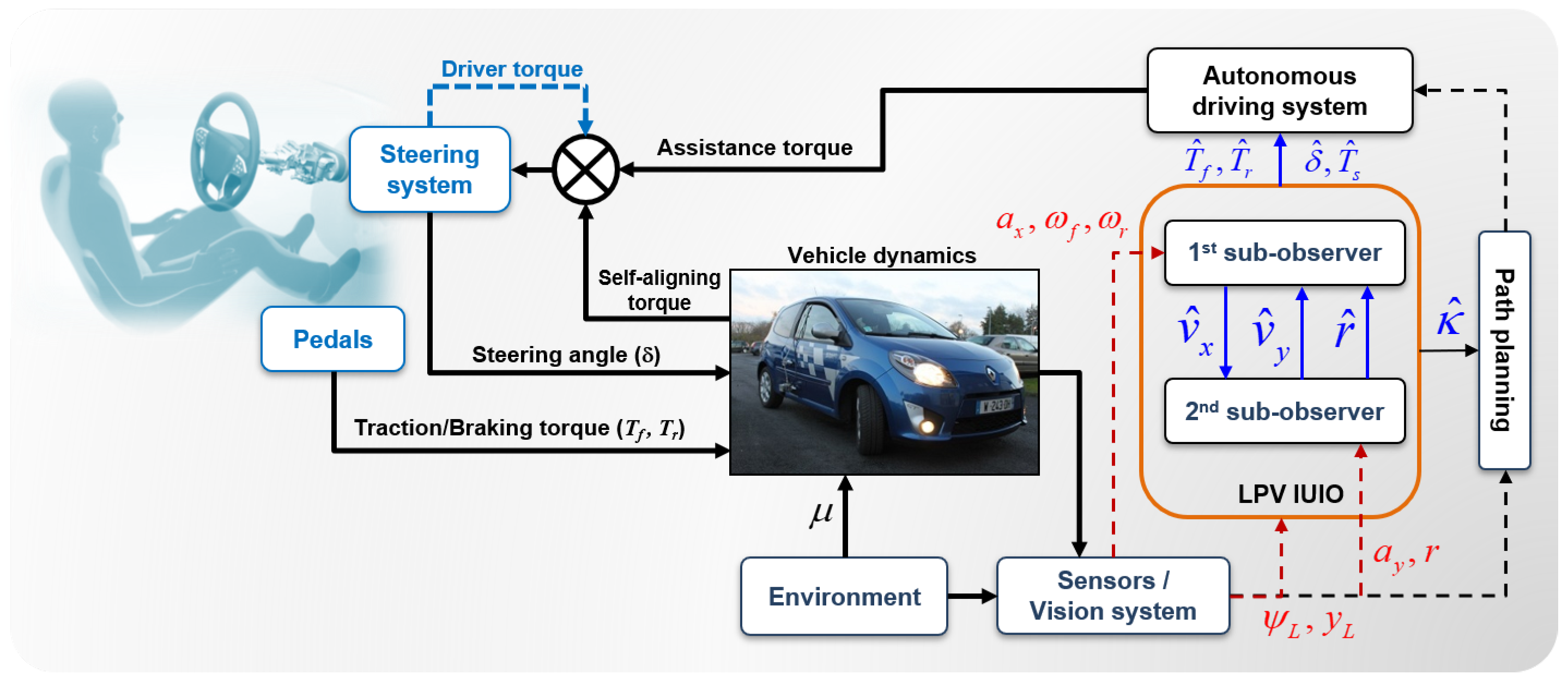
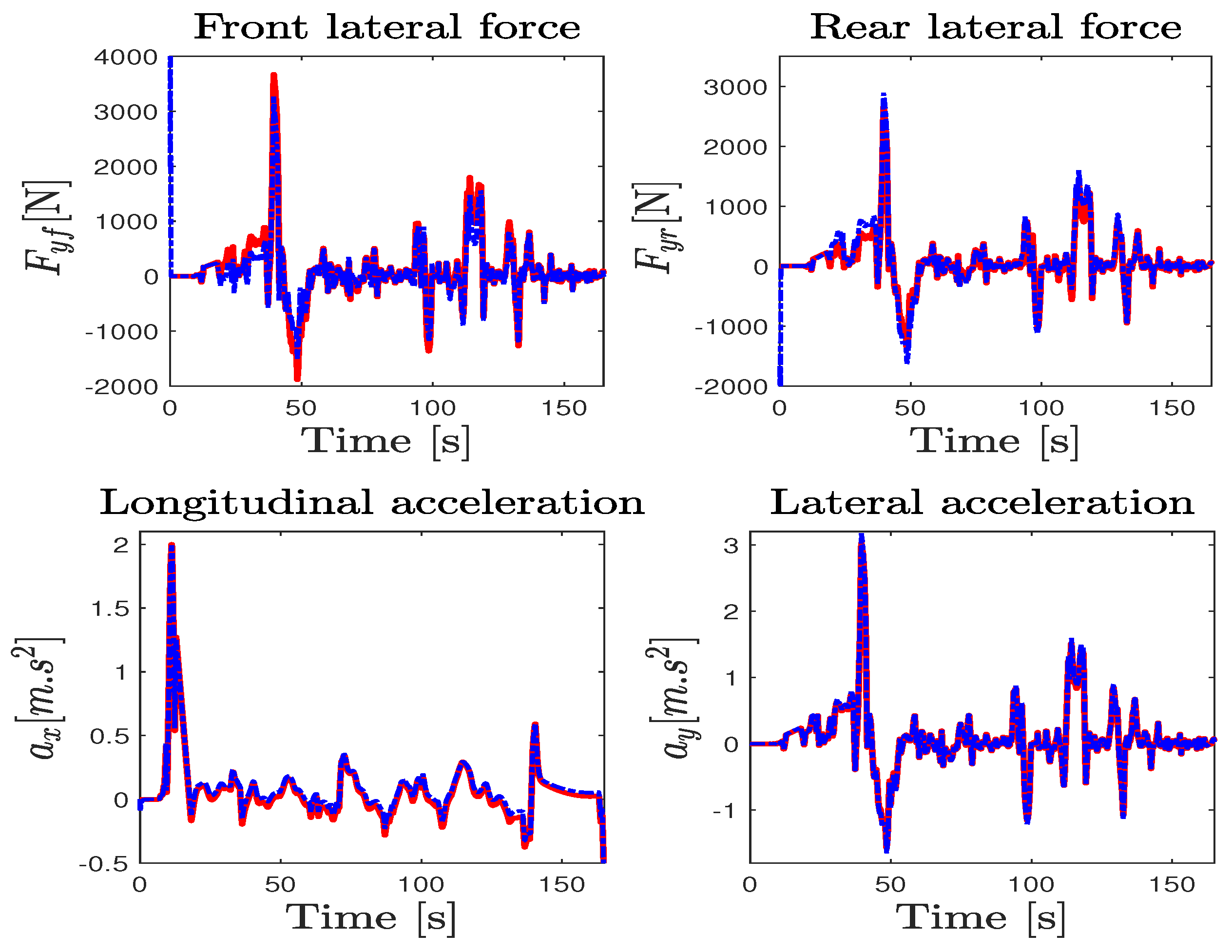
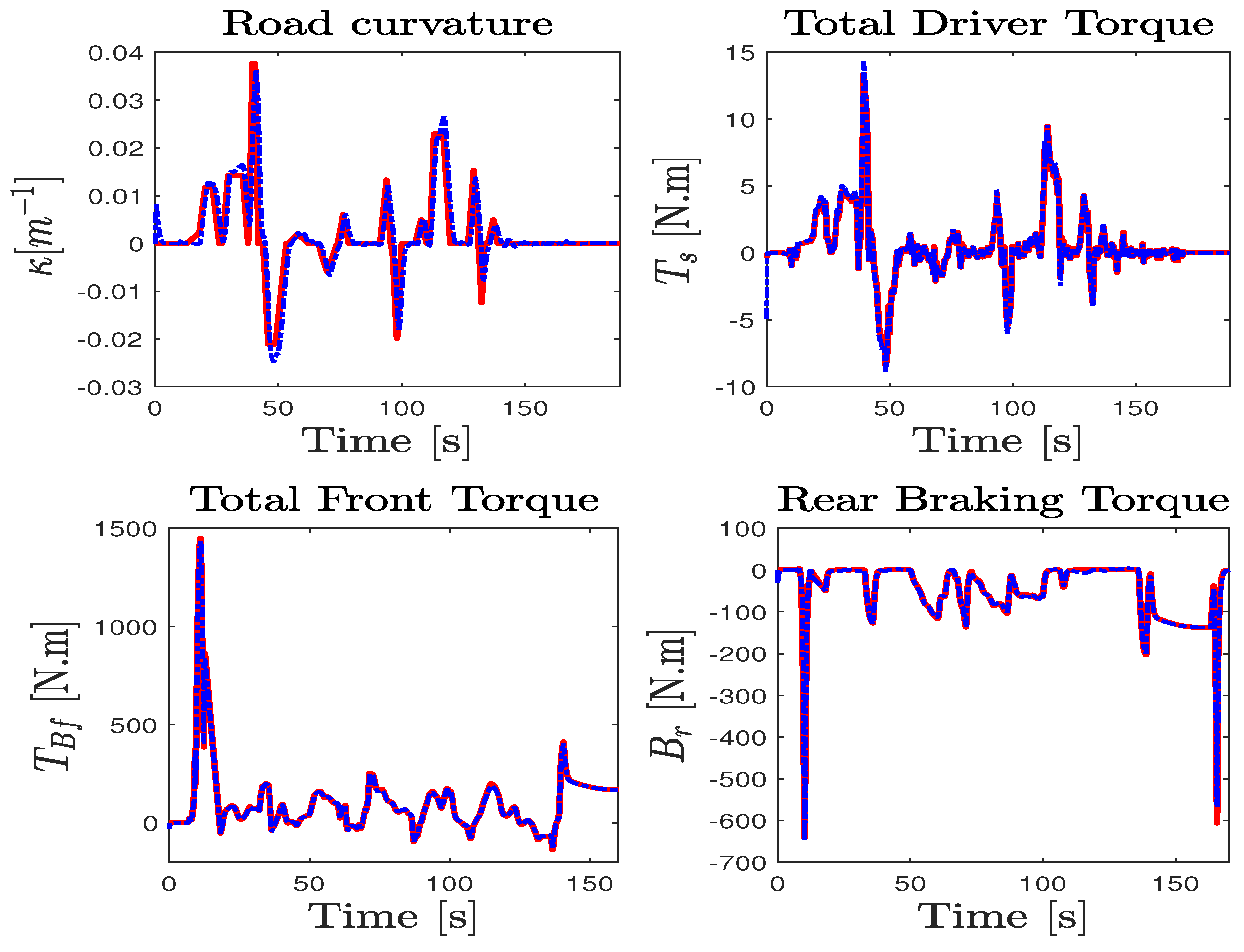
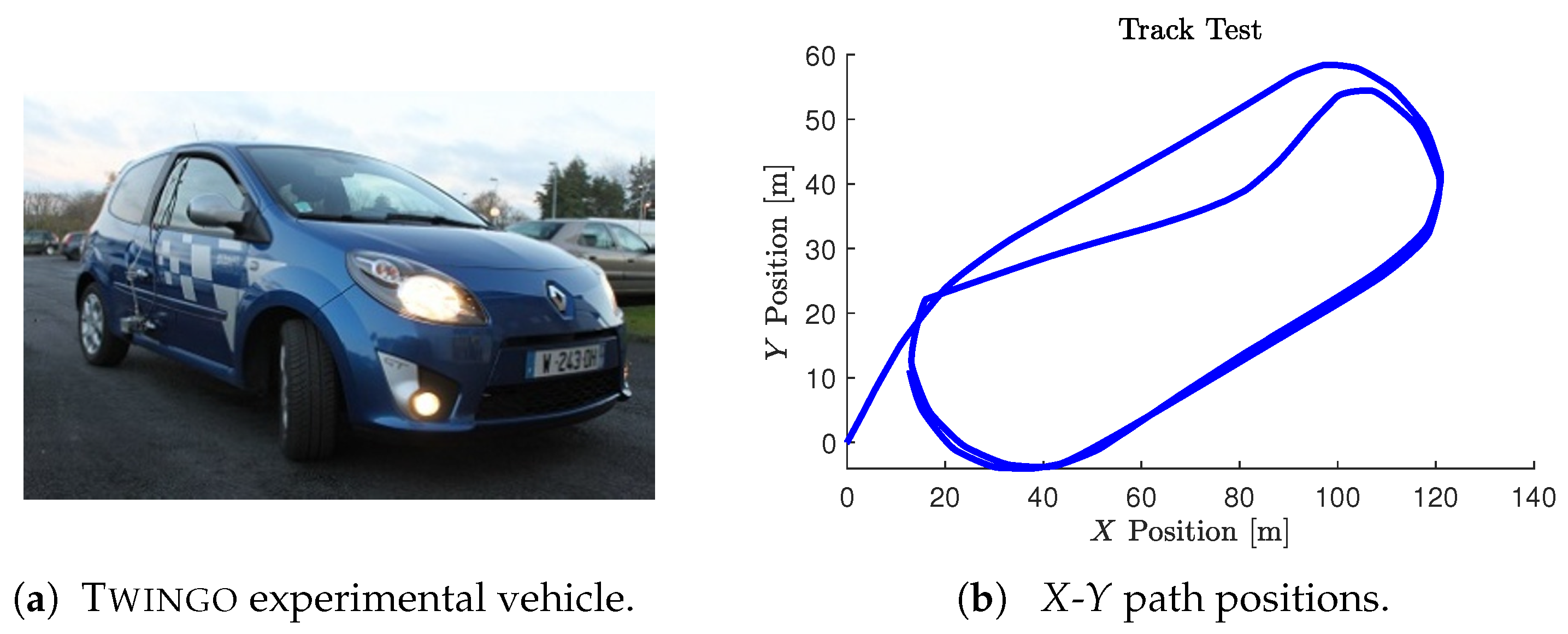
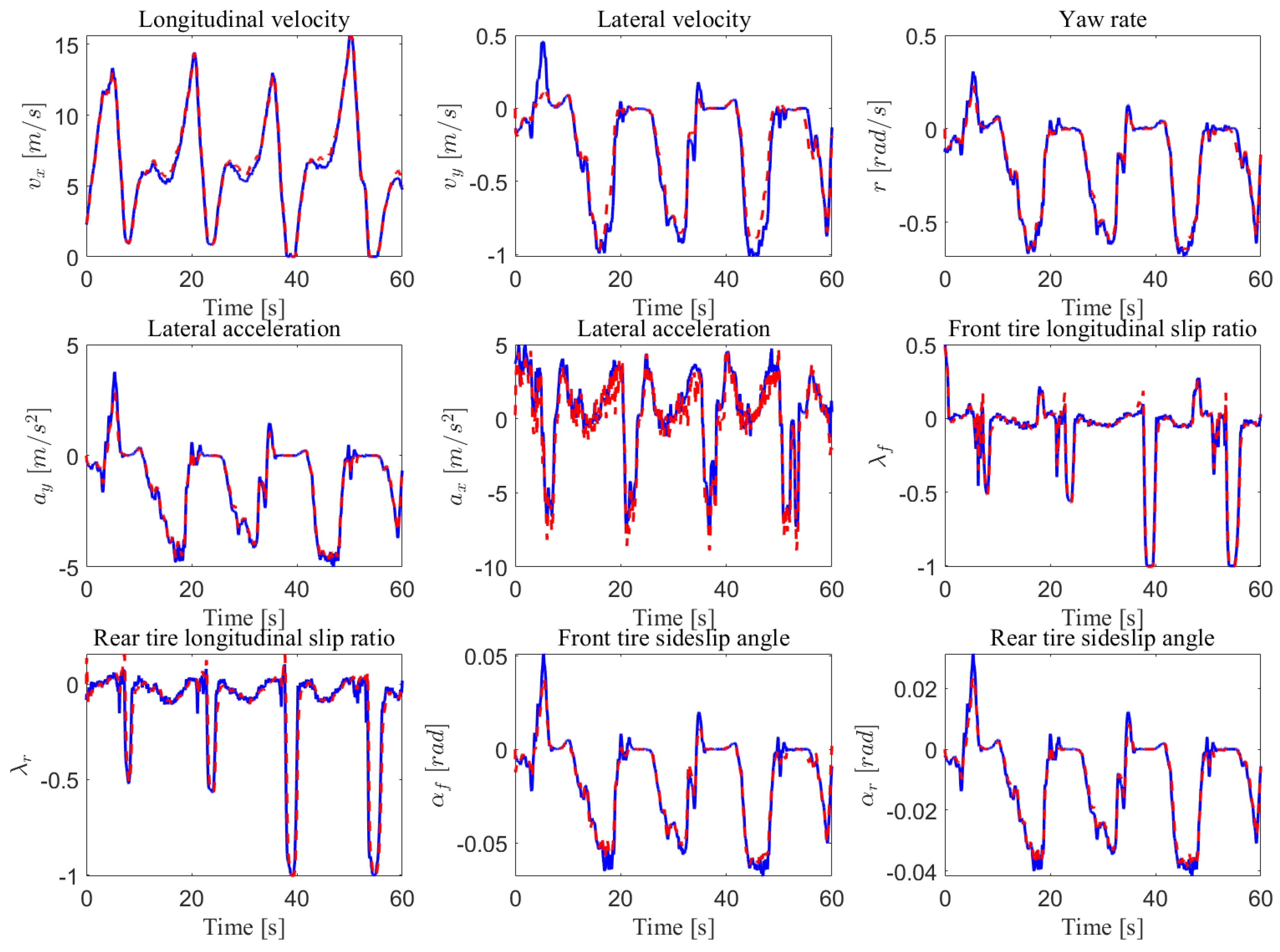
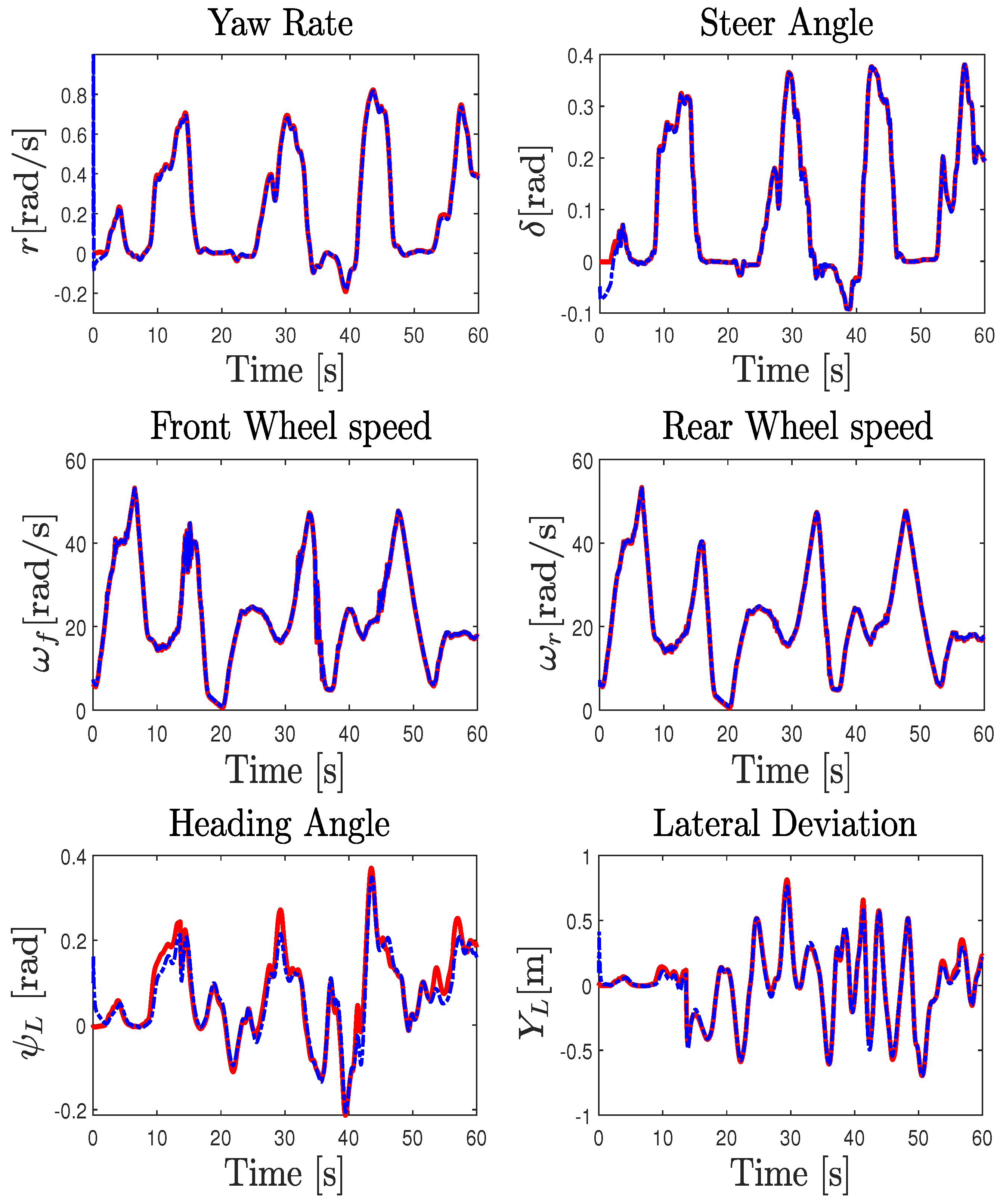
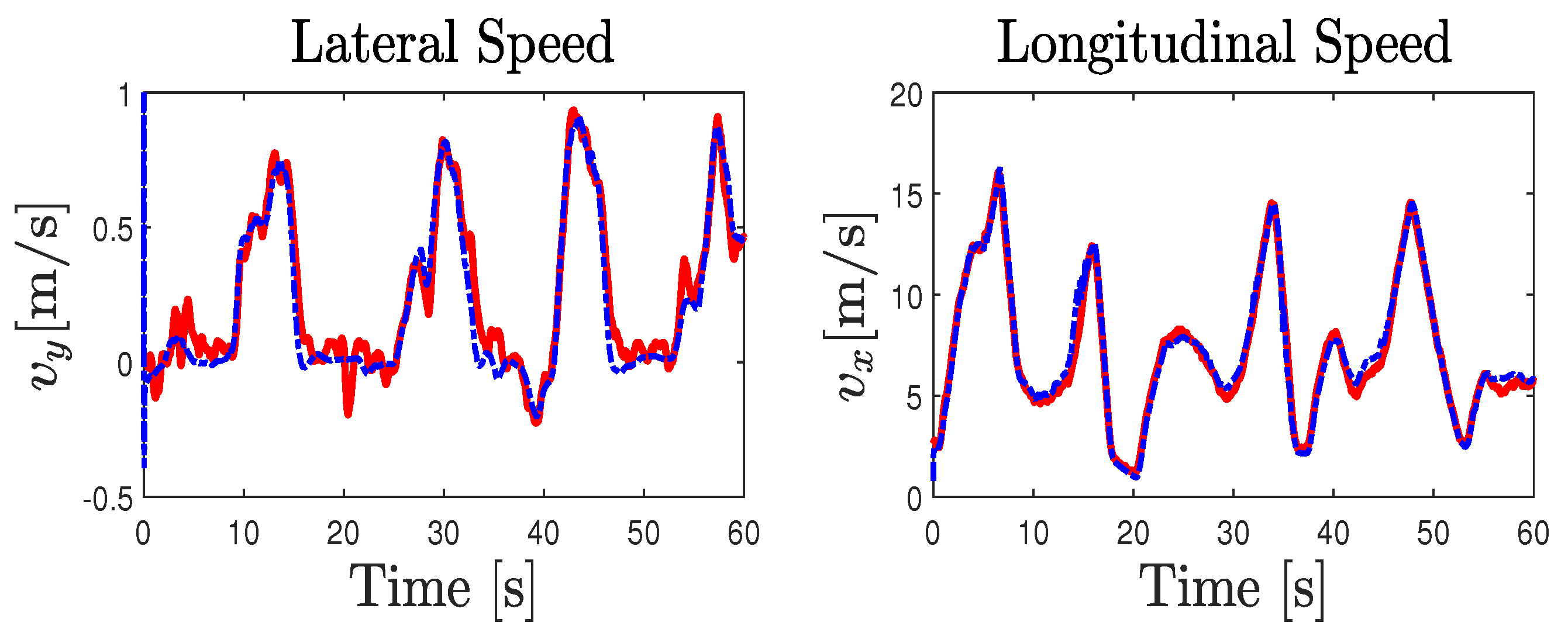
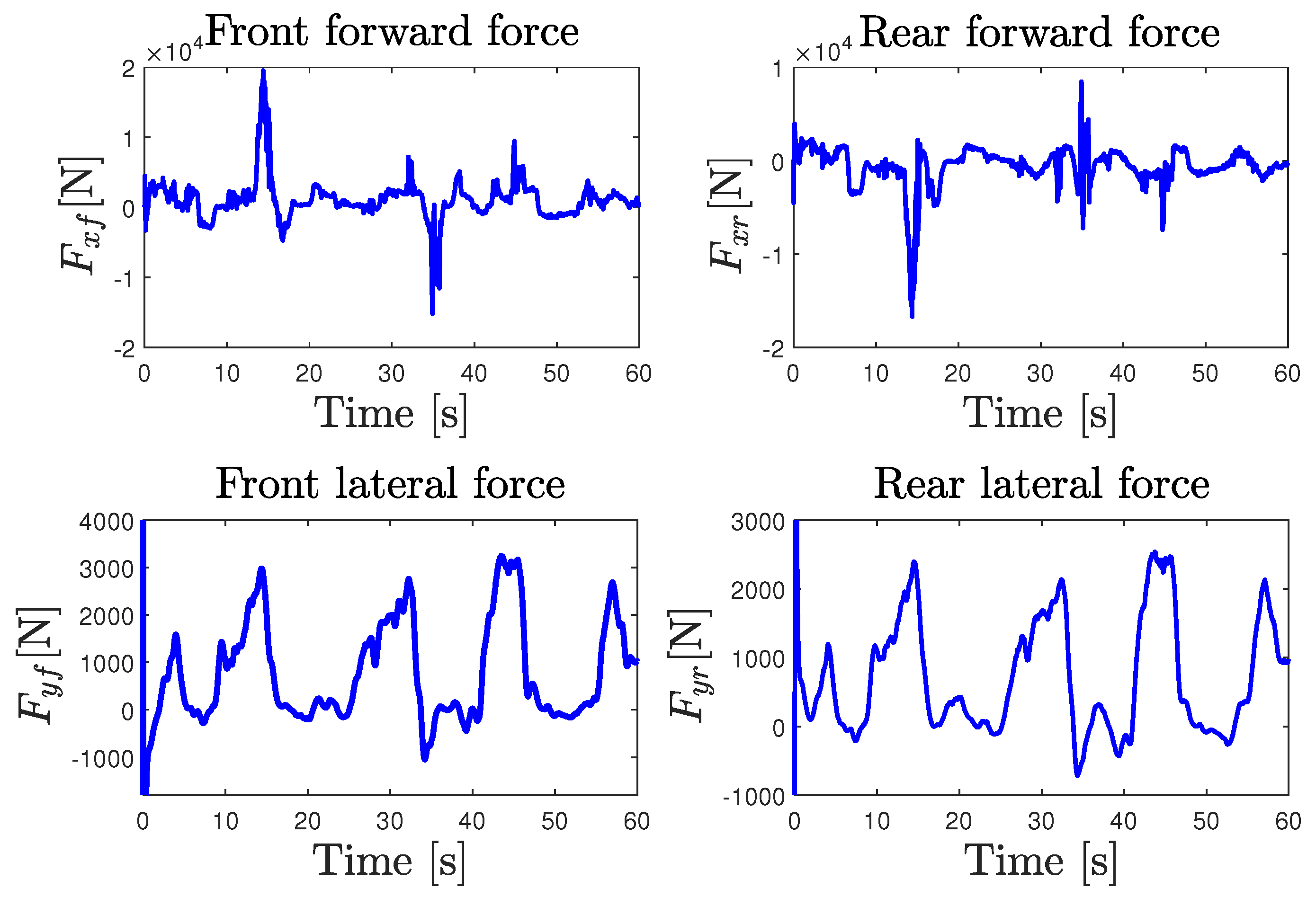
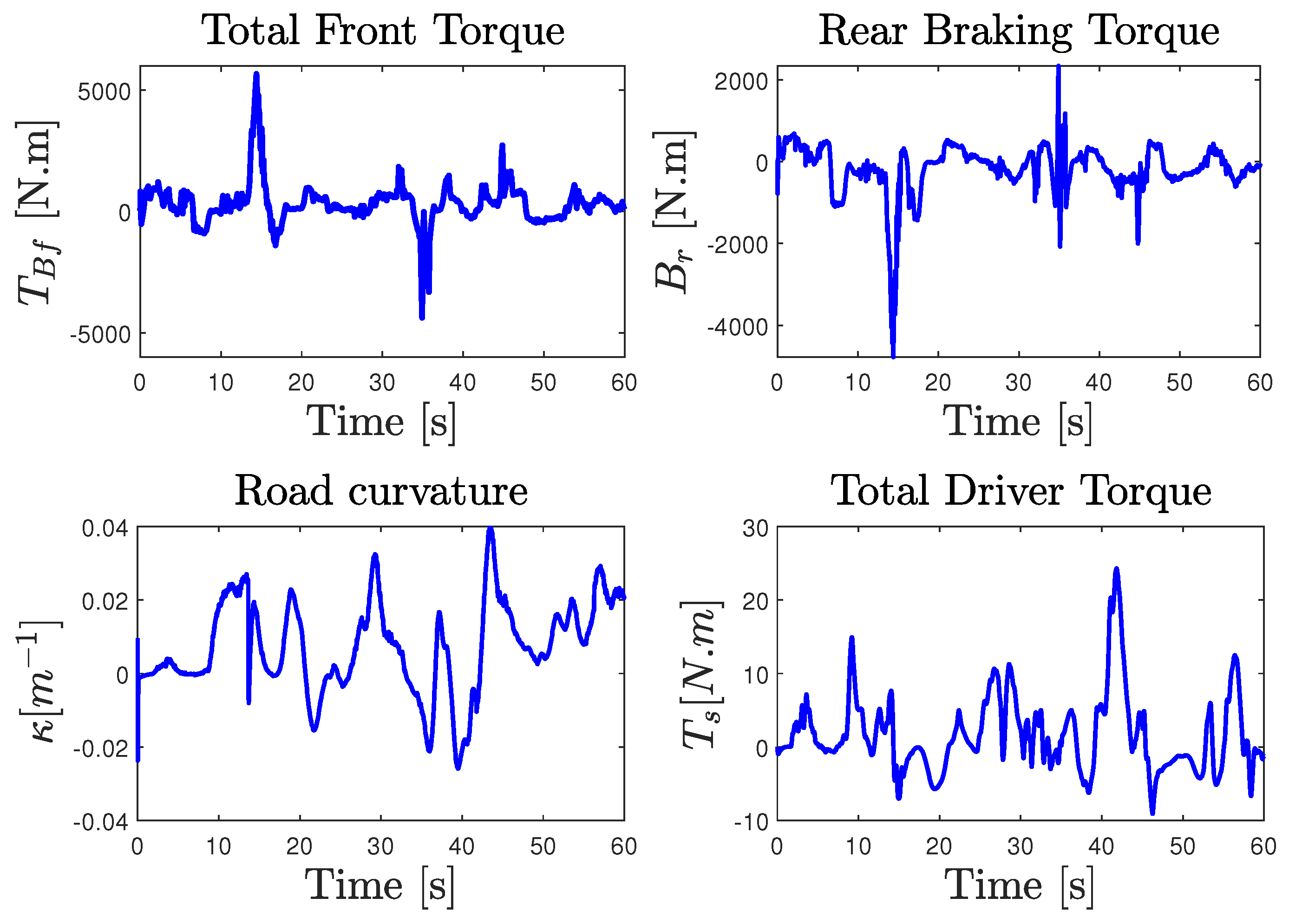
5. Experimental Results and Discussions
5.1. Hardware Experiments
5.2. Observer Sensitivity against Road Friction Uncertainties
5.3. Experiment Validation Procedure and Trials
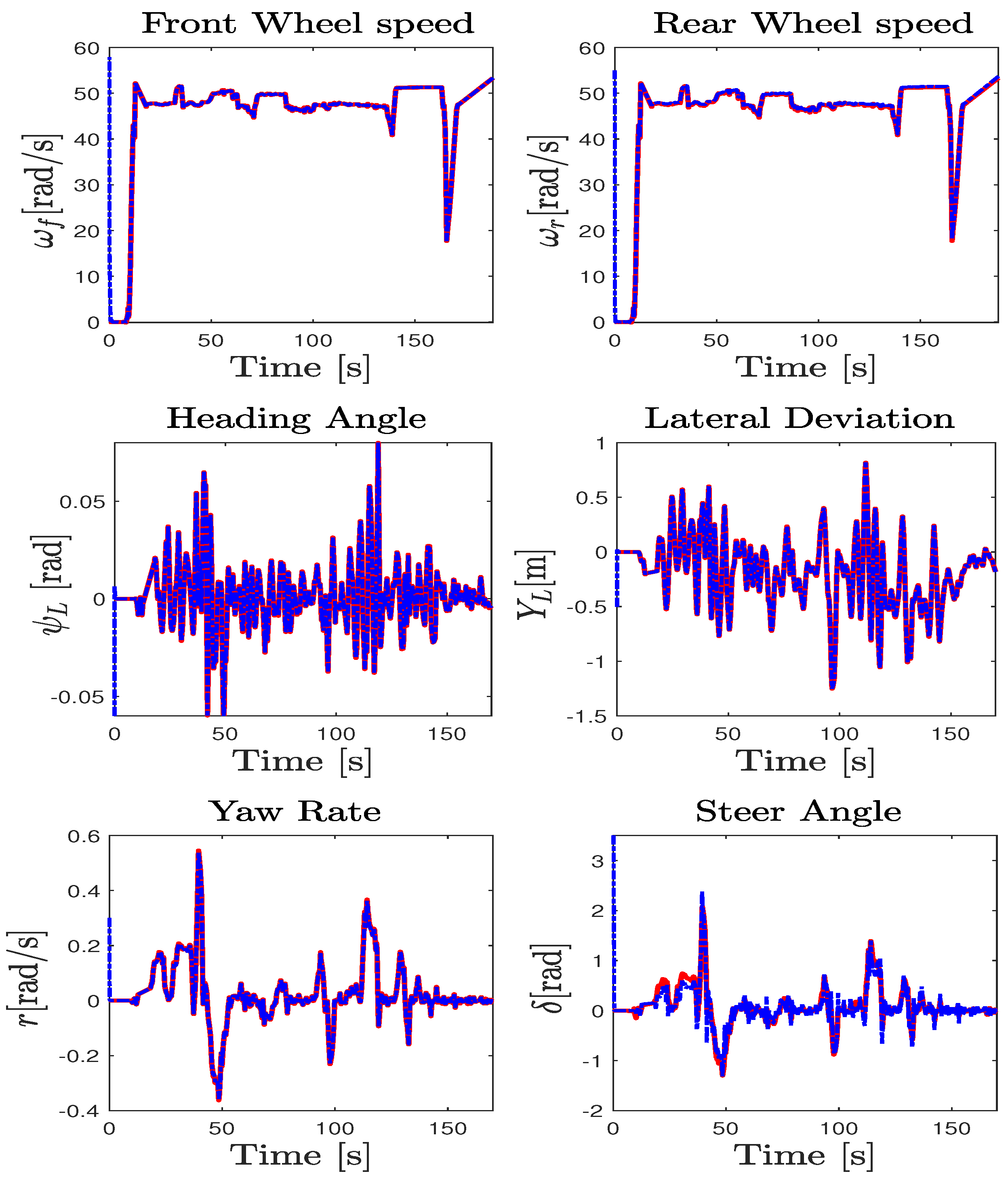
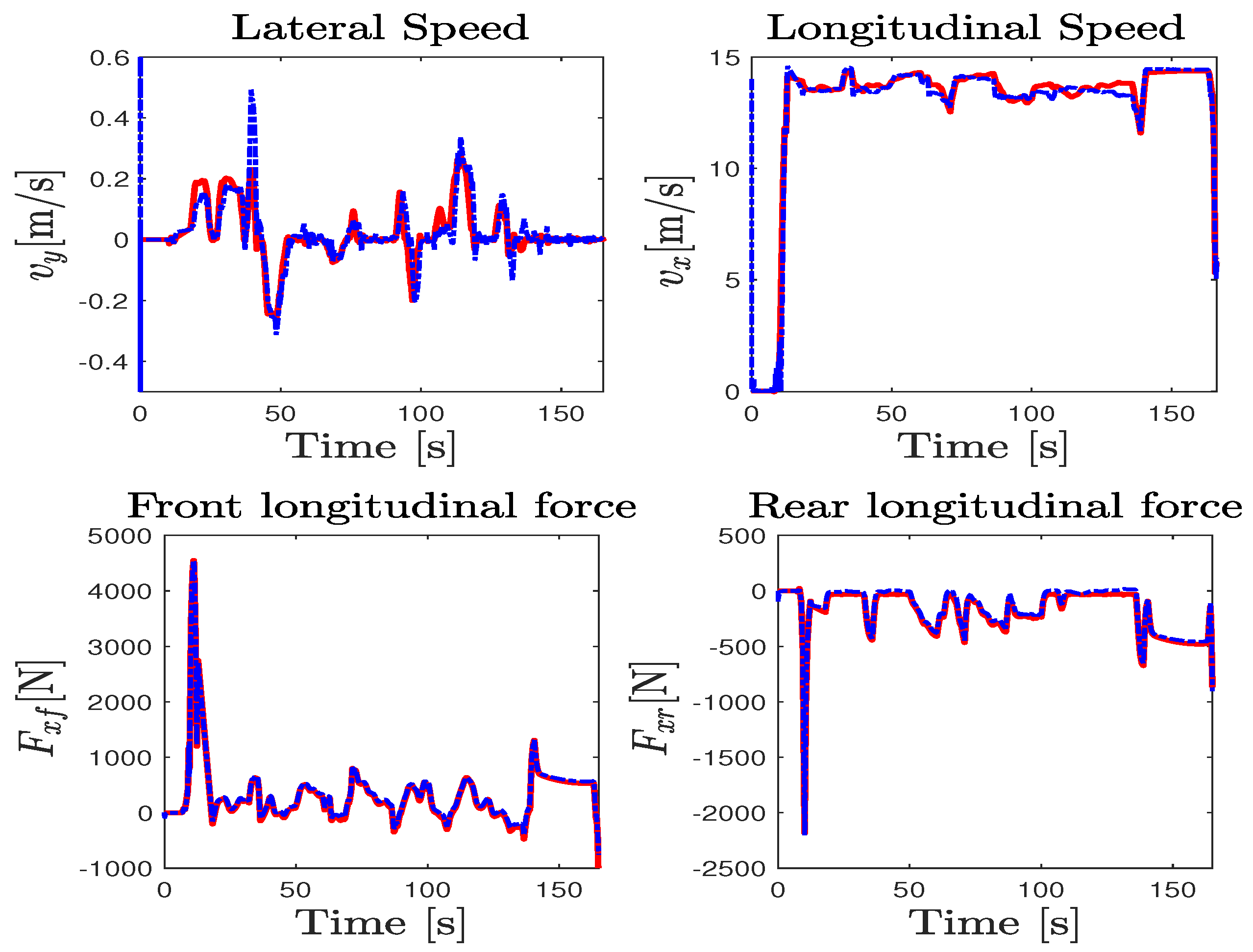
5.4. Vehicle Model Adequacy Evaluation
5.5. NI-UI Observer Validation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Vehicle’s Parameters Nomenclature
| Variable | Description |
| , | Lateral and forward velocities |
| r, , | Yaw rate and Longitudinal/lateral acceleration |
| , | Angular velocities of the front and rear wheels |
| , , | Steering angle, side slip angle, and longitudinal slip ratio |
| , , | Lateral offset and angular displacement, road curvature |
| , , | Cornering/longitudinal forces and lateral wind force |
| , | Aerodynamic and rolling resistance forces |
| , , | Braking torques and engine torque. |
| m, | Vehicle mass and inertia about the z-axis |
| , | Cornering and longitudinal stiffness parameters |
| , | The wheels’ moment of inertia |
| , | Distances between the C.G. and front and rear axles |
| , | Look-ahead distance and distance of wind force action |
| , | Steering system inertia, column–wheels gear ratio |
| R, | Wheel radius and damping coefficient. |
Appendix B. Vehicle’s Parameters Values
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| m | 1210 [kg] | [m] | |
| 1520 [kg.m2] | [m] | ||
| 47135 [N/rad] | 5 [m] | ||
| 56636 [N/rad] | [m] | ||
| 91165 [N/rad] | R | [m] | |
| 62671 [N/rad] | [kg.m2] | ||
| [kg.m2] | [Nm/rad/s] | ||
| [kg.m2] | 16 |
Appendix C
References
- Yu, Z. Review of Vehicle State Estimation Problem under Driving Situation. J. Mech. Eng. 2009, 45, 20. [Google Scholar] [CrossRef]
- Zhao, L.H.; Liu, Z.Y.; Chen, H. Design of a Nonlinear Observer for Vehicle Velocity Estimation and Experiments. IEEE Trans. Control Syst. Technol. 2011, 19, 664–672. [Google Scholar] [CrossRef]
- Sentouh, C.; Nguyen, A.T.; Rath, J.J.; Floris, J.; Popieul, J.C. Human–machine shared control for vehicle lane keeping systems: A Lyapunov-based approach. IET Intell. Transp. Syst. 2019, 13, 63–71. [Google Scholar] [CrossRef]
- Singh, K.B.; Arat, M.A.; Taheri, S. Literature review and fundamental approaches for vehicle and tire state estimation. Veh. Syst. Dyn. 2019, 57, 1643–1665. [Google Scholar] [CrossRef]
- Perozzi, G.; Rath, J.J.; Sentouh, C.; Floris, J.; Popieul, J.C. Lateral shared sliding mode control for lane-keeping assist system in steer-by-wire vehicles: Theory and experiments. IEEE Trans. Intell. Veh. 2021; accepted. [Google Scholar] [CrossRef]
- Perozzi, G.; Oudainia, M.R.; Sentouh, C.; Popieul, J.C.; Rath, J.J. Driver Assisted Lane Keeping with Conflict Management Using Robust Sliding Mode Controller. Sensors 2023, 23, 4. [Google Scholar] [CrossRef]
- Kim, M.s.; Kim, B.j.; Kim, C.i.; So, M.H.; Lee, G.s.; Lim, J.H. Vehicle Dynamics and Road Slope Estimation based on Cascade Extended Kalman Filter. In Proceedings of the 2018 International Conference on Information and Communication Technology Robotics (ICT-ROBOT), Busan, Republic of Korea, 6–8 September 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Peng, Y.; Chen, J.; Ma, Y. Observer-based estimation of velocity and tire-road friction coefficient for vehicle control systems. Nonlinear Dyn. 2019, 96, 363–387. [Google Scholar] [CrossRef]
- García, R.A.; Orihuela, L.; Millán, P.; Rubio, F.R.; Ortega, M.G. Guaranteed estimation and distributed control of vehicle formations. Int. J. Control 2020, 93, 2729–2742. [Google Scholar] [CrossRef]
- Du, M.; Zhao, D.; Yang, M.; Chen, H. Nonlinear extended state observer-based output feedback stabilization control for uncertain nonlinear half-car active suspension systems. Nonlinear Dyn. 2020, 100, 2483–2503. [Google Scholar] [CrossRef]
- Boufadene, M.; Belkheiri, M.; Rabhi, A.; Hajjaji, A.E. Vehicle longitudinal force estimation using adaptive neural network nonlinear observer. Int. J. Veh. Des. 2019, 79, 205–220. [Google Scholar] [CrossRef]
- Davoodabadi, I.; BRamezani, A.A.; Mahmoodi-k, M.; Ahmadizadeh, P. Identification of tire forces using Dual Unscented Kalman Filter algorithm. Nonlinear Dyn. 2014, 78, 1907–1919. [Google Scholar] [CrossRef]
- Jeon, W.; Zemouche, A.; Rajamani, R. Nonlinear Observer for Vehicle Motion Tracking. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Fouka, M.; Nehaoua, L.; Arioui, H. Motorcycle State Estimation and Tire Cornering Stiffness Identification Applied to Road Safety: Using Observer-Based Identifiers. IEEE Trans. Intell. Transp. Syst. 2022, 23, 7017–7027. [Google Scholar] [CrossRef]
- Mahyuddin, M.N.; Na, J.; Herrmann, G.; Ren, X.; Barber, P. Adaptive observer-based parameter estimation with application to road gradient and vehicle mass estimation. IEEE Trans. Ind. Electron. 2013, 61, 2851–2863. [Google Scholar] [CrossRef]
- Youssfi, N.E.; Oudghiri, M.; Bachtiri, R.E. Vehicle lateral dynamics estimation using unknown input observer. Procedia Comput. Sci. 2019, 148, 502–511. [Google Scholar] [CrossRef]
- Boufadene, M.; Rabhi, A.; Belkheiri, M.; Elhajjaji, A. Vehicle online parameter estimation using a nonlinear adaptive observer. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 1006–1010. [Google Scholar] [CrossRef]
- Soualmi, B.; Sentouh, C.; Popieul, J. Both vehicle state and driver’s torque estimation using Unknown Input Proportional Multi-Integral T-S observer. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 2957–2962. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Guerra, T.M.; Sentouh, C.; Zhang, H. Unknown input observers for simultaneous estimation of vehicle dynamics and driver torque: Theoretical design and hardware experiments. IEEE/ASME Trans. Mechatron. 2019, 24, 2508–2518. [Google Scholar] [CrossRef]
- Sentouh, C.; Sebsadji, Y.; Mammar, S.; Glaser, S. Road bank angle and faults estimation using unknown input proportional-integral observer. In Proceedings of the 2007 European Control Conference (ECC), Kos, Greece, 2–5 July 2007; pp. 5131–5138. [Google Scholar] [CrossRef]
- Sentouh, C.; Mammar, S.; Glaser, S. Simultaneous vehicle state and road attributes estimation using unknown input proportional-integral observer. In Proceedings of the 2008 IEEE Intelligent Vehicles Symposium, Eindhoven, The Netherlands, 4–6 June 2008; pp. 690–696. [Google Scholar] [CrossRef]
- Zhang, B.; Du, H.; Lam, J.; Zhang, N.; Li, W. A novel observer design for simultaneous estimation of vehicle steering angle and sideslip angle. IEEE Trans. Ind. Electron. 2016, 63, 4357–4366. [Google Scholar] [CrossRef]
- Fouka, M.; Nehaoua, L.; Ichalal, D.; Arioui, H.; Mammar, S. Road geometry and steering reconstruction for powered two-wheeled vehicles. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 2024–2029. [Google Scholar]
- Jeong, H.B.; Ahn, C.K.; You, S.H.; Sohn, K.M. Finite-Memory Estimation for Vehicle Roll and Road Bank Angles. IEEE Trans. Ind. Electron. 2018, 66, 5423–5432. [Google Scholar] [CrossRef]
- Pan, J.; Nguyen, A.T.; Guerra, T.M.; Sentouh, C.; Wang, S.; Popieul, J.C. Vehicle Actuator Fault Detection With Finite-Frequency Specifications via Takagi-Sugeno Fuzzy Observers: Theory and Experiments. IEEE Trans. Veh. Technol. 2023, 72, 407–417. [Google Scholar] [CrossRef]
- Tanaka, K.; Wang, H.O. Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach; John Wiley & Sons, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Guerra, T.M.; Estrada-Manzo, V.; Lendek, Z. Observer design for Takagi–Sugeno descriptor models: An LMI approach. Automatica 2015, 52, 154–159. [Google Scholar] [CrossRef]
- Chen, X.; Sun, R.; Jiang, W.; Jia, Q.; Zhang, J. A novel two-stage extended Kalman filter algorithm for reaction flywheels fault estimation. Chin. J. Aeronaut. 2016, 29, 462–469. [Google Scholar] [CrossRef]
- Fouka, M.; Nehaoua, L.; Arioui, H.; Mammar, S. Interconnected Observers for a Powered Two-Wheeled Vehicles: Both Lateral and Longitudinal Dynamics Estimation. In Proceedings of the 2019 IEEE 16th International Conference on Networking, Sensing and Control, Banff, AB, Canada, 9–11 May 2019; pp. 163–168. [Google Scholar] [CrossRef]
- Cordeiro, R.A.; Ribeiro, A.M.; Azinheira, J.R.; Victorino, A.C.; Ferreira, P.A.; de Paiva, E.C.; Bueno, S.S. Road grades and tire forces estimation using two-stage extended kalman filter in a delayed interconnected cascade structure. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 115–120. [Google Scholar] [CrossRef]
- Yu, J.; Yu, J.; Chen, F.; Wang, C. Numerical study of tip leakage flow control in turbine cascades using the DBD plasma model improved by the parameter identification method. Aerosp. Sci. Technol. 2019, 84, 856–864. [Google Scholar] [CrossRef]
- Cordeiro, R.A.; Victorino, A.C.; Azinheira, J.R.; Ferreira, P.A.; de Paiva, E.C.; Bueno, S.S. Estimation of vertical, lateral, and longitudinal tire forces in four-wheel vehicles using a delayed interconnected cascade-observer structure. IEEE/ASME Trans. Mechatron. 2019, 24, 561–571. [Google Scholar] [CrossRef]
- Fouka, M.; Sentouh, C.; Popieul, J.C. Quasi-LPV Interconnected Observer Design for Full Vehicle Dynamics Estimation With Hardware Experiments. IEEE/ASME Trans. Mechatron. 2021, 26, 1763–1772. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Sentouh, C.; Popieul, J.C. Driver-automation cooperative approach for shared steering control under multiple system constraints: Design and experiments. IEEE Trans. Ind. Electron. 2016, 64, 3819–3830. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Tuan, H.; Apkarian, P.; Narikiyo, T.; Yamamoto, Y. Parameterized linear matrix inequality techniques in fuzzy control system design. IEEE Trans. Fuzzy Syst. 2001, 9, 324–332. [Google Scholar] [CrossRef]
- Sala, A.; Ariño, C. Asymptotically necessary and sufficient conditions for stability and performance in fuzzy control: Applications of Polya’s theorem. Fuzzy Sets Syst. 2007, 158, 2671–2686. [Google Scholar] [CrossRef]
- Ouhib, L.; Kara, R. Proportional Observer design based on D-stability and Finsler’s Lemma for Takagi-Sugeno systems. Fuzzy Sets Syst. 2023, 452, 61–90. [Google Scholar] [CrossRef]
- Ichalal, D.; Marx, B.; Maquin, D.; Ragot, J. New fault tolerant control strategy for nonlinear systems with multiple model approach. In Proceedings of the 2010 Conference on Control and Fault-Tolerant Systems (SysTol), Nice, France, 6–8 October 2010; pp. 606–611. [Google Scholar] [CrossRef]
- Lazar, M.; De La Peña, D.M.; Heemels, W.; Alamo, T. On input-to-state stability of min–max nonlinear model predictive control. Syst. Control Lett. 2008, 57, 39–48. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Ichalal, D.; Mammar, S. On Unknown Input Observers for LPV Systems. IEEE Trans. Ind. Electron. 2015, 62, 5870–5880. [Google Scholar] [CrossRef]

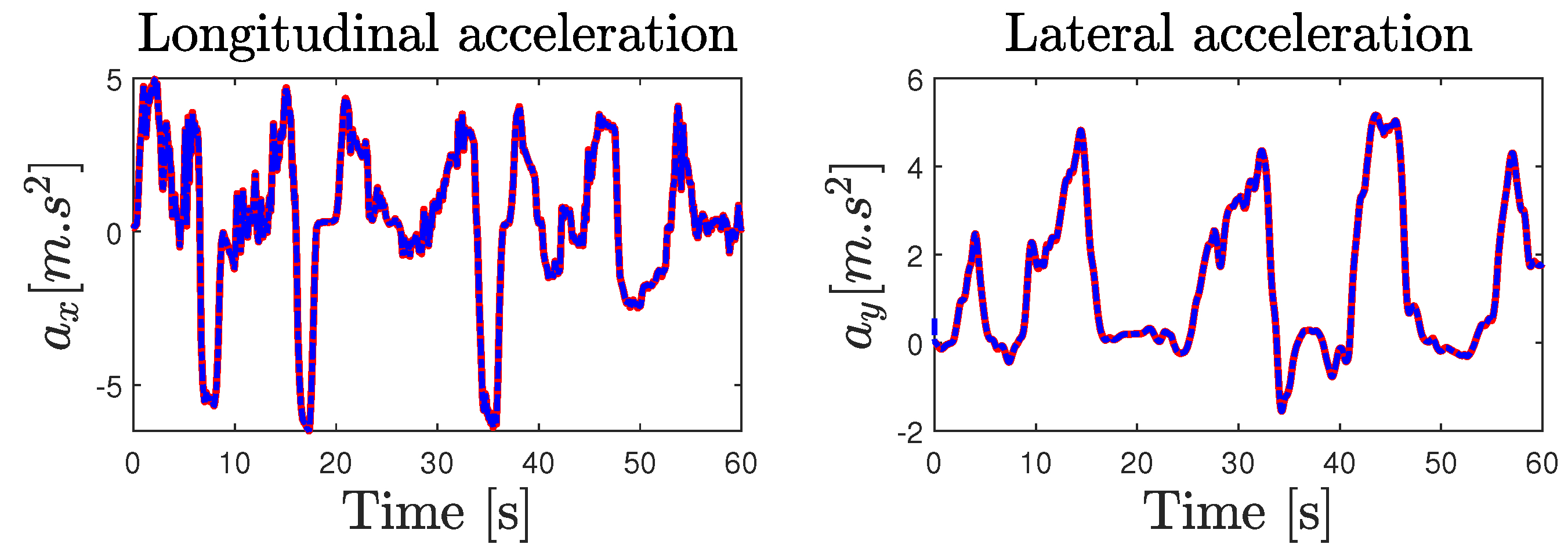
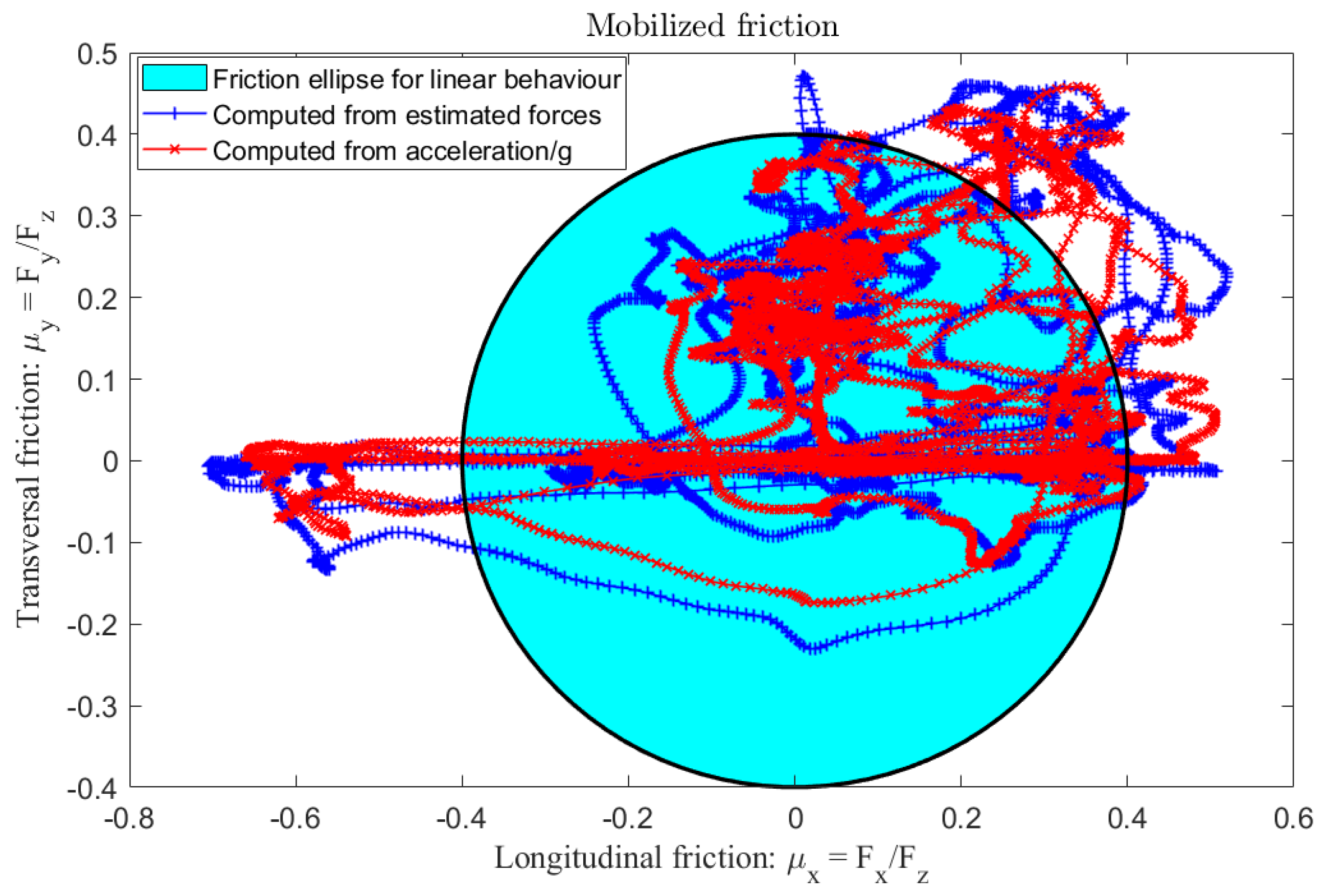
| r (%) | (%) | (%) | (%) | |||||
|---|---|---|---|---|---|---|---|---|
| (%) | (%) | (%) | (%) | |||||
| (%) | (%) | (%) | (%) | |||||
| r | |||||||||
|---|---|---|---|---|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sentouh, C.; Fouka, M.; Popieul, J.-C. Virtual Sensor: Simultaneous State and Input Estimation for Nonlinear Interconnected Ground Vehicle System Dynamics. Sensors 2023, 23, 4236. https://doi.org/10.3390/s23094236
Sentouh C, Fouka M, Popieul J-C. Virtual Sensor: Simultaneous State and Input Estimation for Nonlinear Interconnected Ground Vehicle System Dynamics. Sensors. 2023; 23(9):4236. https://doi.org/10.3390/s23094236
Chicago/Turabian StyleSentouh, Chouki, Majda Fouka, and Jean-Christophe Popieul. 2023. "Virtual Sensor: Simultaneous State and Input Estimation for Nonlinear Interconnected Ground Vehicle System Dynamics" Sensors 23, no. 9: 4236. https://doi.org/10.3390/s23094236
APA StyleSentouh, C., Fouka, M., & Popieul, J.-C. (2023). Virtual Sensor: Simultaneous State and Input Estimation for Nonlinear Interconnected Ground Vehicle System Dynamics. Sensors, 23(9), 4236. https://doi.org/10.3390/s23094236







