Distributed DRL-Based Computation Offloading Scheme for Improving QoE in Edge Computing Environments
Abstract
1. Introduction
2. Background and Related Research
2.1. Computation Offloading
2.2. Reinforcement Learning
2.3. RL Methods
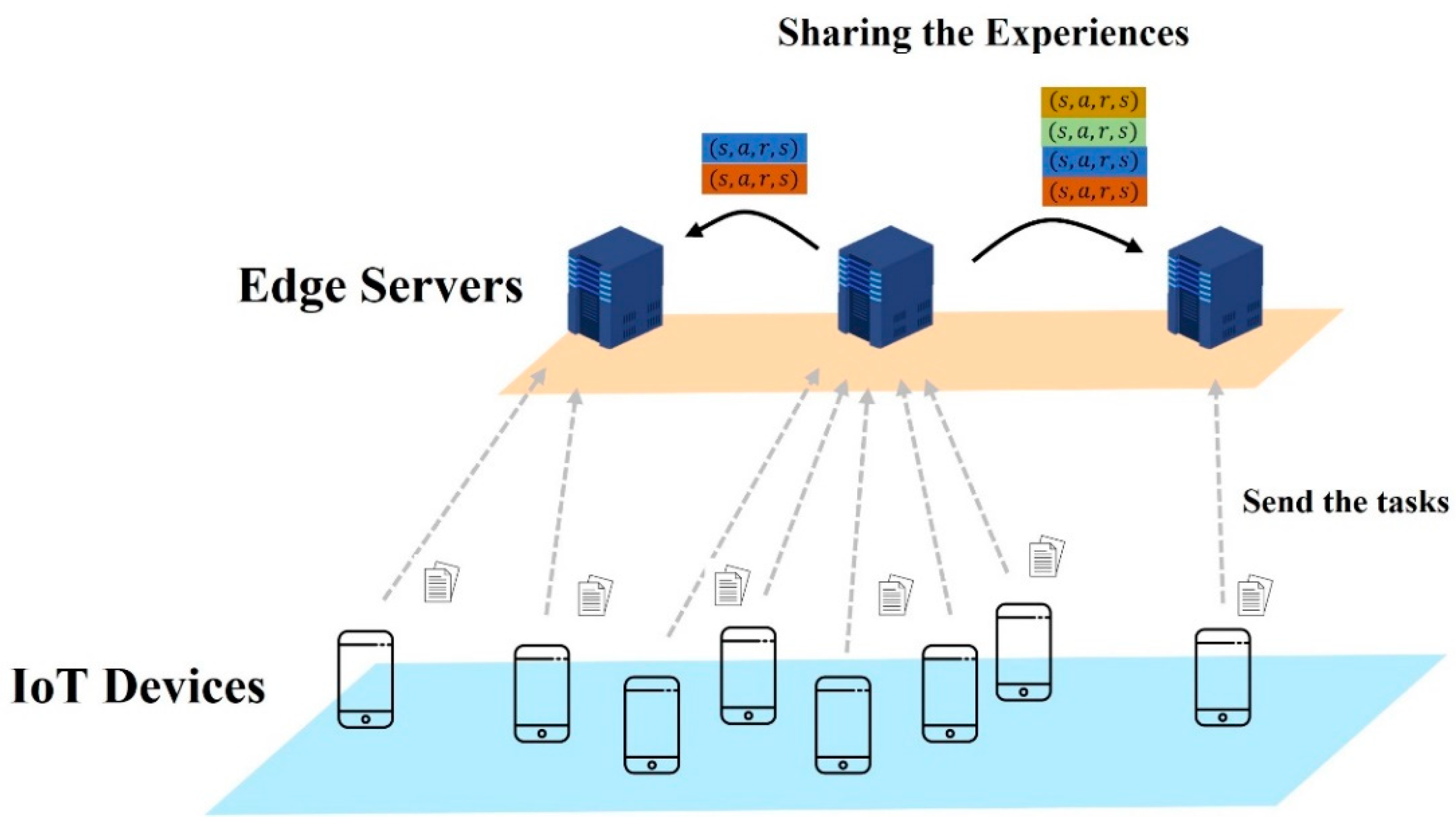
2.4. Edge Collaboration for Computation Offloading
2.5. RL-Based Computation Offloading
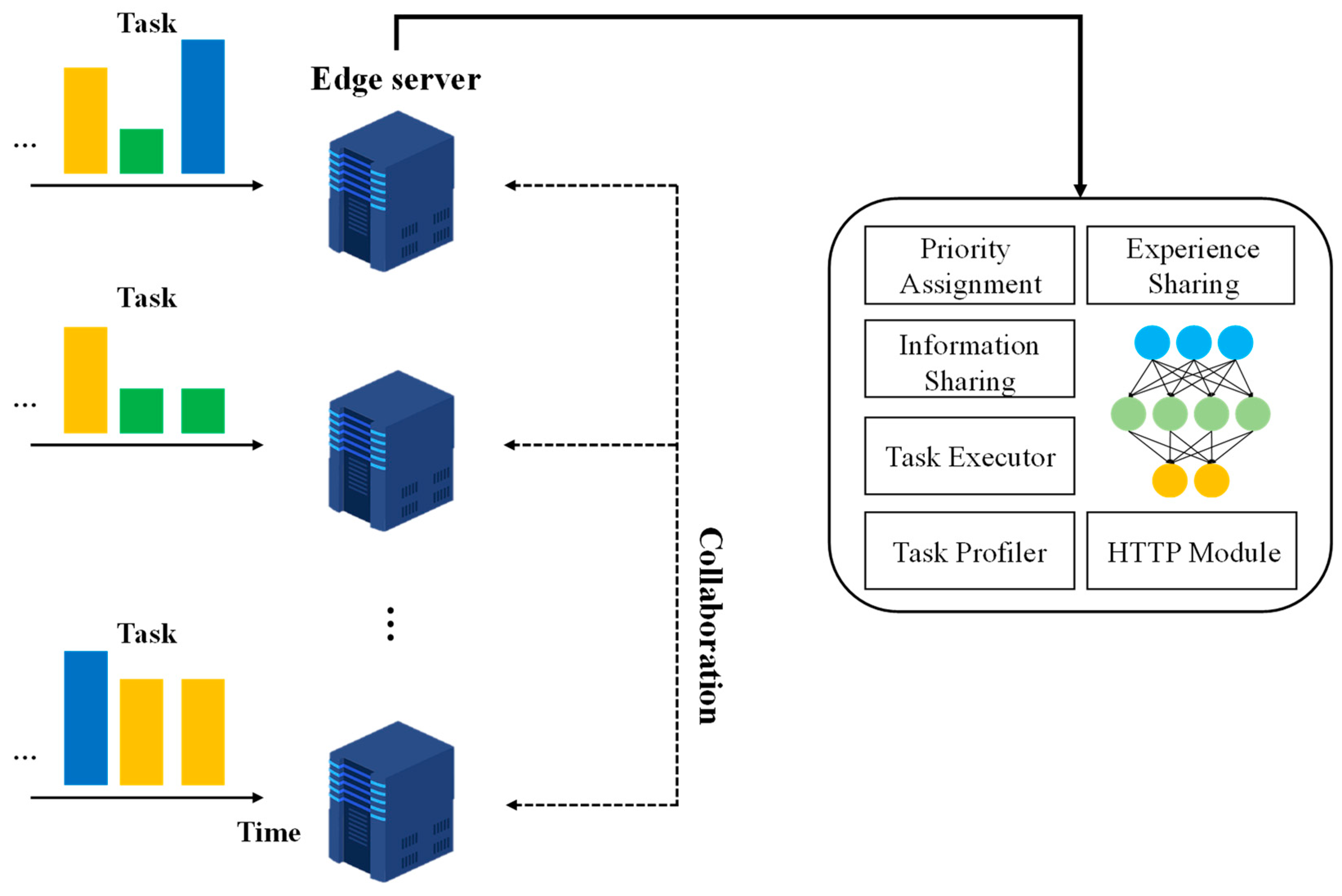
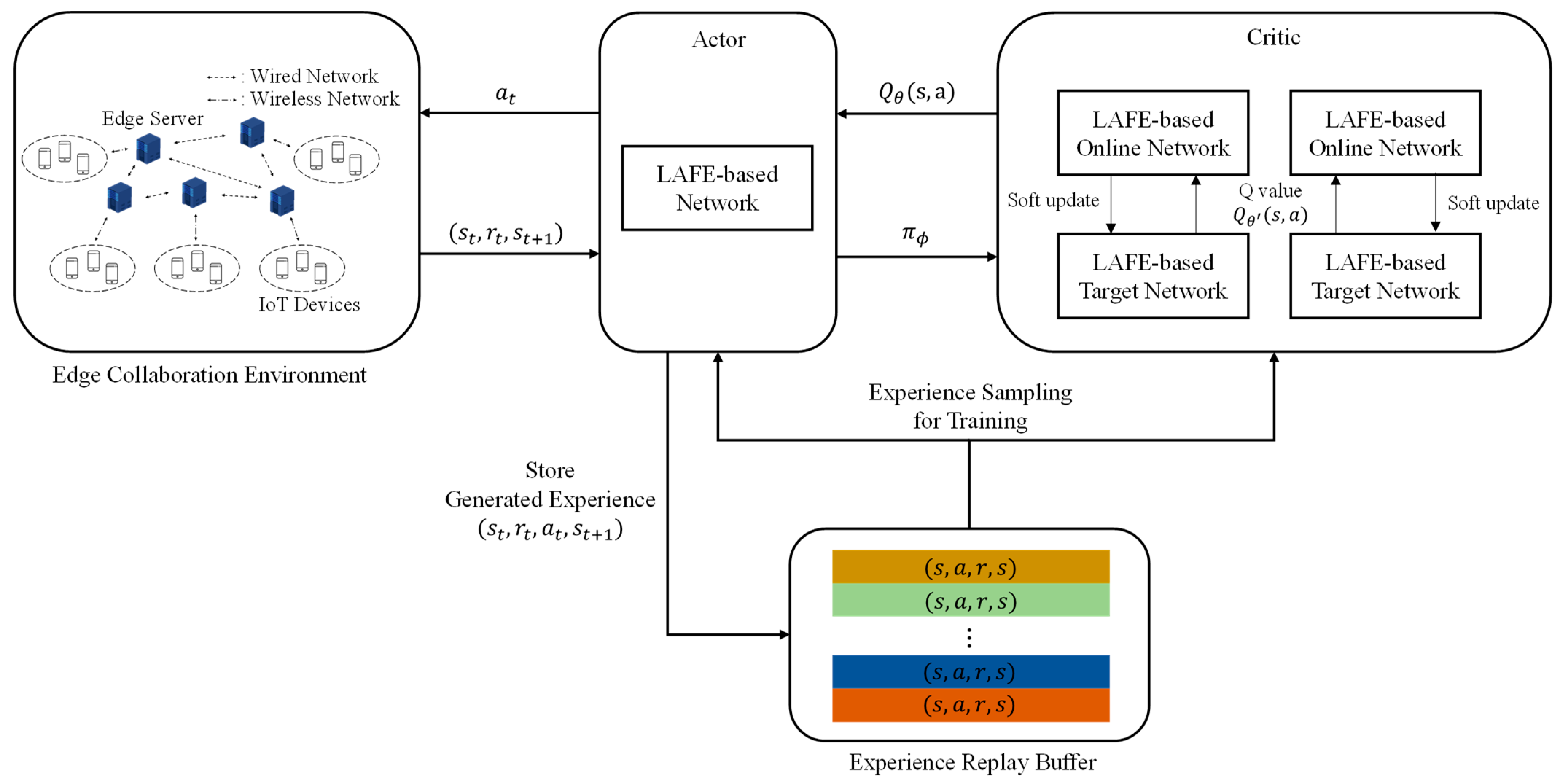
3. Proposed Scheme
3.1. System Model
3.2. Problem Formulation
3.3. Deep Reinforcement Learning Structure
- State: Task size (), task deadline (), set of computing resource capacity of edge server (), set of computing resource usage , set of available bandwidth between edge servers (), and a set of number of stored tasks in edge server’s buffer ().
- Action: The action represents the offloading target. The offloading target is the local edge server or other edge servers.
- Reward: The reward is defined by considering task service time and load balance, as calculated in Equation (9).
| Algorithm 1 RL with Prioritized Experience Sharing | |
| 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16: 17: 18: 19: 20: 21: 22: 23: | Initialize DDPG networks , actor network with random parameters , and random parameters in critic network . Initialize target network parameter for episode = 1 to Mmax do Reset environment state s0 and reward r = 0 for t = 1 to T do Obtain the state st Generate action at by the actor network Obtain reward rt and state s(t+1) using shared information between edge servers Store the experience with TD error and state value Calculate the rank according to the Equation (9) if replay buffer is full then Find the least replayed experience in replay buffer Remove from replay buffer end if end for for to Z do Probabilistically select a sample from replay buffer Calculate according to the Equation (11) Update online network parameter of critic and actor Soft update critic network parameter of critic and actor end for Share the prioritized experience end for |
4. Simulation
4.1. Simulation Setup
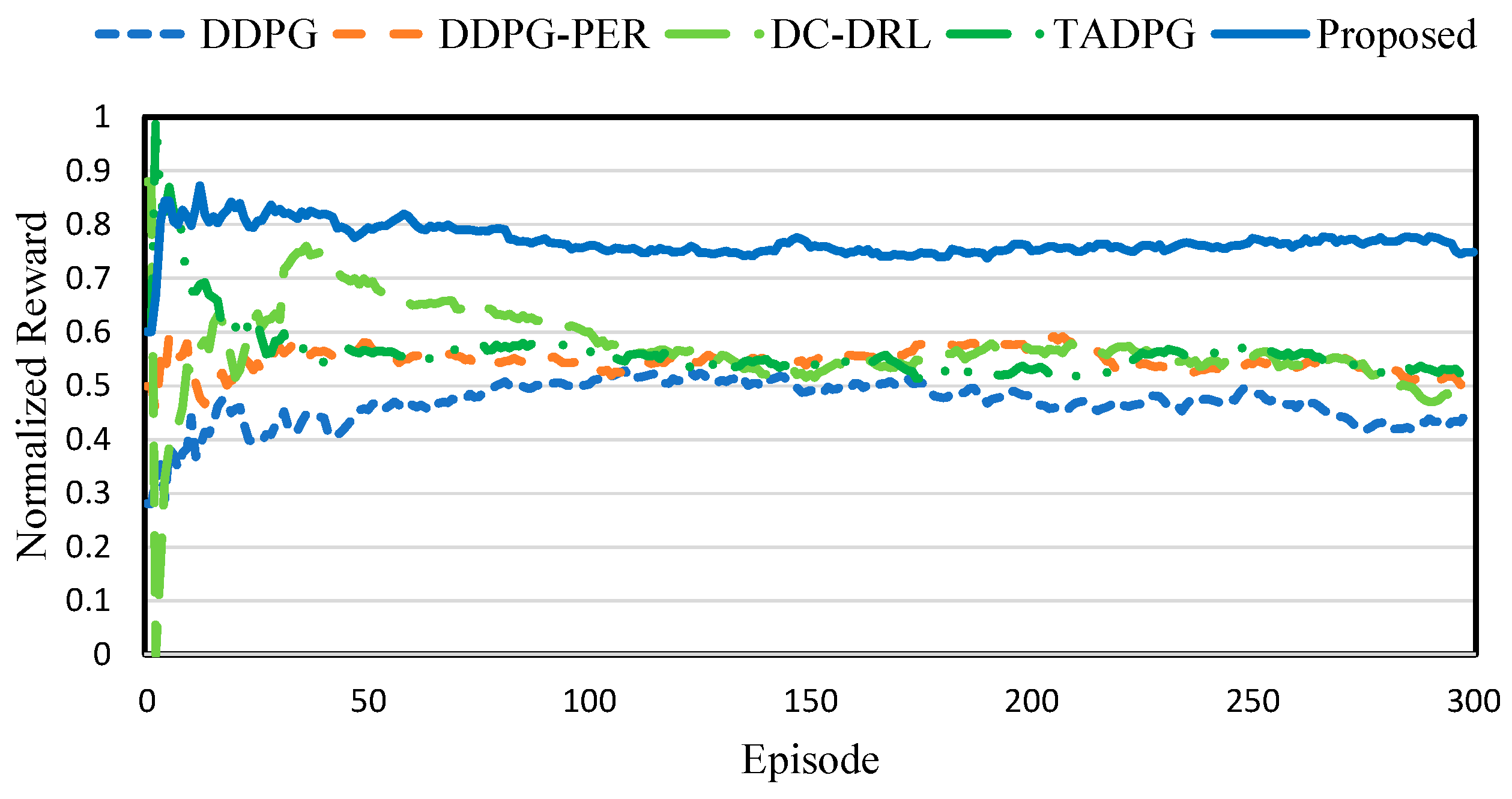
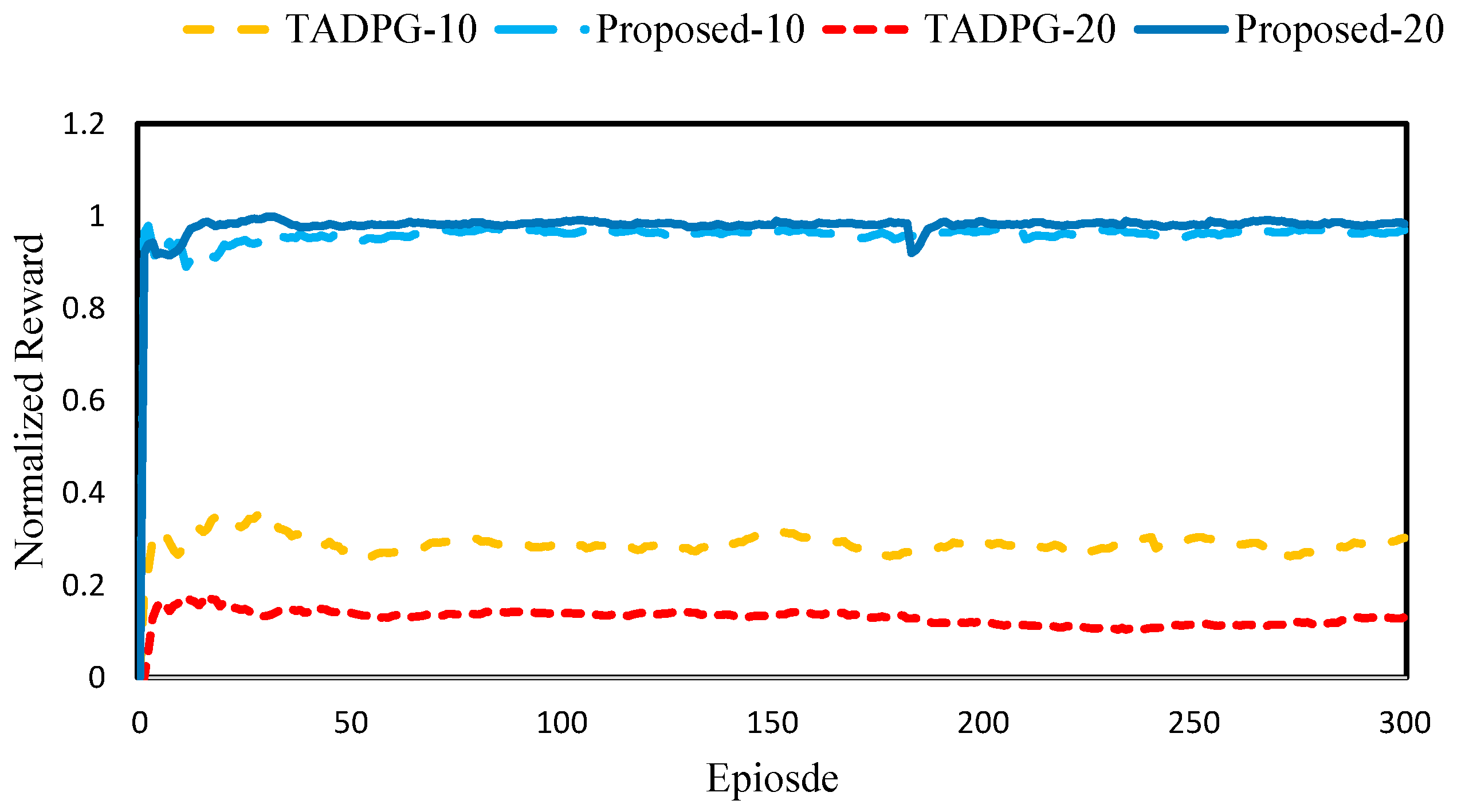
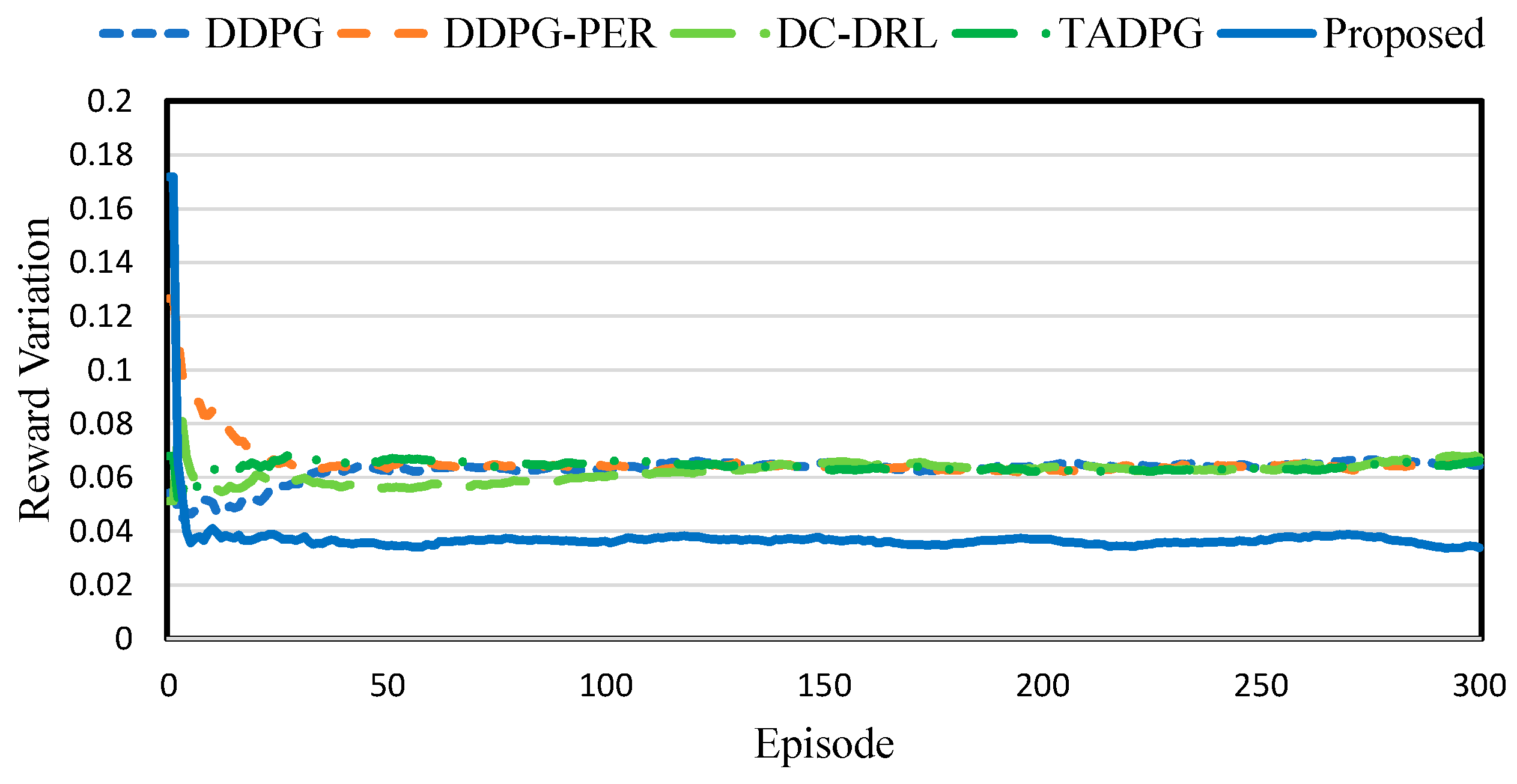
4.2. Performance of RL Training
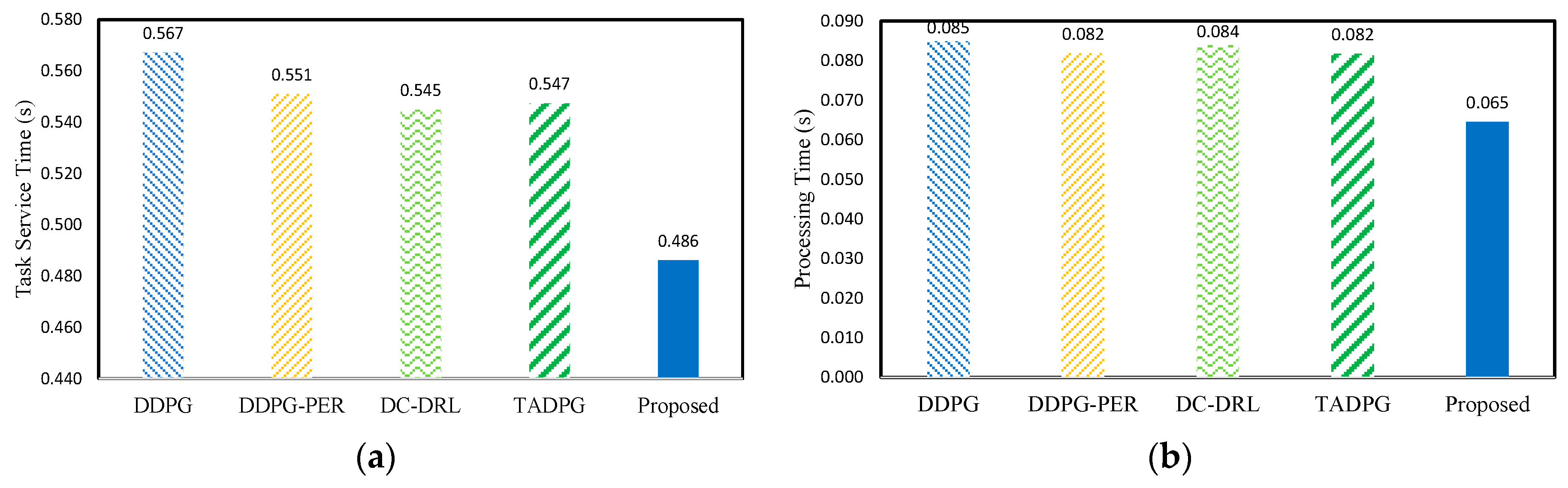
4.3. Performance of QoE
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aslanpour, M.S.; Gill, S.S.; Toosi, A.N. Performance Evaluation Metrics for Cloud, Fog, and Edge Computing: A Review, Taxonomy, Benchmarks, and Standards for Future Research. Internet Things 2020, 12, 100273. [Google Scholar] [CrossRef]
- Khan, W.Z.; Ahmed, E.; Hakak, S.; Yaqqob, I.; Ahmed, A. Edge Computing: A Survey. Future Gener. Comput. Syst. 2019, 97, 219–235. [Google Scholar] [CrossRef]
- Hu, Y.; Zhan, J.; Zhou, G.; Chen, A.; Cai, W.; Guo, K.; Hu, Y.; Li, L. Fast Forest Fire Smoke Detection using MVMNet. Knowl.-Based Syst. 2020, 4, 108219. [Google Scholar] [CrossRef]
- Wang, J.; Pan, J.; Esposito, F.; Calyam, P.; Yang, Z.; Mohapatra, P. Edge Cloud Offloading Algorithms: Issues, Methods, and Perspectives. ACM Comput. Surv. 2020, 52, 1–23. [Google Scholar] [CrossRef]
- Meng, Q.; Wang, K.; Liu, B.; Miyazaki, T.; He, X. QoE-based Big Data Analysis with Deep Learning in Pervasive Edge Environment. In Proceedings of the IEEE International Conference on Communications, Kansas City, MO, USA, 20–24 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Xue, M.; Wu, H.; Peng, G.; Wolter, K. DDPQN: An Efficient DNN Offloading Strategy in Local-Edge-Cloud Collaborative Environments. IEEE Trans. Serv. Comput. 2021, 15, 640–655. [Google Scholar] [CrossRef]
- Qiu, X.; Zhang, W.; Chen, W.; Zhen, Z. Distributed and Collective Deep Reinforcement Learning for Computation Offloading: A Practical Perspective. IEEE Trans. Parallel Distrib. Syst. 2020, 32, 1085–1101. [Google Scholar] [CrossRef]
- Li, Y. Deep Reinforcement Learning: An Overview. arXiv 2017, arXiv:1701.07274. [Google Scholar]
- Lillicrap, T.P.; Hung, J.J.; Pritzel, A.; Heess, H.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous Control with Deep Reinforcement Learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Satyanarayann, M. Pervasive Computing: Vision and Challenges. IEEE Pers. Commun. 2001, 8, 10–17. [Google Scholar] [CrossRef]
- Song, H.; Bai, J.; Yi, Y.; Wu, J.; Liu, L. Artificial Intelligence Enabled Internet of Things: Network Architecture and Spectrum Access. IEEE Comput. Intell. Mag. 2020, 15, 44–51. [Google Scholar] [CrossRef]
- Bonomi, F.; Milito, R.; Zhu, J.; Addepalli, S. Fog Computing and Its Role in the Internet of Things. In International Conference on Mobile Cloud Computing Workshop; Association for Computing Machinery: New York, NY, USA, 2012; pp. 13–16. [Google Scholar]
- Patal, M.; Hu, Y.; Hede, P.; Joubert, J.; Thornton, C.; Naughton, B.; Ramos, J.R.; Chan, C.; Young, V.; Tan, S.J.; et al. Mobile-Edge Computing-Introductory Technical White Paper. ETSI Tech. Represent. 2013, 29, 854–864. [Google Scholar]
- MCEnros, P.; Wang, S.; Liyanage, M. A Survey on the Convergence of Edge Computing and AI for UAVs: Opportunities and Challenges. IEEE Internet Things J. 2022, 9, 15435–15459. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-Learning. AAAI Conf. Artif. Intell. 2016, 30, 1. [Google Scholar] [CrossRef]
- Konda, V.; Tsitsiklis, J. Actor-Critic Algorithms. In Advances in Neural Information Processing Systems 12; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Liu, J.; Mao, Y.; Zhang, J.; Letaief, K.B. Delay-Optimal Computation Task Scheduling for Mobile-Edge Computing Systems. In IEEE International Symposium on Information Theory; IEEE: Barcelona, Spain, 2016; pp. 1451–1455. [Google Scholar]
- Tan, H.; Han, Z.; Li, X.-Y.; Lau, F.C. Online Job Dispatching and Scheduling in Edge-Clouds. In IEEE Conference on Computer Communications; IEEE: New York, NY, USA, 2017; pp. 1–9. [Google Scholar]
- Deng, X.; Li, J.; Liu, E.; Zhang, H. Task Allocation Algorithm and Optimization Model on Edge Collaboration. J. Syst. Archit. 2020, 110, 101778. [Google Scholar] [CrossRef]
- Zhang, Y.; Lan, X.; Ren, J.; Cai, L. Efficient Computing Resource Sharing for Mobile Edge-Cloud Computing Networks. IEEE/ACM Trans. Netw. 2020, 28, 1227–1240. [Google Scholar] [CrossRef]
- Choi, H.; Yu, H.; Lee, E. Latency-Classification-based Deadline-aware Task Offloading Algorithm in Mobile Edge Computing Environments. Appl. Sci. 2019, 9, 4696. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Y.; Sun, R. Task Proactive Caching based Computation Offloading and Resource Allocation in Mobile-Edge Computing Systems. In Proceedings of the IEEE International Wireless Communications & Mobile Computing Conference, Limassol, Cyprus, 25–29 June 2018; pp. 232–237. [Google Scholar]
- Xu, X.; Li, D.; Dai, Z.; Li, S.; Chen, X. A Heuristic Offloading Method for Deep Learning Edge Services in 5G Network. IEEE Access 2019, 7, 67734–67744. [Google Scholar] [CrossRef]
- Jonathan, A.; Chandra, A.; Weissman, J. Locality-aware Load Sharing in Mobile Cloud Computing. In Proceedings of the International Conference on Utility and Cloud Computing, Austin, TX, USA, 5–8 December 2017; pp. 141–150. [Google Scholar]
- Wang, Z.; Liang, W.; Huang, M.; Ma, Y. Delay-Energy Joint Optimization for Task Offloading in Mobile Edge Computing. arXiv 2018, arXiv:1804.10416. [Google Scholar]
- Chen, X.; Jiao, L.; Li, W.; Fu, X. Efficient Multi-User Computation Offloading for Mobile-Edge Cloud Computing. IEEE/ACM Trans. Netw. 2015, 25, 2795–2808. [Google Scholar] [CrossRef]
- Du, M.; Wang, Y.; Ye, K.; Xu, C. Algorithmics of Cost-Driven Computation Offloading in the Edge-Cloud Environment. IEEE Trans. Netw. 2020, 69, 1519–1532. [Google Scholar] [CrossRef]
- Chen, M.; Wang, T.; Zhang, S.; Liu, A. Deep Reinforcement Learning for Computation Offloading in Mobile Edge Computing Environment. Comput. Commun. 2021, 175, 1–12. [Google Scholar] [CrossRef]
- Seid, A.M.; Boaten, G.O.; Anokye, S.; Kwantwi, T.; Usn, G.; Liu, G. Collaborative Computation Offloading and Resource Allocation in Multi-UAV-Assisted IoT Networks: A Deep Reinforcement Learning Approach. IEEE Internet Things J. 2021, 8, 12203–12218. [Google Scholar] [CrossRef]
- Ong, H.Y.; Chavez, K.; Hong, A. Distributed Deep Q-Learning. arXiv 2015, arXiv:1508.04186. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchrounous Methods for Deep Reinforcement Learning. In Proceedings of the 33rd International Conference on International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Barth-Maron, G.; Hoffman, M.W.; Budden, D.; Dabney, W.; Horgan, D.; Tb, D.; Muldal, A.; Hees, N.; Lillicrap, T. Distributed Distributional Deterministic Policy Gradients. arXiv 2018, arXiv:1804.08617. [Google Scholar]
- Chen, J.; Xing, H.; Xiao, Z.; Xu, L.; Tao, T. A DRL Agent for Jointly Optimizing Computation Offloading and Resource Allocation in MEC. IEEE Internet Things J. 2021, 8, 17508–17524. [Google Scholar] [CrossRef]
- Gu, B.; Alzab, M.; Lin, Z.; Hang, X.; Juang, J. AI-enabled Task Offloading for Improving Quality of Computational Experience in Ultra Dense Networks. ACM Trans. Internet Technol. 2022, 22, 1–17. [Google Scholar] [CrossRef]
- Yamansavascilar, B.; Baktir, A.C.; Sonmez, C.; Ozgovde, A.; Ersov, C. DeepEdge: A Deep Reinforcement Learning based Task Orchestrator for Edge Computing. arXiv 2021, arXiv:2110.01863. [Google Scholar] [CrossRef]
- Ale, L.; King, S.A.; Zhang, N.; Sattar, R.; Skandaranivam, J. D3PG: Dirichlet DDPG for Task Partitioning and Offloading with Constrained Hybrid Action Space in Mobile Edge Computing. IEEE Internet Things J. 2022, 9, 19260–19272. [Google Scholar] [CrossRef]
- Qadeer, A.; Lee, M.J. DDPG-Edge-Cloud: A Deep-Deterministic Policy Gradient based Multi-Resource Allocation in Edge-Cloud System. In Proceedings of the IEEE International Conference on Artificial Intelligence in Information and Communication, Jeju Island, Repulic of Korea, 21–24 February 2022; pp. 339–344. [Google Scholar]
- Nachum, O.; Morouzi, M.; Xu, K.; Schuurmans, D. Bridging the Gap Between Value and Policy based Reinforcement Learning. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Jain, R.K.; Chiu, D.-M.W.; Hawe, W.R. A Quantitative Measure of Fairness and Discrimination; Eastern Research Laboratory, Digital Equipment Corporation: Hudson, MA, USA, 1984; Volume 21. [Google Scholar]
- Lai, S.; Fan, X.; Ye, Q.; Tan, Z.; Zhang, Y.; He, X.; Nanda, P. FairEdge: A Fairness-Oriented Task Offloading Scheme for IoT Applications in Mobile Cloudlet Networks. IEEE Access 2020, 8, 13516–13526. [Google Scholar] [CrossRef]
- Zhang, G.; Shen, F.; Yang, Y.; Qian, H.; Yao, W. Fair Task Offloading among Fog Nodes in Fog Computing Networks. In Proceedings of the IEEE International Conference on Communications, Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection via the LASSO: A Retrospective. J. R. Stat. Soc. Ser. B Stat. Methodol. 2011, 73, 273–282. [Google Scholar] [CrossRef]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized Experience Replay. arXiv 2015, arXiv:1511.05952. [Google Scholar]
- Gulli, A.; Pa, S. Deep Learning with Keras; Packet Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]


| Scheme | Temporal State | Experience Priority | Agent |
|---|---|---|---|
| TADPG [34] | ✓ | ✓ | Single-agent |
| B. Gu [35] | ✕ | ✕ | Multi-agent |
| DC-DRL [7] | ✕ | ✕ | Multi-agent |
| L. Ale et al. [37] | ✕ | ✕ | Single-agent |
| A. Oadder et al. [38] | ✓ | ✓ | Single-agent |
| Proposed | ✓ | ✓ | Multi-agent |
| Proposed | TADPG | DC-DRL | DDPG-PER | DDPG | |
| Reward | −0.44977 | −0.51398 | −0.53132 | −0.5213 | −0.53887 |
| Variation | 0.0338 | 0.0661 | 0.0673 | 0.0655 | 0.0645 |
| Proposed-20 | TADPG-20 | Proposed-10 | TADPG-10 | |
|---|---|---|---|---|
| Reward | −0.0523 | −0.0733 | 0.0242 | 0.0156 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Chung, K. Distributed DRL-Based Computation Offloading Scheme for Improving QoE in Edge Computing Environments. Sensors 2023, 23, 4166. https://doi.org/10.3390/s23084166
Park J, Chung K. Distributed DRL-Based Computation Offloading Scheme for Improving QoE in Edge Computing Environments. Sensors. 2023; 23(8):4166. https://doi.org/10.3390/s23084166
Chicago/Turabian StylePark, Jinho, and Kwangsue Chung. 2023. "Distributed DRL-Based Computation Offloading Scheme for Improving QoE in Edge Computing Environments" Sensors 23, no. 8: 4166. https://doi.org/10.3390/s23084166
APA StylePark, J., & Chung, K. (2023). Distributed DRL-Based Computation Offloading Scheme for Improving QoE in Edge Computing Environments. Sensors, 23(8), 4166. https://doi.org/10.3390/s23084166





