A Machine Learning Pipeline for Gait Analysis in a Semi Free-Living Environment
Abstract
:1. Introduction
2. Material and Methods
- The segmentation step uses an adaptive change-point detection algorithm to process IMU recordings. The method searches for significant changes in the time-frequency space at a given scale, i.e., instants where the subject changed their behavior/activity. Signals are thus segmented into several homogeneous regimes that will help to extract knowledge from the global recording.
- Once these homogeneous regimes are segmented, they are classified as walking or non-walking phases through a supervised classification procedure. A second algorithm identifies, within non walking phases, sedentary and non-sedentary regimes, thus providing a full labelization of the regimes. Sedentary regimes correspond to activities that are not walking phases but that imply movements from the recorded subjects (in our case, walking up and down stairs, opening a fire door, and performing a 90° turn). On the other hand, non-sedentary regimes correspond to activities that do not imply movements from participants (in our case, leaning, sitting, standing).
- The next step consists of extracting features from the regimes that have been classified as corresponding to a walking phase. These features were selected in order to assess different aspects of gait (stability, steadiness, sturdiness, and symmetry).
- By using models learned from healthy subjects, each walking regime is then given a score represented by distinct color, allowing visual and intuitive feedback.
2.1. Data and Protocols
2.2. Step 1: Adaptive Changepoint Detection Method
2.2.1. Data Transformation
2.2.2. Changepoint Detection Algorithm
2.2.3. Calibration of β
2.3. Step 2: Classification of Segmented Phases
2.4. Step 3: Feature Extraction
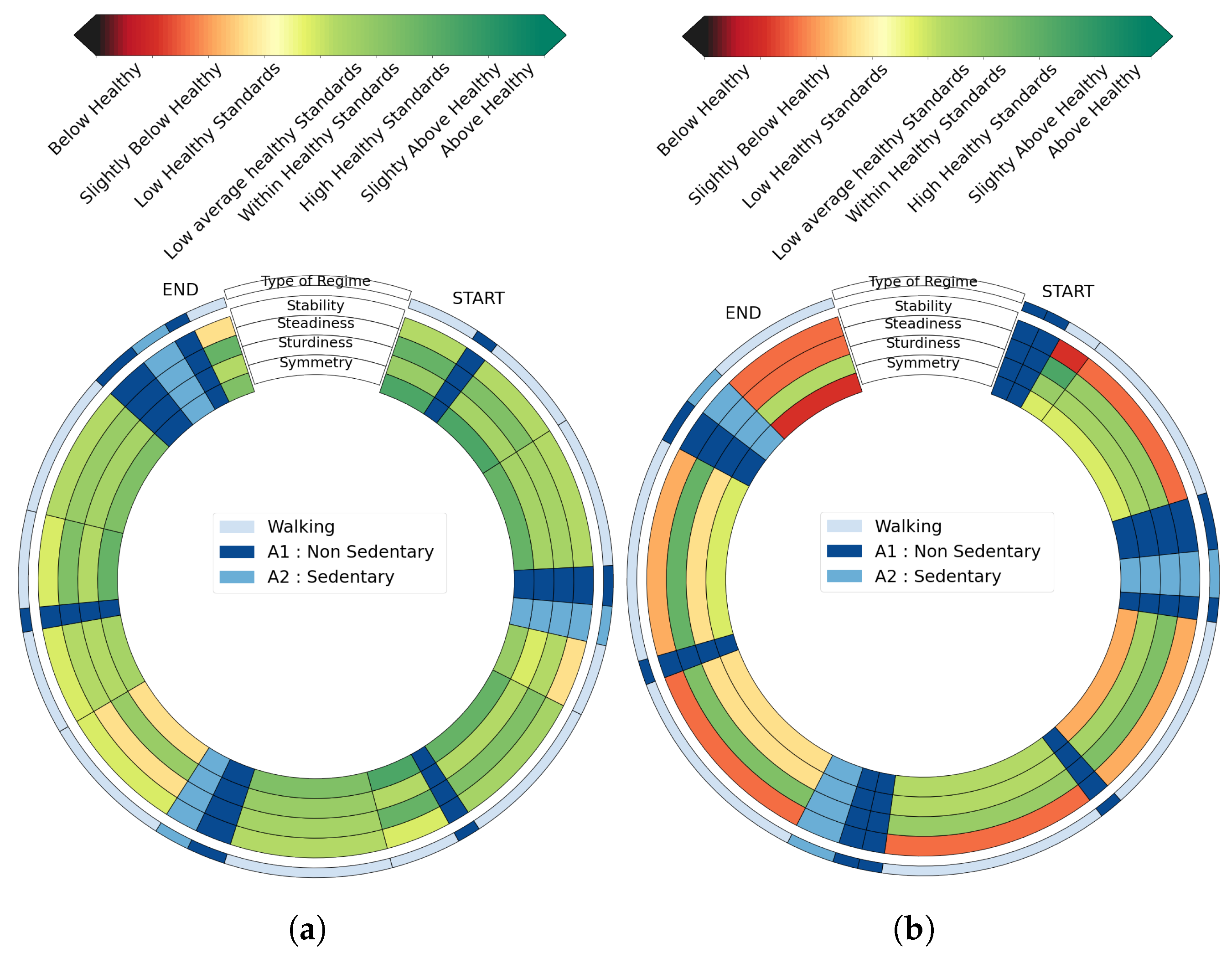
2.5. Step 4: Score Generation and Graphical Feedback
2.6. Evaluation Metrics
2.6.1. Evaluation of the Adaptive Change-Point Detection
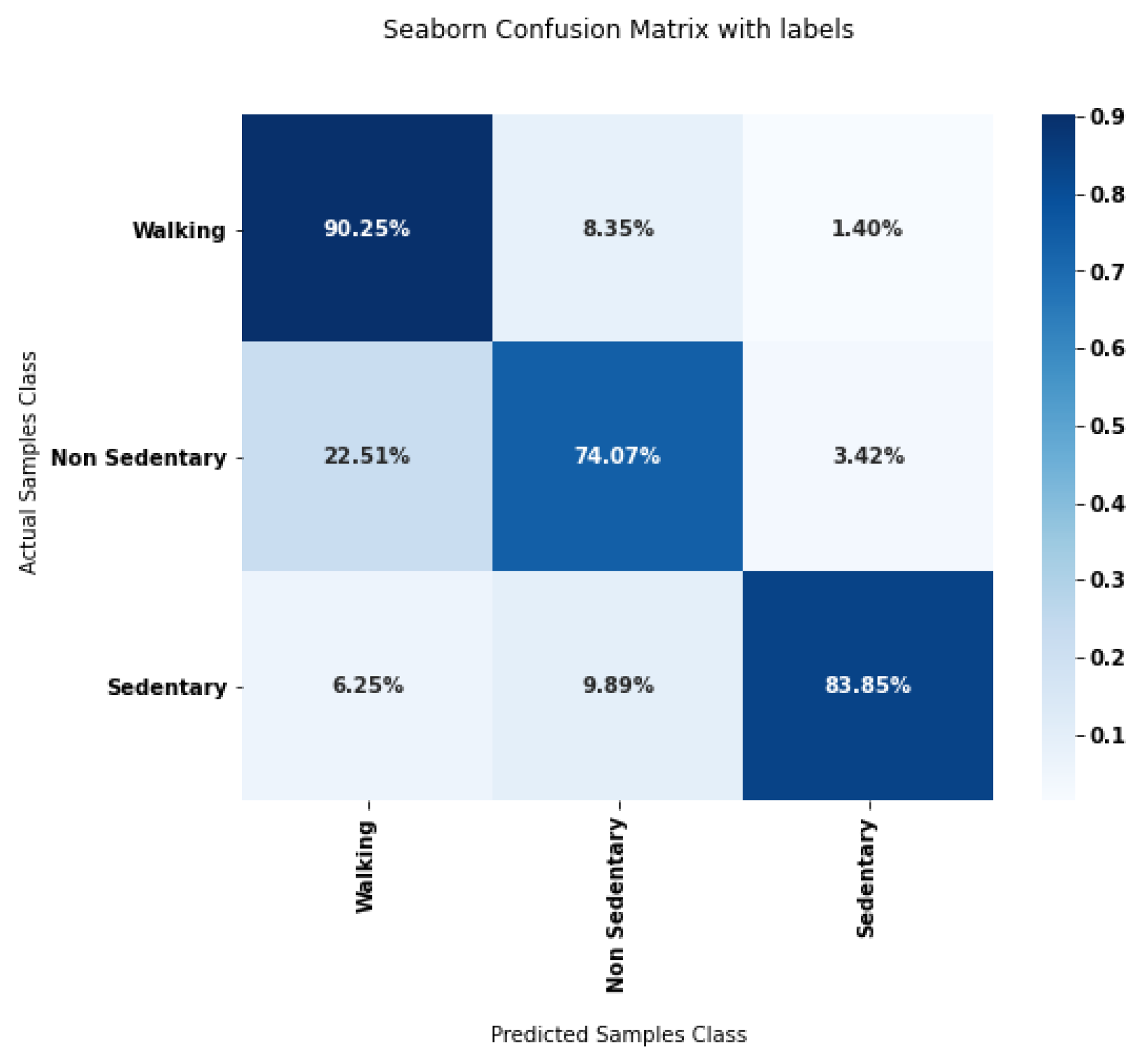
2.6.2. Joint Evaluation of Segmentation and Classification Steps
3. Results
3.1. Adaptive Change-Point Detection
3.2. Joint Evaluation of Segmentation and Classification Steps
3.3. Scores and Graphical Feedback
4. Discussion
4.1. Performances
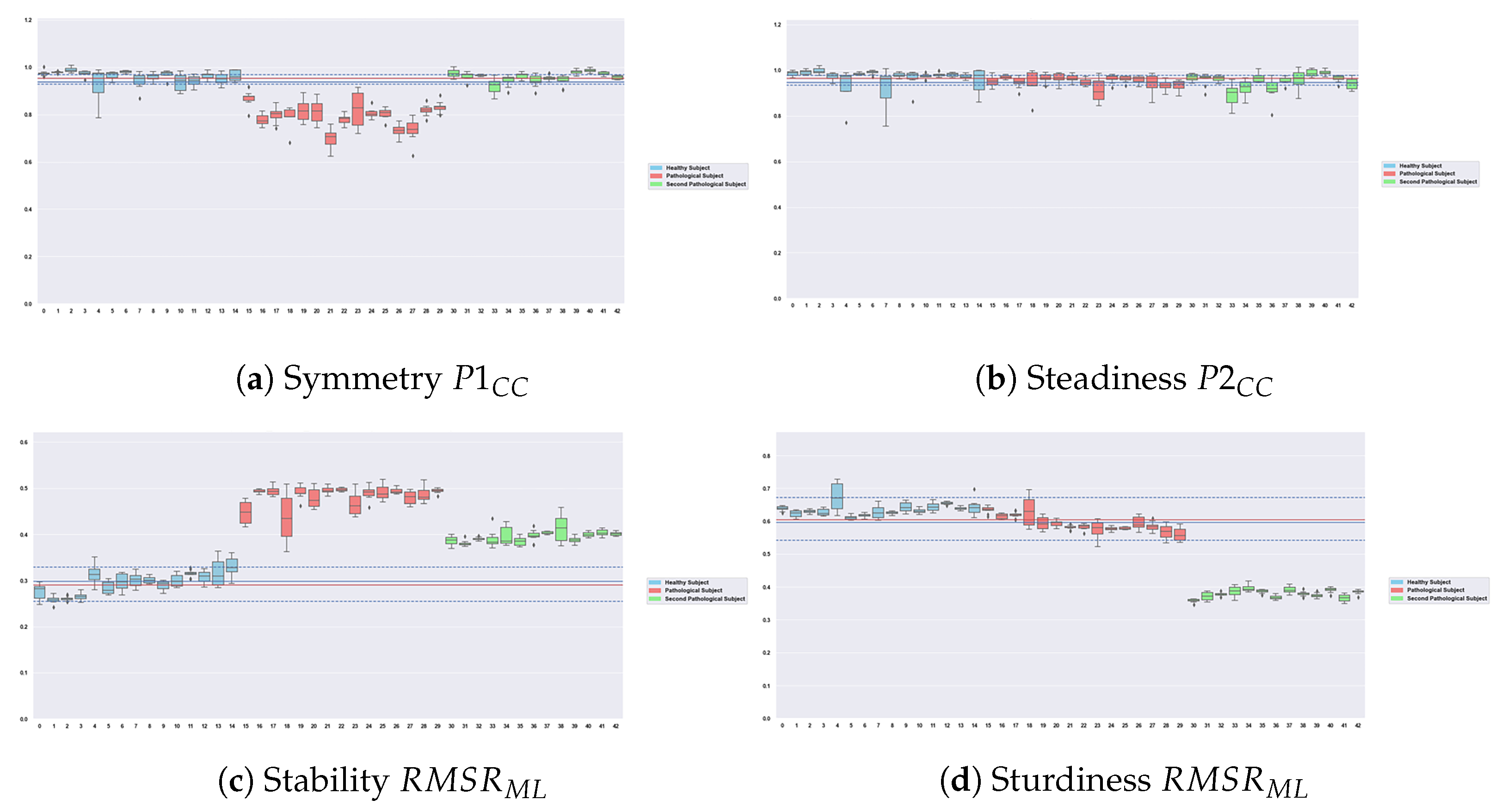
4.2. Robustness of the Features
4.3. Relevance of the Graphical Feedback and Possible Usecases
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FLE | Free-Living Environment |
| Semi FLE | Semi Free-Living Environment |
| HAR | Human Activity Recognition |
| IMU | Inertial Measurement Unit |
References
- Silva de Lima, A.L.; Evers, L.J.; Hahn, T.; Bataille, L.; Hamilton, J.L.; Little, M.A.; Okuma, Y.; Bloem, B.R.; Faber, M.J. Freezing of gait and fall detection in Parkinson’s disease using wearable sensors: A systematic review. J. Neurol. 2017, 264, 1642–1654. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dot, T.; Quijoux, F.; Oudre, L.; Vienne-Jumeau, A.; Moreau, A.; Vidal, P.P.; Ricard, D. Non-Linear Template-Based Approach for the Study of Locomotion. Sensors 2020, 20, 1939. [Google Scholar] [CrossRef] [PubMed]
- Vienne, A.; Barrois, R.P.; Buffat, S.; Ricard, D.; Vidal, P.P. Inertial sensors to assess gait quality in patients with neurological disorders: A systematic review of technical and analytical challenges. Front. Psychol. 2017, 8, 817. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oudre, L.; Barrois-Müller, R.; Moreau, T.; Truong, C.; Vienne-Jumeau, A.; Ricard, D.; Vayatis, N.; Vidal, P.P. Template-based step detection with inertial measurement units. Sensors 2018, 18, 4033. [Google Scholar] [CrossRef] [Green Version]
- Semwal, V.B.; Gaud, N.; Lalwani, P.; Bijalwan, V.; Alok, A.K. Pattern identification of different human joints for different human walking styles using inertial measurement unit (IMU) sensor. Artif. Intell. Rev. 2022, 55, 1149–1169. [Google Scholar] [CrossRef]
- McGrath, T.; Stirling, L. Body-worn IMU-based human hip and knee kinematics estimation during treadmill walking. Sensors 2022, 22, 2544. [Google Scholar] [CrossRef]
- Nouredanesh, M.; Godfrey, A.; Howcroft, J.; Lemaire, E.D.; Tung, J. Fall risk assessment in the wild: A critical examination of wearable sensor use in free-living conditions. Gait Posture 2021, 85, 178–190. [Google Scholar] [CrossRef]
- Halliday, S.J.; Shi, H.; Brittain, E.L.; Hemnes, A.R. Reduced free-living activity levels in pulmonary arterial hypertension patients. Pulm. Circ. 2018, 9, 2045894018814182. [Google Scholar] [CrossRef] [Green Version]
- Brodie, M.A.; Coppens, M.J.; Lord, S.R.; Lovell, N.H.; Gschwind, Y.J.; Redmond, S.J.; Del Rosario, M.B.; Wang, K.; Sturnieks, D.L.; Persiani, M.; et al. Wearable pendant device monitoring using new wavelet-based methods shows daily life and laboratory gaits are different. Med. Biol. Eng. Comput. 2016, 54, 663–674. [Google Scholar] [CrossRef]
- Jung, S.; Michaud, M.; Oudre, L.; Dorveaux, E.; Gorintin, L.; Vayatis, N.; Ricard, D. The Use of Inertial Measurement Units for the Study of Free Living Environment Activity Assessment: A Literature Review. Sensors 2020, 20, 5625. [Google Scholar] [CrossRef]
- Storm, F.A.; Nair, K.; Clarke, A.J.; Van der Meulen, J.M.; Mazzà, C. Free-living and laboratory gait characteristics in patients with multiple sclerosis. PLoS ONE 2018, 13, e0196463. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nazarahari, M.; Rouhani, H. Detection of daily postures and walking modalities using a single chest-mounted tri-axial accelerometer. Med. Eng. Phys. 2018, 57, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Cajamarca, G.; Rodríguez, I.; Herskovic, V.; Campos, M.; Riofrío, J.C. StraightenUp+: Monitoring of posture during daily activities for older persons using wearable sensors. Sensors 2018, 18, 3409. [Google Scholar] [CrossRef] [Green Version]
- Ahmadi, M.; O’Neil, M.; Fragala-Pinkham, M.; Lennon, N.; Trost, S. Machine learning algorithms for activity recognition in ambulant children and adolescents with cerebral palsy. J. NeuroEng. Rehabil. 2018, 15, 105. [Google Scholar] [CrossRef] [Green Version]
- Ellis, K.; Kerr, J.; Godbole, S.; Staudenmayer, J.; Lanckriet, G. Hip and wrist accelerometer algorithms for free-living behavior classification. Med. Sci. Sport. Exerc. 2016, 48, 933–940. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ni, Z.; Wu, T.; Wang, T.; Sun, F.; Li, Y. Deep multi-branch two-stage regression network for accurate energy expenditure estimation with ECG and IMU data. IEEE Trans. Biomed. Eng. 2022, 69, 3224–3233. [Google Scholar] [CrossRef]
- Nouredanesh, M.; Tung, J. IMU, sEMG, or their cross-correlation and temporal similarities: Which signal features detect lateral compensatory balance reactions more accurately? Comput. Methods Programs Biomed. 2019, 182, 105003. [Google Scholar] [CrossRef]
- Choi, A.; Kim, T.H.; Yuhai, O.; Jeong, S.; Kim, K.; Kim, H.; Mun, J.H. Deep learning-based near-fall detection algorithm for fall risk monitoring system using a single inertial measurement unit. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 2385–2394. [Google Scholar] [CrossRef]
- Furtado, S.; Godfrey, A.; Del Din, S.; Rochester, L.; Gerrand, C. Free-living monitoring of ambulatory activity after treatments for lower extremity musculoskeletal cancers using an accelerometer-based wearable—A new paradigm to outcome assessment in musculoskeletal oncology? Disabil. Rehabil. 2022, 1–10. [Google Scholar] [CrossRef]
- Tawaki, Y.; Nishimura, T.; Murakami, T. Monitoring of gait features during outdoor walking by simple foot mounted IMU system. In Proceedings of the 46th Annual Conference of the IEEE Industrial Electronics Society, IECON, Singapore, 18–21 October 2020; pp. 3413–3418. [Google Scholar] [CrossRef]
- Oudre, L.; Jakubowicz, J.; Bianchi, P.; Simon, C. Classification of periodic activities using the Wasserstein distance. IEEE. Trans. Biomed. 2012, 59, 1610–1619. [Google Scholar] [CrossRef]
- Truong, C. Détection de Ruptures Multiples—Application aux Signaux Physiologiques. Ph.D. Thesis, Université Paris-Saclay, Paris, France, 2018. [Google Scholar]
- Nguyen, M.D.; Mun, K.R.; Jung, D.; Han, J.; Park, M.; Kim, J.; Kim, J. IMU-based spectrogram approach with deep convolutional neural networks for gait classification. In Proceedings of the International Conference on Consumer Electronics (ICCE), Online, 4–6 January 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Rehman, R.Z.U.; Klocke, P.; Hryniv, S.; Galna, B.; Rochester, L.; Del Din, S.; Alcock, L. Turning detection during gait: Algorithm validation and influence of sensor location and turning characteristics in the classification of parkinson’s disease. Sensors 2020, 20, 5377. [Google Scholar] [CrossRef]
- Nguyen, H.; Lebel, K.; Bogard, S.; Goubault, E.; Boissy, P.; Duval, C. Using inertial sensors to automatically detect and segment activities of daily living in people with Parkinson’s disease. IEEE Trans. Neural Syst. 2017, 26, 197–204. [Google Scholar] [CrossRef] [PubMed]
- Truong, C.; Oudre, L.; Vayatis, N. Greedy kernel change-point detection. IEEE Trans. Signal Process. 2019, 67, 6204–6214. [Google Scholar] [CrossRef]
- Karantonis, D.M.; Narayanan, M.R.; Mathie, M.; Lovell, N.H.; Celler, B.G. Implementation of a real-time human movement classifier using a triaxial accelerometer for ambulatory monitoring. IEEE Trans. Inf. Technol. 2006, 10, 156–167. [Google Scholar] [CrossRef] [PubMed]
- Killick, R.; Fearnhead, P.; Eckley, I.A. Optimal detection of changepoints with a linear computational cost. J. Am. Stat. Assoc. 2012, 107, 1590–1598. [Google Scholar] [CrossRef]
- Truong, C.; Oudre, L.; Vayatis, N. Penalty learning for changepoint detection. In Proceedings of the 25th European Signal Processing Conference (EUSIPCO), Kos Island, Greece, 28 August–2 September 2017; pp. 1569–1573. [Google Scholar] [CrossRef] [Green Version]
- Jung, S.; Oudre, L.; Truong, C.; Dorveaux, E.; Gorintin, L.; Vayatis, N.; Ricard, D. Adaptive change-point detection for studying human locomotion. In Proceedings of the 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Guadalajara, Mexico, 26 July 2021; pp. 2020–2024. [Google Scholar] [CrossRef]
- Prasanth, H.; Caban, M.; Keller, U.; Courtine, G.; Ijspeert, A.; Vallery, E.; Von Zitzewitz, J. Wearable sensor-based real-time gait detection: A systematic review. Sensors 2021, 21, 2727. [Google Scholar] [CrossRef]
- Rast, F.M.; Labruyère, R. Systematic review on the application of wearable inertial sensors to quantify everyday life motor activity in people with mobility impairments. J. Neuroeng. 2020, 17, 1–19. [Google Scholar] [CrossRef]
- Fiorini, L.; Bonaccorsi, M.; Betti, S.; Esposito, D.; Cavallo, F. Combining wearable physiological and inertial sensors with indoor user localization network to enhance activity recognition. J. Ambient Intell. Smart Environ. 2018, 10, 345–357. [Google Scholar] [CrossRef] [Green Version]
- Kerr, J.; Patterson, R.E.; Ellis, K.; Godbole, S.; Johnson, E.; Lanckriet, G.; Staudenmayer, J. Objective assessment of physical activity: Classifiers for public health. Med. Sci. Sport. Exerc. 2016, 48, 951–957. [Google Scholar] [CrossRef] [Green Version]
- Marcotte, R.T.; Petrucci Jr, G.J.; Cox, M.F.; Freedson, P.S.; Staudenmayer, J.W.; Sirard, J.R. Estimating Sedentary Time from a Hip-and Wrist-Worn Accelerometer. Med. Sci. Sport Exerc. 2020, 52, 225–232. [Google Scholar] [CrossRef]
- Fullerton, E.; Heller, B.; Munoz-Organero, M. Recognizing Human Activity in Free-Living Using Multiple Body-Worn Accelerometers. IEEE Sens. J. 2017, 17, 5290–5297. [Google Scholar] [CrossRef] [Green Version]
- Hsu, C.Y.; Tsai, Y.S.; Yau, C.S.; Shie, H.H.; Wu, C.M. Differences in gait and trunk movement between patients after ankle fracture and healthy subjects. Biomed. Eng. Online 2019, 18, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sekine, M.; Tamura, T.; Yoshida, M.; Suda, Y.; Kimura, Y.; Miyoshi, H.; Kijima, Y.; Higashi, Y.; Fujimoto, T. A gait abnormality measure based on root mean square of trunk acceleration. J. Neuroeng. 2013, 10, 1–7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bahari, H.; Forero, J.; Hall, J.C.; Hebert, J.S.; Vette, A.H.; Rouhani, H. Use of the extended feasible stability region for assessing stability of perturbed walking. Science 2021, 11, 1026. [Google Scholar] [CrossRef] [PubMed]
- Bruijn, S.M.; Meijer, O.; Beek, P.; van Dieen, J.H. Assessing the stability of human locomotion: A review of current measures. J. R. Soc. Interface 2013, 10, 20120999. [Google Scholar] [CrossRef]
- Ben Mansour, K.; Gorce, P.; Rezzoug, N. The Multifeature Gait Score: An accurate way to assess gait quality. PLoS ONE 2017, 12, e0185741. [Google Scholar] [CrossRef] [Green Version]
- Labaune, O.; Deroche, T.; Teulier, C.; Berret, B. Vigor of reaching, walking, and gazing movements: On the consistency of interindividual differences. J. Neurophysiol. 2020, 123, 234–242. [Google Scholar] [CrossRef]
- Kobayashi, H.; Kakihana, W.; Kimura, T. Combined effects of age and gender on gait symmetry and regularity assessed by autocorrelation of trunk acceleration. J. Neuroeng. 2014, 11, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Moe-Nilssen, R.; Helbostad, J.L. Estimation of gait cycle characteristics by trunk accelerometry. J. Biomech. 2004, 37, 121–126. [Google Scholar] [CrossRef]
- Tura, A.; Raggi, M.; Rocchi, L.; Cutti, A.G.; Chiari, L. Gait symmetry and regularity in transfemoral amputees assessed by trunk accelerations. J. Neuroeng. 2010, 7, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Cabral, S. Gait Symmetry Measures and Their Relevance to Gait Retraining. In Handbook of Human Motion; Springer International Publishing: Cham, Switzerland, 2018; pp. 429–447. [Google Scholar] [CrossRef]
- Brard, R.; Bellanger, L.; Chevreuil, L.; Doistau, F.; Drouin, P.; Stamm, A. A novel walking activity recognition model for rotation time series collected by a wearable sensor in a free-living environment. Sensors 2022, 22, 3555. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Rivero, D.; Fernandez-Blanco, E.; Luaces, M.R. A public domain dataset for real-life human activity recognition using smartphone sensors. Sensors 2020, 20, 2200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mo, L.; Zhu, Y.; Zeng, L. A Multi-Label Based Physical Activity Recognition via Cascade Classifier. Sensors 2023, 23, 2593. [Google Scholar] [CrossRef] [PubMed]
- Cescon, M.; Choudhary, D.; Pinsker, J.E.; Dadlani, V.; Church, M.M.; Kudva, Y.C.; Doyle III, F.J.; Dassau, E. Activity detection and classification from wristband accelerometer data collected on people with type 1 diabetes in free-living conditions. Comput. Biol. Med. 2021, 135, 104633. [Google Scholar] [CrossRef] [PubMed]
- Konsolakis, K. PhysicaL Activity Recognition Using Wearable Accelerometers in Controlled and Free-Living Environments. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2018. [Google Scholar]
- Andreu-Perez, J.; Garcia-Gancedo, L.; McKinnell, J.; Van der Drift, A.; Powell, A.; Hamy, V.; Keller, T.; Yang, G.Z. Developing fine-grained actigraphies for rheumatoid arthritis patients from a single accelerometer using machine learning. Sensors 2017, 17, 2113. [Google Scholar] [CrossRef]

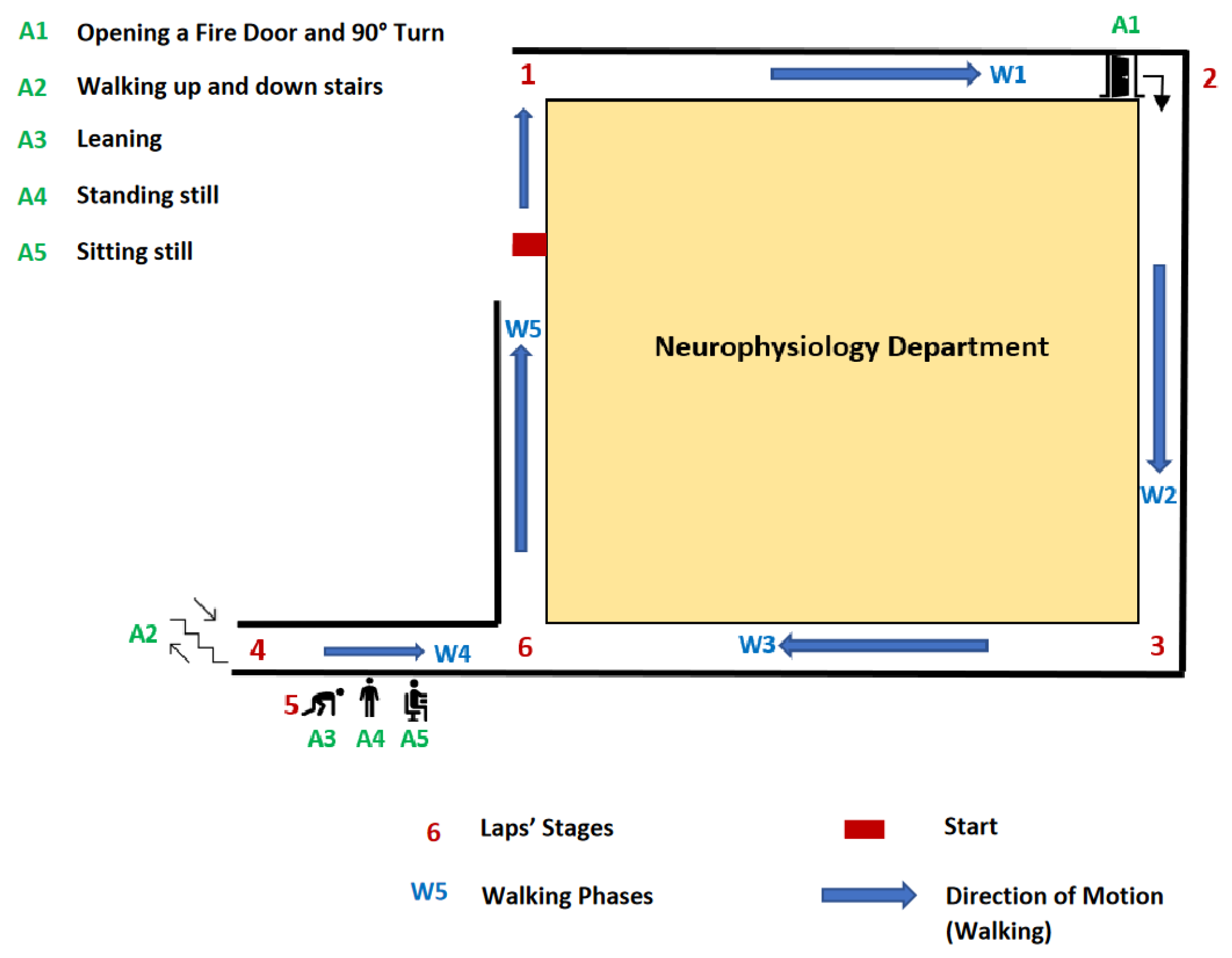


| Transition Identification | Details | Type of Regime |
|---|---|---|
| W1 | Walk (1 → 2) | Walking |
| A1 | Door opening and 90-degree turn | Non-Sedentary |
| W2 | Walk (2 → 3) | Walking |
| W3 | Walk (3 → 4) | Walking |
| A2 | Going up 3 stairs U-turn and going down 3 steps stairs | Non-Sedentary |
| A3 | Leaning | Sedentary |
| A4 | Standing Still | Sedentary |
| A5 | Sitting Still | Sedentary |
| W4 | Walk (5 → 6) | Walking |
| W5 | Walk (6 → 1) | Walking |
| Features | Signal Used for Computation | Description | Domain | Formulas |
|---|---|---|---|---|
| mean_signal | All 6 Signals | Mean | Time | |
| std_signal | All 6 Signals | Standard deviation | Time | |
| var_signal | All 6 Signals | Variance | Time | |
| min_signal | All 6 Signals | Minimum | Time | |
| max_signal | All 6 Signals | Maximum | Time | |
| PD0_signal | All 6 Signals | Power at the first dominant frequency | Frequency | |
| F0_signal | All 6 Signals | First dominant frequency | Frequency | |
| PD2_signal | All 6 Signals | Power at the second dominant frequency | Frequency | |
| F2_signal | All 6 Signals | Second dominant frequency | Frequency | |
| CV_signal | All 6 Signals | Coefficient of variation | Time | |
| p75_signal | All 6 Signals | 75th percentile | Time | Let R be the 75th percentile rank: , p75 corresponds to the Rth value on the sorted X array |
| p25_signal | All 6 Signals | 25th percentile | Time | Let R be the 25th percentile rank: , p25 corresponds to the Rth value on the sorted X array |
| p85_signal | All 6 Signals | 85th percentile | Time | Let R be the 85th percentile rank: , p85 corresponds to the Rth value on the sorted X array |
| p15_signal | All 6 Signals | 15th percentile | Time | Let R be the 15th percentile rank: , p15 corresponds to the Rth value on the sorted X array |
| p95_signal | All 6 Signals | 95th percentile | Time | Let R be the 95th percentile rank: , p95 corresponds to the Rth value on the sorted X array |
| p5_signal | All 6 Signals | 5th percentile | Time | Let R be the 5th percentile rank: , p5 corresponds to the Rth value on the sorted X array |
| p75m_signal | All 6 Signals | 75th percentile at the middle of the signal (2/3 of the signal) | Time | Let R be the 75th percentile rank: , p75 corresponds to the Rth value on the sorted X array |
| p25m_signal | All 6 Signals | 25th percentile at the middle of the signal | Time | Let R be the 25th percentile rank: , p25 corresponds to the Rth value on the sorted X array |
| p85m_signal | All 6 Signals | 85th percentile at the middle of the signal | Time | Let R be the 85th percentile rank: , p85 corresponds to the Rth value on the sorted X array |
| p15m_signal | All 6 Signals | 15th percentile at the middle of the signal | Time | Let R be the 15th percentile rank: , p15 corresponds to the Rth value on the sorted X array |
| RMS_signal | All 6 Signals | Root mean Ssquare | Time | |
| P1_aCC | aCC | First peak of autocorrelation coefficients for craniocaudal acceleration | Time | , P1 is the first peak of ACF |
| P2_aCC | aCC | Second peak of autocorrelation coefficients for craniocaudal acceleration | Time | , P2 is the second peak of ACF |
| VM | All 6 Signals | Vector magnitude of all accelerations (craniocaudal aCC, mediolateral aML, and anteroposterior aAP) | Time |
| Categories | Features | Description | Mathematical Computation |
|---|---|---|---|
| Steadiness | The second peak of the autocorrelation coefficients calculated on craniocaudal accelerations via the Wiener–Khinchin theorem: the higher it is, the more similar the steps are. | , P1 is the first peak of ACF whereas P2 is the second peak | |
| Symmetry | The first peak of the autocorrelation coefficients calculated on craniocaudal accelerations via the Wiener–Khinchin theorem: the higher it is, the more similar the strides are. | P1 is the first peak of ACF whereas P2 is the second peak | |
| Sturdiness | Root mean square ratio on anteroposterior acceleration. The higher it is, the higher the sturdiness is. | , | |
| Stability | Root mean square ratio on mediolateral acceleration. The lower it is, the higher the stability is. | , |
| Type of Classifiers | Reported Performances | Performances on Our Data |
|---|---|---|
| Support Vector Machine SVM | 0.72 [47] | 0.88 ± 0.14 |
| 0.85 [14] | ||
| 0.74 [48] | ||
| Random Forest | 0.88 [49] | 0.85 ± 0.16 |
| 0.88 [50] | ||
| 0.86 [14] | ||
| Decision Tree | 0.82 [47] | 0.77 ± 0.17 |
| 0.83 [51] | ||
| 0.80 [14] | ||
| k Nearest Neighbors | 0.75 [47] | 0.89 ± 0.06 |
| 0.74 [49] | ||
| 0.68 [50] |
| Configurations |
|---|
| All the regime is used (normal configuration) |
| Only the first 3 s of the regime are used |
| Only the first 3.5 s of the regime are used |
| Only the first 4 s of the regime are used |
| Only the first 5 s of the regime are used |
| Only the first 40% of the regime is used |
| Only 40% of the regime is used (with start at 20% of the total duration) |
| Only 40% of the regime is used (with start at 30% of the total duration) |
| Only 40% of the regime is used (with start at 40% of the total duration) |
| Only the last 40% of the regime is used |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, S.; de l’Escalopier, N.; Oudre, L.; Truong, C.; Dorveaux, E.; Gorintin, L.; Ricard, D. A Machine Learning Pipeline for Gait Analysis in a Semi Free-Living Environment. Sensors 2023, 23, 4000. https://doi.org/10.3390/s23084000
Jung S, de l’Escalopier N, Oudre L, Truong C, Dorveaux E, Gorintin L, Ricard D. A Machine Learning Pipeline for Gait Analysis in a Semi Free-Living Environment. Sensors. 2023; 23(8):4000. https://doi.org/10.3390/s23084000
Chicago/Turabian StyleJung, Sylvain, Nicolas de l’Escalopier, Laurent Oudre, Charles Truong, Eric Dorveaux, Louis Gorintin, and Damien Ricard. 2023. "A Machine Learning Pipeline for Gait Analysis in a Semi Free-Living Environment" Sensors 23, no. 8: 4000. https://doi.org/10.3390/s23084000
APA StyleJung, S., de l’Escalopier, N., Oudre, L., Truong, C., Dorveaux, E., Gorintin, L., & Ricard, D. (2023). A Machine Learning Pipeline for Gait Analysis in a Semi Free-Living Environment. Sensors, 23(8), 4000. https://doi.org/10.3390/s23084000





