Structural Health Monitoring (SHM) Study of Polymer Matrix Composite (PMC) Materials Using Nonlinear Vibration Methods Based on Embedded Piezoelectric Transducers
Abstract
1. Introduction
2. Materials
2.1. PVDF Transducers and PMC Material
- Six plies of glass fibers 2/2 twill fabric (thickness 0.2 mm, from Gazechim Composites);
- An orthophthalic unsaturated polyester resin (pre-accelerated) Norester 822 for infusion (from Nord Composites), with a degassing pressure of –0.4 bar during 4 min and an injection pressure of –0.8 bar during the LRI;
- 1% wt. of methyl ethyl ketone peroxide (MEKP) ketanox B180 (from C.O.I.M s.p.a.).
2.2. PVDF Transducers and PMC Material
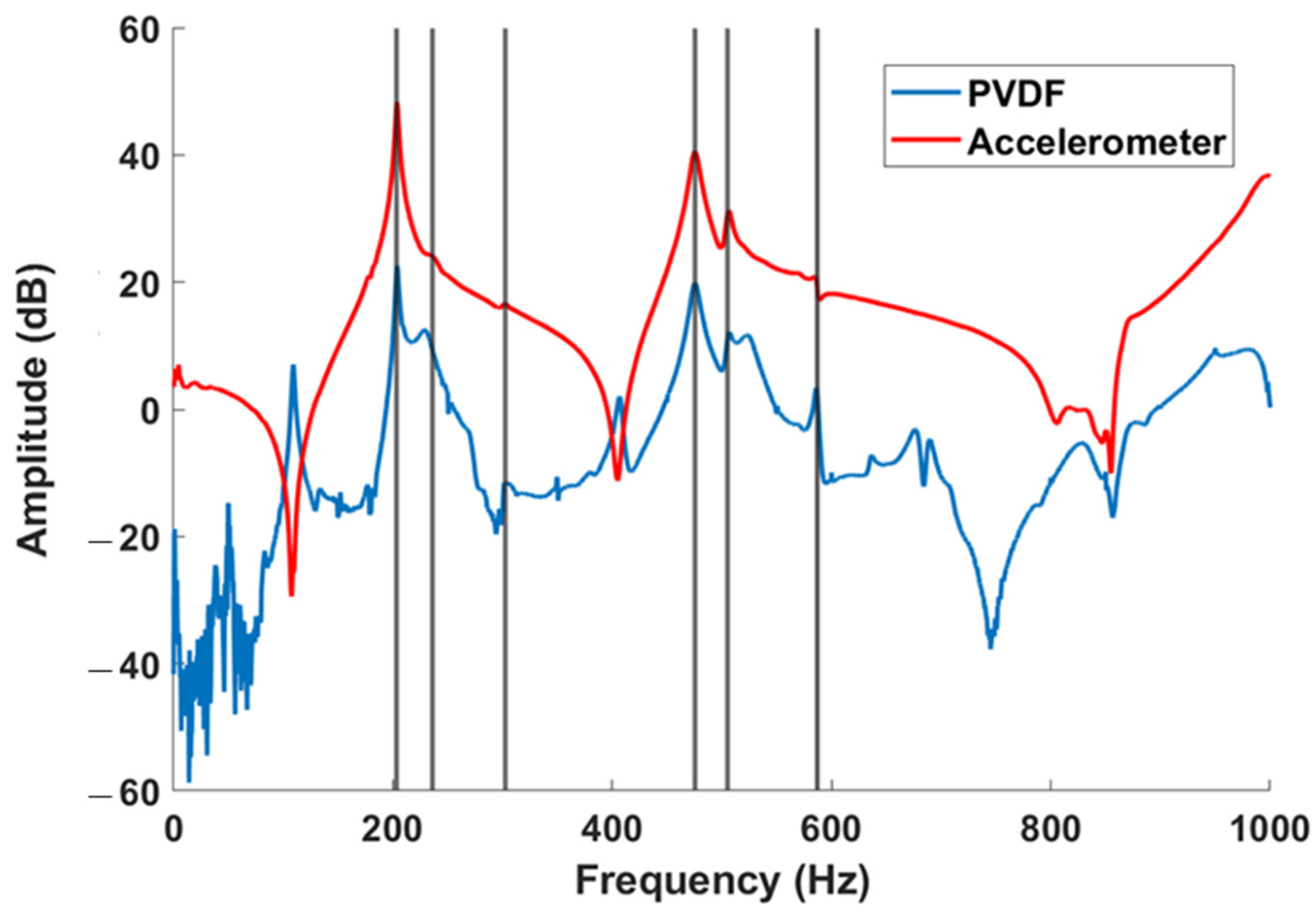
3. Experimental Vibration Setup
4. Nonlinear Methods
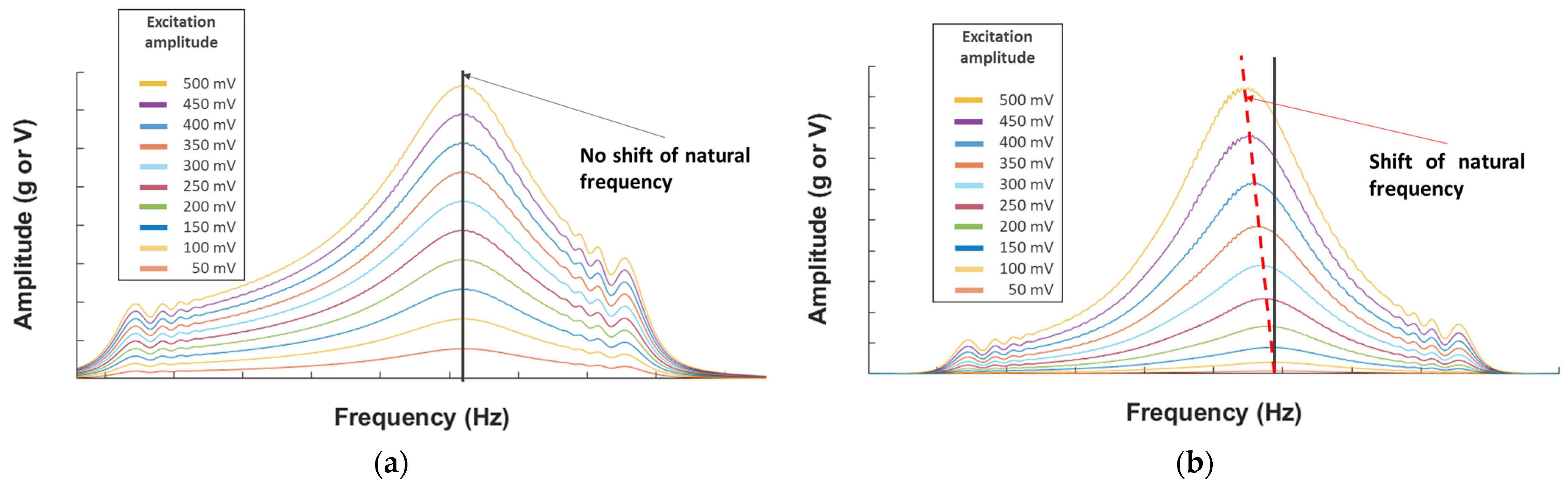
4.1. Nonlinear Resonance
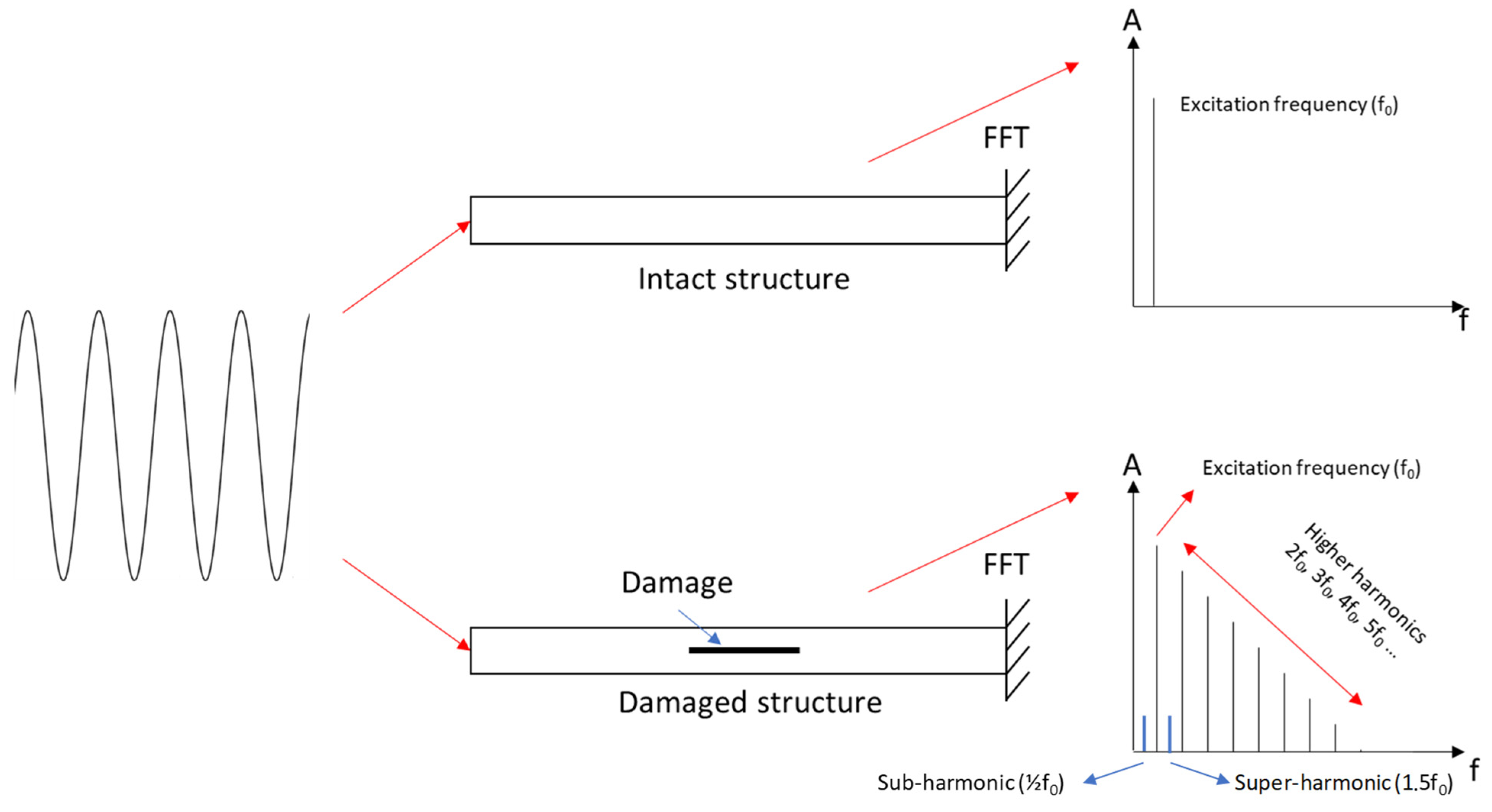
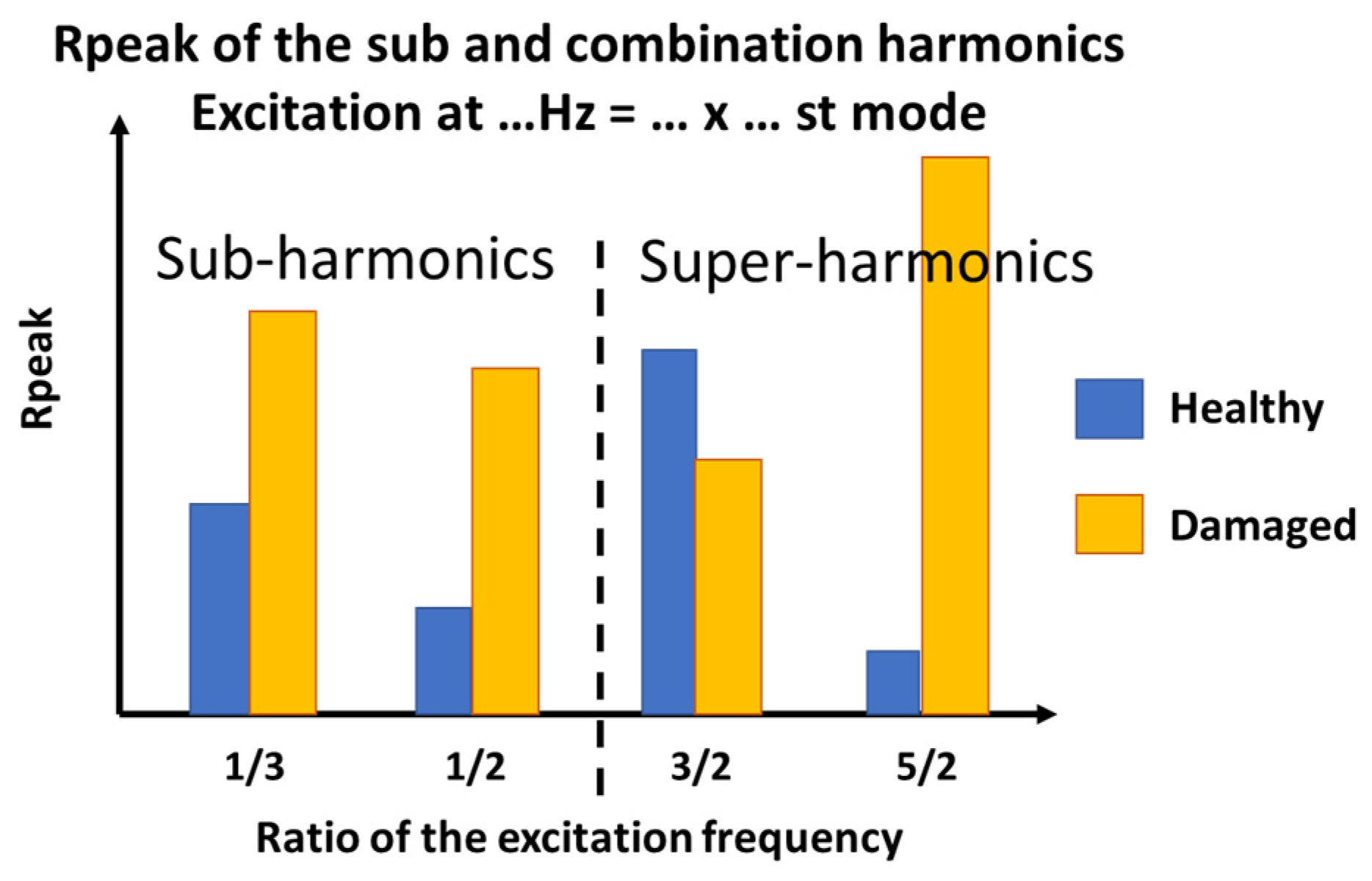
4.2. Sub- and Super-Harmonics Generation
4.3. Experimental Protocol
- Send a white noise at 0.5 V (out of amplifier) with a frequency range of 0–1200 Hz;
- Choose six natural frequencies from the FRF to investigate (this choice was made for the healthy plate regarding the results of PVDF and accelerometer in order to observe the best signals, and the same modes were used for the damaged plates);
- ○
- The modes around 105, 160, 420, 540, 720, and 840 Hz;
- ○
- These values are approximate, each plate and test has its own value (Table 2);
- Send a sweep signal with a frequency range of 40 Hz around the natural frequency excited and increase the amplitude of excitation 10 times (from 50 to 500 mV (out of amplifier));
- Send a harmonic signal corresponding to the frequency of the 1st, 2nd, and 4th modes of vibration (caught by the white noise) and their ratios 1/3, 1/2. The excitation level is 1 V (out of amplifier);
- ○
- Around [105, 52.5, 35] Hz, [160, 80, 53.33] Hz and [420, 210, 140] Hz;
- ○
- These values are approximate, each plate and test has its own value (Table 2);
5. Results and Discussion
5.1. Nonlinear Resonance
5.1.1. Manufactured Damaged Plates
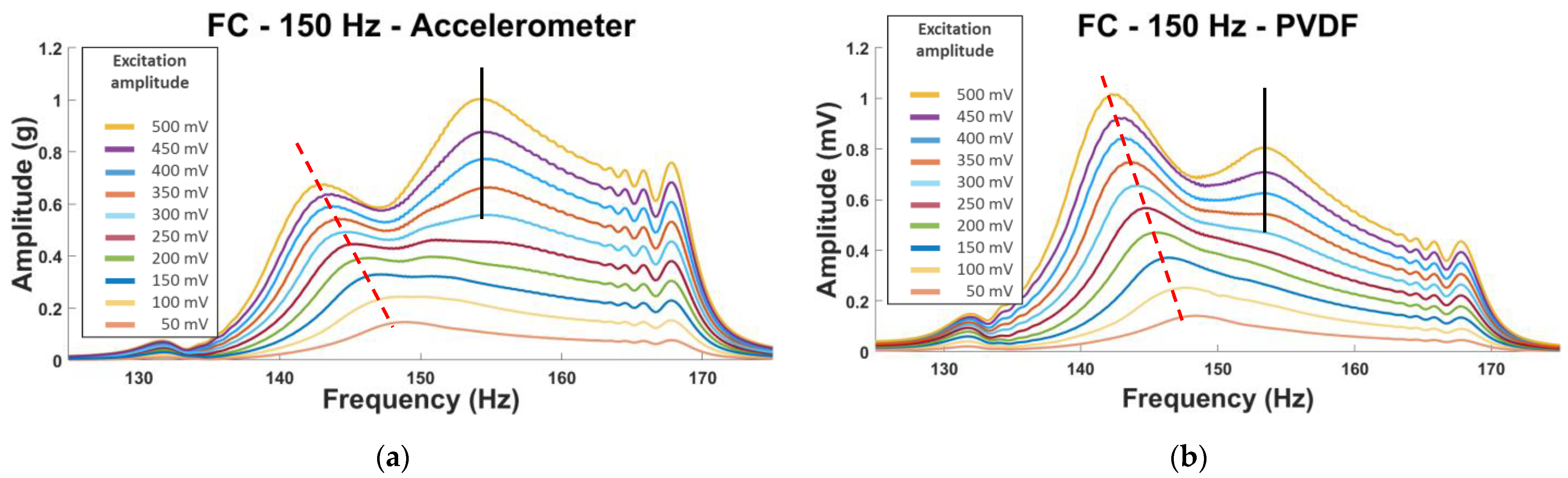
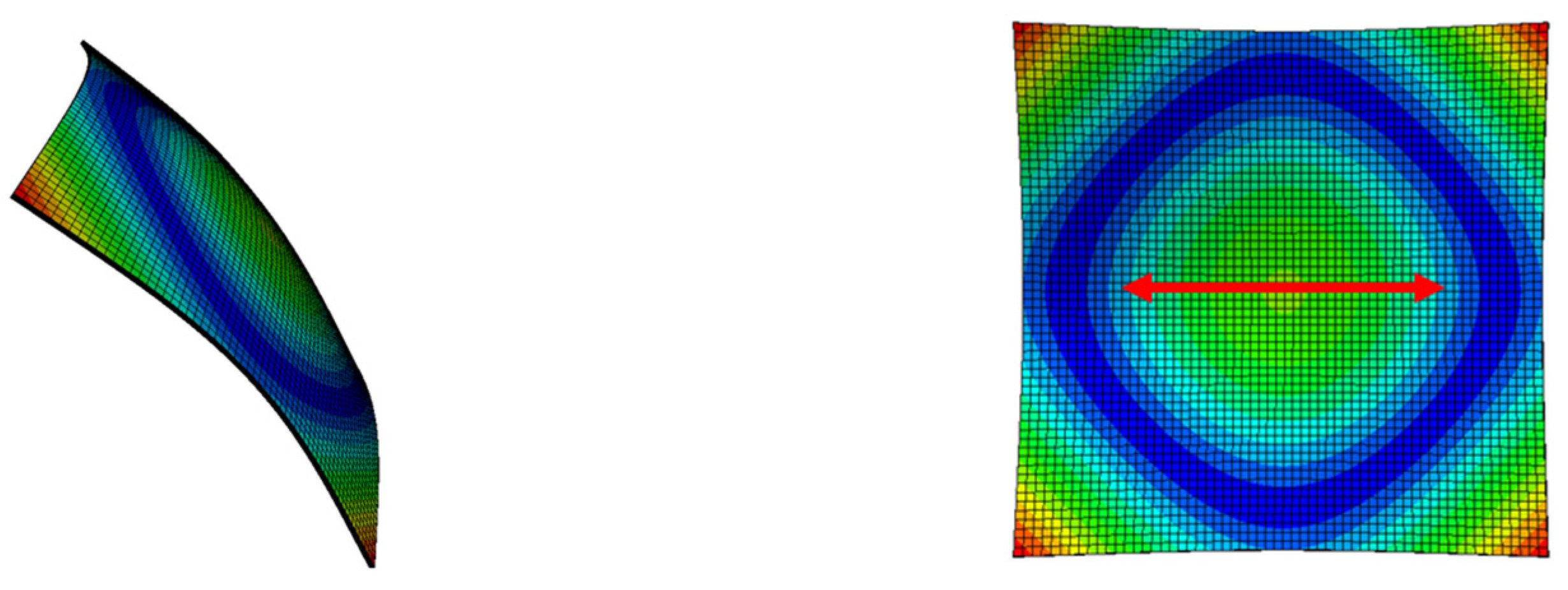
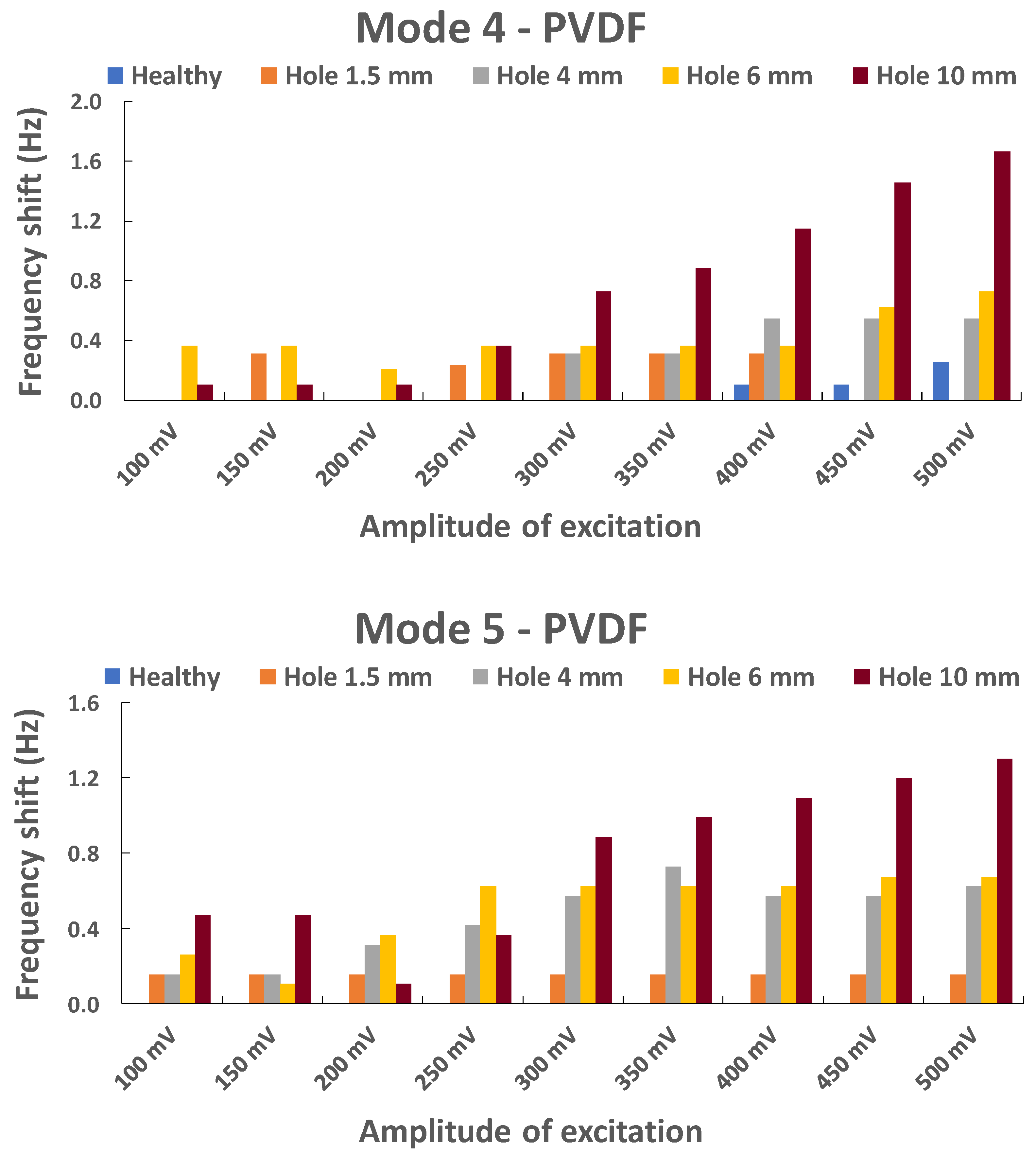
5.1.2. Plate with Holes
5.1.3. Summary of the NLR Method
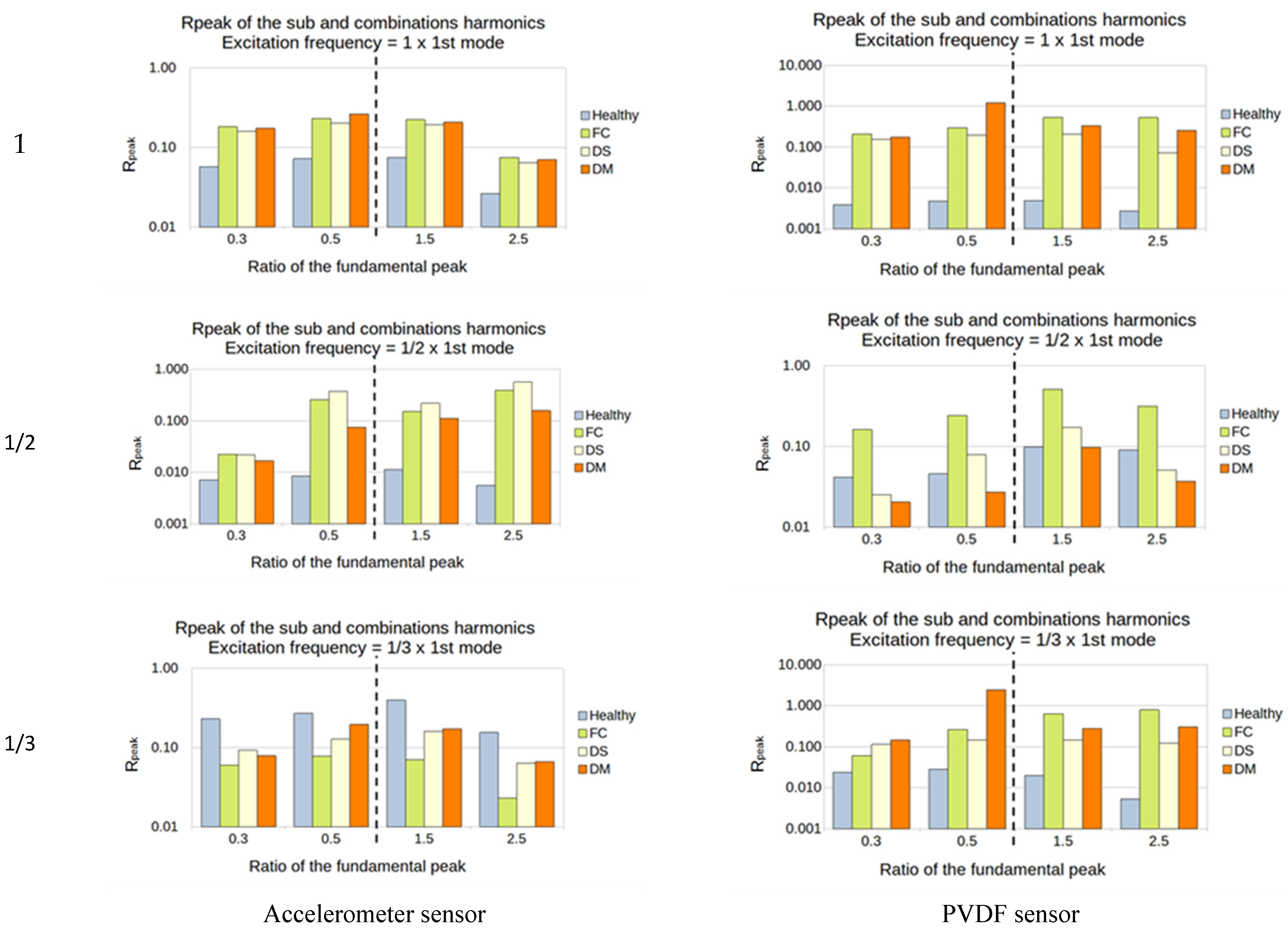
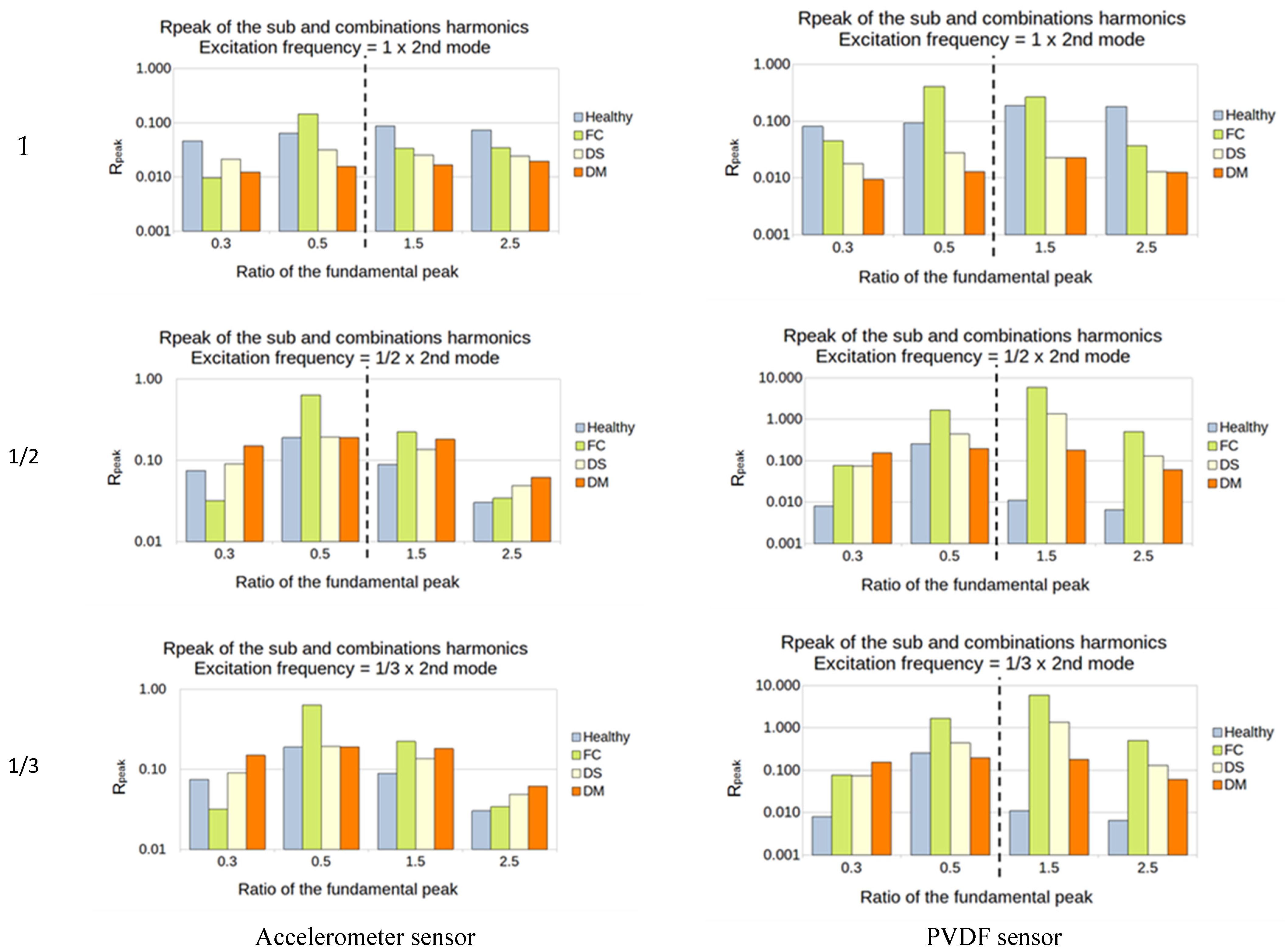
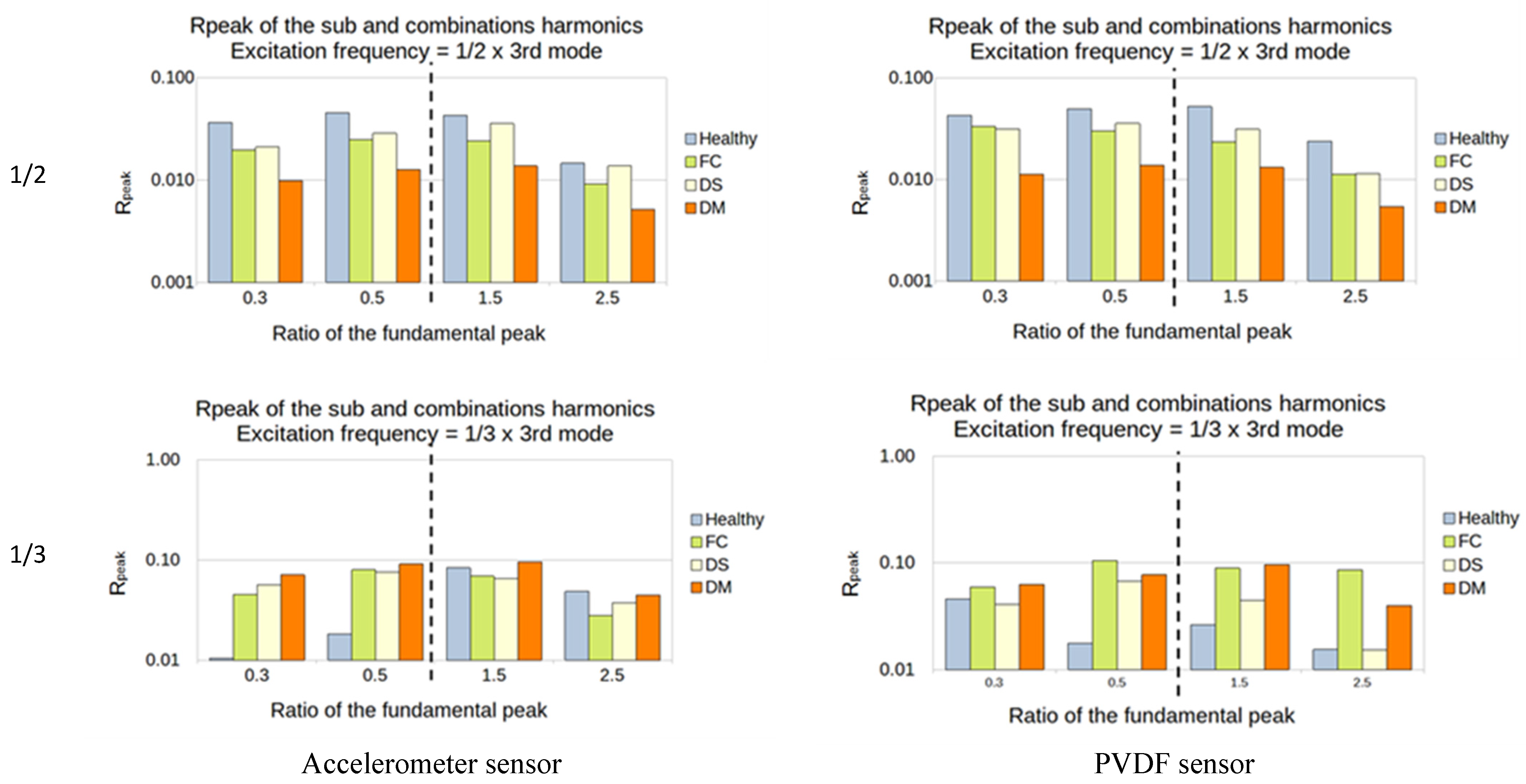
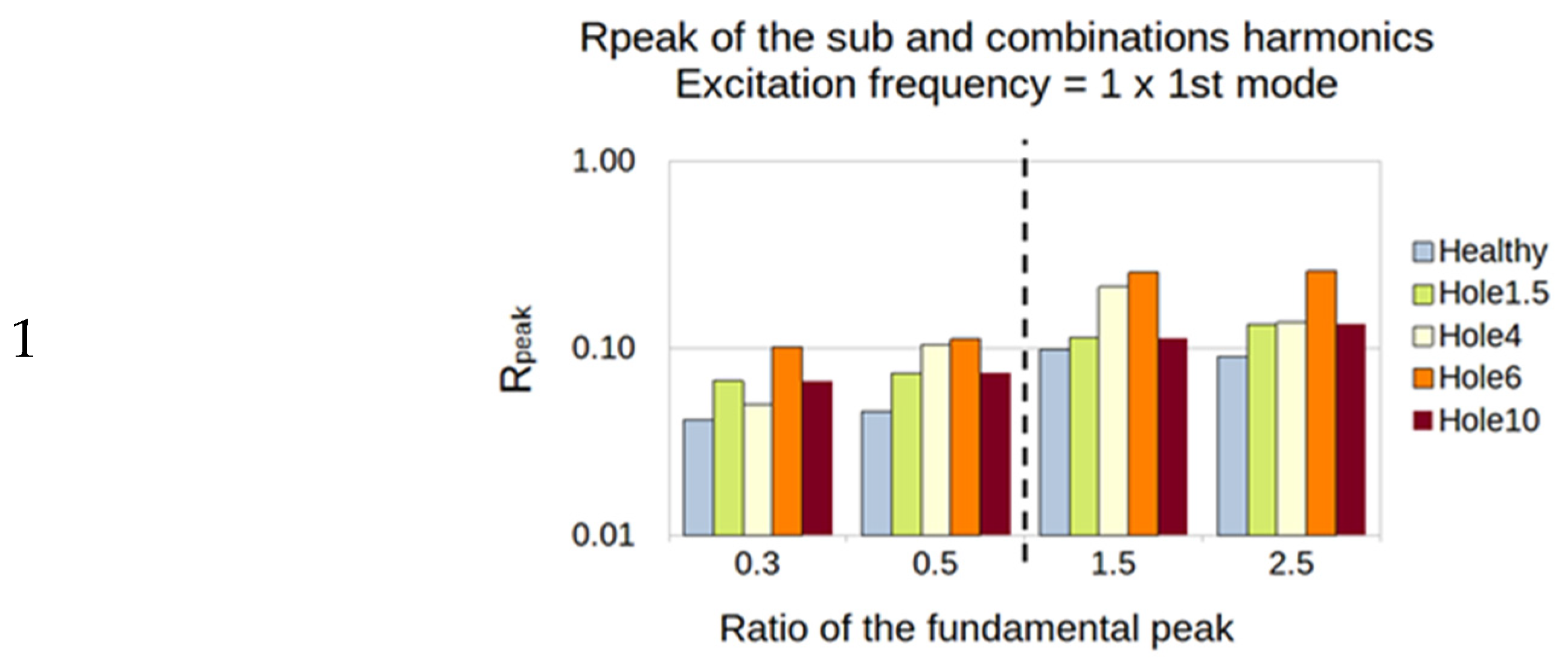
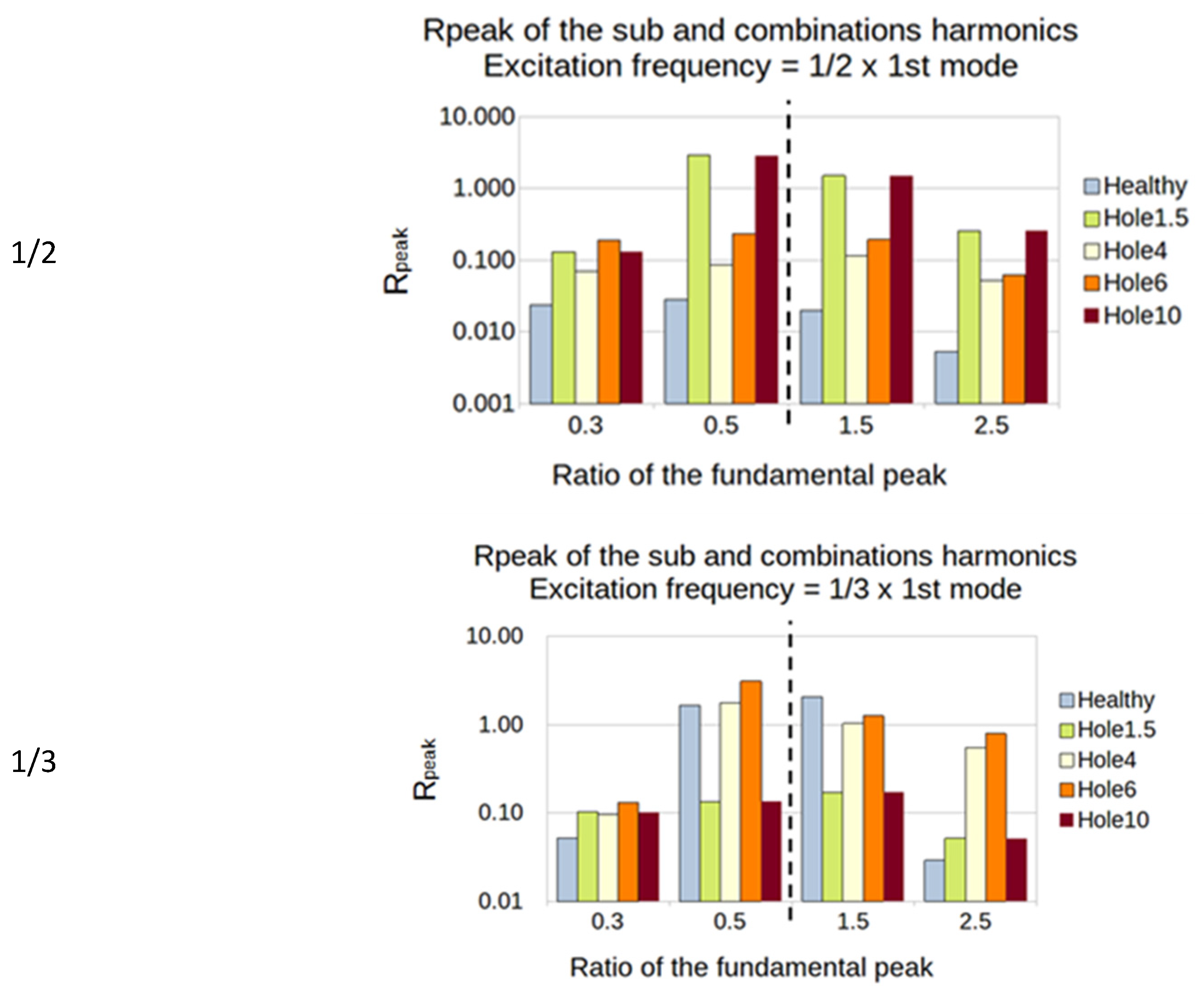
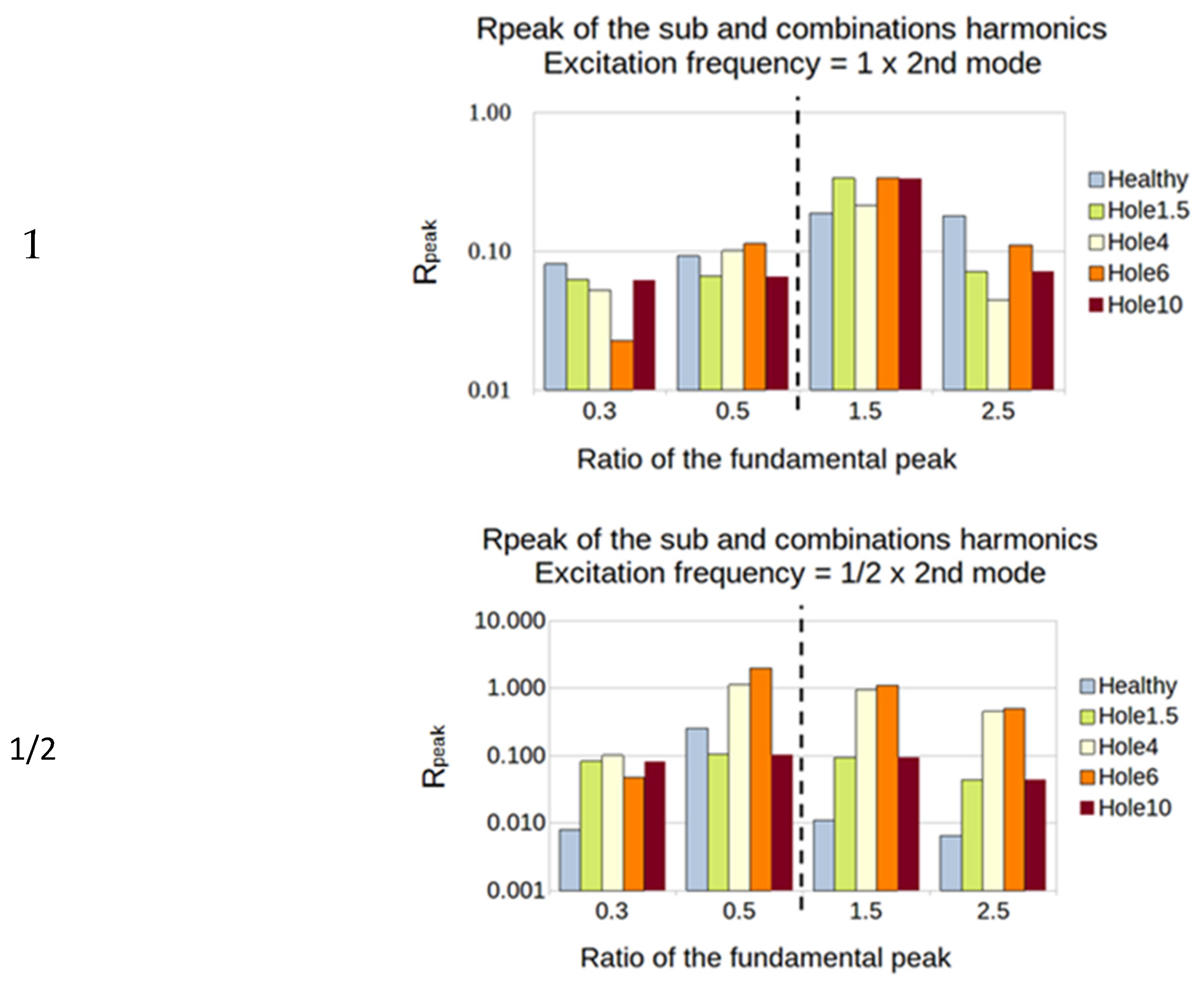
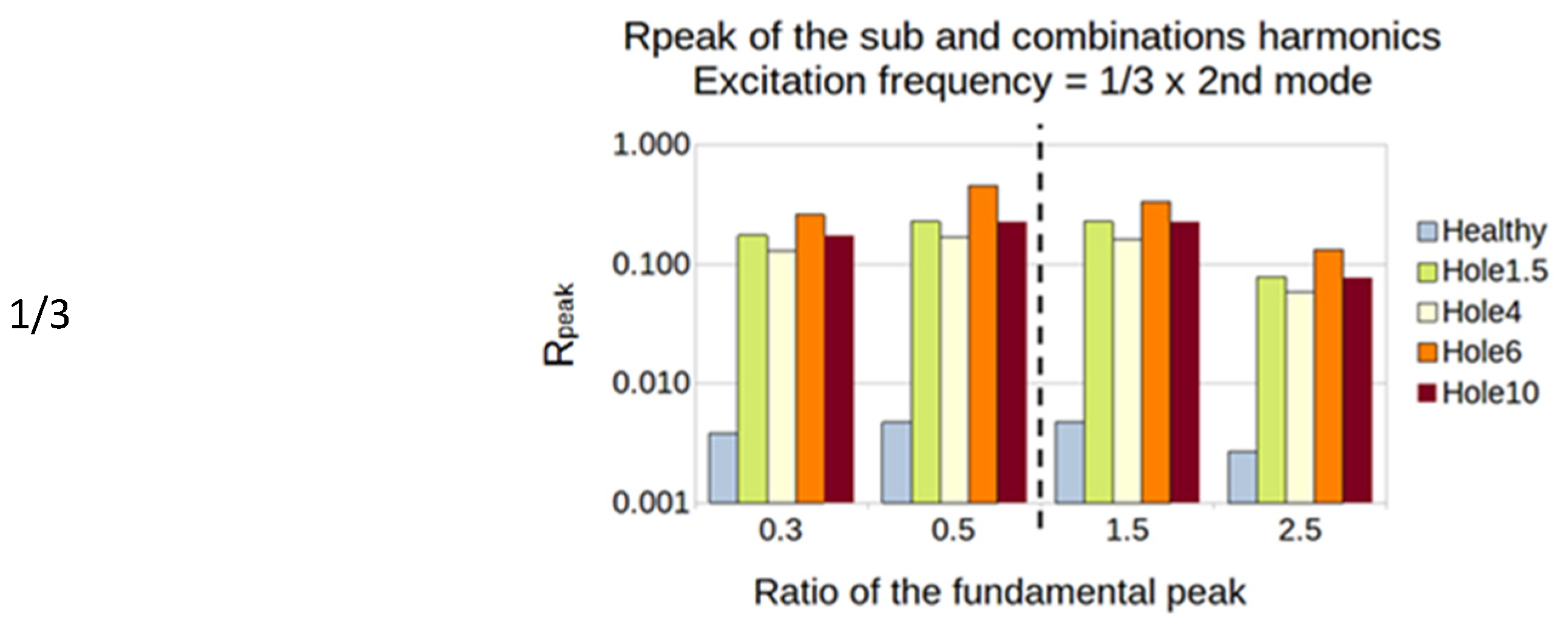
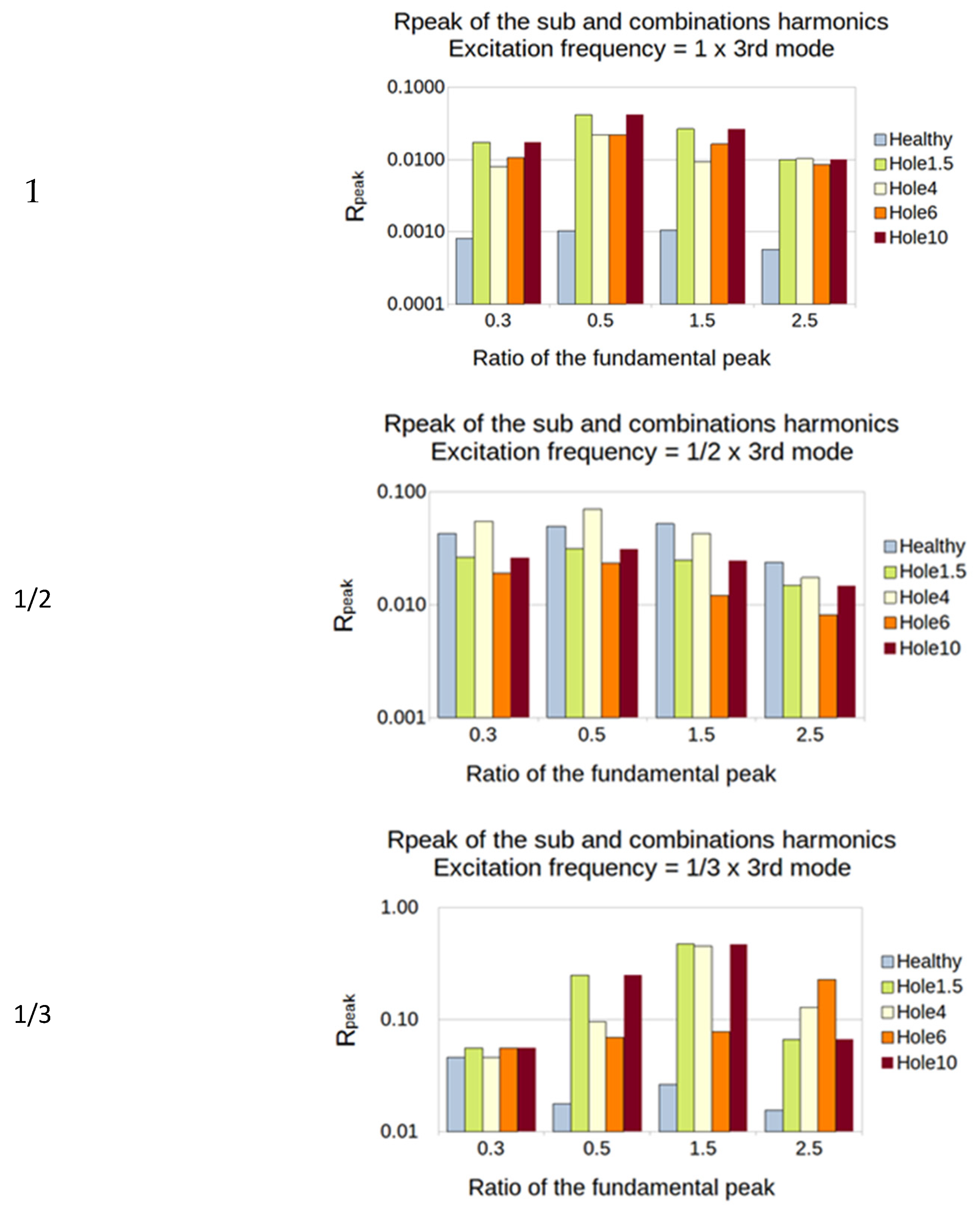
5.2. Sub- and Super-Harmonics Generation
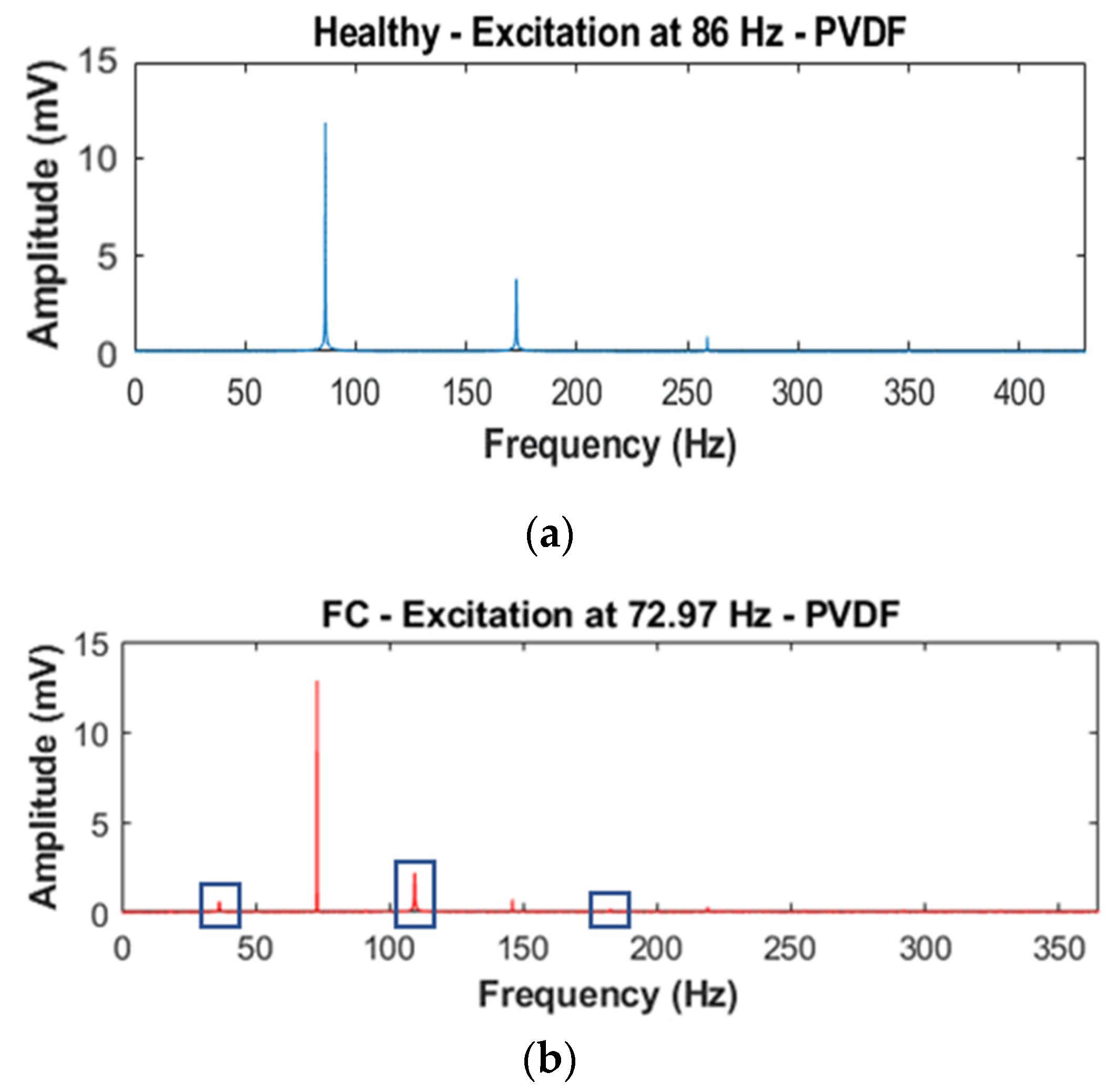
- The excitation frequency is 150 Hz = 1/2 × 3rd mode (the 3rd mode natural frequency is 300 Hz):
- The sub-harmonics (1/3 and 1/2): Rpeak is calculated from the amplitude of the output peaks at 75 and 50 Hz;
- The super-harmonics (1.5 and 2.5): Rpeak is calculated from the amplitude of the output peaks at 225 and 375 Hz;
5.2.1. Manufactured Damaged Plates
5.2.2. Plates with a Hole
5.2.3. Summary of the SFE Method
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Harizi, W. Characterization of Damage to Polymer Matrix Composites by a Non-Destructive Multi-Technique Approach. Ph.D. Thesis, Mines Douai et l’Université de Valenciennes et du Hainaut Cambresis, Douai, France, 2012. [Google Scholar]
- Harizi, W.; Chaki, S.; Bourse, G.; Ourak, M. Characterization of the Damage Mechanisms in Polymer Composite Materials by Ultrasonic Waves, Acoustic Emission and Infrared Thermography. In Proceedings of the ECCM15, Venise, Italy, 24–28 June 2012. [Google Scholar]
- Harizi, W.; Chaki, S.; Bourse, G.; Ourak, M. Mechanical damage characterization of glass fiber-reinforced polymer laminates by ultrasonic maps. Compos. Part B Eng. 2015, 70, 131–137. [Google Scholar] [CrossRef]
- Harizi, W.; Chaki, S.; Bourse, G.; Ourak, M. Mechanical damage assessment of Polymer–Matrix Composites using active infrared thermography. Compos. Part B Eng. 2014, 66, 204–209. [Google Scholar] [CrossRef]
- Al-Haik, M.; Hussaini, M.; Garmestani, H. Prediction of nonlinear viscoelastic behavior of polymeric composites using an artificial neural network. Int. J. Plast. 2006, 22, 1367–1392. [Google Scholar] [CrossRef]
- Sajan, S.; Selvaraj, D.P. A review on polymer matrix composite materials and their applications. Mater. Today Proc. 2021, 47, 5493–5498. [Google Scholar] [CrossRef]
- Jia, Z.; Li, T.; Chiang, F.-P.; Wang, L. An experimental investigation of the temperature effect on the mechanics of carbon fiber reinforced polymer composites. Compos. Sci. Technol. 2018, 154, 53–63. [Google Scholar] [CrossRef]
- Colombo, C.; Vergani, L.; Burman, M. Static and fatigue characterisation of new basalt fibre reinforced composites. Compos. Struct. 2012, 94, 1165–1174. [Google Scholar] [CrossRef]
- Reddy, M.I.; Raju, P.V.K.; Bhargava, N. Experimental Investigation on the Mechanical and Thermal Properties of Sprouts Center Stem (Asian Palmyra) Fiber Reinforced Polymer Composites. Mater. Today Proc. 2018, 5, 7808–7817. [Google Scholar] [CrossRef]
- Saba, N.; Jawaid, M. A review on thermomechanical properties of polymers and fibers reinforced polymer composites. J. Ind. Eng. Chem. 2018, 67, 1–11. [Google Scholar] [CrossRef]
- Harizi, W.; Aboura, Z.; Meyer, Y.; Tuloup, C. Structural Health Monitoring of Smart Polymer-Matrix Composite during Cyclic Loading Using an in-Situ Piezoelectric Sensor. In Proceedings of the 22nd International Conference on Composite Materials (ICCM22), Melbourne, Australia, 11–16 August 2019; pp. 872–878. [Google Scholar]
- Tuloup, C.; Harizi, W.; Aboura, Z.; Meyer, Y. Structural health monitoring of polymer-matrix composite using embedded piezoelectric ceramic transducers during several four-points bending tests. Smart Mater. Struct. 2020, 29, 125011. [Google Scholar] [CrossRef]
- Tuloup, C.; Harizi, W.; Aboura, Z.; Meyer, Y.; Khellil, K.; Lachat, R. On the use of in-situ piezoelectric sensors for the manufacturing and structural health monitoring of polymer-matrix composites: A literature review. Compos. Struct. 2019, 215, 127–149. [Google Scholar] [CrossRef]
- Harizi, W.; Tuloup, C.; Aboura, Z. Evaluation of the crosslinking steps of an unsaturated polyester resin during the infusion process of polymer-matrix composites using embedded PZT transducer. ESAFORM 2021 2021. [Google Scholar] [CrossRef]
- Harizi, W.; Aboura, Z.; Meyer, Y.; Tuloup, C. Real-Time Monitoring of the Infusion Process of a Polymer-Matrix Composite with an Embedded Piezoelectric Transducer. In Proceedings of the IX ECCOMAS Thematic Conference on Smart Structures and Materials, Paris, France, 8–11 July 2019. [Google Scholar]
- Tuloup, C.; Harizi, W.; Aboura, Z.; Meyer, Y.; Ade, B.; Khellil, K. Detection of the key steps during Liquid Resin Infusion manufacturing of a polymer-matrix composite using an in-situ piezoelectric sensor. Mater. Today Commun. 2020, 24, 101077. [Google Scholar] [CrossRef]
- Kim, S.; E Adams, D.; Sohn, H.; Rodriguez-Rivera, G.; Myrent, N.; Bond, R.; Vitek, J.; Carr, S.; Grama, A.; Meyer, J.J. Crack detection technique for operating wind turbine blades using Vibro-Acoustic Modulation. Struct. Heal. Monit. 2014, 13, 660–670. [Google Scholar] [CrossRef]
- Polimeno, U.; Meo, M. Detecting barely visible impact damage detection on aircraft composites structures. Compos. Struct. 2009, 91, 398–402. [Google Scholar] [CrossRef]
- Van Den Abeele, K.E.-A.; Johnson, P.A.; Sutin, A. Nonlinear Elastic Wave Spectroscopy (NEWS) Techniques to Discern Material Damage, Part I: Nonlinear Wave Modulation Spectroscopy (NWMS). Res. Nondestruct. Eval. 2000, 12, 17–30. [Google Scholar] [CrossRef]
- Polimeno, U.; Meo, M. Understanding the effect of boundary conditions on damage identification process when using non-linear elastic wave spectroscopy methods. Int. J. Non-linear Mech. 2008, 43, 187–193. [Google Scholar] [CrossRef]
- Polimeno, U.; Meo, M.; Almond, D. Smart Nonlinear Acoustic Based Structural Health Monitoring System. Adv. Sci. Technol. 2008, 56, 426–434. [Google Scholar] [CrossRef]
- Meo, M.; Polimeno, U.; Zumpano, G. Detecting Damage in Composite Material Using Nonlinear Elastic Wave Spectroscopy Methods. Appl. Compos. Mater. 2008, 15, 115–126. [Google Scholar] [CrossRef]
- Andreades, C.; Ciampa, F. CFRP Composites with Embedded PZT Transducers for Nonlinear Ultrasonic Inspection of Space Structures. In Proceedings of the EWSHM2018, Manchester, UK, 10–13 July 2018. [Google Scholar]
- Andreades, C.; Fierro, G.P.M.; Meo, M. A nonlinear ultrasonic SHM method for impact damage localisation in composite panels using a sparse array of piezoelectric PZT transducers. Ultrasonics 2020, 108, 106181. [Google Scholar] [CrossRef]
- Aymerich, F.; Staszewski, W.J. Impact Damage Detection in Composite Laminates Using Nonlinear Acoustics. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1084–1092. [Google Scholar] [CrossRef]
- Aymerich, F.; Staszewski, W. Experimental Study of Impact-Damage Detection in Composite Laminates using a Cross-Modulation Vibro-Acoustic Technique. Struct. Heal. Monit. 2010, 9, 541–553. [Google Scholar] [CrossRef]
- Loi, G.; Porcu, M.C.; Aymerich, F. Impact Damage Detection in Composite Beams by Analysis of Non-Linearity under Pulse Excitation. J. Compos. Sci. 2021, 5, 39. [Google Scholar] [CrossRef]
- Idriss, M.; El Mahi, A. Linear and nonlinear resonant techniques for characterizing cyclic fatigue damage in composite laminate. Compos. Part B Eng. 2018, 142, 36–46. [Google Scholar] [CrossRef]
- Idriss, M.; El Mahi, A.; El Guerjouma, R. Characterization of sandwich beams with debonding by linear and nonlinear vibration method. Compos. Struct. 2015, 120, 200–207. [Google Scholar] [CrossRef]
- Bentahar, M. Nonlinear Acoustics: Application to Ultrasonic Characterisation of Damage in Heterogeneous Materials and Remaining Life Determination. Ph.D. Thesis, INSA Lyon, Lyon, France, 2005. [Google Scholar]
- Bentahar, M.; El Guerjouma, R.; Monnier, T.; Deville, L. Slow and Fast Dynamics to Control Damage in Heterogeneous Materials: Application to Concrete and Glass/Fibre Polymer. J. Adv. Sci. 2005, 17, 70–75. [Google Scholar] [CrossRef]
- Hassani, S.; Mousavi, M.; Gandomi, A.H. Structural Health Monitoring in Composite Structures: A Comprehensive Review. Sensors 2021, 22, 153. [Google Scholar] [CrossRef]
- Bregar, T.; Starc, B.; Čepon, G.; Boltežar, M. On the Use of PVDF Sensors for Experimental Modal Analysis. In Proceedings of the Conference Proceedings of the Society for Experimental Mechanics Series, Munich, Germany, 14‒17 June 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 279–281. [Google Scholar]
- Guzmán, E.; Cugnoni, J.; Gmür, T. Monitoring of composite structures using a network of integrated PVDF film transducers. Smart Mater. Struct. 2015, 24. [Google Scholar] [CrossRef]
- Mahi, A.; Idriss, M.; Assarar, M.; Guerjouma, R.; Dazel, O. Effets de l’endommagement Sur Le Comportement Vibratoire Des Matériaux Sandwichs Endommagés. In Proceedings of the 19ème Congrès Français de Mécanique, Marseille, France, 24–28 August 2009. [Google Scholar]
- Long, H.; Liu, Y.; Liu, K. Nonlinear Vibration Analysis of a Beam with a Breathing Crack. Appl. Sci. 2019, 9, 3874. [Google Scholar] [CrossRef]
- Singh, A.K. Detection of Defects in Composite Laminates with Vibro-Ultrasonic Methods. Ph.D. Thesis, The National University of Singapore, Singapore, April 2019. [Google Scholar]
- Siemens Company Autopower Function. Available online: https://community.sw.siemens.com/s/article/the-autopower-function-demystified (accessed on 11 March 2022).

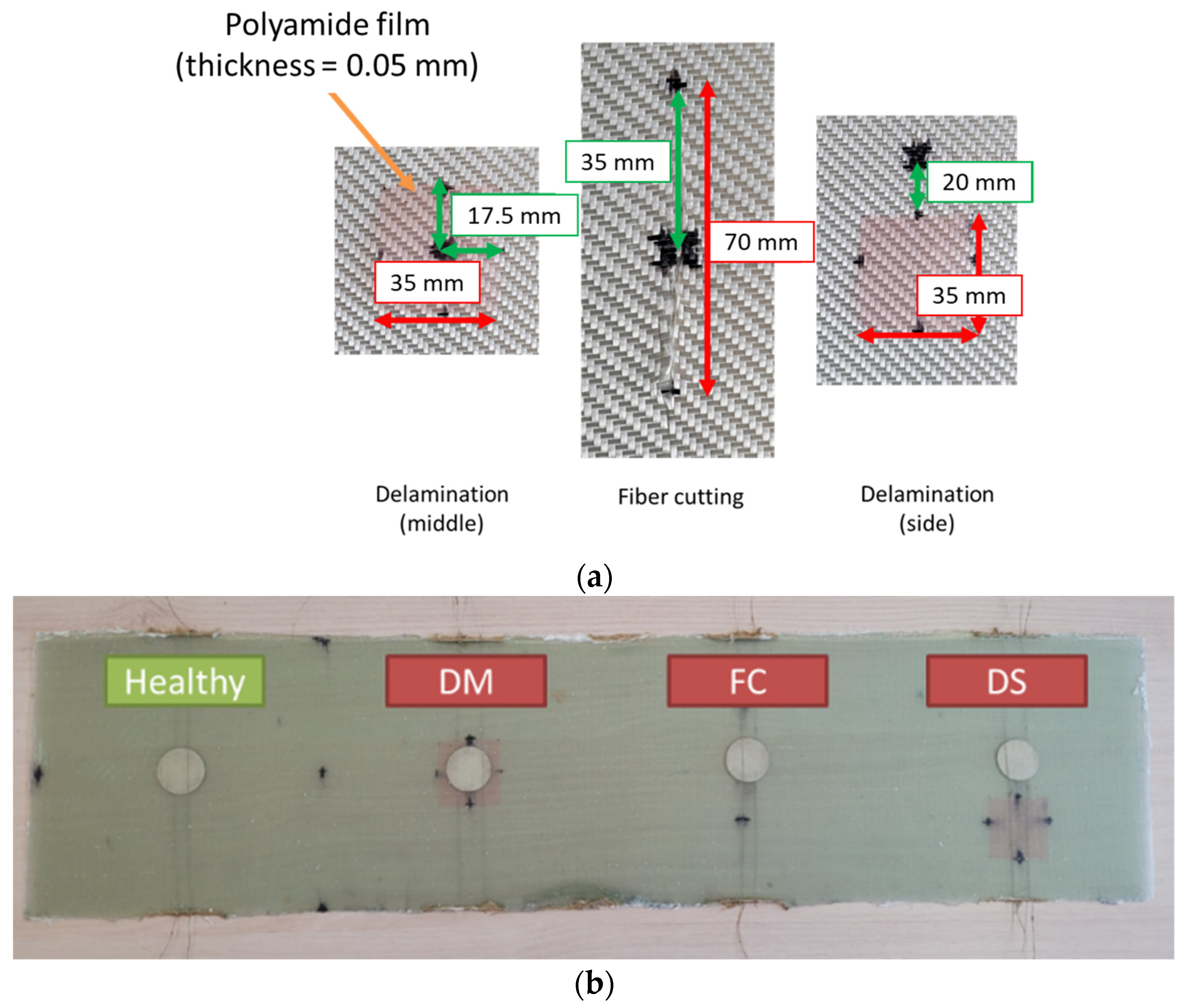






| Name | Description | |
|---|---|---|
| No damage | Healthy |
|
| LRI damaged | DM |
|
| DS |
| |
| FC |
| |
| Hole (mm) damaged | 1.5 |
|
| 4 |
| |
| 6 |
| |
| 10 |
|
| Sensor | Natural Frequency | Healthy | DM | DS | FC | Hole (Diameter mm) | |||
|---|---|---|---|---|---|---|---|---|---|
| 1.5 | 4 | 6 | 10 | ||||||
| Accelerometer | 1 | 107.7 | 108.5 | 115.8 | 107.8 | 106.6 | 106.1 | 104.9 | 105.4 |
| 2 | 169.7 | 167.8 | 169.5 | 151.7 | 165.0 | 155.2 | 158.9 | 158.3 | |
| 3 | 414.4 | 413.2 | 423.9 | 423.4 | 417.7 | 417.6 | 415.6 | 414.2 | |
| 4 | 537.2 | 533.8 | 555.6 | 541.6 | 544.1 | 540.4 | 535.3 | 532.8 | |
| 5 | 730.2 | 720.6 | 760.8 | 732.5 | 730.9 | 731.9 | 728.9 | 727.4 | |
| 6 | 841.7 | 824.5 | 860.1 | 806.6 | 833.6 | 825.1 | 825.5 | 823.3 | |
| PVDF | 1 | 108.4 | 111.5 | 118.6 | 111.5 | 109.6 | 108.4 | 107.4 | 107.3 |
| 2 | 168.2 | 170.1 | 168.2 | 153.2 | 165.8 | 158.6 | 162.1 | 161.6 | |
| 3 | 414.2 | 417.2 | 426.8 | 428.4 | 420.4 | 419.2 | 416.6 | 415.6 | |
| 4 | 535.4 | 532.9 | 556.5 | 542.3 | 546.7 | 542.7 | 537.5 | 534.0 | |
| 5 | 729.3 | 719.6 | 766.5 | 739.2 | 734.8 | 732.3 | 730.7 | 729.6 | |
| 6 | 839.0 | 825.3 | 867.0 | 806.7 | 837.2 | 827.1 | 826.9 | 825.8 | |
| Damage | Natural Frequency | |||||
|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | 5th | 6th | |
| FC | X | OO | X | X | O | X |
| DS | X | X | X | O | X | X |
| DM | X | X | X | O | X | O |
| Hole | X | O | O | OO | OO | O |
| Damage | 1st Frequency | 2nd Frequency | 3rd Frequency | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1/3 | 1/2 | 1 | 1/3 | 1/2 | 1 | 1/3 | 1/2 | 1 | |
| FC | OO | OO | OO | OO | OO | O | OO | X | OO |
| DS | OO | O | OO | OO | OO | X | O | X | OO |
| DM | OO | X | OO | OO | OO | X | OO | X | OO |
| Hole | X | OO | OO | OO | OO | X | OO | X | OO |
| Damage | 1st Frequency | 2nd Frequency | 3rd Frequency | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1/3 | 1/2 | 1 | 1/3 | 1/2 | 1 | 1/3 | 1/2 | 1 | |
| FC | X | O | O | O | O | X | O | X | X |
| DS | X | O | O | O | O | X | O | X | X |
| DM | X | O | O | O | O | X | O | X | X |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dolbachian, L.; Harizi, W.; Aboura, Z. Structural Health Monitoring (SHM) Study of Polymer Matrix Composite (PMC) Materials Using Nonlinear Vibration Methods Based on Embedded Piezoelectric Transducers. Sensors 2023, 23, 3677. https://doi.org/10.3390/s23073677
Dolbachian L, Harizi W, Aboura Z. Structural Health Monitoring (SHM) Study of Polymer Matrix Composite (PMC) Materials Using Nonlinear Vibration Methods Based on Embedded Piezoelectric Transducers. Sensors. 2023; 23(7):3677. https://doi.org/10.3390/s23073677
Chicago/Turabian StyleDolbachian, Loan, Walid Harizi, and Zoheir Aboura. 2023. "Structural Health Monitoring (SHM) Study of Polymer Matrix Composite (PMC) Materials Using Nonlinear Vibration Methods Based on Embedded Piezoelectric Transducers" Sensors 23, no. 7: 3677. https://doi.org/10.3390/s23073677
APA StyleDolbachian, L., Harizi, W., & Aboura, Z. (2023). Structural Health Monitoring (SHM) Study of Polymer Matrix Composite (PMC) Materials Using Nonlinear Vibration Methods Based on Embedded Piezoelectric Transducers. Sensors, 23(7), 3677. https://doi.org/10.3390/s23073677







