Optimizing Cardiac Wireless Implant Communication: A Feasibility Study on Selecting the Frequency and Matching Medium
Abstract
1. Introduction
2. Materials and Methods
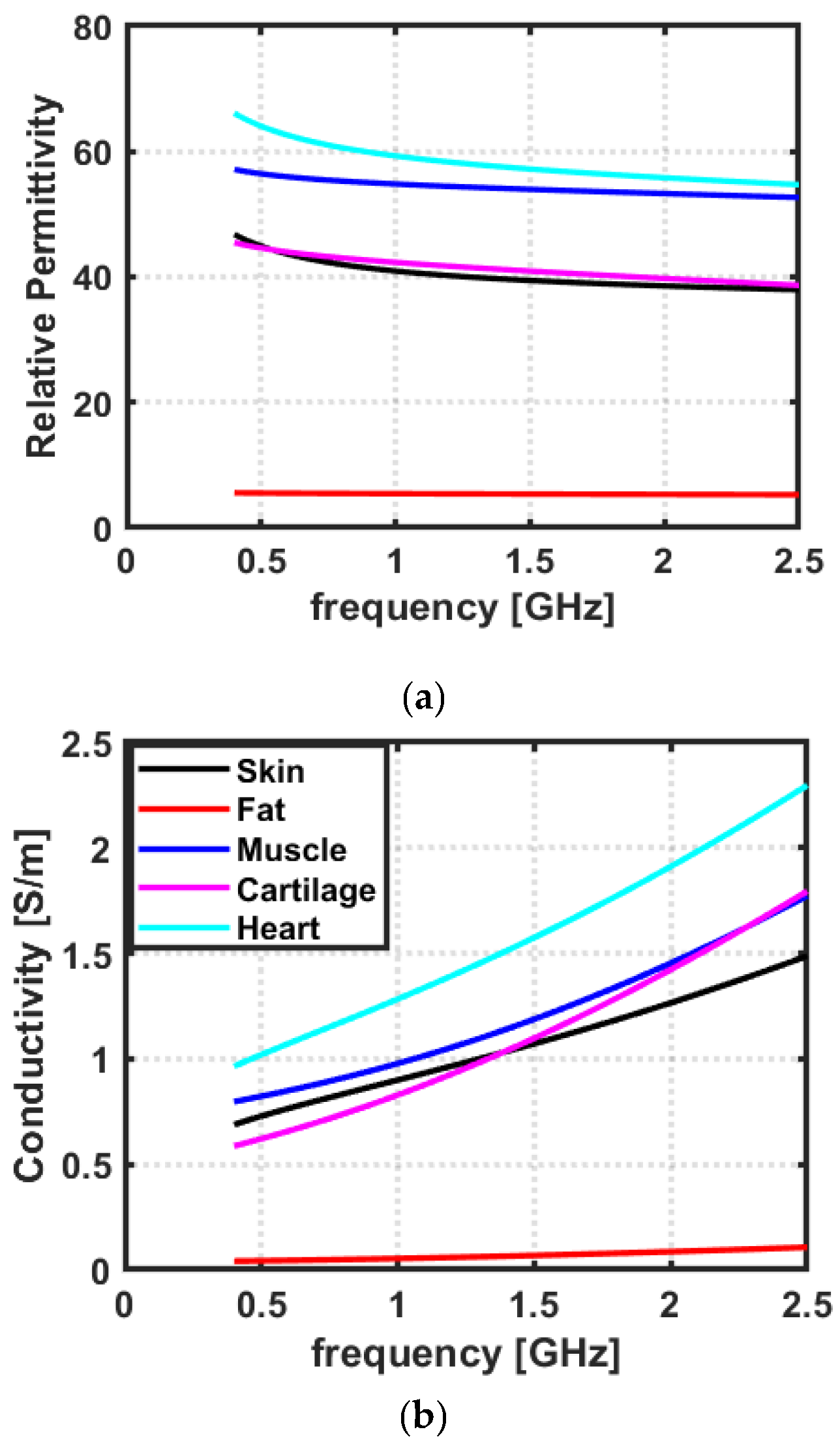
2.1. Dielectric Properties of Biological Tissues
2.2. Penetration Depth of EM Waves in Biological Tissues
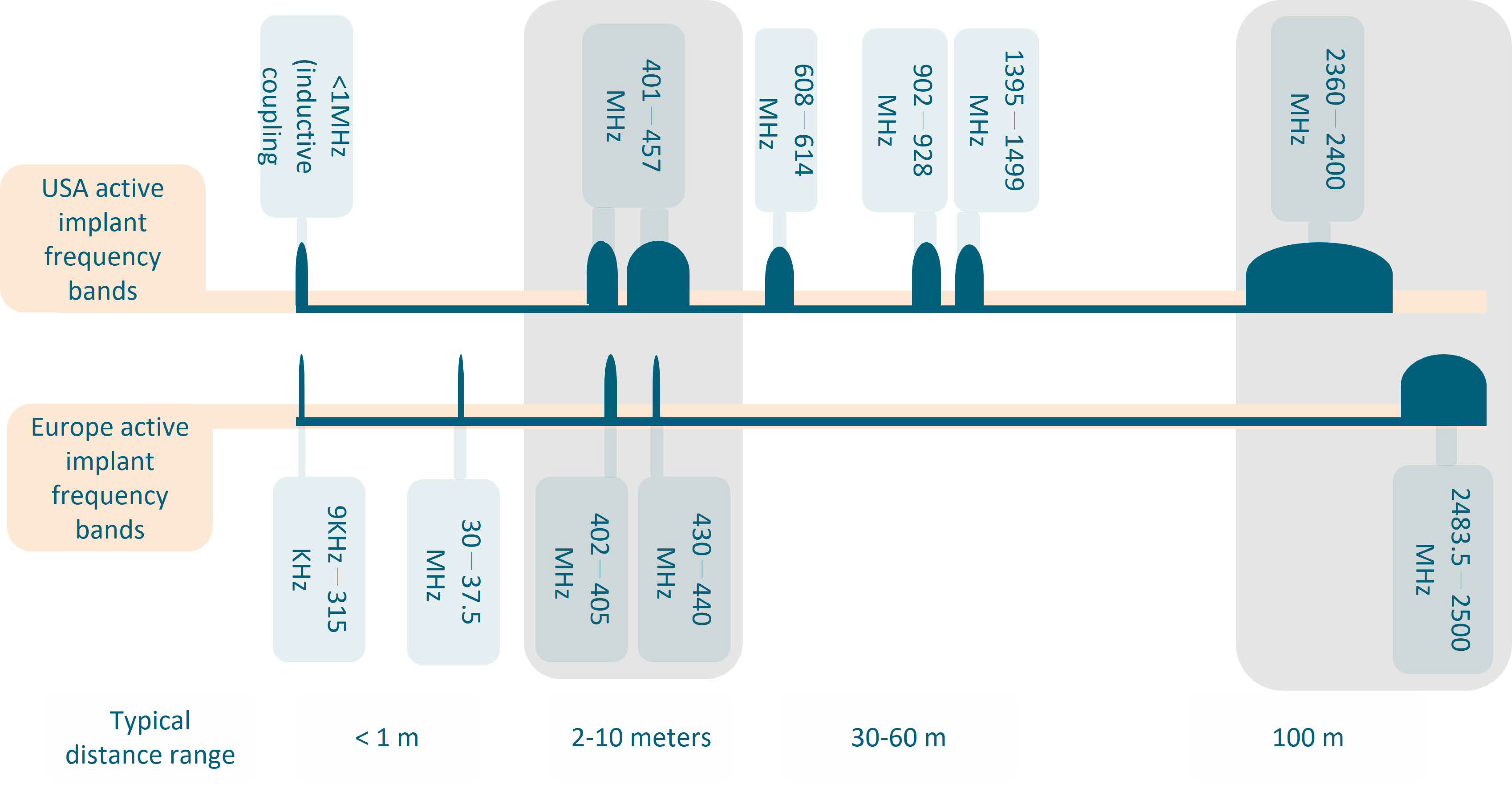
2.3. Choice of Frequency and the Matching Medium
- The first objective is to transfer the maximum power of the incident EM wave to the target tissue, which is the heart in our case;
- The second objective is to achieve the maximum spatial resolution, which is dictated by the wavelength in the matching medium, i.e., the medium where the transmitting/receiving antennas are located [29].
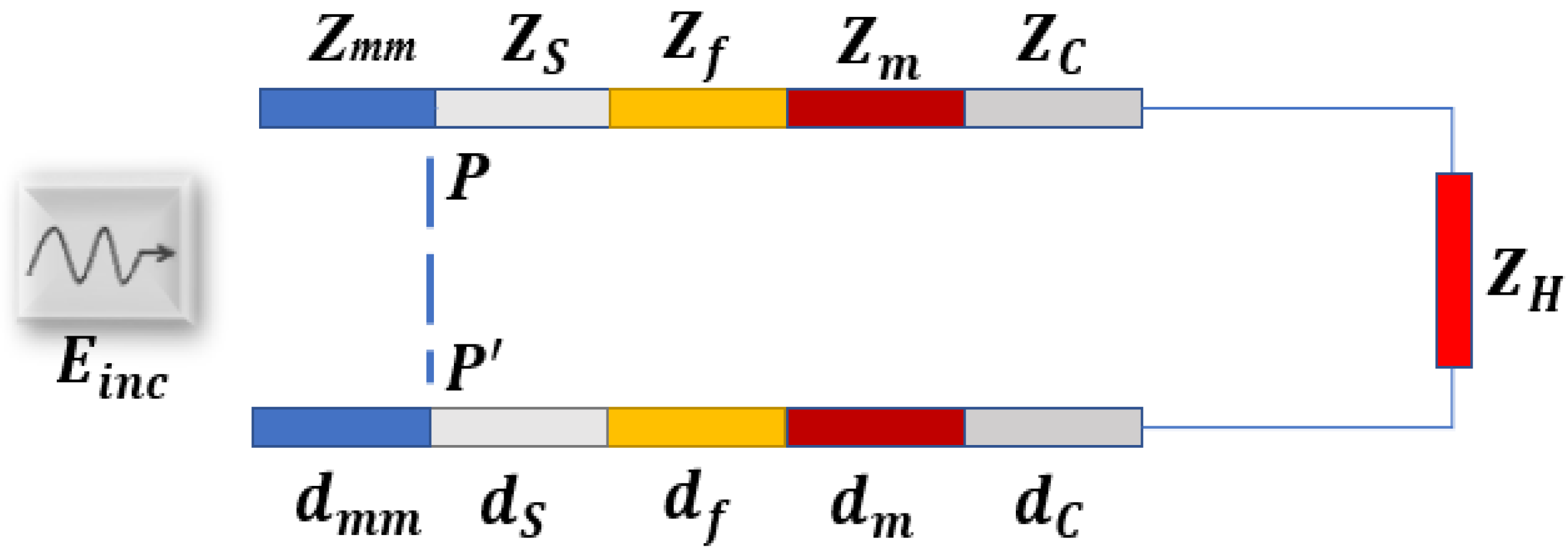
2.3.1. Planar Layered Model
2.4. Experimental Setup for Distance and Signal Quality Measurement for Cardiac Implants
2.5. Liquid Bio-Phantom Preparation
3. Results and Discussion
3.1. Dielectric Properties of Biological Tissues
3.2. Penetration Depth of EM Waves in Biological Tissues
3.3. Choice of Frequency and the Matching Medium (Transmission Line Analysis)
3.4. Liquid Bio-Phantom
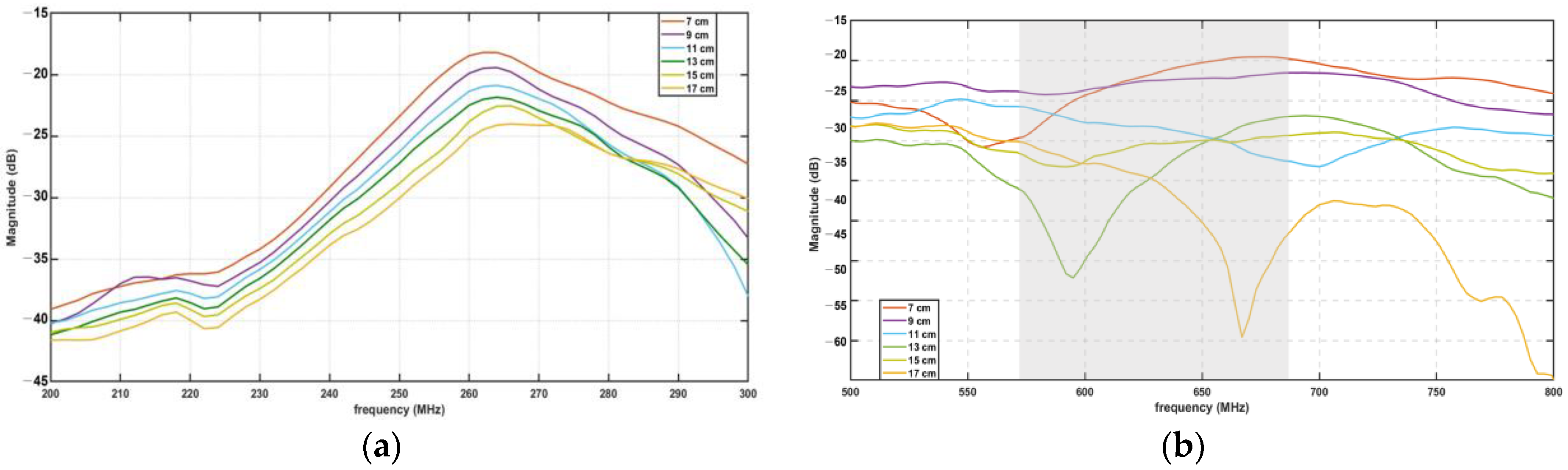
3.5. Experimental Findings for Distance and Signal Quality Measurement for Cardiac Implants
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Timmis, A.; Townsend, N.; Gale, C.P.; Torbica, A.; Lettino, M.; Petersen, S.E.; Mossialos, E.A.; Maggioni, A.P.; Kazakiewicz, D.; May, H.T.; et al. European Society of Cardiology: Cardiovascular disease statistics 2019. Eur. Heart J. 2020, 41, 12–85. [Google Scholar] [CrossRef]
- Roth, G.A.; Mensah, G.A.; Johnson, C.O.; Addolorato, G.; Ammirati, E.; Baddour, L.M.; Barengo, N.C.; Beaton, A.Z.; Benjamin, E.J.; Benziger, C.P.; et al. Global burden of cardiovascular diseases and risk factors, 1990–2019: Update from the GBD 2019 study. J. Am. Coll. Cardiol. 2020, 76, 2982–3021. [Google Scholar] [CrossRef] [PubMed]
- Cox-Pridmore, D.M.; Castro, F.A.; Silva, S.R.P.; Camelliti, P.; Zhao, Y. Emerging Bioelectronic Strategies for Cardiovascular Tissue Engineering and Implantation. Small 2022, 18, 2105281. [Google Scholar] [CrossRef]
- Walsh, P.; Kodoth, V.; McEneaney, D.; Rodrigues, P.; Velasquez, J.; Waterman, N.; Escalona, O. Towards low energy atrial defibrillation. Sensors 2015, 15, 22378–22400. [Google Scholar] [CrossRef]
- Nelson, S.; Whitsel, L.; Khavjou, O.; Phelps, D.; Leib, A. Projections of Cardiovascular Disease Prevalence and Costs; RTI International Research: Triangle Park, NC, USA, 2016; p. 214680. [Google Scholar]
- Santos, J.V.; Vandenberghe, D.; Lobo, M.; Freitas, A. Cost of cardiovascular disease prevention: Towards economic evaluations in prevention programs. Ann. Transl. Med. 2020, 8, 512. [Google Scholar] [CrossRef]
- Anwar, U.; Ajijola, O.A.; Shivkumar, K.; Marković, D. Towards a Leadless Wirelessly Controlled Intravenous Cardiac Pacemaker. IEEE Trans. Biomed. Eng. 2022, 69, 3074–3086. [Google Scholar] [CrossRef] [PubMed]
- Foo, F.S.; Stiles, M.K.; Lee, M.; Looi, K.L.; Clare, G.C.; Webber, M.; Boddington, D.; Jackson, R.; Poppe, K.K.; Kerr, A.J. Ten-year trends in cardiac implantable electronic devices in New Zealand: A national data linkage study (ANZACS-QI 51). Intern. Med. J. 2022, 52, 614–622. [Google Scholar] [CrossRef] [PubMed]
- Bose, P.; Khaleghi, A.; Balasingham, I. In-body and off-body channel modeling for future leadless cardiac pacemakers based on phantom and animal experiments. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 2484–2488. [Google Scholar] [CrossRef]
- Yu, Z.; Chen, J.C.; He, Y.; Alrashdan, F.T.; Avants, B.W.; Singer, A.; Robinson, J.T.; Yang, K. Magnetoelectric bio-implants powered and programmed by a single transmitter for coordinated multisite stimulation. IEEE J. Solid-State Circuits 2021, 57, 818–830. [Google Scholar] [CrossRef]
- Moncion, C.; Balachandar, L.; Bojja-Venkatakrishnan, S.; Riera, J.J.; Volakis, J.L. Fully-passive wireless implant for neuropotential acquisition: An In Vivo validation. IEEE J. Electromagn. RF Microw. Med. Biol. 2019, 3, 199–205. [Google Scholar] [CrossRef]
- Griffiths, S.; Behar, J.M.; Kramer, D.B.; Debney, M.T.; Monkhouse, C.; Lefas, A.Y.; Lowe, M.; Amin, F.; Cantor, E.; Boyalla, V.; et al. The long-term outcomes of cardiac implantable electronic devices implanted via the femoral route. Pacing Clin. Electrophysiol. 2022, 45, 481–490. [Google Scholar] [CrossRef] [PubMed]
- Niedermeier, A.; Vitali-Serdoz, L.; Fischlein, T.; Kirste, W.; Walaschek, J.; Rittger, H.; Bastian, D. Perioperative Sensor and Algorithm Programming in Patients with Implanted ICDs and Pacemakers for Cardiac Resynchronization Therapy. Sensors 2021, 21, 8346. [Google Scholar] [CrossRef] [PubMed]
- Yacoub, M.H.; McLeod, C. The expanding role of implantable devices to monitor heart failure and pulmonary hypertension. Nat. Rev. Cardiol. 2018, 15, 770–779. [Google Scholar] [CrossRef]
- Amin, B.; Shahzad, A.; Crocco, L.; Wang, M.; O’Halloran, M.; González-Suárez, A.; Elahi, M.A. A feasibility study on microwave imaging of bone for osteoporosis monitoring. Med. Biol. Eng. Comput. 2021, 59, 925–936. [Google Scholar] [CrossRef]
- Fang, X.; Ramzan, M.; Wang, Q.; Neumann, N.; Du, X.; Plettemeier, D. Path loss models for wireless cardiac RF communication. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 893–897. [Google Scholar]
- Khaleghi, A.; Balasingham, I. On selecting the frequency for wireless implant communications. In 2015 Loughborough Antennas & Propagation Conference (LAPC); IEEE: Piscataway, NJ, USA, 2015; pp. 1–4. [Google Scholar]
- Chow, E.Y.; Morris, M.M.; Irazoqui, P.P. Implantable RF medical devices: The benefits of high-speed communication and much greater communication distances in biomedical applications. IEEE Microw. Mag. 2013, 14, 64–73. [Google Scholar] [CrossRef]
- Soliman, M.M.; Chowdhury, M.E.H.; Khandakar, A.; Islam, M.T.; Qiblawey, Y.; Musharavati, F.; Nezhad, E.Z. Review on medical implantable antenna technology and imminent research challenges. Sensors 2021, 21, 3163. [Google Scholar]
- Murphy, O.H.; Mcleod, C.N.; Navaratnarajah, M.; Yacoub, M.; Toumazou, C. A Pseudo-Normal-Mode Helical Antenna for Use With Deeply Implanted Wireless Sensors. IEEE Trans. Antennas Propag. 2012; 60, 1135–1139. [Google Scholar]
- Poon, A.S.Y.; O′Driscoll, S.; Meng, T.H. Optimal Frequency for Wireless Power Transmission Into Dispersive Tissue. IEEE Trans. Antennas Propag. 2010, 58, 1739–1750. [Google Scholar] [CrossRef]
- Ho, J.S.; Yeh, A.J.; Neofytou, E.; Kim, S.; Tanabe, Y.; Patlolla, B.; Beygui, R.E.; Poon, A.S.Y. Wireless power transfer to deep-tissue microimplants. Proc. Natl. Acad. Sci. USA 2014, 111, 7974–7979. [Google Scholar] [CrossRef]
- Kim, S.; Ho, J.; Poon, A.S.Y. Midfield Wireless Powering of Subwavelength Autonomous Devices. Phys. Rev. Lett. 2013, 110, 203905. [Google Scholar] [CrossRef]
- Bose, P.; Khaleghi, A.; Albatat, M.; Bergsland, J.; Balasingham, I. RF Channel Modeling for Implant-to-Implant Communication and Implant to Subcutaneous Implant Communication for Future Leadless Cardiac Pacemakers. IEEE Trans. Biomed. Eng. 2018, 65, 2798–2807. [Google Scholar] [CrossRef]
- Gabriel, C.; Gabriel, S.; Corthout, E. The dielectric properties of biological tissues: I. Literature survey. Phys. Med. Biol. Phys. Med. Biol. 1996, 41, 2231–2249. [Google Scholar] [CrossRef] [PubMed]
- Amin, B.; Shahzad, A.; O’Halloran, M.; Elahi, M.A. Microwave Bone Imaging: A Preliminary Investigation on Numerical Bone Phantoms for Bone Health Monitoring. Sensors 2020, 20, 6320. [Google Scholar] [CrossRef] [PubMed]
- Gasperini, D.; Costa, F.; Daniel, L.; Manara, G.; Genovesi, S. Matching Layer Design for Far-Field and Near-Field Penetration Into a Multilayered Lossy Media. IEEE Antennas Propag. Mag. 2022, 64, 86–96. [Google Scholar] [CrossRef]
- Scapaticci, R.; Bjelogrlic, M.; Vasquez, J.A.T.; Vipiana, F.; Mattes, M.; Crocco, L. Microwave technology for brain imaging and monitoring: Physical foundations, potential and limitations. In Emerging Electromagnetic Technologies for Brain Diseases Diagnostics Monitoring and Therapy; Springer: Berlin/Heidelberg, Germany, 2018; pp. 7–35. [Google Scholar]
- Scapaticci, R.; Di Donato, L.; Catapano, I.; Crocco, L. A feasibility study on microwave imaging for brain stroke monitoring. Prog. Electromagn. Res. B 2012, 40, 305–324. [Google Scholar] [CrossRef]
- Wang, M.; Crocco, L.; Cavagnaro, M. On the Design of a Microwave Imaging System to Monitor Thermal Ablation of Liver Tumors. IEEE J. Electromagn. RF Microw. Med. Biol. 2021, 5, 231–237. [Google Scholar] [CrossRef]
- Amin, B.; Shahzad, A.; Kelly, D.; O’Halloran, M.; Elahi, M.A. Anthropomorphic Calcaneus Phantom for Microwave Bone Imaging Applications. IEEE J. Electromagn. RF Microw. Med. Biol. 2020, 5, 206–213. [Google Scholar] [CrossRef]
- Amin, B.; Elahi, M.A.; Shahzad, A.; Porter, E.; McDermott, B.; O’Halloran, M. Dielectric properties of bones for the monitoring of osteoporosis. Med Biol. Eng. Comput. 2018, 57, 1–13. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271. [Google Scholar] [CrossRef]
- Amin, B.; Shahzad, A.; O′Halloran, M.; Mcdermott, B.; Elahi, M.A. Experimental Validation of Microwave Imaging Prototype and DBIM-IMATCS Algorithm for Bone Health Monitoring. IEEE Access 2022, 10, 42589–42600. [Google Scholar] [CrossRef]
- Zou, L.; McLeod, C.; Bahmanyar, M.R. Wireless Interrogation of Implantable SAW Sensors. IEEE Trans. Biomed. Eng. 2020, 67, 1409–1417. [Google Scholar] [CrossRef] [PubMed]
- Carrara, N. Dielectric Properties of Body Tissues in the Frequency Range 10 Hz–100 GHz; Institute for Applied Physics, Italian National Research Council: Rome, Italy, 2015. [Google Scholar]
- Slaney, M.; Kak, A.; Larsen, L. Limitations of Imaging with First-Order Diffraction Tomography. IEEE Trans. Microw. Theory Tech. 1984, 32, 860–874. [Google Scholar] [CrossRef]
- Joachimowicz, N.; Duchêne, B.; Conessa, C.; Meyer, O. Anthropomorphic Breast and Head Phantoms for Microwave Imaging. Diagnostics 2018, 8, 85. [Google Scholar] [CrossRef] [PubMed]
- Amin, B.; Kelly, D.; Shahzad, A.; O’Halloran, M.; Elahi, M.A. Microwave calcaneus phantom for bone imaging applications. In 2020 14th European Conference on Antennas and Propagation (EuCAP); Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Salahuddin, S.; Porter, E.; Krewer, F.; Halloran, M.O. Optimised analytical models of the dielectric properties of biological tissue. Med. Eng. Phys. 2017, 43, 103–111. [Google Scholar] [CrossRef] [PubMed]
- Misiri, J.; Kusumoto, F.; Goldschlager, N. Electromagnetic Interference and Implanted Cardiac Devices: The Medical Environment (Part II). Clin. Cardiol. 2012, 35, 321–328. [Google Scholar] [CrossRef]
- Andreuccetti, D.; Fossi, R.; Petrucci, C. Dielectric Properties of Body Tissues in the Frequency Range 10 Hz–100 GHz. Available online: http://www.niremf.ifac.cnr.it/tissprop/ (accessed on 21 March 2023).
- van der Kruk, J.; Steelman, C.M.; Endres, A.L.; Vereecken, H. Dispersion inversion of electromagnetic pulse propagation within freezing and thawing soil waveguides. Geophys. Res. Lett. 2009, 36, 18. [Google Scholar] [CrossRef]
- Wang, T.; Chen, G.; Zhu, J.; Gong, H.; Zhang, L.; Wu, H. Deep understanding of impedance matching and quarter wavelength theory in electromagnetic wave absorption. J. Colloid Interface Sci. 2021, 595, 1–5. [Google Scholar] [CrossRef]
- Karadima, O.; Rahman, M.; Sotiriou, I.; Ghavami, N.; Lu, P.; Ahsan, S.; Kosmas, P. Experimental Validation of Microwave Tomography with the DBIM-TwIST Algorithm for Brain Stroke Detection and Classification. Sensors 2020, 20, 840. [Google Scholar] [CrossRef]
- McDermott, B.; Porter, E.; Santorelli, A.; Divilly, B.; Morris, L.; Jones, M.; McGinley, B.; O’Halloran, M. Anatomically and dielectrically realistic microwave head phantom with circulation and reconfigurable lesions. Prog. Electromagn. Res. B 2017, 78, 47–60. [Google Scholar] [CrossRef]
- Garrett, J.; Fear, E. Stable and Flexible Materials to Mimic the Dielectric Properties of Human Soft Tissues. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 599–602. [Google Scholar] [CrossRef]








| Tissue | ∆ε | τ | α | ||
|---|---|---|---|---|---|
| Dry Skin | 4 | 32 | 7.23 × 10−12 | 0 | 0.0002 |
| Fat | 2.5 | 3.0 | 7.96 × 10−12 | 0.2 | 0.01 |
| Muscle | 4 | 50 | 7.23 × 10−12 | 0.10 | 0.20 |
| Cartilage | 4.34 | 35.6 | 12.8 × 10−12 | 0.25 | 0.07 |
| Heart | 4 | 50.0 | 7.96 × 10−12 | 0.10 | 0.05 |
| Bio-Phantom | Triton X-100 (Vol %) | De-Ionized Water (Vol %) | Sodium Chloride (g/L) |
|---|---|---|---|
| Blood [38] | 14% | 86% | 9.4 |
| Antenna | A | B |
|---|---|---|
| 433 MHz | 296 MHz | 342 MHz |
| 915 MHz | 697 MHz | 670 MHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amin, B.; Rehman, M.R.u.; Farooq, M.; Elahi, A.; Donaghey, K.; Wijns, W.; Shahzad, A.; Vazquez, P. Optimizing Cardiac Wireless Implant Communication: A Feasibility Study on Selecting the Frequency and Matching Medium. Sensors 2023, 23, 3411. https://doi.org/10.3390/s23073411
Amin B, Rehman MRu, Farooq M, Elahi A, Donaghey K, Wijns W, Shahzad A, Vazquez P. Optimizing Cardiac Wireless Implant Communication: A Feasibility Study on Selecting the Frequency and Matching Medium. Sensors. 2023; 23(7):3411. https://doi.org/10.3390/s23073411
Chicago/Turabian StyleAmin, Bilal, Muhammad Riaz ur Rehman, Muhammad Farooq, Adnan Elahi, Kevin Donaghey, William Wijns, Atif Shahzad, and Patricia Vazquez. 2023. "Optimizing Cardiac Wireless Implant Communication: A Feasibility Study on Selecting the Frequency and Matching Medium" Sensors 23, no. 7: 3411. https://doi.org/10.3390/s23073411
APA StyleAmin, B., Rehman, M. R. u., Farooq, M., Elahi, A., Donaghey, K., Wijns, W., Shahzad, A., & Vazquez, P. (2023). Optimizing Cardiac Wireless Implant Communication: A Feasibility Study on Selecting the Frequency and Matching Medium. Sensors, 23(7), 3411. https://doi.org/10.3390/s23073411








