Plastic Classification Using Optical Parameter Features Measured with the TMF8801 Direct Time-of-Flight Depth Sensor
Abstract
1. Introduction
2. Methods
2.1. Sensor System and Data Acquisition
2.2. Measurements
2.3. Histogram Processing
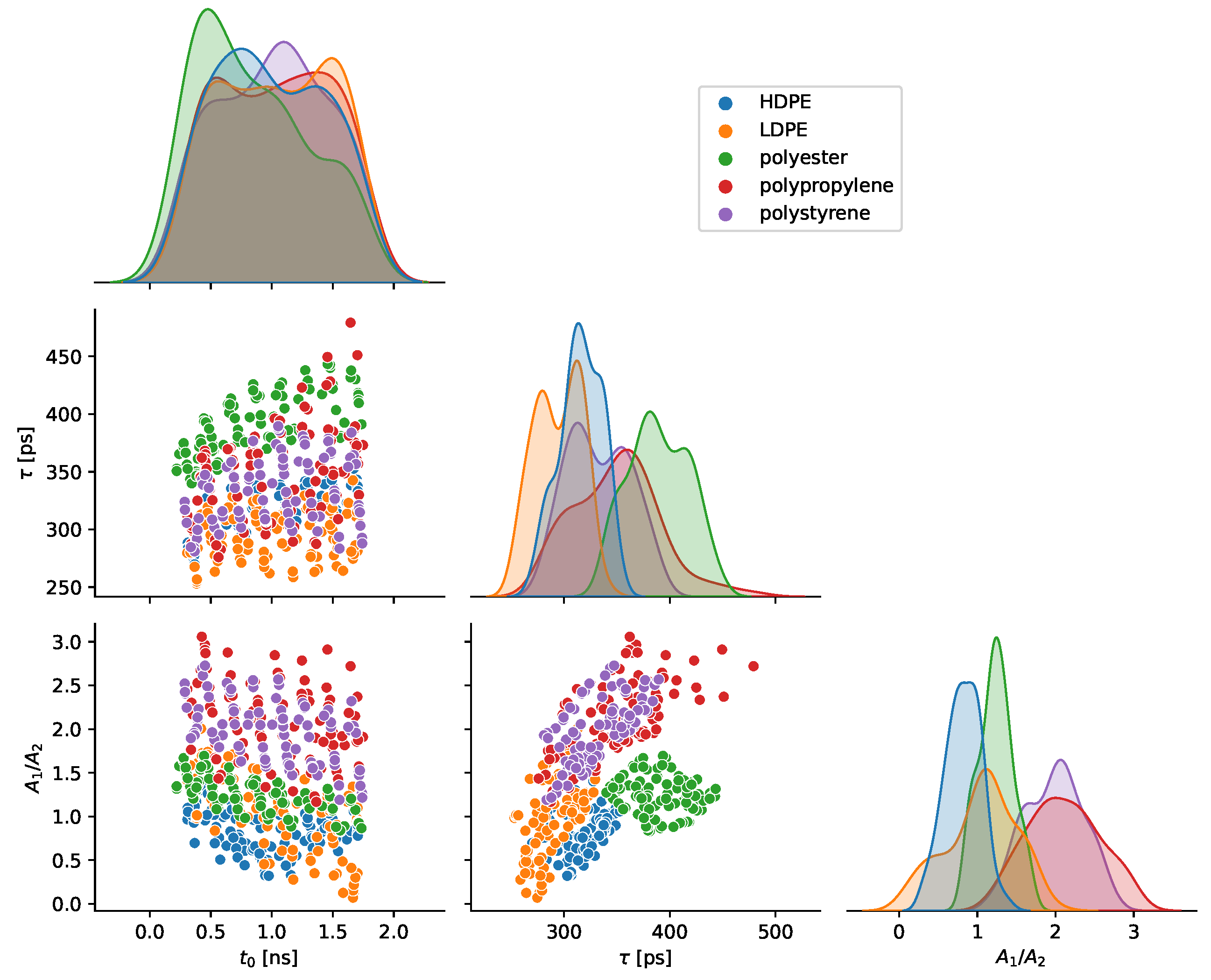
2.4. Optical Parameter Model
2.5. Classifier Creation
3. Results
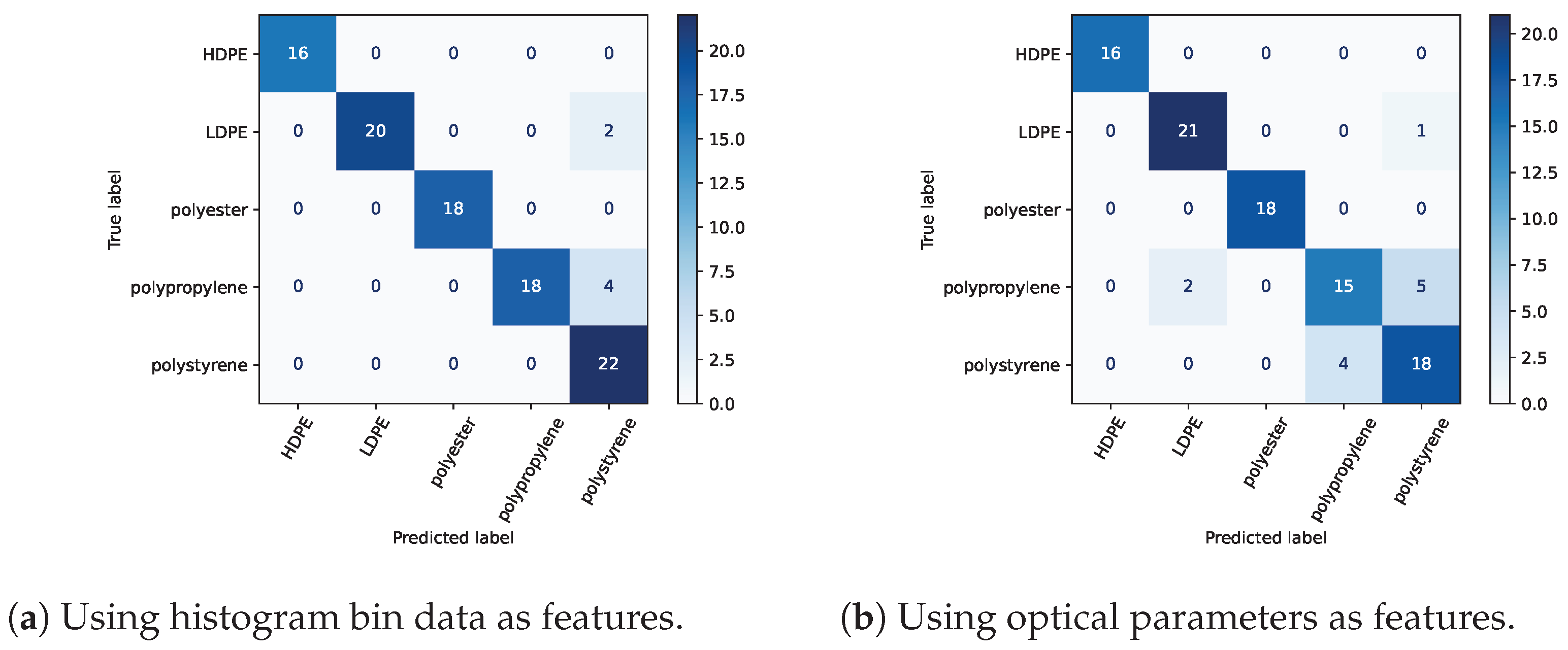
3.1. Sliding Distance Classification with Histogram Data
3.2. Sliding Distance Classification with Optical Parameters
3.3. Fixed-Distance Classification with Optical Parameters
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ToF | Time of flight |
| RGB | red, green, blue |
| MIRF | material impulse response function |
| TPSF | temporal point spread function |
| TDC | time-to-digital converter |
| PMD | photon mixing device |
| ROI | region of interest |
| SPAD | single photon avalanche diode |
| LDPE | low-density polyethylene |
| HDPE | high-density polyethylene |
| A.I. | artificial intelligence |
| k-NN | k-nearest neighbor |
| NB | naive Bayes |
| SVC | support vector classifier |
| RBF | radial basis function |
References
- McCormack, J.; Prine, J.; Trowbridge, B.; Rodriguez, A.C.; Integlia, R. 2D LIDAR as a Distributed Interaction Tool for Virtual and Augmented Reality Video Games. In Proceedings of the 2015 IEEE Games Entertainment Media Conference (GEM), Toronto, ON, Canada, 14–16 October 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Davis, A.; Bouman, K.L.; Chen, J.G.; Rubinstein, M.; Durand, F.; Freeman, W.T. Visual Vibrometry: Estimating Material Properties From Small Motion in Video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5335–5343. [Google Scholar]
- Saponaro, P.; Sorensen, S.; Kolagunda, A.; Kambhamettu, C. Material Classification With Thermal Imagery. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 4649–4656. [Google Scholar]
- Khan, M.J.; Khan, H.S.; Yousaf, A.; Khurshid, K.; Abbas, A. Modern Trends in Hyperspectral Image Analysis: A Review. IEEE Access 2018, 6, 14118–14129. [Google Scholar] [CrossRef]
- Chen, S.Y.; Cheng, Y.C.; Yang, W.L.; Wang, M.Y. Surface Defect Detection of Wet-Blue Leather Using Hyperspectral Imaging. IEEE Access 2021, 9, 127685–127702. [Google Scholar] [CrossRef]
- Stuart, M.B.; Stanger, L.R.; Hobbs, M.J.; Pering, T.D.; Thio, D.; McGonigle, A.J.S.; Willmott, J.R. Low-Cost Hyperspectral Imaging System: Design and Testing for Laboratory-Based Environmental Applications. Sensors 2020, 20, 3293. [Google Scholar] [CrossRef] [PubMed]
- Viitakoski, M. Specim IQ Technical Specifications. Available online: https://www.specim.com/iq/tech-specs/ (accessed on 14 March 2023).
- Caputo, B.; Hayman, E.; Mallikarjuna, P. Class-Specific Material Categorisation. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05) Volume 1, Washington, DC, USA, 17–20 October 2005; pp. 1597–1604. [Google Scholar] [CrossRef]
- Liu, C.; Sharan, L.; Adelson, E.H.; Rosenholtz, R. Exploring Features in a Bayesian Framework for Material Recognition. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 239–246. [Google Scholar] [CrossRef]
- Su, S.; Heide, F.; Swanson, R.; Klein, J.; Callenberg, C.; Hullin, M.; Heidrich, W. Material Classification Using Raw Time-Of-Flight Measurements. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 3503–3511. [Google Scholar]
- Heide, F.; Xiao, L.; Heidrich, W.; Hullin, M.B. Diffuse Mirrors: 3D Reconstruction from Diffuse Indirect Illumination Using Inexpensive Time-of-Flight Sensors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 23–28 June 2014; pp. 3222–3229. [Google Scholar]
- Tanaka, K.; Mukaigawa, Y.; Funatomi, T.; Kubo, H.; Matsushita, Y.; Yagi, Y. Material Classification from Time-of-Flight Distortions. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 2906–2918. [Google Scholar] [CrossRef] [PubMed]
- Conde, M.H. A Material-Sensing Time-of-Flight Camera. IEEE Sens. Lett. 2020, 4, 1–4. [Google Scholar] [CrossRef]
- Morimoto, K.; Iwata, J.; Shinohara, M.; Sekine, H.; Abdelghafar, A.; Tsuchiya, H.; Kuroda, Y.; Tojima, K.; Endo, W.; Maehashi, Y.; et al. 3.2 Megapixel 3D-Stacked Charge Focusing SPAD for Low-Light Imaging and Depth Sensing. In Proceedings of the 2021 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA USA, 11–15 December 2021; pp. 20.2.1–20.2.4. [Google Scholar] [CrossRef]
- Cambou, P.; Ayari, T. With the Apple iPad LiDAR Chip, Sony Landed on the Moon without Us Knowing. Available online: https://www.edge-ai-vision.com/2020/05/with-the-apple-ipad-lidar-chip-sony-landed-on-the-moon-without-us-knowing/ (accessed on 14 March 2023).
- VL53L1X Datasheet, 3rd ed.; STMicroelectronics: Geneva, Switzerland, 2018.
- Callenberg, C.; Shi, Z.; Heide, F.; Hullin, M.B. Low-Cost SPAD Sensing for Non-Line-of-Sight Tracking, Material Classification and Depth Imaging. ACM Trans. Graph. 2021, 40, 1–12. [Google Scholar] [CrossRef]
- AMS. TMF8801 1D Time-of-Flight Sensor Datasheet. 2021. Available online: https://ams.com/en/tmf8801 (accessed on 14 March 2023).
- Delgadillo Bonequi, I.; Stroschein, A.; Koerner, L.J. A Field-Programmable Gate Array (FPGA)-Based Data Acquisition System for Closed-Loop Experiments. Rev. Sci. Instrum. 2022, 93, 114712. [Google Scholar] [CrossRef] [PubMed]
- Stroschein, A.; Bonequi, I.D.; Koerner, L.J. Pyripherals: A Python Package for Communicating with Peripheral Electronic Devices. J. Open Source Softw. 2022, 7, 4762. [Google Scholar] [CrossRef]
- AMS. TMF8X0X Host Driver Communication (AN000597). 2021. Available online: https://ams.com/documents/20143/36005/TMF8X0X_Host_Driver_Communication_AN000597_6-00.pdf/7703ffd6-620d-912e-3010-646d20a8616a (accessed on 14 March 2023).
- Jensen, H.W.; Marschner, S.R.; Levoy, M.; Hanrahan, P. A Practical Model for Subsurface Light Transport. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 12–17 August 2001; pp. 511–518. [Google Scholar] [CrossRef]
- Che, C.; Luan, F.; Zhao, S.; Bala, K.; Gkioulekas, I. Towards Learning-based Inverse Subsurface Scattering. In Proceedings of the 2020 IEEE International Conference on Computational Photography (ICCP), Saint Louis, MO, USA, 24–26 April 2020; pp. 1–12. [Google Scholar] [CrossRef]
- Heide, F.; Xiao, L.; Kolb, A.; Hullin, M.B.; Heidrich, W. Imaging in Scattering Media Using Correlation Image Sensors and Sparse Convolutional Coding. Opt. Express 2014, 22, 26338–26350. [Google Scholar] [CrossRef] [PubMed]
- Jungerman, S.; Ingle, A.; Li, Y.; Gupta, M. 3D Scene Inference from Transient Histograms. In Proceedings of the Computer Vision—ECCV, Tel Aviv, Israel, 23–27 October 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Springer: Cham, Switzerland, 2022; pp. 401–417. [Google Scholar] [CrossRef]
- Sun, F.; Xu, Y.; Wu, Z.; Zhang, J. A Simple Analytic Modeling Method for SPAD Timing Jitter Prediction. IEEE J. Electron Devices Soc. 2019, 7, 261–267. [Google Scholar] [CrossRef]
- Kapoor, S.; Narayanan, A. Leakage and the Reproducibility Crisis in ML-based Science. arXiv 2022, arXiv:2207.07048. [Google Scholar] [CrossRef]
- Geyer, R.; Jambeck, J.R.; Law, K.L. Production, Use, and Fate of All Plastics Ever Made. Sci. Adv. 2017, 3, e1700782. [Google Scholar] [CrossRef] [PubMed]
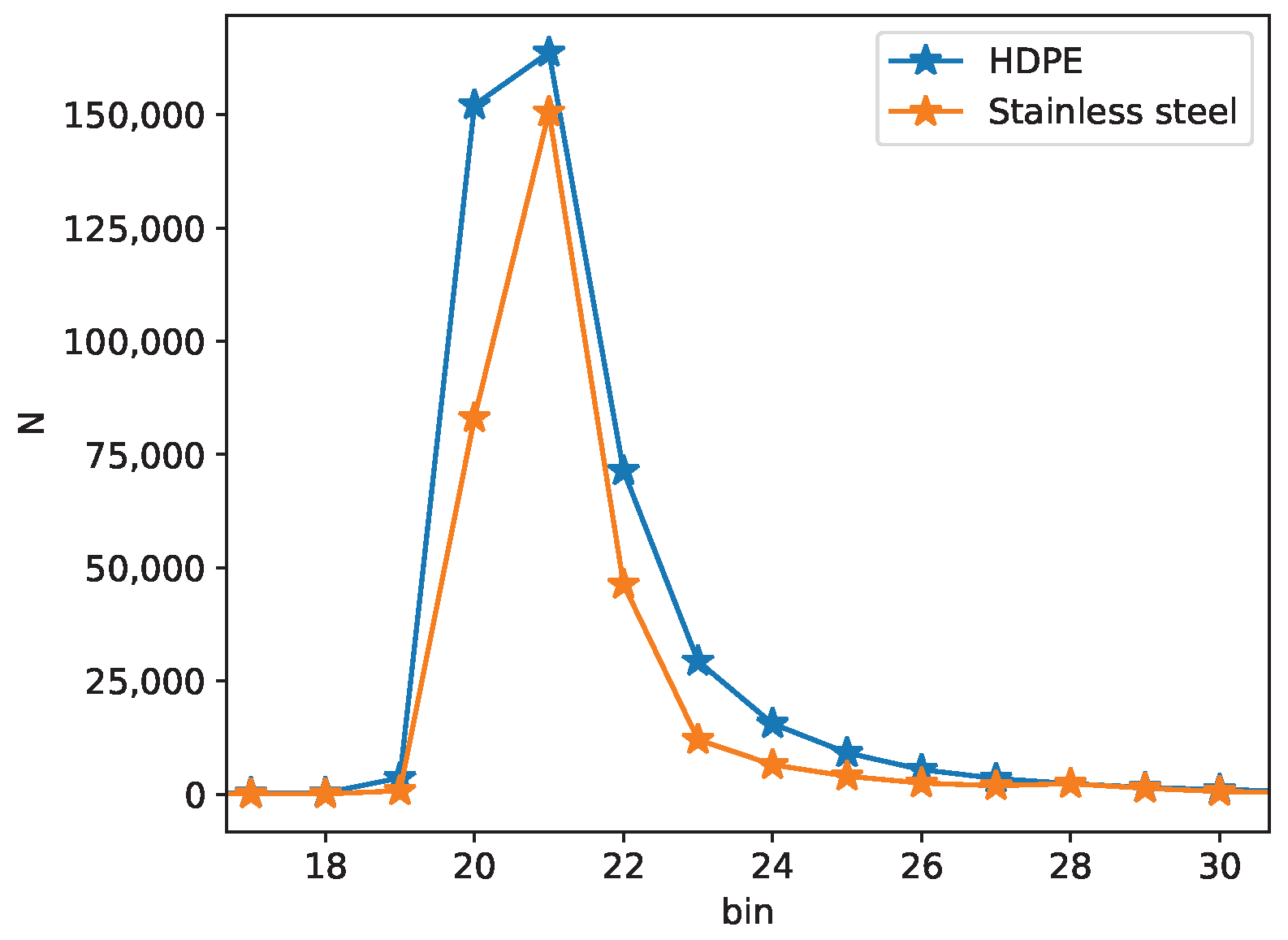




| 0.24 | 0.516 | 0.528 |
| Laser Pulses | Total Photons/Hist. | Classification Accuracy |
|---|---|---|
| 100 k | 58,816.8 | 1.0 |
| 300 k | 162,887.3 | 1.0 |
| 600 k | 319,091.8 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Becker, C.N.; Koerner, L.J. Plastic Classification Using Optical Parameter Features Measured with the TMF8801 Direct Time-of-Flight Depth Sensor. Sensors 2023, 23, 3324. https://doi.org/10.3390/s23063324
Becker CN, Koerner LJ. Plastic Classification Using Optical Parameter Features Measured with the TMF8801 Direct Time-of-Flight Depth Sensor. Sensors. 2023; 23(6):3324. https://doi.org/10.3390/s23063324
Chicago/Turabian StyleBecker, Cienna N., and Lucas J. Koerner. 2023. "Plastic Classification Using Optical Parameter Features Measured with the TMF8801 Direct Time-of-Flight Depth Sensor" Sensors 23, no. 6: 3324. https://doi.org/10.3390/s23063324
APA StyleBecker, C. N., & Koerner, L. J. (2023). Plastic Classification Using Optical Parameter Features Measured with the TMF8801 Direct Time-of-Flight Depth Sensor. Sensors, 23(6), 3324. https://doi.org/10.3390/s23063324






