Spherical Fourier-Transform-Based Real-TimeNear-Field Shaping and Focusing in Beyond-5G Networks
Abstract
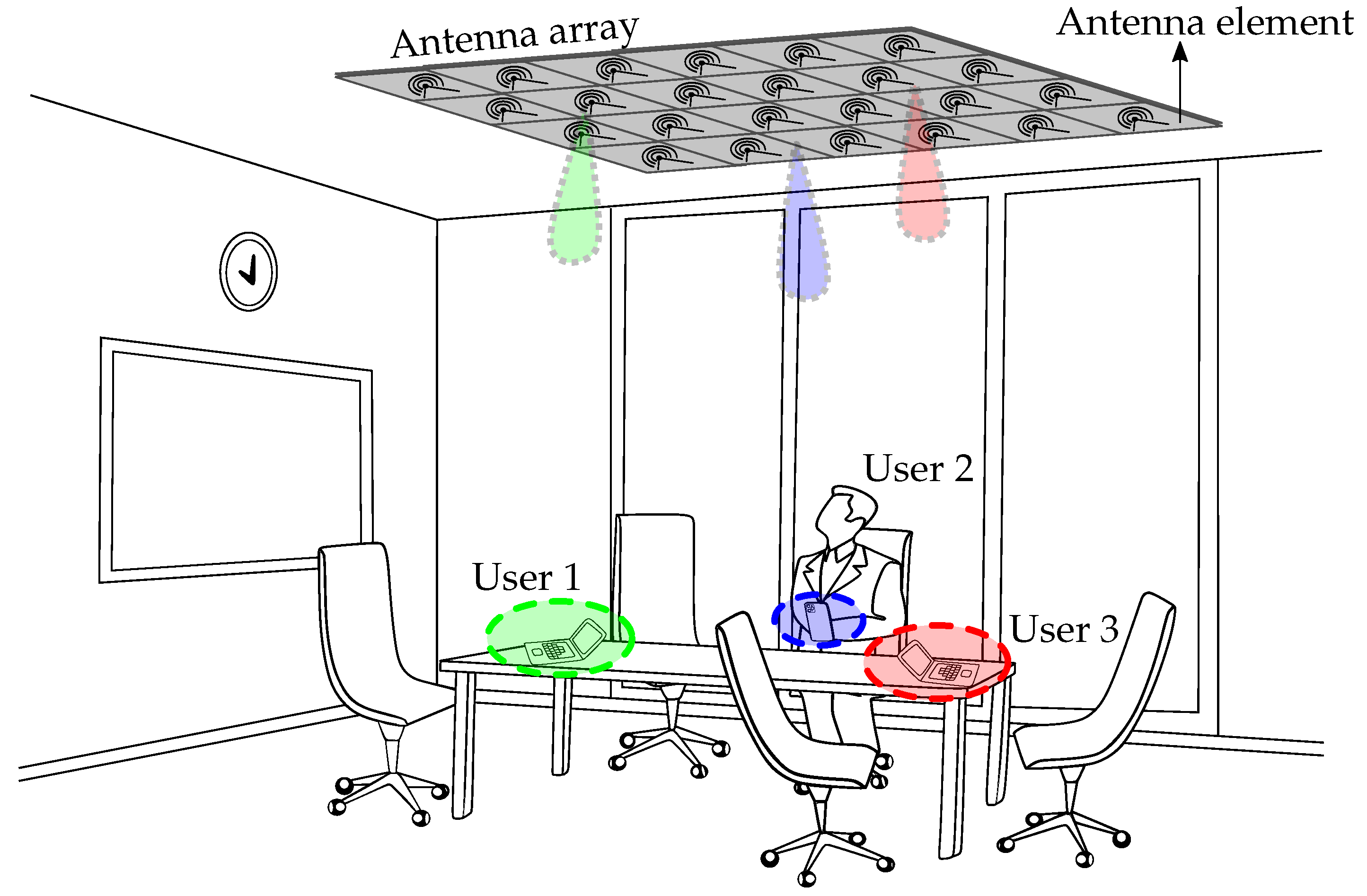
1. Introduction
2. Theory
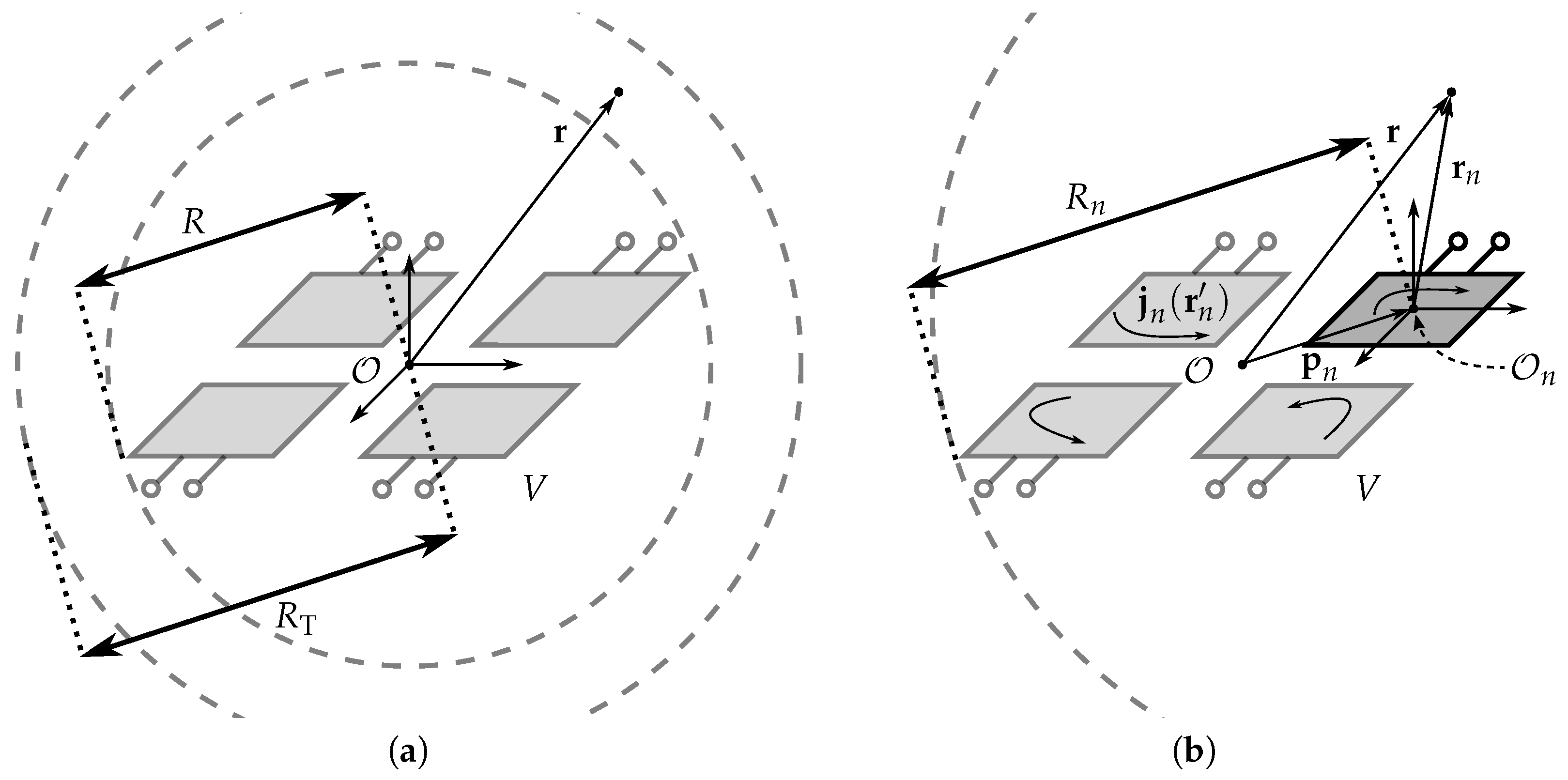
2.1. Problem Statement
2.2. Far-to-Near-Field Transformation
2.3. Phase Center Translation
2.4. Near-Field Intensity Shaping
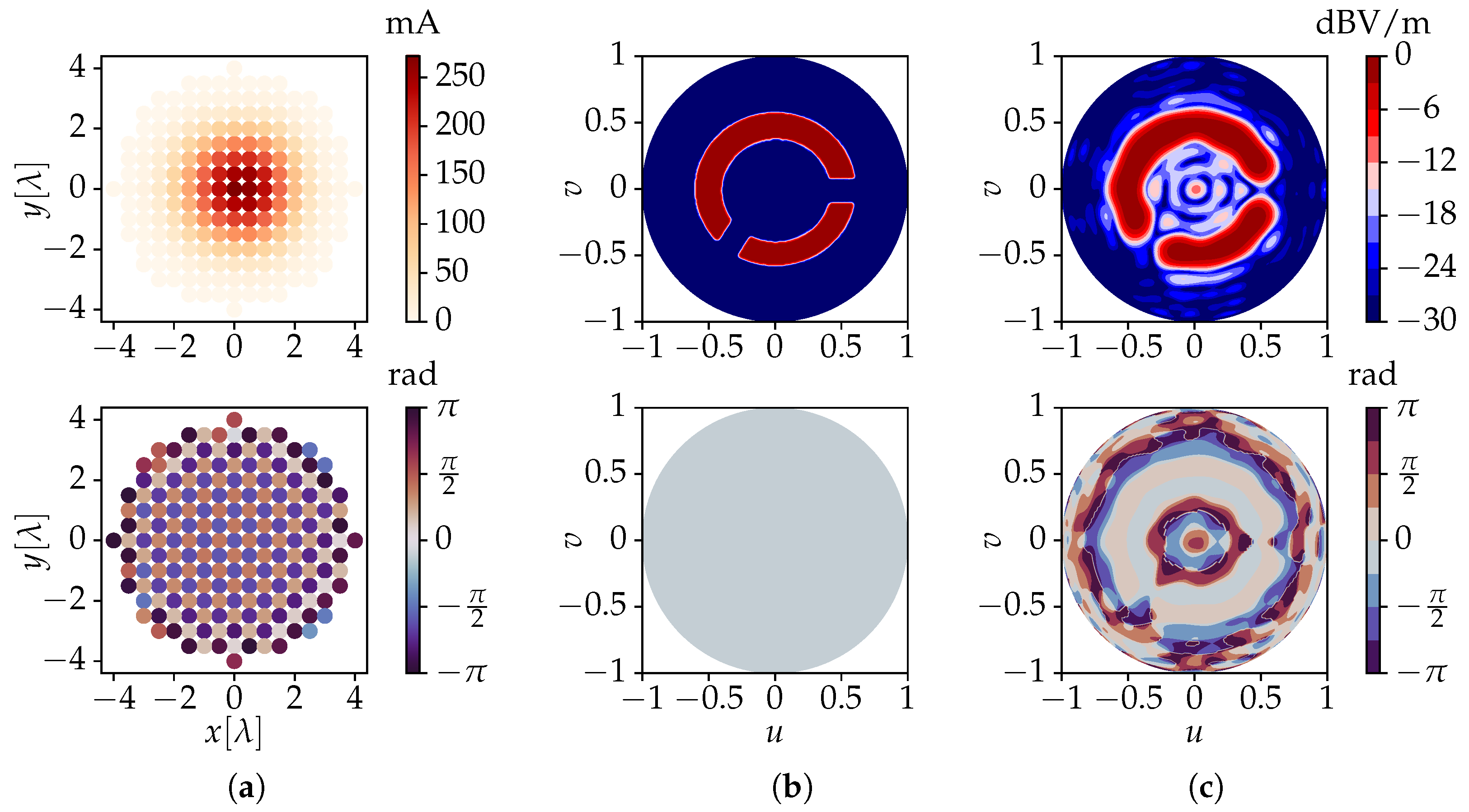
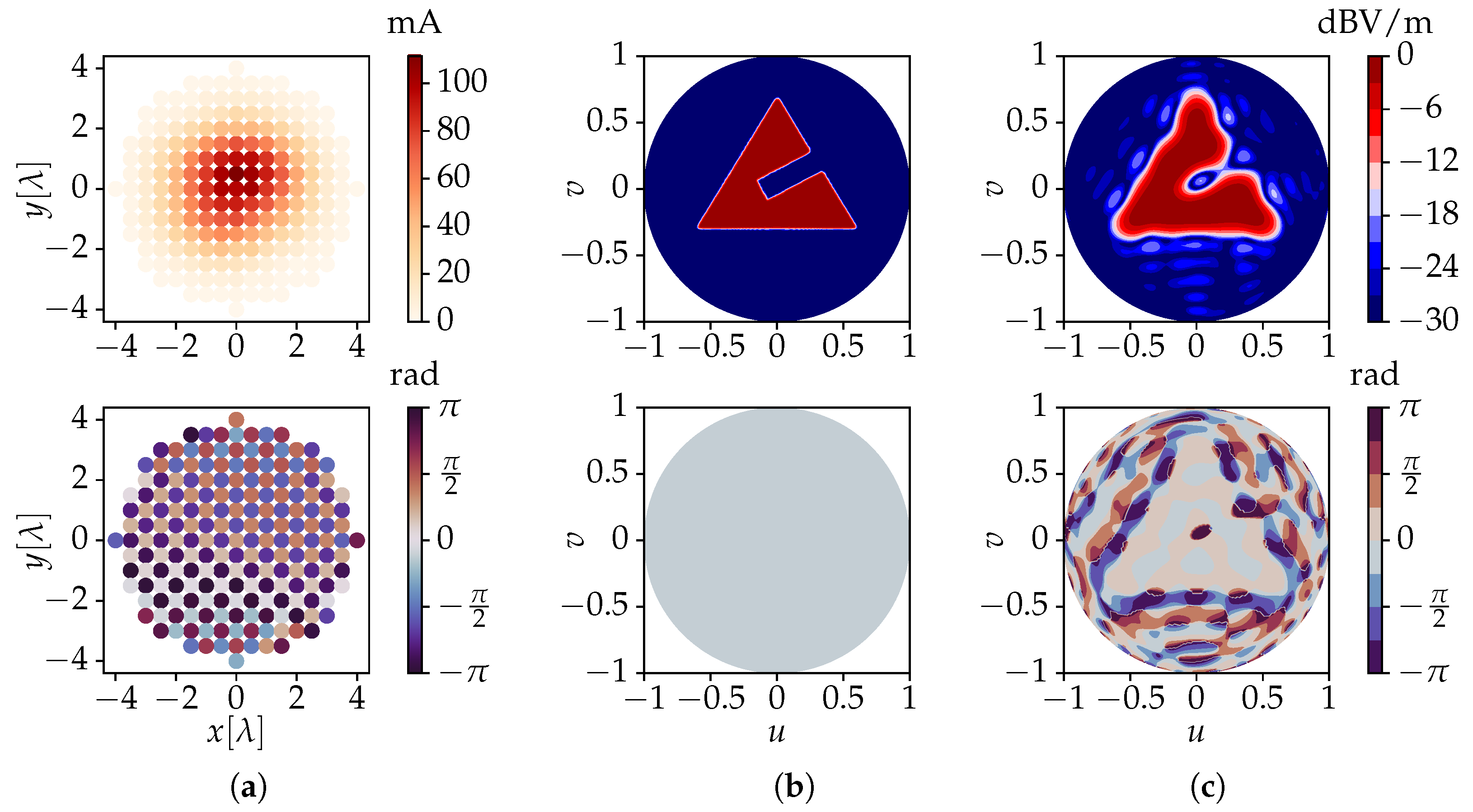
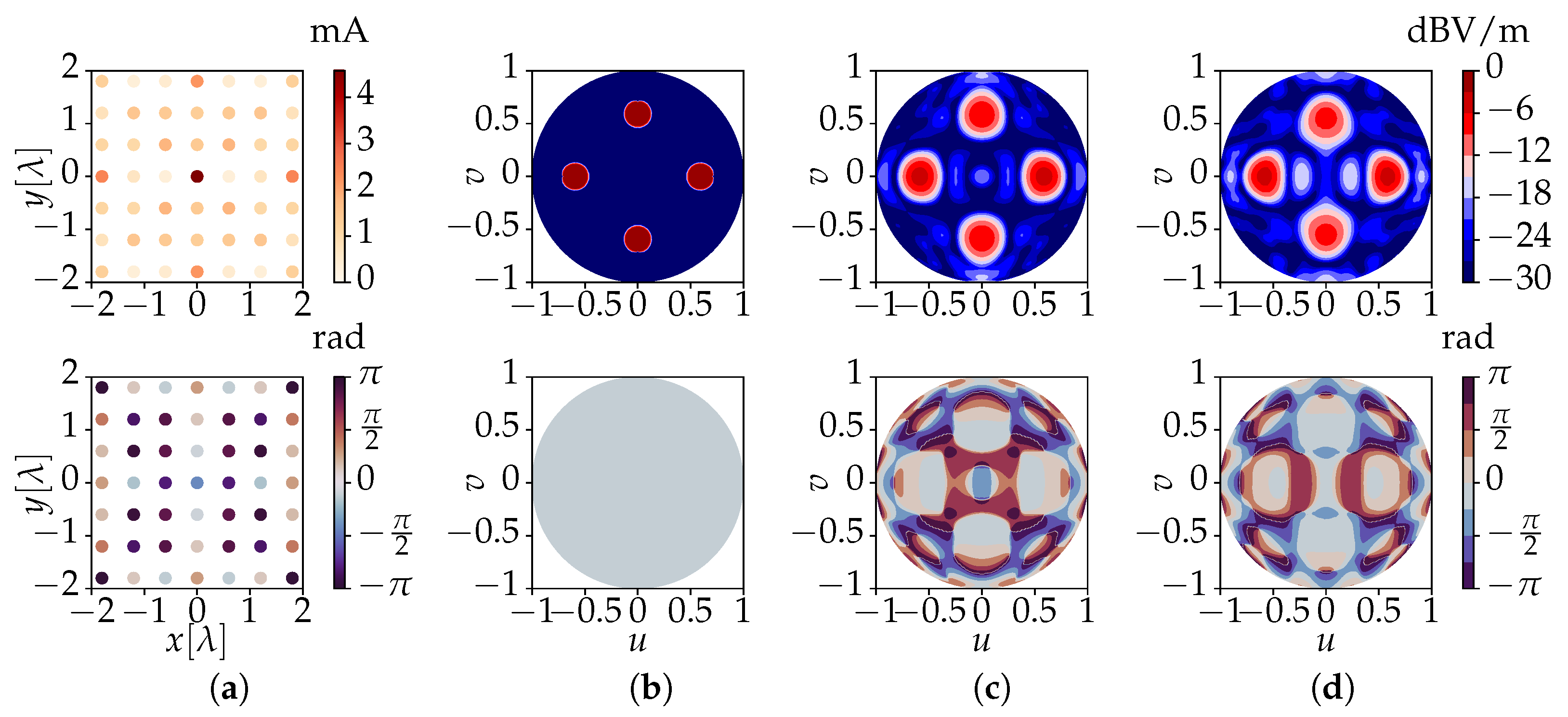
3. Validation
3.1. Numerical Validation
3.2. Full-Wave Validation and Application
3.3. Discussion on Computational Efficiency
- Novel method: The number of operations required is approximately , where is the chosen order of the spherical Fourier transform. For the largest array studied, with N = 200 and = 30, the shaping procedure required around 200 ms and circa 100 MB of pre-computed data.
- O-mt-TR [31]: The amount of operations required is of order , where M are the variables to optimize, and L is the amount of control points used. As the computational time scales exponentially with L, several hours are required to achieve shaping, hence excluding this algorithm from real-time applications. A variation of this technique, being O-mt-LSM [33], does not require any set-up phase, but this results in reduced computational efficiency and resolution.
- Smart skin holography [13]: While a quite good resolution is obtained in near-field shaping, the process required circa 20 min per shape. Again, this algorithm is also not suited to real-time applications.
- Method of Moments (MoM) [30]: A radial slot array is synthesised with an in-house MoM code and tailored for a specific target shape. The amount of time usually required to fill an MoM matrix and solve the matrix system is not compatible with real-time applications.
- Angular spectrum projection method [28]: This method’s efficiency is quantified as largely faster than the O-mt-TR. At the same time, the obtained target shapes exhibit a very poor resolution and are obtained as a discontinuous collection of discrete points.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Green’s Function Multipole Expansion
References
- Bjornson, E.; Sanguinetti, L.; Wymeersch, H.; Hoydis, J.; Marzetta, T.L. Massive MIMO is a reality—What is next?: Five promising research directions for antenna arrays. Digit. Signal Process. 2019, 94, 3–20. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Xing, Y.; Kanhere, O.; Ju, S.; Madanayake, A.; Mandal, S.; Alkhateeb, A.; Trichopoulos, G.C. Wireless communications and applications above 100 GHz: Opportunities and challenges for 6G and beyond. IEEE Access 2019, 7, 78729–78757. [Google Scholar] [CrossRef]
- Massa, A.; Benoni, A.; Da Ru, P.; Goudos, S.K.; Li, B.; Oliveri, G.; Polo, A.; Rocca, P.; Salucci, M. Designing smart electromagnetic environments for next-generation wireless communications. Telecom 2021, 2, 213–221. [Google Scholar] [CrossRef]
- Moerman, A.; Van Kerrebrouck, J.; Caytan, O.; Lima de Paula, I.; Bogaert, L.; Torfs, G.; Demeester, P.; Rogier, H.; Lemey, S. Beyond 5G without obstacles: mmWave-over-fiber distributed antenna systems. IEEE Commun. Mag. 2022, 60, 27–33. [Google Scholar] [CrossRef]
- Lu, H.; Zeng, Y. Communicating with extremely large-scale arrray/surface: Unified modeling and performance analysis. IEEE Trans. Wirel. Commun. 2021, 21, 4039–4053. [Google Scholar] [CrossRef]
- Oliveri, G.; Zardi, F.; Rocca, P.; Salucci, M.; Massa, A. Constrained design of passive static EM skin. IEEE Trans. Antennas Propag. 2023, 71, 1528–1538. [Google Scholar] [CrossRef]
- Bjornson, E.; Demir, O.T.; Sanguinetti, L. A primer on near-field beamforming for arrays and reconfigurable intelligent surfaces. In Proceedings of the Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 31 October–3 November 2021; pp. 105–112. [Google Scholar]
- Hansen, R.C. Focal region characteristics of focused array antennas. IEEE Trans. Antennas Propag. 1985, 33, 1328–1337. [Google Scholar] [CrossRef]
- Sherman, J.W. Properties of focused apertures in the Fresnel region. IRE Trans. Antennas Propag. 1962, 33, 399–408. [Google Scholar] [CrossRef]
- Puglielli, A.; Townley, A.; LaCaille, G.; Milovanovic, V.; Lu, P.; Trotskovsky, K.; Whitcombe, A.; Narevsky, N.; Wright, G.; Courtade, T.; et al. Design of energy- and cost-efficient massive MIMO arrays. Proc. IEEE 2015, 104, 399–408. [Google Scholar] [CrossRef]
- Kapusuz, K.Y.; Lemey, S.; Rogier, H. Dual-polarized 28-GHz air filled SIW phased antenna array for next-generation cellular systems. In Proceedings of the IEEE International Symposium on Phased Array System & Technology, Waltham, MA, USA, 15–18 October 2019; pp. 1–6. [Google Scholar]
- Benoni, A.; Salucci, M.; Oliveri, G.; Rocca, P.; Li, B.; Massa, A. Planning of EM skins for improved quality-of-service in urban areas. IEEE Trans. Antennas Propag. 2022, 70, 8849–8862. [Google Scholar] [CrossRef]
- Oliveri, G.; Rocca, P.; Salucci, M.; Massa, A. Holographic smart EM skins for advanced beam power shaping in next generation wireless environments. IEEE J. Multiscale Multiphys. Comput. Tech. 2021, 6, 171–182. [Google Scholar] [CrossRef]
- Geyi, W. The method of maximum power transmission efficiency for the design of antenna arrays. IEEE Open J. Antennas Propag. 2021, 2, 412–430. [Google Scholar] [CrossRef]
- Inserra, D.; Yang, Z.; Zhao, F.; Huang, Y.; Li, J.; Wen, G. On the design of discrete apertures for high-efficiency wireless power transfer. IEEE Trans. Antennas Propag. 2022, 70, 783–788. [Google Scholar] [CrossRef]
- Cicchetti, R.; Faraone, A.; Testa, O. Energy-based representation of multiport circuits and antennas suitable for near- and far-field syntheses. IEEE Trans. Antennas Propag. 2019, 67, 85–98. [Google Scholar] [CrossRef]
- Prado, D.R.; Vaquero, A.F.; Arrebola, M.; Pino, M.R.; Las-Heras, F. Acceleration of gradient-based algorithms for array antenna synthesis with far-field or near-field constraints. IEEE Trans. Antennas Propag. 2018, 66, 5239–5248. [Google Scholar] [CrossRef]
- Wu, J.W.; Wu, R.Y.; Bo, X.C.; Bao, L.; Fu, X.J.; Cui, T.J. Synthesis algorithm for near-field power pattern control and its experimental verification via metasurfaces. IEEE Trans. Antennas Propag. 2019, 67, 1073–1083. [Google Scholar] [CrossRef]
- Huang, Z.X.; Cheng, Y.J. Near-field pattern synthesis for sparse focusing antenna arrays based on Bayesian compressive sensing and convex optimization. IEEE Trans. Antennas Propag. 2018, 66, 5249–5257. [Google Scholar] [CrossRef]
- Huang, Z.X.; Cheng, Y.J.; Yang, H.N. Synthesis of sparse near field focusing antenna arrays with accurate control of focal distance by reweighted l1 norm optimization. IEEE Trans. Antennas Propag. 2021, 69, 3010–3014. [Google Scholar] [CrossRef]
- Ayestaran, R.G.; Leon, G.; Pino, M.R.; Nepa, P. Wireless power transfer through simultaneous near-field focusing and far-field synthesis. IEEE Trans. Antennas Propag. 2019, 67, 5623–5633. [Google Scholar] [CrossRef]
- Buffi, A.; Serra, A.A.; Nepa, P.; Chou, H.-T.; Manara, G. A focused planar microstrip array for 2.4 GHz RFID readers. IEEE Trans. Antennas Propag. 2010, 58, 1536–1544. [Google Scholar] [CrossRef]
- Tofigh, F.; Nourinia, J.; Azarmanesh, M.; Khazaei, K.M. Near-field focused array microstrip planar antenna for medical applications. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 951–954. [Google Scholar] [CrossRef]
- Zhang, H.; Shlezinger, N.; Guidi, F.; Dardari, D.; Imani, M.F.; Eldar, Y.C. Beam focusing for near-field multiuser MIMO communications. IEEE Trans. Wirel. Commun. 2022, 21, 7476–7490. [Google Scholar] [CrossRef]
- Liu, R.; Wu, K. Antenna array for amplitude and phase specified near-field multifocus. IEEE Trans. Antennas Propag. 2019, 67, 3140–3150. [Google Scholar] [CrossRef]
- Cai, X.; Gu, X.; Geyi, W. Optimal design of antenna arrays focused on multiple targets. IEEE Trans. Antennas Propag. 2020, 68, 4593–4603. [Google Scholar] [CrossRef]
- Zhao, D.; Zhu, M. Generating microwave spatial fields with arbitrary patterns. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1739–1742. [Google Scholar] [CrossRef]
- Guo, S.; Zhao, D.; Wang, B.-Z.; Cao, W. Shaping electric field intensity via angular spectrum projection and the linear superposition principle. IEEE Trans. Antennas Propag. 2020, 68, 8249–8254. [Google Scholar] [CrossRef]
- Piestun, R.; Shamir, J. Synthesis of three-dimensional light fields and applications. Proc. IEEE 2002, 90, 222–244. [Google Scholar] [CrossRef]
- Ettorre, M.; Casaletti, M.; Valerio, G.; Sauleau, R.; Le Coq, L.; Pavone, S.C.; Albani, M. On the near-field shaping and focusing capability of a radial line slot array. IEEE Trans. Antennas Propag. 2014, 62, 1991–1999. [Google Scholar] [CrossRef]
- Bellizzi, G.G.; Bevacqua, M.T.; Crocco, L.; Isernia, T. 3-D field intensity shaping via optimized multi-target time reversal. IEEE Trans. Antennas Propag. 2018, 66, 4380–4385. [Google Scholar] [CrossRef]
- Bellizzi, G.G.; Iero, D.A.M.; Crocco, L.; Isernia, T. Three dimensional field intensity shaping: The scalar case. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 360–363. [Google Scholar] [CrossRef]
- Bellizzi, G.G.; Bevacqua, T. The linear sampling method as a tool for “blind” field intensity shaping. IEEE Trans. Antennas Propag. 2020, 68, 3154–3162. [Google Scholar] [CrossRef]
- Ludwig, A.; Sarris, C.D.; Eleftheriades, G.V. Near-field antenna arrays for steerable sub-wavelength magnetic-field beams. IEEE Trans. Antennas Propag. 2014, 62, 3543–3556. [Google Scholar] [CrossRef]
- Van Bladel, J.G. Electromagnetic Fields; John Wiley & Sons: Hoboken, NJ, USA, 2007; Volume 19. [Google Scholar]
- Felaco, A.; Kapusuz, K.Y.; Rogier, H.; Vande Ginste, D. Efficient modeling of on-body passive UHF RFID systems in the radiative near-field. IEEE Trans. Antennas Propag. 2022, 70, 2979–2989. [Google Scholar] [CrossRef]
- Rahola, J.; Belloni, F.; Richter, A. Modelling of radiation patterns using scalar spherical harmonics with vector coefficients. In Proceedings of the 2009 3rd European Conference on Antennas and Propagation (EuCAP), Berlin, Germany, 23–27 March 2009; pp. 3361–3365. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1964; Volume 55.
- Galdo, G.D.; Lotze, J.; Landmann, M.; Haardt, M. Modelling and manipulation of polarimetric antenna beam patterns via spherical harmonics. In Proceedings of the European Signal Processing Conference, Florence, Italy, 4–8 September 2006; pp. 1–5. [Google Scholar]
- Rahmat-Samii, Y. Useful coordinate transformations for antenna applications. IEEE Trans. Antennas Propag. 1979, 27, 571–574. [Google Scholar] [CrossRef]
- Beentjes, C.H.L. Quadrature on a Spherical Surface. University of Oxford, 2015. Available online: https://bit.ly/3cGAETV (accessed on 9 February 2023).
- Cappellin, C.; Breinbjerg, O.; Frandsen, A. Properties of the transformation from the spherical wave expansion to the plane wave expansion. Radio Sci. 2008, 43, RS1012. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, W.; Cai, W. Fast multipole method for 3-D Helmholtz equation in layered media. SIAM J. Sci. Comput. 2019, 41, A3954–A3981. [Google Scholar] [CrossRef]
- Cruzan, O.R. Translational addition theorems for spherical vector wave functions. Appl. Math. 2019, 20, 33–40. [Google Scholar]
- Chew, W.C.; Jin, J.-M.; Michielssen, E. Fast and Efficient Algorithms in Computational Electromagnetics; Artech House: Norwood, MA, USA, 2001. [Google Scholar]
- CST Studio Suite 2019. Available online: https://bit.ly/3fn96Um (accessed on 9 February 2023).
- Python 3.10.7. Available online: http://bitly.ws/yRtm (accessed on 9 February 2023).
- Balanis, C.A. Antenna Theory: Analysis and Design, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Stratton, J.A. Electromagnetic Theory; John Wiley & Sons: Hoboken, NJ, USA, 2007; Volume 33. [Google Scholar]
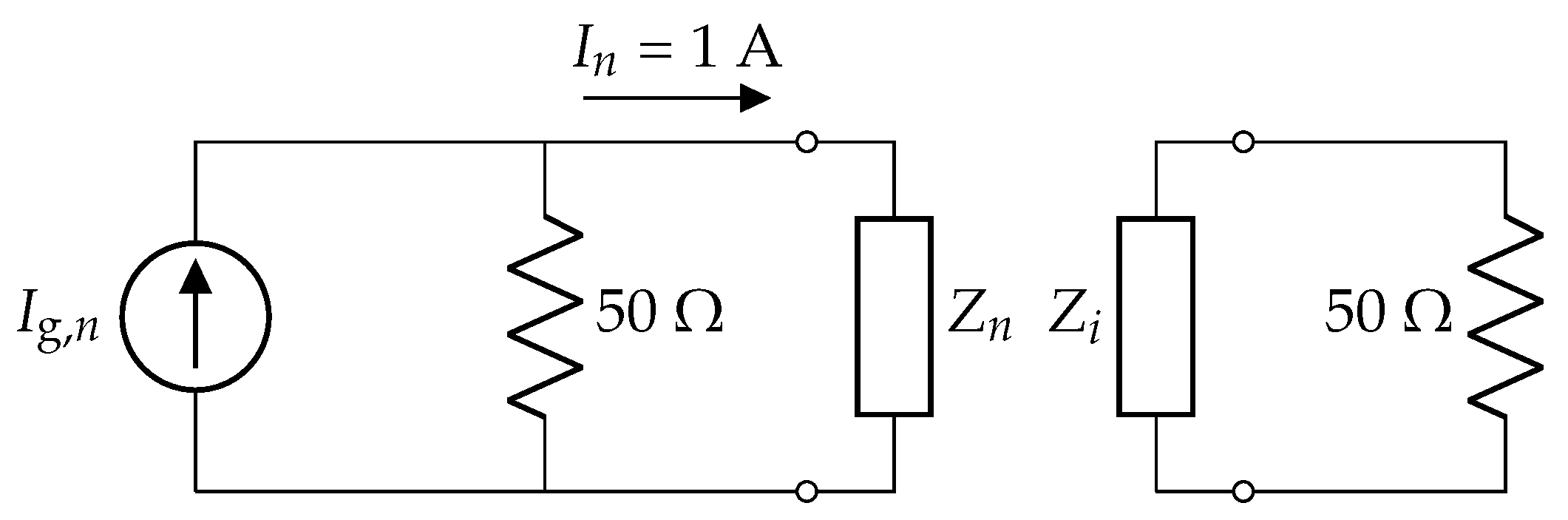
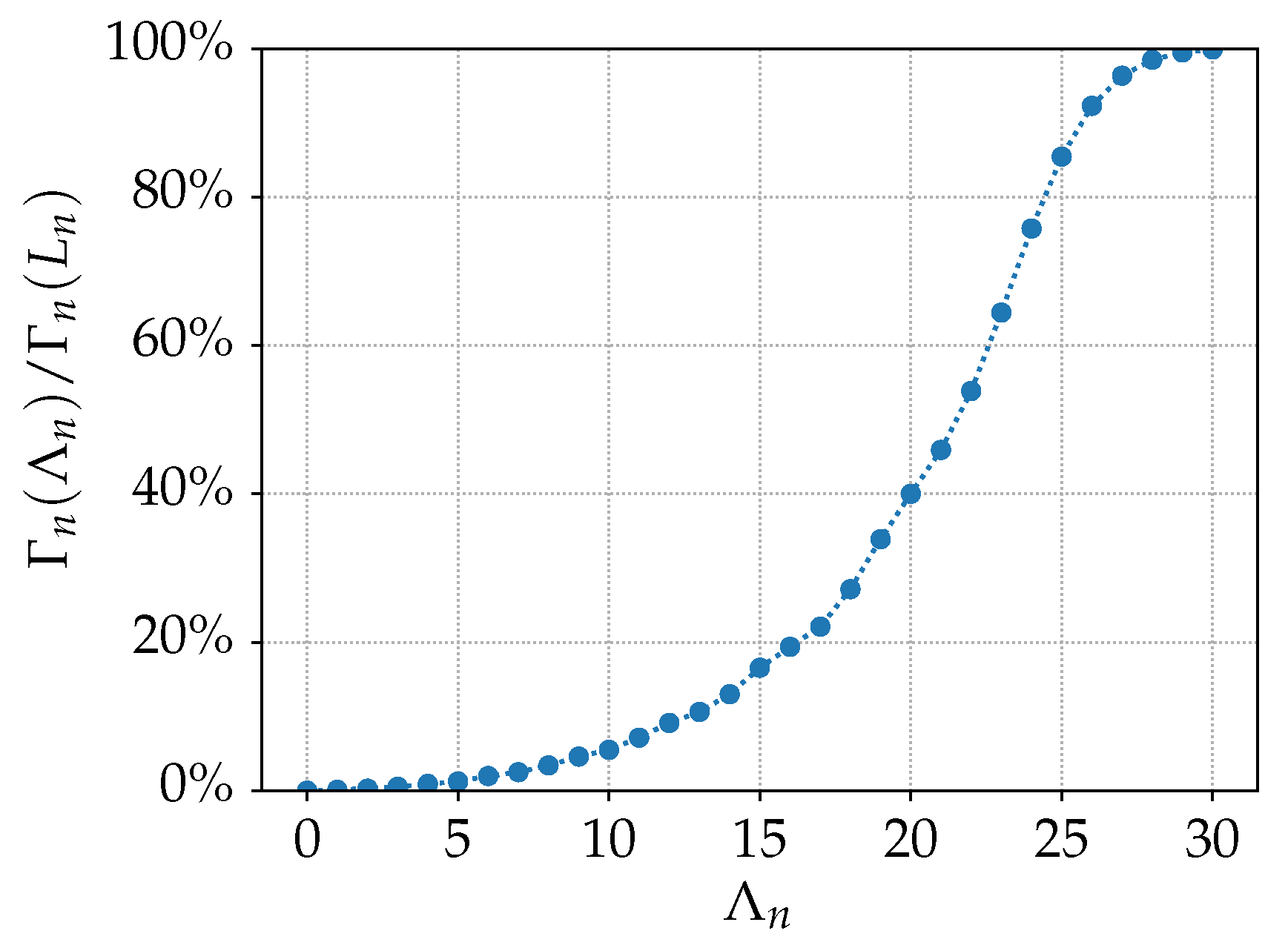

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Felaco, A.; Kapusuz, K.Y.; Rogier, H.; Vande Ginste, D. Spherical Fourier-Transform-Based Real-TimeNear-Field Shaping and Focusing in Beyond-5G Networks. Sensors 2023, 23, 3323. https://doi.org/10.3390/s23063323
Felaco A, Kapusuz KY, Rogier H, Vande Ginste D. Spherical Fourier-Transform-Based Real-TimeNear-Field Shaping and Focusing in Beyond-5G Networks. Sensors. 2023; 23(6):3323. https://doi.org/10.3390/s23063323
Chicago/Turabian StyleFelaco, Alessandro, Kamil Yavuz Kapusuz, Hendrik Rogier, and Dries Vande Ginste. 2023. "Spherical Fourier-Transform-Based Real-TimeNear-Field Shaping and Focusing in Beyond-5G Networks" Sensors 23, no. 6: 3323. https://doi.org/10.3390/s23063323
APA StyleFelaco, A., Kapusuz, K. Y., Rogier, H., & Vande Ginste, D. (2023). Spherical Fourier-Transform-Based Real-TimeNear-Field Shaping and Focusing in Beyond-5G Networks. Sensors, 23(6), 3323. https://doi.org/10.3390/s23063323








