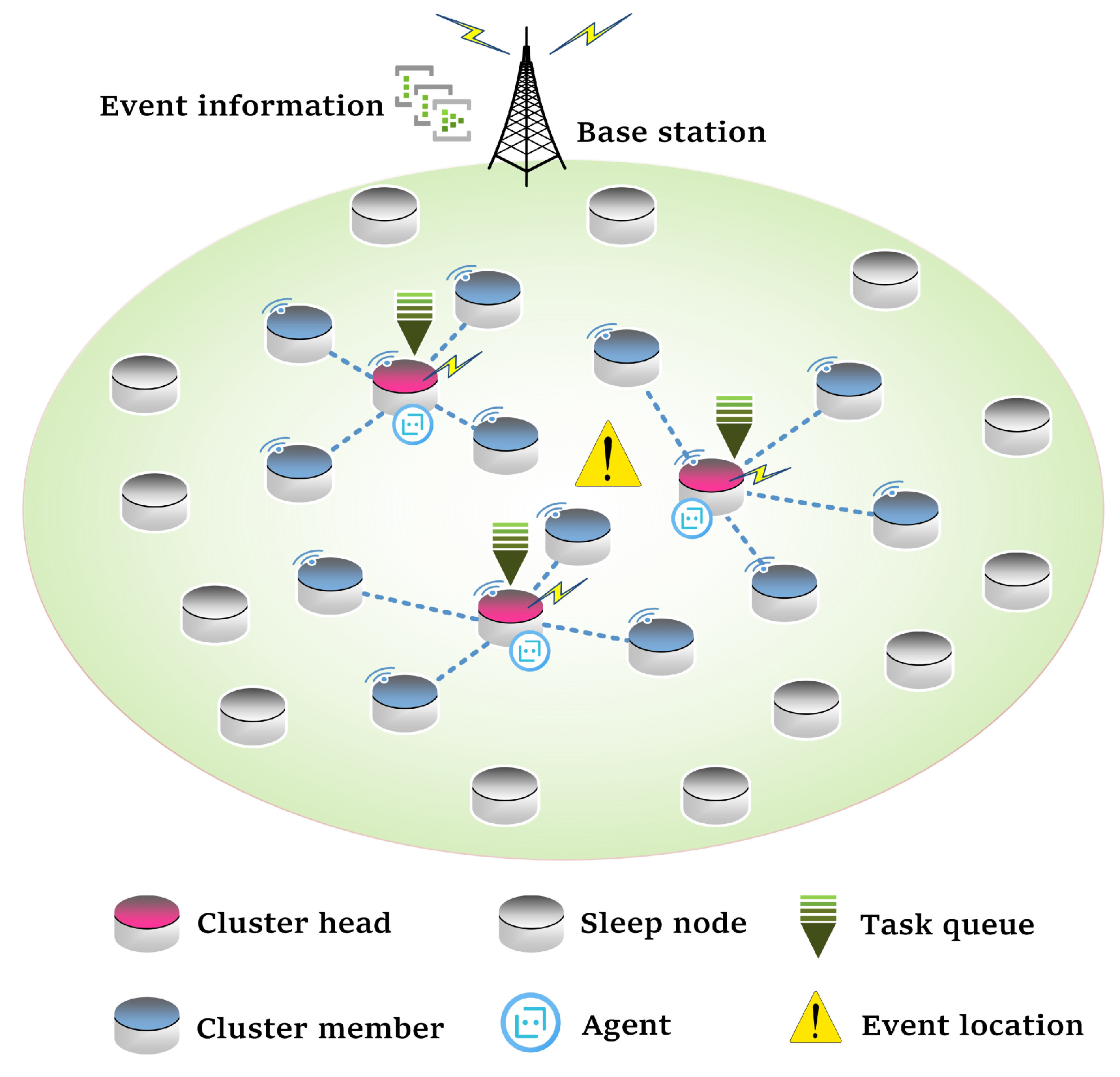
In this section, we evaluate the performance of DDPG-based one-to-multiple cooperative computing for large-scale event-driven WSNs. The simulations are carried out on the Python platform, where the Pytorch module is used to build the neural network model, and the Gym module is used to complete the environment construction.
7.1. Simulation Environment Setting
Since the training and inference of the algorithm are separated, the training is carried out in a single cluster, and the inference is carried out in the whole WSN. Therefore, we set up two environments for training and inference. In order to obtain better algorithm performance, the training environment should be similar to the inference environment. The initial N value is four in the simulation.
For the training environment, we need to simulate a single cluster cooperative computing environment and build a deep neural network. We randomly deploy (
N + 1) nodes in the 20 × 20 m
monitoring area and randomly select a cluster head from them. All nodes have the same initial energy and can communicate with each other. In a training episode, the cluster head successively receives computation tasks and makes offloading decisions until the cluster head energy is exhausted. The two task parameters
and
are also randomly set from their ranges. The value of the node sensing radius
is related to node density, which is discussed in the simulation results. The parameters used in the training environment are shown in
Table 1, in which some parameter settings are referred to in the literature [
3,
33,
37]. The hidden layer of DDPG’s actor networks and critic networks is a three-layer structure, and the number of neurons is 256, 128, 64, respectively. The setting of the reward parameters
in (
16) has an influence on the convergence of the algorithm to the optimal value. These two parameters need to be manually adjusted and slightly changed according to different
N values. We will discuss this in the simulation results. The other hyperparameters of neural networks are shown in
Table 2.
For the inference environment, we simulate the full life cycle of the WSN. The the monitored area is
m
. A set of two-dimensional coordinates are randomly generated to represent the random deployment of nodes in the monitored area. Then, BS can obtain the node coordinates and notify every node. A communication channel is ideal so that the communication between nodes is stable and reliable. A randomly generated event queue demotes the event set
, and each event contains two elements: event location and a set of computation tasks. Event location is a two-dimensional coordinate randomly generated within the monitored area. For each computation task, the setting methods of parameters
and
are the same as in the training environment. The nodes within the range centered on the event location with the radius of
are activated and divided into several clusters by the dynamic clustering algorithm. The parameter
of inter-cluster task assignment in (
12) is set as 0.5. The actor network structure is consistent with that in the training environment. The other parameters are the same as the training environment.
7.2. Comparative Algorithms
To better evaluate the performance of the algorithm, there are five other offloading methods compared with the proposed algorithm.
(1) DQN-based offloading algorithm: Since the DQN algorithm can only deal with discrete action space, we selected a set of representative actions for different values of N. For example, when N = 4, we have 100 sampling actions, such as (0.2, 0.2, 0.2, 0.2, 0.2), (0.6, 0.2, 0.1, 0.1, 0), and so on. Similar to the DDPG algorithm, DQN also obtains neural network parameters by training in a single cluster environment and then performs an inference test in the whole WSN.
(2) Exhaustive search: For each task, the cluster head searches all the actions with a step size of 0.01 and then calculates the delay and energy consumption after executing each action. The action with the least energy consumption is selected as the optimal solution with the constraint of delay. With the increase in N, the computational complexity of this algorithm will increase explosively.
(3) Local computing: The cluster head completes all the computation tasks and does not cooperate with the cluster members.
(4) Random offloading: The cluster head randomly selects an action in the action space and performs the corresponding computation offloading.
(5) Average offloading: The cluster head divides computation tasks into N + 1 parts on average, and the cluster head and each member all participate in computing. This algorithm can make full use of the computing resources of clusters but also causes high energy consumption.
7.3. Simulation Results
In this section, we first observe the convergence of the DDPG algorithm in the training process and then compare it with the performance of other algorithms from the perspective of a single event and the whole WSN lifetime. In the simulation, we conducted 10 groups of comparative experiments for each parameter test point. In the same group of comparison experiments, the performance of all algorithms are compared under the same node distribution and the same event set, while in different groups of comparison experiments, the node distribution and event set are different. The final result is the average of 10 experiments (The Statistical Program for Social Sciences (SPSS) was utilized to analyze the statistical significance of the experimental data by the paired sample T test. The results show that the experimental data obtained by each algorithm at each parameter test point have significant differences (p < 0.05).).
(1) The convergence of the DDPG algorithm.
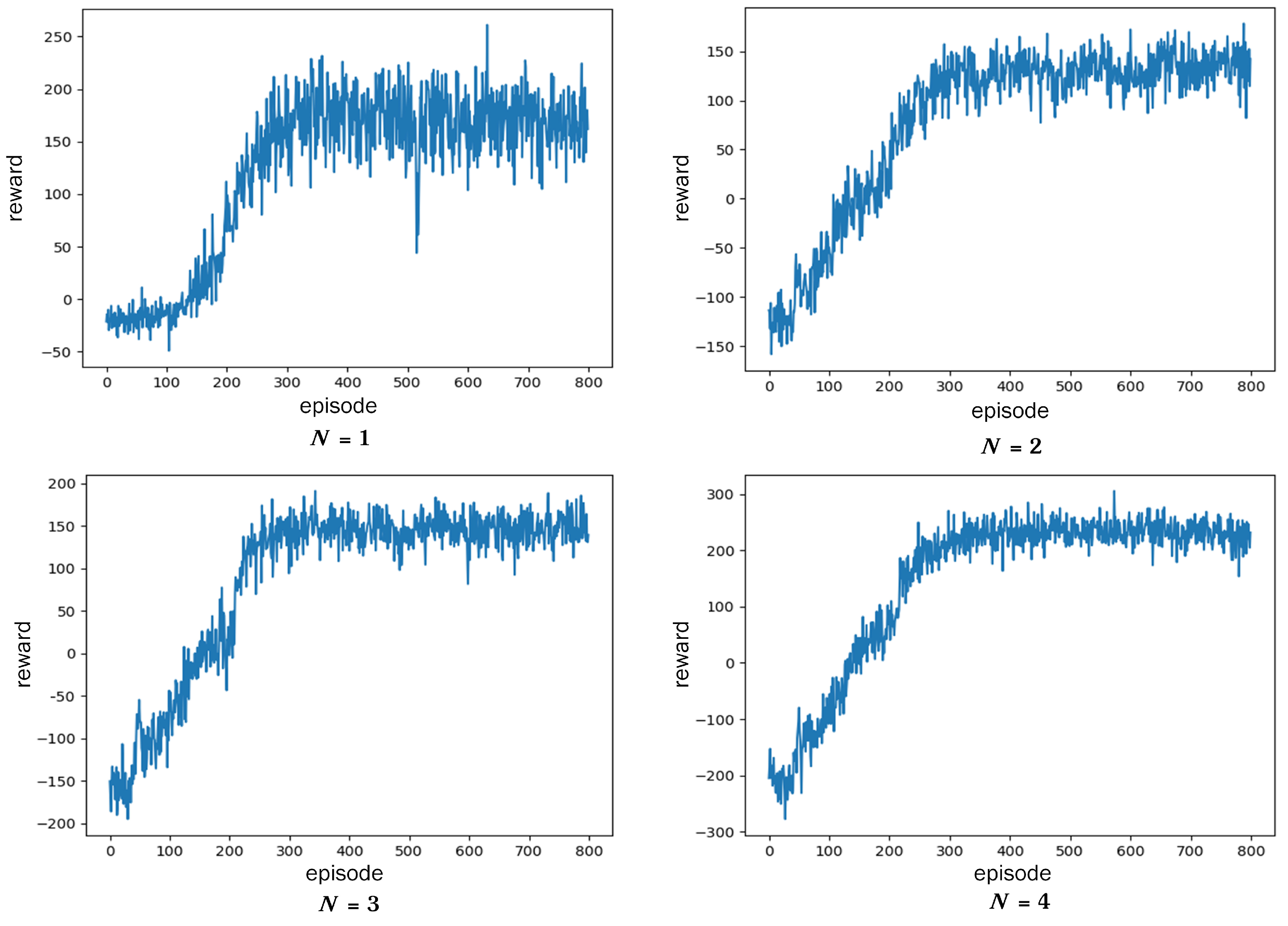
Figure 5 shows the reward curve of the DDPG algorithm when
N is equal to 1, 2, 3, 4. At the beginning of training, due to the random selection of actions, a large number of tasks cannot be completed, so the reward is negative. As the number of iterations increases, the reward rises rapidly and reaches a relatively stable level after the 300th round. The fluctuation of reward value is caused by the randomness of the task bit amount
and deadline
. Relatively, the smaller the
N, the bigger the reward fluctuations. This is because low computing capacity makes it difficult to meet the needs of some urgent tasks.
In addition, the setting of reward parameters has an influence on whether the algorithm converges to the optimal solution. The values of parameters
in (
16) need to be adjusted manually to help fast and stable convergence of the algorithm. A useful tip of adjustment is to firstly set the ratio of
and
to about 1:1 by adjusting
, and then fine-tune it according to the convergence trend. The reference value of
is shown in
Table 3. This table also shows the comparison of the task completion rate in one episode after the algorithm converges. As the
N value goes down, the task completion rate will decrease due to the lack of computing capacity. When
N = 1, the task completion rate is only 80% (lower than 95%), indicating that only one cooperative node cannot complete the event monitoring. In the process of algorithm inference, emergency tasks will be assigned to the clusters with high computing capacity (large
N value), while the clusters with low computing capacity mainly complete lightweight tasks. Thus, the completion rate of tasks in one event can exceed 95% for the whole WSN.
(2) Relationship between sensing radius and task completion rate.
Figure 6 shows the relationship between the task completion rate of an event and node sensing radius
for DDPG when the monitored area is 30 × 30 m, the number of nodes is 200, and the number of tasks in a single event is 800. With the same node density,
affects the number of nodes activated by this event. If
is small, the number of activated nodes is small. If the number of tasks is huge, the nodes will die due to excessive energy consumption, and the event cannot be completed. The same is true for other competitive algorithms. More nodes should participate in cooperative computing, which can effectively improve the task completion rate. As we can see, when node density is 200/900 = 0.22
,
greater than 6.5 m can ensure that the task completion rate of a single event is more than 95%.
(3) Comparison for single event completion. In this subsection, we discuss the reaction time of the task, the task completion rate, and energy consumption of a single event in inference environment.
The reaction time of tasks: The time of event processing is divided into several uneven time slots, and one task is processed in each time slot. In addition, the main difference in each algorithm is the scheme of cooperative computing for tasks within the cluster, while for the algorithm of clustering and task allocation, they adopt the same scheme. Therefore, the reaction time of tasks is considered an important indicator of algorithm performance.
Table 4 shows the average reaction time of different algorithms when the monitored area is 30 × 30 m, the number of nodes is 200, and the number of tasks is 3000. We can see that the reaction time of executing the DDPG algorithm is slightly higher than that of other algorithms but significantly lower than that of the exhaustive algorithm. The reaction time for the exhaustive algorithm to perform a computation task is about 0.5 s, which becomes unacceptable for processing events containing a large number of tasks. In addition, we can see that the reaction time of DQN is slightly less than that of the DDPG algorithm. This is because the neural network structure of the DQN algorithm is the same as that of the DDPG algorithm except for the Softmax function. Similar to the analysis in
Section 6.4, it can be seen that the computational complexity of generating an action of the cluster head for DQN is
, which is slightly lower than the DDPG algorithm.
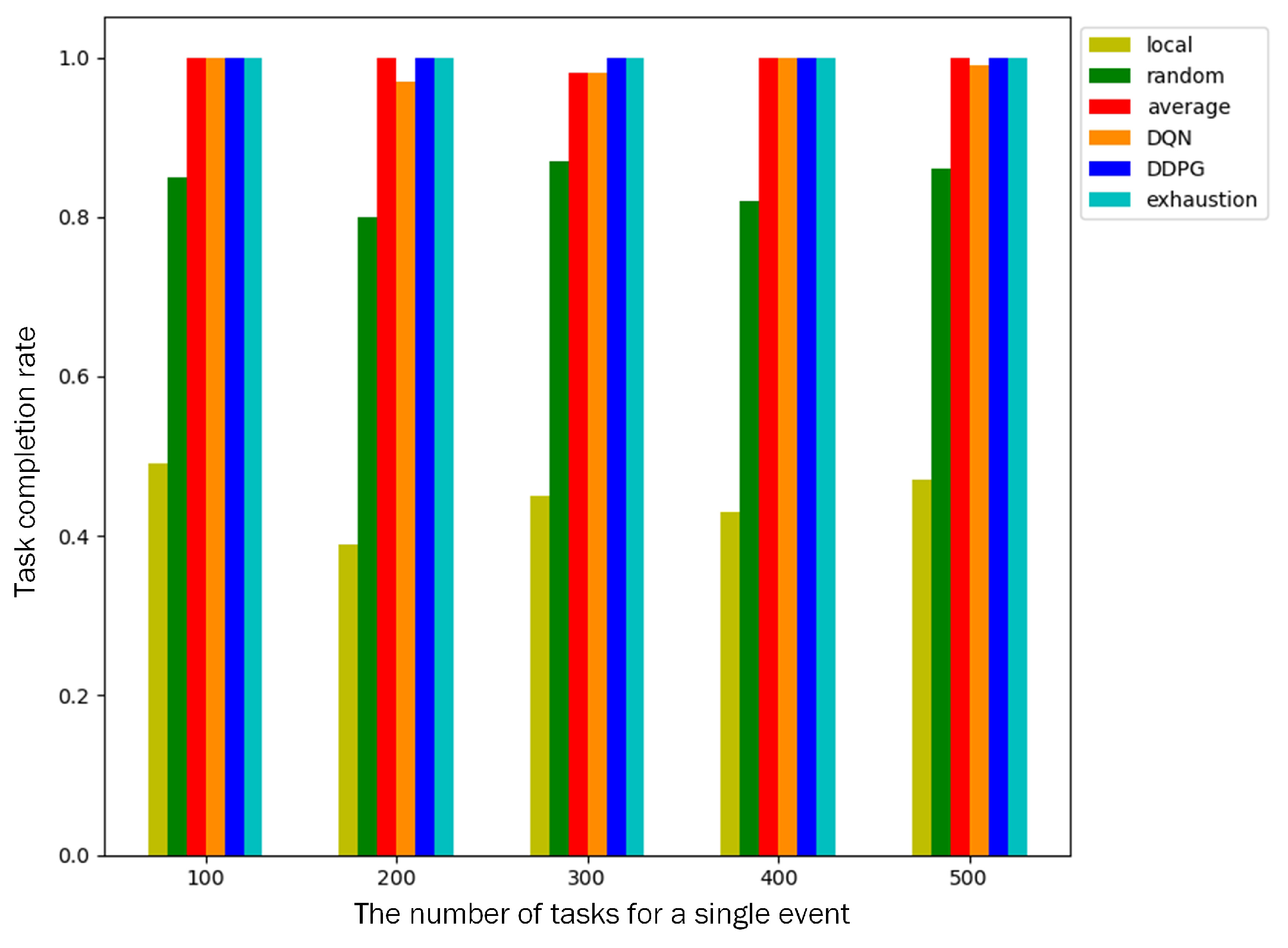
Task completion rate: A total of 200 nodes are deployed in the monitored area, and a single event contains 100–500 computation tasks. We compare the task completion rates of different algorithms. As shown in
Figure 7, the task completion rate of local computing is only about 40% because only cluster heads participate in the computation and cannot complete the task with a low deadline. The task completion rate of random offloading is about 80%. Both algorithms failed to complete the event because the task completion rate is less than 95%. The other four algorithms can make full use of cluster members to participate in cooperative computing, and the task completion rate of an event is above 96%.
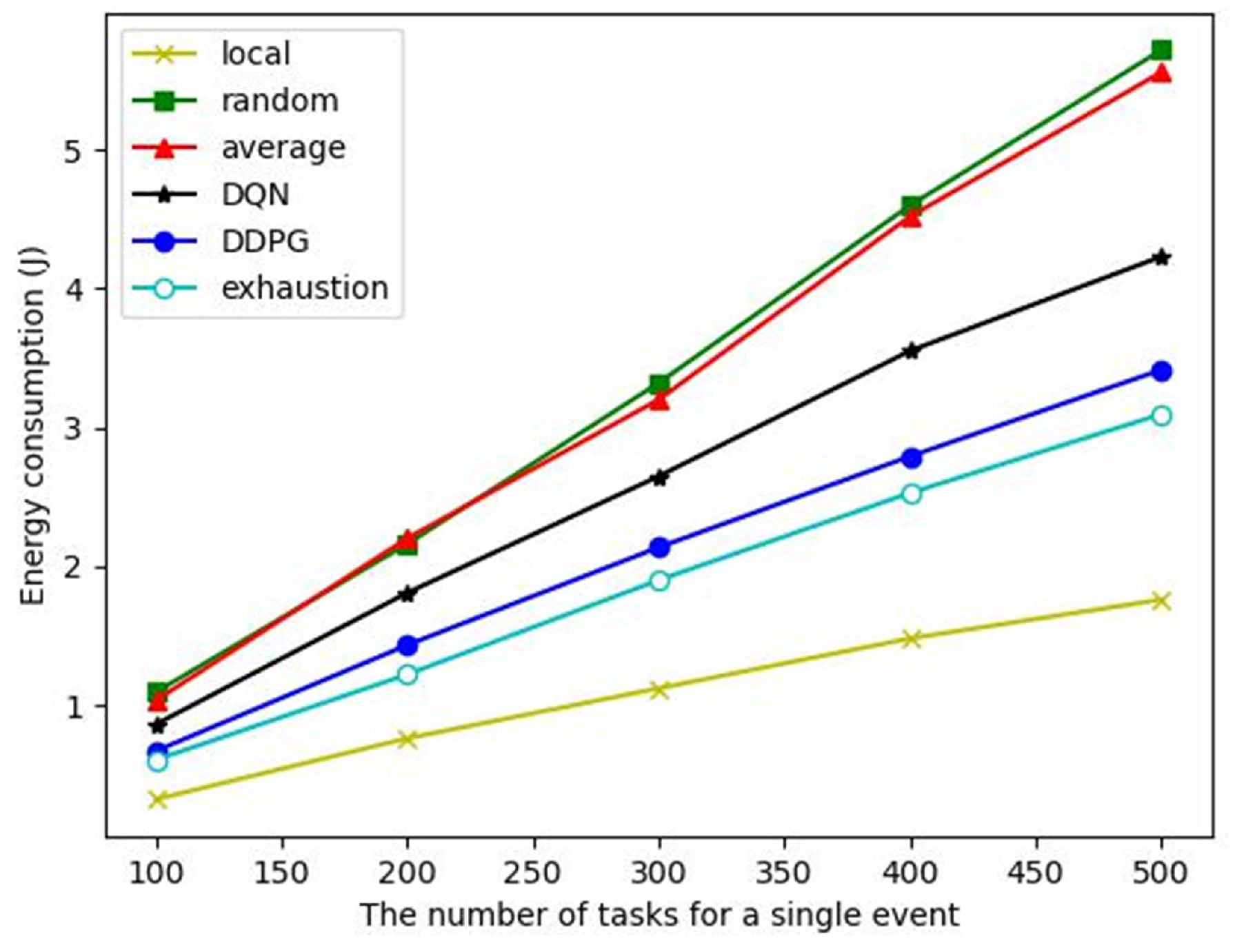
Energy consumption: As shown in
Figure 8, although the local computing algorithm has the lowest energy consumption, its task completion rate is only 40% (see
Figure 7), which cannot complete the event monitoring. The energy consumption of the DDPG algorithm to complete a single event is close to that of the exhaustive algorithm but significantly lower than that of other comparison algorithms. The average offloading algorithm cannot dynamically offload computation according to the task and node state. Although it can ensure the completion of tasks, it consumes a lot of energy. Therefore, even though it can ensure that the event monitoring is completed, the energy consumption is very high. The action selection of the DQN algorithm is a discrete sampling, which cannot effectively cover the optimal action selection. The action space of the DDPG algorithm is continuous, so better actions can be selected to achieve a performance close to the exhaustive algorithm.
In summary, when 200 nodes are deployed, we give a comprehensive comparison of the algorithms on the reaction time of tasks, task completion rate, and energy consumption, as shown in
Table 5. The proposed DDPG algorithm is superior to other algorithms and is close to the exhaustive algorithm in terms of energy consumption. At the same time, it can also ensure that the task completion rate exceeds 95% and the reaction time can be acceptable in practical applications.
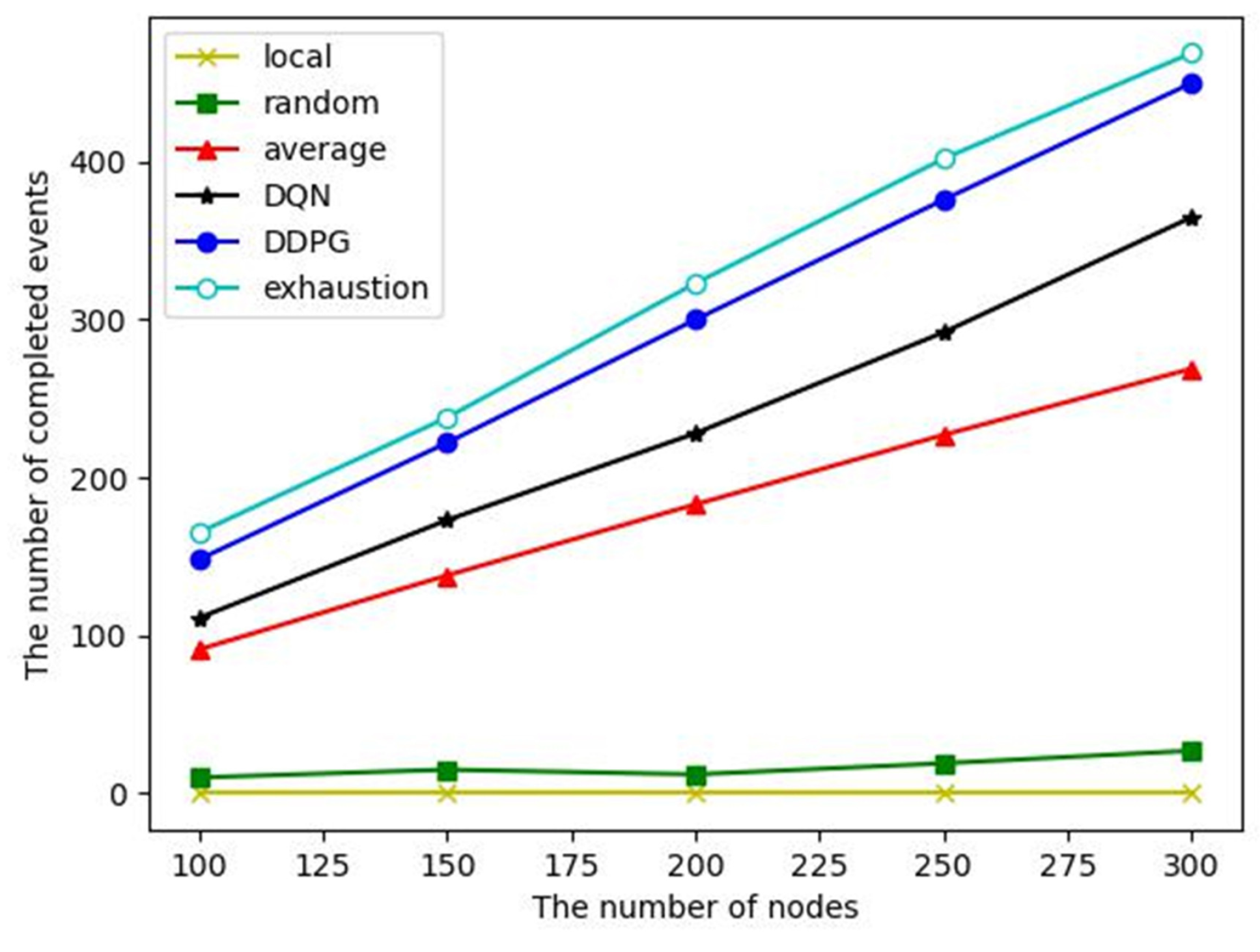
(4) Comparison for the whole WSN lifetime: In the whole lifetime of the WSN, we mainly investigate the number of completed events and the number of alive nodes, which can reflect the effectiveness and energy balance of the WSN.
The number of completed events: Event monitoring completion is defined as a task completion rate of more than 95%. From the above analysis, it can be seen that the task completion rates of local computing and random offloading are low, so the number of completed events of them are small, as shown in
Figure 9. Despite the average offloading, DQN and DDPG algorithms have similar task completion rates of a single event, and the energy consumption of the DDPG algorithm to complete an event is significantly lower than that of the other two algorithms, so it can complete more events in the whole WSN lifetime.
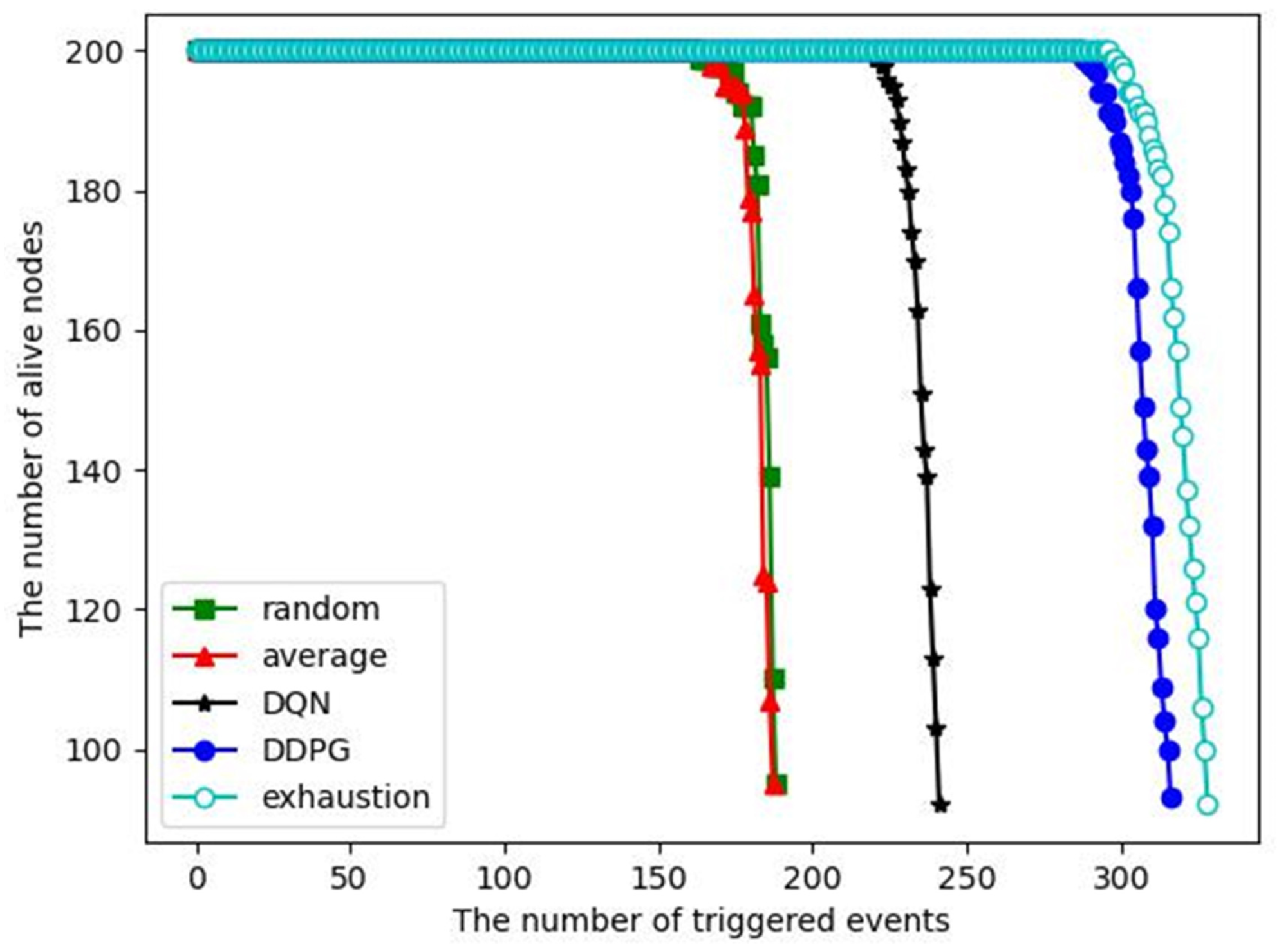
The number of alive nodes versus the number of triggered events:
Figure 10 shows that when 200 nodes are deployed in the monitored area, the number of alive nodes changes as the number of triggered events increases. As the number of events processed increases, the energy of the nodes decreases and some nodes may die (run out of energy). When the number of dead nodes exceeds half of the total number of nodes, we consider the entire network to have failed. Therefore, we want to have as many events processed as possible before the network crashes. In addition, if the energy consumption of each node is not balanced, some nodes will die prematurely due to taking on too many tasks, which will cause coverage holes. As we can see, the first node death only occurs at the end of the WSN lifetime for each algorithm, indicating that the dynamic clustering algorithm and inter-cluster task allocation can achieve an energy consumption balance. For the DDPG algorithm, more than 300 events are processed before the network crash, which is close to the exhaustive algorithm and significantly better than the other competitive algorithms. It indicates that the DDPG algorithm has better energy saving and energy consumption balance compared with the competitive algorithms. Local computing is not included in this comparison because it cannot complete event monitoring.