A Novel Method for Automatic Detection and Elimination of the Jumps Caused by the Instantaneous Disturbance Torque in the Maglev Gyro Signal
Abstract
1. Introduction
2. Materials and Methods
2.1. North-Seeking Principles of the GAT
2.2. HSA-KS Method
2.2.1. Main Principle of HSA Applied to the GAT Signal
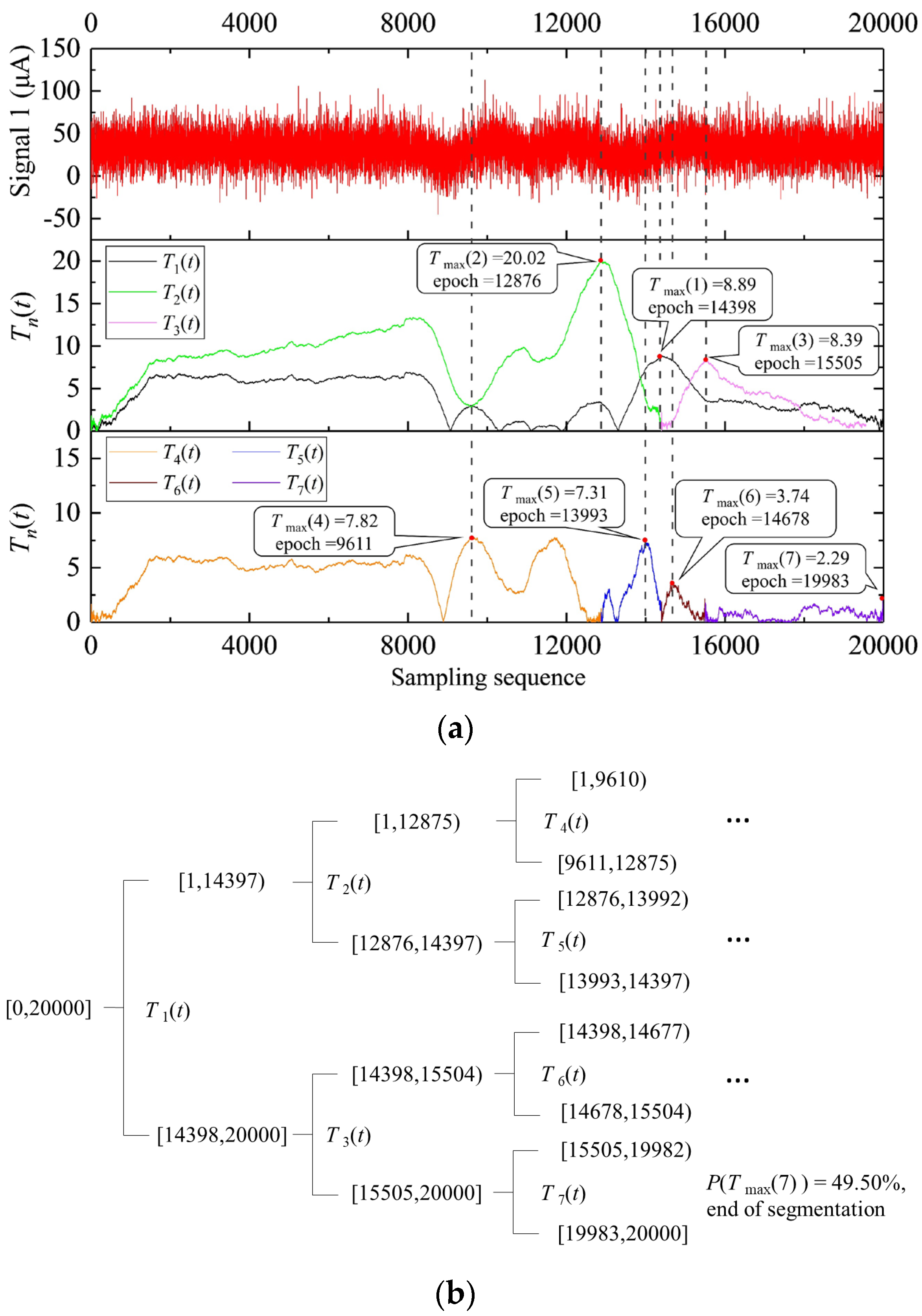
2.2.2. Determination of the Categorical Stationary Subsequence
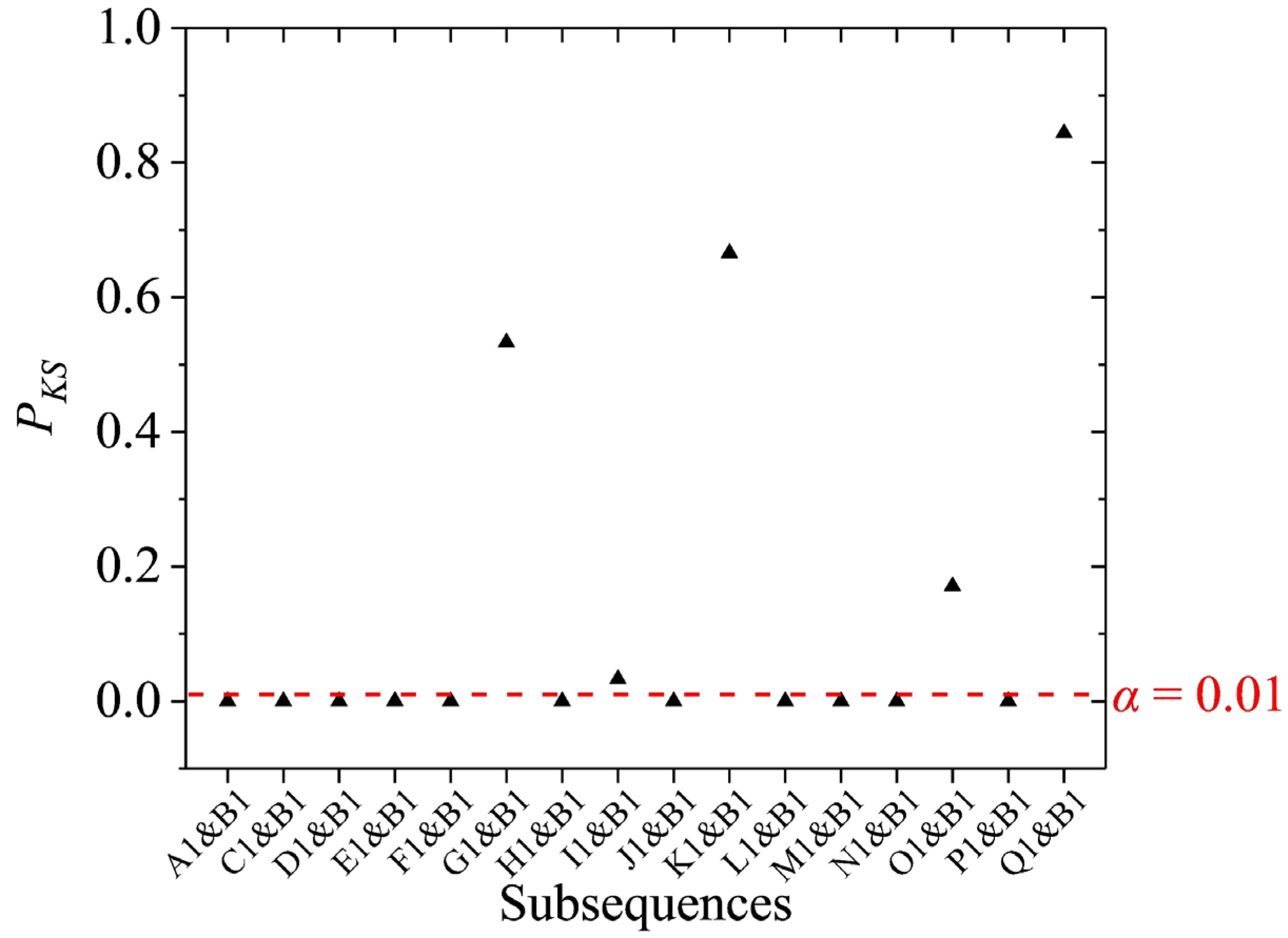
2.2.3. Two-Sample Kolmogorov-Smirnov Test
2.2.4. Specific Steps of the HSA-KS Method
2.3. Experimental Design
2.3.1. Field Experiment
2.3.2. Three Schemes for Processing GAT Signals
3. Results and Discussion
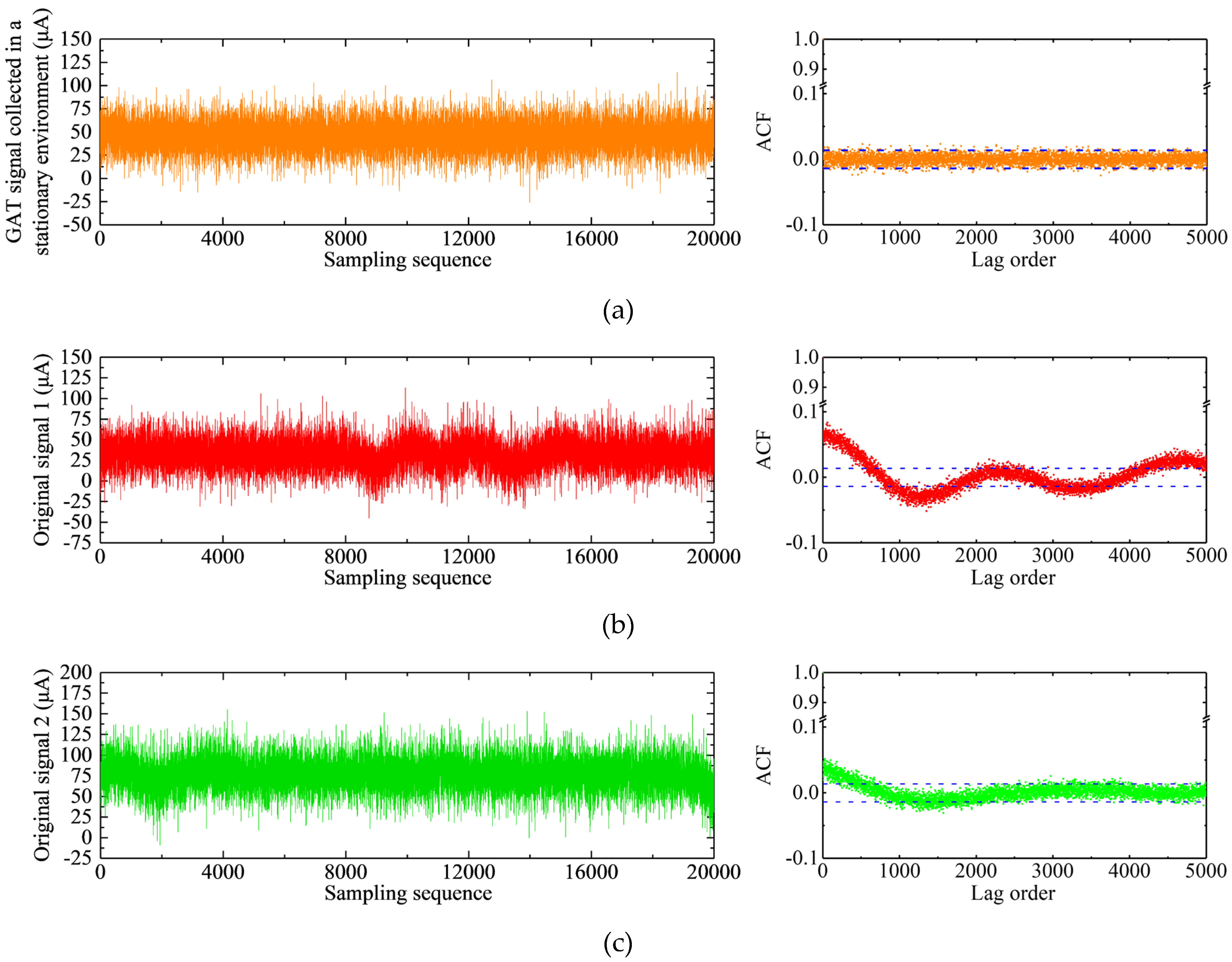
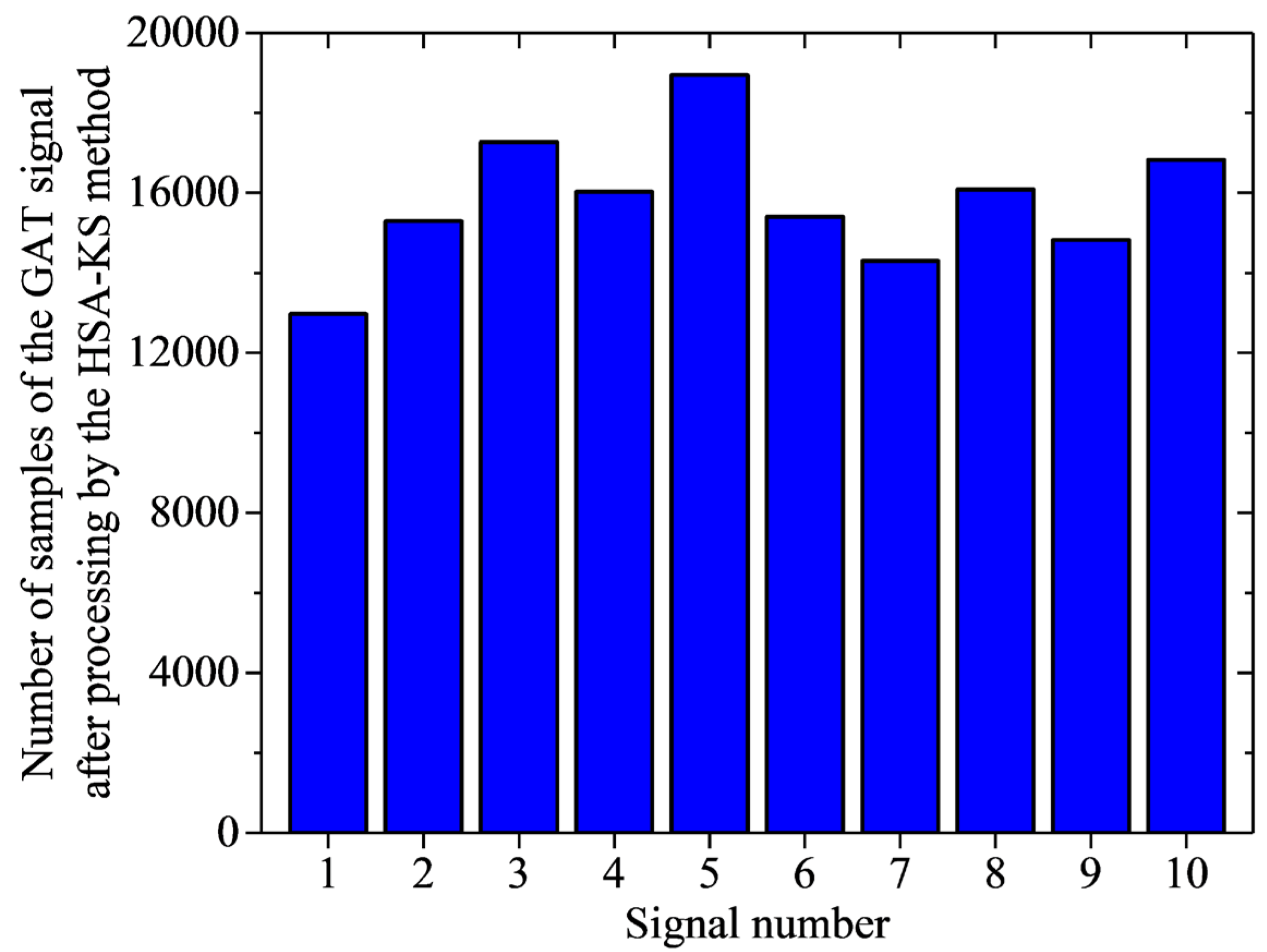
3.1. Typical GAT Signals
3.2. Signal Processing Results
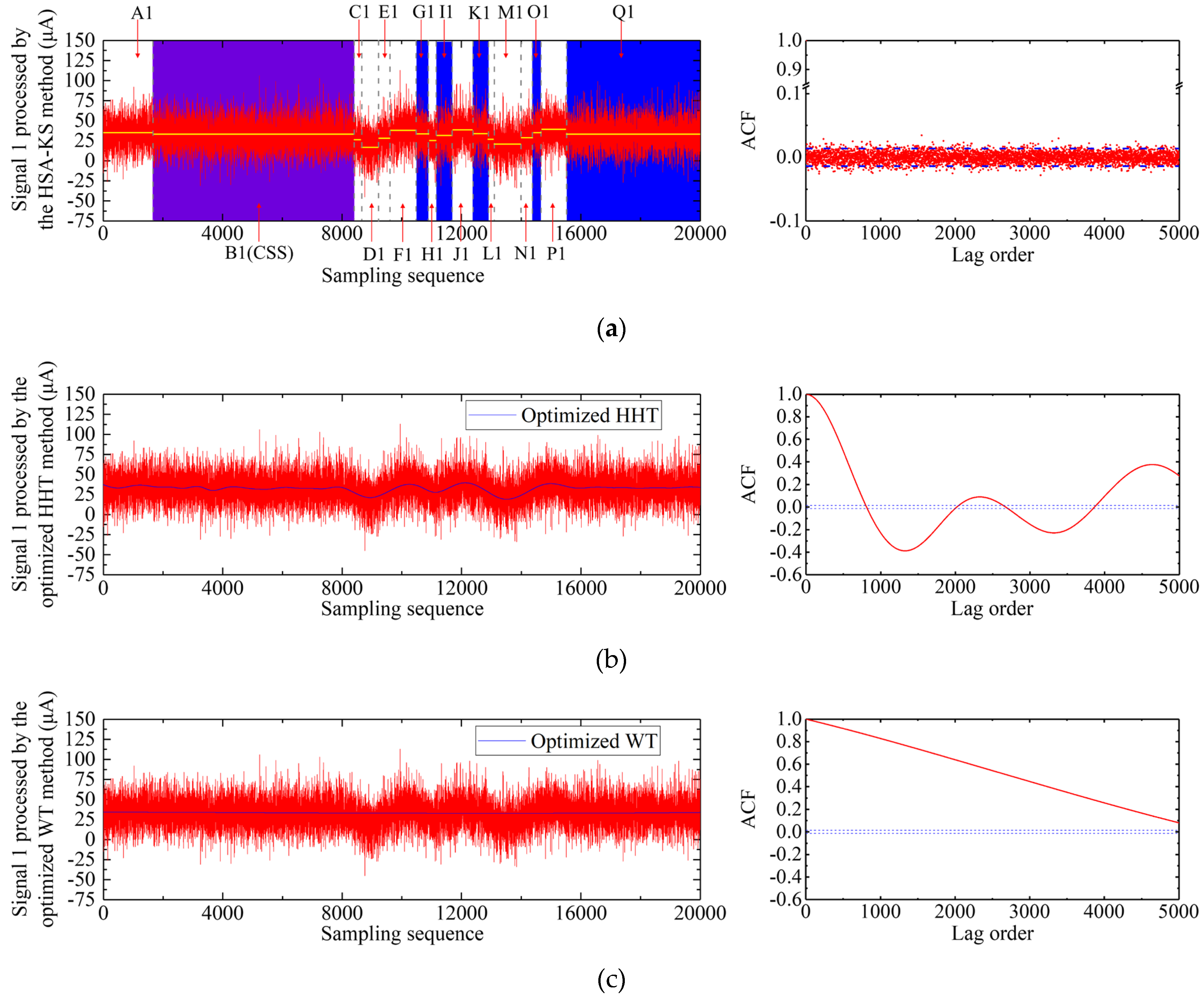
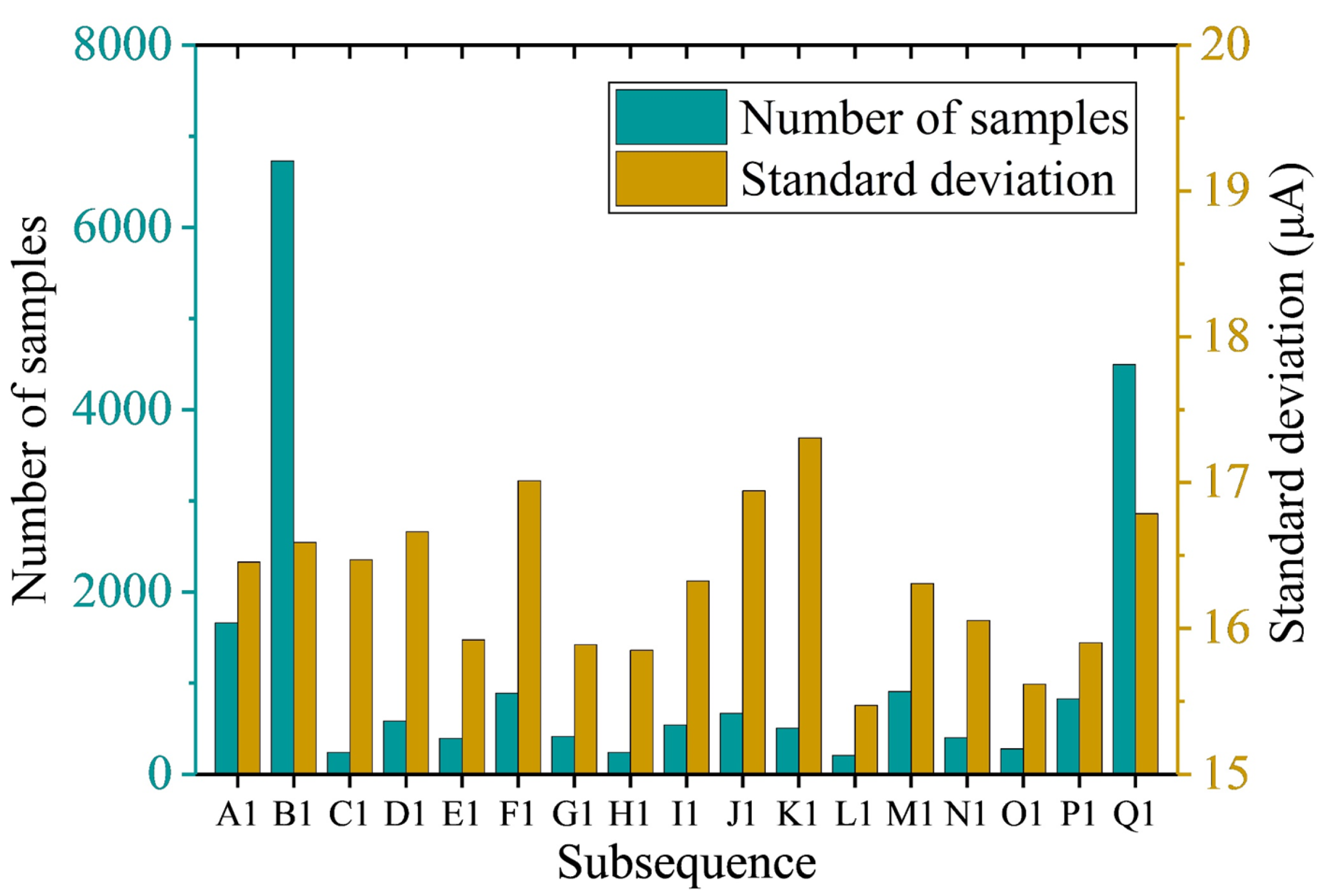
3.2.1. Signal 1 Processing Result
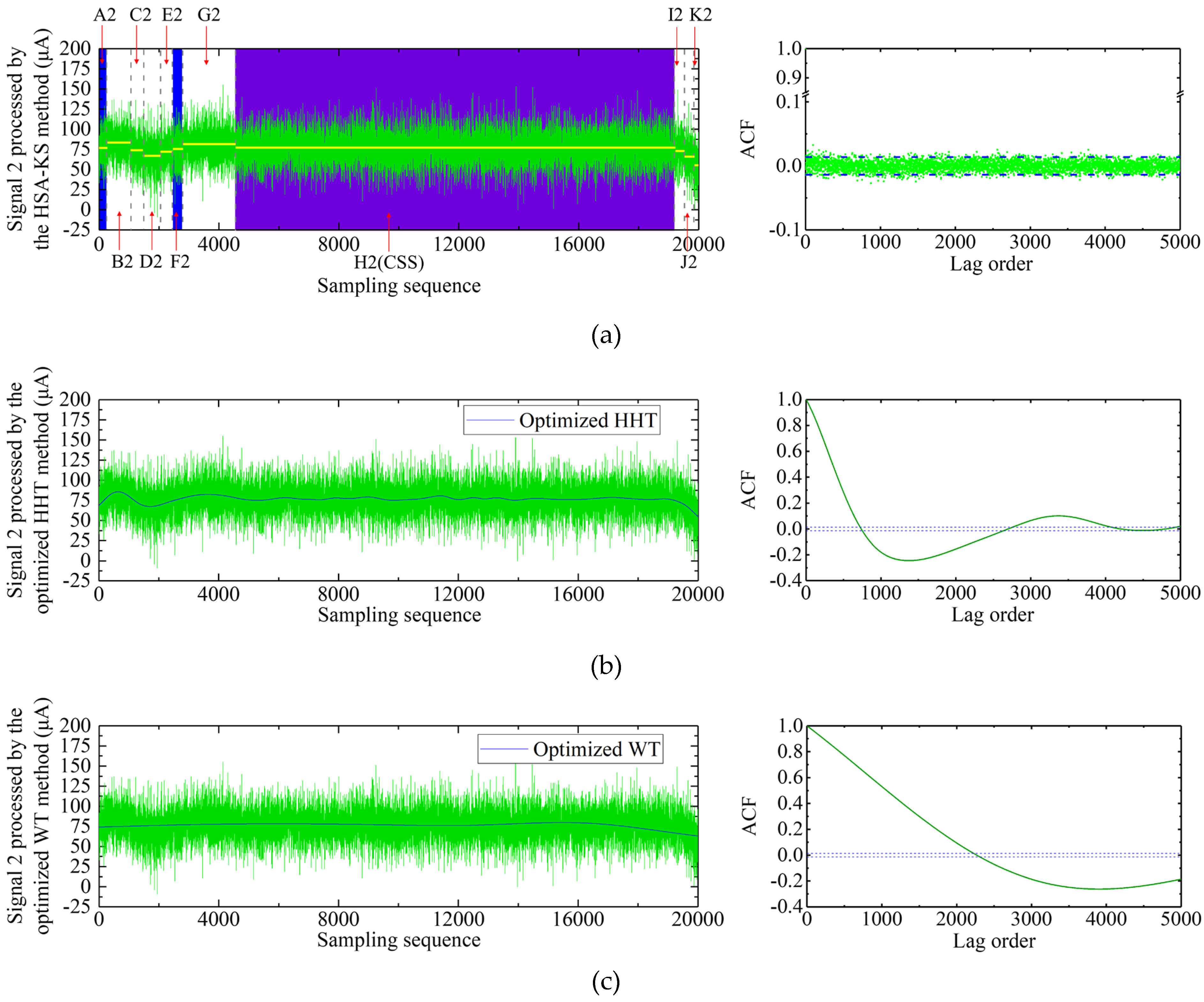
3.2.2. Signal 2 Processing Result
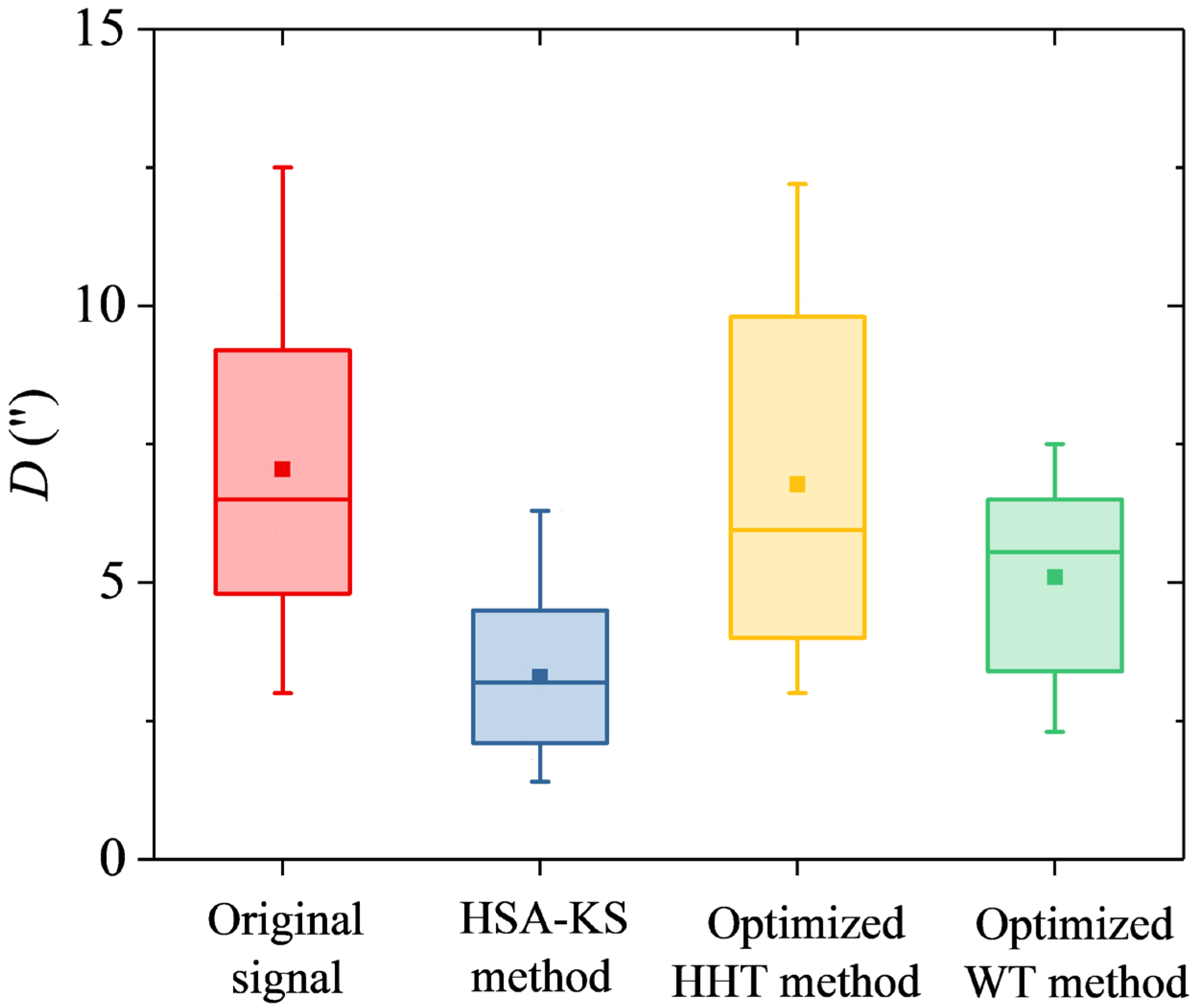
3.3. Results of the D-Values
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACF | autocorrelation function |
| CSS | categorical stationary subsequence |
| EMD | empirical mode decomposition |
| GAT | maglev gyro total station |
| GPS | global positioning system |
| HHT | Hilbert-Huang transform |
| HSA | heuristic segmentation algorithm |
| IMF | intrinsic mode function |
| KS | Kolmogorov-Smirnov |
| RMSE | root mean square error |
| WT | wavelet transform |
| gyro north azimuth | |
| N | total number of the current samples |
| collected real-time rotor current value of the torquer | |
| collected real-time stator current value of the torquer | |
| Ti(t) | statistics sequence in the HSA-KS method of the i-th segmentation |
| Tmax(i) | maximum value of Ti(t) |
| P(Tmax) | the statistical significance |
| l | the total number of samples of the signal to be segmented |
| I0(t) | signal sequence of the CSS |
| Ih(t) | subsequence with CSS for the two-sample KS test |
| KS statistic | |
| PKS | significance level of |
| α | significance level |
| m | number of the subsequences segmented from the original signal |
| A1, B1, C1, …, and Q1 | subsequences segmented by the signal 1 |
| A2, B2, C2, …, and K2 | subsequences segmented by the signal 2 |
| D-value | absolute difference between the gyro and high-precision GPS north azimuths |
References
- Thomas, T.L. The Six Methods of Finding North Using a Suspended Gyroscope. Surv. Rev. Dir. 1982, 26, 257–272. [Google Scholar] [CrossRef]
- Yang, Z.; Shi, Z.; Yang, J. North Seeking Principle and Measurement Application of Magnetically Suspended Gyroscope; Surveying and Mapping Press: Beijing, China, 2017. [Google Scholar]
- Filatov, Y.V.; Pavlov, P.A.; Velikoseltsev, A.A.; Schreiber, K.U. Precision Angle Measurement Systems on the Basis of Ring Laser Gyro. Sensors 2020, 20, 6930. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Y. Integrated Geographical Latitude Measurement and North-Seeking Technology and Method of Maglev Gyro Total Station in Confined Space of Mining. Insights Min. Sci. Technol. 2022, 3, 555618. [Google Scholar]
- Shi, Z.; Yang, Z.; He, K. Azimuth information processing optimization method for a magnetically suspended gyroscope. J. Intell. Fuzzy Syst. 2018, 34, 787–796. [Google Scholar] [CrossRef]
- Huo, Z.; Wang, F.; Shen, H.; Sun, X.; Zhang, J.; Li, Y.; Chu, H. Optimal Compensation of MEMS Gyroscope Noise Kalman Filter Based on Conv-DAE and MultiTCN-Attention Model in Static Base Environment. Sensors 2022, 22, 7249. [Google Scholar] [CrossRef]
- Yang, J. Automation of the GAT Magnet Suspended Gyro-Total-Station and the Gyroscope’s Data Analysis. Ph.D. Thesis, Chang’an University, Xi’an, China, 2011. [Google Scholar]
- Ma, J. Research on Key Technology of Maglev Gyroscope Orientation Measurement for Super Long Tunnel under Complex Environment. Ph.D. Thesis, Chang’an University, Xi’an, China, 2019. [Google Scholar]
- Wang, Y.; Yang, Z.; Shi, Z.; Ma, J.; Liu, D.; Shi, L. Periodic error detection and separation of magnetic levitation gyroscope signals based on continuous wavelet transform and singular spectrum analysis. Meas. Sci. Technol. 2022, 33, 065107. [Google Scholar] [CrossRef]
- Ma, J.; Yang, Z.; Shi, Z.; Zhang, X.; Liu, C. Application and Optimization of Wavelet Transform Filter for North-Seeking Gyroscope Sensor Exposed to Vibration. Sensors 2019, 19, 3624. [Google Scholar] [CrossRef]
- Liu, D.; Yang, Z.; Wang, D.; Li, H. Research on Noise Reduction of Rotor Signal of Maglev Gyroscope Based on Local Mean Decomposition. J. Electron. Meas. Instrum. 2022, 36, 20–27. [Google Scholar] [CrossRef]
- Peesapati, R.; Sabat, S.L.; Karthik, K.P.; Nayak, J.; Giribabu, N. Efficient Hybrid Kalman Filter for Denoising Fiber Optic Gyroscope Signal. Optik 2013, 124, 4549–4556. [Google Scholar] [CrossRef]
- Song, J.; Shi, Z.; Wang, L.; Wang, H. Random Error Analysis of MEMS Gyroscope Based on an Improved DAVAR Algorithm. Micromachines 2018, 9, 373. [Google Scholar] [CrossRef]
- Zhang, X. Research on Data Processing of Maglev Gyroscope Based on Frequency Domain Analysis and Multivariate Filtering. MEng Thesis, Chang’an University, Xi’an, China, 2019. [Google Scholar]
- Liu, C. Research on Key Technologies of Positioning and Orientation Measurement of Fiber Optic Gyro Strapdown Inertial Navigation System in Confined Space. Ph.D. Thesis, Chang’an University, Xi’an, China, 2021. [Google Scholar]
- Fraedrich, K.; Hang, H.; Gerstengarbe, F.W.; Werner, P.C. Multiscale Detection of Abrupt Climate Changes: Application to River Nile Flood Levels. Int. J. Climatol. 1997, 17, 1301–1315. [Google Scholar] [CrossRef]
- Zhongwei, Y.; Duzheng, Y.; Cun, W. Climatic jumps in the flood/drought historical chronology of central China. Clim. Dyn. 1992, 6, 153–160. [Google Scholar] [CrossRef]
- Mann, H.B. Non-Parametric Test Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Feng, G.; Gong, Z.; Zhi, R.; Zhang, D. Analysis of Precipitation Characteristics of South and North China Based on the Power-Law Tail Exponents. Chinese Phys. B 2008, 17, 2745–2752. [Google Scholar] [CrossRef]
- Feng, G.; Gong, Z.; Dong, W.; Li, J. Abrupt Climate Change Detection Based on Heuristic Segmentation Algorithm. Acta Phys. Sin. 2005, 54, 5494–5499. [Google Scholar] [CrossRef]
- Bernaola-Galván, P.; Ivanov, P.C.; Amaral, L.A.N.; Stanley, H.E. Scale Invariance in the Nonstationarity of Human Heart Rate. Phys. Rev. Lett. 2001, 87, 168105. [Google Scholar] [CrossRef]
- Huang, S.; Liu, D.; Huang, Q.; Chen, Y. Contributions of climate variability and human activities to the variation of runoff in the Wei River Basin, China. Hydrol. Sci. J. 2016, 61, 1026–1039. [Google Scholar] [CrossRef]
- Fukuda, K.; Stanley, H.E.; Amaral, L. Heuristic segmentation of a nonstationary time series. Phys. Rev. E 2004, 69, 21108. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, L.; Xiao, Y.; Chang, C.-C.; Zhi, X.; Shen, Z. New framework for assessing urban stormwater management measures in the context of climate change. Sci. Total. Environ. 2021, 813, 151901. [Google Scholar] [CrossRef]
- Dos Reis, J.; Oliveira Costa, C.; Sá da Costa, J. Local Validation of Structural Health Monitoring Strain Measurements. Measurement 2019, 136, 143–153. [Google Scholar] [CrossRef]
- Wang, M.; Jiang, S.; Ren, L.; Xu, C.-Y.; Wei, L.; Cui, H.; Yuan, F.; Liu, Y.; Yang, X. The Development of a Nonstationary Standardised Streamflow Index Using Climate and Reservoir Indices as Covariates. Water Resour. Manag. 2022, 36, 1377–1392. [Google Scholar] [CrossRef]
- Feller, W. An Introduction to Probability Theory and Its Applications, 2nd ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 1971. [Google Scholar]
- Massey, F.J., Jr. The Kolmogorov-Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in Fortran 77: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK; New York, NY, USA; Port Chester, NY, USA; Melbourne, VIC, Australia; Sydney, NSW, Australia, 1993. [Google Scholar]
- Stephens, M.A. Use of the Kolmogorov-Smirnov, Cramér-Von Mises and Related Statistics without Extensive Tables. J. R. Stat. Soc. Ser. B 1970, 32, 115–122. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Snin, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hubert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Battista, B.; Knapp, C.; McGee, T.; Goebel, V. Application of the empirical mode decomposition and Hilbert-Huang transform to seismic reflection data. Geophysics 2007, 72, H29–H37. [Google Scholar] [CrossRef]
- Mallat, S.G. Multiresolution Approximations and Wavelet Orthonormal Bases of L 2 (R). Trans. Am. Math. Soc. 1989, 315, 69. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.M.; Kerkyacharian, G.; Picard, D. Density estimation by wavelet thresholding. Ann. Stat. 1996, 24, 508–539. [Google Scholar] [CrossRef]
- Liu, H.; Wang, W.; Xiang, C.; Han, L.; Nie, H. A de-noising method using the improved wavelet threshold function based on noise variance estimation. Mech. Syst. Signal Process. 2018, 99, 30–46. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons, Inc.: Hoboken, Hoboken, NJ, USA, 2015. [Google Scholar]
- Cryer, J.D.; Chan, K.-S. Time Series Analysis: With Applications in R, 2nd ed.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, VIC, Australia, 2018. [Google Scholar]
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 2020. [Google Scholar]
- Ma, J.; Yang, Z.; Shi, Z.; Liu, C.; Yin, H.; Zhang, X. Adjustment options for a survey network with magnetic levitation gyro data in an immersed under-sea tunnel. Surv. Rev. 2018, 51, 373–386. [Google Scholar] [CrossRef]


| Scheme | Original Signal | HSA-KS Method | Optimized HHT Method | Optimized WT Method |
|---|---|---|---|---|
| Signal 1 | 9.2 | 3.5 | 10.1 | 3.3 |
| Signal 2 | 3.5 | 1.4 | 4.0 | 7.5 |
| Scheme | Original Signal | HSA-KS Method | Optimized HHT Method | Optimized WT Method |
|---|---|---|---|---|
| Mean value | 7.1 | 3.3 | 6.8 | 5.1 |
| Improvement | — | 53.5% | — | 28.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yang, Z.; Ma, J.; Shi, Z.; Liu, D.; Shi, L.; Li, H. A Novel Method for Automatic Detection and Elimination of the Jumps Caused by the Instantaneous Disturbance Torque in the Maglev Gyro Signal. Sensors 2023, 23, 2763. https://doi.org/10.3390/s23052763
Wang Y, Yang Z, Ma J, Shi Z, Liu D, Shi L, Li H. A Novel Method for Automatic Detection and Elimination of the Jumps Caused by the Instantaneous Disturbance Torque in the Maglev Gyro Signal. Sensors. 2023; 23(5):2763. https://doi.org/10.3390/s23052763
Chicago/Turabian StyleWang, Yiwen, Zhiqiang Yang, Ji Ma, Zhen Shi, Di Liu, Ling Shi, and Hang Li. 2023. "A Novel Method for Automatic Detection and Elimination of the Jumps Caused by the Instantaneous Disturbance Torque in the Maglev Gyro Signal" Sensors 23, no. 5: 2763. https://doi.org/10.3390/s23052763
APA StyleWang, Y., Yang, Z., Ma, J., Shi, Z., Liu, D., Shi, L., & Li, H. (2023). A Novel Method for Automatic Detection and Elimination of the Jumps Caused by the Instantaneous Disturbance Torque in the Maglev Gyro Signal. Sensors, 23(5), 2763. https://doi.org/10.3390/s23052763






