Morphological and Spectral Features of Ionospheric Structures at E- and F-Region Altitudes over Poker Flat Analyzed Using Modeling and Observations
Abstract
1. Introduction
1.1. Background
1.2. Motivation
2. Data and Methodology
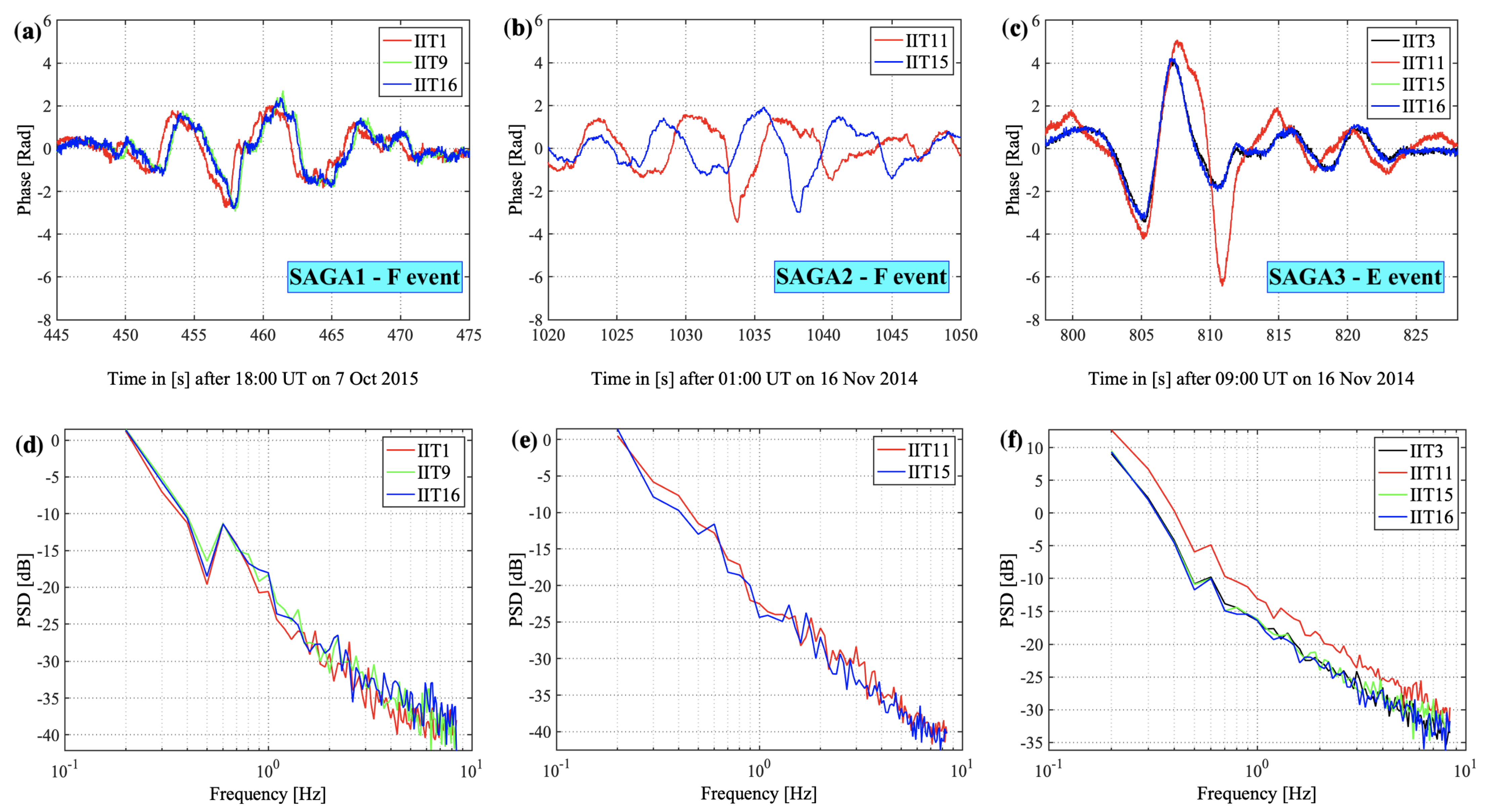
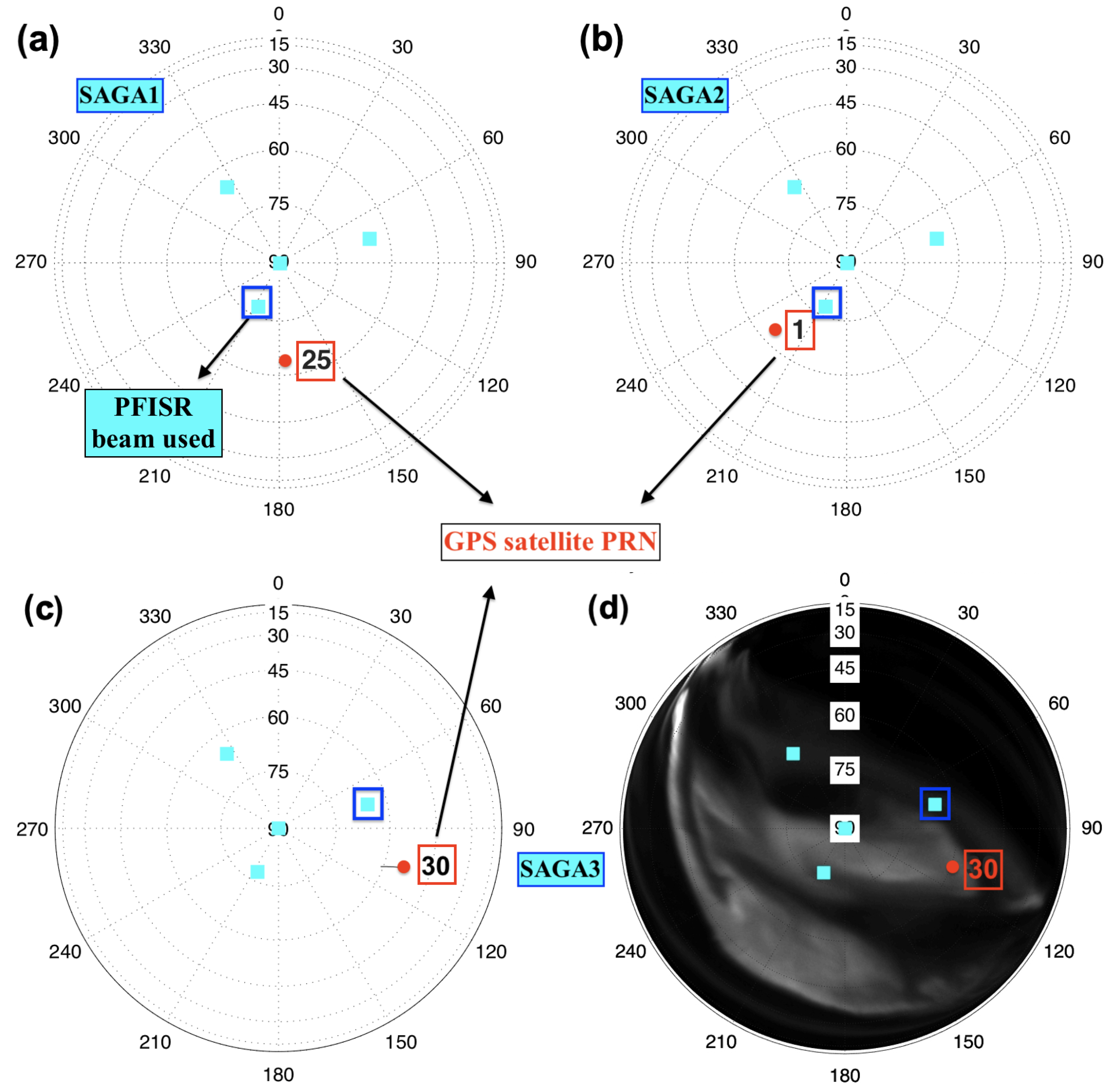
2.1. Observational Data
2.2. Modeling
3. Results
4. Discussion
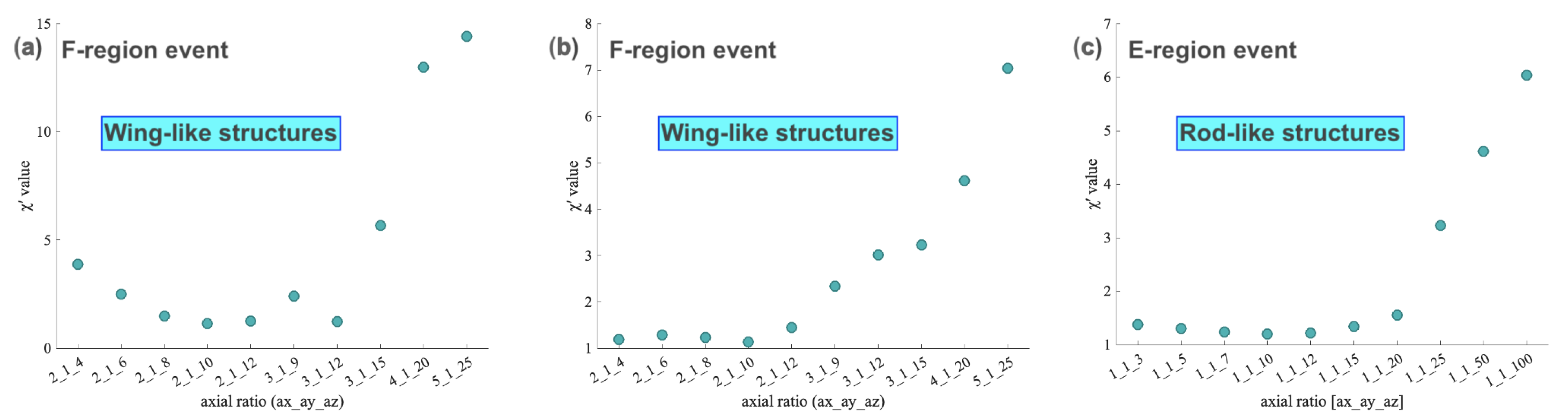
4.1. Morphology of the Irregularity Structures at E and F Heights
- The axial ratios estimated using our inverse analysis indicate that rod-like irregularity structures are more prominent for the E-region event (SAGA3 E-event from Table 2).
- Wing-type irregularity structures are likely responsible for the F-region phase fluctuations for both events (SAGA1 and SAGA2 F-events from Table 2).
- Additionally, the sensitivity analysis shown in Figure 5 support the results that the rod-like irregularities are responsible for E-region phase fluctuations and wing-like irregularities for F-region phase fluctuations.
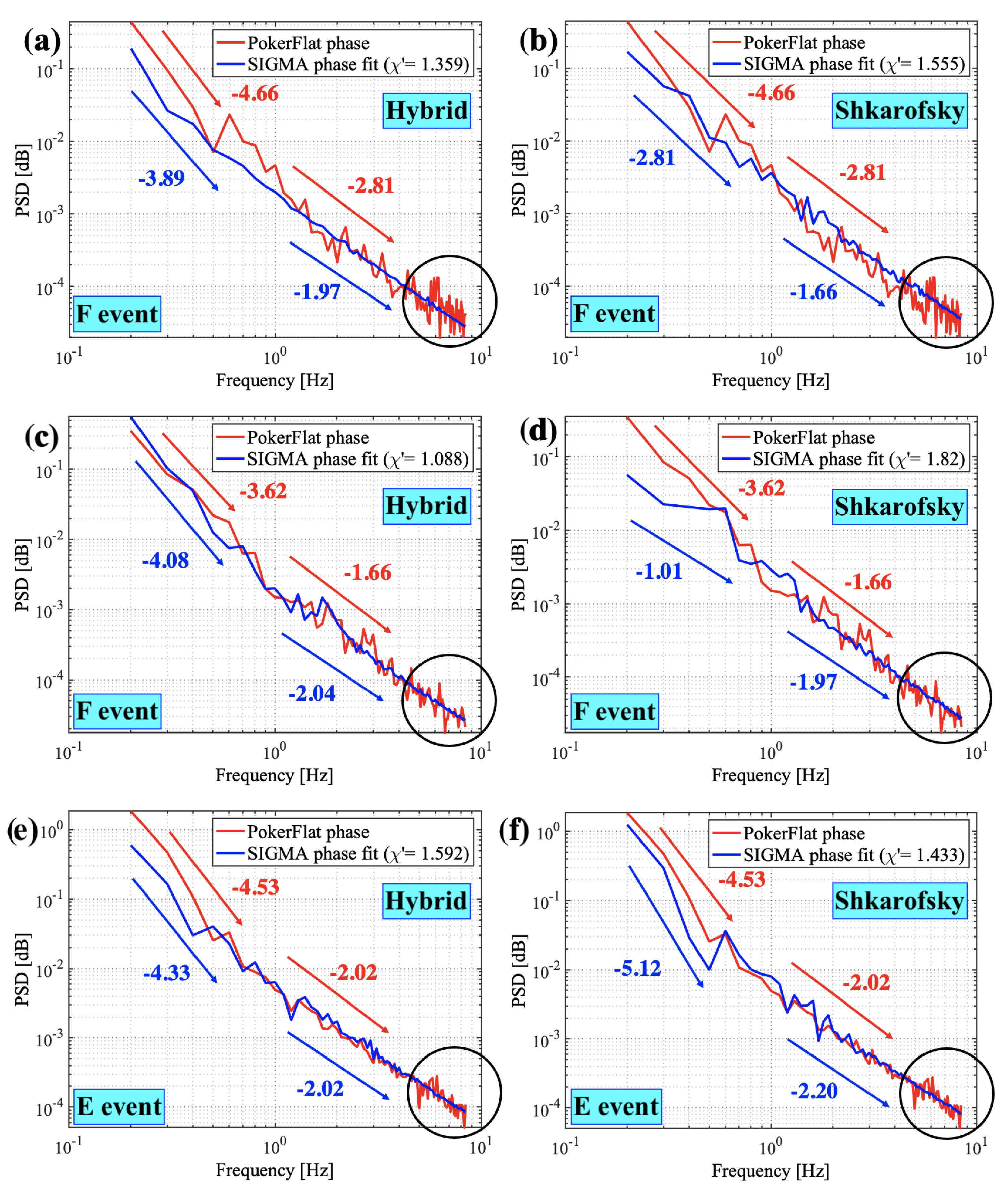
4.2. Variation of the Spectral Index at E- and F-Region Heights
- We analyzed spectral indices at irregularity layer height for the selected E- and F-region events. We found that the E-region power law index is less than those for the F-region cases (see Table 2);
- Spectral slopes of the PSDs of the phase time series on the ground are steeper at frequencies below 1 Hz compared to those above 1 Hz irrespective of E- or F-region scintillations (see Figure 7);
- The spectral slope of the scintillation spectrum on the ground is less than the spectral index at irregularity layer height.
5. Conclusions
- The axial ratio analyzed for the E-region event reveals that the irregularities are more elongated along the magnetic field lines having rod-like structures. On the other hand, the F-region irregularities have wing/sheet-like structures with irregularity axial ratios extending both along and across the field lines.
- The spectral indices analyzed at E- and F-region irregularity heights show that the E-region spectral index is less than the F-region spectral indices.
- Spectral slope analysis compares the slopes on the ground with those at the irregularity layer. We found that the spectral slopes on the ground are less than the slopes at the irregularity layer height for E- and F-region events, consistent with what is expected.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GPS | Global Positioning System |
| GNSS | Global Navigation Satellite System |
| GDI | Gradient Drift Instability |
| KHI | Kelvin-Helmholtz Instability |
| MLT | Magnetic Local Time |
| PSD | Power Spectral Density |
References
- Yeh, K.C.; Liu, C.H. Radio wave scintillations in the ionosphere. Proc. IEEE 1982, 70, 324–360. [Google Scholar]
- Bhattacharyya, A.; Yeh, K.; Franke, S.J. Deducing turbulence parameters from transionospheric scintillation measurements. Space Sci. Rev. 1992, 61, 335–386. [Google Scholar] [CrossRef]
- Wernik, A.W.; Alfonsi, L.; Materassi, M. Ionospheric irregularities, scintillation and its effect on systems. Acta Geophys. Pol. 2004, 52, 237–249. [Google Scholar]
- Coster, A.; Komjathy, A. Space weather and the global positioning system. Space Weather 2008, 6. [Google Scholar] [CrossRef]
- Yonezawa, T. Theory of formation of the ionosphere. Space Sci. Rev. 1966, 5, 3–56. [Google Scholar] [CrossRef]
- Ivanov-Kholodny, G.; Mikhailov, A. The Theory of Ionosphere Formation. In The Prediction of Ionospheric Conditions; Springer: Berlin/Heidelberg, Germany, 1986; pp. 15–52. [Google Scholar]
- Aarons, J. Global morphology of ionospheric scintillations. Proc. IEEE 1982, 70, 360–378. [Google Scholar] [CrossRef]
- Kintner, P.M.; Ledvina, B.M.; De Paula, E. GPS and ionospheric scintillations. Space Weather 2007, 5. [Google Scholar] [CrossRef]
- Jin, Y.; Moen, J.I.; Oksavik, K.; Spicher, A.; Clausen, L.B.; Miloch, W.J. GPS scintillations associated with cusp dynamics and polar cap patches. J. Space Weather. Space Clim. 2017, 7, A23. [Google Scholar] [CrossRef]
- Nishimura, Y.; Verkhoglyadova, O.; Deng, Y.; Zhang, S.R. Cross-Scale Coupling and Energy Transfer in the Magnetosphere-Ionosphere-Thermosphere System; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Kelley, M.C.; Vickrey, J.F.; Carlson, C.; Torbert, R. On the origin and spatial extent of high-latitude F region irregularities. J. Geophys. Res. Space Phys. 1982, 87, 4469–4475. [Google Scholar] [CrossRef]
- Kinrade, J.; Mitchell, C.N.; Smith, N.D.; Ebihara, Y.; Weatherwax, A.T.; Bust, G.S. GPS phase scintillation associated with optical auroral emissions: First statistical results from the geographic South Pole. J. Geophys. Res. Space Phys. 2013, 118, 2490–2502. [Google Scholar] [CrossRef]
- Prikryl, P.; Zhang, Y.; Ebihara, Y.; Ghoddousi-Fard, R.; Jayachandran, P.T.; Kinrade, J.; Mitchell, C.N.; Weatherwax, A.T.; Bust, G.; Cilliers, P.J.; et al. An interhemispheric comparison of GPS phase scintillation with auroral emission observed at South Pole and from DMSP satellite. Ann. Geophys. 2013, 56, 15. [Google Scholar] [CrossRef]
- Mrak, S.; Semeter, J.; Hirsch, M.; Starr, G.; Hampton, D.; Varney, R.H.; Reimer, A.S.; Swoboda, J.; Erickson, P.J.; Lind, F.; et al. Field-aligned GPS scintillation: Multisensor data fusion. J. Geophys. Res. Space Phys. 2018, 123, 974–992. [Google Scholar] [CrossRef]
- Jiao, Y.; Morton, Y.T.; Taylor, S.; Pelgrum, W. Characterization of high-latitude ionospheric scintillation of GPS signals. Radio Sci. 2013, 48, 698–708. [Google Scholar] [CrossRef]
- Fredricks, R.; Coroniti, F. Ambiguities in the deduction of rest frame fluctuation spectrums from spectrums computed in moving frames. J. Geophys. Res. 1976, 81, 5591–5595. [Google Scholar] [CrossRef]
- Wernik, A.; Liu, C.; Franke, S.J.; Gola, M. High-latitude irregularity spectra deduced from scintillation measurements. Radio Sci. 1990, 25, 883–895. [Google Scholar] [CrossRef]
- Rino, C.; Livingston, R. On the analysis and interpretation of spaced-receiver measurements of transionospheric radio waves. Radio Sci. 1982, 17, 845–854. [Google Scholar] [CrossRef]
- Livingston, R.C.; Rino, C.; Owen, J.; Tsunoda, R.T. The anisotropy of high-latitude nighttime F region irregularities. J. Geophys. Res. Space Phys. 1982, 87, 10519–10526. [Google Scholar] [CrossRef]
- Costa, E.; Fougere, P.F. Cross-spectral analysis of spaced-receiver measurements. Radio Sci. 1988, 23, 129–139. [Google Scholar] [CrossRef]
- Rino, C.; Livingston, R.; Matthews, S. Evidence for sheet-like auroral ionospheric irregularities. Geophys. Res. Lett. 1978, 5, 1039–1042. [Google Scholar] [CrossRef]
- Rino, C.; Owen, J. The structure of localized nighttime auroral zone scintillation enhancements. J. Geophys. Res. Space Phys. 1980, 85, 2941–2948. [Google Scholar] [CrossRef]
- Keskinen, M.J.; Ossakow, S. Nonlinear evolution of plasma enhancements in the auroral ionosphere, 1, Long wavelength irregularities. J. Geophys. Res. Space Phys. 1982, 87, 144–150. [Google Scholar] [CrossRef]
- Keskinen, M.J.; Ossakow, S. Theories of high-latitude ionospheric irregularities: A review. Radio Sci. 1983, 18, 1077–1091. [Google Scholar] [CrossRef]
- Bowles, K.; Balsley, B.; Cohen, R. Field-aligned E-region irregularities identified with acoustic plasma waves. J. Geophys. Res. 1963, 68, 2485–2501. [Google Scholar] [CrossRef]
- Greenwald, R.; Ecklund, W.; Balsley, B. Auroral currents, irregularities, and luminosity. J. Geophys. Res. 1973, 78, 8193–8203. [Google Scholar] [CrossRef]
- Costa, E.; Kelley, M. Ionospheric scintillation calculations based on in situ irregularity spectra. Radio Sci. 1977, 12, 797–809. [Google Scholar] [CrossRef]
- Rufenach, C.L. Ionospheric scintillation by a random phase screen: Spectral approach. Radio Sci. 1975, 10, 155–165. [Google Scholar] [CrossRef]
- Kersley, L.; Chandra, H. Power spectra of VHF intensity scintillations from F2-and E-region ionospheric irregularities. J. Atmos. Terr. Phys. 1984, 46, 667–672. [Google Scholar] [CrossRef]
- Conroy, J.P.; Deshpande, K.; Kunduri, B.; Varney, R.H.; Scales, W.; Zaghloul, A. Ionospheric scintillation data inversion to characterize the structures associated with a series of polar cap patches. Radio Sci. 2021, 56, e2020RS007235. [Google Scholar] [CrossRef]
- Deshpande, K.; Bust, G.; Clauer, C.; Rino, C.; Carrano, C. Satellite-beacon Ionospheric-scintillation Global Model of the upper Atmosphere (SIGMA) I: High-latitude sensitivity study of the model parameters. J. Geophys. Res. Space Phys. 2014, 119, 4026–4043. [Google Scholar] [CrossRef]
- Deshpande, K.; Bust, G.; Clauer, C.; Scales, W.; Frissell, N.; Ruohoniemi, J.; Spogli, L.; Mitchell, C.; Weatherwax, A.T. Satellite-beacon Ionospheric-scintillation Global Model of the upper Atmosphere (SIGMA) II: Inverse modeling with high-latitude observations to deduce irregularity physics. J. Geophys. Res. Space Phys. 2016, 121, 9188–9203. [Google Scholar] [CrossRef]
- Datta-Barua, S.; Su, Y.; Deshpande, K.; Miladinovich, D.; Bust, G.; Hampton, D.; Crowley, G. First light from a kilometer-baseline Scintillation Auroral GPS Array. Geophys. Res. Lett. 2015, 42, 3639–3646. [Google Scholar] [CrossRef] [PubMed]
- Deshpande, K.; Bust, G.; Clauer, C.; Kim, H.; Macon, J.; Humphreys, T.; Bhatti, J.; Musko, S.; Crowley, G.; Weatherwax, A. Initial GPS scintillation results from CASES receiver at South Pole, Antarctica. Radio Sci. 2012, 47, 1–10. [Google Scholar] [CrossRef]
- Ghobadi, H.; Spogli, L.; Alfonsi, L.; Cesaroni, C.; Cicone, A.; Linty, N.; Romano, V.; Cafaro, M. Disentangling ionospheric refraction and diffraction effects in GNSS raw phase through fast iterative filtering technique. GPS Solut. 2020, 24, 1–13. [Google Scholar] [CrossRef]
- Sreenivash, V.; Su, Y.; Datta-Barua, S. Automated Ionospheric Scattering Layer Hypothesis Generation for Detected and Classified Auroral Global Positioning System Scintillation Events. Radio Sci. 2020, 55, e2018RS006779. [Google Scholar] [CrossRef]
- Matzka, J.; Stolle, C.; Yamazaki, Y.; Bronkalla, O.; Morschhauser, A. The geomagnetic Kp index and derived indices of geomagnetic activity. Space Weather 2021, 19, e2020SW002641. [Google Scholar] [CrossRef]
- Su, Y.; Datta-Barua, S.; Bust, G.S.; Deshpande, K.B. Distributed sensing of ionospheric irregularities with a GNSS receiver array. Radio Sci. 2017, 52, 988–1003. [Google Scholar] [CrossRef]
- Nicolls, M.J.; Heinselman, C.J. Three-dimensional measurements of traveling ionospheric disturbances with the Poker Flat Incoherent Scatter Radar. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Carrano, C.S.; Groves, K.M.; Caton, R.G. Simulating the impacts of ionospheric scintillation on L band SAR image formation. Radio Sci. 2012, 47, 1–14. [Google Scholar] [CrossRef]
- Press, W.H. Numerical Recipes in C The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Martin, E.; Aarons, J. F layer scintillations and the aurora. J. Geophys. Res. 1977, 82, 2717–2722. [Google Scholar] [CrossRef]
- Rino, C.; Matthews, S. On the morphology of auroral zone radio wave scintillation. J. Geophys. Res. Space Phys. 1980, 85, 4139–4151. [Google Scholar] [CrossRef]
- Rino, C.; Livingston, R.; Tsunoda, R.; Robinson, R.; Vickrey, J.; Senior, C.; Cousins, M.; Owen, J.; Klobuchar, J. Recent studies of the structure and morphology of auroral zone F region irregularities. Radio Sci. 1983, 18, 1167–1180. [Google Scholar] [CrossRef]
- Fejer, B.G.; Kelley, M. Ionospheric irregularities. Rev. Geophys. 1980, 18, 401–454. [Google Scholar] [CrossRef]
- Basu, S.; Vesprini, R.L.; Aarons, J. Field-aligned ionospheric E-region irregularities and sporadic E. Radio Sci. 1973, 8, 235–246. [Google Scholar] [CrossRef]
- Yokoyama, T.; Yamamoto, M.; Fukao, S. Computer simulation of polarization electric fields as a source of midlatitude field-aligned irregularities. J. Geophys. Res. Space Phys. 2003, 108. [Google Scholar] [CrossRef]
- Elkins, T.J.; Papagiannis, M.D. Measurement and interpretation of power spectrums of ionospheric scintillation at a sub-auroral location. J. Geophys. Res. 1969, 74, 4105–4115. [Google Scholar] [CrossRef]
- Rufenach, C.L. Power-law wavenumber spectrum deduced from ionospheric scintillation observations. J. Geophys. Res. 1972, 77, 4761–4772. [Google Scholar] [CrossRef]
- Crane, R. Spectra of ionospheric scintillation. J. Geophys. Res. 1976, 81, 2041–2050. [Google Scholar] [CrossRef]
- Basu, S.; Basu, S.; MacKenzie, E.; Coley, W.; Hanson, W.; Lin, C. F region electron density irregularity spectra near auroral acceleration and shear regions. J. Geophys. Res. Space Phys. 1984, 89, 5554–5564. [Google Scholar] [CrossRef]
- Livingston, R.C.; Rino, C.L.; McClure, J.; Hanson, W. Spectral characteristics of medium-scale equatorial F region irregularities. J. Geophys. Res. Space Phys. 1981, 86, 2421–2428. [Google Scholar] [CrossRef]
- Zettergren, M.; Semeter, J. Ionospheric plasma transport and loss in auroral downward current regions. J. Geophys. Res. Space Phys. 2012, 117. [Google Scholar] [CrossRef]
- Zettergren, M.; Lynch, K.; Hampton, D.; Nicolls, M.; Wright, B.; Conde, M.; Moen, J.; Lessard, M.; Miceli, R.; Powell, S. Auroral ionospheric F region density cavity formation and evolution: MICA campaign results. J. Geophys. Res. Space Phys. 2014, 119, 3162–3178. [Google Scholar] [CrossRef]
- Zettergren, M.; Snively, J. Ionospheric response to infrasonic-acoustic waves generated by natural hazard events. J. Geophys. Res. Space Phys. 2015, 120, 8002–8024. [Google Scholar] [CrossRef]




| SAGA1—F Event | SAGA2—F Event | SAGA3—E Event | ||||
|---|---|---|---|---|---|---|
| Parameter | Observed | Simulated | Observed | Simulated | Observed | Simulated |
| Hybrid Spectrum | ||||||
| (el/m3) | (0.2–0.4) × 1012 | 0.2 × 1012 | (0.7–1.1) × 1012 | 0.75 × 1012 | (0.7–1.1) × 1012 | 1.05 × 1012 |
| (m/s) | 1000–1500 (1500) | 1550 | 450–700 (500) | 550 | 500–800 | 500 |
| 130–200 (140) | 160 | 290–360 (290) | 300 | 130–200 | 160 | |
| Shkarofsky Spectrum | ||||||
| (el/m3) | (0.2–0.4) × 1012 | 0.27 × 1012 | (0.7–1.1) × 1012 | 1.05 × 1012 | (0.7–1.1) × 1012 | 0.74 × 1012 |
| (m/s) | 1000–1500 (1500) | 1500 | 450–700 (500) | 500 | 500–800 | 825 |
| 130–200 (140) | 140 | 290–360 (290) | 290 | 130–200 | 130 | |
| SAGA1 F—Event | SAGA2 F—Event | SAGA3 E—Event | ||||
|---|---|---|---|---|---|---|
| Parameter | Hybrid | Shkarofsky | Hybrid | Shkarofsky | Hybrid | Shkarofsky |
| Axial Ratio | 5 | a = 2, a = 1, a = 10 | 5 | a = 2, a = 1, a = 10 | 6 | a = 1, a = 1, a = 10 |
| Wing-like | Wing-like | Rod-like | ||||
| Spectral Index | 4.5 | 4.5 | 4 | 4.5 | 3 | 3.5 |
| SAGA1 F—Event | SAGA2 F—Event | SAGA3 E—Event | |
|---|---|---|---|
| Wings | |||
| Sheets | |||
| Rods |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaggu, P.R.; Deshpande, K.B.; Datta-Barua, S.; Bust, G.S.; Hampton, D.L.; Rubio, A.L.; Conroy, J.P. Morphological and Spectral Features of Ionospheric Structures at E- and F-Region Altitudes over Poker Flat Analyzed Using Modeling and Observations. Sensors 2023, 23, 2477. https://doi.org/10.3390/s23052477
Vaggu PR, Deshpande KB, Datta-Barua S, Bust GS, Hampton DL, Rubio AL, Conroy JP. Morphological and Spectral Features of Ionospheric Structures at E- and F-Region Altitudes over Poker Flat Analyzed Using Modeling and Observations. Sensors. 2023; 23(5):2477. https://doi.org/10.3390/s23052477
Chicago/Turabian StyleVaggu, Pralay Raj, Kshitija B. Deshpande, Seebany Datta-Barua, Gary S. Bust, Donald L. Hampton, Aurora López Rubio, and James P. Conroy. 2023. "Morphological and Spectral Features of Ionospheric Structures at E- and F-Region Altitudes over Poker Flat Analyzed Using Modeling and Observations" Sensors 23, no. 5: 2477. https://doi.org/10.3390/s23052477
APA StyleVaggu, P. R., Deshpande, K. B., Datta-Barua, S., Bust, G. S., Hampton, D. L., Rubio, A. L., & Conroy, J. P. (2023). Morphological and Spectral Features of Ionospheric Structures at E- and F-Region Altitudes over Poker Flat Analyzed Using Modeling and Observations. Sensors, 23(5), 2477. https://doi.org/10.3390/s23052477






