The Use of a PVDF Array to Measure the Stress Field Inside an Elastic Material
Abstract
1. Introduction
2. Vertical PVDF Array
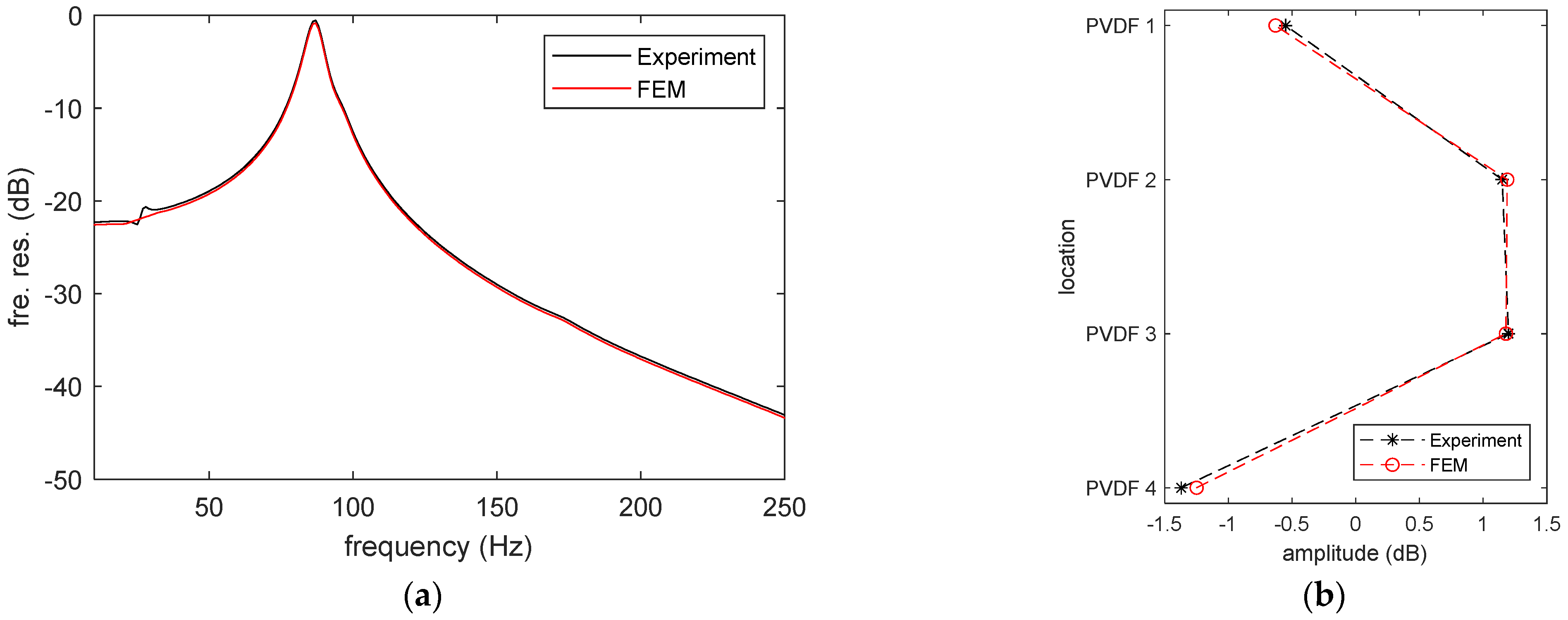
2.1. Experimental Description of Cylinder 1
2.2. Results of Cylinder 1 and Discussion
3. Horizontal PVDF Array
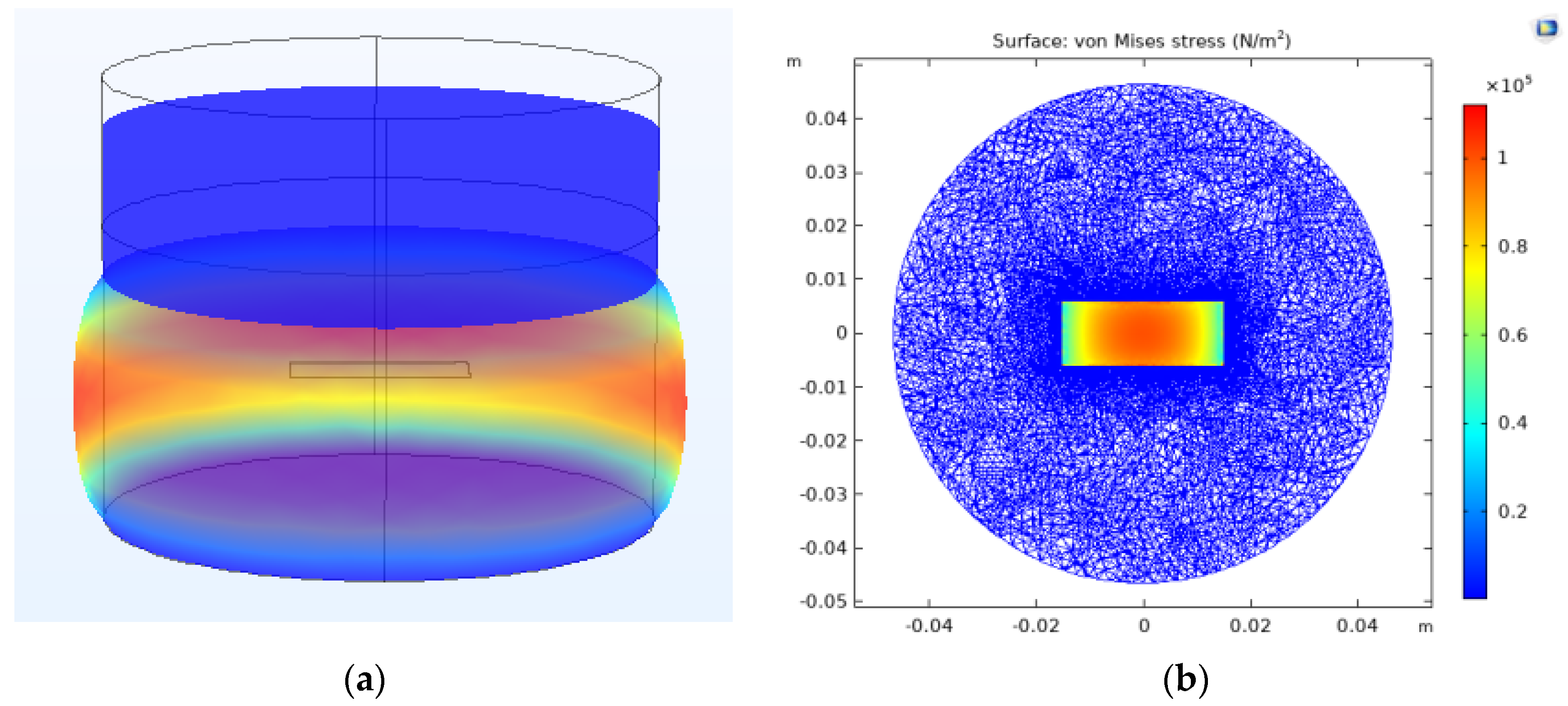
3.1. Experimental Description of Cylinder 2
3.2. Results of Cylinder 2 and Discussion
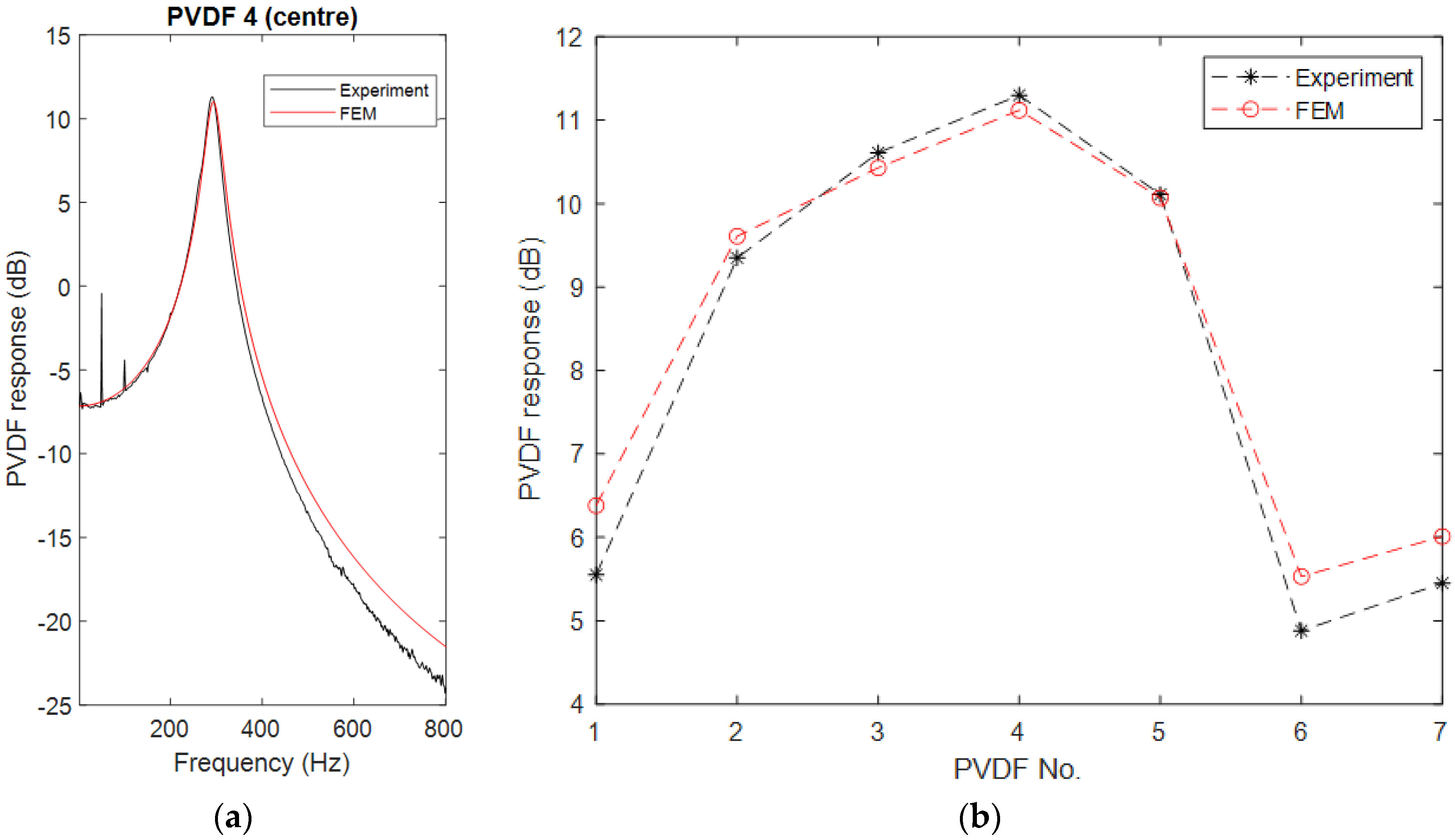
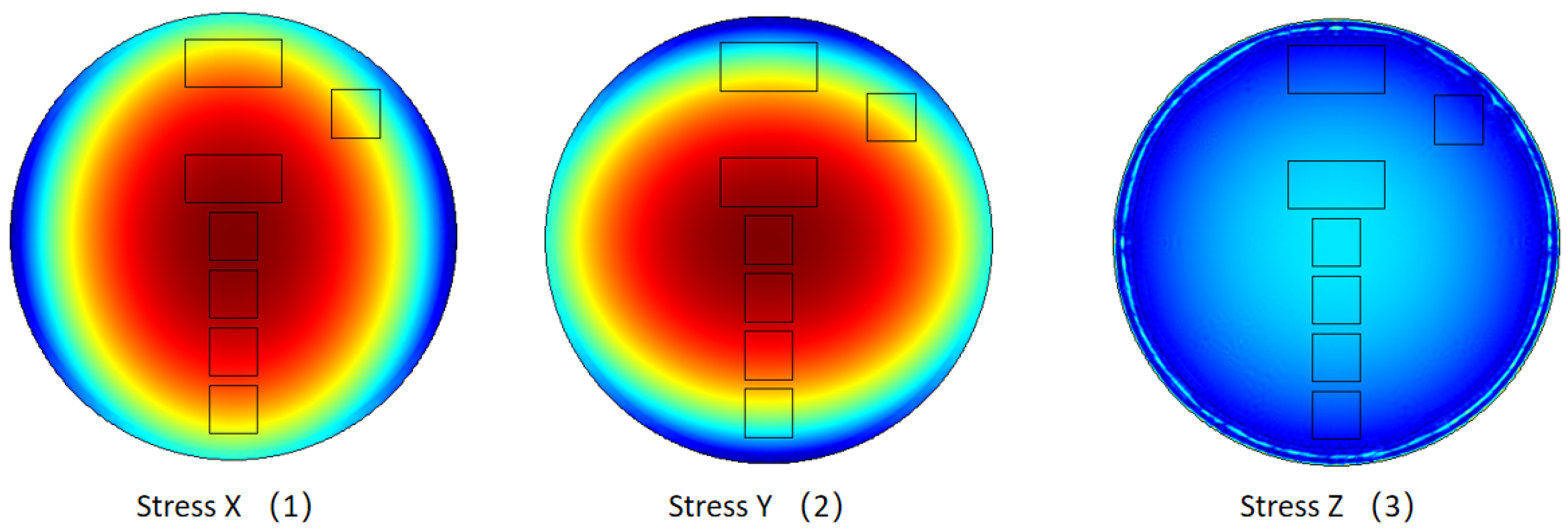
- In the horizontal direction, the PVDF element closer to the center of the cylinder has a larger output. Both experiment and the FE model indicate that the central element, i.e., PVDF 4, has the largest output and it gradually decreases from PVDF 4 at the center to PVDF 1 close to the edge of the cylinder.
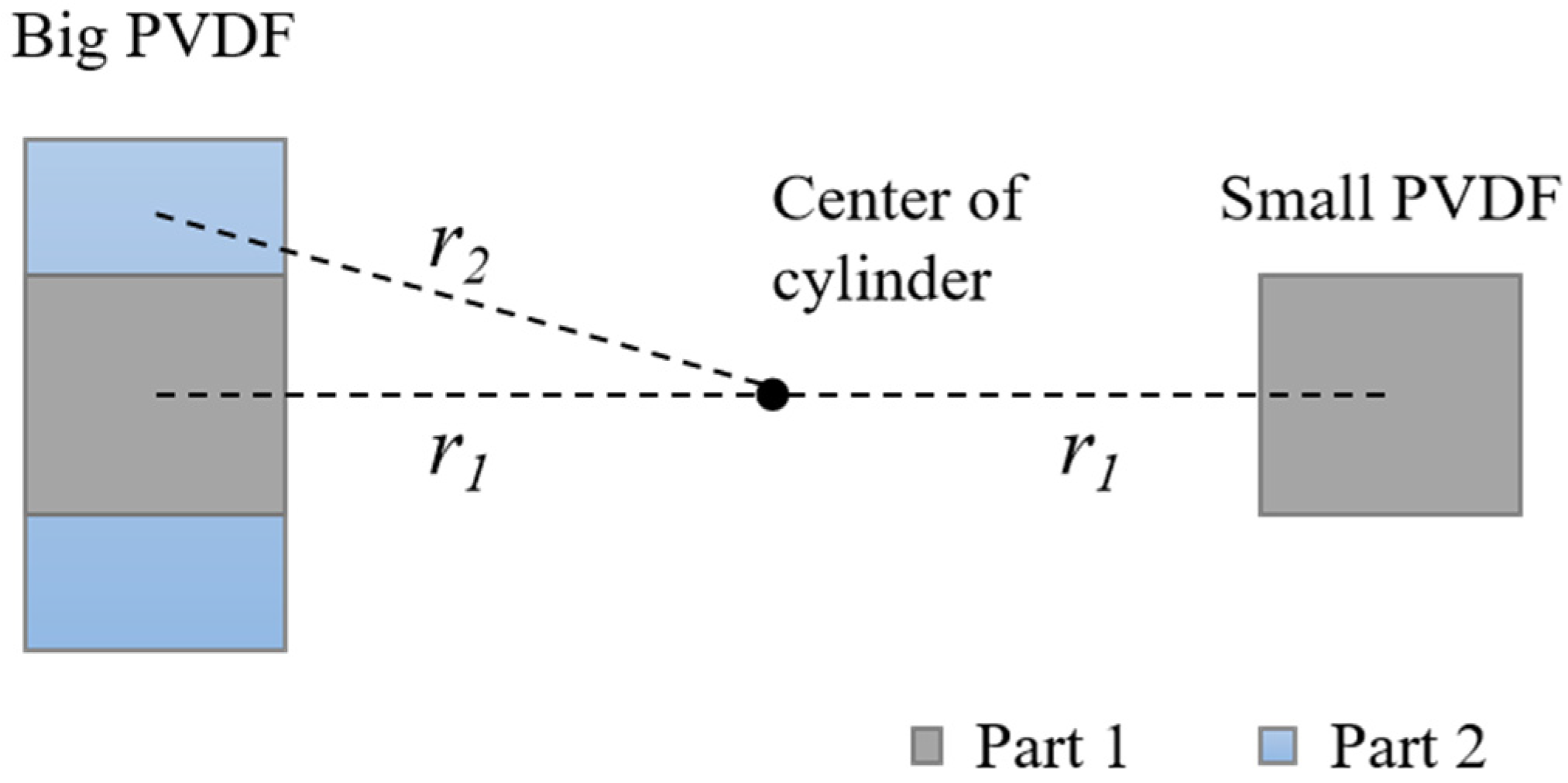
- The PVDF with the larger electrode areas have smaller outputs compared to their symmetric partners. There are two pairs of PVDF elements whose centers are at symmetrical positions but have different electrode size. One pair is PVDF 1 and PVDF 7, and the other pair is PVDF 3 and PVDF 5. Both the experiment and the FE model demonstrate that the output of the larger elements is slightly less than that of the smaller elements.
- Although the centers of PVDF 1 and PVDF 6 are at the same radial position and their size is also the same, the output of PVDF 1 is slightly bigger than PVDF 6.
4. Conclusions
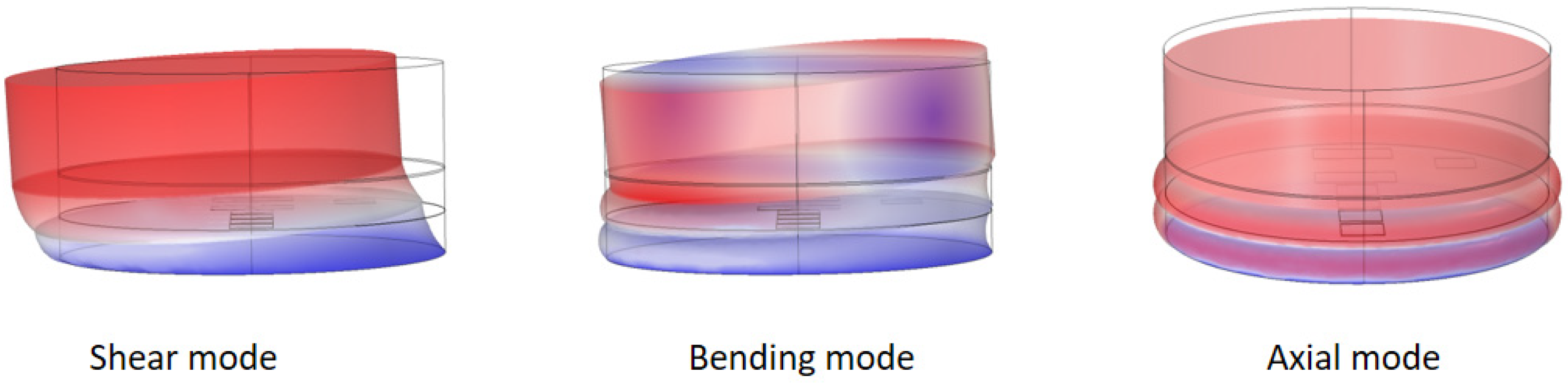
- The output of embedded PVDF is significantly affected by the elastic material around it. Even when the excitation is only in the normal direction, the Poisson effect of the elastic material can generate large in-plane stress which dominates the output of embedded PVDF.
- The output of embedded PVDF is determined by the averaged volume stress applied on it. The size of embedded PVDF does not directly link to its sensitivity. Increasing the size may even lead to an opposite result. Therefore, it is particularly important to carefully choose the size of embedded PVDF for various applications. In fact, if the stress distribution of the structure can be determined, a higher sensitivity can be obtained by placing a small-sized PVDF at the antinode of the stress field.
- To improve the sensitivity of embedded PVDF, its directivity should be considered. For anisotropic PVDF, the sensitivity in the x1 direction can be tens of times that in the x2 direction. Therefore, in practical applications, it should be ensured that the x1 direction of PVDF is aligned with the direction of high stress.
- When the embedded PVDF is located at the center point of an asymmetrical mode of the elastic material, the positive and negative stress applied on it will cancel with each other so that the sensitivity to this mode significantly decreases. This location should be avoided if this mode is important in the measurement. On the other hand, this phenomenon can also be exploited to avoid interference from an unwanted mode.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, R.K.; Lye, S.W.; Miao, J. PVDF nanofiber sensor for vibration measurement in a string. Sensors 2019, 19, 3739. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Xing, J.; Shang, D.; Wang, Y. A flow velocity measurement method based on a PVDF piezoelectric sensor. Sensors 2019, 19, 1657. [Google Scholar] [CrossRef] [PubMed]
- Sun, P.; Gao, Y.; Jin, B.; Brennan, M.J. Use of PVDF wire sensors for leakage localization in a fluid-filled pipe. Sensors 2020, 20, 692. [Google Scholar] [CrossRef]
- Du, G.; Li, Z.; Song, G. A PVDF-based sensor for internal stress monitoring of a concrete-filled steel tubular (CFST) column subject to impact loads. Sensors 2018, 18, 1682. [Google Scholar] [CrossRef]
- Youssef, A.; Matthews, D.; Guzzomi, A.; Pan, J. Measurement of pressure fluctuations inside a model thrust bearing using PVDF sensors. Sensors 2017, 17, 878. [Google Scholar] [CrossRef] [PubMed]
- Killeen, D.; Legg, M.; Matthews, D. A prototype PVDF underwater pressure-gradient acoustic intensity probe. In Proceedings of the Acoustics, Adelaide, Australia, 23–25 November 2009. [Google Scholar]
- Wang, N.; Pan, J.; Matthews, D. Acoustical intensity probe based on a polyvinylidene fluoride bimorph. J. Acoust. Soc. Am. 2021, 150, 4083–4094. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.K. Theory of laminated piezoelectric plates for the design of distributed sensors/actuators. Part I: Governing equations and reciprocal relationships. J. Acoust. Soc. Am. 1990, 87, 1144–1158. [Google Scholar] [CrossRef]
- Shapiro, Y.; Kósa, G.; Wolf, A. Shape tracking of planar hyper-flexible beams via embedded PVDF deflection sensors. IEEE/ASME Trans. Mechatron. 2013, 19, 1260–1267. [Google Scholar] [CrossRef]
- Cho, Y.; Je, Y.; Jeong, W.-B. A miniaturized acoustic vector sensor with PIN-PMN-PT single crystal cantilever beam accelerometers. Acta Acust. 2020, 4, 17. [Google Scholar] [CrossRef]
- Luo, M.; Luo, H.; Axinte, D.; Liu, D.; Mei, J.; Liao, Z. A wireless instrumented milling cutter system with embedded PVDF sensors. Mech. Syst. Signal Process. 2018, 110, 556–568. [Google Scholar] [CrossRef]
- Caneva, C.; De Rosa, I.M.; Sarasini, F. Acoustic emission monitoring of flexurally loaded aramid/epoxy composites by embedded PVDF sensors. J. Acoust. Emiss. 2007, 25, 80–91. [Google Scholar]
- Suh, J.B. Stress Analysis of Rubber Blocks under Vertical Loading and Shear Loading. Ph.D. Thesis, University of Akron, Akron, OH, USA, 2007. [Google Scholar]
- Fatima, I.D.; Shafi, N.; Anjum, H. Viscoelastic Properties of Rubber Material Modelling. In 2019 International Conference on Applied and Engineering Mathematics, Taxila, Pakistan, 27–29 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 117–121. [Google Scholar]
- Measurement Specialties Inc. Piezo Film Sensors Technical Manual; Measurement Specialties Inc.: Hampton, VA, USA, 1999. [Google Scholar]
- Jin, M.; Matthews, D.; Pan, J. Experimental investigation into the sensitivity of elastically coated piezoelectric polyvinylidene fluoride films to an impact force. Appl. Acoust. 2022, 192, 108713. [Google Scholar] [CrossRef]
- Qi, G.; Yan, H.; Qi, D.; Li, H.; Zhang, Z. The Aging Performance of PVDF in Acid Oil and Gas Medium. Polymers 2022, 14, 4244. [Google Scholar] [CrossRef] [PubMed]
- Sencadas, V.; Moreira, V.M.; Lanceros-Mendéz, S.; Pouzada, A.S.; Gregório, R., Jr. α-to-β Transformation on PVDF Films Obtained by Uniaxial Stretch. Mater. Sci. Forum 2006, 514, 872–876. [Google Scholar] [CrossRef]





| Rubber | Density (kg/m3) | Young’s Modulus (Pa) | Loss Factor | Poisson’s Ratio |
| 1050 | 2.3 × 106 | 0.15 | 0.495 | |
| PVDF | Density (kg/m3) | Young’s modulus (Pa) | Loss factor | Poisson’s ratio |
| 1780 | 4.6 × 109 | 0 | 0.35 | |
| g31 (Vm/N) | g32 (Vm/N) | g33 (Vm/N) | ||
| 0.21 | 0.042 | −0.30 |
| PVDF 1 | 4.36 × 105 Pa | 2.57 × 105 Pa | −4.30 × 103 Pa |
| PVDF 2 | 6.60 × 105 Pa | 3.86 × 105 Pa | −5.24 × 103 Pa |
| PVDF 3 | 6.64 × 105 Pa | 3.92 × 105 Pa | −5.33 × 103 Pa |
| PVDF 4 | 4.47 × 105 Pa | 2.62 × 105 Pa | −4.54 × 103 Pa |
| Group 1 | Group 2 | |||
|---|---|---|---|---|
| PVDF 1 (Small) | PVDF 7 (Big) | PVDF 3 (Small) | PVDF 5 (Big) | |
| 3.56 × 105 Pa | 3.30 × 105 Pa | 4.98 × 105 Pa | 4.63 × 105 Pa | |
| 2.65 × 105 Pa | 2.49 × 105 Pa | 4.90 × 105 Pa | 4.56 × 105 Pa | |
| −9.60 × 103 Pa | −9.23 × 105 Pa | −1.72 × 104 Pa | −1.60 × 104 Pa | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, M.; Matthews, D.; Wang, N.; Pan, J. The Use of a PVDF Array to Measure the Stress Field Inside an Elastic Material. Sensors 2023, 23, 2144. https://doi.org/10.3390/s23042144
Jin M, Matthews D, Wang N, Pan J. The Use of a PVDF Array to Measure the Stress Field Inside an Elastic Material. Sensors. 2023; 23(4):2144. https://doi.org/10.3390/s23042144
Chicago/Turabian StyleJin, Ming, David Matthews, Ning Wang, and Jie Pan. 2023. "The Use of a PVDF Array to Measure the Stress Field Inside an Elastic Material" Sensors 23, no. 4: 2144. https://doi.org/10.3390/s23042144
APA StyleJin, M., Matthews, D., Wang, N., & Pan, J. (2023). The Use of a PVDF Array to Measure the Stress Field Inside an Elastic Material. Sensors, 23(4), 2144. https://doi.org/10.3390/s23042144








