Improved Estimation of Exercise Intensity Thresholds by Combining Dual Non-Invasive Biomarker Concepts: Correlation Properties of Heart Rate Variability and Respiratory Frequency
Abstract
:1. Introduction
2. Methods
2.1. Participants
2.2. Data Processing
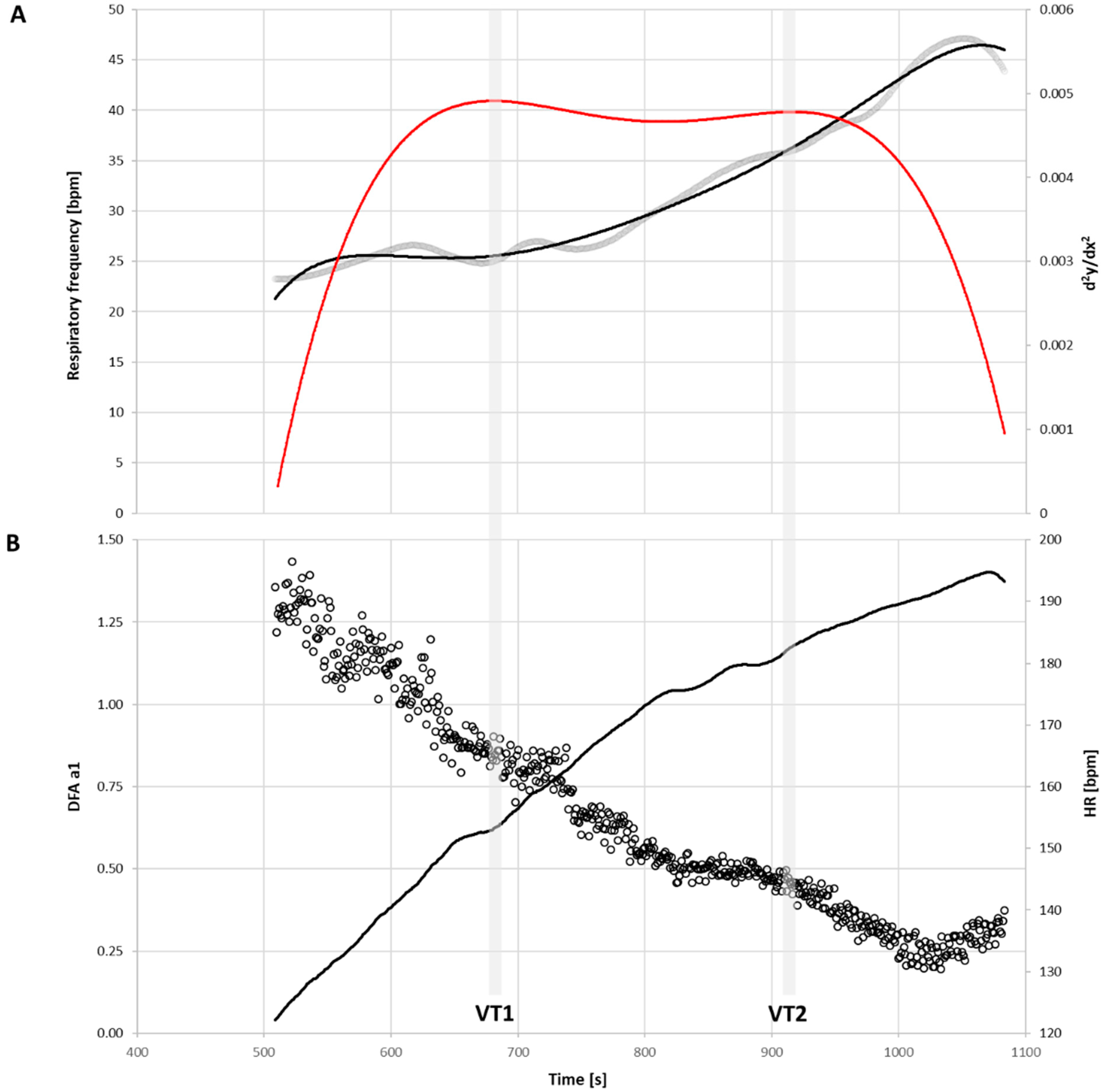
2.3. Calculation of VTs
2.4. Calculation of the HRVTs
2.5. Calculation of the EDRTs
2.6. Calculation of HRVT and EDRT Combination
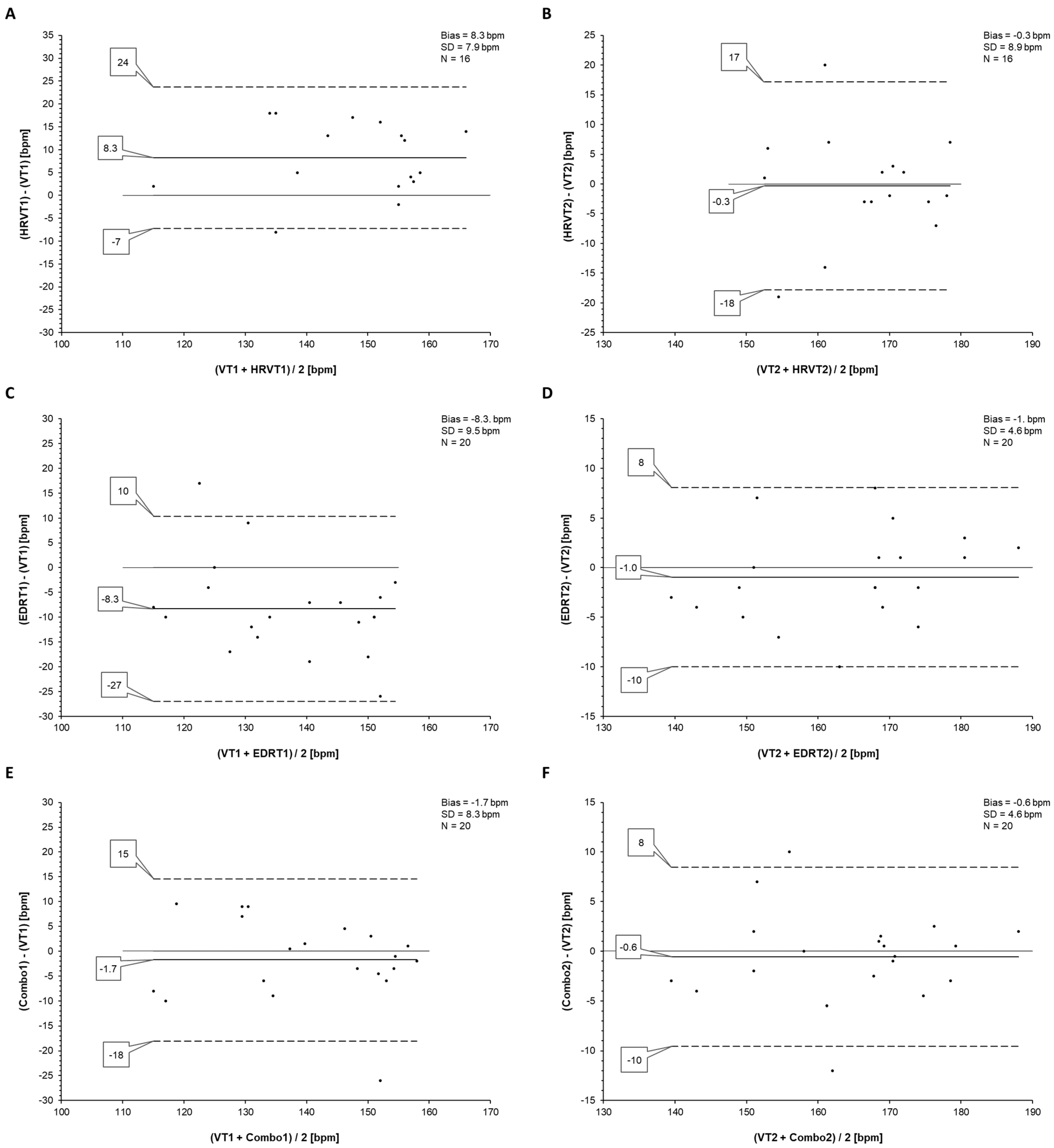
3. Statistics
4. Results
EDRT, HRVT and Combo Agreement to VTs
5. Discussion
6. Limitations
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jamnick, N.A.; Pettitt, R.W.; Granata, C.; Pyne, D.B.; Bishop, D.J. An Examination and Critique of Current Methods to Determine Exercise Intensity. Sports Med. 2020, 50, 1729–1756. [Google Scholar] [CrossRef] [PubMed]
- Iannetta, D.; Keir, D.A.; Fontana, F.Y.; Inglis, E.C.; Mattu, A.T.; Paterson, D.H.; Pogliaghi, S.; Murias, J.M. Evaluating the Accuracy of Using Fixed Ranges of METs to Categorize Exertional Intensity in a Heterogeneous Group of Healthy Individuals: Implications for Cardiorespiratory Fitness and Health Outcomes. Sports Med. 2021, 51, 2411–2421. [Google Scholar] [CrossRef] [PubMed]
- Iannetta, D.; Inglis, E.C.; Mattu, A.T.; Fontana, F.Y.; Pogliaghi, S.; Keir, D.A.; Murias, J.M. A Critical Evaluation of Current Methods for Exercise Prescription in Women and Men. Med. Sci. Sports Exerc. 2020, 52, 466–473. [Google Scholar] [CrossRef] [PubMed]
- Iannetta, D.; Zhang, J.; Murias, J.M.; Aboodarda, S.J. Neuromuscular and perceptual mechanisms of fatigue accompanying task failure in response to moderate-, heavy-, severe-, and extreme-intensity cycling. J. Appl. Physiol. 2022, 133, 323–334. [Google Scholar] [CrossRef]
- Iannetta, D.; Inglis, E.C.; Fullerton, C.; Passfield, L.; Murias, J.M. Metabolic and performance-related consequences of exercising at and slightly above MLSS. Scand. J. Med. Sci. Sports 2018, 28, 2481–2493. [Google Scholar] [CrossRef] [PubMed]
- Keir, D.A.; Fontana, F.Y.; Robertson, T.C.; Murias, J.M.; Paterson, D.H.; Kowalchuk, J.M.; Pogliaghi, S. Exercise Intensity Thresholds: Identifying the Boundaries of Sustainable Performance. Med. Sci. Sports Exerc. 2015, 47, 1932–1940. [Google Scholar] [CrossRef]
- Stöggl, T.L.; Sperlich, B. Editorial: Training Intensity, Volume and Recovery Distribution Among Elite and Recreational Endurance Athletes. Front. Physiol. 2019, 10, 592. [Google Scholar] [CrossRef]
- Hofmann, P.; Tschakert, G. Intensity- and Duration-Based Options to Regulate Endurance Training. Front. Physiol. 2017, 8, 337. [Google Scholar] [CrossRef]
- Bellotti, C.; Calabria, E.; Capelli, C.; Pogliaghi, S. Determination of Maximal Lactate Steady State in Healthy Adults: Can NIRS help? Med. Sci. Sports Exerc. 2013, 45, 1208–1216. [Google Scholar] [CrossRef]
- Rogers, B.; Giles, D.; Draper, N.; Hoos, O.; Gronwald, T. A New Detection Method Defining the Aerobic Threshold for Endurance Exercise and Training Prescription Based on Fractal Correlation Properties of Heart Rate Variability. Front. Physiol. 2021, 11, 596567. [Google Scholar] [CrossRef]
- Rogers, B.; Giles, D.; Draper, N.; Mourot, L.; Gronwald, T. Detection of the Anaerobic Threshold in Endurance Sports: Validation of a New Method Using Correlation Properties of Heart Rate Variability. J. Funct. Morphol. Kinesiol. 2021, 6, 38. [Google Scholar] [CrossRef]
- Bok, D.; Rakovac, M.; Foster, C. An Examination and Critique of Subjective Methods to Determine Exercise Intensity: The Talk Test, Feeling Scale, and Rating of Perceived Exertion. Sports Med. 2022, 52, 2085–2109. [Google Scholar] [CrossRef]
- Mann, T.; Lamberts, R.P.; Lambert, M.I. Methods of prescribing relative exercise intensity: Physiological and practical considerations. Sports Med. 2013, 43, 613–625. [Google Scholar] [CrossRef]
- Maturana, F.M.; Fontana, F.Y.; Pogliaghi, S.; Passfield, L.; Murias, J.M. Critical power: How different protocols and models affect its determination. J. Sci. Med. Sport 2018, 21, 742–747. [Google Scholar] [CrossRef] [PubMed]
- Klitzke Borszcz, F.; Ferreira Tramontin, A.; Pereira Costa, V. Is the Functional Threshold Power Interchangeable with the Maximal Lactate Steady State in Trained Cyclists? Int. J. Sports Physiol. Perform. 2019, 14, 1029–1035. [Google Scholar] [CrossRef]
- Rogers, B.; Giles, D.; Draper, N.; Mourot, L.; Gronwald, T. Influence of Artefact Correction and Recording Device Type on the Practical Application of a Non-Linear Heart Rate Variability Biomarker for Aerobic Threshold Determination. Sensors 2021, 21, 821. [Google Scholar] [CrossRef]
- Ferrari, M.; Mottola, L.; Quaresima, V. Principles, Techniques, and Limitations of Near Infrared Spectroscopy. Can. J. Appl. Physiol. 2004, 29, 463–487. [Google Scholar] [CrossRef]
- Gandia-Soriano, A.; Salas-Montoro, J.-A.; Javaloyes, A.; Lorente-Casaus, C.; Zabala, M.; Priego-Quesada, J.I.; March, M.M. Validity and Reliability of Two Near-infrared Spectroscopy Devices to Measure Resting Hemoglobin in Elite Cyclists. Int. J. Sports Med. 2022, 43, 875–880. [Google Scholar] [CrossRef]
- Gaskill, S.E.; Ruby, B.C.; Walker, A.J.; Sanchez, O.A.; Serfass, R.C.; Leon, A.S. Validity and reliability of combining three methods to determine ventilatory threshold. Med. Sci. Sports Exerc. 2001, 33, 1841–1848. [Google Scholar] [CrossRef]
- Rogers, B.; Gronwald, T. Fractal Correlation Properties of Heart Rate Variability as a Biomarker for Intensity Distribution and Training Prescription in Endurance Exercise: An Update. Front. Physiol. 2022, 13, 879071. [Google Scholar] [CrossRef]
- Schaffarczyk, M.; Rogers, B.; Reer, R.; Gronwald, T. Validation of a non-linear index of heart rate variability to determine aerobic and anaerobic thresholds during incremental cycling exercise in women. Eur. J. Appl. Physiol. 2022, 123, 299–309. [Google Scholar] [CrossRef] [PubMed]
- Michael, S.; Graham, K.S.; Davis, G.M. Cardiac Autonomic Responses during Exercise and Post-exercise Recovery Using Heart Rate Variability and Systolic Time Intervals—A Review. Front. Physiol. 2017, 8, 301. [Google Scholar] [CrossRef]
- Rogers, B.; Schaffarczyk, M.; Gronwald, T. Estimation of Respiratory Frequency in Women and Men by Kubios HRV Software Using the Polar H10 or Movesense Medical ECG Sensor during an Exercise Ramp. Sensors 2022, 22, 7156. [Google Scholar] [CrossRef] [PubMed]
- Cross, T.J.; Morris, N.R.; Schneider, D.A.; Sabapathy, S. Evidence of break-points in breathing pattern at the gas-exchange thresholds during incremental cycling in young, healthy subjects. Eur. J. Appl. Physiol. 2012, 112, 1067–1076. [Google Scholar] [CrossRef] [PubMed]
- García, D.; Kontaxis, S.; Hernández-Vicente, A.; Hernando, D.; Milagro, J.; Pueyo, E.; Garatachea, N.; Bailon, R.; Lázaro, J. Ventilatory Thresholds Estimation Based on ECG-derived Respiratory Rate. In Proceedings of the 2021 Computing in Cardiology (CinC), Brno, Czech Republic, 13–15 September 2021; pp. 1–4. [Google Scholar]
- Tipton, M.J.; Harper, A.; Paton, J.F.R.; Costello, J.T. The human ventilatory response to stress: Rate or depth? J. Physiol. 2017, 595, 5729–5752. [Google Scholar] [CrossRef]
- Nicolò, A.; Sacchetti, M. Differential control of respiratory frequency and tidal volume during exercise. Eur. J. Appl. Physiol. 2022, 123, 215–242. [Google Scholar] [CrossRef]
- Reis, V.M.; Tillaar, R.V.D.; Marques, M.C. Higher Precision of Heart Rate Compared with VO2 to Predict Exercise Intensity in Endurance-Trained Runners. J. Sports Sci. Med. 2011, 10, 164–168. [Google Scholar]
- Binder, R.K.; Wonisch, M.; Corra, U.; Cohen-Solal, A.; Vanhees, L.; Saner, H.; Schmid, J.-P. Methodological approach to the first and second lactate threshold in incremental cardiopulmonary exercise testing. Eur. J. Cardiovasc. Prev. Rehabil. 2008, 15, 726–734. [Google Scholar] [CrossRef]
- Chan, Y.H. Biostatistics 104: Correlational analysis. Singapore Med. J. 2003, 44, 614–619. [Google Scholar]
- Cicchetti, D.V. Guidelines, criteria, and rules of thumb for evaluating normed and standardized assessment instruments in psychology. Psychol. Assess. 1994, 6, 284–290. [Google Scholar] [CrossRef]
- Bland, J.; Altman, D. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef]
- Ludbrook, J. Confidence in Altman-Bland plots: A critical review of the method of differences. Clin. Exp. Pharmacol. Physiol. 2010, 37, 143–149. [Google Scholar] [CrossRef] [PubMed]
- Mateo-March, M.; Moya-Ramón, M.; Javaloyes, A.; Sánchez-Muñoz, C.; Clemente-Suárez, V.J. Validity of Detrended Fluctuation Analysis of Heart Rate Variability to Determine Intensity Thresholds in Elite Cyclists. Eur. J. Sport Sci. 2022, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Rogers, B.; Berk, S.; Gronwald, T. An Index of Non-Linear HRV as a Proxy of the Aerobic Threshold Based on Blood Lactate Concentration in Elite Triathletes. Sports 2022, 10, 25. [Google Scholar] [CrossRef]
- Gronwald, T.; Rogers, B.; Hoos, O. Fractal Correlation Properties of Heart Rate Variability: A New Biomarker for Intensity Distribution in Endurance Exercise and Training Prescription? Front. Physiol. 2020, 11, 550572. [Google Scholar] [CrossRef]
- Balagué, N.; Hristovski, R.; Almarcha, M.D.C.; Garcia-Retortillo, S.; Ivanov, P.C. Network Physiology of Exercise: Vision and Perspectives. Front. Physiol. 2020, 11, 611550. [Google Scholar] [CrossRef]
- Gourine, A.V.; Machhada, A.; Trapp, S.; Spyer, K.M. Cardiac vagal preganglionic neurones: An update. Auton. Neurosci. 2016, 199, 24–28. [Google Scholar] [CrossRef] [PubMed]
- Ernst, G. Heart-Rate Variability—More than Heart Beats? Front. Public Health 2017, 5, 240. [Google Scholar] [CrossRef]
- Devarajan, A.; Wang, K.; Shannon, K.; Su, Y.; Verheyden, J.; Sun, X.; Vaseghi, M. Convergent cardiorespiratory neurons represent a significant portion of cardiac and respiratory neurons in the vagal ganglia. Front. Cardiovasc. Med. 2022, 9, 959815. [Google Scholar] [CrossRef] [PubMed]
- Rogers, B.; Schaffarczyk, M.; Clauß, M.; Mourot, L.; Gronwald, T. The Movesense Medical Sensor Chest Belt Device as Single Channel ECG for RR Interval Detection and HRV Analysis during Resting State and Incremental Exercise: A Cross-Sectional Validation Study. Sensors 2022, 22, 2032. [Google Scholar] [CrossRef]
- Yeh, M.P.; Gardner, R.M.; Adams, T.D.; Yanowitz, F.G.; Crapo, R.O. “Anaerobic threshold”: Problems of determination and validation. J. Appl. Physiol. 1983, 55, 1178–1186. [Google Scholar] [CrossRef]
- Keir, D.A.; Iannetta, D.; Maturana, F.M.; Kowalchuk, J.M.; Murias, J.M. Identification of Non-Invasive Exercise Thresholds: Methods, Strategies, and an Online App. Sports Med. 2022, 52, 237–255. [Google Scholar] [CrossRef]
- Pallarés, J.G.; Morán-Navarro, R.; Ortega, J.F.; Fernández-Elías, V.E.; Mora-Rodriguez, R. Validity and Reliability of Ventilatory and Blood Lactate Thresholds in Well-Trained Cyclists. PLoS ONE 2016, 11, e0163389. [Google Scholar] [CrossRef]
- Ekkekakis, P.; Lind, E.; Hall, E.E.; Petruzzello, S. Do regression-based computer algorithms for determining the ventilatory threshold agree? J. Sports Sci. 2008, 26, 967–976. [Google Scholar] [CrossRef]
- Faude, O.; Kindermann, W.; Meyer, T. Lactate Threshold Concepts. Sports Med. 2009, 39, 469–490. [Google Scholar] [CrossRef]

| Sex | Age [Years] | Height [cm] | Body Weight [kg] | HRMAX [bpm] | VO2MAX [mL/kg/min] |
|---|---|---|---|---|---|
| M (N = 12) | 42.8 (±12.9) | 178.2 (±7.8) | 83.3 (±13.3) | 176.3 (±15.4) | 41.4 (±8.8) |
| F (N = 8) | 35.8 (±10.9) | 169.4 (±4.4) | 65.6 (±9.8) | 174.4 (±6.3) | 40.2 (±4.9) |
| VT1 HR | HRVT1 HR | EDRT1 HR | Combo1 HR | VT2 HR | HRVT2 HR | EDRT2 HR | Combo2 HR | |
|---|---|---|---|---|---|---|---|---|
| N = 20 | N = 16 | N = 20 | N = 20 | N = 20 | N = 16 | N = 20 | N = 20 | |
| 156 | 161 | 153 | 157 | 179 | 177 | 182 | 180 | |
| 150 | 162 | 131 | 147 | 169 | 172 | 167 | 170 | |
| 125 | 143 | 125 | 134 | 152 | 153 | 147 | 150 | |
| 137 | 150 | 125 | 138 | 151 | 171 | 151 | 161 | |
| 156 | 159 | 146 | 153 | 171 | 173 | 167 | 170 | |
| 165 | - | 139 | 139 | 187 | - | 189 | 189 | |
| 119 | - | 111 | 111 | 145 | - | 141 | 141 | |
| 159 | 173 | 141 | 157 | 175 | 182 | 173 | 178 | |
| 126 | - | 135 | 135 | 148 | - | 155 | 155 | |
| 122 | - | 112 | 112 | 141 | - | 138 | 138 | |
| 139 | 131 | 129 | 130 | 158 | 165 | 151 | 158 | |
| 154 | 156 | 143 | 150 | 180 | 173 | 181 | 177 | |
| 126 | 144 | 122 | 133 | 150 | 156 | 148 | 152 | |
| 155 | 159 | 149 | 154 | 177 | 174 | 171 | 173 | |
| 136 | 141 | 119 | 130 | 168 | 154 | 158 | 156 | |
| 139 | 156 | 125 | 141 | 169 | 166 | 167 | 167 | |
| 144 | 160 | 137 | 149 | 168 | 170 | 169 | 170 | |
| 156 | 154 | 146 | 150 | 168 | 165 | 173 | 169 | |
| 149 | 162 | 142 | 152 | 171 | 169 | 172 | 171 | |
| 114 | 116 | 131 | 124 | 164 | 145 | 172 | 159 | |
| Mean ± SD | 141 ± 15 | 152 ± 14 | 133 ± 12 | 140 ± 13 | 165 ± 13 | 167 ± 10 | 164 ± 14 | 164 ± 13 |
| r | - | 0.83 | 0.78 | 0.84 | - | 0.58 | 0.95 | 0.94 |
| p | - | <0.001 | <0.001 | 0.36 | - | 0.89 | 0.36 | 0.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rogers, B.; Schaffarczyk, M.; Gronwald, T. Improved Estimation of Exercise Intensity Thresholds by Combining Dual Non-Invasive Biomarker Concepts: Correlation Properties of Heart Rate Variability and Respiratory Frequency. Sensors 2023, 23, 1973. https://doi.org/10.3390/s23041973
Rogers B, Schaffarczyk M, Gronwald T. Improved Estimation of Exercise Intensity Thresholds by Combining Dual Non-Invasive Biomarker Concepts: Correlation Properties of Heart Rate Variability and Respiratory Frequency. Sensors. 2023; 23(4):1973. https://doi.org/10.3390/s23041973
Chicago/Turabian StyleRogers, Bruce, Marcelle Schaffarczyk, and Thomas Gronwald. 2023. "Improved Estimation of Exercise Intensity Thresholds by Combining Dual Non-Invasive Biomarker Concepts: Correlation Properties of Heart Rate Variability and Respiratory Frequency" Sensors 23, no. 4: 1973. https://doi.org/10.3390/s23041973
APA StyleRogers, B., Schaffarczyk, M., & Gronwald, T. (2023). Improved Estimation of Exercise Intensity Thresholds by Combining Dual Non-Invasive Biomarker Concepts: Correlation Properties of Heart Rate Variability and Respiratory Frequency. Sensors, 23(4), 1973. https://doi.org/10.3390/s23041973









