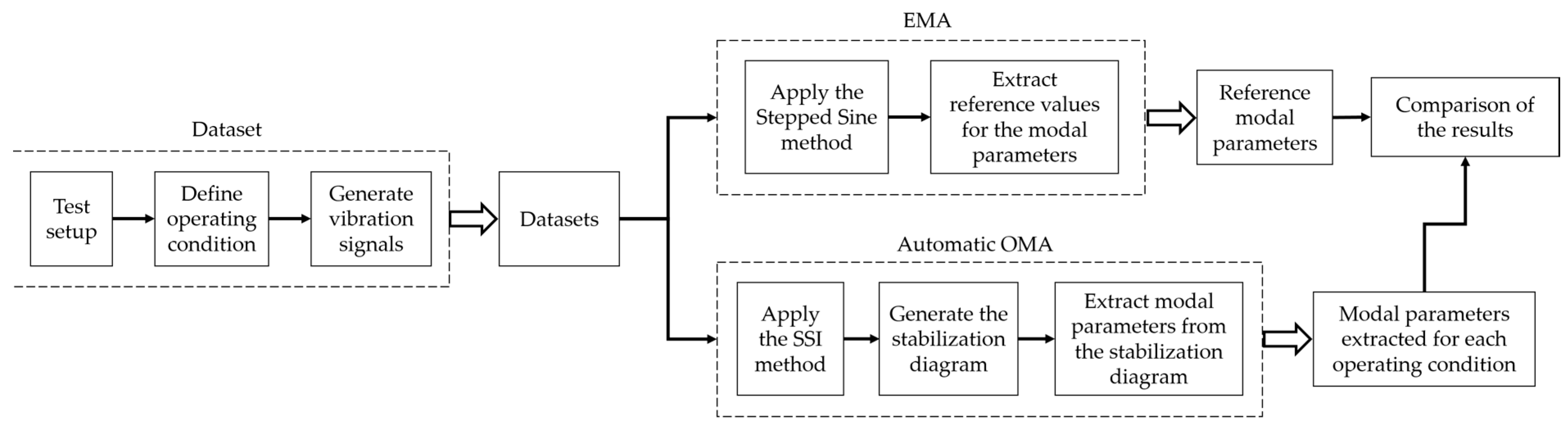
The proposed algorithm is applied to two different datasets: response measurements of a test rig with a rotor supported by hydrodynamic bearings, and response measurements of a test rig with a rotor supported by rolling bearings.
The algorithm, as well as the SSI-DATA method, were implemented in the programming language Python™.
3.1. Test Rig with Hydrodynamic Bearings
The stabilization limits considered in the following analysis were 0.2% for the frequency variation, 2% for the damping ratio variation, and 95% for the minimum MAC value, all of them conservatively chosen. The range was used as the damping ratio limit. All stabilization diagrams were built with a maximum order of 100, with fixed 100 block rows.
Figure 3 displays the stabilization diagram of the first test of
Table 1, excitation with white noise (medium intensity) and a sampling frequency of 2048 Hz. The diagram is presented in the frequency range of 0 Hz to 256 Hz, the range of interest in this analysis. From the diagram, one can observe that there are three alignments of spurious poles, the first at 75 Hz (the rotor’s rotating speed), two at 150 Hz (first harmonic), and the last at 225 Hz (second harmonic). The identification of the rotating speed and its harmonics as spurious was possible due to the HVC related to the damping ratio. In addition, several mathematical poles were also classified as spurious and, therefore, will not enter the following analysis. One can also observe that, close to the first rotor’s mode, two poles are predominantly identified in each order, which could lead to the idea that both forward and backward frequencies are identified. However, the second poles of each order are mostly identified with a high damping ratio (>7%), being inadequate to represent any rotor’s frequency.
The MPC (computed as described in [
26]) and the MPD (computed as described in [
6]) values of each pole were computed to perform additional analysis. The MPC value ranged from 63% to 99% for the first rotor’s mode, the highest ones (>86%) being outliers because of the high damping ratio (>5%), as will be seen in a further outlier analysis. For the second one, the range was 98% to 100%. For the foundation mode of 241.9 Hz, the values were much more stable, ranging from 94% to 98%. The MPD value, in contrast, ranged from 8% to 35% for the first rotor’s mode, the lowest ones (<19%) being outliers because of the high damping ratio (>5%). For the second one, the range was 3% to 6%. For the foundation mode of 241.9 Hz, the range was 11% to 16%. Therefore, if any clustering algorithm or HVC based on the MPC or MPD values were employed, the first rotor’s mode could be identified due to its great dispersion as spurious, and the identification algorithm would fail to provide reliable information.
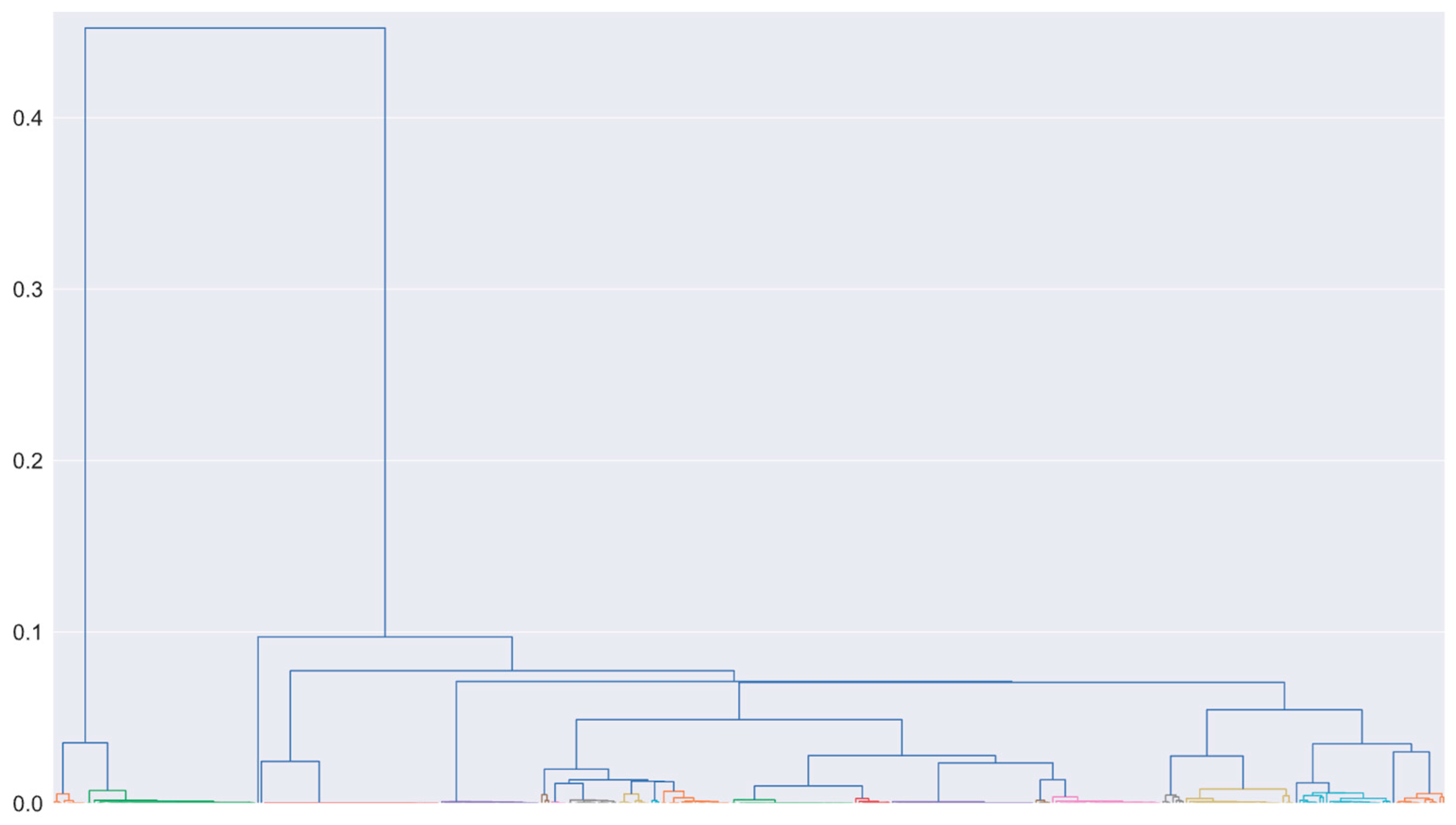
After building the stabilization diagram and applying the HVC, the hierarchical clustering was performed. For the selected threshold definition, the distance between the known difference of closely spaced modes was employed. The difference between the first and second frequencies of the first mode, according to Equation (13), is 0.006. For the second mode, the difference is 0.002. Tests considering thresholds near these values were evaluated, resulting in a selected threshold of 0.01. It is important to emphasize that this threshold proved itself adequate for all other tests of
Table 1, demonstrating how simple it is to select a value that works in different operating conditions of the same system.
Figure 4 displays the obtained dendrogram, in which each cluster is represented by a different color in the bottom of the dendrogram and whose x-axis is organized with the frequency range of 53 Hz to 250 Hz, distributed in an ascending order.
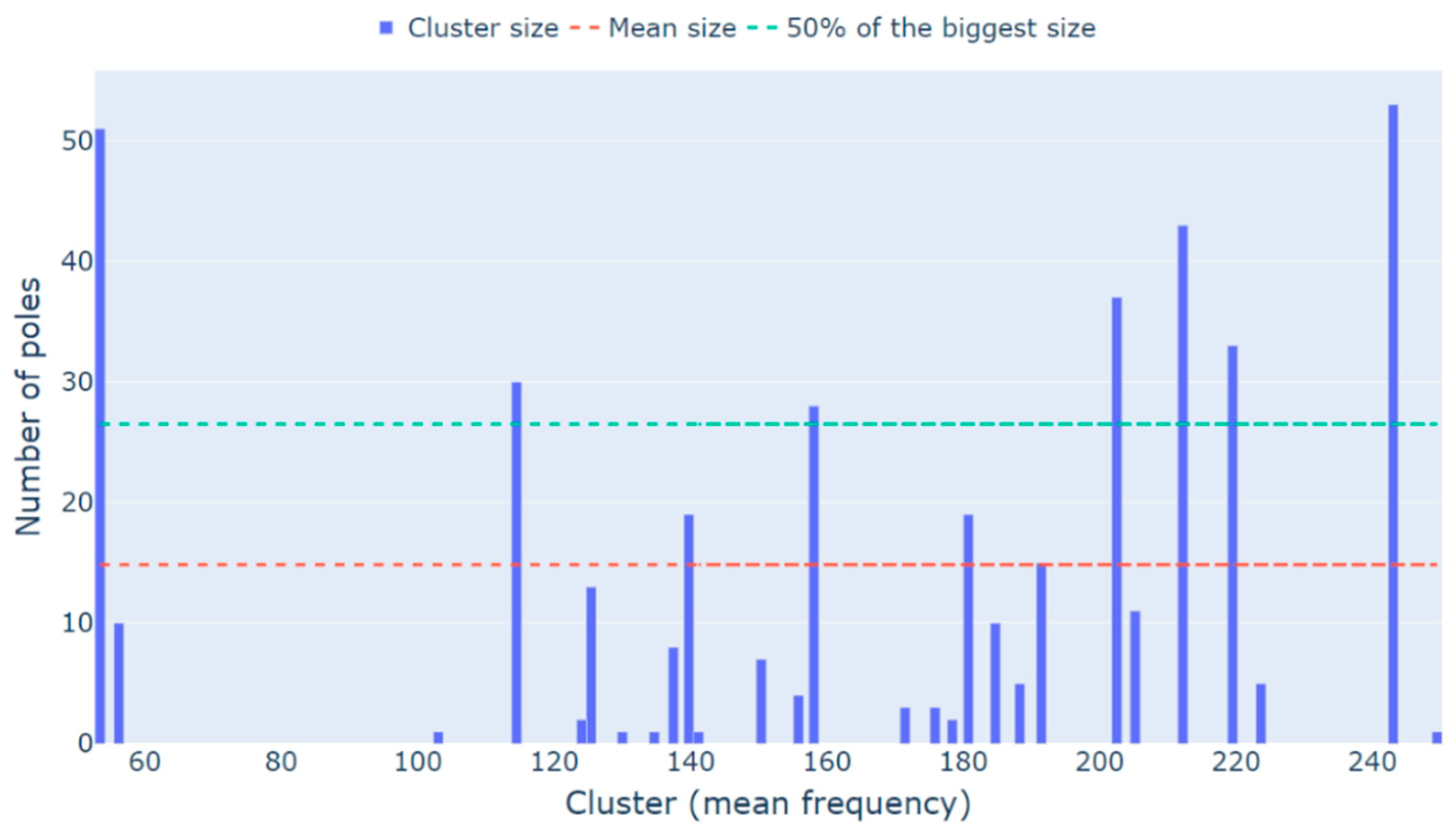
Figure 5 displays the diagram of each cluster’s size, along with the limits proposed by this paper and by [
7] to remove small clusters. From
Figure 5, one can see that if the limit proposed by [
7] was considered, the 6th and the 8th foundation modes would not be identified by the algorithm. There are also cases in which the first rotor’s mode is below the limit proposed by the authors, as the signals obtained from test 3 show. Therefore, the limit defined by the mean size is justified.
The outlier analysis was performed within the 10 clusters that remained from the previous analysis.
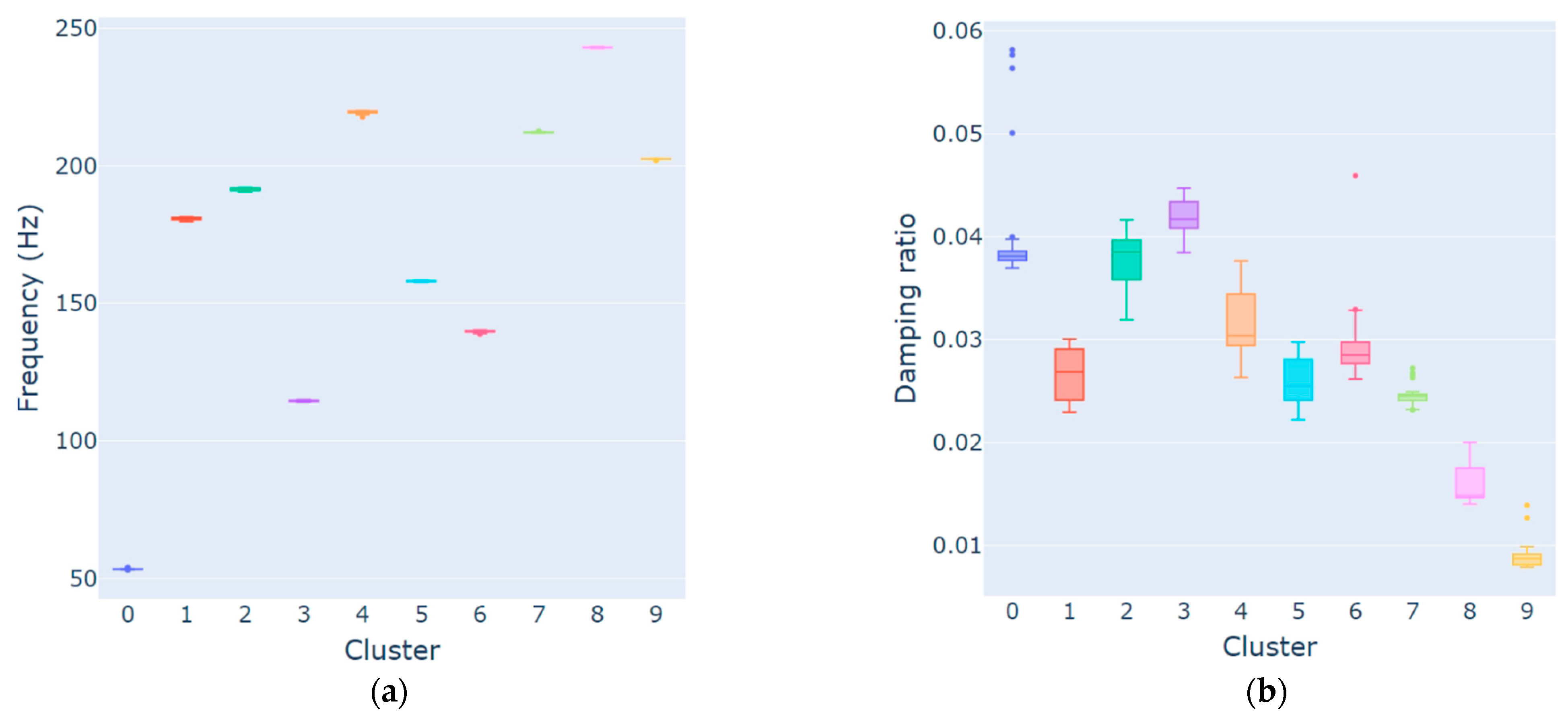
Figure 6 displays the boxplot of both frequency and damping ratio values. Points out of the box range are considered outliers. Taking the first cluster as an example, which represents the first rotor mode, there are outliers in both frequency and damping ratio, although the first ones (53.16 Hz, 53.24 Hz, and 53.94) are less pronounced than the last ones (all damping ratios above 4%). From
Figure 6, it is possible to see that the outlier analysis was adequate to remove outliers from all modes.
Concluding all essential steps proposed by the algorithm, the averages of the frequencies and of the damping ratios of the poles inside each cluster are extracted. The results are displayed in
Table 6, along with the standard deviation of these parameters, the difference between the maximum and minimum values within the cluster that originated them, the errors in relation to the EMA references, the size of the cluster, and the lowest value in the MAC matrix, which will be further employed in the optional step to obtain sets of poles with high correlation mode shapes. From
Table 6, one can see that most of the identified modes presented low standard deviations and low differences between maximum and minimum, for both frequency and damping ratio, and bigger cluster sizes.
It is important to mention that, although the first two modes of the rotor are composed by two frequencies, the backward and the forward ones (
Table 2), the algorithm was not able to identify both of them. Since the similarity measure encompasses only the frequency difference between the poles, as presented in Equation (13), and considering the fact that the frequency and the damping ratio of the backward and forward frequencies are significantly close, it would be possible that both frequencies were grouped in the same cluster. However, the minimum MAC value for this mode was 98%, indicating a high correlation between all mode shapes within the cluster. Since some difference is expected from the mode shapes of the forward and backward frequencies, it is more likely that only poles of one of these frequencies are present in the cluster, indicating that the proximity of these two frequencies lead the SSI method to identify only one of them.
It is also important to mention that not only the rotor’s modes were identified, but also several modes from the foundation. Comparing
Table 6 with
Table 3, one can see that the modes identified with the OMA algorithm do not have the exact same parameters as the modes identified by EMA (but are relatively close). However, one must also recall that the EMA test was performed without the shaft and this variation of the modal parameters was already expected. Comparing the foundation’s results with the rotor’s results, one can observe that the errors were similar, highlighting the algorithms’ ability to extract accurate modal parameters for both the rotor and the foundation.
Moreover,
Table 7 displays the errors between the EMA values and estimated values of the rotor’s modal parameters using the proposed algorithm, in which all but one parameter presented a low error. The highest error was on the damping factor of the first mode, whose occurrence can be traced back to the SSI method’s ability to estimate this parameter.
Table 6 and
Table 7 demonstrate the proposed algorithm’s capability of extracting the modal parameters of a rotating machine.
With the clusters of each global mode and the lowest value in their MAC matrices, the additional step of the algorithm can be performed. The modes of 53.4 Hz, 114.5 Hz, 139.9 Hz, 202.06, 212.2 Hz, and 243.1 Hz presented good results, since the minimum values on their MAC matrix were greater than the MAC limit of the stabilization diagram (95%), an expected value from poles from the same mode. Therefore, no alteration will be performed in the clusters of these modes. However, the other modes (158.1 Hz, 180.8 Hz, 191.5 Hz and 219.5) presented values lower than the MAC limit of the stabilization diagram. Hence, hierarchical clustering based on the MAC values was performed, obtaining, for each mode, a new set of poles from which the mean, the standard deviation, and the difference between the maximum and minimum values of the modal parameters were computed. The results are displayed in
Table 8, from which one can verify that the minimum MAC value of all modes is now at least 95%, indicating that the obtained clusters present mode shapes with high correlation and, therefore, the mean of the mode shapes of each cluster is adequate to represent these modes. It is also possible to verify that no significant alteration occurred on the mean values of the modal parameters. In addition, the standard deviation and the difference between the maximum and minimum of most of the clusters achieved lower values (values highlighted in green), whereas only two modes exhibited an increase in standard deviation (values highlighted in red).
After these analyzes, the proposed algorithm, ignoring the additional step, was applied to all tests of
Table 1 and the results obtained for the rotor’s modes are displayed in
Table 9. As
Table 9 shows, the proposed algorithm was able to extract the rotor’s modes from all tests, these having a small standard deviation and with mean values close to the values selected via EMA. It is important to mention that the main reason for the high errors in the damping ratio estimations is the low magnitude of this parameter. Moreover, the estimation of damping ratios is a challenge even when well consolidated EMA techniques are used for the modal identification, and high errors are also obtained when the results of different EMA techniques are compared. In this context, the estimations displayed in
Table 9 are very good.
As occurred in Test 1, the application of the proposed algorithm to the remaining tests of
Table 1 also enabled the identification of several foundation modes. In order to summarize the results,
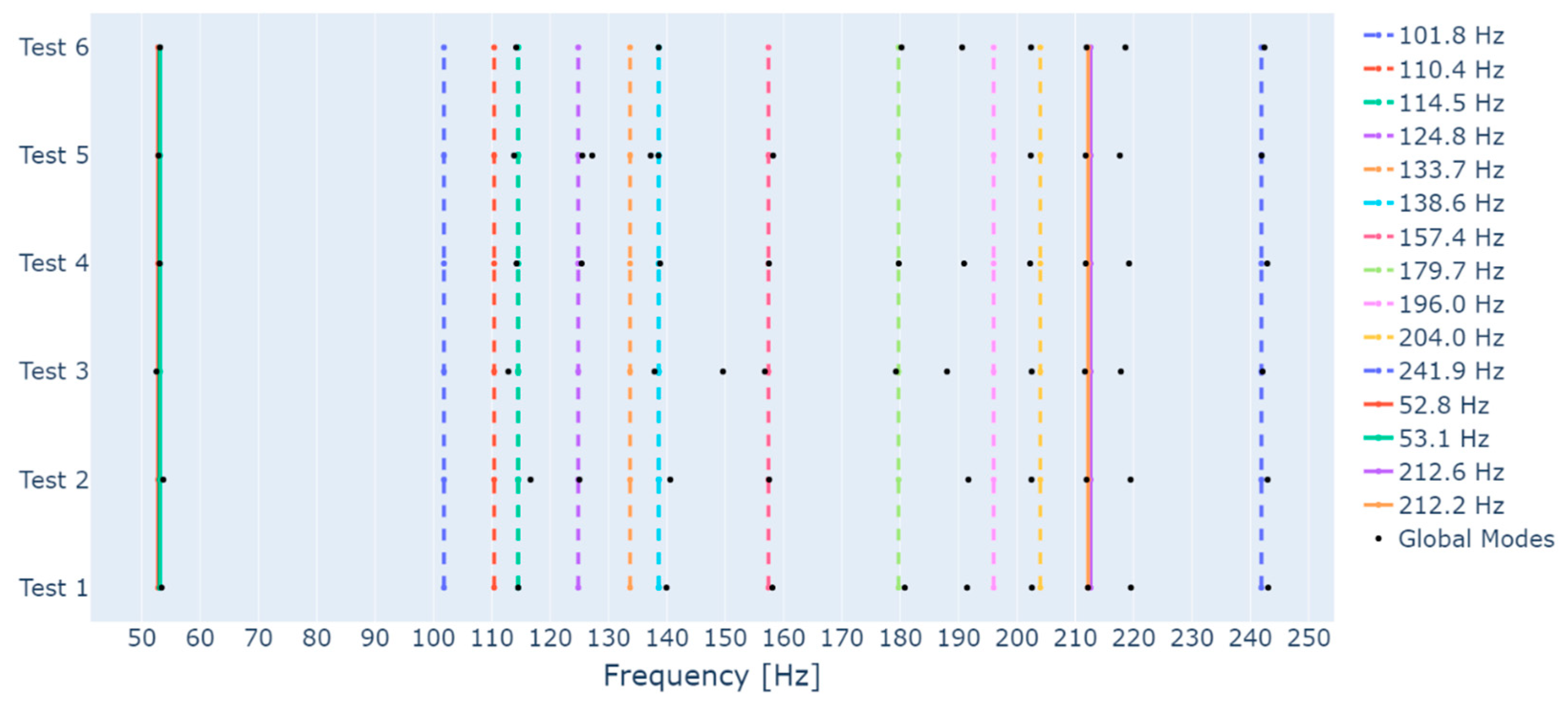
Figure 7 displays all modes estimated through the proposed algorithm as black dots, all rotor modes as continuous lines, and all foundation modes estimated by EMA as dashed lines. The frequency is presented in the x-axis and the data used to estimate the modes is presented in the y-axis. As indicated by
Figure 7, most foundation modes were identified. Recalling the stabilization diagram of
Figure 3, obtained with the data with medium intensity white noise, one can see that there are some frequency ranges in which the stabilization is irregular. Therefore, the absence of some foundation modes can be, once more, associated with the challenges in the SSI method.
With these analyses, an investigation was performed to evaluate the differences between dividing the hierarchical clustering in two steps, one based only on the frequency difference between the poles, and other based only on the MAC value, as proposed in this paper, and applying the hierarchical clustering in one single step, considering both the frequency difference and the MAC value, as proposed by other papers in the literature. In this case, the third step of the algorithm was modified so that the similarity measure comprised the frequency difference and the MAC value. Then, it was applied to all tests of
Table 1, without the additional step, and considering four different threshold values (0.04, 0.06, 0.08 and 0.1). The results are displayed on
Figure 8, along with the results from the proposed algorithm with the additional step to facilitate the comparison. In some cases, the modified algorithm identified global modes with very close frequencies. Due to the frequency range of
Figure 8, these cases would not be visible. Therefore, the icons representing them have been modified, and are represented with solid icons rather than hollow ones.
From
Figure 8, one can see that most of the frequencies identified by the proposed algorithm were also identified by the modified one. However, there are several cases in which two very close frequencies are identified, especially when the threshold of 0.04 is used. Analyzing the frequency range of the first rotor;s mode, one can see that the threshold of 0.04 identified two frequencies of approximately 53 Hz for Tests 1, 4, 5, and 6, and the thresholds of 0.06, 0.08, and 0.1 performed the same for Test 6. When the stabilization diagram of
Figure 3 was analyzed, it was verified that this frequency range indeed presented the stabilization of two different modes. However, the damping factor of one of them made it inadequate to represent any rotor’s frequency. That is also the case for all other tests. Therefore, the identification of two frequencies near the rotor modes by the modified algorithm represents a disadvantage of using one single hierarchical clustering with similarity distance that comprises both the frequency difference and the MAC value.
Evaluating other frequency ranges, it is possible to identify the same phenomenon in some foundation modes (124.8 Hz, 138.6 Hz, 157.4 Hz, 196.0 Hz and 204.0 Hz), mostly in the results from the modified algorithm (only the foundation modes of 124.8 Hz and 138.6 Hz of test 5 for the proposed algorithm). Analyzing each stabilization diagram, it was observed that most pairs of close frequencies were identified because poles from a single physical mode happened to be divided into more than one cluster by the algorithms due to irregularities in the stabilization diagram. The exceptions were the frequencies near 124.8 Hz of Tests 4 and 5, since the stabilization diagrams of these tests really present the alignment of two modes. However, it is possible that one of the alignments is actually an alignment of spurious modes rather than a closely spaced mode of the foundation, as occurred for the first rotor’s frequency.
Furthermore, there are some cases in which a foundation mode was identified by one of the algorithms and not by the other. These cases occurred 16 times, for both algorithms and all thresholds, and occurred for the foundation modes of 124.8 Hz (Tests 1 and 6), 157.4 Hz (Tests 1 and 3), and 196.0 Hz (Tests 4, 5 and 6). In five of these cases, the employed algorithm was the modified one with a threshold of 0.08. The modified algorithm with thresholds of 0.06 and 0.10 were responsible for three cases each, and the modified algorithm with a threshold of 0.04 was responsible for two cases. The proposed algorithm, in turn, was responsible for three cases.
Moreover, when the modified algorithm is employed, there is no guarantee that the minimum MAC value between the poles of a global mode is above the limit established for the stabilization diagram. Considering the global modes identified in all tests, when the threshold of 0.04 is used, 7 of the 74 identified global modes presented MAC values below 95%, with the minimum being 91%. When the threshold of 0.06 is used, 21 of the 66 identified global modes present values below 95%, with a minimum of 88%. When the threshold of 0.08 is used, 30 of the 62 identified global modes present values below 95%, with a minimum of 80%. Finally, when the threshold of 0.10 is used, 32 of the 64 identified global modes present values below 95%, with a minimum of 80%.
Considering the results presented here and that only one threshold value was selected for all tests of the proposed algorithm, some findings must be summarized. When the modified algorithm with low thresholds is used, there is a tendency to increase the division of poles belonging to the same physical mode into more than one cluster, which represents a disadvantage to the modal identification. If the threshold increased, the tendency decreases, but even when the threshold of 0.10 was used, the number of times that the division happened was higher than when the proposed algorithm was used. In addition, the increase of the threshold value proved to increase the number of global modes with a minimum MAC value below the limit of the stabilization diagram, and decrease these minimum values, which could lead to inaccuracies in the mode shapes’ mean. As to the non-identification of some foundation modes, both algorithms performed in the same manner. However, considering that the objective of this paper is the correct identification of the rotor’s modes, the identification of a spurious global mode near the first rotor’s
Frequency, along with the other findings, demonstrated the superiority of the proposed algorithm’s performance.
3.2. Test Rig with Rolling Bearings
To verify the robustness of the proposed algorithm, a distinct system will be analyzed. All data presented in
Table 4 will be verified and the results will be briefly presented here, with focus on the identification of the rotor’s modes.
For the construction of the stabilization diagrams, the same stabilization and damping ratio limits and stabilization diagram parameters were considered throughout the results showed in this section.
Figure 9 displays the stabilization diagram of Test 1 as an example. When compared to the one of
Figure 3, this stabilization diagram shows fewer well-defined alignments of stable poles and more poles classified as not stable. However, it is also possible to identify in
Figure 9 two well-defined alignments of stable poles near the rotor’s modes (
Table 5), which, unlike the stabilization diagram of
Figure 3, have modal parameters that make them adequate to represent both backward and forward frequencies. These particularities characterize this data set as a source of information about the modal parameters of closely spaced modes and as a real challenge to the identification of the foundation’s modes.
After building all stabilization diagrams, the algorithm follows by considering the threshold of 0.01 for the hierarchical clustering of all data sets, and the same one is used in the analyses from the previous section, demonstrating again how easy it is to select this threshold. The additional step was also considered to generate the results of the test rig supported by rolling bearings. The results for the rotor’s modes are displayed in
Table 10, from which one can see that, even with unfavorable excitation conditions, the algorithm can extract representative global modes for the rotor, with low standard deviations and modal parameters close to the ones estimated by EMA.
Comparing
Table 9 and
Table 10, one can observe that the estimation’s errors are really close to each other, demonstrating the algorithms’ robustness to different datasets.
As mentioned in the previous section, it is expected that the forward and backward frequencies present different mode shapes. Since the test rig supported by rolling bearings provided good results for both frequencies, their mode shapes were compared. Test 1 of
Table 4 was once more taken as an example and the MAC value was computed between the mode shapes of all poles from the backward frequency and the mode shapes of all poles from the forward frequencies, producing a MAC matrix of 75 × 68 (the number of poles from the clusters of the backward and forward frequencies, respectively). The mean, maximum, and minimum MAC values of the matrix were 75%, 82%, and 67%, confirming the expected difference.
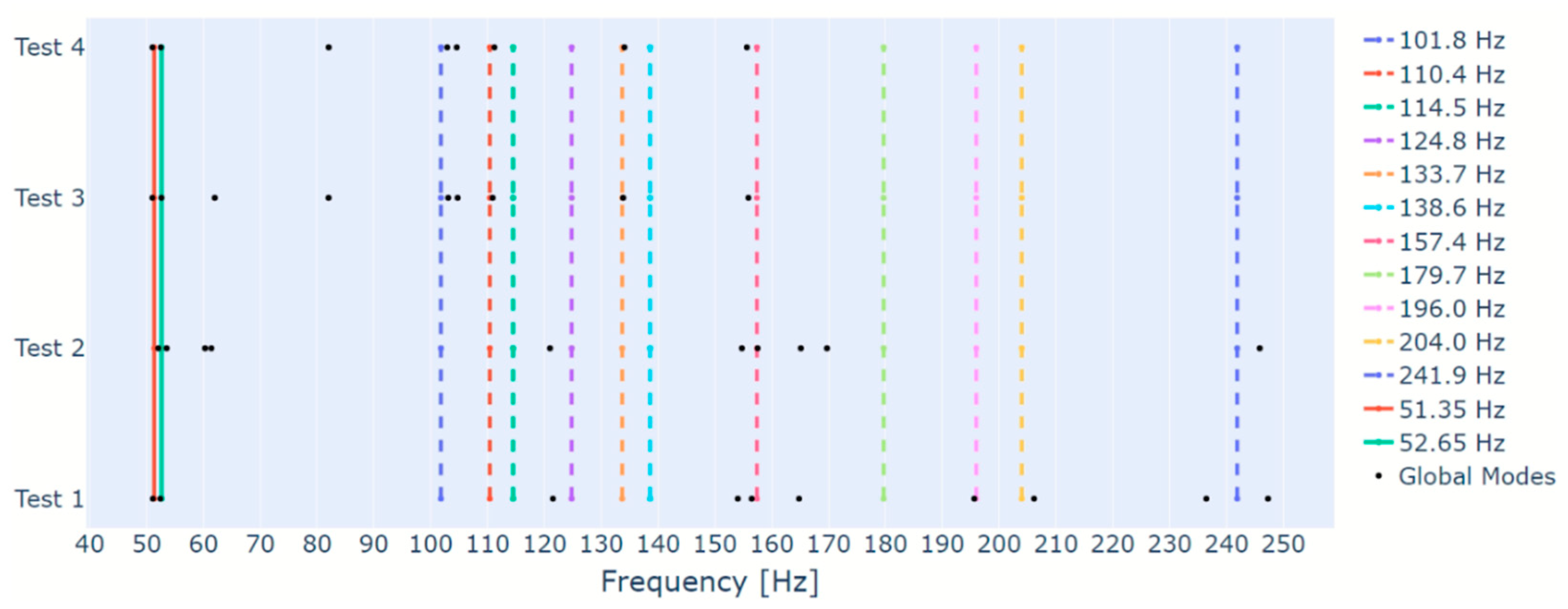
Moreover, in order to evaluate the ability of the proposed algorithm to extract the foundation’s modes when a different system is considered,
Figure 10 displays the extracted modes as black dots, the rotor’s modes as continuous lines, and the foundation’s modes as dashed lines. From
Figure 10, one can see that the algorithm was able to extract several of the foundation’s modes from the data of Test 1. When data from different tests are employed, only a few foundation’s modes are identified, which could be associated to unfavorable test conditions, and some modes out of the investigated frequency range (80 Hz to 320 Hz) appear. Moreover, the algorithm identifies some extra modes near the foundation mode of 157.4 Hz when data from Tests 1 and 2 are employed. Investigations performed with the same test rig by [
25] detected a mode associated to the bearings housing near the frequency of 155 Hz, which would explain these extra identified modes. Therefore, the proposed algorithm demonstrated a good ability to identify the foundation’s modes.
As already mentioned, the results of this section were generated considering the additional step; however, the algorithm considering only the essential steps would also be capable of identifying accurate frequencies and damping ratios of all rotors’ modes, which was also observed in the results from the test rig supported by hydrodynamic bearings. Hence, the additional step is recommended when a higher precision in the mode shapes estimation is required or when a MAC criterion inside each cluster needs to be respected.