Frequency Comb-Based Ground-Penetrating Bioradar: System Implementation and Signal Processing
Abstract
1. Introduction
2. Basics
2.1. Bioradar Measuring Principle
2.2. Frequency Comb CW Radar
- Requirement 1:
- Requirement 2:
2.3. Ground-Penetrating Bioradar
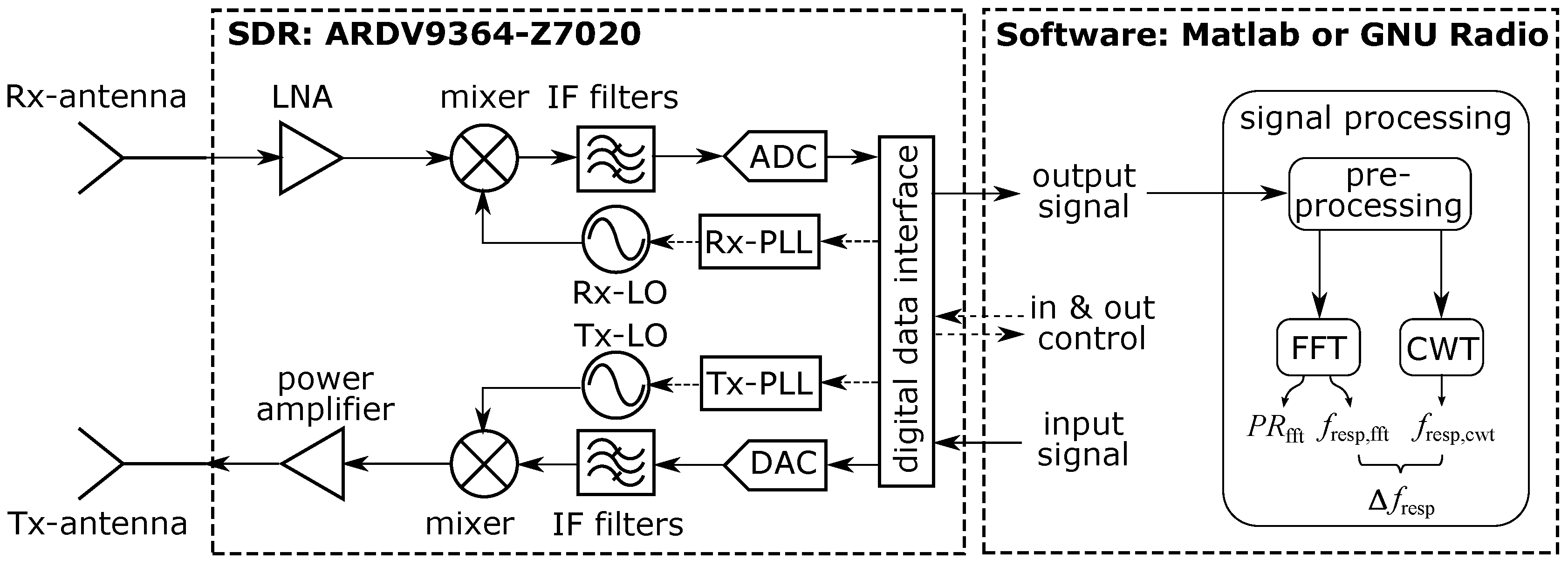
3. System Description: SDR-Based Bioradar
4. Signal Processing
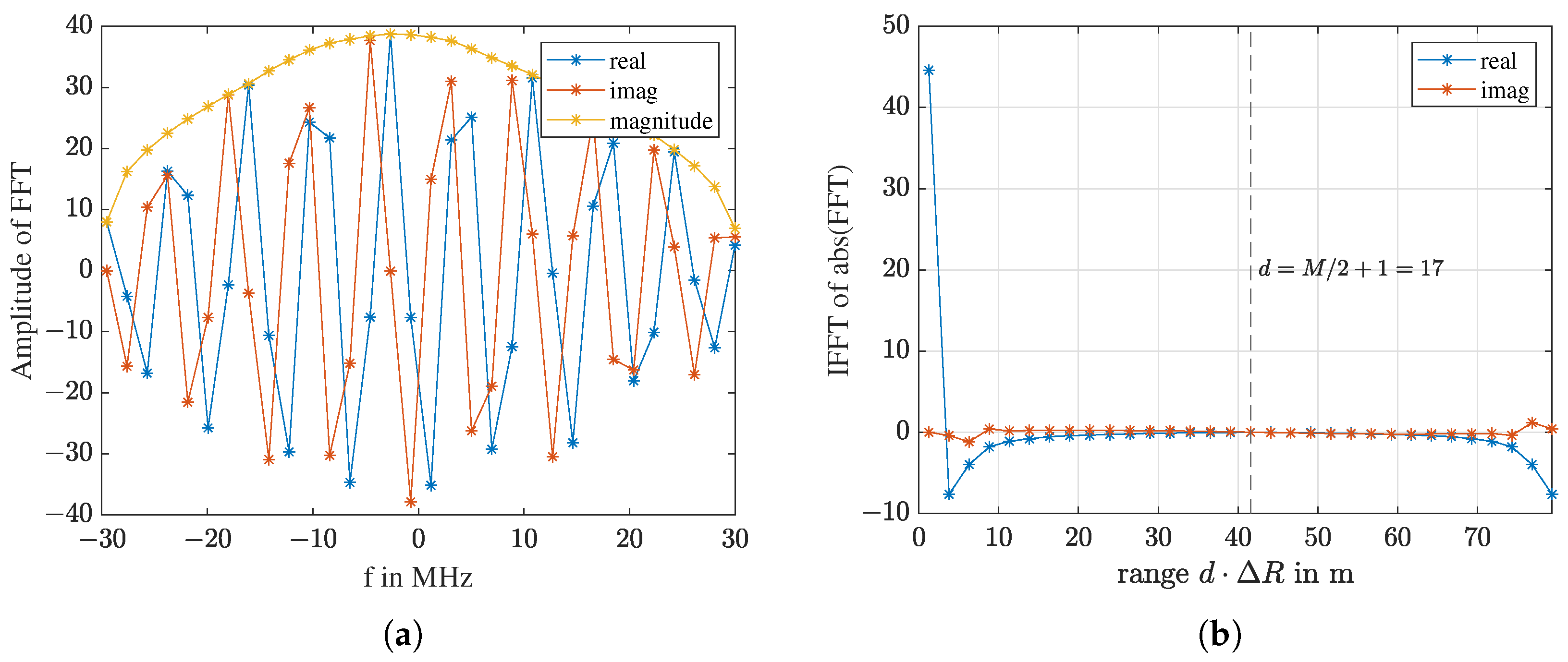
4.1. Pre-Processing: Radar Frequency Domain to Spatial Domain
4.2. FFT: Time Domain to Breathing Frequency Domain
4.3. Continuous Wavelet Transform (CWT): Time–Frequency Analysis
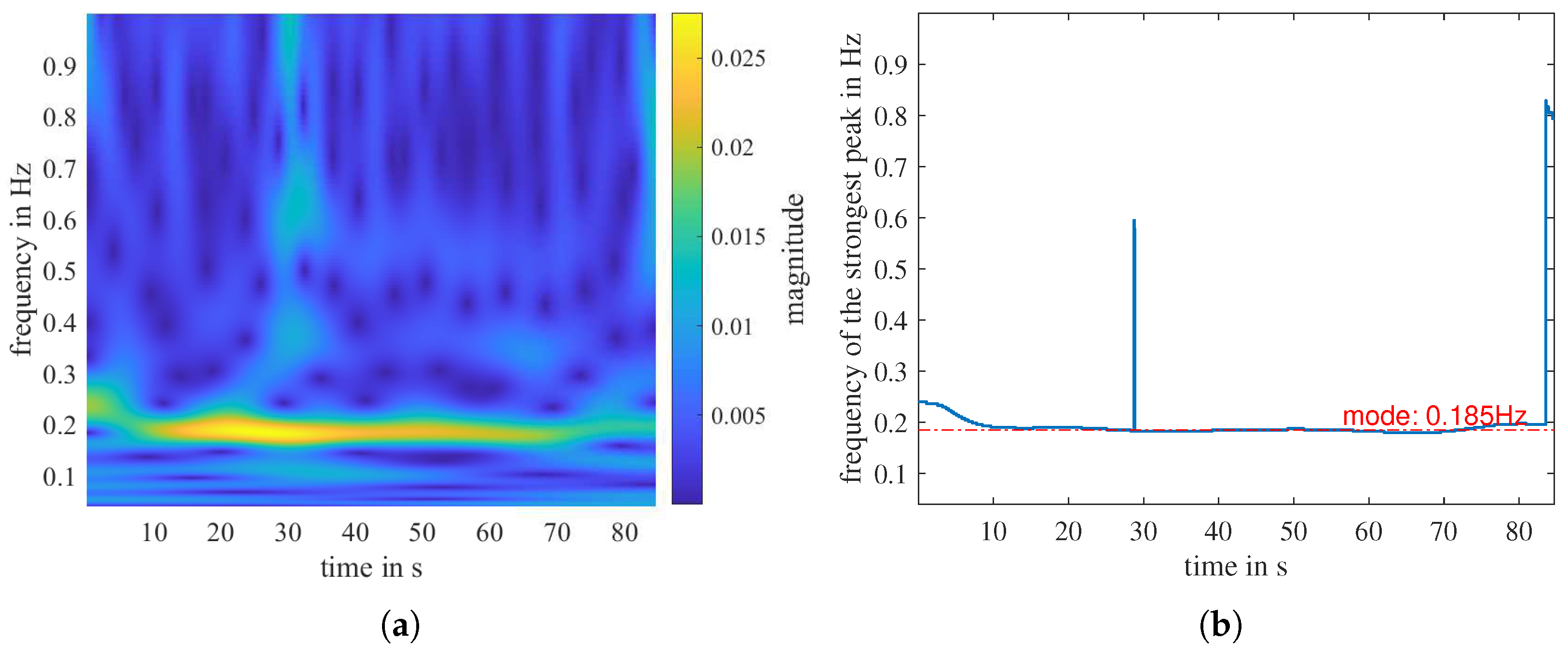
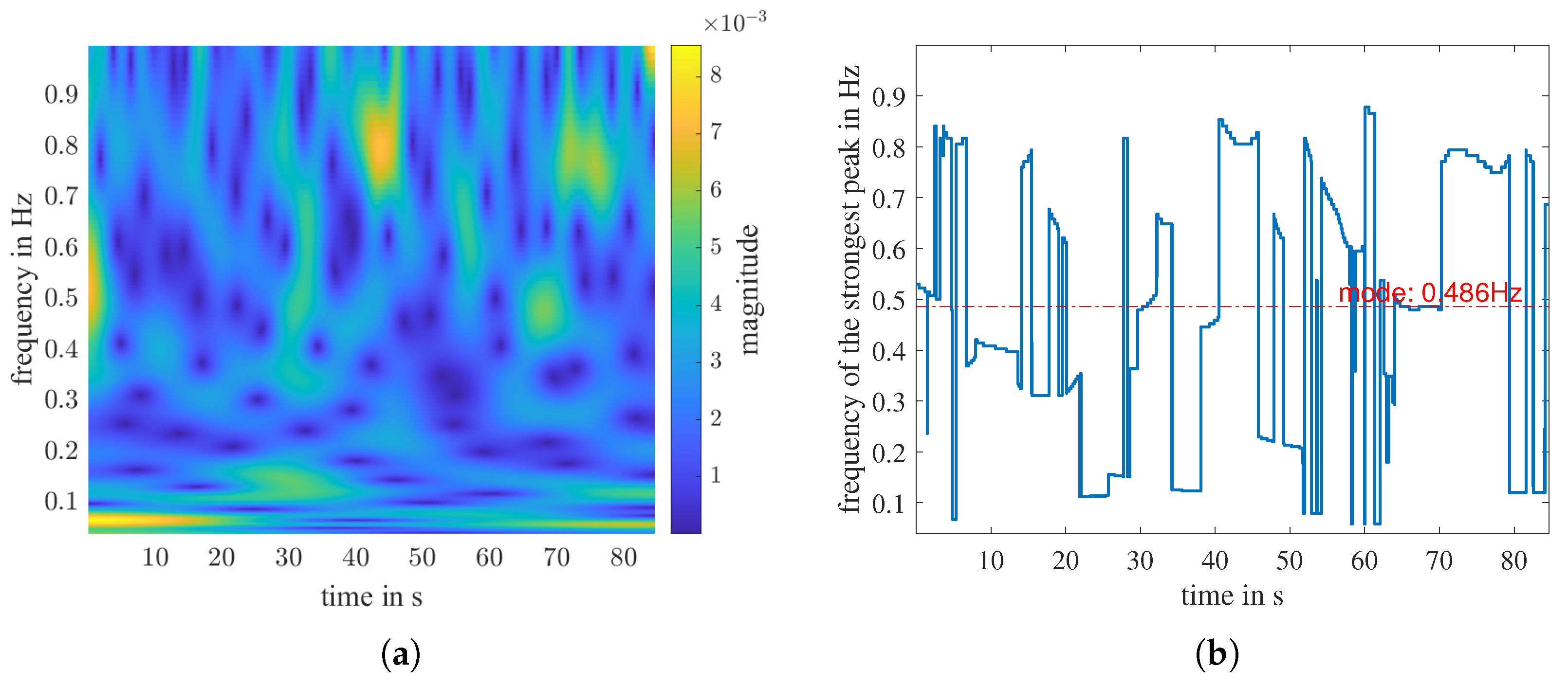
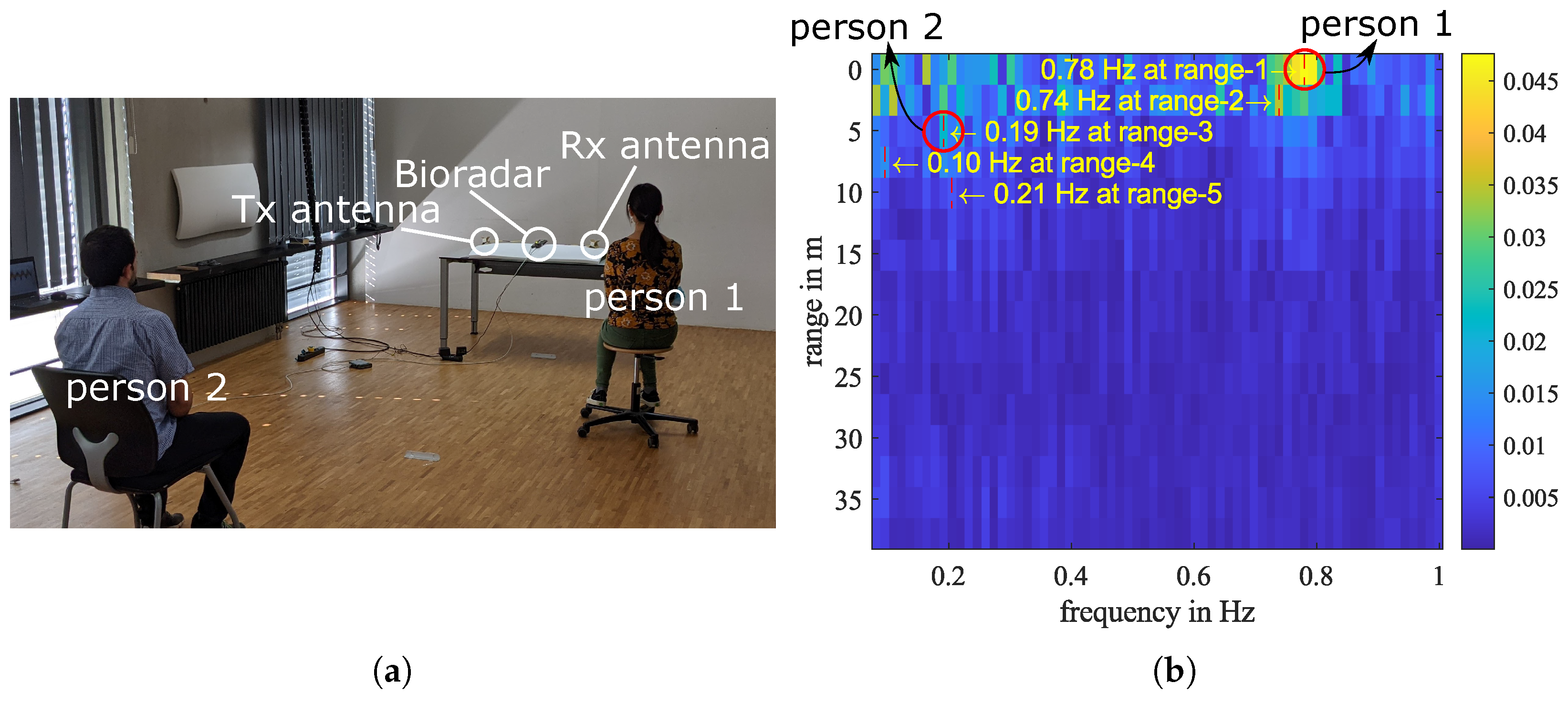
5. Experiment with Two Persons
6. Field Measurement
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
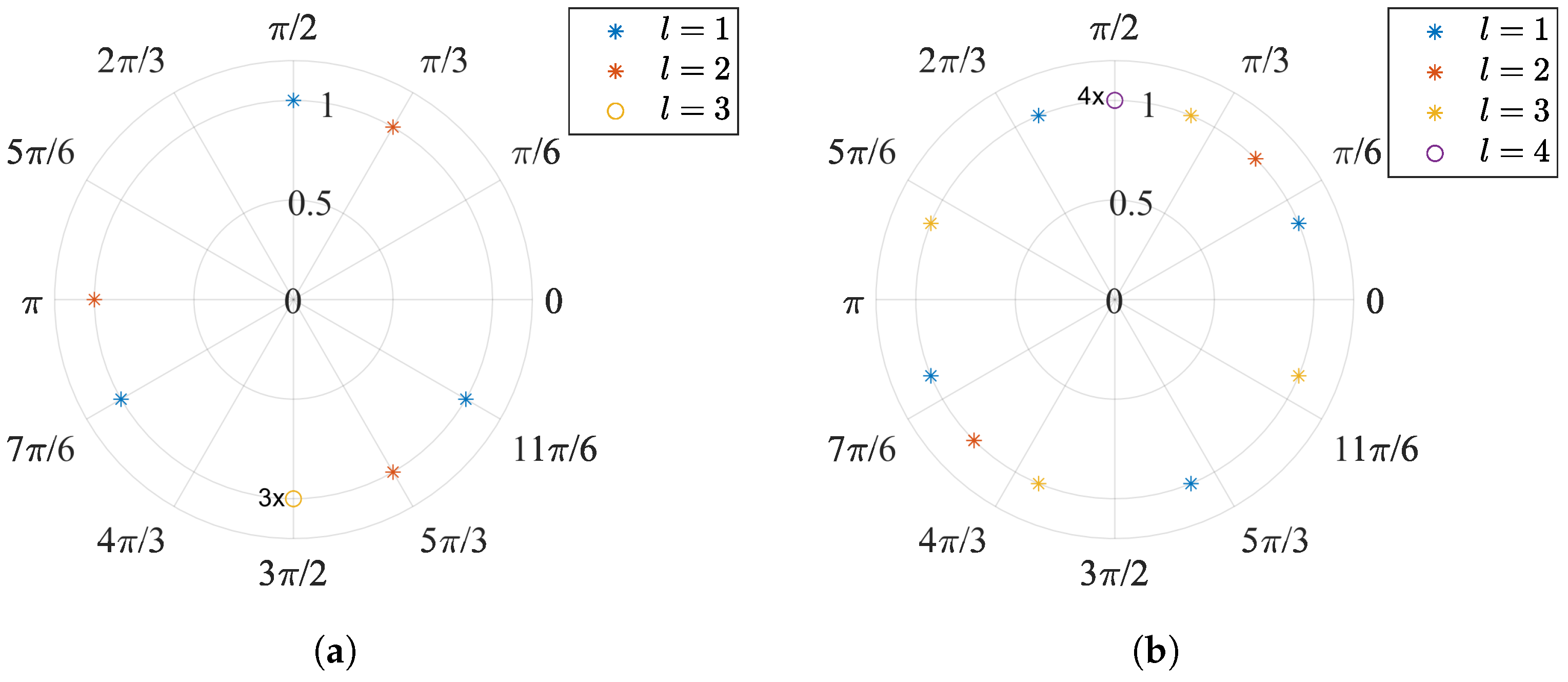
Appendix A. GNU Radio Flow Graph

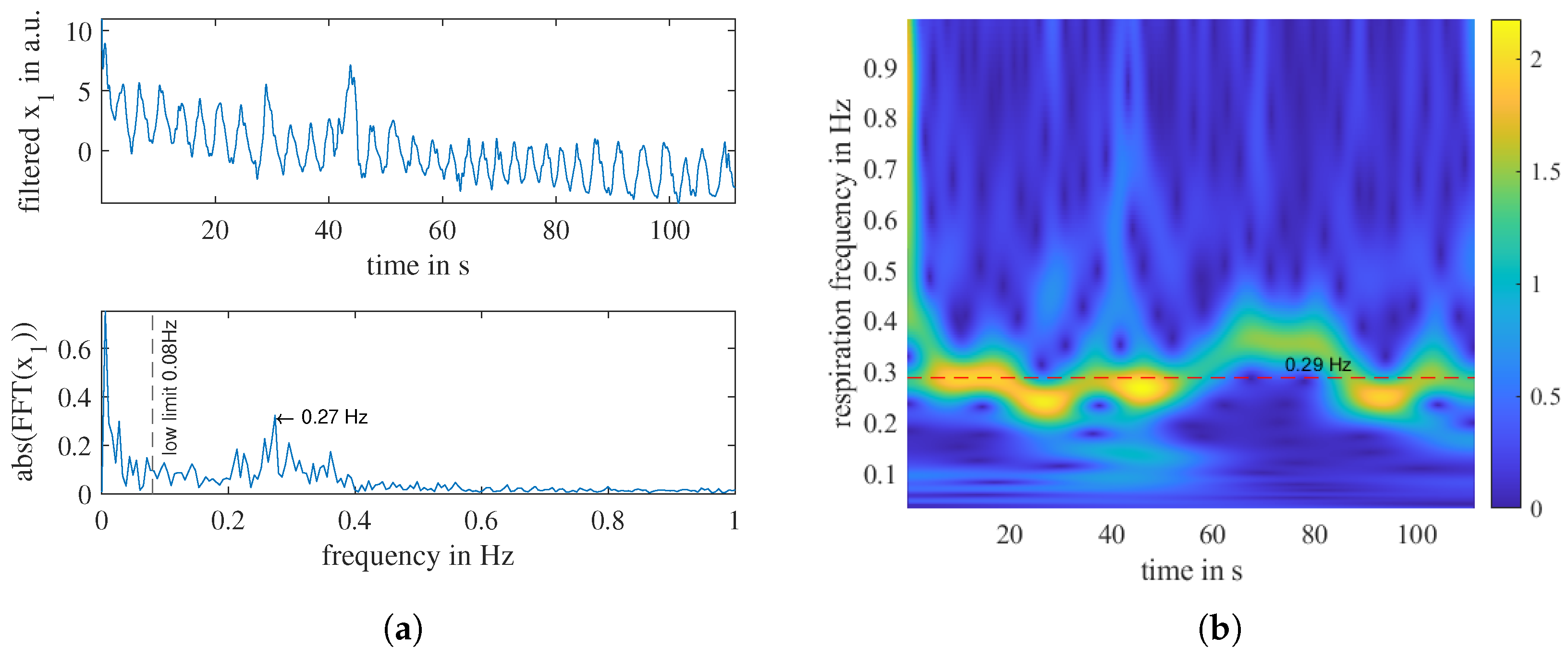
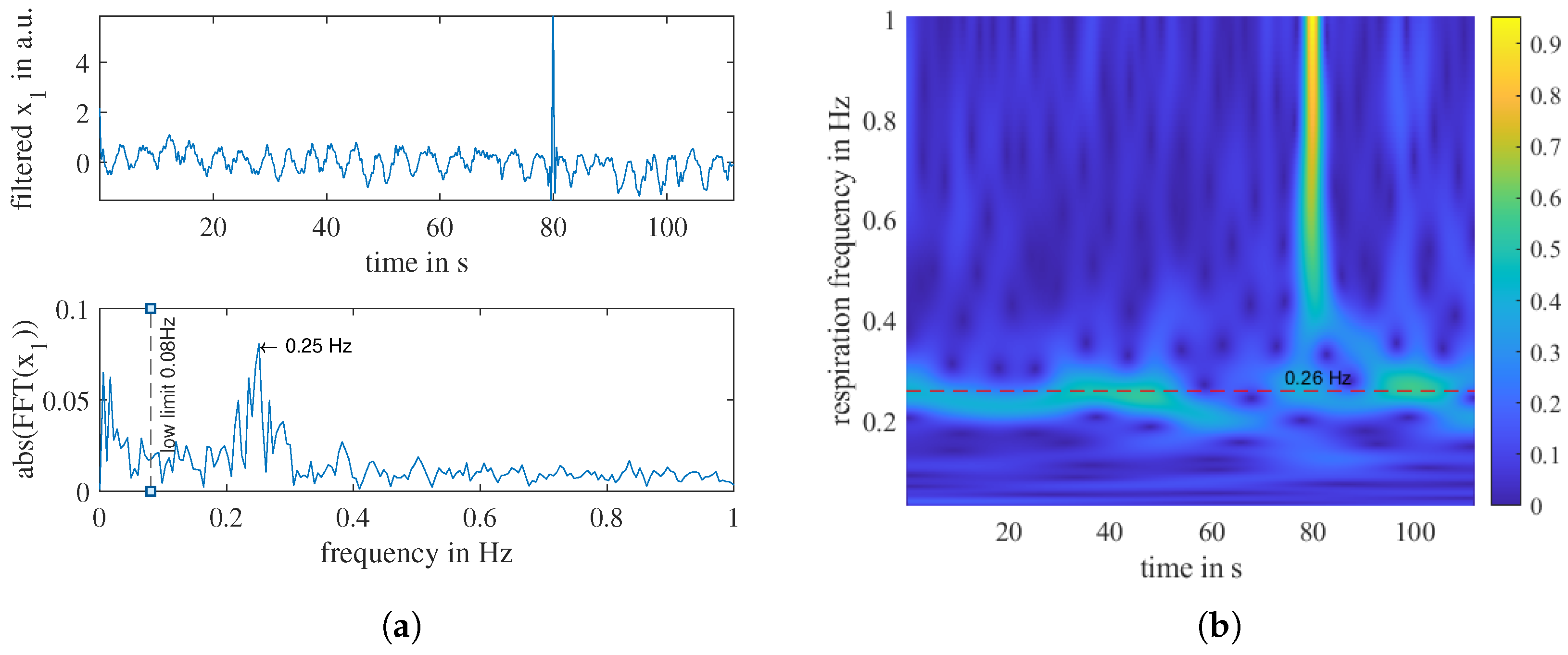
Appendix B. Field Measurement Plots


References
- Hänsch, T.W. Nobel lecture: Passion for precision. Rev. Mod. Phys. 2006, 78, 1297–1309. [Google Scholar] [CrossRef]
- Hall, J.L. Nobel lecture: Defining and measuring optical frequencies. Rev. Mod. Phys. 2006, 78, 1279–1295. [Google Scholar] [CrossRef]
- Bin Nesar, M.S.; Trippe, K.; Stapley, R.; Whitaker, B.M.; Hill, B. Improving touchless respiratory monitoring via lidar orientation and thermal imaging. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2022. [Google Scholar] [CrossRef]
- Gu, C.; Li, C.; Lin, J.; Long, J.; Huangfu, J.; Ran, L. Instrument-based noncontact doppler radar vital sign detection system using heterodyne digital quadrature demodulation architecture. IEEE Trans. Instrum. Meas. 2010, 59, 1580–1588. [Google Scholar] [CrossRef]
- Koelpin, A.; Lurz, F.; Linz, S.; Mann, S.; Will, C.; Lindner, S. Six-port based interferometry for precise radar and sensing applications. Sensors 2016, 16, 1556. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.K.; Kim, Y. Quadrature frequency-group radar and its center estimation algorithms for small vibrational displacement. Sci. Rep. 2019, 9, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Zakrzewski, M.; Raittinen, H.; Vanhala, J. Comparison of center estimation algorithms for heart and respiration monitoring with microwave doppler radar. IEEE Sens. J. 2012, 12, 627–634. [Google Scholar] [CrossRef]
- Li, C.; Lubecke, V.M.; Boric-Lubecke, O.; Lin, J. A review on recent advances in doppler radar sensors for noncontact healthcare monitoring. IEEE Trans. Microw. Theory Tech. 2013, 61, 2046–2060. [Google Scholar] [CrossRef]
- Li, C.; Lin, J. Recent advances in Doppler radar sensors for pervasive healthcare monitoring. In Proceedings of the Microwave Conference Proceedings (APMC), Yokohama, Japan, 7–10 December 2010; pp. 283–290. [Google Scholar]
- Baboli, M.; Singh, A.; Soll, B.; Boric-Lubecke, O.; Lubecke, V.M. Wireless sleep apnea detection using continuous wave quadrature Doppler radar. IEEE Sens. J. 2020, 20, 538–545. [Google Scholar] [CrossRef]
- Yee Siong, L.; Pathirana, P.N.; Steinfort, C.L.; Caelli, T. Monitoring and analysis of respiratory patterns using microwave Doppler radar. IEEE J. Transl. Eng. Health Med. 2014, 2, 1–12. [Google Scholar] [CrossRef]
- Will, C.; Shi, K.; Schellenberger, S.; Steigleder, T.; Michler, F.; Weigel, R.; Ostgathe, C.; Koelpin, A. Local pulse wave detection using continuous wave radar systems. IEEE J. Electromagn. RF Microwaves Med. Biol. 2017, 1, 81–89. [Google Scholar] [CrossRef]
- Lin, F.; Song, C.; Zhuang, Y.; Xu, W.; Li, C.; Ren, K. Cardiac scan: A non-contact and continuous heart-based user authentication system. In Proceedings of the Annual International Conference on Mobile Computing and Networking, MOBICOM, Snowbird, UT, USA, 16–20 October 2017; Part F1312. pp. 315–328. [Google Scholar] [CrossRef]
- Li, C.; Lubecke, V.M.; Boric-Lubecke, O.; Lin, J. Sensing of life activities at the human-microwave frontier. IEEE J. Microwaves 2021, 1, 66–78. [Google Scholar] [CrossRef]
- Zhang, Y.; Qi, F.; Lv, H.; Liang, F.; Wang, J. Bioradar Technolology. IEEE Microw. Mag. 2019, 20, 58–73. [Google Scholar] [CrossRef]
- Ossberger, G.; Buchegger, T.; Schimback, E.; Stelzer, A.; Weigel, R. Non-invasive respiratory movement detection and monitoring of hidden humans using ultra wideband pulse radar. In Proceedings of the 2004 International Workshop on Ultra Wideband Systems Joint with Conference on Ultra Wideband Systems and Technologies. Joint UWBST & IWUWBS 2004 (IEEE Cat. No.04EX812), Kyoto, Japan, 18–21 May 2004; pp. 395–399. [Google Scholar] [CrossRef]
- Nezirović, A.; Yarovoy, A.G.; Ligthart, L.P. Signal processing for improved detection of trapped victims using UWB radar. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2005–2014. [Google Scholar] [CrossRef]
- Sachs, J.; Helbig, M.; Herrmann, R.; Kmec, M.; Schilling, K.; Zaikov, E. Remote vital sign detection for rescue, security, and medical care by ultra-wideband pseudo-noise radar. Ad Hoc Netw. 2014, 13, 42–53. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, S.; Chen, C.; Chen, J.; Fang, G. A novel method for automatic detection of trapped victims by ultrawideband radar. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3132–3142. [Google Scholar] [CrossRef]
- Andersen, N.; Granhaug, K.; Michaelsen, J.A.; Bagga, S.; Hjortland, H.A.; Knutsen, M.R.; Lande, T.S.; Wisland, D.T. A 118-mW pulse-based radar SoC in 55-nm CMOS for non-contact human vital signs detection. IEEE J. Solid-State Circuits 2017, 52, 3421–3433. [Google Scholar] [CrossRef]
- Wang, H.; Dang, V.; Ren, L.; Liu, Q.; Ren, L.; Mao, E.; Kilik, O.; Fathy, A.E. An elegant solution: An aternative ultra-wideband transceiver based on stepped-frequency continuous-wave operation and compressive sensing. IEEE Microw. Mag. 2016, 17, 53–63. [Google Scholar] [CrossRef]
- Ren, L.; Kong, L.; Foroughian, F.; Wang, H.; Theilmann, P.; Fathy, A.E. Comparison study of noncontact vital signs detection using a doppler stepped-frequency continuous-wave radar and camera-based imaging photoplethysmography. IEEE Trans. Microw. Theory Tech. 2017, 65, 3519–3529. [Google Scholar] [CrossRef]
- Peng, Z.; Ran, L.; Li, C. A κ-band portable FMCW radar with beamforming array for short-range localization and vital-Doppler targets discrimination. IEEE Trans. Microw. Theory Tech. 2017, 65, 3443–3452. [Google Scholar] [CrossRef]
- Loschonsky, M.; Feige, C.H.; Rogall, O.; Fisun, S.; Reindl, L.M. Detection technology for trapped and buried people. In Proceedings of the IEEE MTT-S International Microwave Workshop Series on Wireless Sensing, Local Positioning and RFID, IMWS 2009, Cavtat, Croatia, 24–25 September 2009; pp. 2–7. [Google Scholar] [CrossRef]
- Liu, L.; Liu, S. Remote detection of human vital sign with stepped-frequency continuous wave radar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 775–782. [Google Scholar] [CrossRef]
- Fu, L.; Liu, S.; Liu, L.; Lei, L. Development of an airborne ground penetrating radar system: Antenna design, laboratory experiment, and numerical simulation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 761–766. [Google Scholar] [CrossRef]
- Shi, D.; Aftab, T.; Yousaf, A.; Reindl, L.M. Design of a small size biquad-UWB-patch-antenna and signal processing for detecting respiration of trapped victims. In Proceedings of the Progress in Electromagnetics Research Symposium, Singapore, 19–22 November 2017; Volume 2017, pp. 1774–1779. [Google Scholar] [CrossRef]
- Oyan, M.J.; Hamran, S.E.; Hanssen, L.; Berger, T.; Plettemeier, D. Ultrawideband gated step frequency ground-penetrating radar. IEEE Trans. Geosci. Remote Sens. 2012, 50, 212–220. [Google Scholar] [CrossRef]
- Lathi, B.P.; Ding, Z. Modern Digital and Analog Communication Systems, 4th ed.; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Stralka, J.P. Applications of Orthogonal Frequency-Division Multiplexing (OFDM) to Radar. Ph.D. Thesis, The Johns Hopkins University, Baltimore, MD, USA, 2008. [Google Scholar]
- Badawy, J.; Nguyen, O.K.; Clark, C.; Halm, E.A.; Makam, A.N. Is everyone really breathing 20 times a minute? Assessing epidemiology and variation in recorded respiratory rate in hospitalised adults. BMJ Qual. Saf. 2017, 26, 832–836. [Google Scholar] [CrossRef]
- Fleming, S.; Thompson, M.; Stevens, R.; Heneghan, C.; Plüddemann, A.; MacOnochie, I.; Tarassenko, L.; Mant, D. Normal ranges of heart rate and respiratory rate in children from birth to 18 years of age: A systematic review of observational studies. Lancet 2011, 377, 1011–1018. [Google Scholar] [CrossRef]
- Semler, M.W.; Stover, D.G.; Copland, A.P.; Hong, G.; Johnson, M.J.; Kriss, M.S.; Otepka, H.; Wang, L.; Christman, B.W.; Rice, T.W. Flash mob research: A single-day, multicenter, resident-directed study of respiratory rate. Chest 2013, 143, 1740–1744. [Google Scholar] [CrossRef]
- Snyder, F.; Hobson, J.A.; Morrison, D.F.; Goldfrank, F. Changes in respiration, heart rate, and systolic blood pressure in human sleep. J. Appl. Physiol. 1964, 19, 417–422. [Google Scholar] [CrossRef]
- Skolnik, M.l. Introduction to Radar Systems, 3rd ed.; McGraw-Hill Higher Education: New York, NY, USA, 2001. [Google Scholar]
- Daniels, D.J. (Ed.) Ground Penetrating Radar; Institution of Engineering and Technology: London, UK, 2004. [Google Scholar] [CrossRef]
- Bradford, J.H. Frequency-dependent attenuation analysis of ground-penetrating radar data. Geophysics 2007, 72. [Google Scholar] [CrossRef]
- Shi, D.; Aftab, T.; Gidion, G.; Sayed, F.; Reindl, L.M. A novel electrically small ground-penetrating radar patch antenna with a parasitic ring for respiration detection. Sensors 2021, 21, 1930. [Google Scholar] [CrossRef] [PubMed]
- Collins, T.F.; Getz, R.; Pu, D.; Wyglinsk, A.M. Software-Defined Radio for Engineers; Artech House: New York, NY, USA, 2018. [Google Scholar]
- Analog Devices. AD9364: RF Agile Transceiver Data Sheet (Rev. c); Analog Devices: Wilmington, MA, USA, 2014. [Google Scholar]
- Analog Devices. AD936x Family Transceiver; Analog Devices: Wilmington, MA, USA; Available online: https://www.analog.com/en/applications/technology/sdr-radioverse-pavilion-home/wideband-transceivers.html (accessed on 5 September 2021).
- Robert, F.C.J.; Sylvar, D.M.; Ulcek, J.L. Evaluating compliance with FCC guidelines for human exposure to radiofrequency electromagnetic fields. FCC OET Bull. 1997, 65, 1–79. [Google Scholar]
- Olhede, S.C.; Walden, A.T. Generalized Morse wavelets. IEEE Trans. Signal Process. 2002, 50, 2661–2670. [Google Scholar] [CrossRef]
- Lilly, J.M.; Olhede, S.C. Generalized Morse wavelets as a superfamily of analytic wavelets. IEEE Trans. Signal Process. 2012, 60, 6036–6041. [Google Scholar] [CrossRef]
- Lilly, J.M.; Olhede, S.C. Higher-order properties of analytic wavelets. IEEE Trans. Signal Process. 2009, 57, 146–160. [Google Scholar] [CrossRef]
- Brunetti, G.; Armenise, M.N.; Ciminelli, C. Chip-scaled Ka-band photonic linearly chirped microwave waveform generator. Front. Phys. 2022, 10, 1–13. [Google Scholar] [CrossRef]

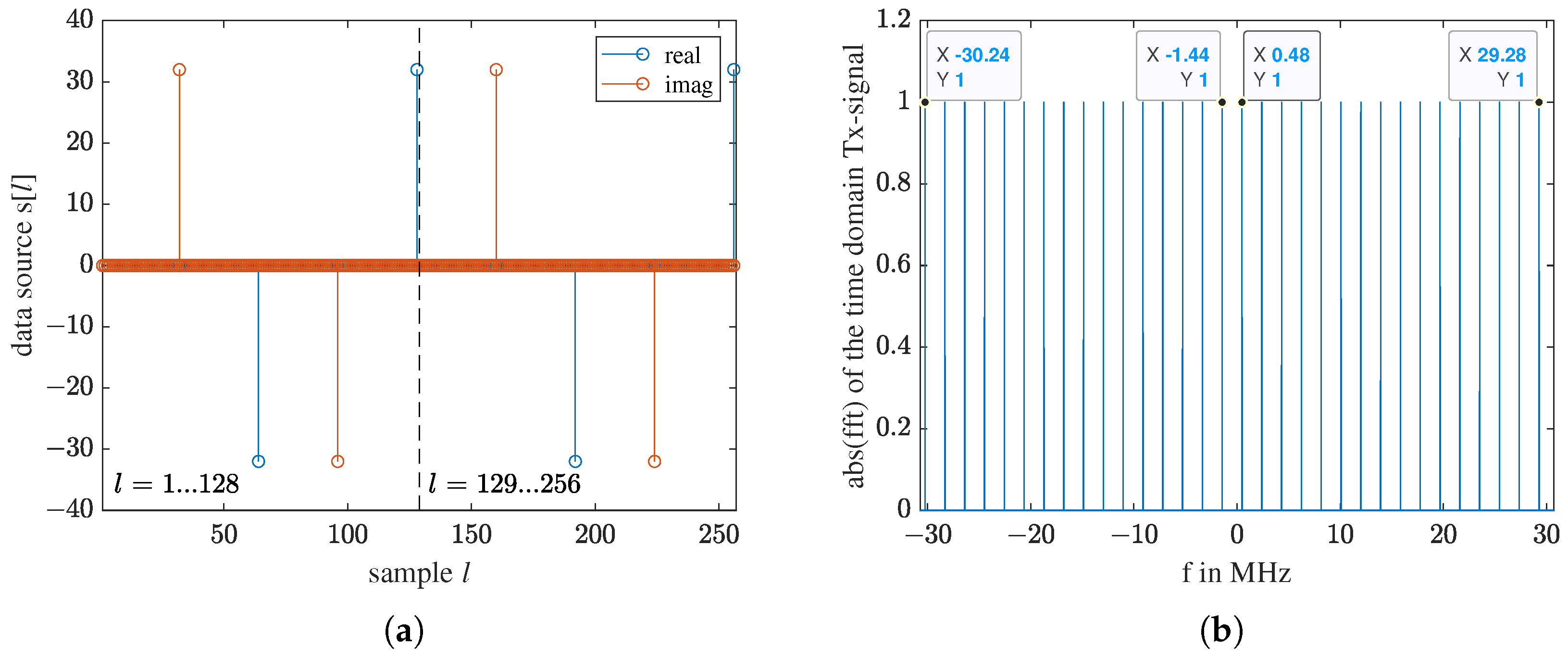








| Parameter | Symbol | Value |
|---|---|---|
| sampling frequency | MHz | |
| number of tones in the frequency comb | M | 32 |
| number of samples in waveform | L | 4096 |
| bandwidth | MHz | |
| start frequency | MHz | |
| stop frequency | MHz |
| Parameter | Symbol | Value |
|---|---|---|
| sampling frequency | MHz | |
| LO-frequency of the receiver | GHz | |
| LO-frequency of the transmitter | GHz | |
| transmitting waveform | see Equation (5) and Table 1 | |
| number of samples per receiving frame | L | 4096 |
| number of frames | N | 20k |
| frame rate | 225 Hz | |
| measurement duration | about 86 s |
| Nr. | Scenario | Life Detected | ||||
|---|---|---|---|---|---|---|
| 1 | (a) | Hz | Hz | dB | yes | |
| 2 | (a) | Hz | Hz | dB | yes | |
| 3 | (b) | Hz | Hz | dB | yes | |
| 4 | (b) | Hz | Hz | dB | no | |
| 5 | (c) | Hz | Hz | dB | yes | |
| 6 | (c) | Hz | Hz | dB | yes | |
| 7 | (d) | Hz | Hz | dB | no | |
| 8 | (d) | Hz | Hz | dB | no |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, D.; Gidion, G.; Aftab, T.; Reindl, L.M.; Rupitsch, S.J. Frequency Comb-Based Ground-Penetrating Bioradar: System Implementation and Signal Processing. Sensors 2023, 23, 1335. https://doi.org/10.3390/s23031335
Shi D, Gidion G, Aftab T, Reindl LM, Rupitsch SJ. Frequency Comb-Based Ground-Penetrating Bioradar: System Implementation and Signal Processing. Sensors. 2023; 23(3):1335. https://doi.org/10.3390/s23031335
Chicago/Turabian StyleShi, Di, Gunnar Gidion, Taimur Aftab, Leonhard M. Reindl, and Stefan J. Rupitsch. 2023. "Frequency Comb-Based Ground-Penetrating Bioradar: System Implementation and Signal Processing" Sensors 23, no. 3: 1335. https://doi.org/10.3390/s23031335
APA StyleShi, D., Gidion, G., Aftab, T., Reindl, L. M., & Rupitsch, S. J. (2023). Frequency Comb-Based Ground-Penetrating Bioradar: System Implementation and Signal Processing. Sensors, 23(3), 1335. https://doi.org/10.3390/s23031335







