Hybrid CNN-SVR Blood Pressure Estimation Model Using ECG and PPG Signals
Abstract
1. Introduction
2. Materials and Methods
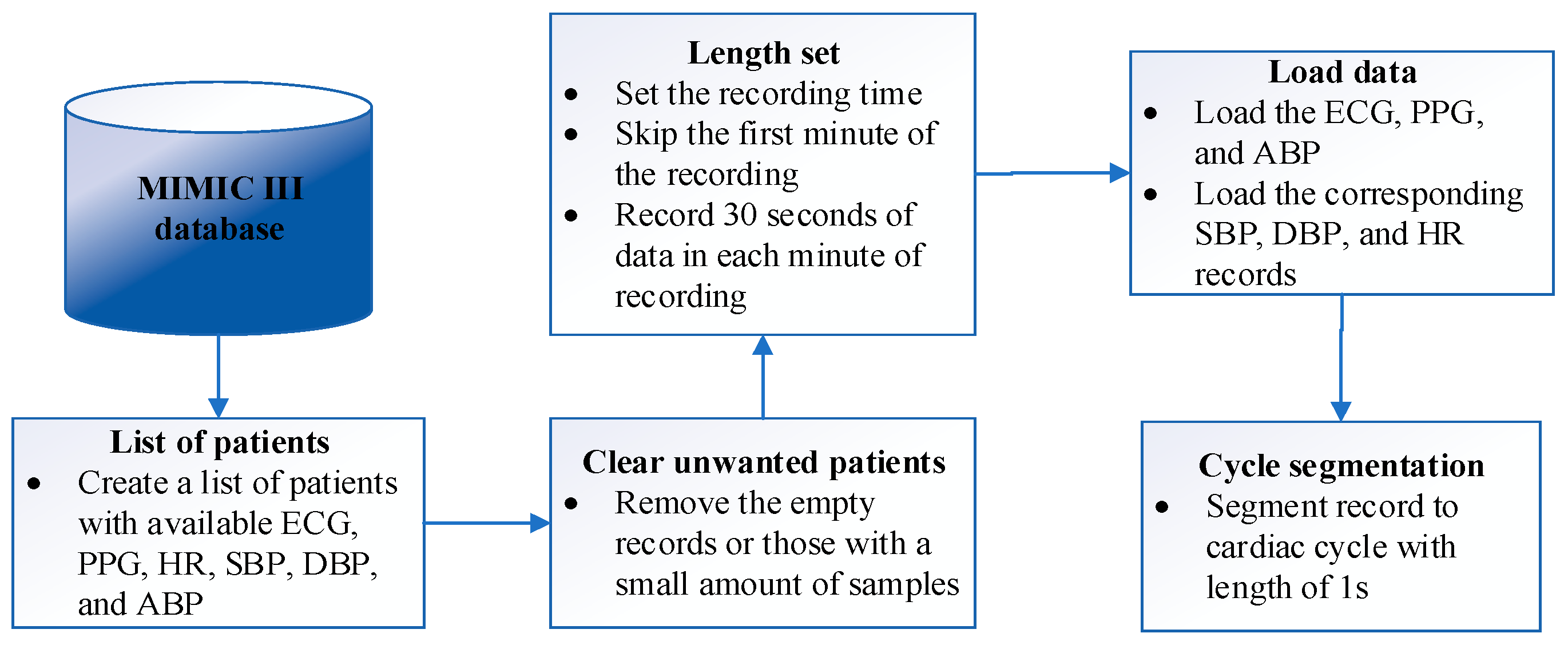
2.1. Database
- The duration of recording was specified and based on the requirement of this study; seven minutes of data were collected for each patient.
- Most of the missing samples occurred within the first minute of recording; all records were collected after one minute of the actual recording time.
- A 30 s gap was allowed between each one-minute collection interval to avoid recording consecutive pulses.
- Five ECG signals from leads I, II, III, AVR, and V were available during portions of some ECG records in the MIMIC III waveform database. However, these five ECG signals were not all available simultaneously. We employed the ECG lead AVR in this study due to better signal quality and availability in most records. The ECG and PPG waveforms were loaded into the MATLAB environment as a matrix with two labelled columns.
- The corresponding SBP and DBP specified as ABP Sys and ABP Dias, respectively, were loaded as a matrix with three labeled columns.
- Both matrices of steps 4 and 5 were concatenated together and saved in CSV format for training and testing the network.
- As each cardiac cycle interval was considered to be 0.6 s to 1 s, the signals were segmented into the cardiac cycle with a length of 1 s as one beat [13].
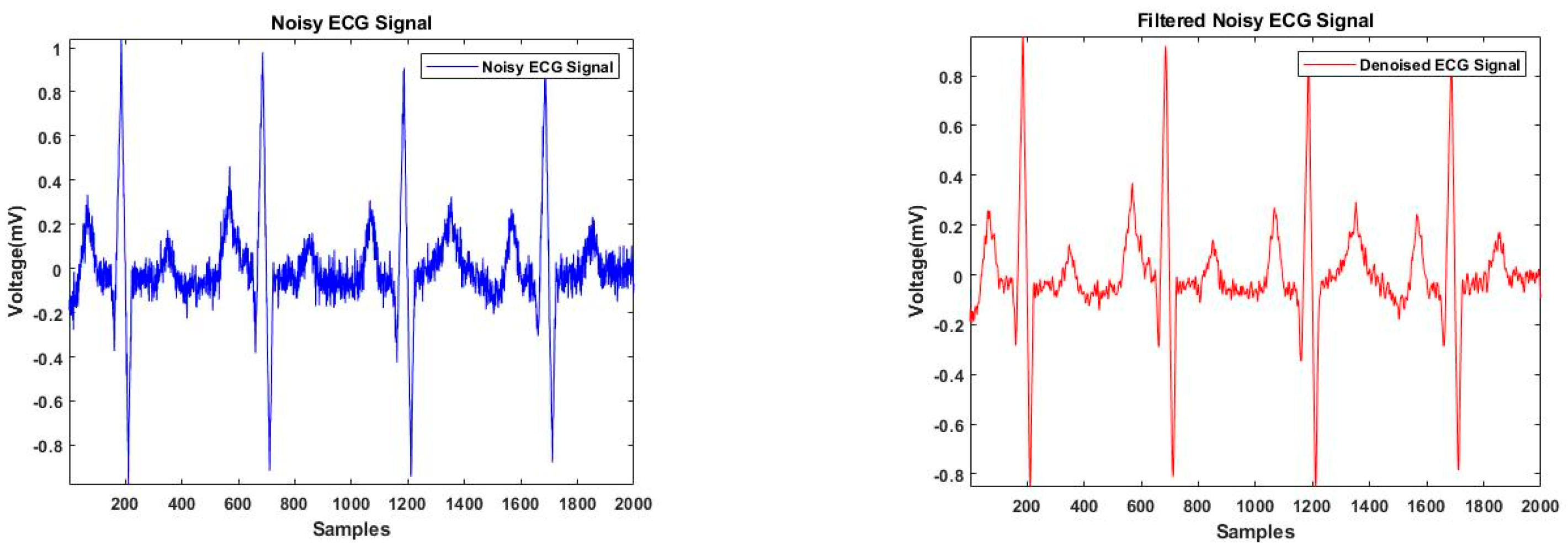
2.2. Pre-Processing
2.3. R-Peak Detection
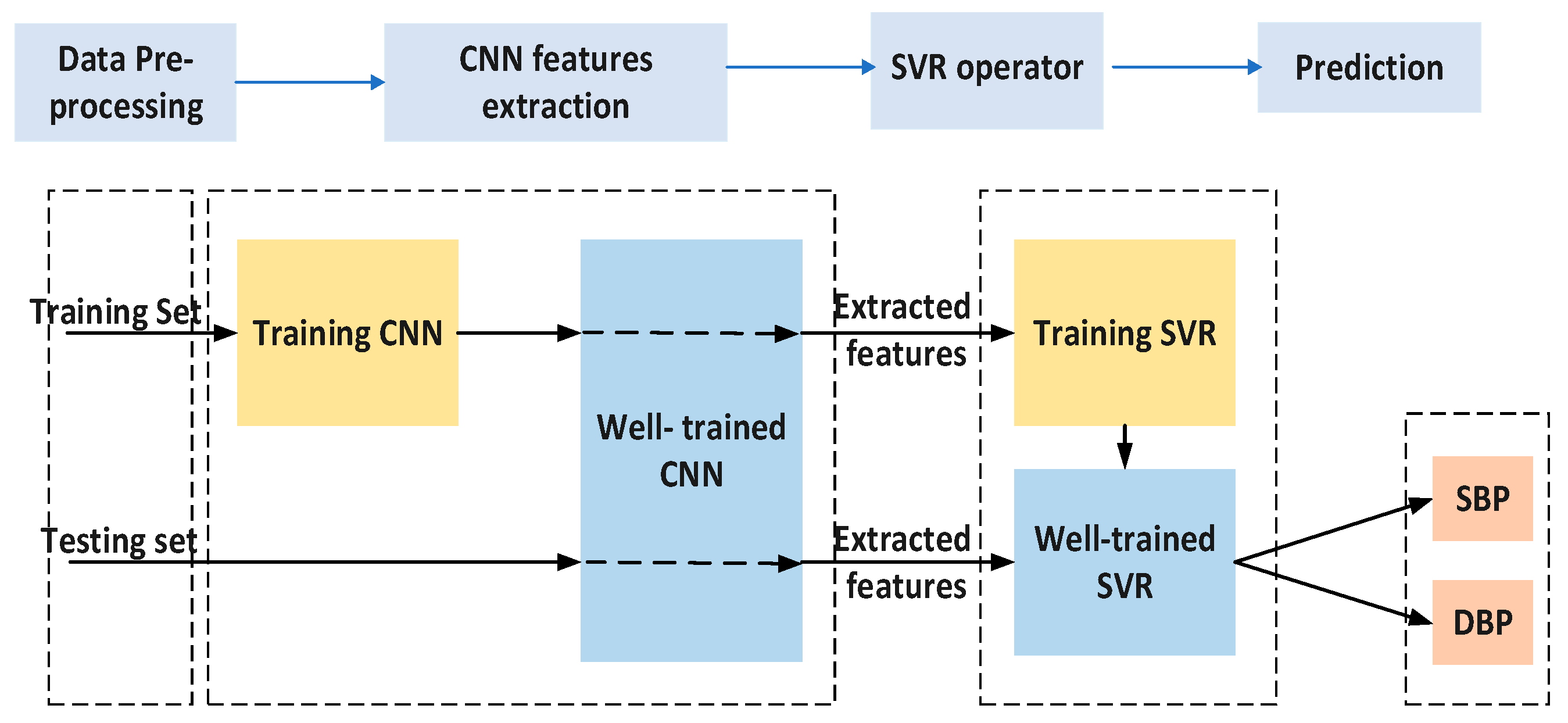
2.4. Hybrid CNN-SVR Model
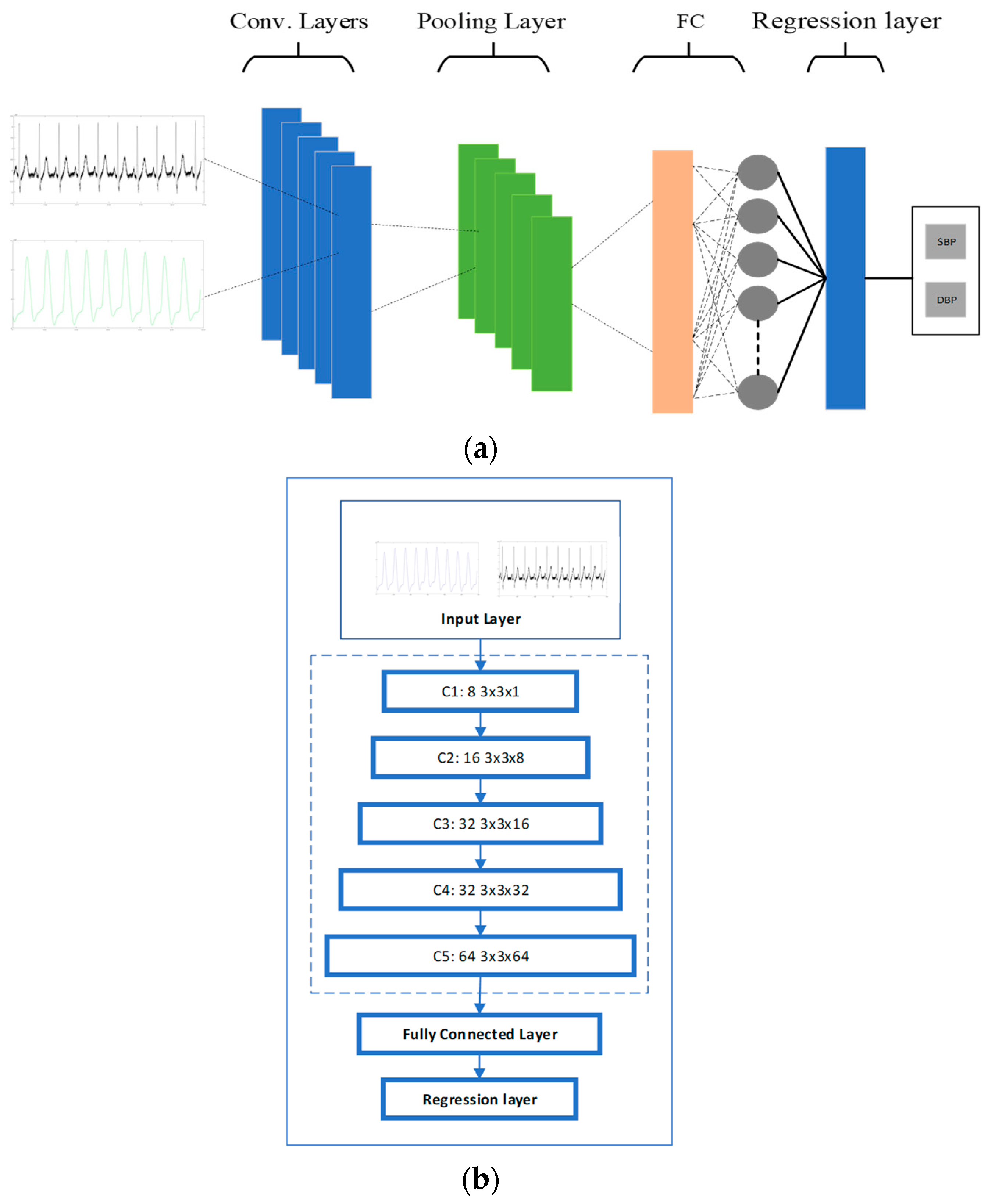
2.4.1. Convolutional Neural Networks
2.4.2. CNN Model for BP Estimation
2.4.3. SVR Model
Kernel Function Selection
Description of the Proposed SVR
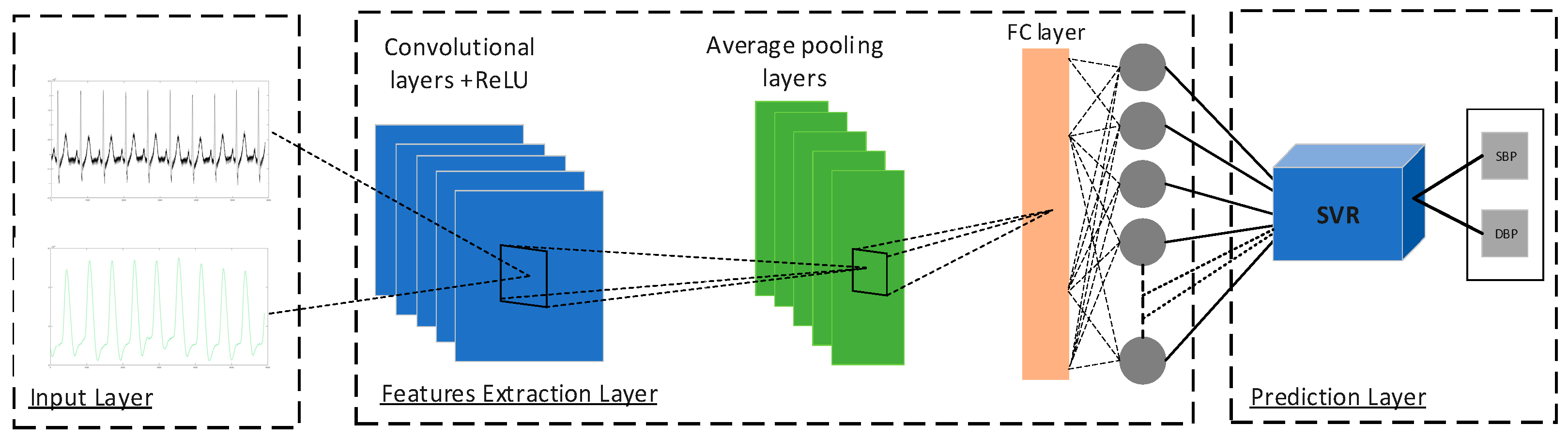
2.5. The Architecture of the Proposed Hybrid CNN-SVR Model
3. Model Training and Experimental Results
3.1. Accuracy Performance
3.2. Comparison of the Results with the Related Works
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, R.; Huang, Z.P.; Ji, L.Y.; Wu, J.K.; Li, H.; Zhang, Z.Q. Beat-to-Beat Ambulatory Blood Pressure Estimation Based on Random Forest. In Proceedings of the 2016 IEEE 13th International Conference on Wearable and Implantable Body Sensor Networks (BSN), San Francisco, CA, USA, 14–17 June 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Xu, J.; Jiang, J.; Zhou, H.; Yan, Z. A Novel Blood Pressure Estimation Method Combing Pulse Wave Transit Time Model and Neural Network Model. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Republic of Korea, 11–15 July 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Zhang, Y.; Feng, Z. A SVM Method for Continuous Blood Pressure Estimation from a PPG Signal. In Proceedings of the 9th International Conference on Machine Learning and Computing, Singapore, 24–26 February 2017; ACM: New York, NY, USA, 2017. [Google Scholar]
- Arza, A.; Lázaro, J.; Gil, E.; Laguna, P.; Aguiló, J.; Bailon, R. Pulse transit time and pulse width as potential measure for estimating beat-to-beat systolic and diastolic blood pressure. In Proceedings of the Computing in Cardiology 2013, Zaragoza, Spain, 22–25 September 2013. [Google Scholar]
- Goli, S.; Jayanthi, T. Cuff less continuous non-invasive blood pressure measurement using pulse transit time measurement. Int. J. Recent Dev. Eng. Technol. 2014, 2, 16–86. [Google Scholar]
- Padilla, J.M.; Berjano, E.J.; Saiz, J.; Facila, L.; Diaz, P.; Merce, S. Assessment of relationships between blood pressure, pulse wave velocity and digital volume pulse. In Proceedings of the 2006 Computers in Cardiology, Valencia, Spain, 17–20 September 2006. [Google Scholar]
- Wong, M.Y.-M.; Poon, C.C.-Y.; Zhang, Y.-T. An evaluation of the cuffless blood pressure estimation based on pulse transit time technique: A half year study on normotensive subjects. Cardiovasc. Eng. 2009, 9, 32–38. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekaran, V.; Dantu, R.; Jonnada, S.; Thiyagaraja, S.; Subbu, K.P. Cuffless differential blood pressure estimation using smart phones. IEEE Trans. Biomed. Eng. 2012, 60, 1080–1089. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, J.C.; Amadu, A.M.; Dastidar, A.G.; McIntyre, B.; Szantho, G.V.; Lyen, S.; Godsave, C.; Ratcliffe, L.E.; Burchell, A.E.; Hart, E.C.; et al. ECG strain pattern in hypertension is associated with myocardial cellular expansion and diffuse interstitial fibrosis: A multi-parametric cardiac magnetic resonance study. Eur. Heart J. Cardiovasc. Imaging 2016, 18, 441–450. [Google Scholar] [CrossRef] [PubMed]
- Madani, A.; Arnaout, R.; Mofrad, M.; Arnaout, R. Fast and accurate view classification of echocardiograms using deep learning. NPJ Digit. Med. 2018, 1, 6. [Google Scholar] [CrossRef]
- Johnson, A.E.W.; Pollard, T.J.; Shen, L.; Lehman, L.-W.H.; Feng, M.; Ghassemi, M.; Moody, B.; Szolovits, P.; Celi, L.A.; Mark, R.G. MIMIC-III, a freely accessible critical care database. Sci. Data 2016, 3, 160035. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef]
- Ding, X.; Wang, Y.; Hao, Y.; Lv, Y.; Chen, R.; Yan, H. A New Measure of Pulse Rate Variability and Detection of Atrial Fibrillation Based on Improved Time Synchronous Averaging. Comput. Math. Methods Med. 2021, 2021, 9. [Google Scholar] [CrossRef]
- Rai, H.M.; Trivedi, A.; Shukla, S. ECG signal processing for abnormalities detection using multi-resolution wavelet transform and Artificial Neural Network classifier. Measurement 2013, 46, 3238–3246. [Google Scholar] [CrossRef]
- AlMahamdy, M.; Riley, H.B. Performance study of different denoising methods for ECG signals. Procedia Comput. Sci. 2014, 37, 325–332. [Google Scholar] [CrossRef]
- Arvinti, B.; Costache, M.; Toader, D.; Oltean, M.; Isar, A. ECG statistical denoising in the wavelet domain. In Proceedings of the 9th International Symposium on Electronics and Telecommunications, Timisoara, Romania, 11–12 November 2010. [Google Scholar]
- Al-Qawasmi, A.; Daqrouq, K. ECG signal enhancement using wavelet transform. WSEAS Trans. Biol. Biomed. 2010, 7, 62–72. [Google Scholar]
- Prasad, V.; Latha, T.; Suresh, M. Denoising of biological signals using wavelets. Int. J. Curr. Eng. Technol. 2013, 3, 863–866. [Google Scholar]
- Kania, M.; Fereniec, M.; Maniewski, R. Wavelet denoising for multi-lead high resolution ECG signals. Meas. Sci. Rev. 2007, 7, 30–33. [Google Scholar]
- Awal, M.A.; Mostafa, S.; Ahmad, M. Performance analysis of Savitzky-Golay smoothing filter using ECG signal. Int. J. Comput. Inf. Technol. 2011, 1, 24. [Google Scholar]
- Hargittai, S. Savitzky-Golay least-squares polynomial filters in ECG signal processing. In Proceedings of the Computers in Cardiology, Lyon, France, 25–28 September 2005. [Google Scholar]
- Chandrakar, C.; Kowar, M. Denoising ECG signals using adaptive filter algorithm. Int. J. Soft Comput. Eng. 2012, 2, 120–123. [Google Scholar]
- Savitzky, A.; Golay, M. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Payne, R.A.; Symeonides, C.N.; Webb, D.J.; Maxwell, S.R.J. Pulse transit time measured from the ECG: An unreliable marker of beat-to-beat blood pressure. J. Appl. Physiol. 2006, 100, 136–141. [Google Scholar] [CrossRef]
- Ding, X.; Dai, W.; Luo, N.; Liu, J.; Zhao, N.; Zhang, Y. A Flexible Tonoarteriography-Based Body Sensor Network for Cuffless Measurement of Arterial Blood Pressure. In Proceedings of the IEEE 12th International Conference on Wearable and Implantable Body Sensor Networks (BSN), Cambridge, MA, USA, 9–12 June 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Tsinalis, O.; Matthews, P.M.; Guo, Y.; Zafeiriou, S. Automatic Sleep Stage Scoring with Single-Channel EEG Using Convolutional Neural Networks; Cornell University: Ithaca, NY, USA, 2016. [Google Scholar]
- Badshah, A.M.; Ahmad, J.; Rahim, N.; Baik, S.W. Speech emotion recognition from spectrograms with deep convolutional neural network. In Proceedings of the 2017 International Conference on Platform Technology and Service (PlatCon), Busan, Repblic of Korea, 13–15 February 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Mao, Q.; Dong, M.; Huang, Z.; Zhan, Y. Learning salient features for speech emotion recognition using convolutional neural networks. IEEE Trans. Multimed. 2014, 16, 2203–2213. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Luo, P.; Wang, X.; Shao, W.; Peng, Z. Towards understanding regularization in batch normalization. arXiv 2018, arXiv:1809.00846. [Google Scholar]
- Kalchbrenner, N.; Grefenstette, E.; Blunsom, P. A convolutional neural network for modelling sentences. arXiv 2014, arXiv:1404.2188. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, Y.; Cao, H.; Zhang, S.; Zhou, Y. Nonlinear regression with high-dimensional space mapping for blood component spectral quantitative analysis. J. Spectrosc. 2018, 2018, 2689750. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, Y.F. FS_SFS: A novel feature selection method for support vector machines. Pattern Recognit. 2006, 39, 1333–1345. [Google Scholar] [CrossRef]
- Qian, N. On the momentum term in gradient descent learning algorithms. Neural Netw. 1999, 12, 145–151. [Google Scholar] [CrossRef]
- Zhang, B.; Ren, H.; Huang, G.; Cheng, Y.; Hu, C. Predicting blood pressure from physiological index data using the SVR algorithm. BMC Bioinform. 2019, 20, 109. [Google Scholar] [CrossRef]
- Kachuee, M.; Kiani, M.M.; Mohammadzade, H.; Shabany, M. Cuffless blood pressure estimation algorithms for continuous health-care monitoring. IEEE Trans. Biomed. Eng. 2016, 64, 859–869. [Google Scholar] [CrossRef]
- Slapničar, G.; Mlakar, N.; Luštrek, M. Blood pressure estimation from photoplethysmogram using a spectro-temporal deep neural network. Sensors 2019, 19, 3420. [Google Scholar] [CrossRef]
- Chen, S.; Ji, Z.; Wu, H.; Xu, Y. A Non-Invasive Continuous Blood Pressure Estimation Approach Based on Machine Learning. Sensors 2019, 19, 2585. [Google Scholar] [CrossRef]
- Khalid, S.G.; Zhang, J.; Chen, F.; Zheng, D. Blood pressure estimation using photoplethysmography only: Comparison between different machine learning approaches. J. Healthc. Eng. 2018, 2018, 1548647. [Google Scholar] [CrossRef]
- Ertuğrul, F.; Sezgin, N. A noninvasive time-frequency-based approach to estimate cuffless arterial blood pressure. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 2260–2274. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, W.; Xing, Y.; Zhou, X. A novel neural network model for blood pressure estimation using photoplethesmography without electrocardiogram. J. Healthc. Eng. 2018, 2018, 7804243. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wu, D.; Li, Y. Cuff-less and Calibration-free Blood Pressure Estimation Using Convolutional Autoencoder with Unsupervised Feature Extraction. In Proceedings of the 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Baek, S.; Jang, J.; Yoon, S. End-to-End Blood Pressure Prediction via Fully Convolutional Networks. IEEE Access 2019, 7, 185458–185468. [Google Scholar] [CrossRef]



| MAE | Standard Deviation | Subjects | ||
|---|---|---|---|---|
| AAMI standard | SB, DBP | 5 (mmHg) | 8 (mmHg) | 85 |
| Hybrid CNN-SVR Model | SBP | 1.23 | 2.45 | 120 |
| DBP | 3.08 | 5.67 | ||
| Model | Number of Subjects | Engineered Feature | MAE SBP (mmHg) | MAE DBP (mmHg) |
|---|---|---|---|---|
| Classical ML [38] | MIMIC-II, 1000 subjects | Yes | 11.17 | 5.35 |
| ResNet [39] | MIMIC-III, 510 subjects | Yes | 9.43 | 6.88 |
| GA-SVR [40] | MIMIC-III, 772 waveforms | Yes | 3.27 | 1.16 |
| Regression tree [41] | Queensland, 32 subjects | Yes | 4.82 | 3.25 |
| ELM [42] | MIMIC-II, 4254 records | Yes | 4.25 | 3.95 |
| ANN [43] | MIMIC-II, 90 subjects | Yes | 4.02 | 2.27 |
| CNN [44] | Unspecified, 62 Subjects | No | 9.61 | 6.73 |
| CNN [45] | MIMIC-II, 379 Subjects | No | 9.30 | 5.12 |
| Hybrid CNN-SVR | MIMIC-III, 120 subjects | No | 1.23 | 3.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rastegar, S.; Gholam Hosseini, H.; Lowe, A. Hybrid CNN-SVR Blood Pressure Estimation Model Using ECG and PPG Signals. Sensors 2023, 23, 1259. https://doi.org/10.3390/s23031259
Rastegar S, Gholam Hosseini H, Lowe A. Hybrid CNN-SVR Blood Pressure Estimation Model Using ECG and PPG Signals. Sensors. 2023; 23(3):1259. https://doi.org/10.3390/s23031259
Chicago/Turabian StyleRastegar, Solmaz, Hamid Gholam Hosseini, and Andrew Lowe. 2023. "Hybrid CNN-SVR Blood Pressure Estimation Model Using ECG and PPG Signals" Sensors 23, no. 3: 1259. https://doi.org/10.3390/s23031259
APA StyleRastegar, S., Gholam Hosseini, H., & Lowe, A. (2023). Hybrid CNN-SVR Blood Pressure Estimation Model Using ECG and PPG Signals. Sensors, 23(3), 1259. https://doi.org/10.3390/s23031259






