Optimal Channel Training Design for Secure Short-Packet Communications
Abstract
1. Introduction
- Based on the finite blocklength information theory, we derive a closed-form expression to approximate the average achievable secrecy throughput, which provides an efficient means to comprehensively evaluate the impact of key system parameters, e.g., the channel training length and blocklength, on the latency-reliability tradeoff.
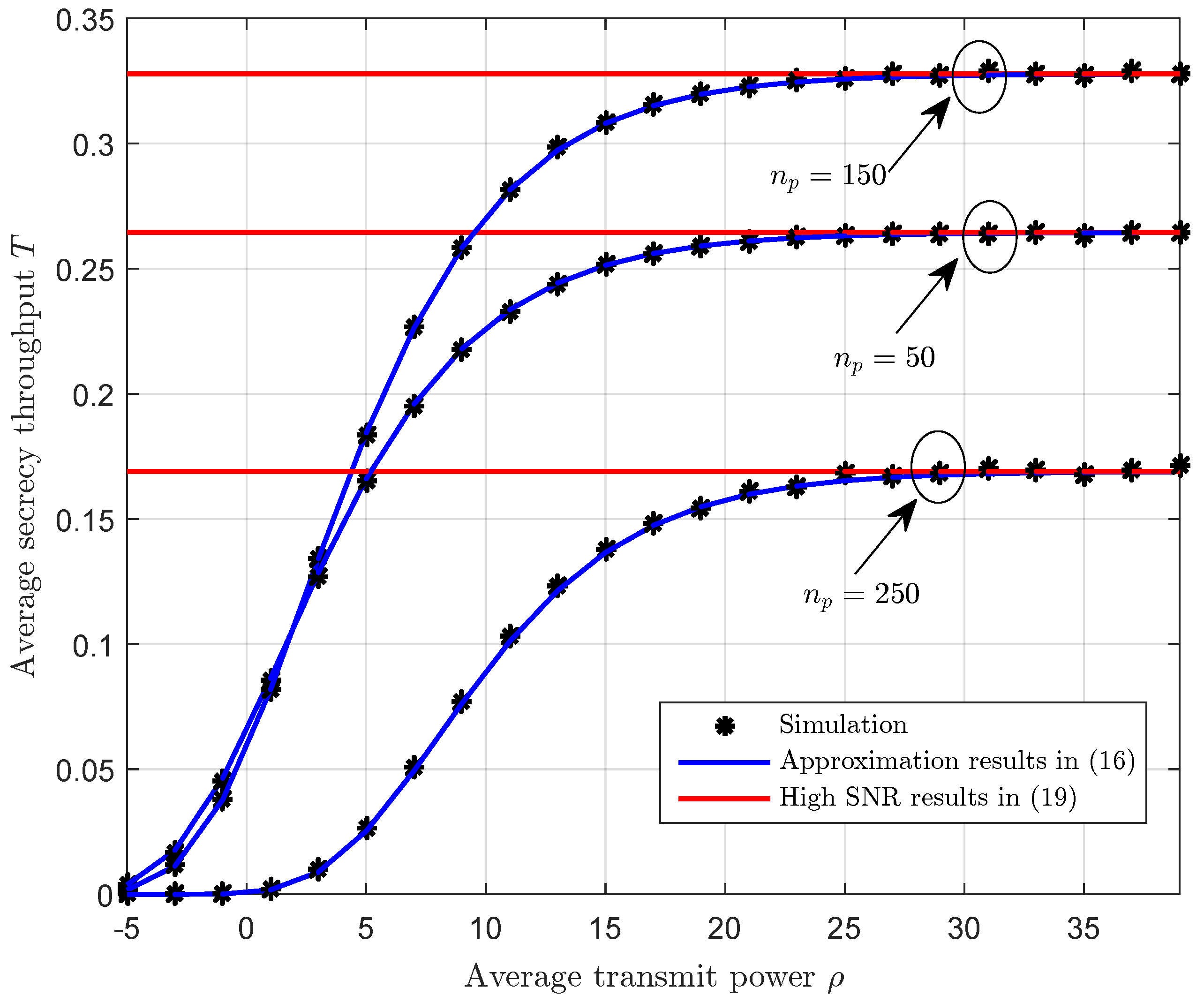
- To achieve additional insights on the application of the channel training scheme for secure short-packet communications into the practical design, we also present the asymptotic closed-form expressions for the average secrecy throughput under two special cases, i.e., high signal-to-noise ratio (SNR) and infinite blocklength.
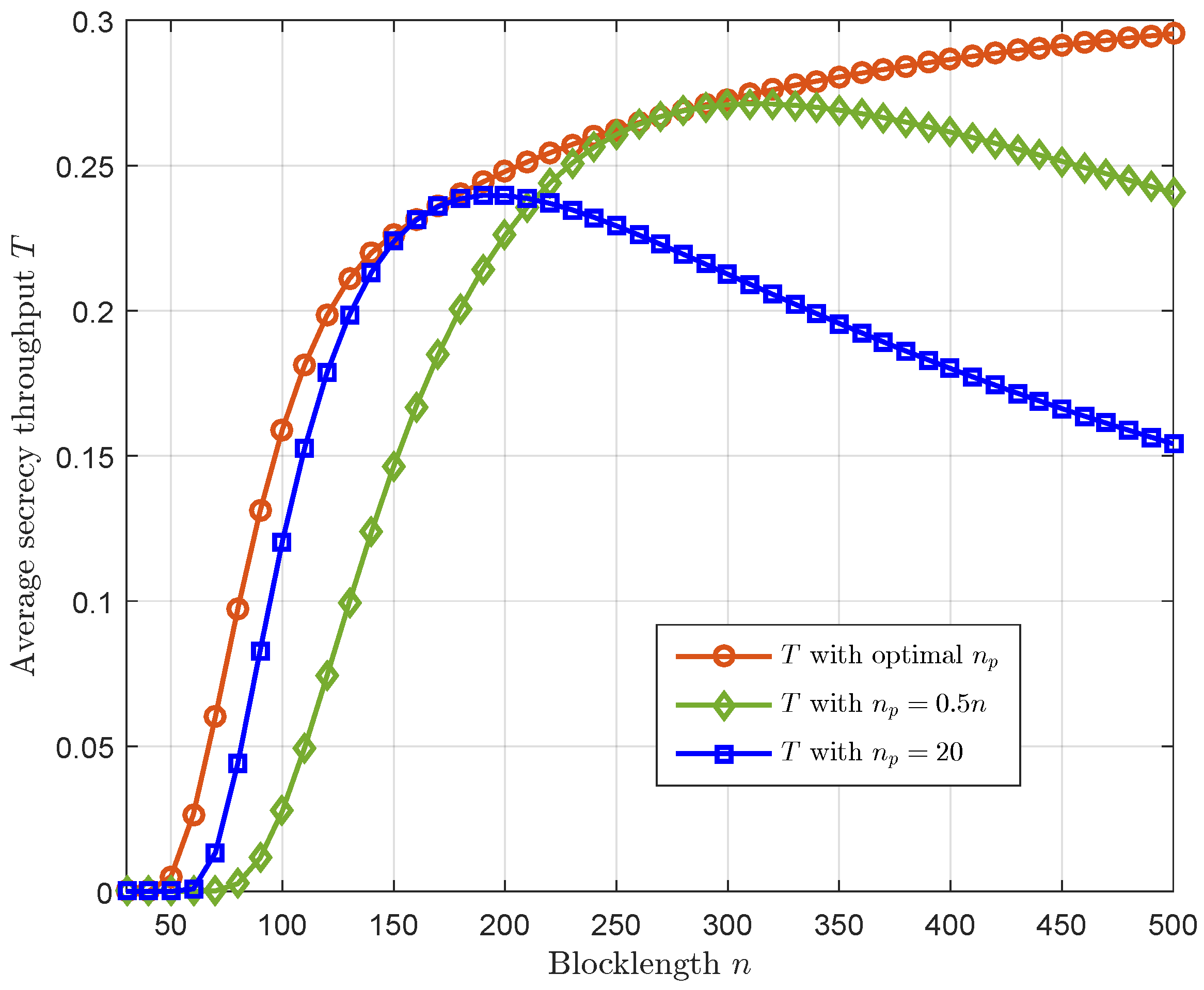
- We determine the optimal channel training length to maximize the average secrecy throughput under the reliability constraint and given blocklength. Numerical results demonstrate the performance gain achieved by the optimal channel training length is remarkable relative to the fixed-ratio channel training length and fixed channel training length schemes.
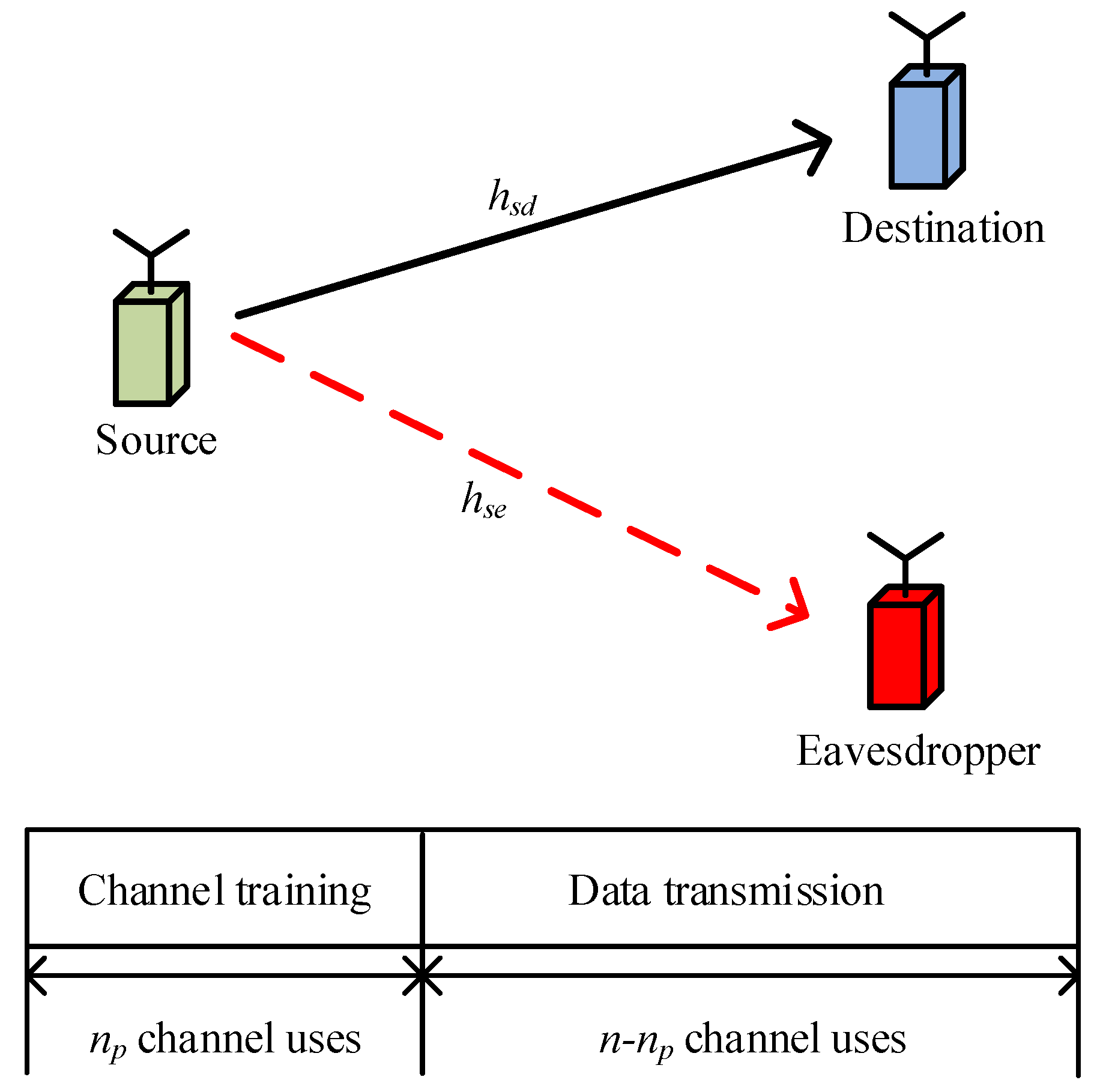
2. System Model
3. Secrecy Performance Analysis
3.1. Secrecy Throughput Approximation
3.2. High SNR Regime
3.3. The Class Case with Infinite Blocklength
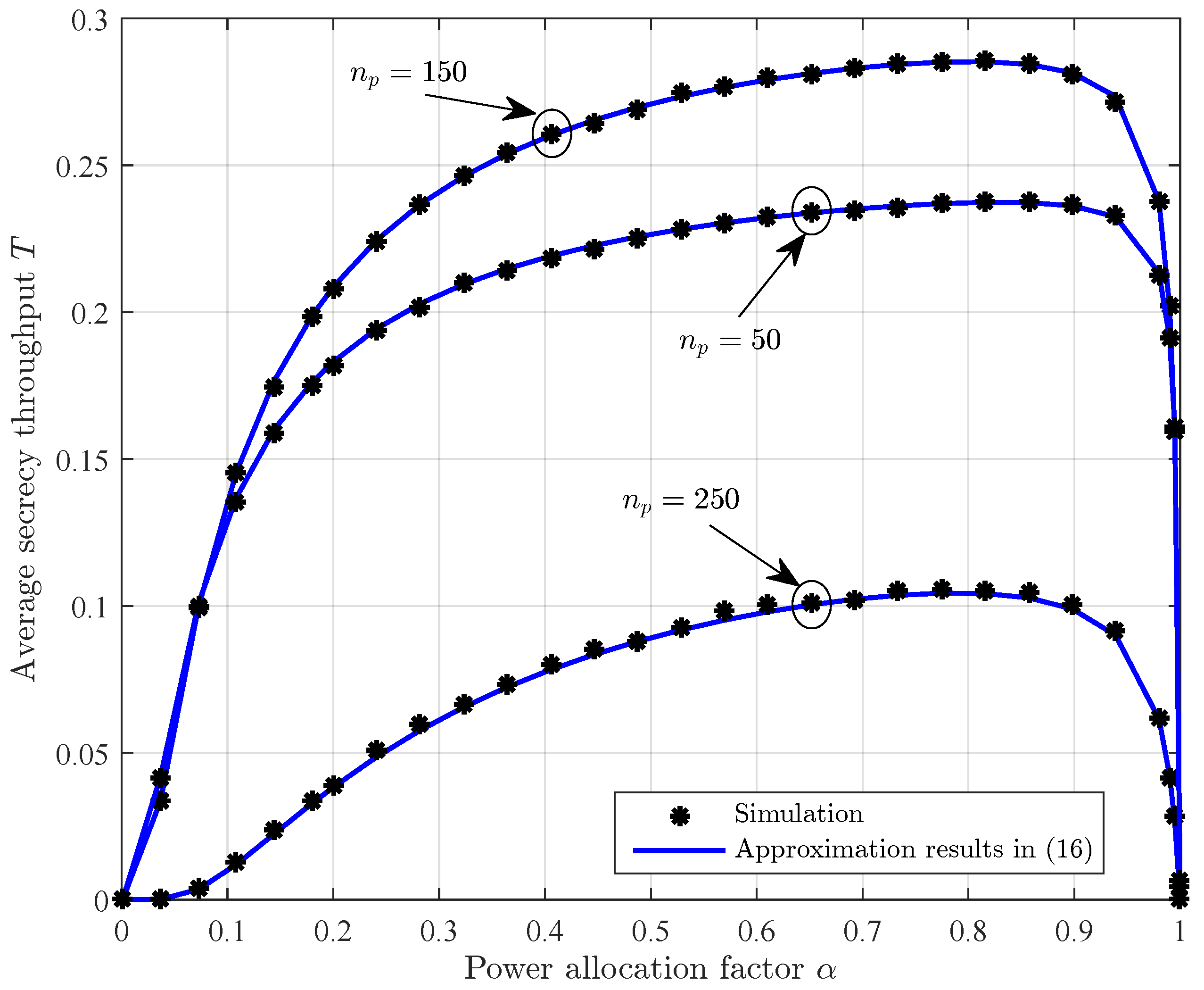
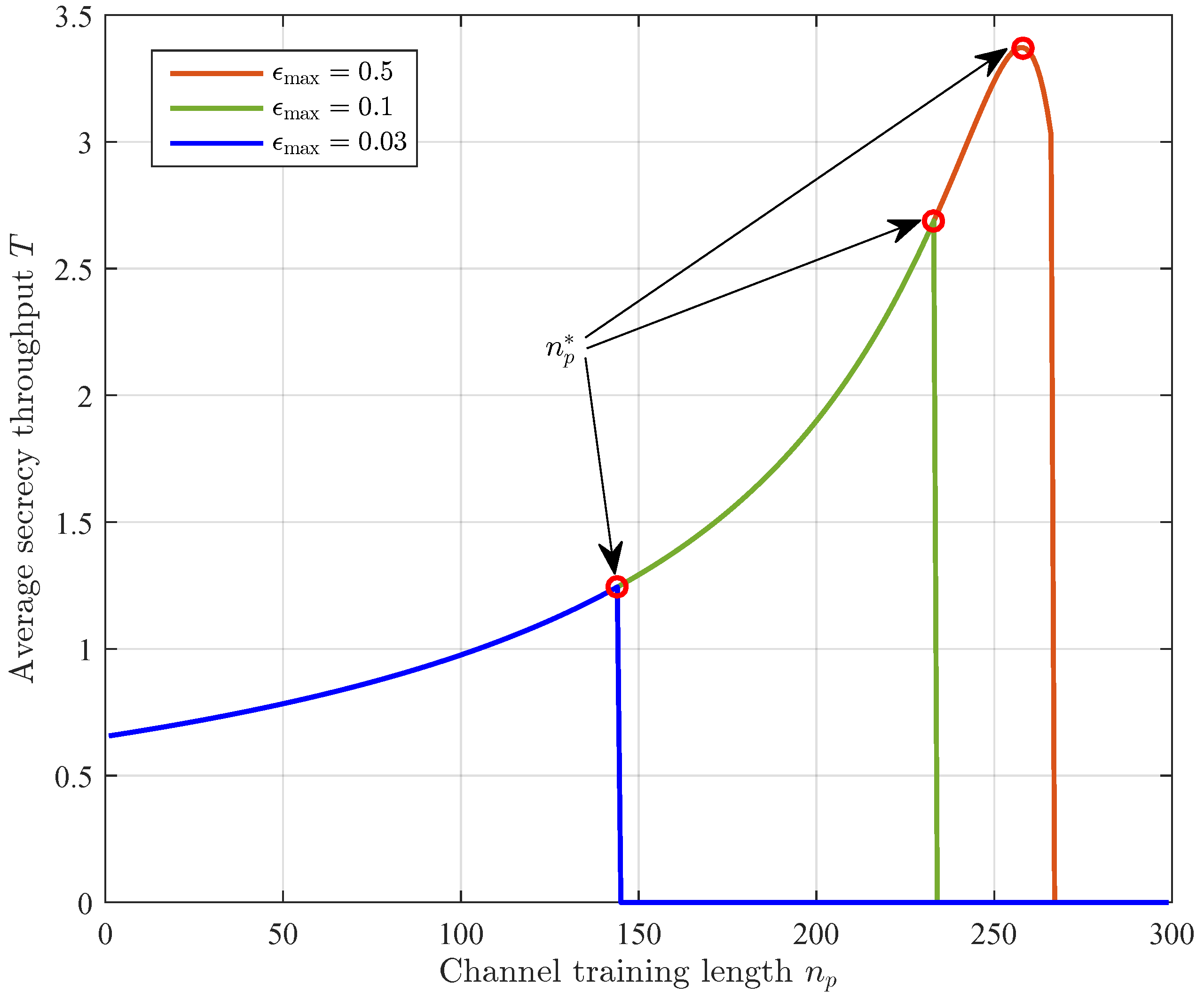
3.4. Optimal Transmission Design
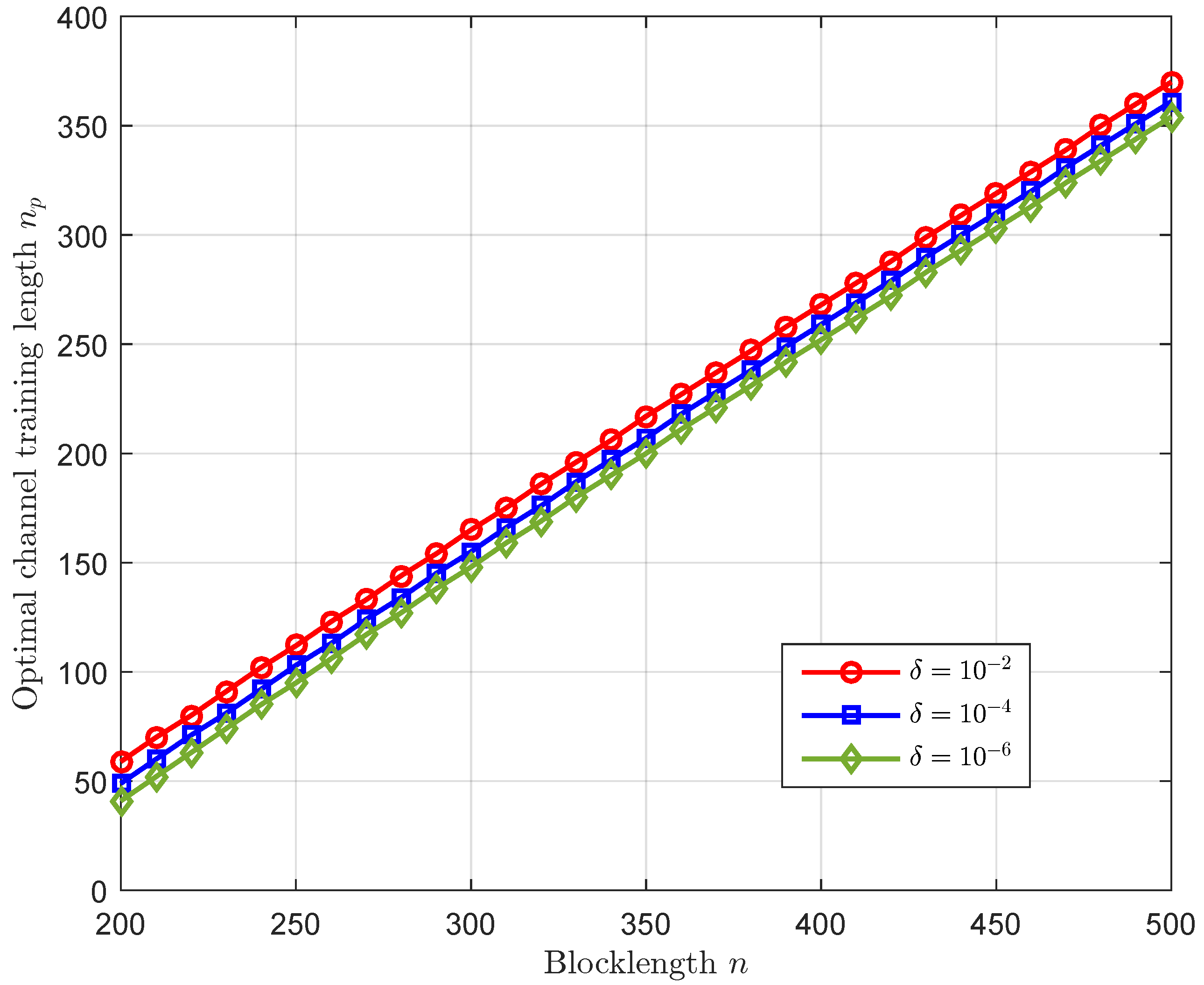
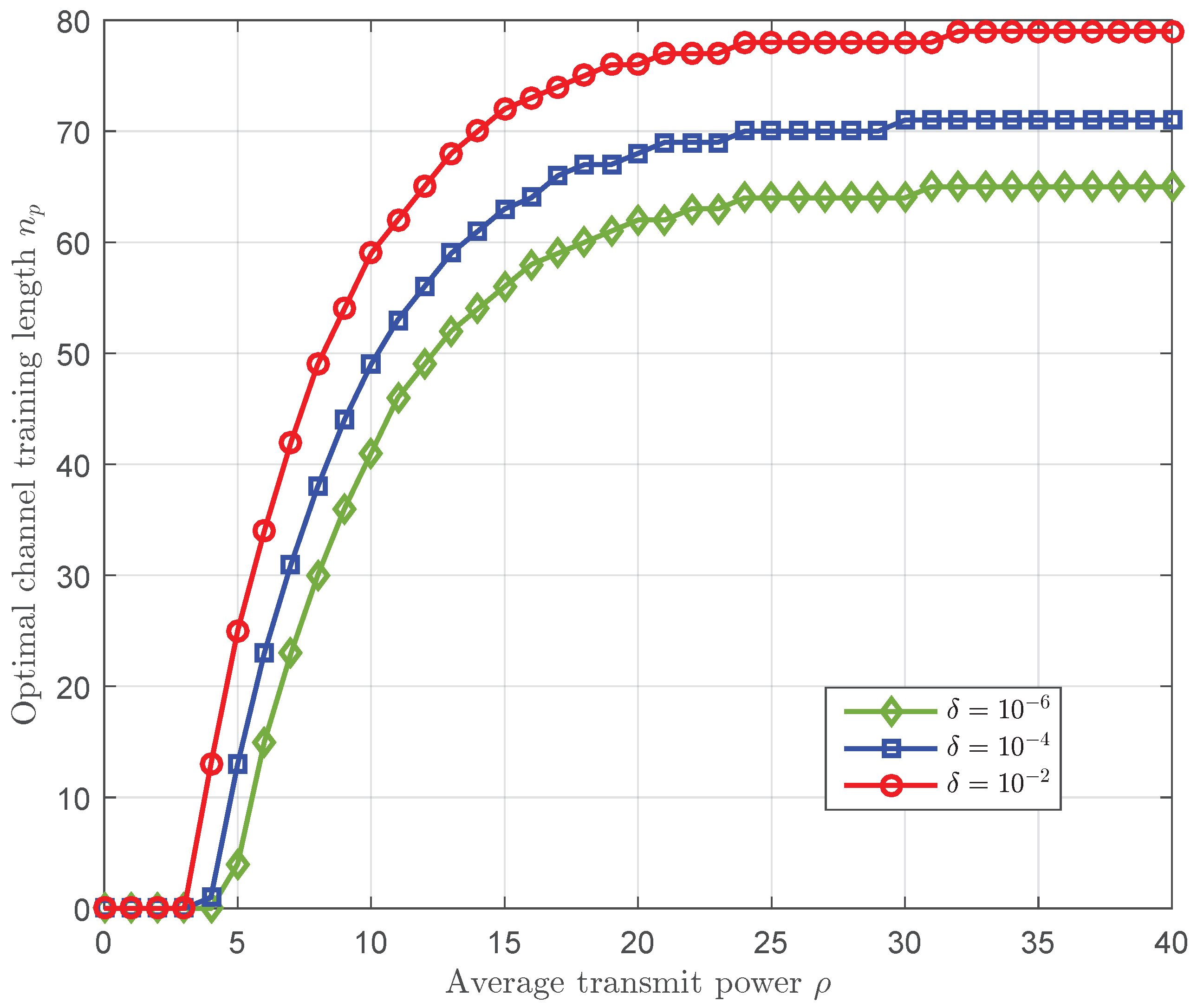
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Parvez, I.; Rahmati, A.; Guvenc, I.; Sarwat, A.I.; Dai, H. A Survey on Low Latency Towards 5G: RAN, Core Network and Caching Solutions. IEEE Commun. Surv. Tutor. 2018, 20, 3098–3130. [Google Scholar] [CrossRef]
- Durisi, G.; Koch, T.; Popovski, P. Toward Massive, Ultrareliable, and Low-Latency Wireless Communication with Short Packets. Proc. IEEE 2016, 104, 1711–1726. [Google Scholar] [CrossRef]
- Feng, D.; She, C.; Ying, K.; Lai, L.; Hou, Z.; Quek, T.Q.S.; Li, Y.; Vucetic, B. Toward Ultrareliable Low-Latency Communications: Typical Scenarios, Possible Solutions, and Open Issues. IEEE Veh. Technol. Mag. 2019, 14, 94–102. [Google Scholar] [CrossRef]
- Ashraf, S.A.; Aktas, I.; Eriksson, E.; Helmersson, K.W.; Ansari, J. Ultra-Reliable and Low-Latency Communication for Wireless Factory Automation: From LTE to 5G. In Proceedings of the 2016 IEEE 21st International Conference on Emerging Technologies and Factory Automation, Berlin, Germany, 6–9 September 2016. [Google Scholar]
- Polyanskiy, Y.; Poor, H.V.; Verdu, S. Channel Coding Rate in the Finite Blocklength Regime. IEEE Trans. Inf. Theory 2010, 56, 2307–2359. [Google Scholar] [CrossRef]
- Xiang, Z.; Yang, W.; Cai, Y.; Ding, Z.; Song, Y.; Zou, Y. NOMA-Assisted Secure Short-Packet Communications in IoT. IEEE Wirel. Commun. 2020, 27, 8–15. [Google Scholar] [CrossRef]
- Feng, C.; Wang, H.M. Secure Short-Packet Communications at the Physical Layer for 5G and Beyond. IEEE Commun. Stand. Mag. 2021, 5, 96–102. [Google Scholar] [CrossRef]
- Wang, H.M.; Yang, Q.; Ding, Z.; Poor, H.V. Secure Short-Packet Communications for Mission-Critical IoT Applications. IEEE Trans. Wireless Commun. 2019, 18, 2565–2578. [Google Scholar] [CrossRef]
- Ren, H.; Pan, C.; Deng, Y.; Elkashlan, M.; Nallanathan, A. Resource Allocation for Secure URLLC in Mission-Critical IoT Scenarios. IEEE Trans. Wireless Commun. 2020, 68, 5793–5807. [Google Scholar] [CrossRef]
- Hu, J.; Cai, Y.; Yang, N. Secure Transmission Design with Feedback Compression for the Internet of Things. IEEE Trans. Signal Process. 2018, 66, 1580–1593. [Google Scholar] [CrossRef]
- Zou, Y.; Zhu, J.; Wang, X.; Hanzo, L. A Survey on Wireless Security: Technical Challenges, Recent Advances, and Future Trends. Proc. IEEE 2016, 104, 1727–1765. [Google Scholar] [CrossRef]
- Yang, W.; Schaefer, R.F.; Poor, H.V. Wiretap channels: Nonasymptotic fundamental limits. IEEE Trans. Inf. Theory 2019, 65, 4069–4093. [Google Scholar] [CrossRef]
- Feng, C.; Wang, H.M.; Poor, H.V. Reliable and Secure Short-Packet Communications. IEEE Trans. Wirel. Commun. 2022, 21, 1913–1926. [Google Scholar] [CrossRef]
- Farhat, J.; Brante, G.; Souza, R.D.; Vilela, J.P. On the Secure Spectral Efficiency of URLLC With Randomly Located Colluding Eavesdroppers. IEEE Internet Things J. 2021, 8, 14672–14682. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Yu, B.; Zhang, T.; Cai, Y. Relay-Assisted Secure Short-Packet Transmission in Cognitive IoT with Spectrum Sensing. China Commun. 2021, 18, 37–50. [Google Scholar] [CrossRef]
- Lai, X.; Wu, T.; Zhang, Q.; Qin, J. Average Secure BLER Analysis of NOMA Downlink Short-Packet Communication Systems in Flat Rayleigh Fading Channels. IEEE Trans. Wirel. Commun. 2021, 20, 2948–2960. [Google Scholar] [CrossRef]
- Lv, S.; Xu, X.; Han, S.; Tao, X.; Zhang, P. Energy-Efficient Secure Short-Packet Transmission in NOMA-Assisted mMTC Networks With Relaying. IEEE Trans. Veh. Technol. 2022, 71, 1699–1712. [Google Scholar] [CrossRef]
- Xiang, Z.; Yang, W.; Cai, Y.; Xiong, J.; Ding, Z.; Song, Y. Secure Transmission in a NOMA-Assisted IoT Network With Diversified Communication Requirements. IEEE Internet Things J. 2020, 7, 11157–11169. [Google Scholar] [CrossRef]
- Wei, L.; Yang, Y.; Jiao, B. Secrecy Throughput in Full-Duplex Multiuser MIMO Short-Packet Communications. IEEE Wirel. Commun. Lett. 2021, 10, 1339–1343. [Google Scholar] [CrossRef]
- Li, C.; She, C.; Yang, N.; Quek, T.Q.S. Secure Transmission Rate of Short Packets With Queueing Delay Requirement. IEEE Trans. Wirel. Commun. 2022, 21, 203–218. [Google Scholar] [CrossRef]
- Xie, Y.; Ren, P.; Xu, D.; Li, Q. Security and Reliability Performance Analysis for URLLC With Randomly Distributed Eavesdroppers. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021. [Google Scholar]
- Xie, Y.; Ren, P. Optimizing Training and Transmission Overheads for Secure URLLC Against Randomly Distributed Eavesdroppers. IEEE Trans. Veh. Technol. 2022, 71, 11921–11935. [Google Scholar] [CrossRef]
- Li, C.; Yang, N.; Yan, S. Optimal Transmission of Short-Packet Communications in Multiple-Input Single-Output Systems. IEEE Trans. Veh. Technol. 2019, 68, 7199–7203. [Google Scholar] [CrossRef]
- Lee, B.; Park, S.; Love, D.J.; Ji, H.; Shim, B. Packet Structure and Receiver Design for Low Latency Wireless Communications with Ultra-Short Packets. IEEE Trans. Commun. 2018, 66, 796–807. [Google Scholar] [CrossRef]
- Gursoy, M.C. On the capacity and energy efficiency of training-based transmissions over fading channels. IEEE Trans. Inf. Theory 2009, 55, 4543–4567. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series, and Products, 7th ed.; Academic Press, Inc.: Cambridge, MA, USA, 2007. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Li, J.; Hu, J.; Zhang, X.; Zhang, S. Optimal Channel Training Design for Secure Short-Packet Communications. Sensors 2023, 23, 1068. https://doi.org/10.3390/s23031068
Chen D, Li J, Hu J, Zhang X, Zhang S. Optimal Channel Training Design for Secure Short-Packet Communications. Sensors. 2023; 23(3):1068. https://doi.org/10.3390/s23031068
Chicago/Turabian StyleChen, Dechuan, Jin Li, Jianwei Hu, Xingang Zhang, and Shuai Zhang. 2023. "Optimal Channel Training Design for Secure Short-Packet Communications" Sensors 23, no. 3: 1068. https://doi.org/10.3390/s23031068
APA StyleChen, D., Li, J., Hu, J., Zhang, X., & Zhang, S. (2023). Optimal Channel Training Design for Secure Short-Packet Communications. Sensors, 23(3), 1068. https://doi.org/10.3390/s23031068







