Data Augmentation for a Virtual-Sensor-Based Nitrogen and Phosphorus Monitoring
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.3. Work Objective
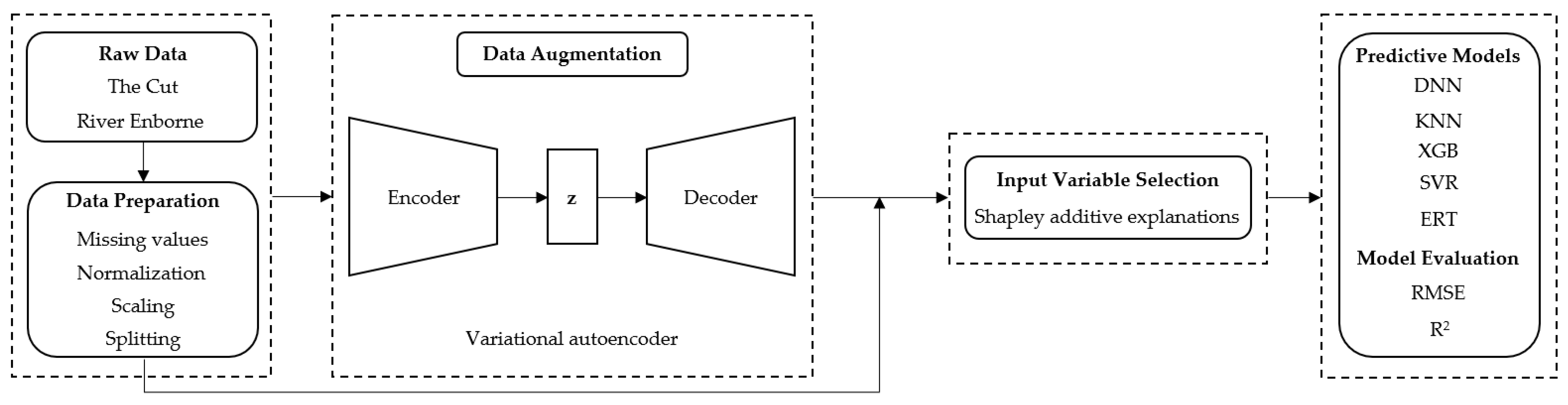
2. Materials and Methods
2.1. Study Area and Water-Quality Data
2.2. Data Analysis Frameworks
- Pandas (1.0.5): used for data manipulation and analysis;
- TensorFlow (2.10.0): used for building a deep neural network (further discussed in Section 2.5.1);
- Scikit-learn (1.1.0): used for implementing the k-nearest neighbors, extremely randomized trees, and support vector regression models (further discussed in Section 2.5.2, Section 2.5.3 and Section 2.5.4, respectively);
- XGBoost (2.0.0): an implementation of a gradient-boosted decision tree algorithm;
- PyTorch (1.12.1): used for developing the VAE. It was chosen because it has a resilient backpropagation optimizer, which was the most effective in our case.
2.3. Virtual Sensor Development
2.3.1. Data Preprocessing
2.3.2. Data Division
2.3.3. Input Variable Selection
2.3.4. Model Selection
2.3.5. Model Evaluation
2.4. Data Augmentation: A Variational Autoencoder
2.4.1. Architecture
2.4.2. Formulation
2.4.3. Loss Function
2.4.4. Reparameterization Trick
2.4.5. Implementation
2.5. Predictive Models
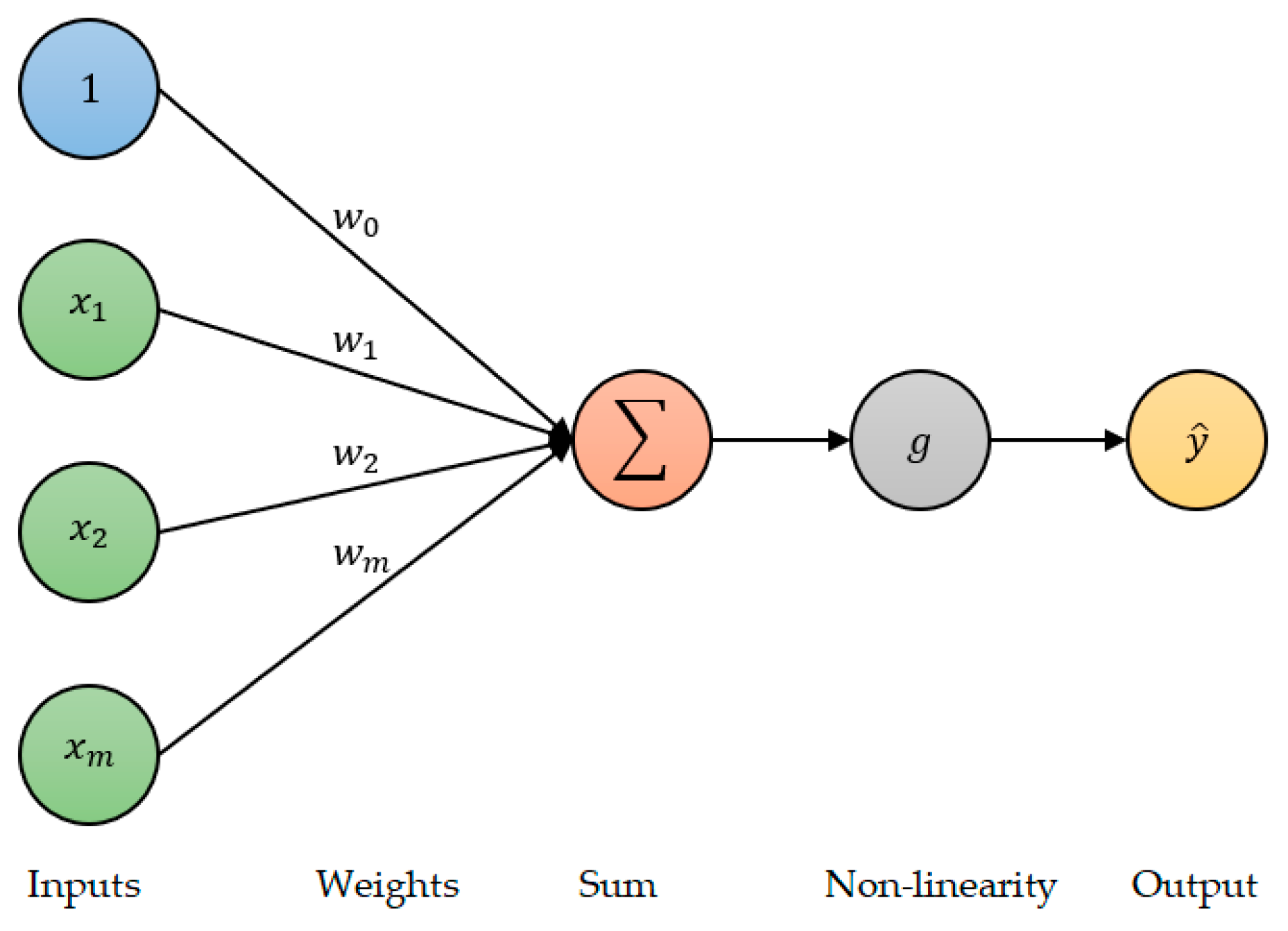
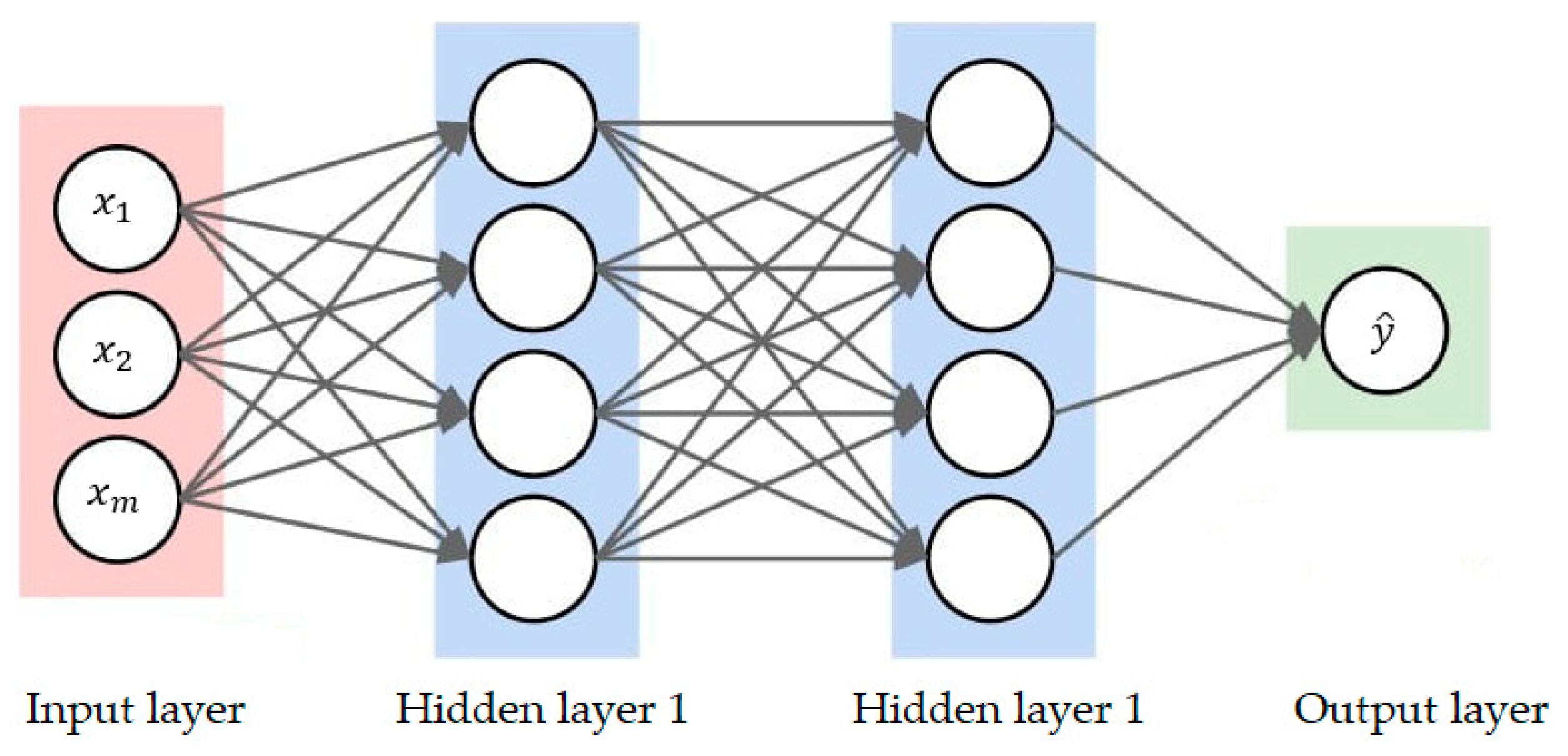
2.5.1. Deep Neural Network (DNN)
2.5.2. K-Nearest Neighbors (KNN)
2.5.3. Extremely Randomized Trees (ERT)
2.5.4. Support Vector Regression (SVR)
2.5.5. Extreme Gradient Boosting (XGB)
3. Results and Discussion
3.1. Model Optimization
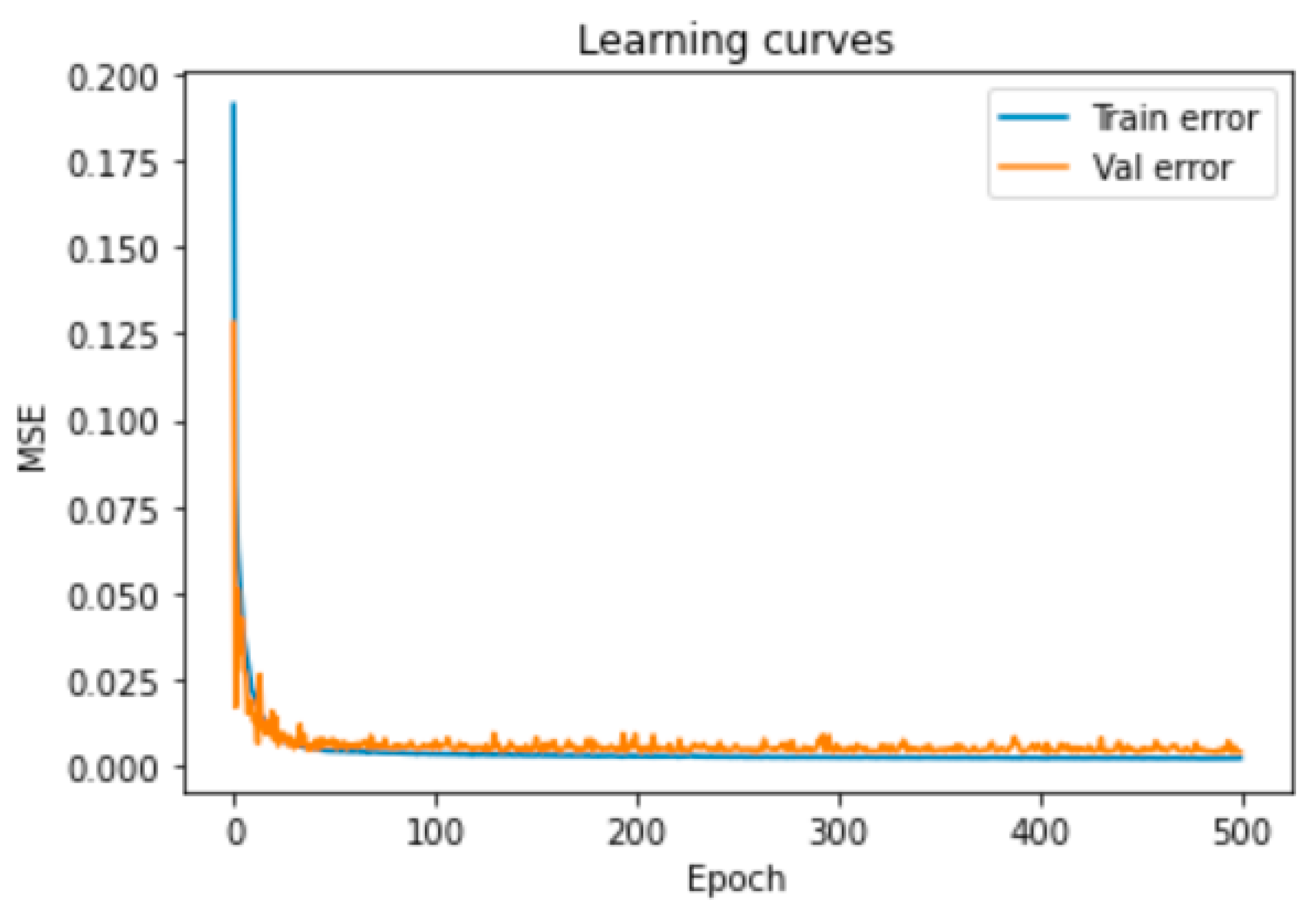
3.1.1. DNN Optimization
3.1.2. VAE Optimization
3.1.3. KNN Optimization
3.1.4. ERT Optimization
3.1.5. SVR Optimization
3.1.6. XGB Optimization
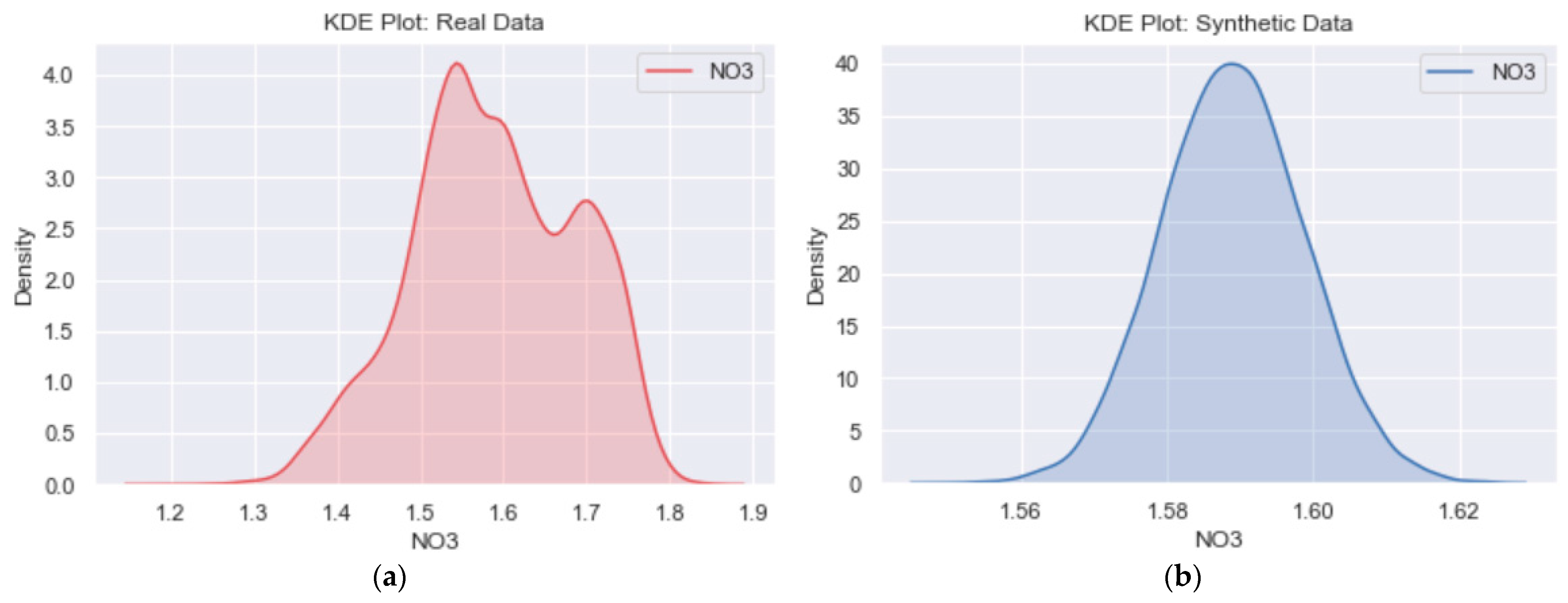
3.2. Likeness between Real and Generated Samples
3.3. Virtual Sensor Performance with Increasing Dataset Size
3.4. Performance Based on Predictor Importance: Comparison with the Current Benchmark
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, X.E.; Wu, X.; Hao, H.L.; He, Z.L. Mechanisms and assessment of water eutrophication. J. Zhejiang Univ. Sci. B 2008, 9, 197–209. [Google Scholar] [CrossRef] [PubMed]
- Xia, R.; Zhang, Y.; Critto, A.; Wu, J.; Fan, J.; Zheng, Z.; Zhang, Y. The Potential Impacts of Climate Change Factors on Freshwater Eutrophication: Implications for Research and Countermeasures of Water Management in China. Sustainability 2016, 8, 229. [Google Scholar] [CrossRef]
- Van Ginkel, C. Eutrophication: Present reality and future challenges for South Africa. Water SA 2011, 37, 693–702. [Google Scholar] [CrossRef]
- Kakade, A.; Salama, E.-S.; Han, H.; Zheng, Y.; Kulshrestha, S.; Jalalah, M.; Harraz, F.A.; Alsareii, S.A.; Li, X. World eutrophic pollution of lake and river: Biotreatment potential and future perspectives. Environ. Technol. Innov. 2021, 23, 101604. [Google Scholar] [CrossRef]
- Pellerin, B.A.; Stauffer, B.A.; Young, D.A.; Sullivan, D.J.; Bricker, S.B.; Walbridge, M.R.; Clyde, G.A., Jr.; Shaw, D.M. Emerging Tools for Continuous Nutrient Monitoring Networks: Sensors Advancing Science and Water Resources Protection. J. Am. Water Resour. Assoc. 2016, 52, 993–1008. [Google Scholar] [CrossRef]
- Paepae, T.; Bokoro, P.N.; Kyamakya, K. From Fully Physical to Virtual Sensing for Water Quality Assessment: A Comprehensive Review of the Relevant State-of-the-Art. Sensors 2021, 21, 6971. [Google Scholar] [CrossRef]
- Blaen, P.J.; Khamis, K.; Lloyd, C.E.; Bradley, C.; Hannah, D.; Krause, S. Real-time monitoring of nutrients and dissolved organic matter in rivers: Capturing event dynamics, technological opportunities and future directions. Sci. Total Environ. 2016, 569–570, 647–660. [Google Scholar] [CrossRef]
- Cassidy, R.; Jordan, P. Limitations of instantaneous water quality sampling in surface-water catchments: Comparison with near-continuous phosphorus time-series data. J. Hydrol. 2011, 405, 182–193. [Google Scholar] [CrossRef]
- Paepae, T.; Bokoro, P.N.; Kyamakya, K. A Virtual Sensing Concept for Nitrogen and Phosphorus Monitoring Using Machine Learning Techniques. Sensors 2022, 22, 7338. [Google Scholar] [CrossRef]
- Matthews, M.W.; Bernard, S. Eutrophication and cyanobacteria in South Africa’s standing water bodies: A view from space. S. Afr. J. Sci. 2015, 111, 7. [Google Scholar] [CrossRef]
- Murphy, K.; Heery, B.; Sullivan, T.; Zhang, D.; Paludetti, L.; Lau, K.T.; Diamond, D.; Costa, E.; O’connor, N.; Regan, F. A low-cost autonomous optical sensor for water quality monitoring. Talanta 2015, 132, 520–527. [Google Scholar] [CrossRef] [PubMed]
- Castrillo, M.; García, L. Estimation of high frequency nutrient concentrations from water quality surrogates using machine learning methods. Water Res. 2020, 172, 115490. [Google Scholar] [CrossRef] [PubMed]
- Ha, N.-T.; Nguyen, H.Q.; Truong, N.C.Q.; Le, T.L.; Thai, V.N.; Pham, T.L. Estimation of nitrogen and phosphorus concentrations from water quality surrogates using machine learning in the Tri An Reservoir, Vietnam. Environ. Monit. Assess. 2020, 192, 789. [Google Scholar] [CrossRef] [PubMed]
- Dilmi, S. Calcium Soft Sensor Based on the Combination of Support Vector Regression and 1-D Digital Filter for Water Quality Monitoring. Arab. J. Sci. Eng. 2022, 1–26. [Google Scholar] [CrossRef]
- Zhu, Q.-X.; Zhang, X.-H.; He, Y.-L. Novel Virtual Sample Generation Based on Locally Linear Embedding for Optimizing the Small Sample Problem: Case of Soft Sensor Applications. Ind. Eng. Chem. Res. 2020, 59, 17977–17986. [Google Scholar] [CrossRef]
- Zhang, X.-H.; Xu, Y.; He, Y.-L.; Zhu, Q.-X. Novel manifold learning based virtual sample generation for optimizing soft sensor with small data. ISA Trans. 2020, 109, 229–241. [Google Scholar] [CrossRef]
- He, Y.-L.; Hua, Q.; Zhu, Q.-X.; Lu, S. Enhanced virtual sample generation based on manifold features: Applications to developing soft sensor using small data. ISA Trans. 2022, 126, 398–406. [Google Scholar] [CrossRef]
- Kadlec, P.; Gabrys, B.; Strandt, S. Data-driven Soft Sensors in the process industry. Comput. Chem. Eng. 2009, 33, 795–814. [Google Scholar] [CrossRef]
- Wang, X.; Liu, H. Data supplement for a soft sensor using a new generative model based on a variational autoencoder and Wasserstein GAN. J. Process Control 2020, 85, 91–99. [Google Scholar] [CrossRef]
- Gao, S.; Qiu, S.; Ma, Z.; Tian, R.; Liu, Y. SVAE-WGAN-Based Soft Sensor Data Supplement Method for Process Industry. IEEE Sens. J. 2022, 22, 601–610. [Google Scholar] [CrossRef]
- Yuan, X.; Ou, C.; Wang, Y.; Yang, C.; Gui, W. A Layer-Wise Data Augmentation Strategy for Deep Learning Networks and Its Soft Sensor Application in an Industrial Hydrocracking Process. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3296–3305. [Google Scholar] [CrossRef]
- Chen, Z.-S.; Hou, K.-R.; Zhu, M.-Y.; Xu, Y.; Zhu, Q.-X. A virtual sample generation approach based on a modified conditional GAN and centroidal Voronoi tessellation sampling to cope with small sample size problems: Application to soft sensing for chemical process. Appl. Soft Comput. 2021, 101, 107070. [Google Scholar] [CrossRef]
- Zhu, Q.-X.; Hou, K.-R.; Chen, Z.-S.; Gao, Z.-S.; Xu, Y.; He, Y.-L. Novel virtual sample generation using conditional GAN for developing soft sensor with small data. Eng. Appl. Artif. Intell. 2021, 106, 104497. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, Y.; Zhu, Q.-X.; He, Y.-L. Novel Virtual Sample Generation Using Target-Relevant Autoencoder for Small Data-Based Soft Sensor. IEEE Trans. Instrum. Meas. 2021, 70, 2515910. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, Q.; Tian, R.; Ma, Z.; Dang, X. Horizontal Data Augmentation Strategy for Industrial Quality Prediction. ACS Omega 2022, 7, 30782–30793. [Google Scholar] [CrossRef]
- Jiang, X.; Ge, Z. Improving the Performance of Just-In-Time Learning-Based Soft Sensor Through Data Augmentation. IEEE Trans. Ind. Electron. 2022, 69, 13716–13726. [Google Scholar] [CrossRef]
- Foschi, J.; Turolla, A.; Antonelli, M. Soft sensor predictor of E. coli concentration based on conventional monitoring parameters for wastewater disinfection control. Water Res. 2021, 191, 116806. [Google Scholar] [CrossRef]
- Bowes, M.J.; Gozzard, E.; Newman, J.; Loewenthal, M.; Halliday, S.; Skeffington, R.; Jarvie, H.; Wade, A.; Palmer-Felgate, E. Hourly physical and nutrient monitoring data for The Cut, Berkshire (2009–2012). In Environmental Information Platform; NERC Environmental Information Data Centre: Lancaster, UK, 2015. [Google Scholar] [CrossRef]
- Wade, A.J.; Palmer-Felgate, E.J.; Halliday, S.J.; Skeffington, R.A.; Loewenthal, M.; Jarvie, H.P.; Bowes, M.J.; Greenway, G.M.; Haswell, S.J.; Bell, I.M.; et al. Hydrochemical processes in lowland rivers: Insights from in situ, high-resolution monitoring. Hydrol. Earth Syst. Sci. 2012, 16, 4323–4342. [Google Scholar] [CrossRef]
- Halliday, S.J.; Skeffington, R.A.; Wade, A.J.; Bowes, M.J.; Gozzard, E.; Newman, J.R.; Loewenthal, M.; Palmer-Felgate, E.J.; Jarvie, H.P. High-frequency water quality monitoring in an urban catchment: Hydrochemical dynamics, primary production and implications for the Water Framework Directive. Hydrol. Process. 2015, 29, 3388–3407. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. Available online: http://scikit-learn.sourceforge.net (accessed on 19 November 2022).
- Kingma, D.P.; Welling, M. An Introduction to Variational Autoencoders. Found. Trends® Mach. Learn. 2019, 12, 307–392. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Wei, S.; Chen, Z.; Arumugasamy, S.K.; Chew, I.M.L. Data augmentation and machine learning techniques for control strategy development in bio-polymerization process. Environ. Sci. Ecotechnol. 2022, 11, 100172. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: London, UK, 2016. [Google Scholar]
- Ma, J.; Ding, Y.; Cheng, J.C.; Jiang, F.; Xu, Z. Soft detection of 5-day BOD with sparse matrix in city harbor water using deep learning techniques. Water Res. 2019, 170, 115350. [Google Scholar] [CrossRef]
- Harrison, J.W.; Lucius, M.A.; Farrell, J.L.; Eichler, L.W.; Relyea, R.A. Prediction of stream nitrogen and phosphorus concentrations from high-frequency sensors using Random Forests Regression. Sci. Total Environ. 2021, 763, 143005. [Google Scholar] [CrossRef] [PubMed]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Zhang, H.; Zhang, L.; Jiang, Y. Overfitting and Underfitting Analysis for Deep Learning Based End-to-end Communication Systems. In Proceedings of the 2019 11th International Conference on Wireless Communications and Signal Processing (WCSP), Xi’an, China, 23–25 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar] [CrossRef]
- MathWorks. Train Variational Autoencoder (VAE) to Generate Images. 2019. Available online: https://www.mathworks.com/help/deeplearning/ug/train-a-variational-autoencoder-vae-to-generate-images.html#responsive_offcanvas (accessed on 4 December 2022).
- Osán, T.; Bussandri, D.; Lamberti, P. Quantum metrics based upon classical Jensen–Shannon divergence. Phys. A Stat. Mech. Its Appl. 2022, 594, 127001. [Google Scholar] [CrossRef]



| Ref. | Year | Generative Models | Application |
|---|---|---|---|
| [21] | 2019 | Stacked autoencoder | Hydrocracking process |
| [19] | 2020 | Metropolis–Hastings algorithm, | Thermal power-plant boiler |
| variational autoencoder (VAE), | |||
| generative adversarial network (GAN), VAE-GAN | |||
| [20] | 2021 | GAN, stacked VAE (SVAE), SVAE-GAN | Thermal power-plant boiler |
| [22] | 2021 | Centroidal Voronoi tessellation sampling, | Polyethylene process |
| conditional GAN (CGAN) | |||
| [23] | 2021 | CGAN | High-density polyethylene |
| [24] | 2021 | Monte Carlo with particle swarm optimization, | Purified terephthalic acid |
| noise-injection, target-relevant AE, VAE | Ethylene production system | ||
| [25] | 2022 | Combined AE data augmentation strategy | Industrial debutanizer |
| [26] | 2022 | VAE, GAN | Industrial reformer |
| Variable | Transformation | |
|---|---|---|
| The Cut | River Enborne | |
| Turbidity | Reciprocal | Reciprocal |
| Flow rate | Reciprocal | Logarithm |
| Chlorophyll | Logarithm | Logarithm |
| Dissolved oxygen | Square root | Logarithm |
| Nitrate (as NH4 or NO3) | Cube root | Cube root |
| Total Reactive Phosphorus | None | Cube root |
| pH | None | Reciprocal |
| Temperature | None | None |
| Conductivity | None | None |
| Total Phosphorus | Square root | |
| Hyperparameter | Value |
|---|---|
| Hidden layers | 4 |
| Hidden neurons | 50,75,100,200 |
| Activation function | Rectified linear unit |
| Batch size | 300 |
| Number of epochs | 500 |
| Weight initialization | Normal |
| Optimization algorithm | Root mean square propagation |
| Hyperparameter | Value |
|---|---|
| Encoder and decoder hidden layers | 3 |
| Encoder and decoder neurons | 50,15,12 |
| Activation function | Rectified linear unit |
| Latent dimensions | 2 |
| Learning rate | 0.01 |
| Batch size | 4 |
| Number of epochs | 200 |
| Weight initialization | Normal |
| Optimization algorithm | Resilient backpropagation |
| Default Settings | Performance | Optimized Settings | Performance | ||||
|---|---|---|---|---|---|---|---|
| Parameter | Value | RMSE | R2 | Parameter | Value | RMSE | R2 |
| k | 5 | 0.0183 | 0.9656 | k | 3 | 0.0146 | 0.9781 |
| Weight | Uniform | Weight | Distance | ||||
| Metric | Minkowski | Metric | Manhattan | ||||
| Default Settings | Performance | Optimized Settings | Performance | ||||
|---|---|---|---|---|---|---|---|
| Parameter | Value | RMSE | R2 | Parameter | Value | RMSE | R2 |
| n_estimators | 100 | 0.0142 | 0.9796 | n_estimators | 700 | 0.0139 | 0.9802 |
| max_features | Auto | max_features | auto | ||||
| Default Settings | Performance | Optimized Settings | Performance | ||||
|---|---|---|---|---|---|---|---|
| Parameter | Value | RMSE | R2 | Parameter | Value | RMSE | R2 |
| Kernel | rbf | 0.0369 | 0.8611 | Kernel | rbf | 0.0342 | 0.8806 |
| Gamma | Scale | Gamma | Scale | ||||
| C | 1 | C | 200 | ||||
| Default Settings | Performance | Optimized Settings | Performance | ||||
|---|---|---|---|---|---|---|---|
| Parameter | Value | RMSE | R2 | Parameter | Value | RMSE | R2 |
| Max depth | 6 | 0.0209 | 0.9554 | Max depth | 10 | 0.0159 | 0.9740 |
| n_estimators | 100 | n_estimators | 900 | ||||
| Learning rate | 0.3 | Learning rate | 0.05 | ||||
| Variable | The Cut | ||||
| Original Size 8934 | Increased by 2234 | Increased by 4468 | Increased by 6702 | Increased by 8934 | |
| TRP | 0.0344 | 0.0312 | 0.0288 | 0.0274 | 0.0260 |
| TP | 0.0073 | 0.0066 | 0.0061 | 0.0058 | 0.0055 |
| EC | 0.0028 | 0.0026 | 0.0024 | 0.0023 | 0.0022 |
| Turb | 0.1436 | 0.1306 | 0.1226 | 0.1161 | 0.1105 |
| DO | 0.0044 | 0.0040 | 0.0037 | 0.0035 | 0.0034 |
| Temp | 0.0248 | 0.0224 | 0.0207 | 0.0196 | 0.0187 |
| NH4 | 0.0073 | 0.0067 | 0.0061 | 0.0057 | 0.0055 |
| Variable | River Enborne | ||||
| Original Size 12,723 | Increased by 3181 | Increased by 6362 | Increased by 9543 | Increased by 12,723 | |
| TRP | 0.0108 | 0.0098 | 0.0090 | 0.0085 | 0.0081 |
| EC | 0.0069 | 0.0062 | 0.0058 | 0.0055 | 0.0052 |
| Turb | 0.0602 | 0.0545 | 0.0507 | 0.0476 | 0.0457 |
| DO | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 |
| pH | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 |
| Temp | 0.0501 | 0.0451 | 0.0420 | 0.0395 | 0.0379 |
| NO3 | 0.0010 | 0.0009 | 0.0008 | 0.0008 | 0.0007 |
| Model | NH4 in The Cut | Predictive Performance Improvement | ||||
| 8934 | Increased by 2234 | Increased by 4468 | Increased by 6702 | Increased by 8934 | ||
| SVR | 0.0704 | 0.0671 | 0.0619 | 0.0584 | 0.0550 | 22% |
| KNN | 0.0337 | 0.0308 | 0.0290 | 0.0274 | 0.0260 | 23% |
| XGB | 0.0426 | 0.0409 | 0.0387 | 0.0356 | 0.0332 | 22% |
| ERT | 0.0379 | 0.0349 | 0.0326 | 0.0306 | 0.0288 | 24% |
| DNN | 0.0439 | 0.0383 | 0.0332 | 0.0308 | 0.0302 | 31% |
| TRP in The Cut | ||||||
| SVR | 0.1169 | 0.1074 | 0.1005 | 0.0945 | 0.0895 | 23% |
| KNN | 0.0781 | 0.0708 | 0.0663 | 0.0612 | 0.0582 | 25% |
| XGB | 0.0829 | 0.0751 | 0.0690 | 0.0653 | 0.0611 | 26% |
| ERT | 0.0790 | 0.0713 | 0.0661 | 0.0616 | 0.0583 | 26% |
| DNN | 0.0905 | 0.0818 | 0.0766 | 0.0682 | 0.0622 | 31% |
| TP in The Cut | ||||||
| SVR | 0.0710 | 0.0645 | 0.0601 | 0.0563 | 0.0532 | 25% |
| KNN | 0.0477 | 0.0432 | 0.0404 | 0.0374 | 0.0355 | 26% |
| XGB | 0.0516 | 0.0460 | 0.0425 | 0.0401 | 0.0380 | 26% |
| ERT | 0.0489 | 0.0440 | 0.0407 | 0.0380 | 0.0359 | 27% |
| DNN | 0.0585 | 0.0532 | 0.0494 | 0.0424 | 0.0407 | 30% |
| Model | NO3 in the Enborne | Predictive Performance Improvement | ||||
| 12,723 | Increased by 3181 | Increased by 6362 | Increased by 9543 | Increased by 12,723 | ||
| SVR | 0.0342 | 0.0317 | 0.0295 | 0.0281 | 0.0270 | 21% |
| KNN | 0.0146 | 0.0141 | 0.0136 | 0.0133 | 0.0132 | 10% |
| XGB | 0.0166 | 0.0161 | 0.0152 | 0.0147 | 0.0142 | 14% |
| ERT | 0.0140 | 0.0134 | 0.0128 | 0.0125 | 0.0121 | 14% |
| DNN | 0.0365 | 0.0297 | 0.0268 | 0.0256 | 0.0236 | 35% |
| TRP in the Enborne | ||||||
| SVR | 0.0395 | 0.0368 | 0.0346 | 0.0332 | 0.0322 | 18% |
| KNN | 0.0215 | 0.0201 | 0.0191 | 0.0183 | 0.0177 | 18% |
| XGB | 0.0224 | 0.0208 | 0.0195 | 0.0183 | 0.0175 | 22% |
| ERT | 0.0203 | 0.0188 | 0.0177 | 0.0169 | 0.0163 | 20% |
| DNN | 0.0318 | 0.0267 | 0.0264 | 0.0228 | 0.0223 | 30% |
| Predictors | Benchmark | This Work | Improvements of This Work Compared to a Benchmark | |||
|---|---|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | RMSE | R2 | |
| NH4 in The Cut | ||||||
| Temp | 0.1312 | 0.1620 | 0.0882 | 0.1022 | 33% | −59% |
| Temp, Chl | 0.1342 | 0.1220 | 0.0681 | 0.4634 | 49% | 74% |
| Temp, Chl, Turb | 0.0907 | 0.5986 | 0.0493 | 0.7190 | 46% | 17% |
| Temp, Chl, Turb, EC | 0.0655 | 0.7895 | 0.0376 | 0.8362 | 43% | 6% |
| Temp, Chl, Turb, EC, DO | 0.0526 | 0.8647 | 0.0310 | 0.8887 | 41% | 3% |
| Temp, Chl, Turb, EC, DO, pH | 0.0429 | 0.9101 | 0.0260 | 0.9216 | 39% | 1% |
| TP in The Cut | ||||||
| EC | 0.1213 | 0.1697 | 0.0924 | 0.0513 | 24% | −231% |
| EC, DO | 0.1291 | 0.0593 | 0.0737 | 0.3961 | 43% | 85% |
| EC, DO, Turb | 0.0956 | 0.4853 | 0.0585 | 0.6196 | 39% | 22% |
| EC, DO, Turb, Temp | 0.0680 | 0.7382 | 0.0434 | 0.7900 | 36% | 7% |
| EC, DO, Turb, Temp, Chl | 0.0610 | 0.7880 | 0.0390 | 0.8308 | 36% | 5% |
| EC, DO, Turb, Temp, Chl, pH | 0.0556 | 0.8253 | 0.0355 | 0.8593 | 36% | 4% |
| TRP in The Cut | ||||||
| EC | 0.1952 | 0.1820 | 0.1506 | 0.0399 | 23% | −356% |
| EC, Turb | 0.2037 | 0.1072 | 0.1127 | 0.4609 | 45% | 77% |
| EC, Turb, DO | 0.1554 | 0.4813 | 0.0955 | 0.6136 | 39% | 22% |
| EC, Turb, DO, Temp | 0.1101 | 0.7401 | 0.0704 | 0.7897 | 36% | 6% |
| EC, Turb, DO, Temp, Chl | 0.0999 | 0.7864 | 0.0639 | 0.8265 | 36% | 5% |
| EC, Turb, DO, Temp, Chl, pH | 0.0907 | 0.8219 | 0.0581 | 0.8566 | 36% | 4% |
| TRP in River Enborne | ||||||
| EC | 0.0666 | 0.5637 | 0.0396 | 0.7371 | 41% | 24% |
| EC, DO | 0.0608 | 0.6355 | 0.0258 | 0.8882 | 58% | 28% |
| EC, DO, Temp | 0.0343 | 0.8848 | 0.0178 | 0.9466 | 48% | 7% |
| EC, DO, Temp, Turb | 0.0257 | 0.9345 | 0.0161 | 0.9567 | 37% | 2% |
| EC, DO, Temp, Turb, pH | 0.0213 | 0.9559 | 0.0157 | 0.9587 | 26% | 0% |
| EC, DO, Temp, Turb, pH, Chl | 0.0212 | 0.9558 | 0.0162 | 0.9556 | 24% | 0% |
| NO3 in River Enborne | ||||||
| EC | 0.0617 | 0.6107 | 0.0378 | 0.7113 | 39% | 14% |
| EC, Temp | 0.0559 | 0.6818 | 0.0206 | 0.9137 | 63% | 25% |
| EC, Temp, pH | 0.0274 | 0.9223 | 0.0138 | 0.9617 | 50% | 4% |
| EC, Temp, pH, DO | 0.0205 | 0.9566 | 0.0125 | 0.9684 | 39% | 1% |
| EC, Temp, pH, DO, Turb | 0.0172 | 0.9695 | 0.0119 | 0.9714 | 31% | 0% |
| EC, Temp, pH, DO, Turb, Chl | 0.0177 | 0.9681 | 0.0122 | 0.9704 | 31% | 0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paepae, T.; Bokoro, P.N.; Kyamakya, K. Data Augmentation for a Virtual-Sensor-Based Nitrogen and Phosphorus Monitoring. Sensors 2023, 23, 1061. https://doi.org/10.3390/s23031061
Paepae T, Bokoro PN, Kyamakya K. Data Augmentation for a Virtual-Sensor-Based Nitrogen and Phosphorus Monitoring. Sensors. 2023; 23(3):1061. https://doi.org/10.3390/s23031061
Chicago/Turabian StylePaepae, Thulane, Pitshou N. Bokoro, and Kyandoghere Kyamakya. 2023. "Data Augmentation for a Virtual-Sensor-Based Nitrogen and Phosphorus Monitoring" Sensors 23, no. 3: 1061. https://doi.org/10.3390/s23031061
APA StylePaepae, T., Bokoro, P. N., & Kyamakya, K. (2023). Data Augmentation for a Virtual-Sensor-Based Nitrogen and Phosphorus Monitoring. Sensors, 23(3), 1061. https://doi.org/10.3390/s23031061







