Quantum Key Distribution for Critical Infrastructures: Towards Cyber-Physical Security for Hydropower and Dams
Abstract
:1. Introduction
2. Objective
3. Quantum Key Distribution and Its Implementation
4. Approach
4.1. Use Case for Quantum Security in Hydro
- securing remote interactive access (control, maintenance, and repairs);
- remote monitoring (remote sensors for control/safety/monitoring, remote monitoring only centers with unidirectional traffic);
- vendor monitoring;
- supply chain security (validation of the authenticity of software and supply chain communications).
- document how it capitalizes on the specific environment of the dam/hydro facility or hydro testbed from a security point of view;
- identify security benefits/disadvantages of the QKD relative to traditional methods, in the identified use cases;
- document how it highlights the practical (logistical) suitability/applicability of the QKD for implementation within the dam/hydro environment/testbed;
- document a reference architecture for deployment in the selected use case;
- identify operational impacts on QKD deployment;
- highlight how the use case contributes to the missions of hydropower research facilities.
4.2. Integration of the QKD System with the Hydro Communications System

5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Simplified Examples of Classical and Quantum Keys for Encryption
Appendix A.1. Classical Key Encryption
Appendix A.2. Quantum Key Encryption
- Step 1: Preparation and Transmission by Alice
- Alice randomly selects bits and their corresponding bases. The bases can be:
- –
- Rectilinear, represented as Z-basis: and .
- –
- Diagonal, represented as X-basis: and .
- For demonstration, consider the binary of “dam”: 1100100 1100001 1101101. Alice selects the first three bits: 110.
- –
- For the first bit (1), Alice chooses the rectilinear basis and sends .
- –
- For the second bit (1), Alice chooses the diagonal basis and sends .
- –
- For the third bit (0), Alice chooses the rectilinear basis and sends .
- Step 2: Measurement by Bob
- Bob randomly selects a basis for each received qubit and performs a measurement.
- –
- For the first qubit, he chooses rectilinear and measures 1.
- –
- For the second qubit, he chooses rectilinear (a mismatch with Alice) and obtains a random result, say 0.
- –
- For the third qubit, he chooses rectilinear and measures 0.
- Step 3: Basis Discussion
- Alice and Bob publicly disclose the bases they used.
- They compare their choices:
- –
- For the first bit, both chose rectilinear—they retain Bob’s result.
- –
- For the second bit, they used different bases—they discard Bob’s result.
- –
- For the third bit, both chose rectilinear—they retain Bob’s result.
- Their resulting raw key is now 10.
- Step 4: Error Estimation
- A subset of the raw key is selected for error testing.
- They compare their respective bits in this subset publicly.
- Calculate QBER = (number of errors in subset)/(size of subset).
- If QBER exceeds a threshold, the protocol is aborted due to potential eavesdropping.
- Step 5: Privacy Amplification
- Aims to reduce any potential eavesdropper’s information to an insignificant level.
- Two-universal hash functions might be applied to the key to produce a shorter, more secure key. For example, take the raw key to be 1011010101. Consider a very basic hash function defined as follows:
- –
- Break the string into groups of 2.
- –
- For each group:
- ∗
- If it is 00, it maps to 0.
- ∗
- If it is 01 or 10, it maps to 1.
- ∗
- If it is 11, it maps to 0.
- –
- Given the original key, applying the hash function produces which is shorter than the original key as a result of a specific transformation.
- Classical error-correcting codes can be used to rectify errors introduced by the quantum channel. For example, consider the Hamming(7,4) code [69]:
- –
- Designed to encode four bits of data into seven bits by adding three parity bits.
- –
- Given a four-bit data ‘1101’, encoding adds parity bits to produce 0 0 1 0 1 1 0.
- –
- If an error flips the sixth bit during transmission, we receive 0 0 1 0 1 0 0.
- –
- The error is detected and corrected using the parity bits, restoring the original encoded string.
Appendix B. Glossary
| Term | Definition |
|---|---|
| a | Fiber’s Attenuation: Represented in units of dB/km, it is the property of the optical fiber that quantifies the loss of signal strength per unit length of fiber. |
| Alice and Bob | Conventionally used names to denote the sender and receiver in cryptographic communications, including in QKD systems. |
| Attenuation | The reduction of signal strength as it travels through a medium, such as an optical fiber, due to absorption, scattering, and other loss mechanisms. |
| BB84 | A quantum key distribution protocol developed in 1984 by Bennett and Brassard, using two non-orthogonal bases [56]. |
| Binary Entropy Function | A function quantifying the maximum possible information about the total key based on shared bits between parties. Typically denoted as , it represents the uncertainty of a binary random variable and is defined as [49,56]:
|
| Channel Loss Parameter () | A dimensionless parameter derived from the total optical loss () and representing the linear loss. |
| Coherent States | A coherent quantum state is defined as:
|
| Continuous Variable-Quantum Key Distribution (CV-QKD) | CV-QKD employs continuous quantum variables such as the quadratures of the electromagnetic field to encode information. The most common CV-QKD protocols are based on coherent states using Gaussian modulation of amplitude and phase, and they use homodyne or heterodyne detection for the decoding process. This approach has the advantage of being compatible with conventional telecom technology, potentially allowing for more straightforward integration into existing networks. However, it typically makes more assumptions that detector noise can be “trusted”, and calibrated away. |
| Dark Counts | False positive detector counts, usually due to detector noise. |
| Decoy State QKD | A variation of the BB84 QKD protocol which employs additional signal states to improve security against photon number splitting attacks. |
| Discrete Variable (DV) QKD | Discrete Variable (DV) QKD leverages the quantum properties of individual photons to distribute shared symmetric random numbers. It typically operates using polarization or phase encoding schemes to encode the random quantum information. Protocols such as BB84, B92, and SARG04 are well-known in the DV-QKD [22,52]. |
| Error Correction | A process to identify and correct errors in the quantum key transmission. |
| Error Rate in the X Basis () | A parameter representing the rate of error in the x basis of the key during QKD operations. |
| Error Reconciliation | A procedure in QKD to correct any discrepancies in the key between the two parties. |
| Eve | Conventionally used name to denote a potential attacker trying to gain unauthorized access to the quantum transmissions. All errors are typically attributed to her. |
| Fiber-Based Loss | Refers to the loss of signal in optical fibers, affecting the transmission of quantum signals. |
| Fiber Length (L) | The physical distance covered by the optical fiber, usually represented in kilometers. |
| Finite Size Effects | Describes the effects or limitations of having a finite number of measured signals in QKD. |
| Homodyne Detection | A technique used in quantum cryptography for measuring a quantum signal through interference with a local oscillator using balanced difference detection. |
| Hydropower | The generation of power through the use of the gravitational force of falling or fast-running water. |
| Information Theoretical Security (ITS) | A security paradigm that assures confidentiality regardless of the computational resources of an adversary. |
| Leakage During Error Correction () | The segment of key information that might be exposed to any potential adversary during error correction procedures in the QKD protocol. |
| Misalignment Angle | In polarization encoded QKD, refers to the variation in the angle of the initial polarization state, which can be caused by factors such as thermal fluctuations or physical stress on the fiber. |
| One-Time Pad (OTP) | A method of encryption where a message is combined with a one-time-use key using exclusive OR (XOR) operation. |
| Phase Modulation | The modulation of the phase of a carrier signal to encode information, often used in QKD systems to encode quantum information. |
| Avalanche Photo Detectors (APD) | Photodetectors that can detect low-intensity light down to single photons, often used in QKD receivers. |
| Polarization | Refers to the orientation of oscillations in electromagnetic waves, used to encode information in quantum states in the context of QKD. |
| Quantum Bit Error Ratio (QBER) | The ratio of errors that occur during quantum transmission. |
| Quantum Cryptography (QC) | A method of cryptography with a trust anchor rooted in quantum mechanics principles. |
| Quantum Key Distribution (QKD) | A cryptographic protocol based on quantum mechanics to securely distribute random private keys between two parties. |
| Secure Key Length (L) | The length of the secure key. |
| Secure Key Rate (SKR) | The rate at which a QKD system can produce secure shared private keys, influenced by factors like distance and error rate. A metric to evaluate the performance of a QKD system |
| Secure Rate Formula | A mathematical representation of the rate at which a QKD system can generate secure keys. |
| Total Optical Loss () | Represented in units of dB, it measures the total loss in the system, arising due to the fiber’s attenuation (a), imperfect components, and the length of the fiber (L). |
References
- Rass, S.; Schauer, S.; König, S.; Zhu, Q. Cyber-Security in Critical Infrastructures; Springer: Berlin/Heidelberg, Germany, 2020; Volume 297. [Google Scholar]
- Whyatt, M.; Whyatt, M.V.; Thorsen, D.E.; Watson, M.D.; Ham, K.D.; Pederson, P.A.; McKinnon, A.D.; DeSomber, K.R. Toward a Resilient Cybersecure Hydropower Fleet: Cybersecurity Landscape and Roadmap 2021; Technical Report PNNL-32053; PNNL: Richland, WA, USA, 2021.
- Dams Sector Landscape; Technical Report; CISA, U.S. Department of Homeland Security, Cybersecurity and Infrastructure Security Agency: Washington, DC, USA, 2019. Available online: https://damsafety-prod.s3.amazonaws.com/s3fs-public/files/6.%20Dams%20Sector%20Landscape.pdf (accessed on 4 December 2023).
- Singh, P.; Singh, S.; Vardhan, S.; Patnaik, A. Sustainability of maintenance management practices in hydropower plant: A conceptual framework. Mater. Today Proc. 2020, 28, 1569–1574. [Google Scholar] [CrossRef]
- Ratnam, E.L.; Baldwin, K.G.; Mancarella, P.; Howden, M.; Seebeck, L. Electricity system resilience in a world of increased climate change and cybersecurity risk. Electr. J. 2020, 33, 106833. [Google Scholar] [CrossRef]
- Alrefaei, A.S. An Overview of Securing SCADA Systems: The Gap in the Physical Security Measure. In Proceedings of the 2022 Fifth National Conference of Saudi Computers Colleges (NCCC), Makkah, Saudi Arabia, 17–18 December 2022; pp. 88–91. [Google Scholar]
- Urbina, D.I.; Giraldo, J.A.; Cardenas, A.A.; Tippenhauer, N.O. Survey and new directions for physics-based attack detection in process control systems. In Proceedings of the IFIP Annual Conference on Data and Applications Security and Privacy, Trento, Italy, 18–20 July 2016; Springer: Cham, Switzerland, 2016; pp. 65–81. [Google Scholar]
- Chen, T.M.; Abu-Nimeh, S. Lessons from Stuxnet. Computer 2011, 44, 91–93. [Google Scholar] [CrossRef]
- Lee, R.M.; Assante, M.J.; Conway, T. Analysis of the Cyber Attack on the Ukrainian Power Grid; Technical Report; Electricity Information Sharing and Analysis Center (E-ISAC): Washington, DC, USA, 2016. [Google Scholar]
- Passian, A.; Imam, N. Nanosystems, edge computing, and the next generation computing systems. Sensors 2019, 19, 4048. [Google Scholar] [CrossRef]
- Farahi, R.; Passian, A.; Tetard, L.; Thundat, T. Critical issues in sensor science to aid food and water safety. ACS Nano 2012, 6, 4548–4556. [Google Scholar] [CrossRef]
- Alshowkan, M.; Evans, P.G.; Starke, M.; Earl, D.; Peters, N.A. Authentication of smart grid communications using quantum key distribution. Sci. Rep. 2022, 12, 12731. [Google Scholar] [CrossRef]
- Evans, P.G.; Alshowkan, M.; Earl, D.; Mulkey, D.; Newell, R.T.; Peterson, G.; Safi, C.L.; Tripp, J.L.; Peters, N.A. Trusted Node QKD at an Electrical Utility. IEEE Access 2021, 9, 105220–105229. [Google Scholar] [CrossRef]
- Grice, W.; Evans, P.; Pooser, R. Quantum Key Distribution for the Smart Grid. In IEEE Vision for Smart Grid Communications: 2030 and Beyond; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kuruganti, T. Quantum Key Distribution Applicability to Smart Grid Cybersecurity Systems. Internal Technical Report, ORNL. 2014; GridSQuARe Project. Available online: https://www.ornl.gov/research-library#stq=%22Quantum%20Key%20Distribution%20Applicability%20to%20Smart%20Grid%20Cybersecurity%20Systems.%22&stp=1 (accessed on 4 December 2023).
- Dunjko, V.; Wallden, P.; Andersson, E. Quantum Digital Signatures without Quantum Memory. Phys. Rev. Lett. 2014, 112, 040502. [Google Scholar] [CrossRef]
- Chen, Y.A.; Zhang, A.N.; Zhao, Z.; Zhou, X.Q.; Lu, C.Y.; Peng, C.Z.; Yang, T.; Pan, J.W. Experimental Quantum Secret Sharing and Third-Man Quantum Cryptography. Phys. Rev. Lett. 2005, 95, 200502. [Google Scholar] [CrossRef] [PubMed]
- Long, G.l.; Deng, F.g.; Wang, C.; Li, X.h.; Wen, K.; Wang, W.y. Quantum secure direct communication and deterministic secure quantum communication. Front. Phys. China 2007, 2, 251–272. [Google Scholar] [CrossRef]
- Cao, Z.; Lu, Y.; Chai, G.; Yu, H.; Liang, K.; Wang, L. Realization of Quantum Secure Direct Communication with Continuous Variable. Research 2023, 6, 193. [Google Scholar] [CrossRef]
- Rothe, S.; Besser, K.L.; Krause, D.; Kuschmierz, R.; Koukourakis, N.; Jorswieck, E.; Czarske, J.W. Securing Data in Multimode Fibers by Exploiting Mode-Dependent Light Propagation Effects. Research 2023, 6, 65. [Google Scholar] [CrossRef]
- Diamanti, E.; Lo, H.K.; Qi, B.; Yuan, Z. Practical challenges in quantum key distribution. NPJ Quantum Inf. 2016, 2, 16025. [Google Scholar] [CrossRef]
- Nandal, R.; Nandal, A.; Joshi, K.; Rathee, A.K. A survey and comparison of some of the most prominent QKD protocols. SSRN Electron. J. 2021. [Google Scholar] [CrossRef]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301. [Google Scholar] [CrossRef]
- Gobby, C.; Yuan, Z.; Shields, A. Quantum key distribution over 122 km of standard telecom fiber. Appl. Phys. Lett. 2004, 84, 3762–3764. [Google Scholar] [CrossRef]
- Yuan, Z.; Kardynal, B.; Sharpe, A.; Shields, A. High speed single photon detection in the near infrared. Appl. Phys. Lett. 2007, 91, 041114. [Google Scholar] [CrossRef]
- Rosenberg, D.; Peterson, C.G.; Harrington, J.W.; Rice, P.R.; Dallmann, N.; Tyagi, K.T.; McCabe, K.P.; Nam, S.; Baek, B.; Hadfield, R.H.; et al. Practical long-distance quantum key distribution system using decoy levels. New J. Phys. 2005, 7, 71. [Google Scholar] [CrossRef]
- Hiskett, P.A.; Rosenberg, D.; Peterson, C.G.; Hughes, R.J.; Nam, S.; Lita, A.E.; Miller, A.J.; Nordholt, J.E. Long-distance quantum key distribution in optical fibre. New J. Phys. 2007, 8, 193. [Google Scholar] [CrossRef]
- Ouellet, S.M.; Dettmer, J.; Olivier, G.; DeWit, T.; Lato, M. Advanced monitoring of tailings dam performance using seismic noise and stress models. Commun. Earth Environ. 2022, 3, 301. [Google Scholar] [CrossRef]
- Antonovskaya, G.; Kapustian, N.; Basakina, I.; Afonin, N.; Moshkunov, K. Hydropower Dam State and Its Foundation Soil Survey Using Industrial Seismic Oscillations. Geosciences 2019, 9, 187. [Google Scholar] [CrossRef]
- Baron, P.; Kočiško, M.; Hlavatá, S.; Franas, E. Vibrodiagnostics as a predictive maintenance tool in the operation of turbo generators of a small hydropower plant. Adv. Mech. Eng. 2022, 14, 16878132221101023. [Google Scholar] [CrossRef]
- Mohanta, R.K.; Chelliah, T.R.; Allamsetty, S.; Akula, A.; Ghosh, R. Sources of vibration and their treatment in hydro power stations-A review. Eng. Sci. Technol. Int. J. 2017, 20, 637–648. [Google Scholar] [CrossRef]
- Quaranta, E.; Müller, G. Noise Generation and Acoustic Impact of Free Surface Hydropower Machines: Focus on Water Wheels and Emerging Challenges. Int. J. Environ. Res. Public Health 2021, 18, 13051. [Google Scholar] [CrossRef]
- Philippe, S.; d’Errico, F. A physical unclonable neutron sensor for nuclear arms control inspections. Sci. Rep. 2020, 10, 20605. [Google Scholar] [CrossRef]
- Ijaz, S.; Rana, A.S.; Ahmad, Z.; Zubair, M.; Massoud, Y.; Mehmood, M.Q. The Dawn of Metadevices: From Contemporary Designs to Exotic Applications. Adv. Devices Instrum. 2022, 2022, 9861078. [Google Scholar] [CrossRef]
- Kwek, L.C.; Cao, L.; Luo, W.; Wang, Y.; Sun, S.; Wang, X.; Liu, A.Q. Chip-based quantum key distribution. AAPPS Bull. 2021, 31, 15. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, N.; Huang, Z.; Lai, J.; Liu, J.; Deng, G.; Wang, X.; Zhao, W. High-Sensitivity Force Sensors Based on Novel Materials. Adv. Devices Instrum. 2023, 4, 19. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, F. Squeezing for cosmic symphony. AAPPS Bull. 2023, 33, 5. [Google Scholar] [CrossRef]
- Lawrence, J.; Hollern, J.; Geddes, B.; Geddes, B.; Freeman, S.; Reif, M.; Reiger, C. Fossil Power Plant Cyber Security Life-Cycle Risk Reduction, a Practical Framework for Implementation; Technical Report; Southern Engineering Services: Aberdeen, NC, USA, 2020. [Google Scholar] [CrossRef]
- Bharani, P.; Chandra, K.; Potnuru, D. A nonlinear load frequency controller for hydropower plants. Int. J. Ambient. Energy 2021, 42, 203–210. [Google Scholar] [CrossRef]
- Wang, S.; Yin, Z.Q.; He, D.Y.; Chen, W.; Wang, R.Q.; Ye, P.; Han, Z.F. Twin-field quantum key distribution over 830-km fibre. Nat. Photonics 2022, 16, 154–161. [Google Scholar] [CrossRef]
- Liao, S.; Cai, W.Q.; Liu, W.Y.; Zhang, L.; Li, Y.; Ren, J.G.; Pan, J.W. Satellite-to-ground quantum key distribution. Nature 2017, 549, 43–47. [Google Scholar] [CrossRef]
- Yin, J.; Li, Y.H.; Liao, S.K.; Yang, M.; Cao, Y.; Zhang, L.; Pan, J.W. Entanglement-based secure quantum cryptography over 1120 kilometres. Nature 2020, 582, 501–505. [Google Scholar] [CrossRef]
- Sharma, P.; Agrawal, A.; Bhatia, V.; Prakash, S.; Mishra, A.K. Quantum Key Distribution Secured Optical Networks: A Survey. IEEE Open J. Commun. Soc. 2021, 2, 2049–2083. [Google Scholar] [CrossRef]
- Qi, B.; Zhu, W.; Qian, L.; Lo, H.K. Feasibility of quantum key distribution through a dense wavelength division multiplexing network. New J. Phys. 2010, 12, 103042. [Google Scholar] [CrossRef]
- Scherer, A.; Sanders, B.C.; Tittel, W. Long-distance practical quantum key distribution by entanglement swapping. Opt. Express 2011, 19, 3004–3018. [Google Scholar] [CrossRef]
- Lo, H.K.; Ma, X.; Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef]
- Lütkenhaus, N. Security against eavesdropping in quantum cryptography. Phys. Rev. A 2000, 61, 052304. [Google Scholar] [CrossRef]
- Makarov, V.; Khan, J. Optical attacks on practical continuous-variable quantum key distribution systems (or ‘how to hack a quantum cryptosystem’). Opt. Lett. 2006, 30, 1043–1045. [Google Scholar]
- Wolf, R. Quantum Key Distribution; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Pljonkin, A.; Singh, P.K. The Review of the Commercial Quantum Key Distribution System. In Proceedings of the 2018 Fifth International Conference on Parallel, Distributed and Grid Computing (PDGC), Solan, India, 22–22 December 2018; pp. 795–799. [Google Scholar] [CrossRef]
- Moreno Escobar, J.J.; Morales Matamoros, O.; Tejeida Padilla, R.; Lina Reyes, I.; Quintana Espinosa, H. A comprehensive review on smart grids: Challenges and opportunities. Sensors 2021, 21, 6978. [Google Scholar] [CrossRef] [PubMed]
- Kong, P.Y. A review of quantum key distribution protocols in the perspective of smart grid communication security. IEEE Syst. J. 2020, 16, 41–54. [Google Scholar] [CrossRef]
- Gopstein, A.; Nguyen, C.; O’Fallon, C.; Hastings, N.; Wollman, D. NIST Framework and Roadmap for Smart Grid Interoperability Standards. National Institute of Standards and Technology Special Publication (NIST SP), Release 2 (Latest 4). 2021. Available online: https://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.1108r4.pdf (accessed on 4 December 2023).
- US Department of Energy. 21 Steps to Improve Cyber Security of SCADA Network; US Department of Energy: Washington, DC, USA, 2001. Available online: https://www.energy.gov/sites/prod/files/oeprod/DocumentsandMedia/21_Steps_-_SCADA.pdf (accessed on 4 December 2023).
- Lim, C.; Curty, M.; Walenta, N.; Xu, F.; Zbinden, H. Concise security bounds for practical decoy-state quantum key distribution. Phys. Rev. 2014, 89, 022307. [Google Scholar] [CrossRef]
- Wilde, M.M. Preface to the Second Edition. In Quantum Information Theory, 2nd ed.; Cambridge University Press: Cambridge, UK, 2017; pp. 11–12. [Google Scholar] [CrossRef]
- Moschandreou, E.; Rollick, B.J.; Qi, B.; Siopsis, G. Experimental decoy-state Bennett-Brassard 1984 quantum key distribution through a turbulent channel. Phys. Rev. A 2021, 103, 032614. [Google Scholar] [CrossRef]
- Ding, Y.Y.; Chen, H.; Wang, S.; He, D.Y.; Yin, Z.Q.; Chen, W.; Zhou, Z.; Guo, G.C.; Han, Z.F. Polarization variations in installed fibers and their influence on quantum key distribution systems. Opt. Express 2017, 25, 27923–27936. [Google Scholar] [CrossRef] [PubMed]
- Mekhtiev, E.; Gerasin, I.; Rudavin, N.; Duplinsky, A.; Kurochkin, Y. Polarization control algorithm for QKD systems. Proc. J. Phys. Conf. Ser. 2021, 2086, 012092. [Google Scholar] [CrossRef]
- Wu, G.; Chen, J.; Li, Y.; Zeng, H. Stable polarization-encoded quantum key distribution in fiber. arXiv 2006, arXiv:quant-ph/0606108. [Google Scholar]
- Inaudi, D.; Blin, E.R. Monitoring Dams with Distributed Fiber Optic Sensing. In Proceedings of the International Conference on Dam Engineering, Philadelphia, PA, USA, 11–14 September 2016; Available online: https://api.semanticscholar.org/CorpusID:229311780 (accessed on 4 December 2023).
- de la Torre, O.; Floris, I.; Sales, S.; Escaler, X. Fiber Bragg Grating Sensors for Underwater Vibration Measurement: Potential Hydropower Applications. Sensors 2021, 21, 4272. [Google Scholar] [CrossRef]
- Li, H.W.; Zhang, C.M.; Jiang, M.S.; Cai, Q.Y. Improving the performance of practical decoy-state quantum key distribution with advantage distillation technology. Commun. Phys. 2022, 5, 53. [Google Scholar] [CrossRef]
- Peters, N.A.; Toliver, P.; Chapuran, T.E.; Runser, R.J.; McNown, S.R.; Peterson, C.G.; Rosenberg, D.; Dallmann, N.; Hughes, R.J.; McCabe, K.P.; et al. Dense wavelength multiplexing of 1550 nm QKD with strong classical channels in reconfigurable networking environments. New J. Phys. 2009, 11, 045012. [Google Scholar] [CrossRef]
- Chapuran, T.E.; Toliver, P.; Peters, N.A.; Jackel, J.; Goodman, M.S.; Runser, R.J.; McNown, S.R.; Dallmann, N.; Hughes, R.J.; McCabe, K.P.; et al. Optical networking for quantum key distribution and quantum communications. New J. Phys. 2009, 11, 105001. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhao, Z.; Mao, K.; Chen, X.; Liu, W.; Wu, Q. A Real-Time Hardware Emulator for 3D Non-Stationary U2V Channels. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3951–3964. [Google Scholar] [CrossRef]
- Hua, B.; Ni, H.; Zhu, Q.; Wang, C.X.; Zhou, T.; Mao, K.; Bao, J.; Zhang, X. Channel Modeling for UAV-to-Ground Communications With Posture Variation and Fuselage Scattering Effect. IEEE Trans. Commun. 2023, 71, 3103–3116. [Google Scholar] [CrossRef]
- Bloom, Y.; Fields, I.; Maslennikov, A.; Rozenman, G.G. Quantum Cryptography–A Simplified Undergraduate Experiment and Simulation. Physics 2022, 4, 104–123. [Google Scholar] [CrossRef]
- Siehler, J.A. The Hamming(7,4) Code. Wolfram Demonstrations Project, 7 March 2011. Available online: http://demonstrations.wolfram.com/TheHamming74Code/ (accessed on 4 December 2023).
- Loudon, R. The Quantum Theory of Light; OUP Oxford: Oxford, UK, 2000. [Google Scholar]
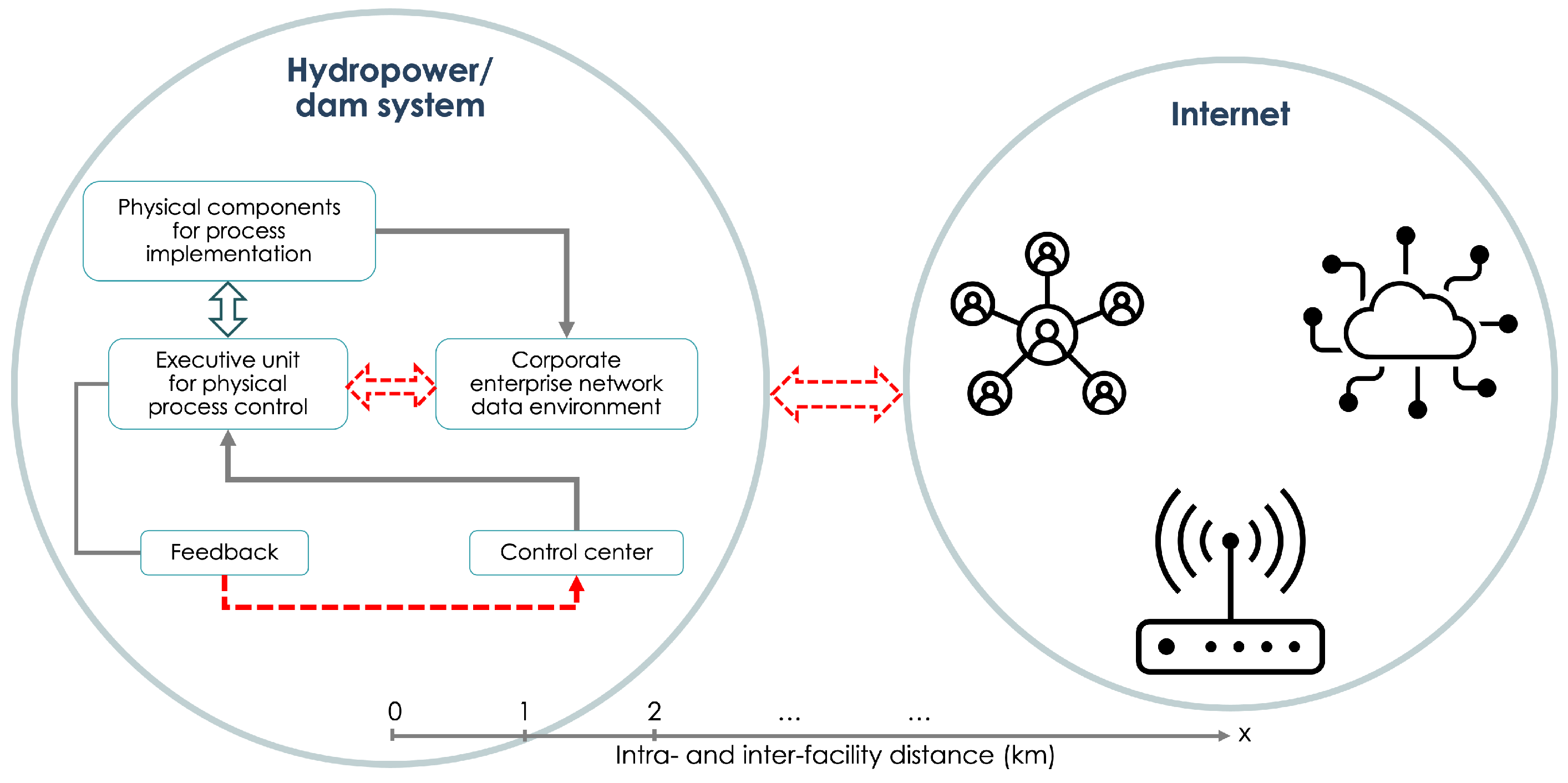

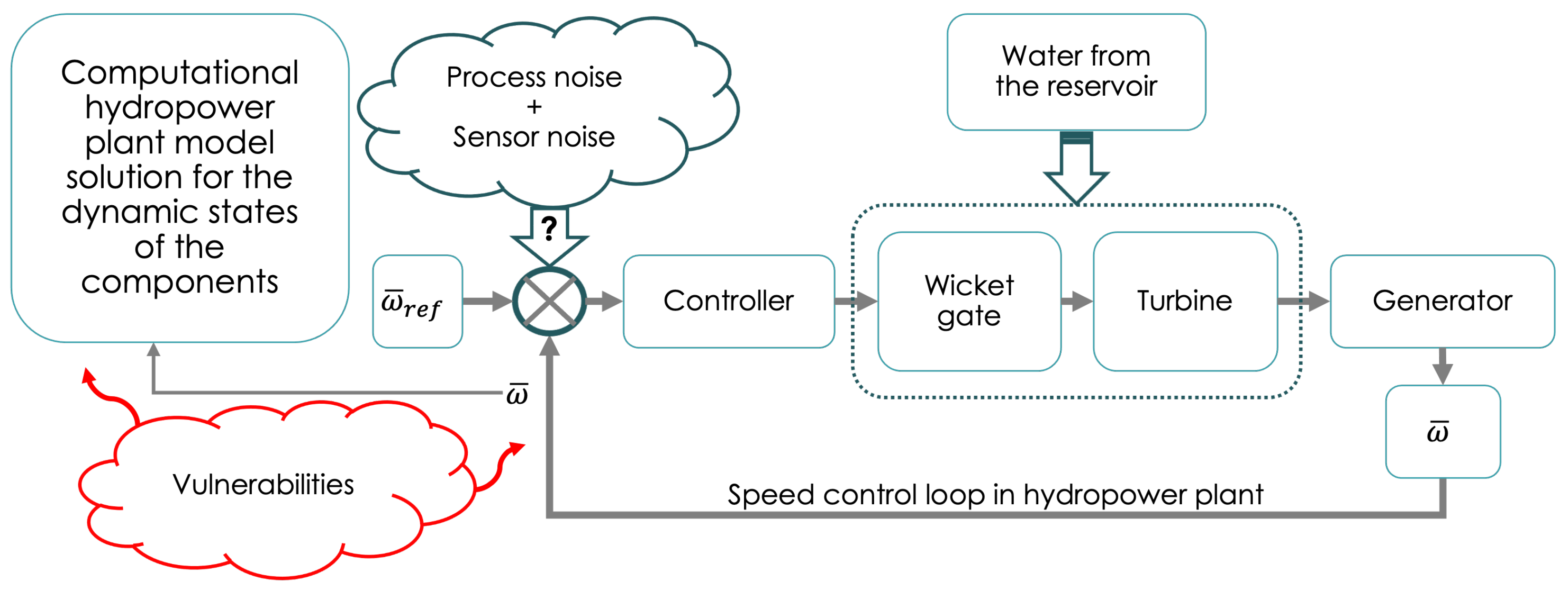

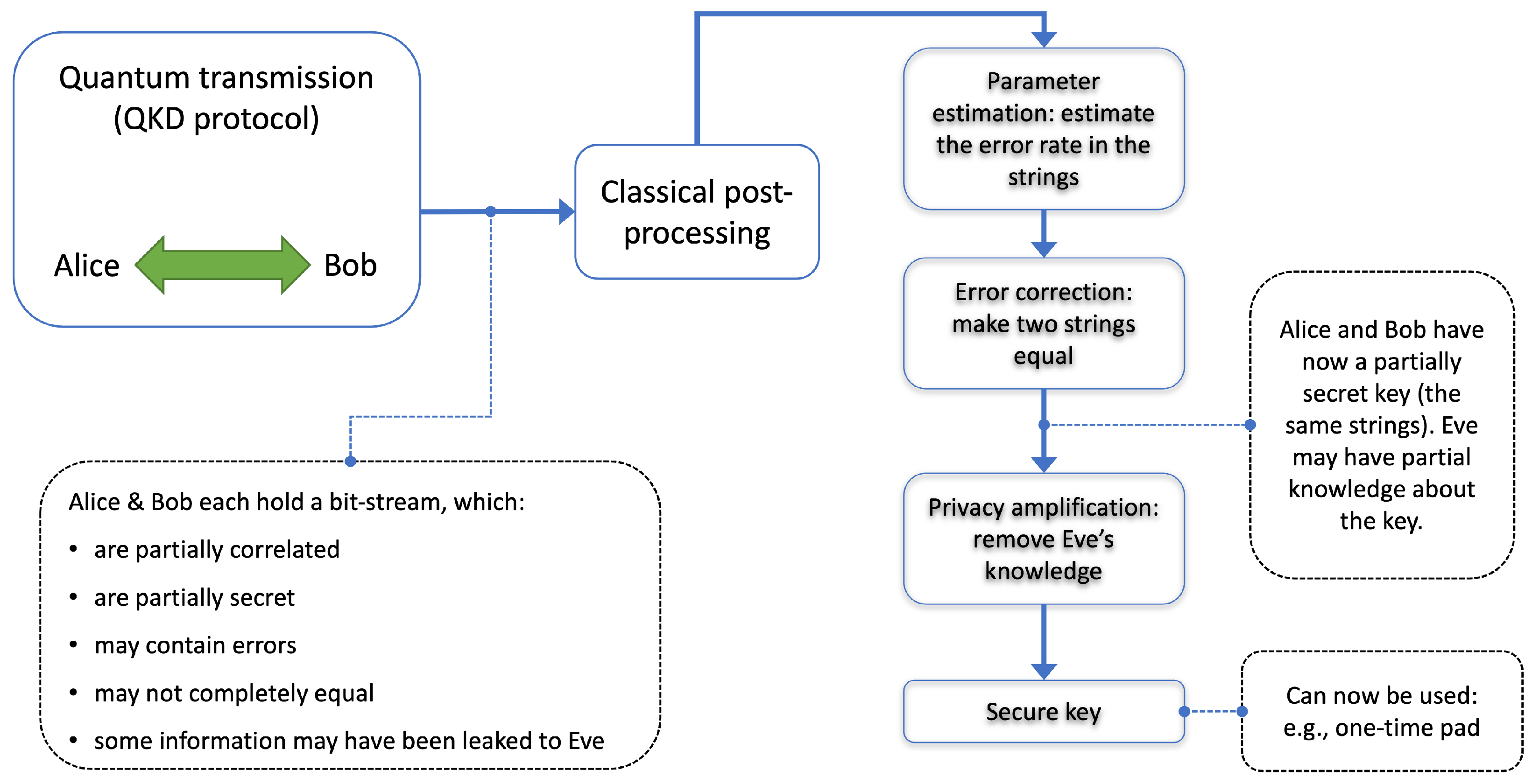
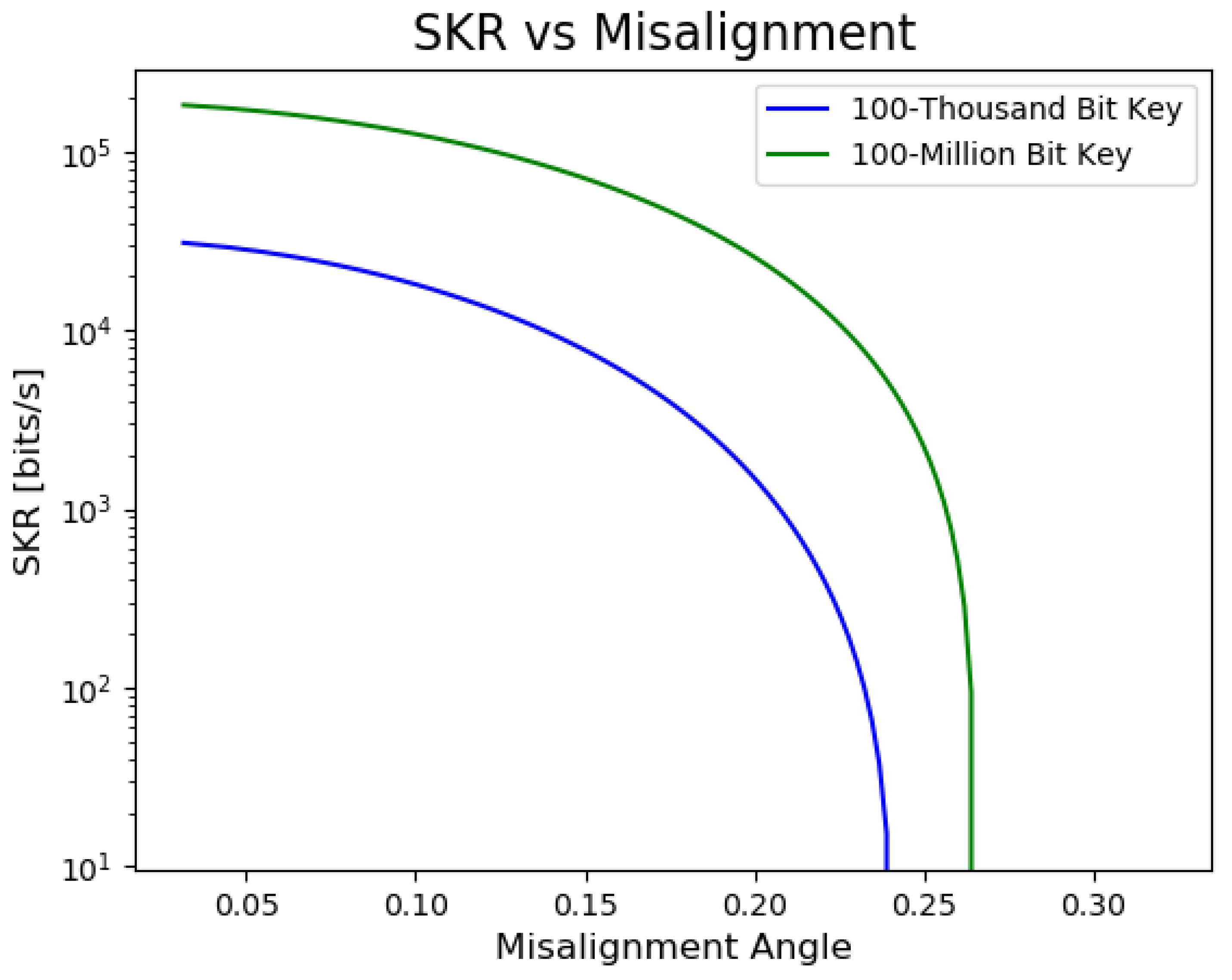
| Cybersecurity Issue | Description | Impact | Role of QKD |
|---|---|---|---|
| Remote Control System Attacks | Compromise of SCADA [6] systems controlling dam operations. | Dam failure, potential loss of life, and environmental damage. | Secure keys via QKD encrypt communication, thwarting unauthorized access to the control system. |
| Sensor Spoofing [7] | Interference with sensors, leading to inaccurate readings and unsafe operations. | Dam failure, potential loss of life, and environmental damage. | Secure or authenticated communication between sensors and control system, reveals data tampering. |
| Communication Interception [8] | Interception or injection of malicious commands in communication channels. | Dam failure, potential loss of life, and environmental damage. | Secure all communications, hindering interception or data tampering. |
| Denial of Service (DoS) Attacks [9] | Overloading communication channels or control systems. | Operational disruption leading to flooding or other issues. | Indirectly aids by protecting from vulnerabilities exploited in DoS. |
| Physical Security Breaches | Tampering of equipment or insertion of malicious hardware/software. | Dam failure, potential loss of life, and environmental damage. | Indirectly aids by strengthening overall cybersecurity infrastructure. |
| Supply Chain Attacks | Pre-installation compromise of hardware or software. | Compromised dam components leading to security breaches. | Indirectly aids by protecting from vulnerabilities exploited due to compromised components. |
| Insider Threats | Misuse of sensitive systems by authorized individuals. | Operational disruption or sabotage. | Secure communication between control systems and authorized personnel, preventing unauthorized access. |
| QKD Modality | Hydropower System’s Requirements |
|---|---|
| BB84 Protocol (see, e.g., Nadal et al. [22] for other protocols) |
|
| Decoy State QKD |
|
| Continuous-Variable QKD |
|
| MDI-QKD |
|
| Satellite-based QKD |
|
| Other Considerations |
|
| Noise Source | Description |
|---|---|
| Quantum Bit Error Ratio (QBER) | Represents the ratio of bits that are received in error. Though not a direct noise source, QBER quantifies the impact of various technical factors and imperfections in QKD systems. |
| Dark Counts | False counts arising in photon detectors due to thermal fluctuations or other non-signal measurement events. |
| Dead Time | Time taken by a detector to recover after detecting a photon. Photons arriving during this interval can lead to loss. |
| Detector Jitter | Uncertainty in a detector’s time response when it receives a signal, arising from electronic and photonic fluctuations. |
| Beam Splitting/Coupling Inefficiencies | Imperfections in beam splitters or inefficient coupling into optical fibers leading to photon loss. |
| Fiber or Channel Attenuation | Losses in the optical channel or the transmission fiber. |
| Multi-Photon Emissions | Occurrences when sources produce multi-photon pulses, introducing vulnerabilities and noise. |
| Phase Fluctuations | In protocols like Differential Phase Shift QKD, phase fluctuations in transmission fiber can cause errors. |
| Timing Jitter/Synchronization | Uncertainty or variations in the timing of a system’s clock or reference signal, affecting synchronization. |
| Quantum State Preparation | Imperfections in preparing quantum states for example, specific polarization state encoding. |
| Spatial Mode Mismatches | Mismatches when transmitting quantum states over channels, leading to decreased detection probabilities. |
| Back Reflections/Scattering | Reflections from interfaces or scattering within components introducing noise photons. |
| Noise Source | Description | Typical Sensor |
|---|---|---|
| Turbine Operations | Noise from turbine movement both in air and underwater. Frequencies (0.5–30) Hz with amplitudes mm. | Hydrophone (underwater), Microphone (airborne) |
| Gates and Valves | Noise due to dam gate or spillway operations. Varies based on size and operation speed. | Vibration sensors, Microphone |
| Pumps and Machinery | Noise from operational machinery. Typically (10–200) Hz. | Microphone, Vibration sensors |
| Flow Turbulence | Noise from rapid and turbulent water flow. (1–100) Hz. | Hydrophone |
| Waterfall/Spill | Noise due to water spillage. Frequency depends on water volume and height of fall. | Hydrophone, Microphone |
| Bubble Formation | Noise due to bubble formation and collapse. (5–50) Hz. | Hydrophone |
| Transformer Operations | Buzzing or humming from transformers. Typically at 50 Hz or 60 Hz. | Magnetic field sensors, Microphone |
| High Voltage Equipment | Noise from insulator discharges. Broadband noise typically spanning 10 Hz to 1 kHz. | Electromagnetic sensors, Microphone |
| Vibration | Vibrations inherent to dam structures. Spanning from very low frequencies (<1 Hz) due to seismic activities to high frequencies (>100 Hz) from machinery operations. | Accelerometers, Vibration sensors |
| Thermal Expansion/Contraction | Noise from temperature-induced structural changes. Frequency varies based on structure size and material. | Vibration sensors, Microphone |
| Wildlife Activities | Sounds from local fauna. Frequencies are species-specific, ranging broadly from 1 Hz to 10 kHz. | Microphone, Hydrophone |
| Weather Patterns | Noise from atmospheric disturbances, thunder, tornado. Broad frequency range from <1 Hz (thunder rumble) to >10 kHz (lightning crack). | Wind sensors, Microphone |
| Vehicle Traffic | Noise from vehicular activities. Frequencies range from 20 Hz (engine hum) to 2 kHz (horn). | Accelerometers, Vibration sensors, Microphone |
| Construction/Maintenance | Noise from maintenance or construction work. Broad frequency range depending on tools and machinery. | Accelerometers, Microphone, Vibration sensors |
| Temperature Fluctuations | Ambient temperature changes affecting equipment. Changes can cause material contractions or expansions leading to noise. | Thermocouples, Infrared sensors |
| Moisture/Condensation | Moisture interference with equipment. Can cause electrical noises or material deformations. | Humidity sensors, Moisture meters |
| Step | Description/Equation |
|---|---|
| Error Estimation | |
| Information Reconciliation | Uses error-correcting codes to rectify key discrepancies. The Cascade protocol is popular; it entails key division, shuffling, and parity comparison. |
| Privacy Amplification | Aims to eliminate any eavesdropper’s partial information. Typically employs universal hash functions, represented as: . |
| Key Sifting | Particularly relevant in the BB84 protocol. Alice and Bob publicly disclose the bases chosen for each qubit. Qubits with differing bases are discarded. |
| Authentication | Confirms genuine communication between Alice and Bob. Utilizes classical authentication methods in tandem with previously shared secret keys. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Green, A.; Lawrence, J.; Siopsis, G.; Peters, N.A.; Passian, A. Quantum Key Distribution for Critical Infrastructures: Towards Cyber-Physical Security for Hydropower and Dams. Sensors 2023, 23, 9818. https://doi.org/10.3390/s23249818
Green A, Lawrence J, Siopsis G, Peters NA, Passian A. Quantum Key Distribution for Critical Infrastructures: Towards Cyber-Physical Security for Hydropower and Dams. Sensors. 2023; 23(24):9818. https://doi.org/10.3390/s23249818
Chicago/Turabian StyleGreen, Adrien, Jeremy Lawrence, George Siopsis, Nicholas A. Peters, and Ali Passian. 2023. "Quantum Key Distribution for Critical Infrastructures: Towards Cyber-Physical Security for Hydropower and Dams" Sensors 23, no. 24: 9818. https://doi.org/10.3390/s23249818
APA StyleGreen, A., Lawrence, J., Siopsis, G., Peters, N. A., & Passian, A. (2023). Quantum Key Distribution for Critical Infrastructures: Towards Cyber-Physical Security for Hydropower and Dams. Sensors, 23(24), 9818. https://doi.org/10.3390/s23249818







