Abstract
The photon point clouds collected by the high-sensitivity single-photon detector on the Ice, Cloud, and Land Elevation Satellite-2 (ICESat-2) are utilized in various applications. However, the discretely distributed noise among the signal photons greatly increases the difficulty of signal extraction, especially the edge noise adjacent to signals. To detect signal photons from vegetation coverage areas at different slopes, this paper proposes a density-based multilevel terrain-adaptive noise removal method (MTANR) that identifies noise in a coarse-to-fine strategy based on the distribution of noise photons and is evaluated with high-precision airborne LiDAR data. First, the histogram-based successive denoising method was used as a coarse denoising process to remove distant noise and part of the sparse noise, thereby increasing the fault tolerance of the subsequent steps. Second, a rotatable ellipse that adaptively corrects the direction and shape based on the slope was utilized to search for the optimal filtering direction (OFD). Based on the direction, sparse noise removal was accomplished robustly using the Otsu’s method in conjunction with the ordering points to identify the clustering structure (OPTICS) and provide a nearly noise-free environment for edge searching. Finally, the edge noise was removed by near-ground edge searching, and the signal photons were better preserved by the surface lines. The proposed MTANR was validated in four typical experimental areas: two in Baishan, China, and two in Taranaki, New Zealand. A comparison was made with three other representative methods, namely differential, regressive, and Gaussian adaptive nearest neighbor (DRAGANN), used in ATL08 products, local distance statistics (LDS), and horizontal ellipse-based OPTICS. The results demonstrated that the values of the F1 score for the signal photon identification achieved by the proposed MTANR were 0.9762, 0.9857, 0.9839, and 0.9534, respectively, which were higher than those of the other methods mentioned above. In addition, the qualitative and quantitative results demonstrated that MTANR outperformed in scenes with steep slopes, abrupt terrain changes, and uneven vegetation coverage.
1. Introduction
Spaceborne LiDAR has been widely used in global forest canopy height estimation [1,2,3] due to its rapid and cost-effective detection of surface typography and vertical forest structure [2,4,5,6]. The accuracy of global forest height data evaluated by the Geoscience Laser Altimeter System (GLAS) onboard the Ice, Cloud, and Land Elevation Satellite (ICESat) has been proven over the past few decades [7]. However, limitations such as a large footprint size (70 m) and low sampling density (along-track spacing of 170 m) restrict its application in complex terrains [8]. To address these issues, the ICESat-2, equipped with the advanced topographic laser altimeter system (ATLAS) [9], was launched and put into operation in September 2018. In contrast to the full waveform LiDAR system from the GLAS, ATLAS is a photon-counting LiDAR that utilizes high-frequency pulses [10] with an emission energy of 160/40 μj at 10 kHz and 0.7 m along-track resolution for precise surface measurements [11,12], providing a high sampling rate, a small footprint size (10 m), and a nearly continuous along-track strip of point cloud data [13]. However, the original data from ATLAS, particularly the daytime data, are heavily contaminated by background noise arising from solar radiation and dark current returns [14] and feature a random and wide distribution. In vegetation coverage areas, the abundant noise distributed adjacent to the canopy and the ground surface poses significant challenges for identifying the canopy and ground signals in photon-counting LiDAR data. In this sense, signal photon discrimination from the original data is necessary to address these challenges.
Many excellent signal detection algorithms for photon point clouds have been developed. The algorithms can be broadly classified into three categories: grid-based two-dimensional image processing techniques, local parameters statistics, and density-based clustering algorithms [15]. For image-based techniques, the rasterization of point clouds tends to lead to poor accuracy, so dominant studies mainly focus on the last two types. Local statistical methods separate signals from noise by constructing point cloud features, followed by global or local thresholds. The selection of thresholds in such methods influences the resulting measurements, such as DRAGANN [16,17,18] used in ATL08 products and local distance statistics (LDS) [19]. Density clustering methods utilize a priori information that ICESat-2 point clouds are densely concentrated in the signal photons in comparison to the noise photons for denoising purposes. This type of method imposes no requirements on the shape of clusters [20], but it is sensitive to the parameter settings, such as Bayesian [21], dense-based spatial clustering of applications with noise (DBSCAN) [22], and OPTICS [23]. Notably, OPTICS does not generate explicit clusters and is more robust than the other clustering approaches.
At present, most improvements towards the algorithms above [16,19,20,21,22,23] mainly focus on four aspects: improving the search domain, enhancing parameter determination, employing several characteristics with machine learning methods, and combining several single-level methods to achieve better accuracy. When it comes to search domain improvement, horizontal ellipse-based OPTICS was developed by Zhu et al. [24], which demonstrated greater robustness than the optimized DBSCAN [24]. Gao et al. [25] enhanced the DRAGANN algorithm with a multi-scale search radius for solving the residual noise caused by a fixed radius. In terms of parameter determination, Huang et al. [26] and Zhang et al. [27] improved the self-adaptability of density-based methods based on a genetic algorithm and a particle swarm algorithm. Li et al. [28] and He et al. [29] proposed a relative neighboring relationship (RNR) and local outlier factor algorithm with a rotating search area (LOFR) to improve the local parameter statistics algorithm. For supervised machine learning techniques, Li et al. [30] and Chen et al. [31] proposed the neighboring forward local density difference (NFLDD) and K-nearest neighbors distance to characterize the differences between the signals and noise. Supervised methods, such as random forest and support vector machine, were used to classify the photons, which achieved good accuracy, but these methods rely on a large number of training samples. There are no unified tools and standards for preparing samples, making it difficult apply them widely. However, there is residual noise after single-level filtering algorithms [24,25,26,27,28,29,30,31,32,33], especially noise adjacent to the signal in complex terrains.
Several multilevel approaches combined with single-level methods have been gradually developed. For example, Huang et al. [34] proposed a multilevel strategy that combined an adaptive filter TS-SCABR, empirical mode decomposition, and percentile statistics method to extract the canopy-top. Wu et al. [35] created a multilevel technique that incorporated an RNR-DCM filter and a sliding detection window and fitted a straight-line model to accurately distinguish the sub-canopy photons. To effectively achieve daytime data denoising, You et al. [36] proposed a hybrid algorithm that combined OPTICS and RNR-KNNB. These multi-level methods mainly include three steps, namely preprocessing, fine denoising, and residual noise processing [15], which usually focus on three problems: (1) Changing the traditional search domain to improve the adaptability and provide a stable denoising result in areas with complex terrains. (2) Constructing features or developing algorithms that increase the separability between the signal photons and the noise distributed around them by amplifying the differences between the two. (3) Exploring the adaptation of parameters for different data to make the algorithm more robust.
However, there are relatively few studies that consider all three factors above simultaneously. In this study, we propose a density-based multilevel terrain-adaptive noise removal method (MTANR) with a coarse-to-fine denoising strategy to address the issue. It is challenging to remove the noise adjacent to the signal and the removal requires a nearly noise-free environment; therefore, we categorized noise into three types [25,30]: cloud-caused high-altitude distant noise, sparse noise in medium distance, and edge noise adjacent to signal, as shown in Figure 1. Based on the classification of noise photons, the denoising process was divided into three steps: (1) Distant noise and part of sparse noise were removed using a histogram-based successive method which gradually tightened conditions as a coarse denoising process. (2) The residual sparse noise was identified by the terrain-adaptive OPTICS with a rotating search domain, and a nearly noise-free environment was provided. (3) Based on the directional distribution of local densities at the internal and boundary points in photon clusters, edge searching was employed to remove the edge noise, followed by surface line constraints, which further preserved the signal photons. The steps (2) and (3) are called fine denoising.
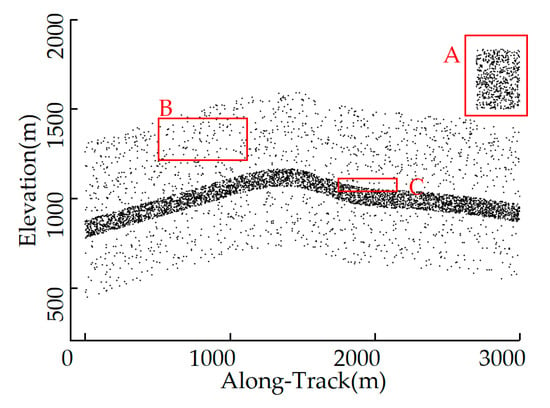
Figure 1.
Schematic diagram of the noise distribution and types: A (cloud-caused high-altitude distant noise), B (sparse noise in medium distance), and C (edge noise adjacent to signal).
The main contributions of this study are as follows: (1) The proposed MTANR robustly preserves the signal photons in steep areas, abrupt terrain changes, and uneven vegetation coverage by automatically determining the terrain-based filtering direction and alternating the shapes of the search domain. (2) Edge searching improves edge noise removal capabilities and reduces edge noise’s impacts on ICESat2 data applications such as canopy height inversion.
The paper is organized as follows. In Section 2, the experiment and validation data are described. The details of the method are presented in Section 3. Experiments with four datasets are presented in Section 4 where the experimental results and analyses are presented. This is followed by some concluding remarks.
2. Materials
2.1. ICESat2 Data
The ATL03 photons and ATL08 product used for this study are accessible from the National Snow and Ice Data Center (https://nsidc.org/data/icesat-2/data, accessed on 4 March 2023), including information such as the signal confidence, elevation, latitude, and longitude. Considering the impacts of slope and vegetation coverage factors on denoising, this study opted to test two representative vegetation coverage study areas [37]. The profiles of the raw data selected are shown in Figure 2, and the details are displayed in Table 1. One study area is located in the vegetation coverage region near the southern foothills of the Changbai Mountain in Baishan City, Jilin Province, China. This area is characterized by medium to high and uneven vegetation. The other experimental region is situated in the Taranaki region of New Zealand, with relatively sparse vegetation and complex terrains. In this area, we selected two ATL03 strips with a total length of approximately 13 km. Figure 2c represents a strip extending from the mountain foot to the summit, covering gentle slopes, mountain peaks, and abrupt terrain changes. Figure 2d depicts a mountainous area with steep terrain and rapid changes in the slope. These two study areas exhibit obvious slope variations, uneven vegetation coverage distribution, and different background noise patterns. These factors collectively challenge the algorithm’s robustness and the precision of noise reduction [37].
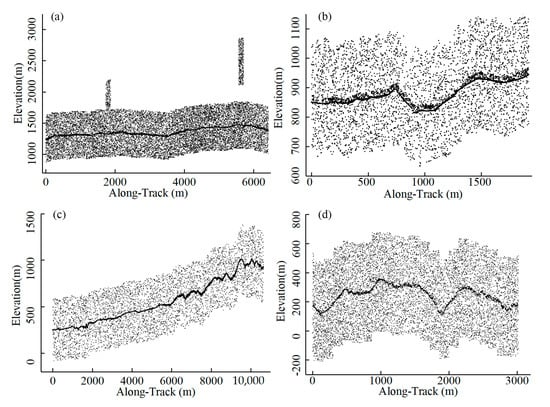
Figure 2.
The raw ATL03 photon data: (a,b) in Baishan, China, and (c,d) in New Zealand.

Table 1.
The ICESat-2 data acquisition time and name details.
2.2. Validation Data
ATL03 provides an initial classification of photons as signal [38] or background. Additionally, ATL08 also provides classification labels, and the photons in ATL03 can be easily reversed and indexed using the identified parameters [16,17,18]. For more information, see Table A1 in Appendix A. However, they are not accurate enough to serve as references for complex topographies such as hilly and mountainous terrains. Some existing approaches for quantitative denoising output assessment typically rely on the manual interpretation of Google Earth satellite images to construct validation datasets [39,40]. In this sense, these subjectively labeled references may be imprecise. For this reason, we employed the airborne point cloud with high density as the reference data to evaluate the signal extraction algorithm presented in this work [39], which provides an increasingly objective benchmark to quantify denoising accuracy. For supplementary validation, the digital terrain model (DTM) and digital surface model (DSM) with a horizontal resolution of 1 m from the airborne LiDAR data of approximately 10 pts/m2 were used to serve as boundaries for the signal photons. A photon is labeled as a signal when its elevation is within the DTM and DSM, and considered as noise when surpassing the threshold. Using airborne data as a constraint reduces subjectivity compared to manual classification, promising robust characterization over vegetation coverage areas.
Although it is ideal that the acquisition time of validation data and ICESat2/ATL03 data should be closely matched, this is often not possible due to the significant cost and time involved in airborne LiDAR missions and manual field surveys [41]. In addition, if there are no major disasters such as earthquakes, landslides, or forest fires, the changes in surface elevation and canopy height due to natural variability and vegetation growth should be minimal [42]. Despite differences in collection time, airborne data continue to be the best option for validation data, which have been used in several recent relevant studies [36,41,43,44,45] such as references for satellite-based forest canopy height inversion. Therefore, it is reasonable to assume that the airborne data provide good references. The acquisition time between airborne and spaceborne data is less than one year in New Zealand, and the airborne data can serve as references directly. The airborne data in Baishan was collected in 2014, a few years ahead of ICESat 2’s acquisition time. So in this area, we set a 0.5 m buffer zone to mitigate the impact of changes over time, according to the research of Huang et al. [39].
3. Method
A density-based multilevel terrain-adaptive noise removal method was designed to remove the high background noise, especially the edge noise of ICESat-2 photon data in study areas with complex terrain and vegetation coverage.
As shown in the flowchart presented in Figure 3, different types of noise were removed using a coarse-to-fine strategy. First, the histogram-based successive denoising as a coarse denoising process was applied to remove distant noise and part of the sparse noise, reducing the computation in subsequent steps and increasing the fault tolerance in further denoising it to the maximum. Secondly, based on the coarse denoising result, fitted approximate terrain curves serve as an aid to the adaptive rotated ellipse to find the OFD. Then, the OPTICS algorithm was applied in the OFD to remove the residual sparse noise. Next, according to the directional distribution of local densities of the internal signal and edge noise in residual photon clusters, the OFD and the direction vertical to optimal filtering direction (VOFD) ellipses were used as search domains to characterize this distributional difference. As a result, the edge noise was removed well during the fine denoising process. In addition, surface lines were fitted to further preserve the signals between them. At last, the results were evaluated using the reference data from airborne LiDAR.
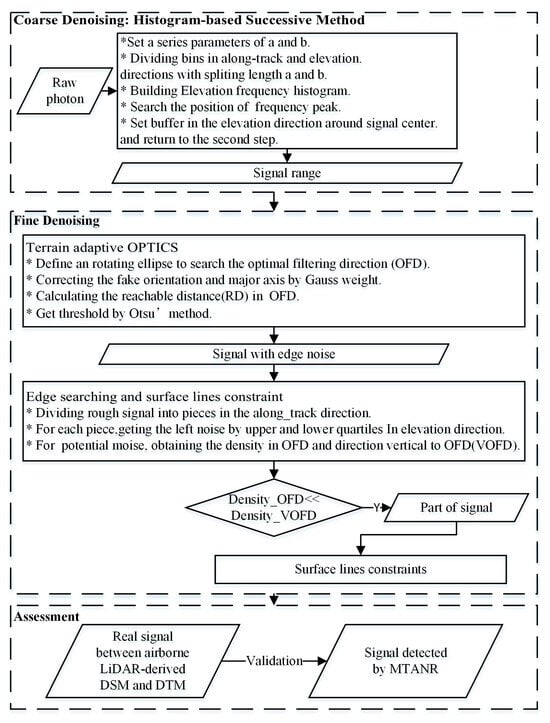
Figure 3.
The flowchart of the noise removal algorithm.
3.1. Preprocessing
The main purpose of preprocessing is to remove cloud-caused distant noise and part of the sparse noise as a coarse denoising process. The cloud-caused noise clusters exhibit similar spatial distribution with signal photons, making it challenging to distinguish them from the signal at a global scale based solely on local density or distance features. Therefore, the handling of the residual portions will pose a challenge. Based on the significantly higher elevation of noise photons compared to signal photons, a histogram-based successive denoising method was designed to remove them. The specific steps of this method are as follows: (1) Grid partitioning: All photons were divided into several bins in the along-track and elevation directions with a certain step size. (2) Frequency histogram building: The number of photons in each bin was counted, and the signal centers were determined based on the elevation of the bin with the maximum quantity. To reduce the influence of individual extreme outliers, the signal center elevation was set as the arithmetic average of the median and the mean. (3) Buffer zone determination: A buffer zone was defined as the range of potential signal photons by taking a certain distance above and below the signal center. Figure 4 shows that by applying strict constraints, a single uniform split step size may identify the noise bins in the sky or below the ground as signals in areas with low surface coverage and sparse signal photons. Though using loose constraints may avoid this problem, our purpose of searching exact signal range will not be achieved. Above all, we devised a series of values, starting with a large partitioning interval and buffer, and successively tightening the parameters to restrict the signal photons within an increasingly fine range.
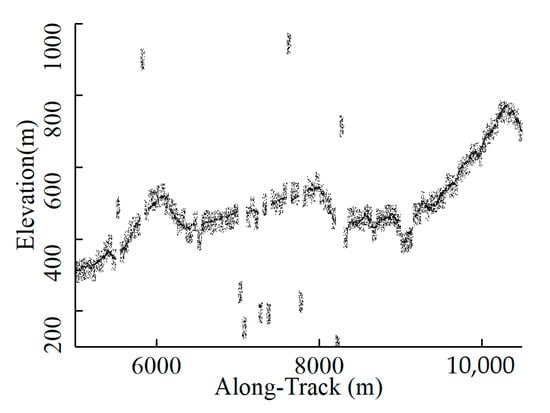
Figure 4.
Schematic diagram: Misclassification of single-level histogram.
3.2. Terrain-Adaptive OPTICS Algorithm
OPTICS is an improvement in the DBSCAN algorithm. Consistent with the DBSCAN algorithm, it also has parameters such as neighborhood radius (, ) and minimum number of points in the neighborhood (). After giving the parameters, DBSCAN directly presents the clustering results. Compared to DBSCAN, the OPTICS algorithm does not directly output cluster assignments. Instead, it produces an ordered list of data points ranked by reachability distance (RD) in the hierarchical density-based cluster structure. By setting a threshold on RD, implicit clusters can be extracted. Thus, the cluster ordering from OPTICS is invariant to input parameters, while DBSCAN can produce various clusters with different parameters.
3.2.1. Definition of Rotating Ellipsoidal OPTICS
Previous studies have found that ATL03 photons have a higher density in the along-track direction than in the across-track orientation [46]. To utilize this terrain-induced difference, we employed a rotating ellipsoidal search domain adapting to the local topography instead of the traditional circular neighborhood in OPTICS. For photon and photon , the ellipsoidal distance between them is defined as Equation (1):
where and represent the along-track distance and the elevation between the two photons; a and b are the lengths of the major and minor axes of the search ellipse. When distance , photon q is considered within the search ellipse centered at photon p; otherwise, photon q is outside the search ellipse. In areas of terrain relief, the search ellipse needs to be rotated to adapt to changes in the surfaces. In this case, the along-track and vertical distances are projected onto the major and minor axis directions of the rotated ellipse. The conversion method of and is illustrated in Equation (2), where θ is the counterclockwise angle between the major axis and the along-track direction.
In the OPTICS algorithm, -neighborhood, reachability distance (RD), and core distance (CD) are used to describe the relationship between photons, and here, we follow their definitions.
-neighborhood: For a point in the full dataset D, its -neighborhood is defined as the set of points and manifested as . It includes all data points in D that are within a distance away from the point p, which can also be represented as . The number of samples contained in is denoted as .
CD: Given and , the CD of a photon o can be expressed as Equation (3). When , photon o is called the core point. In , the k-th closest point to the photon o is denoted as , and its RD can be marked as . If ≤ , is identified as .
RD: As shown in Equation (4), if photon o is a core point, the RD of data point p to point o is defined as the maximum of and . If photon o is not a core point, then is determined as .
3.2.2. Optimal Filtering Direction Searching and Parameter Correction
For a photon p, by changing the rotation angle θ, the number of neighborhood points in any direction and the OFD of photon p can be obtained (e.g., photon A in Figure 5a). To improve computational efficiency, the approximate direction was first searched at a step of 10°. Within a 10° range above and below this direction, the neighborhood counts were computed every 3°, and the OFD was determined as the direction with the maximum count. However, for near-ground edge noise photon B as shown in Figure 5a, this determination typically leads to searching in the wrong direction, decreasing the recognition rate for such photons.
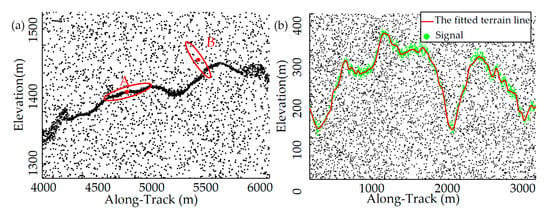
Figure 5.
Schematic diagram: (a) false directions; (b) the fitted terrain line.
In this sense, we identified these photons and corrected false directions by defining local weighted density [27]. For any given point p, its density is assayed by Equation (5), where represents the Euclidean distance between the k-th neighboring and the central photon, k denotes the number of photons in the neighborhood, indicates the variance of the Gaussian function, stands for the weight corresponding to the i-th neighborhood photon, and D is the density of the central photon.
The weight increases with the increasing distance between the neighborhood and central photons, and vice versa. This phenomenon significantly increases the density difference between signal and noise photons. By dividing the search ellipse into two parts based on the short axis, the densities were calculated separately for each part. When the density on one side is three times greater than the other, it is considered an excessive difference in neighboring densities. In such cases, the optimal filtering direction is considered false [47].
After a histogram-based successive coarse denoising, the signal centers along the trajectory were obtained. As shown in Figure 5b, a curve that roughly depicts the topography of this region was produced after sampling and fitting these signal centers. For photons detected in false directions, the wrong direction will be replaced by the tangent direction of the corresponding curve at the along-track distance during neighborhood search.
In addition, to ensure the consistency of the search ellipse in the along-track direction, the ellipse size needs to be modified based on the slope angle during the neighborhood search, considering that during the ground detection of ATLAS photons, the sensor collects point clouds over sloped and flat terrains with consistent firing and sampling rates. As shown in Figure 6, when the search direction exhibits an oblique angle to the ground, the along-track coverage of the ellipse will be shortened when using a fixed-size filtering kernel. Consequently, in sloped regions, a fixed search domain will therefore cover fewer pulses, thereby underestimating the photon density and influencing the denoising performance. Thus, the major axis of the search ellipse in sloped regions can be corrected by Equation (6), where a′ is the major axis over the flat terrain, θ denotes the angle between the search and horizontal directions, and a′ represents the major axis over the sloped terrain.
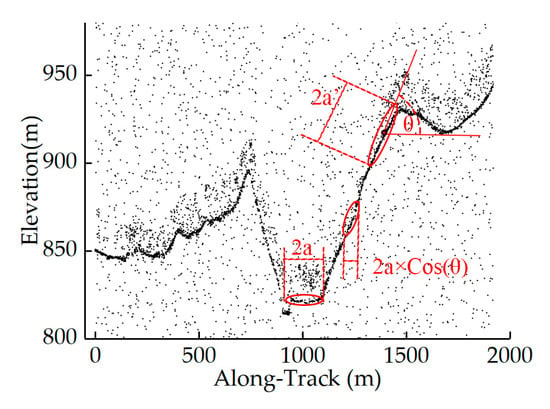
Figure 6.
Schematic diagram: correction of search domain shape.
Given that for a photon there may be multiple RDs for it, the minimum RD is set as the optimal RD for it. After computing the optimal RDs for all photons, a threshold was obtained using Otsu’s method [24,48,49,50]. Based on the sparse distribution of noise photons, we identified photons with RDs greater than the threshold as noise. Considering that noise densities may vary over segments, the photons were divided into 1000 m segments to mitigate this effect, and Otsu’s method was applied independently within each segment.
3.3. Edge Searching and Surface Lines Constraints
After the processing of histogram-based successive denoising and the terrain-adaptive OPTICS, most noise photons were removed. The remaining photons were considered to comprise only signal photons and edge noise. For the noise shown in Figure 7, the number of neighboring points for photon p is significantly lower in the OFD than in the VOFD. Based on these characteristics, a signal can be distinguished from the edge noise.
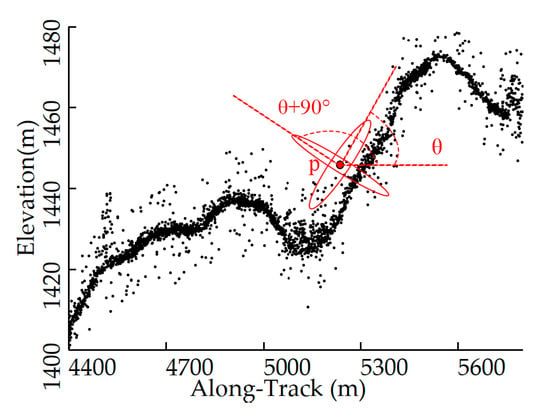
Figure 7.
Schematic diagram: the principle of edge searching.
Within a local window, noise photons may exist in the elevation percentile ranges of 0–25% and 75–100%, which were selected to define potential noise across each along-track segment [25]. Next, iteration through these potential noise points was conducted. For each photon, we searched along and perpendicular to the OFD and compared the point counts in both directions. When the number in the VOFD is greater than that in the OFD, it is labeled noise. Otherwise, it is corrected to be signal. After this process, the remaining photons were all considered signals. However, the laser pulse may be reflected by branches and leaves, decreasing the number of photons penetrating the ground. Consequently, the understory points exhibit relatively sparse distribution and may be incorrectly clustered as noise. To preserve these photons, the highest and lowest points per segment were fitted after the previous process, the approximate DTM and DSM were fitted, and the photons with elevations between the fitted models were reserved. Both Section 3.2 and Section 3.3 contain the fine-denoising process.
3.4. Accuracy Assessment
In this paper, the performance of the algorithm on the ATL03 data is evaluated both qualitatively and quantitatively. For quantitative assessments, recall of recall (R), precision (P), and the value of F1 score (F) are adopted. In addition, the recall rate of signal (Rs) and removal rate of noise (Rn) are used to evaluate the performance of preprocessing. These accuracy metrics can be calculated by Equation (7).
As Table 2 shows, TP represents photons with true and predicted labels as signals; FN denotes photons with a true label as a signal but the predicted as a noise; FP implies photons with a true label as a noise but a predicted one as a signal; TN indicates photons with both true and predicted labels as noise.

Table 2.
Confusion metrics.
For better qualitative assessment, type 1 error and type 2 error indicators are used to qualitatively evaluate the performance of different algorithms [51]. The type 1 error is used to indicate when noise photons are misclassified as signal photons, and the type 2 error indicator is used to indicate when signal photons are misclassified as noise photons.
4. Experiment Results and Analysis
4.1. Coarse Denoising: Histogram-Based Successive Denoising
The results of the four selected datasets subjected to histogram-based successive coarse denoising are shown in Figure 8. The distant noise and most sparse noise have been removed and the signal photons have been restricted to a range that is as accurate as possible, but the residual noise still needs further fine-tuning. Considering the purpose and nature of coarse denoising, for quantitative evaluation, we only compute the recall rate of signal and noise, which is shown in Table 3. As Table 3 shows, in four datasets, the Rs values of the proposed coarse denoising method all reach 1 and the Rn values are above 0.8, indicating that the method removes most of the noise photons and preserves all the signals.
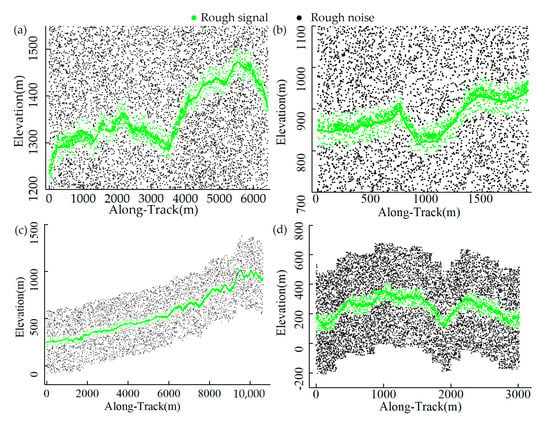
Figure 8.
Results of the histogram-based successive denoising: (a) Data 1, (b) Data 2, (c) Data 3, and (d) Data 4.

Table 3.
Evaluation of histogram-based successive denoising.
4.2. Fine Denoising: Terrain-Adaptive OPTICS and Edge Searching
Fine denoising assignment, which consists of adaptive OPTICS, edge searching, and surface constraints, was utilized to remove the noise distributed around the signal, and the detailed results are shown in Figure 9.
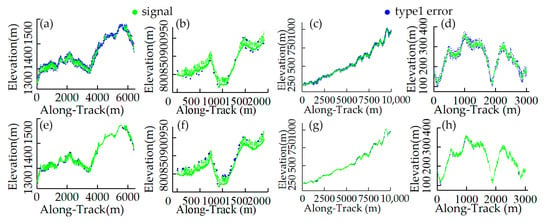
Figure 9.
Results of fine denoising. (a–d) are the denoising results of adaptive OPTICS, and (e–h) are the denoising results after edge searching.
From Figure 9a–d, adaptive OPTICS correctly detected almost all of the sparse noise and adapted well to the four datasets with different slopes. However, there were still some noise photons adjacent to the signal, especially in regions covered by sparse vegetation. Edge searching was applied to characterize the difference between edge noise and the spatial distribution of the signal, thereby allowing the removal of the noise, as shown in Figure 9e–h. The misclassified edge noise photons were almost identified by edge searching, and the change in accuracy metrics is shown in the last two columns of Table 4. From Table 4, it is clear that for terrain-adaptive OPTICS, the F values for four datasets are all above 0.94, but the p values for Data 1 and Data 4 are a little low due to the effect of the large amount of misclassified noise photons. After edge searching, the F values and p values of the four regions are improved to varying degrees due to the removal of most of the residual noise, although there is a slight decrease in the R values. For sparse noise photons, OPTICS does well in removing them, but it tends to fail in identifying the edge noise recognized by edge searching, which is consistent with the results of the visual analysis above.

Table 4.
Performance evaluation of ATL08, LDS, horizontal OPTICS, and MTANR.
4.3. Comparative Analysis of Several Methods in Typical Areas
To better evaluate the performance of our algorithm, raw photons were also processed by ATL08, LDS, and the horizontal ellipse-based OPTICS [24] on the selected datasets. Figure 10 depicts the details of point clouds in Baishan based on different methods. In three typical situations, ATL08 and the MTANR demonstrate good denoising outputs, removing most of the noise photons while maximally retaining the signal photons. Although most signal photons are preserved through LDS, this method fails to identify the edge noise (e.g., type 1 error in Figure 10). The horizontal OPTICS is less affected by edge noise than the LDS. However, lots of sparse signal photons under the canopy (e.g., type 2 error in Figure 10a,b) are misidentified as noise, causing discontinuities in the ground surface. Apparently, these errors will greatly influence the extracted canopy height and DEM in this situation.
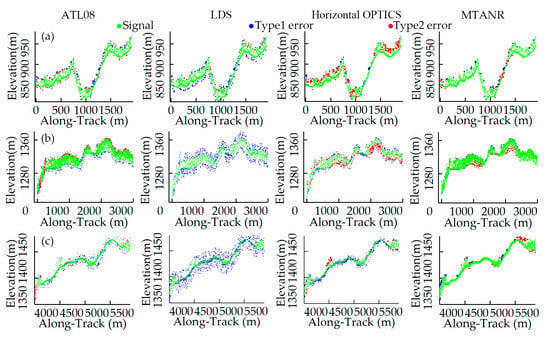
Figure 10.
Zoom-in view of denoising results using different methods in Data 1 and Data 2: (a) areas covered by asymmetric vegetation, (b) areas covered by tall trees, and (c) low fraction vegetation coverage.
The reason for this phenomenon is that the vegetation cover is uneven under the influence of slopes. Flat areas with high fractional vegetation coverage are endowed with tall trees, and the vegetation in rugged areas is short and sparse. For photons beneath trees, canopy occlusion exerts varying effects depending on vegetation density. In sparse vegetation zones, the canopy has less blockage of laser pulses, leading to denser understory points. By contrast, lush vegetation areas with a denser canopy display sparser understory returns. These sparse photons differ slightly from noise. In rugged terrains, the horizontal elliptical search window cannot effectively leverage the terrain information, misclassifying the sparse ground photons. Based on a terrain-adaptive ellipse search window, the MTANR acclimates to the altered terrain, improving the extraction of signal photons in different slopes. Additionally, the edge searching and strengthened constraints for surface lines further preserve understory sparse photons and amplify the variability between photons and edge noise. From Table 4, the MTANR outperforms the other methods pronouncedly in terms of p and F in the experimental sites, which is consistent with Figure 10. Although LDS has the highest R values, it exhibits a poor ability to distinguish edge noise. To summarize, in a rugged and uneven vegetated area, our method is more suitable for signal extraction than the other three methods.
Figure 11 presents a detailed comparison of denoising outputs from compared methods over mountain peaks, terrain with abrupt changes, and steep slopes. As shown in Figure 11a,b, ATL08 typically retains signal photons and misses sparse signals (type 2 error) across terrain discontinuities and steep slopes covered by short vegetation, resulting in discontinuous ground photons. Due to the limitations of horizontal ellipse search space, sparse signals in the two steep regions and abrupt changes in the terrain are misclassified as noise (e.g., type 2 error of Horizontal OPTICS in Figure 11) by horizontal OPTICS. LDS preserves more photons in this test region than ATL08 and horizontal OPTICS, avoiding sparse signal loss, but more edge noise photons (e.g., type 1 error in Figure 11) are also preserved. This phenomenon can be primarily attributed to two factors. For one thing, even with a high-frequency micro-pulse laser detecting height values at a resolution of 0.7 m, ICESat-2 only records 0–4 photons from a reflected laser pulse over vegetation. For another, ICESat-2 has consistent pulse frequencies and sampling rates over surfaces with different slopes. For the same distance along the track, there are fewer returning photons in steep terrain than in flat areas with the slopes increasing [47,52]. It is necessary to expand the search domain to contain more photons for canopy detection. Therefore, there is a reasonable chance that the signals are inadequately characterized by the fixed search domain [53], accounting for the interrupted signal segments in the ATL08 and horizontal OPTICS denoising results, as shown in Figure 11a. According to the quantitative metrics in Table 4, LDS outperforms ATL08 in the R values, but its p values are significantly lower than the other methods. In both areas, the MTANR balances the R and p values and exhibits higher F values than the prior methods. Overall, in areas with steep slopes and sparse vegetation cover, this method exerts the best denoising performance among these approaches and is advantageous in detecting abrupt terrain changes and edge noise.
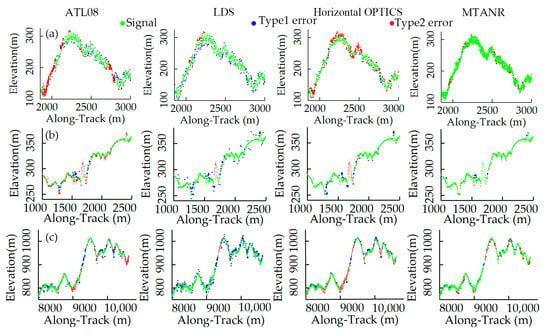
Figure 11.
Zoom-in view of denoising results from different methods in Data 3 and Data 4: (a) steep areas, (b) terrain with abrupt changes, and (c) mountaintop.
4.4. Algorithm Robustness Analysis
To explore how the parameter MinPts affects MTANR’s performance, a series of MinPts were set in each dataset, and the F value in every input parameter is shown in Figure 12. As depicted in Figure 12, with the MinPts increasing from 3 to 15 at a step length of 1, it remains at an overall high level, although it fluctuates a little. For OPTICS-derived algorithms, though the CD values and RD values of photons may vary with different parameters, they change at roughly similar magnitudes, so there is no apparent variation in the order of photons in the RD list [24]. Therefore, the denoising results perform stably under different conditions.
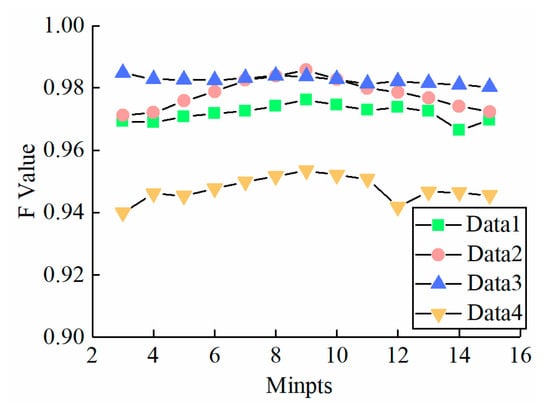
Figure 12.
F value of MTANR for different input parameters of each test data.
4.5. Challenge under Extremely Dense Vegetation
From the experiment, we found that the proposed MTANR may misidentify near-ground photons for noise in regions with extremely dense canopy cover (e.g., the red point in Figure 13), which could lead to errors in ground elevation extraction. This is primarily caused by two factors. First, ATLAS is unable to penetrate dense canopies due to limitations in its detection mechanism and laser intensity [41]. As fraction vegetation coverage (FVC) increases, more photons will be reflected from the canopy, resulting in a reduction in the amount of ground-returned photons [16]. Secondly, density-based denoising methods remove noise by assuming that the spatial distribution of the signal is dense, whereas the noise distribution is relatively sparse. In this instance, the density of the sparse ground photons is comparable to that of the noise, making them readily misclassified [16,35,54]. Therefore, density clustering may not be appropriate in locations with dense canopies. Possible solutions [35,55,56] might be correcting and compensating the missing ground photons based on local ground continuity after edge searching.
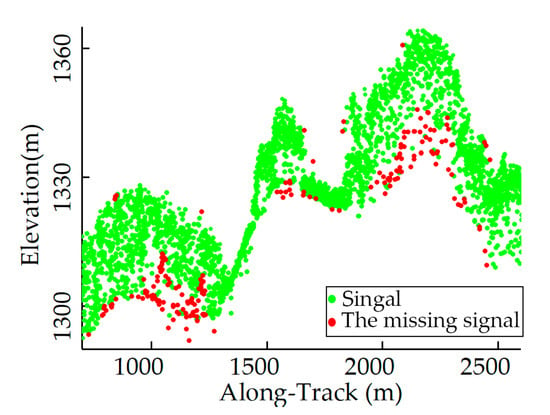
Figure 13.
The missing signals under extremely dense vegetation.
5. Conclusions
This research presents a terrain-adaptive multilevel noise removal method (MTANR) with a coarse-to-fine denoising strategy. Preprocessing is achieved through histogram-based successive denoising to realize a coarse noise removal and provide an accurate range of signals to the maximum. In fine denoising, terrain-adaptive OPTICS and Otsu’s method were used to remove most of the sparse noise photons and create a near-noise-free environment for edge noise detection. Finally, edge searching was used to identify edge noise in residual photon clusters, and the signals were further maintained.
Based on the testing of experimental areas, we have drawn the following conclusions:
- (1)
- The rotatably elliptical search domain can adapt to complex terrains and effectively utilize slope information. Compared to typical algorithms with fixed search domains, the proposed MTANR robustly retains sparse signals in steep areas and terrains with abrupt changes.
- (2)
- Edge searching improves the ability to distinguish between signal and edge noise, which effectively improves denoising performance and minimizes the effects of edge noise in ICESat2 data applications like canopy height inversion.
In the future, we will investigate the ground-returned photon detection approach and denoising performance in dense vegetation.
Author Contributions
Conceptualization, L.W., Y.Z. and X.Z.; methodology, L.W., Y.Z. and X.Z.; validation, L.W.; formal analysis, L.W., Y.Z. and F.C.; resources, L.W., X.Z. and S.D.; data curation, L.W. and T.S.; writing—original draft preparation, L.W.; writing—review and editing, L.W., Y.Z. and X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
Access Funding provided by Jilin University. This research was funded by the National Natural Science Foundation of China (Grant Nos. 42077242, 41820104001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The open data used in this article (access to the data is listed in the article) and the ICESat-2 data can be obtained by accessing the the Earthdata website (https://search.earthdata.nasa.gov, accessed on 4 March 2023), and the airborne data can be obtained by accessing the Toitū Te Whenua Land Information New Zealand website (https://data.linz.govt.nz, accessed on 18 March 2023).
Acknowledgments
Special thanks to NSIDC for providing the datasets for free.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
The details of parameters used for matching ATL03 and ATL08.
Table A1.
The details of parameters used for matching ATL03 and ATL08.
| Datasets | Parameters | Descriptions [17,18] |
|---|---|---|
| ATL03 | signal_conf_ph | Confidence level associated with each photon event selected as the signal. (0 = noise, 1 = added to allow for buffering but the algorithm classifies it as background, 2 = low, 3 = med, and 4 = high.) |
| segment_id | A 7-digit number identifies the along-track geolocation segment number. | |
| ATL08 | classed_pc_flag | Land Vegetation ATBD classification flag for each photon as either noise, ground, canopy, or top of canopy. (0 = noise, 1 = ground, 2 = canopy, and 3 = top of canopy.) |
| classed_pc_indx | Index (1-based) of the ATL08 classified signal photon from the start of the ATL03 geolocation segment specified on the ATL08 product at the photon rate in the corresponding parameter, ph_segment_id. This index traces back to the specific photon within a 20 m segment_id on ATL03. | |
| ph_segment_id | Segment ID of photons tracing back to specific 20 m segment_id on ATL03. |
References
- Lin, X.; Shang, R.; Chen, J.M.; Zhao, G.; Zhang, X.; Huang, Y.; Yu, G.; He, N.; Xu, L.; Jiao, W. High-resolution forest age mapping based on forest height maps derived from GEDI and ICESat-2 space-borne lidar data. Agric. For. Meteorol. 2023, 339, 109592. [Google Scholar] [CrossRef]
- Akturk, E.; Popescu, S.C.C.; Malambo, L. ICESat-2 for Canopy Cover Estimation at Large-Scale on a Cloud-Based Platform. Sensors 2023, 23, 3394. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Zhu, J.; Fu, H. A Rapid and Easy Way for National Forest Heights Retrieval in China Using ICESat-2/ATL08 in 2019. Forests 2023, 14, 1270. [Google Scholar] [CrossRef]
- Swatantran, A.; Tang, H.; Barrett, T.; DeCola, P.; Dubayah, R. Rapid, High-Resolution Forest Structure and Terrain Mapping over Large Areas using Single Photon Lidar. Sci. Rep. 2016, 6, 28277. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhu, J.; Fu, H.; Zhou, C.; Zuo, T. Evaluation of the Vertical Accuracy of Open Global DEMs over Steep Terrain Regions Using ICESat Data: A Case Study over Hunan Province, China. Sensors 2020, 20, 4865. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Ma, Y.; Zhang, J.; Zhang, H.; Zhu, H.; Leng, Z.; Zhang, X.; Cui, A. A noise removal algorithm based on adaptive elevation difference thresholding for ICESat-2 photon-counting data. Int. J. Appl. Earth Obs. Geoinf. 2023, 117, 103207. [Google Scholar] [CrossRef]
- Zhang, G.; Ganguly, S.; Nemani, R.R.; White, M.A.; Milesi, C.; Hashimoto, H.; Wang, W.L.; Saatchi, S.; Yu, Y.F.; Myneni, R.B. Estimation of forest aboveground biomass in California using canopy height and leaf area index estimated from satellite data. Remote Sens. Environ. 2014, 151, 44–56. [Google Scholar] [CrossRef]
- Neuenschwander, A.L.; Magruder, L.A. Canopy and Terrain Height Retrievals with ICESat-2: A First Look. Remote Sens. 2019, 11, 1721. [Google Scholar] [CrossRef]
- An, Z.; Chen, P.; Tang, F.; Yang, X.; Wang, R.; Wang, Z. Evaluating the Performance of Seven Ongoing Satellite Altimetry Missions for Measuring Inland Water Levels of the Great Lakes. Sensors 2022, 22, 9718. [Google Scholar] [CrossRef]
- Jang, J.-Y.; Cho, M. Lensless Three-Dimensional Imaging under Photon-Starved Conditions. Sensors 2023, 23, 2336. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Magruder, L.; Guenther, E.; Hancock, S.; Purslow, M. Radiometric Assessment of ICESat-2 over Vegetated Surfaces. Remote Sens. 2022, 14, 787. [Google Scholar] [CrossRef]
- Jasinski, M.F.; Stoll, J.D.; Cook, W.B.; Ondrusek, M.; Stengel, E.; Brunt, K. Inland and Near-Shore Water Profiles Derived from the High-Altitude Multiple Altimeter Beam Experimental Lidar (MABEL). J. Coast. Res. 2016, 76, 44–55. [Google Scholar] [CrossRef]
- Brunt, K.M.; Neumann, T.A.; Walsh, K.M.; Markus, T. Determination of Local Slope on the Greenland Ice Sheet Using a Multibeam Photon-Counting Lidar in Preparation for the ICESat-2 Mission. IEEE Geosci. Remote Sens. Lett. 2014, 11, 935–939. [Google Scholar] [CrossRef]
- Zhu, X.X.; Nie, S.; Wang, C.; Xi, X.H.; Hu, Z.Y. A Ground Elevation and Vegetation Height Retrieval Algorithm Using Micro-Pulse Photon-Counting Lidar Data. Remote Sens. 2018, 10, 1962. [Google Scholar] [CrossRef]
- Xie, H.; Xu, Q.; Ye, D.; Jia, J.; Sun, Y.; Huang, P.; Li, M.; Liu, S.; Xie, F.; Hao, X.; et al. A Comparison and Review of Surface Detection Methods Using MBL, MABEL, and ICESat-2 Photon-Counting Laser Altimetry Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7604–7623. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K. The ATL08 land and vegetation product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K.; Jelley, B.; Robbins, J.; Markel, J.; Popescu, S.; Nelson, R.; Harding, D.; Pederson, D.; Klotz, B.; et al. Ice, Cloud, and Land Elevation Satellite-2 (ICESat-2). Algorithm Theoretical Basis Document (ATBD) for Land—Vegetation Along-Track Products ATL08, (Version 4); NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2021. [Google Scholar]
- Neuenschwander, A.; Pitts, K.; Jelley, B.; Robbins, J.; Markel, J.; Popescu, S.; Nelson, R.; Harding, D.; Pederson, D.; Klotz, B.; et al. ATLAS/ICESat-2 L3A Land and Vegetation Height, Version 5; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2021. [Google Scholar]
- Xia, S.; Wang, C.; Xi, X.; Luo, S.; Zeng, H. Point cloud filtering and tree height estimation using airborne experiment data of ICESat-2. Yaogan Xuebao/J. Remote Sens. 2014, 18, 1199–1207. [Google Scholar] [CrossRef]
- Wang, C.; Ji, M.; Wang, J.; Wen, W.; Li, T.; Sun, Y. An Improved DBSCAN Method for LiDAR Data Segmentation with Automatic Eps Estimation. Sensors 2019, 19, 172. [Google Scholar] [CrossRef]
- Wang, X.; Pan, Z.; Glennie, C. A Novel Noise Filtering Model for Photon-Counting Laser Altimeter Data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 947–951. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD’96), Oregon, Portland, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.-P.; Sander, J.J.A.S.r. OPTICS: Ordering points to identify the clustering structure. In Proceedings of the ACM SIGMOD International Conference on Management of Data (SIGMOD 1999), Philadelphia, PA, USA, 1–3 June 1999; Volume 28, pp. 49–60. [Google Scholar]
- Zhu, X.; Nie, S.; Wang, C.; Xi, X.; Wang, J.; Li, D.; Zhou, H. A Noise Removal Algorithm Based on OPTICS for Photon-Counting LiDAR Data. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1471–1475. [Google Scholar] [CrossRef]
- Gao, S.; Li, Y.; Zhu, J.; Fu, H.; Zhou, C. Retrieving Forest Canopy Height From ICESat-2 Data by an Improved DRAGANN Filtering Method and Canopy Top Photons Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 2505505. [Google Scholar] [CrossRef]
- Huang, J.; Xing, Y.; You, H.; Qin, L.; Tian, J.; Ma, J. Particle Swarm Optimization-Based Noise Filtering Algorithm for Photon Cloud Data in Forest Area. Remote Sens. 2019, 11, 980. [Google Scholar] [CrossRef]
- Zhang, G.; Lian, W.; Li, S.; Cui, H.; Jing, M.; Chen, Z. A Self-Adaptive Denoising Algorithm Based on Genetic Algorithm for Photon-Counting Lidar Data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6501405. [Google Scholar] [CrossRef]
- Li, Y.; Fu, H.; Zhu, J.; Wang, C. A Filtering Method for ICESat-2 Photon Point Cloud Data Based on Relative Neighboring Relationship and Local Weighted Distance Statistics. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1891–1895. [Google Scholar] [CrossRef]
- He, L.; Pang, Y.; Zhang, Z.; Liang, X.; Chen, B. ICESat-2 data classification and estimation of terrain height and canopy height. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103233. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, J.; Fu, H.; Gao, S.; Wang, C. Filtering Photon Cloud Data in Forested Areas Based on Elliptical Distance Parameters and Machine Learning Approach. Forests 2022, 13, 663. [Google Scholar] [CrossRef]
- Chen, B.; Pang, Y.; Li, Z.; Lu, H.; Liang, X. Photon counting LiDAR point cloud data filtering based on random forest algorithm. J. Geo-Inf. Sci. 2019, 21, 898–906. [Google Scholar] [CrossRef]
- Kui, M.; Xu, Y.; Wang, J.; Cheng, F. Research on the Adaptability of Typical Denoising Algorithms Based on ICESat-2 Data. Remote Sens. 2023, 15, 3884. [Google Scholar] [CrossRef]
- Zhang, J.; Kerekes, J. An Adaptive Density-Based Model for Extracting Surface Returns From Photon-Counting Laser Altimeter Data. IEEE Geosci. Remote Sens. Lett. 2015, 12, 726–730. [Google Scholar] [CrossRef]
- Huang, X.; Cheng, F.; Wang, J.; Duan, P.; Wang, J. Forest Canopy Height Extraction Method Based on ICESat-2/ATLAS Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5700814. [Google Scholar] [CrossRef]
- Wu, Y.; Zhao, R.; Hu, Q.; Zhang, Y.; Zhang, K. Retrieving Sub-Canopy Terrain from ICESat-2 Data Based on the RNR-DCM Filtering and Erroneous Ground Photons Correction Approach. Remote Sens. 2023, 15, 3904. [Google Scholar] [CrossRef]
- You, H.; Li, Y.; Qin, Z.; Lei, P.; Chen, J.; Shi, X. Research on Multilevel Filtering Algorithm Used for Denoising Strong and Weak Beams of Daytime Photon Cloud Data with High Background Noise. Remote Sens. 2023, 15, 4260. [Google Scholar] [CrossRef]
- Liu, A.; Cheng, X.; Chen, Z. Performance evaluation of GEDI and ICESat-2 laser altimeter data for terrain and canopy height retrievals. Remote Sens. Environ. 2021, 264, 112571. [Google Scholar] [CrossRef]
- Gibbons, A.; Neumann, T.; Hancock, D.; Harbeck, K.; Lee, J. On-Orbit Radiometric Performance on ICESat-2. Earth Space Sci. 2021, 8, e2020EA001503. [Google Scholar] [CrossRef]
- Huang, J.; Xing, Y.; Shuai, Y.; Zhu, H. A Novel Noise Filtering Evaluation Criterion of ICESat-2 Signal Photon Data in Forest Environments. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7003805. [Google Scholar] [CrossRef]
- Nan, Y.; Feng, Z.; Li, B.; Liu, E. Multiscale Fusion Signal Extraction for Spaceborne Photon-Counting Laser Altimeter in Complex and Low Signal-to-Noise Ratio Scenarios. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1000105. [Google Scholar] [CrossRef]
- Rodda, S.R.; Nidamanuri, R.R.; Fararoda, R.; Mayamanikandan, T.; Rajashekar, G. Evaluation of Height Metrics and Above-Ground Biomass Density from GEDI and ICESat-2 Over Indian Tropical Dry Forests using Airborne LiDAR Data. J. Indian Soc. Remote Sens. 2023. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, D. Improving ICESat-2-based boreal forest height estimation by a multivariate sample quality control approach. Methods Ecol. Evol. 2023, 14, 1623–1638. [Google Scholar] [CrossRef]
- Adam, M.; Urbazaev, M.; Dubois, C.; Schmullius, C. Accuracy Assessment of GEDI Terrain Elevation and Canopy Height Estimates in European Temperate Forests: Influence of Environmental and Acquisition Parameters. Remote Sens. 2020, 12, 3948. [Google Scholar] [CrossRef]
- Lahssini, K.; Baghdadi, N.; le Maire, G.; Fayad, I. Influence of GEDI Acquisition and Processing Parameters on Canopy Height Estimates over Tropical Forests. Remote Sens. 2022, 14, 6264. [Google Scholar] [CrossRef]
- Sothe, C.; Gonsamo, A.; Lourenco, R.B.; Kurz, W.A.; Snider, J. Spatially Continuous Mapping of Forest Canopy Height in Canada by Combining GEDI and ICESat-2 with PALSAR and Sentinel. Remote Sens. 2022, 14, 5158. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Xi, X.; Luo, S.; Li, G.; Tian, J.; Wang, H. Estimating the vegetation canopy height using micro-pulse photon-counting LiDAR data. Opt. Express 2018, 26, A520–A540. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Ye, D.; Xu, Q.; Sun, Y.; Huang, P.; Tong, X.; Guo, Y.; Liu, X.; Liu, S. A Density-Based Adaptive Ground and Canopy Detecting Method for ICESat-2 Photon-Counting Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4411813. [Google Scholar] [CrossRef]
- Barros, W.K.P.; Dias, L.A.; Fernandes, M.A.C. Fully Parallel Implementation of Otsu Automatic Image Thresholding Algorithm on FPGA. Sensors 2021, 21, 4151. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Fu, H.; Zhu, J.; Li, Y.; Wang, C. An Elliptical Distance Based Photon Point Cloud Filtering Method in Forest Area. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6504705. [Google Scholar] [CrossRef]
- Chen, X.; Li, J.; Huang, S.; Cui, H.; Liu, P.; Sun, Q. An Automatic Concrete Crack-Detection Method Fusing Point Clouds and Images Based on Improved Otsu’s Algorithm. Sensors 2021, 21, 1581. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Fu, H.; Zhu, J.; Wang, L.; Zhao, R.; Wang, C. A Photon Cloud Filtering Method in Forested Areas Considering the Density Difference Between Canopy Photons and Ground Photons. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4403114. [Google Scholar] [CrossRef]
- Shuaitai, Z.; Guoyuan, L.; Xiaoqing, Z.; Jiaqi, Y.; Jinquan, G.; Xinming, T. Single photon point cloud denoising algorithm based on multi-features adaptive. Infrared Laser Eng. 2022, 51, 20210949. [Google Scholar] [CrossRef]
- Malambo, L.; Popescu, S.C. Assessing the agreement of ICESat-2 terrain and canopy height with airborne lidar over US ecozones. Remote Sens. Environ. 2021, 266, 112711. [Google Scholar] [CrossRef]
- Dong, J.; Ni, W.; Zhang, Z.; Sun, G. Performance of ICESat-2 ATL08 product on the estimation of forest height by referencing to small footprint LiDAR data. Natl. Remote Sens. Bull. 2021, 25, 1294–1307. [Google Scholar] [CrossRef]
- Tian, X.; Shan, J. Detection of Signal and Ground Photons From ICESat-2 ATL03 Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5700314. [Google Scholar] [CrossRef]
- Li, B.; Xie, H.; Tong, X.; Liu, S.; Xu, Q.; Sun, Y. Extracting accurate terrain in vegetated areas from ICESat-2 data. Int. J. Appl. Earth Obs. Geoinf. 2023, 117, 103200. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).