Real Aperture Radar Super-Resolution Imaging for Sea Surface Monitoring Based on a Hybrid Model
Abstract
:1. Introduction
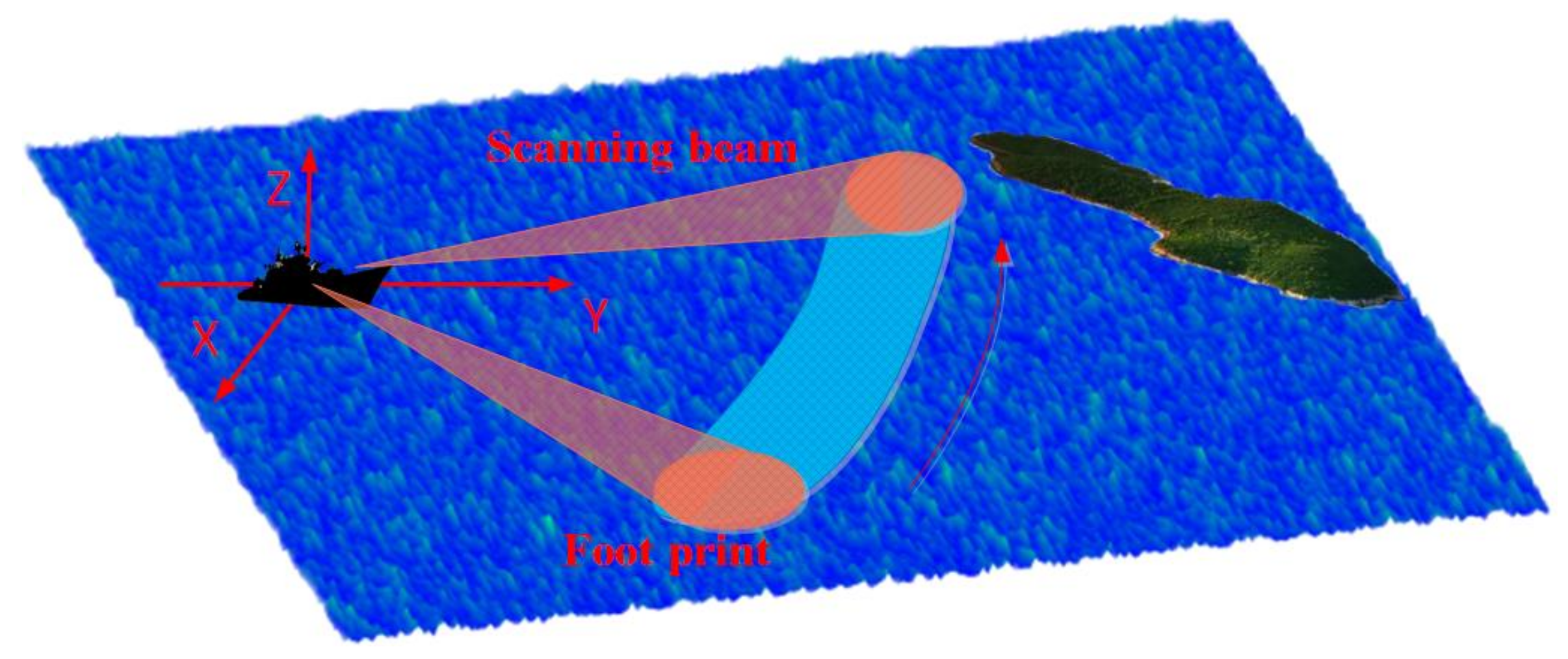
2. Establishment of Echo Model for RASR
3. Methodology
3.1. Likelihood Function Based on the New Observation Model
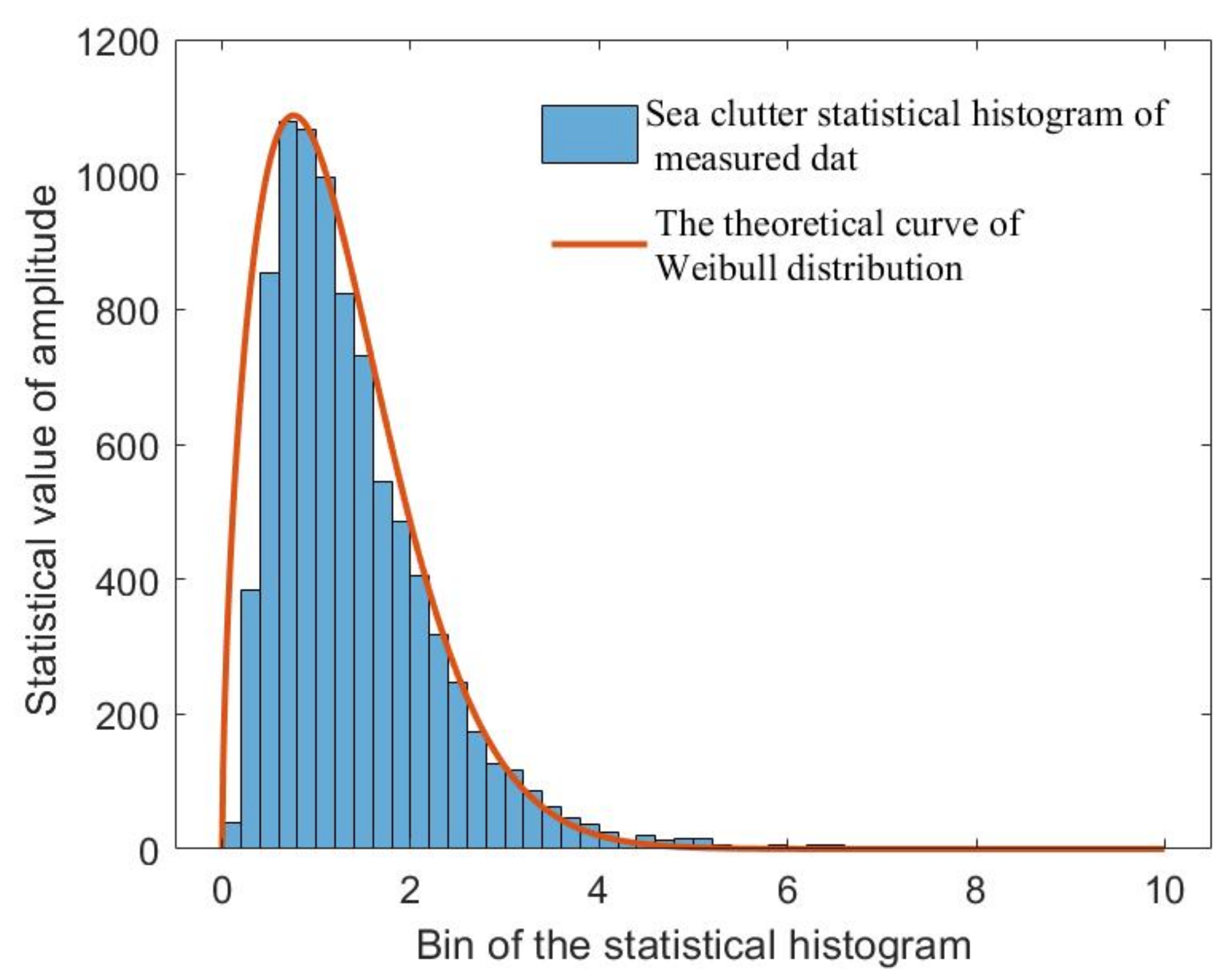
3.2. Target Prior Information
3.3. Solution to the Objective Function
| Algorithm 1: The implementation steps of the proposed hybrid-model method. |
Initialization: Estimate noise variance and determine the regularization parameters and Estimate shape , scale parameters of clutter Step 1: Initialize acceleration step size: Give to the initial iterative matrix and prediction matrix Step k ( ): Repeat j = 2 : M − 1 Extract the j-th distance unit data from Calculate the next iterative value using the predicted result by iteration formula Until (j = M − 1) Update the acceleration step size Update the prediction matrix Until (convergence) Export the final image |
4. Numerical Results
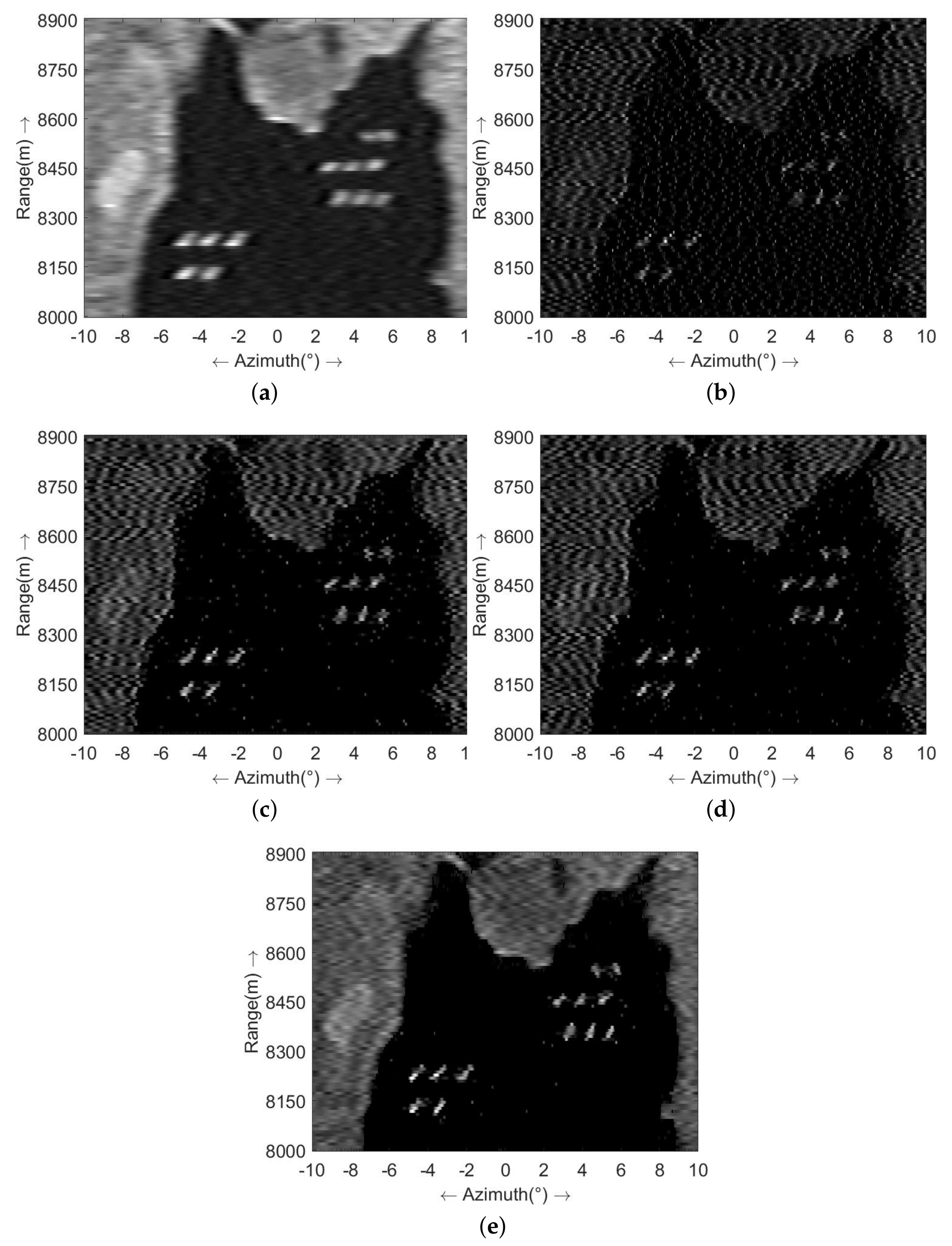
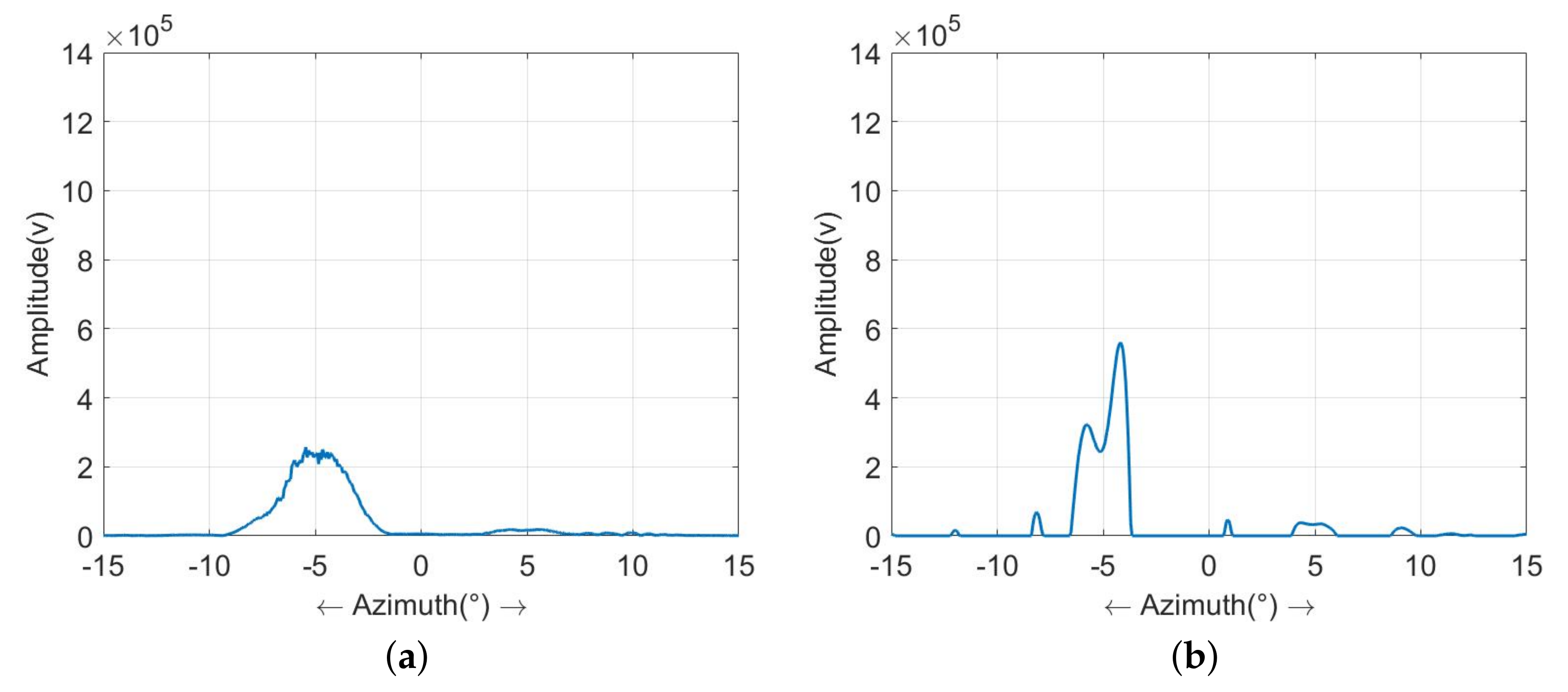
4.1. Simulation Experiment
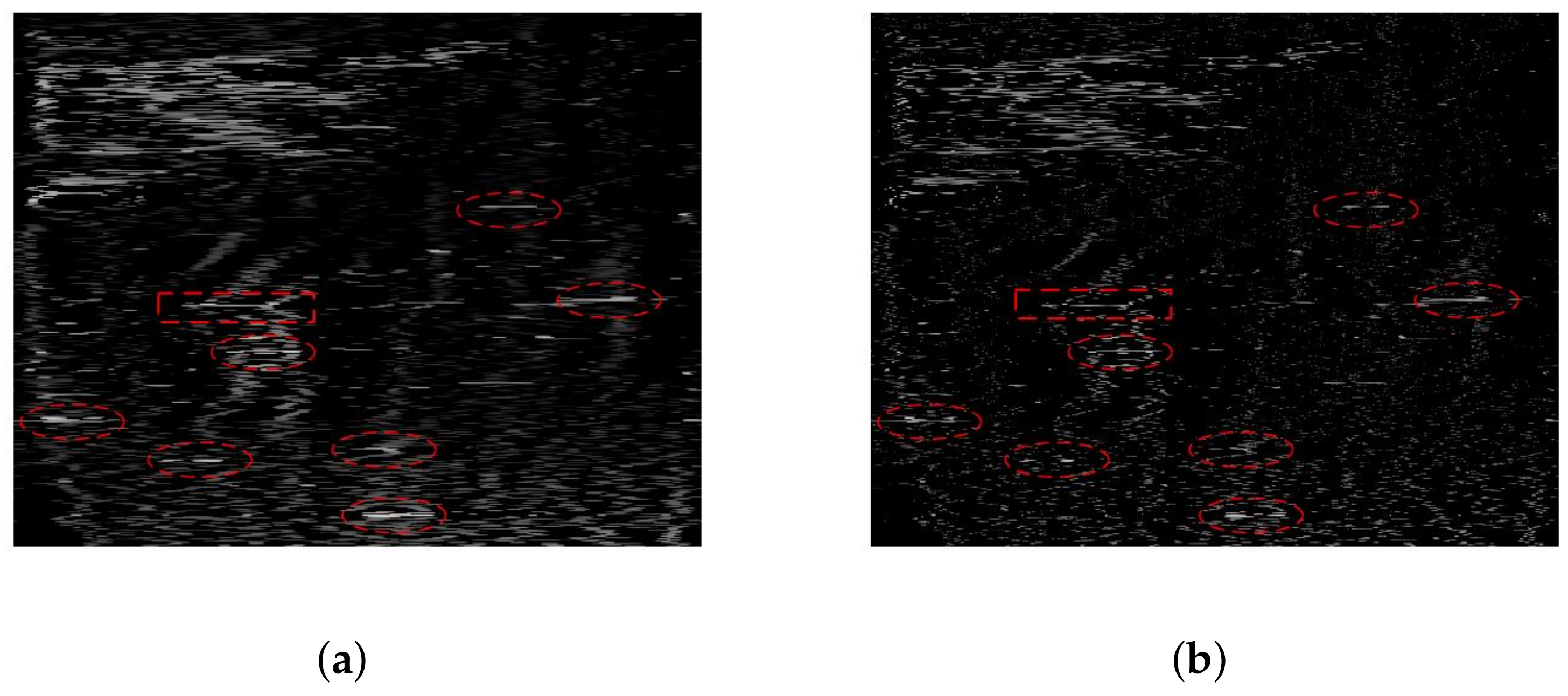
4.2. Real Data Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hauser, D.; Soussi, E.; Thouvenot, E.; Rey, L. SWIMSAT: A real-aperture radar to measure directional spectra of ocean waves from space—Main characteristics and performance simulation. J. Atmos. Ocean. Tech. 2001, 18, 421–437. [Google Scholar] [CrossRef]
- Ly, C.; Dropkin, H.; Manitius, A.Z. Extension of the music algorithm to millimeter-wave (mmw) real-beam radar scanning antennas. In Proceedings of the Radar Sensor Technology and Data Visualization, Orlando, FL, USA, 30 July 2002; pp. 96–107. [Google Scholar]
- Chen, L.; Jiang, X.; Huang, P.; Zhang, Y.; Liu, X. Efficient nonconvex regularization for azimuth resolution enhancement of real beam scanning radar. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; pp. 692–695. [Google Scholar]
- Sadjadi, F. Radar beam sharpening using an optimum FIR filter. Circ. Syst. Sig. Proces. 2000, 19, 121–129. [Google Scholar] [CrossRef]
- Richards, M.A. Iterative noncoherent angular superresolution (radar). In Proceedings of the IEEE National Radar Conference, Arbor, MI, USA, 20–21 April 1988; pp. 100–105. [Google Scholar]
- Zhang, G.; Liang, Y.; Chen, S.; Xing, M.; Li, Z. Super-resolution forward-looking imaging method for manoeuvering platform with optimised dictionary and extended sparsity adaptive matching pursuit. IET Rad. Son. Navi. 2022, 16, 912–923. [Google Scholar] [CrossRef]
- Tuo, X.; Mao, D.; Zhang, Y.; Zhang, Y.; Huang, Y.; Yang, J. Radar Forward-Looking Super-Resolution Imaging Using a Two-Step Regularization Strategy. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 4218–4231. [Google Scholar] [CrossRef]
- Huo, W.; Zhang, Q.; Zhang, Y.; Zhang, Y.; Huang, Y.; Yang, J. A superfast super-resolution method for radar forward-looking imaging. IEEE Sensors 2021, 21, 817. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Li, M.; Zuo, L.; Chen, H.; Wu, Y.; Zhuo, Z. A Computationally efficient airborne forward-looking super-Resolution imaging method based on sparse bayesian Learning. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–13. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, D.; Zhu, D.; Jiang, P. An airborne/missile-borne array radar forward-looking imaging algorithm based on super-resolution method. In Proceedings of the 10th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Shanghai, China, 14–16 October 2017; pp. 1–5. [Google Scholar]
- Chen, H.; Lu, Y.; Mu, H.; Yi, X.; Liu, J.; Wang, Z. Li, M. Knowledge-aided mono-pulse forward-looking imaging for airborne radar by exploiting the antenna pattern information. Electron. Lett. 2017, 53, 566–568. [Google Scholar] [CrossRef]
- Zhang, Y.; Mao, D.; Zhang, Q.; Zhang, Y.; Huang, Y.; Yang, J. Airborne forward-looking radar super-resolution imaging using iterative adaptive approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2044–2054. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, D.; Li, Q.; Zhang, P.; Liang, Y. FIAA-Based Super-Resolution Forward-Looking Radar Imaging Method for Maneuvering Platforms. In Proceedings of the 3rd China International SAR Symposium (CISS), Shanghai, China, 2–4 November 2022; pp. 1–5. [Google Scholar]
- Tuo, X.; Zhang, Y.; Huang, Y.; Yang, J. Fast sparse-TSVD super-resolution method of real aperture radar forward-looking imaging. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6609–6620. [Google Scholar] [CrossRef]
- Shu, Z.; Zong, Z.; Huang, L.; Huang, L. Forward-looking radar super-resolution imaging combined TSVD with l1 norm constraint. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 2559–2562. [Google Scholar]
- Egger, H.; Engl, H.W. Tikhonov regularization applied to the inverse problem of option pricing: Convergence analysis and rates. Inv. Prob. 2005, 21, 1027. [Google Scholar] [CrossRef]
- Nguyen, N.; Milanfar, P.; Golub, G. A computationally efficient superresolution image reconstruction algorithm. IEEE Trans. Image Process 2001, 10, 573–583. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.M.; Li, M.; Wang, Z.; Lu, Y.; Zhang, P.; Wu, Y. Sparse super-resolution imaging for airborne single channel forward-looking radar in expanded beam space via lp regularisation. Electron. Lett. 2015, 51, 863–865. [Google Scholar] [CrossRef]
- Han, J.; Zhang, S.; Zheng, S.; Wang, M.; Ding, H.; Yan, Q. Bias Analysis and Correction for Ill-Posed Inversion Problem with Sparsity Regularization Based on L1 Norm for Azimuth Super-Resolution of Radar Forward-Looking Imaging. Remote Sens. 2022, 14, 5792. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, Y.; Zhang, Y.; Huang, Y.; Yang, J. Airborne radar super-resolution imaging based on fast total variation method. Remote Sens. 2021, 13, 549. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, Y.; Huang, Y.; Zhang, Y.; Pei, J.; Yi, Q.; Yang, J. TV-sparse super-resolution method for radar forward-looking imaging. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6534–6549. [Google Scholar] [CrossRef]
- Chen, H.; Li, Y.; Gao, W.; Zhang, W.; Sun, H.; Guo, L.; Yu, J. Bayesian forward-looking superresolution imaging using Doppler deconvolution in expanded beam space for high-speed platform. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Tan, K.; Lu, X.; Yang, J.; Su, W.; Gu, H. A novel Bayesian super-resolution method for radar forward-looking imaging based on Markov random field model. Remote Sens. 2021, 13, 4115. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Z.; Zhang, Y.; Jin, X.; Gao, W.; Yu, J. Data-driven airborne bayesian forward-looking superresolution imaging based on generalized Gaussian distribution. Front. Signal Process. 2023, 3, 1093203. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Huang, Y.; Yang, J. A sparse Bayesian approach for forward-looking superresolution radar imaging. Sensors 2017, 17, 1353. [Google Scholar] [CrossRef]
- Tan, K.; Li, W.; Zhang, Q.; Huang, Y.; Wu, J.; Yang, J. Penalized maximum likelihood angular super-resolution method for scanning radar forward-looking imaging. Sensors 2018, 18, 912. [Google Scholar] [CrossRef]
- Li, W.; Li, M.; Zuo, L.; Chen, H.; Wu, Y. Real aperture radar forward-looking imaging based on variational Bayesian in presence of outliers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q.; Li, C.; Zhang, Y.; Huang, Y.; Yang, J. Sea-surface target angular superresolution in forward-looking radar imaging based on maximum a posteriori algorithm. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 2822–2834. [Google Scholar] [CrossRef]
- Yang, J.; Kang, Y.; Zhang, Y.; Huang, Y.; Zhang, Y. A Bayesian angular superresolution method with lognormal constraint for sea-surface target. IEEE Access 2020, 8, 13419–13428. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, J.; Tuo, X.; Yang, H.; Zhang, Y.; Huang, Y.; Yang, J. Scanning radar forward-looking superresolution imaging based on the Weibull distribution for a sea-surface target. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Li, W.; Li, M.; Zuo, L.; Sun, H.; Chen, H.; Li, Y. Forward-looking super-resolution imaging for sea-surface target with multi-prior Bayesian method. Remote Sens. 2021, 14, 26. [Google Scholar] [CrossRef]
- Li, W.; Yang, J.; Huang, Y. Keystone transform-based space-variant range migration correction for airborne forward-looking scanning radar. Electron. Lett. 2012, 48, 121–122. [Google Scholar] [CrossRef]
- Ward, K.D.; Watts, S. Use of sea clutter models in radar design and development. IET Radar Sonar Navig. 2010, 4, 146–157. [Google Scholar] [CrossRef]
- Sayama, S. Detection of target and suppression of sea and weather clutter in stormy weather by Weibull/CFAR. IEEJ Trans. Electr. Electron. Eng. 2010, 16, 180–187. [Google Scholar] [CrossRef]
- Conte, E.; De Maio, A.; Galdi, C. Statistical analysis of real clutter at different range resolutions. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 903–918. [Google Scholar] [CrossRef]
- Gleich, D. Markov random field models for non-quadratic regularization of complex SAR images. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2012, 5, 952–961. [Google Scholar] [CrossRef]
- Paul, T.; Chi, P.W.; Wu, P.M.; Wu, M.K. Computation of distribution of relaxation times by Tikhonov regularization for Li ion batteries: Usage of L-curve method. Sci. Rep. 2021, 11, 1487–1503. [Google Scholar] [CrossRef] [PubMed]
- Chambolle, A.; Dossal, C. On the convergence of the iterates of the fast iterative shrinkage/thresholding algorithm. J. Opt. Theor. Appl. 2015, 166, 968–982. [Google Scholar] [CrossRef]
- Rangaswamy, M.; Weiner, D.; Ozturk, A. Computer generation of correlated non-Gaussian radar clutter. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 106–116. [Google Scholar] [CrossRef]







| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Carrier frequency | 9.5 GHz | Velocity of the platform | 50 m/s |
| Pulse repetition frequency | 2000 Hz | Signal bandwidth | 25 MHz |
| Grazing angle | Pulse width | 40 us | |
| Near range | 8 km | Main-lobe beam width | |
| Antenna scanning area | −10∼ | Antenna scanning velocity |
| Methods | ReErr | SSIM |
|---|---|---|
| Tikhonov | 0.7132 | 0.6307 |
| Sparse-MAP | 0.8831 | 0.5260 |
| MRF-MAP | 0.7093 | 0.6608 |
| Weibull-MAP | 0.5113 | 0.7906 |
| The proposed method | 0.2761 | 0.9214 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, K.; Zhou, S.; Lu, X.; Yang, J.; Su, W.; Gu, H. Real Aperture Radar Super-Resolution Imaging for Sea Surface Monitoring Based on a Hybrid Model. Sensors 2023, 23, 9609. https://doi.org/10.3390/s23239609
Tan K, Zhou S, Lu X, Yang J, Su W, Gu H. Real Aperture Radar Super-Resolution Imaging for Sea Surface Monitoring Based on a Hybrid Model. Sensors. 2023; 23(23):9609. https://doi.org/10.3390/s23239609
Chicago/Turabian StyleTan, Ke, Shengqi Zhou, Xingyu Lu, Jianchao Yang, Weimin Su, and Hong Gu. 2023. "Real Aperture Radar Super-Resolution Imaging for Sea Surface Monitoring Based on a Hybrid Model" Sensors 23, no. 23: 9609. https://doi.org/10.3390/s23239609
APA StyleTan, K., Zhou, S., Lu, X., Yang, J., Su, W., & Gu, H. (2023). Real Aperture Radar Super-Resolution Imaging for Sea Surface Monitoring Based on a Hybrid Model. Sensors, 23(23), 9609. https://doi.org/10.3390/s23239609







