A Missing Traffic Data Imputation Method Based on a Diffusion Convolutional Neural Network–Generative Adversarial Network
Abstract
:1. Introduction
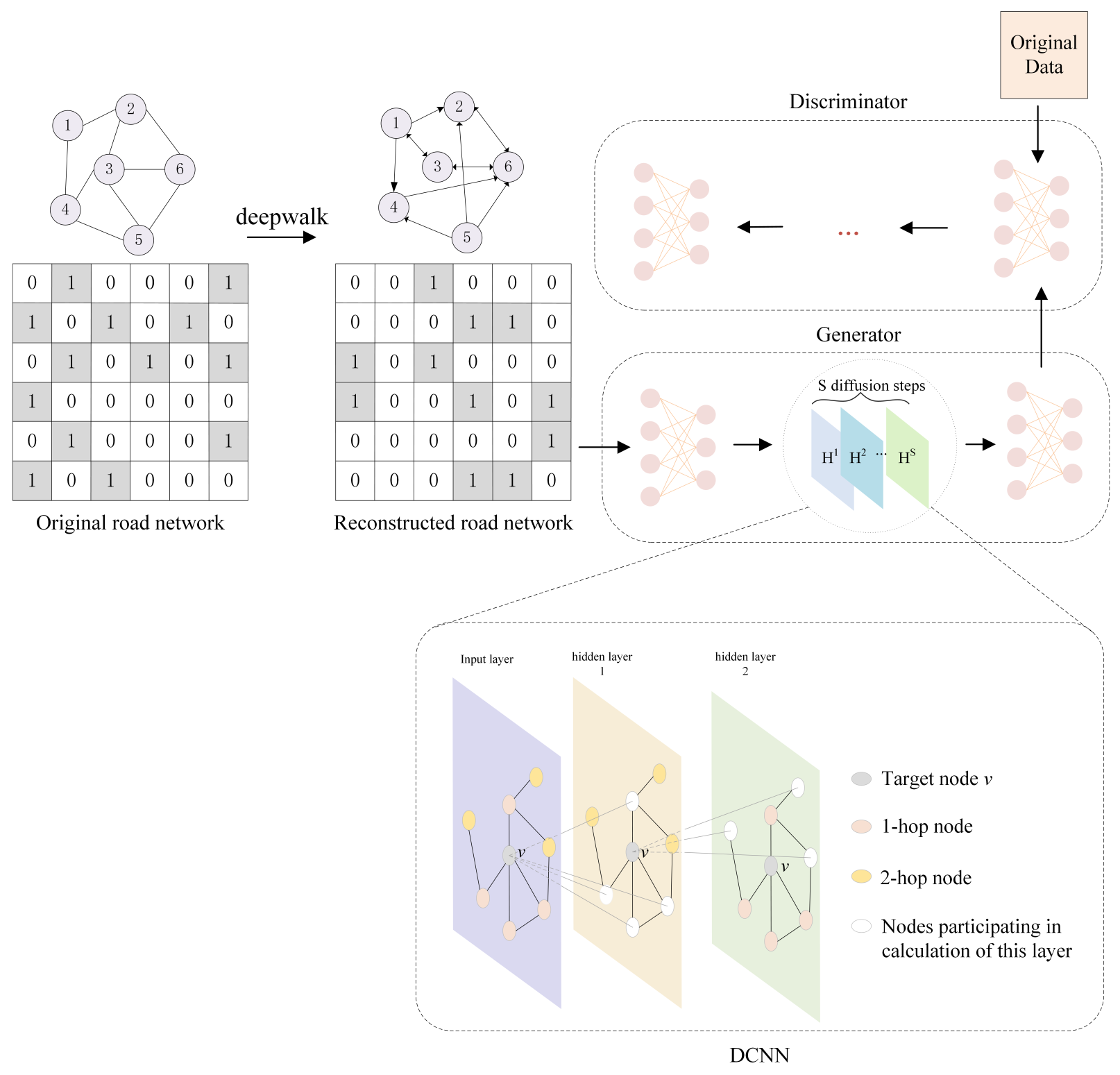
- Deepwalk is used to reconstruct the road network and obtain the node set with the highest spatial correlation of each node as the neighborhood of the node reconstructed to improve the temporal and spatial correlation.
- DCNN is used to capture the dynamic spatial characteristics and consider the forward and reverse traffic flow diffusion to further enhance adaptability and accuracy.
- During experimental analysis, two real datasets and several classical missing traffic state data imputation models are selected for comparative experiments to verify the accuracy and robustness of the proposed model.
2. Related Work
3. Methodology
3.1. Data Definition
3.2. Road Network Reconstruction
3.3. Generation of Traffic Data
4. Experimental Results
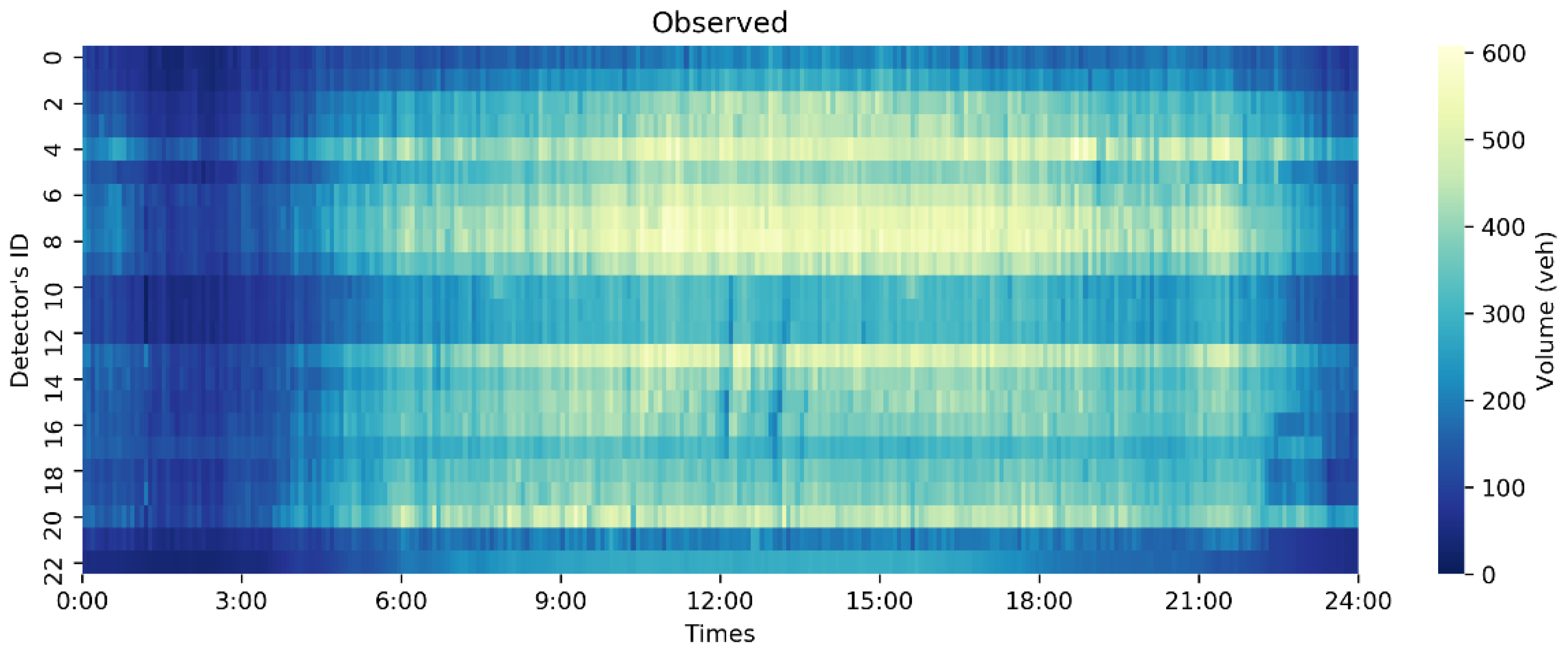
4.1. Experimental Design
4.2. Model Settings and Evaluation Criteria
4.3. Baseline Methods
4.4. The Effect of DCNN and Best Diffusion
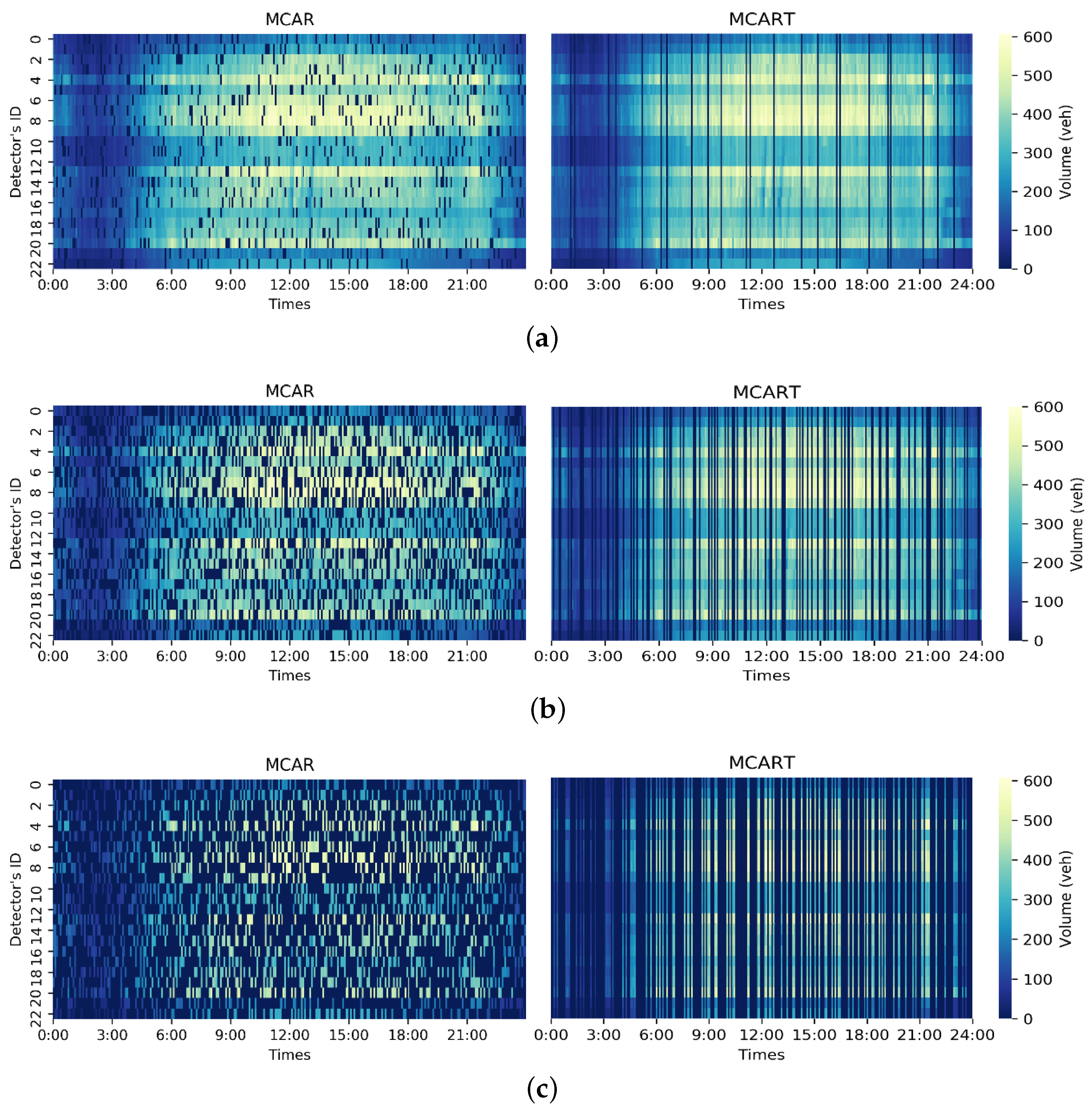
4.5. Experiment and Analysis of PEMS-BAY Dataset
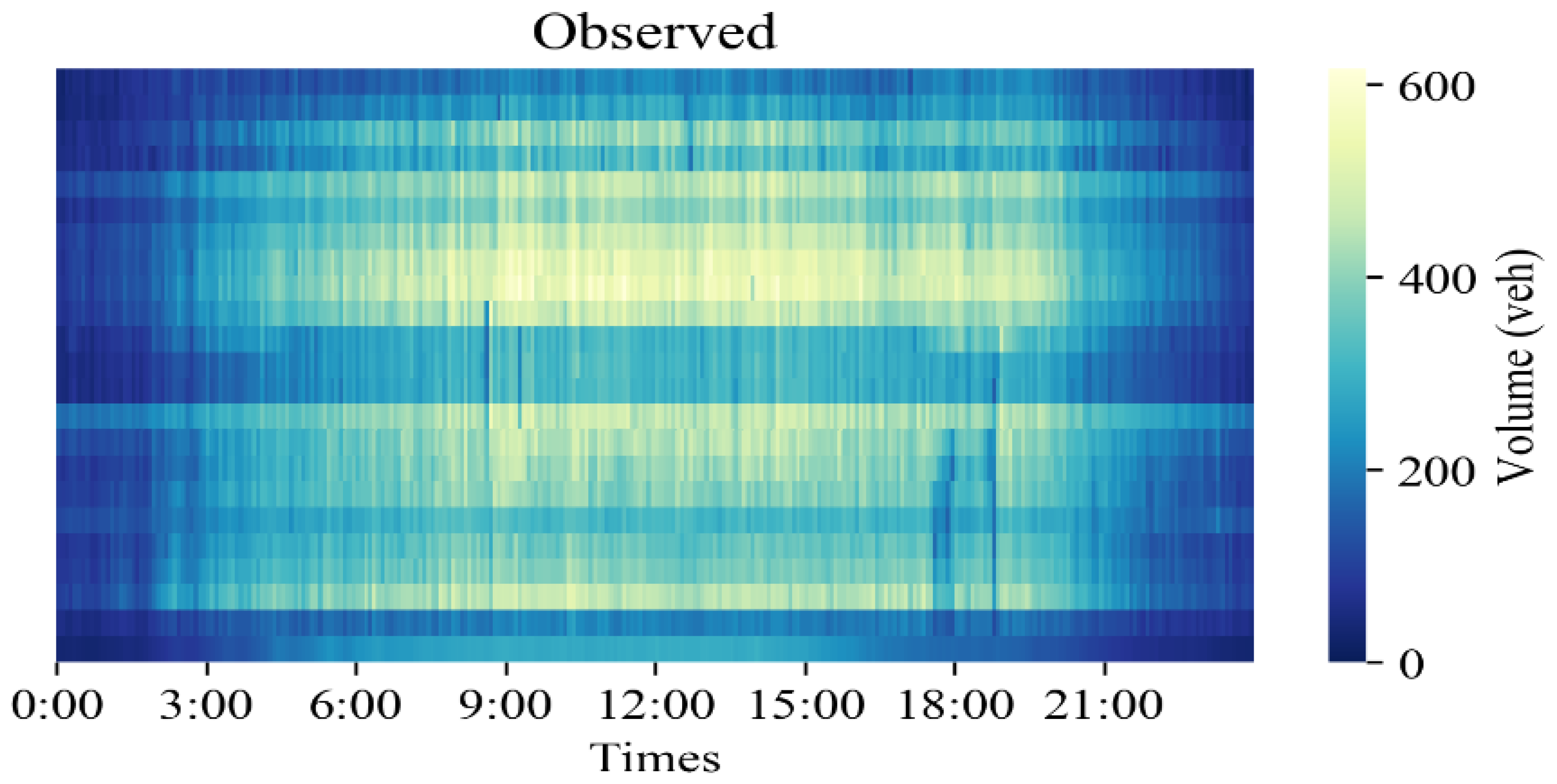
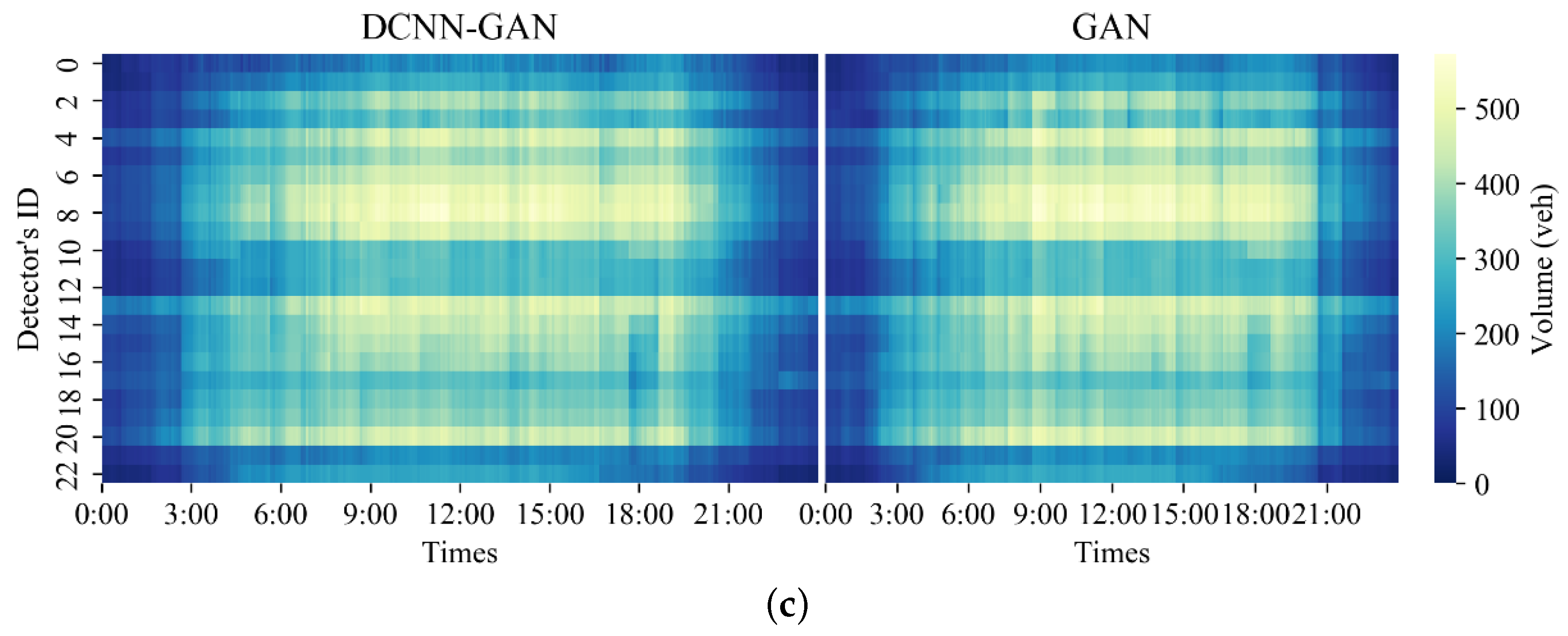
4.6. Experiment and Analysis of Seattle Dataset
4.7. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nie, T.; Qin, G.; Sun, J. Truncated tensor Schatten p-norm based approach for spatiotemporal traffic data imputation with complicated missing patterns. Transp. Res. Part C Emerg. Technol. 2022, 141, 103737. [Google Scholar] [CrossRef]
- Chen, C.; Kwon, J.; Rice, J.; Skabardonis, A.; Varaiya, P. Detecting errors and imputing missing data for single-loop surveillance systems. Transp. Res. Rec. 2003, 1855, 160–167. [Google Scholar] [CrossRef]
- Li, L.; Zhang, J.; Wang, Y.; Ran, B. Missing value imputation for traffic-related time series data based on a multi-view learning method. IEEE Trans. Intell. Transp. Syst. 2018, 20, 2933–2943. [Google Scholar] [CrossRef]
- Liang, Y.; Zhao, Z.; Sun, L. Memory-augmented dynamic graph convolution networks for traffic data imputation with diverse missing patterns. Transp. Res. Part C Emerg. Technol. 2022, 143, 103826. [Google Scholar] [CrossRef]
- Little, R.J.; Rubin, D.B. Statistical Analysis with Missing Data; John Wiley & Sons: Hoboken, NJ, USA, 2019; Volume 793. [Google Scholar]
- Shang, Q.; Yang, Z.; Gao, S.; Tan, D. An imputation method for missing traffic data based on FCM optimized by PSO-SVR. J. Adv. Transp. 2018, 2018, 2935248. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Li, Z. Efficient missing data imputing for traffic flow by considering temporal and spatial dependence. Transp. Res. Part C Emerg. Technol. 2013, 34, 108–120. [Google Scholar] [CrossRef]
- Tan, H.; Feng, G.; Feng, J.; Wang, W.; Zhang, Y.J.; Li, F. A tensor-based method for missing traffic data completion. Transp. Res. Part C Emerg. Technol. 2013, 28, 15–27. [Google Scholar] [CrossRef]
- Sharma, S.; Lingras, P.; Zhong, M. Effect of missing value imputations on traffic parameters estimations from permanent traffic counts. Transp. Res. Board 2003, 1836, 132–142. [Google Scholar]
- Julie, M.D.; Kannan, B. Attribute reduction and missing value imputing with ANN: Prediction of learning disabilities. Neural Comput. Appl. 2012, 21, 1757–1763. [Google Scholar] [CrossRef]
- Raghunathan, T.E.; Lepkowski, J.M.; Van Hoewyk, J.; Solenberger, P. A multivariate technique for multiply imputing missing values using a sequence of regression models. Surv. Methodol. 2001, 27, 85–96. [Google Scholar]
- Luo, X.; Meng, X.; Gan, W.; Chen, Y. Traffic data imputation algorithm based on improved low-rank matrix decomposition. J. Sens. 2019, 2019, 7092713. [Google Scholar] [CrossRef]
- Xu, D.w.; Wang, Y.d.; Jia, L.m.; Zhang, G.j.; Guo, H.f. Real-time road traffic states estimation based on kernel-KNN matching of road traffic spatial characteristics. J. Cent. South Univ. 2016, 23, 2453–2464. [Google Scholar] [CrossRef]
- Yang, H.; Yang, J.; Han, L.D.; Liu, X.; Pu, L.; Chin, S.m.; Hwang, H.l. A Kriging based spatiotemporal approach for traffic volume data imputation. PLoS ONE 2018, 13, e0195957. [Google Scholar] [CrossRef]
- Audigier, V.; Husson, F.; Josse, J. Multiple imputation for continuous variables using a Bayesian principal component analysis. J. Stat. Comput. Simul. 2016, 86, 2140–2156. [Google Scholar] [CrossRef]
- Xu, D.; Peng, H.; Wei, C.; Shang, X.; Li, H. Traffic state data imputation: An efficient generating method based on the graph aggregator. IEEE Trans. Intell. Transp. Syst. 2021, 23, 13084–13093. [Google Scholar] [CrossRef]
- Bao, J.; Chen, D.; Wen, F.; Li, H.; Hua, G. CVAE-GAN: Fine-grained image generation through asymmetric training. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2745–2754. [Google Scholar]
- Xie, Q.; Huang, J.; Du, P.; Peng, M.; Nie, J.Y. Inductive Topic Variational Graph Auto-Encoder for Text Classification. In Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Online, 6–11 June 2021; pp. 4218–4227. [Google Scholar]
- Zhang, Y.; Yin, Y.; Zimmermann, R.; Wang, G.; Varadarajan, J.; Ng, S.K. An enhanced gan model for automatic satellite-to-map image conversion. IEEE Access 2020, 8, 176704–176716. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the NIPS’14: 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. Infogan: Interpretable representation learning by information maximizing generative adversarial nets. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 2180–2188. [Google Scholar]
- Shrivastava, A.; Pfister, T.; Tuzel, O.; Susskind, J.; Wang, W.; Webb, R. Learning from simulated and unsupervised images through adversarial training. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2107–2116. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Li, J.; Monroe, W.; Shi, T.; Jean, S.; Ritter, A.; Jurafsky, D. Adversarial learning for neural dialogue generation. arXiv 2017, arXiv:1701.06547. [Google Scholar]
- Zhang, K.; Jia, N.; Zheng, L.; Liu, Z. A novel generative adversarial network for estimation of trip travel time distribution with trajectory data. Transp. Res. Part C Emerg. Technol. 2019, 108, 223–244. [Google Scholar] [CrossRef]
- Xu, D.; Gao, G.; Qiu, Q.; Li, H. A car-following model considering missing data based on TransGAN networks. IEEE Trans. Intell. Veh. 2023, 1–13. [Google Scholar] [CrossRef]
- Yu, J.J.Q.; Gu, J. Real-time traffic speed estimation with graph convolutional generative autoencoder. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3940–3951. [Google Scholar] [CrossRef]
- Lin, Y.; Dai, X.; Li, L.; Wang, F.Y. Pattern sensitive prediction of traffic flow based on generative adversarial framework. IEEE Trans. Intell. Transp. Syst. 2018, 20, 2395–2400. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Xu, D.; Shang, X.; Peng, H.; Li, H. MVHGN: Multi-View Adaptive Hierarchical Spatial Graph Convolution Network Based Trajectory Prediction for Heterogeneous Traffic-Agents. IEEE Trans. Intell. Transp. Syst. 2023, 24, 6217–6226. [Google Scholar] [CrossRef]
- Xu, D.; Shang, X.; Liu, Y.; Peng, H.; Li, H. Group vehicle trajectory prediction with global spatio-temporal graph. IEEE Trans. Intell. Veh. 2022, 8, 1219–1229. [Google Scholar] [CrossRef]
- Xu, D.; Liu, P.; Li, H.; Guo, H.; Xie, Z.; Xuan, Q. Multi-View Graph Convolution Network Reinforcement Learning for CAVs Cooperative Control in Highway Mixed Traffic. IEEE Trans. Intell. Veh. 2023, 1–12. [Google Scholar] [CrossRef]
- Wang, C.; Pan, S.; Celina, P.Y.; Hu, R.; Long, G.; Zhang, C. Deep neighbor-aware embedding for node clustering in attributed graphs. Pattern Recognit. 2022, 122, 108230. [Google Scholar] [CrossRef]
- Zeb, A.; Saif, S.; Chen, J.; Haq, A.U.; Gong, Z.; Zhang, D. Complex graph convolutional network for link prediction in knowledge graphs. Expert Syst. Appl. 2022, 200, 116796. [Google Scholar] [CrossRef]
- Yang, S.; Cai, B.; Cai, T.; Song, X.; Jiang, J.; Li, B.; Li, J. Robust cross-network node classification via constrained graph mutual information. Knowl.-Based Syst. 2022, 257, 109852. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Xu, D.; Wei, C.; Peng, P.; Xuan, Q.; Guo, H. GE-GAN: A novel deep learning framework for road traffic state estimation. Transp. Res. Part C Emerg. Technol. 2020, 117, 102635. [Google Scholar] [CrossRef]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2016; pp. 855–864. [Google Scholar]
- Wang, D.; Cui, P.; Zhu, W. Structural deep network embedding. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2016; pp. 1225–1234. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 3111–3119. [Google Scholar]
- Chen, X.; He, Z.; Sun, L. A Bayesian tensor decomposition approach for spatiotemporal traffic data imputation. Transp. Res. Part C Emerg. Technol. 2019, 98, 73–84. [Google Scholar] [CrossRef]
- Duan, Y.; Lv, Y.; Liu, Y.L.; Wang, F.Y. An efficient realization of deep learning for traffic data imputation. Transp. Res. Part C Emerg. Technol. 2016, 72, 168–181. [Google Scholar] [CrossRef]

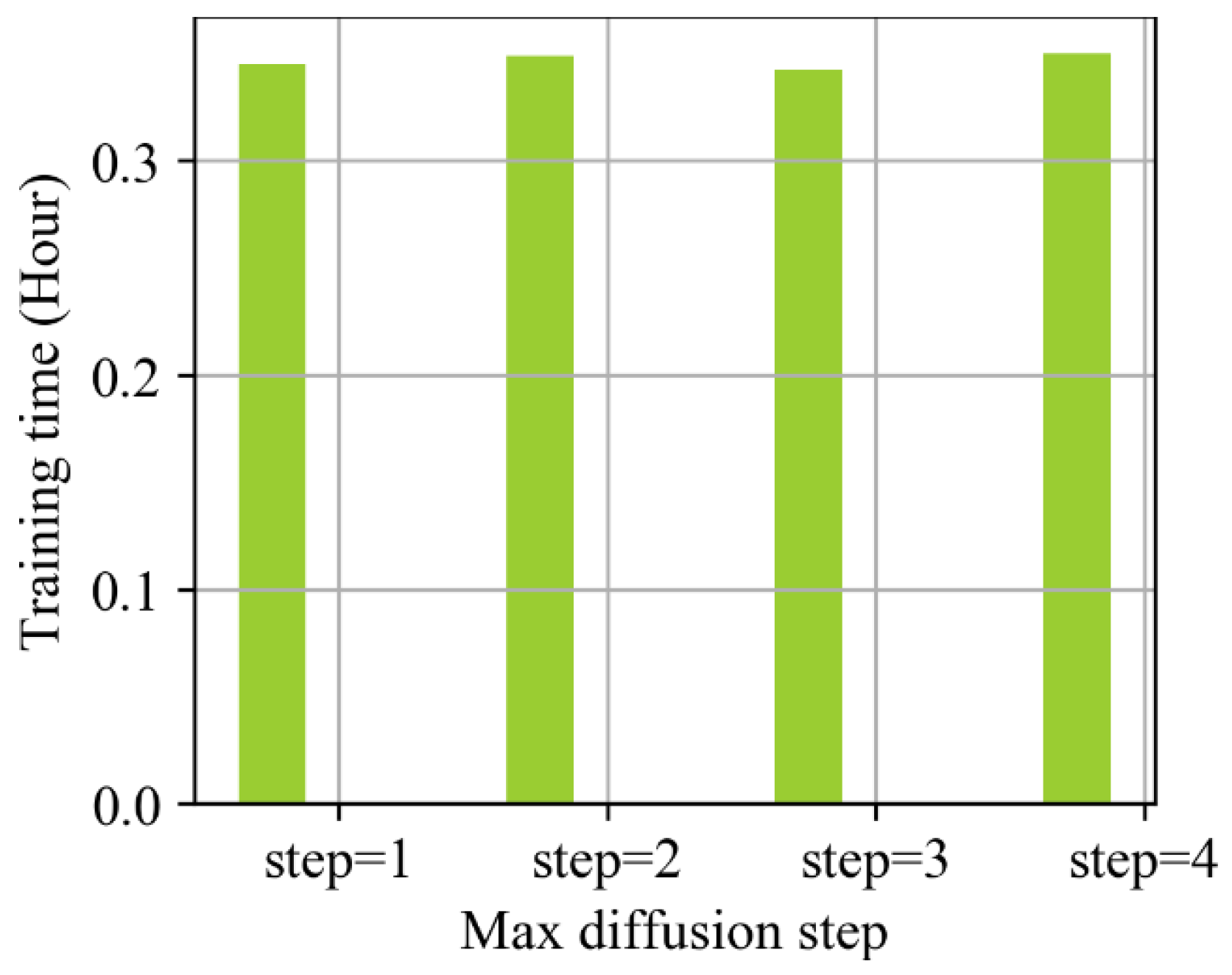





| Diffusion Convolution Step Size | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| RMSE | 25.77 | 25.25 | 25.63 | 25.38 |
| MAE | 19.23 | 19.04 | 19.18 | 19.07 |
| MAPE | 7.94 | 7.75 | 7.88 | 7.82 |
| Missing Type | MCAR | MCART (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | DSAE | GAN | BGCP | DCNN-GAN | DSAE | GAN | BGCP | DCNN-GAN | ||
| RMSE | 32.49 | 27.91 | 31.87 | 25.69 | 32.08 | 28.89 | 29.34 | 25.18 | ||
| 10 | MAE | 24.78 | 20.47 | 22.6 | 19.16 | 24.15 | 20.64 | 21.46 | 18.67 | |
| MAPE | 9.65 | 8.15 | 9.02 | 7.81 | 9.21 | 8.68 | 8.66 | 7.39 | ||
| RMSE | 34.57 | 28.12 | 35.38 | 26.19 | 33.94 | 29.82 | 29.51 | 25.21 | ||
| 20 | MAE | 25.15 | 20.88 | 24.82 | 19.74 | 24.78 | 20.97 | 21.55 | 18.67 | |
| MAPE | 9.96 | 8.82 | 9.77 | 8.12 | 9.67 | 8.85 | 8.68 | 7.69 | ||
| RMSE | 35.29 | 29.15 | 38.24 | 25.55 | 34.64 | 30.67 | 29.89 | 26.09 | ||
| 30 | MAE | 25.62 | 21.53 | 26.59 | 19.16 | 25.13 | 20.14 | 21.68 | 19.41 | |
| MAPE | 10.34 | 8.72 | 10.36 | 8.10 | 10.15 | 8.74 | 8.87 | 7.92 | ||
| RMSE | 37.28 | 30.31 | 39.35 | 26.34 | 36.67 | 31.78 | 39.57 | 29.17 | ||
| Missing rate (%) | 40 | MAE | 26.67 | 22.18 | 28.27 | 19.4 | 25.82 | 22.33 | 22.39 | 21.16 |
| MAPE | 10.85 | 9.28 | 11.09 | 8.21 | 10.63 | 9.48 | 9.34 | 8.63 | ||
| RMSE | 38.32 | 31.13 | 42.32 | 30.96 | 37.24 | 31.87 | 30.77 | 28.71 | ||
| 50 | MAE | 27.29 | 20.07 | 30.59 | 21.31 | 26.45 | 22.29 | 22.96 | 21.37 | |
| MAPE | 11.24 | 8.43 | 11.89 | 8.74 | 10.96 | 9.44 | 9.75 | 8.79 | ||
| RMSE | 39.56 | 32.84 | 45.13 | 31.11 | 38.42 | 32.74 | 31.52 | 30.23 | ||
| 60 | MAE | 27.86 | 21.96 | 32.37 | 21.33 | 27.53 | 23.31 | 23.58 | 22.33 | |
| MAPE | 11.59 | 9.44 | 12.61 | 9.17 | 11.25 | 10.28 | 10.55 | 9.19 | ||
| RMSE | 41.38 | 47.08 | 47.65 | 44.70 | 39.74 | 34.02 | 32.17 | 30.88 | ||
| 70 | MAE | 28.43 | 25.93 | 34.12 | 25.74 | 28.19 | 24.04 | 24.27 | 22.85 | |
| MAPE | 12.16 | 11.24 | 13.32 | 10.84 | 11.82 | 11.54 | 10.83 | 9.18 |
| Missing Type | MCAR | MCART (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | DSAE | GAN | BGCP | DCNN-GAN | DSAE | GAN | BGCP | DCNN-GAN | ||
| RMSE | 5.09 | 4.28 | 4.70 | 3.32 | 5.72 | 4.15 | 4.76 | 3.12 | ||
| 10 | MAE | 3.94 | 2.97 | 3.09 | 2.19 | 3.67 | 3.11 | 3.14 | 2.08 | |
| MAPE | 11.07 | 6.87 | 8.60 | 4.95 | 10.62 | 6.65 | 8.76 | 4.59 | ||
| RMSE | 6.22 | 4.38 | 4.71 | 3.39 | 5.81 | 4.28 | 4.77 | 3.22 | ||
| 20 | MAE | 4.15 | 3.05 | 3.09 | 2.22 | 3.72 | 2.97 | 3.14 | 2.17 | |
| MAPE | 11.46 | 7.09 | 8.61 | 5.12 | 10.7 | 6.58 | 8.71 | 4.75 | ||
| RMSE | 6.56 | 4.52 | 4.72 | 3.5 | 5.71 | 4.28 | 4.79 | 3.33 | ||
| 30 | MAE | 4.38 | 2.98 | 3.10 | 2.26 | 3.67 | 3.05 | 3.16 | 2.24 | |
| MAPE | 12.1 | 7.52 | 8.63 | 5.27 | 10.45 | 6.85 | 8.78 | 5.04 | ||
| RMSE | 6.96 | 4.69 | 4.74 | 3.66 | 5.75 | 4.63 | 4.77 | 3.40 | ||
| Missing rate (%) | 40 | MAE | 4.71 | 3.07 | 3.11 | 2.33 | 3.69 | 3.04 | 3.15 | 2.27 |
| MAPE | 12.98 | 7.84 | 8.67 | 5.55 | 10.68 | 7.17 | 8.74 | 5.10 | ||
| RMSE | 7.33 | 5.02 | 4.74 | 4.03 | 5.77 | 4.74 | 4.85 | 3.64 | ||
| 50 | MAE | 4.94 | 3.44 | 3.12 | 2.45 | 3.7 | 3.14 | 3.19 | 2.34 | |
| MAPE | 13.69 | 7.94 | 8.67 | 5.96 | 10.72 | 7.25 | 8.87 | 5.49 | ||
| RMSE | 7.81 | 6.02 | 4.78 | 5.02 | 5.82 | 4.64 | 4.89 | 3.8 | ||
| 60 | MAE | 5.27 | 3.72 | 3.13 | 2.69 | 3.72 | 3.15 | 3.22 | 2.42 | |
| MAPE | 14.7 | 8.50 | 8.74 | 6.52 | 10.79 | 7.71 | 8.93 | 5.76 | ||
| RMSE | 8.22 | 7.60 | 4.81 | 6.59 | 5.83 | 4.72 | 4.97 | 3.95 | ||
| 70 | MAE | 5.55 | 4.36 | 3.16 | 3.35 | 3.73 | 3.17 | 3.27 | 2.54 | |
| MAPE | 15.56 | 9.01 | 8.82 | 7.96 | 10.76 | 8.34 | 9.08 | 6.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Zhou, L.; Xiao, X.; Xu, D. A Missing Traffic Data Imputation Method Based on a Diffusion Convolutional Neural Network–Generative Adversarial Network. Sensors 2023, 23, 9601. https://doi.org/10.3390/s23239601
Zhang C, Zhou L, Xiao X, Xu D. A Missing Traffic Data Imputation Method Based on a Diffusion Convolutional Neural Network–Generative Adversarial Network. Sensors. 2023; 23(23):9601. https://doi.org/10.3390/s23239601
Chicago/Turabian StyleZhang, Chenchen, Lei Zhou, Xuemei Xiao, and Dongwei Xu. 2023. "A Missing Traffic Data Imputation Method Based on a Diffusion Convolutional Neural Network–Generative Adversarial Network" Sensors 23, no. 23: 9601. https://doi.org/10.3390/s23239601
APA StyleZhang, C., Zhou, L., Xiao, X., & Xu, D. (2023). A Missing Traffic Data Imputation Method Based on a Diffusion Convolutional Neural Network–Generative Adversarial Network. Sensors, 23(23), 9601. https://doi.org/10.3390/s23239601




