A Programmable Crypto-Processor for National Institute of Standards and Technology Post-Quantum Cryptography Standardization Based on the RISC-V Architecture
Abstract
:1. Introduction
2. Target PQC Algorithms
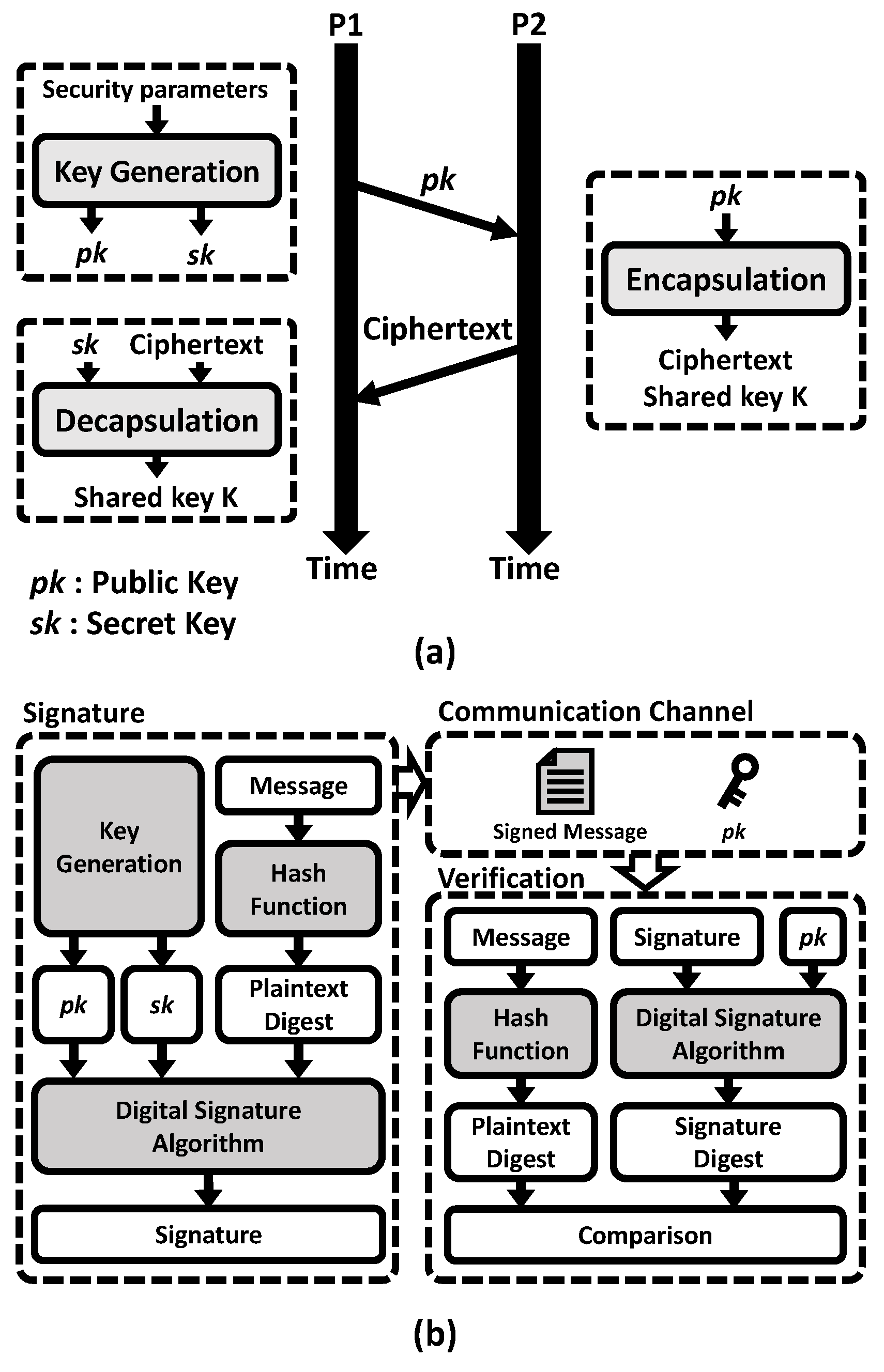
2.1. NIST PQC Standard and Round 4 Algorithms
2.2. Core Operations for Post-Quantum Cryptography
| Algorithm 1: Keccak-f [1600] Permutation |
 |
| Algorithm 2: Montgomery Reduction for PQC algorithms |
 |
| Algorithm 3: Sampling based on Centered Binomial Distribution |
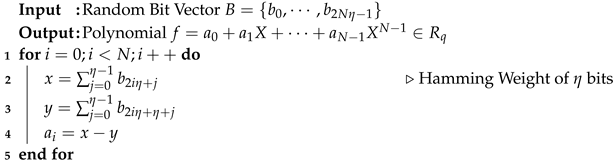 |
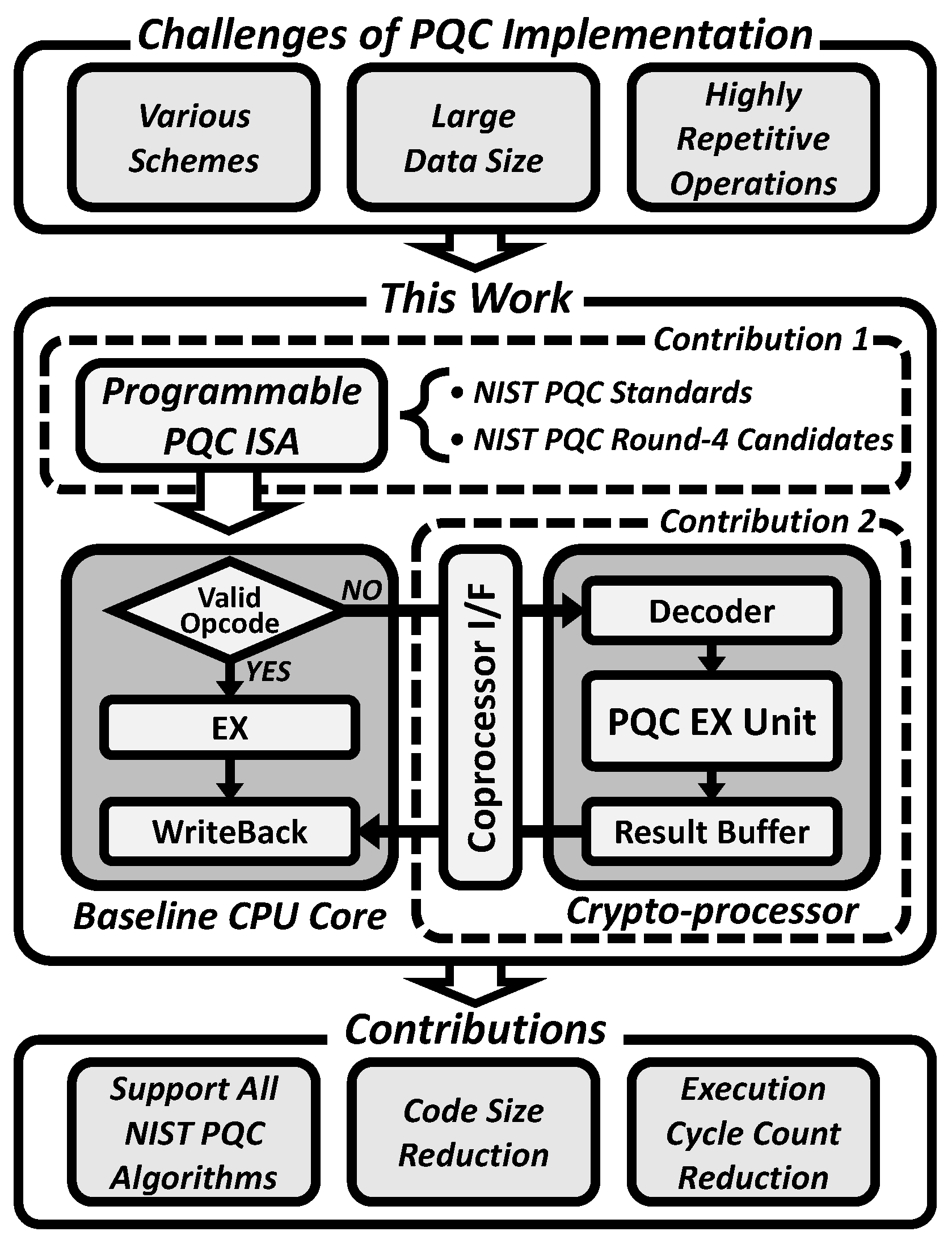
3. Proposed Crypto-Processor Architecture with PQC Instructions
3.1. Proposed RISC-V Instruction Set Extension
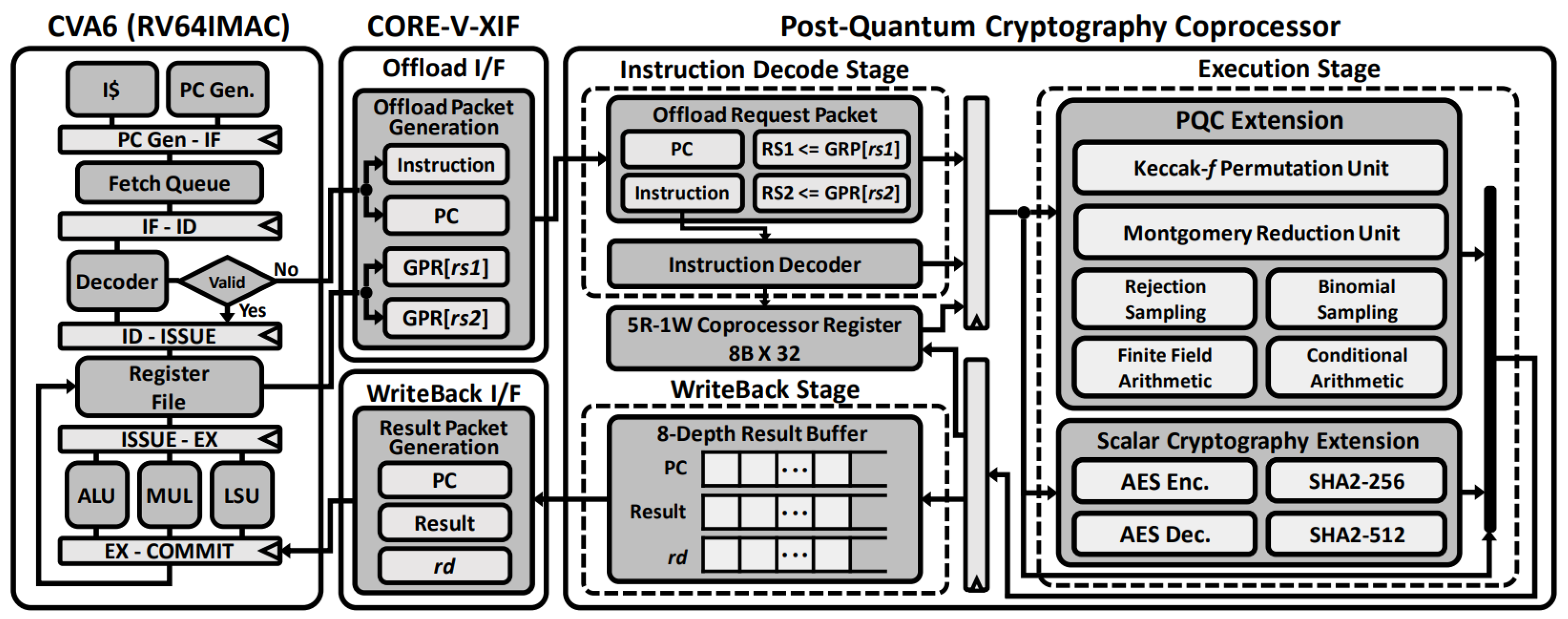
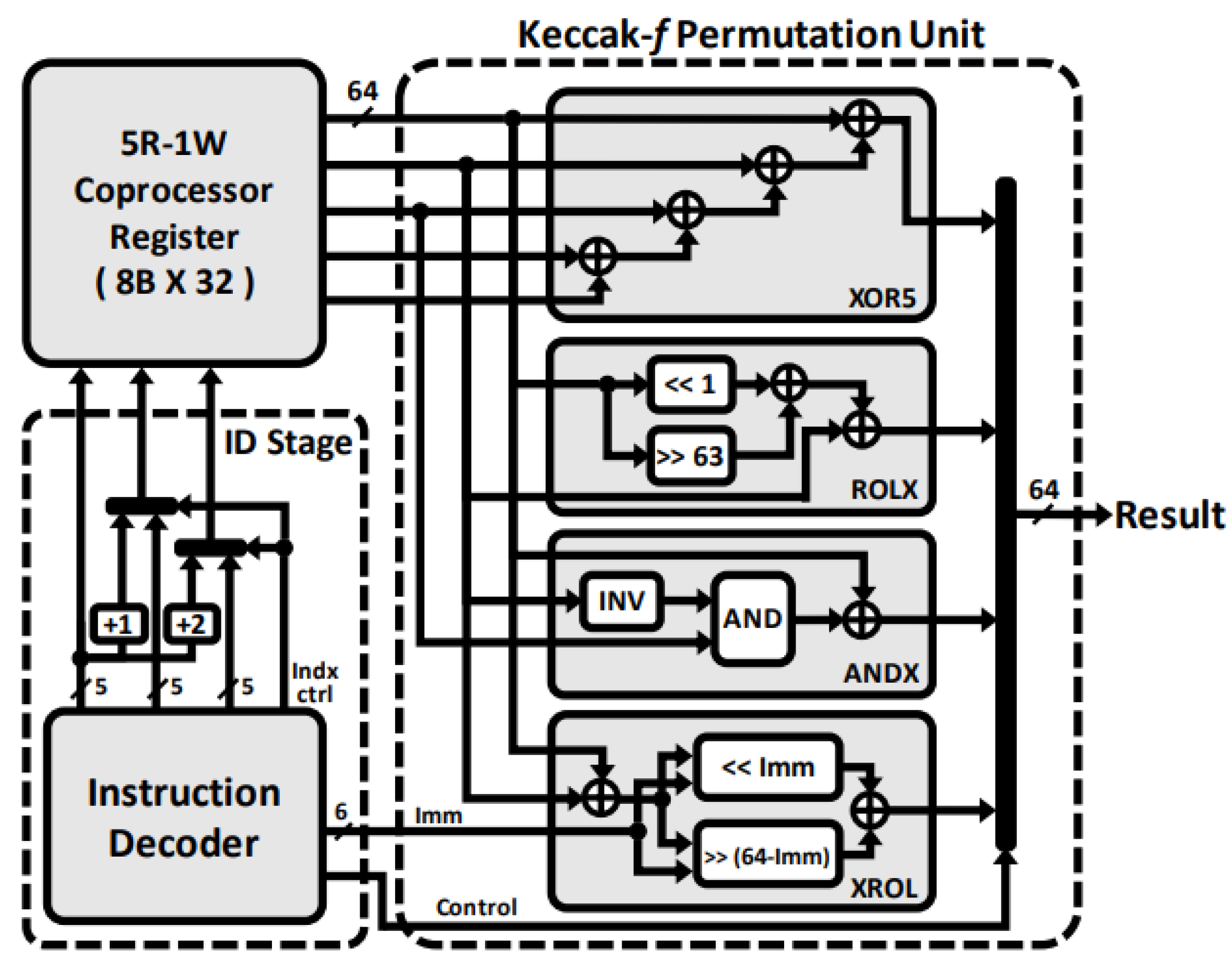
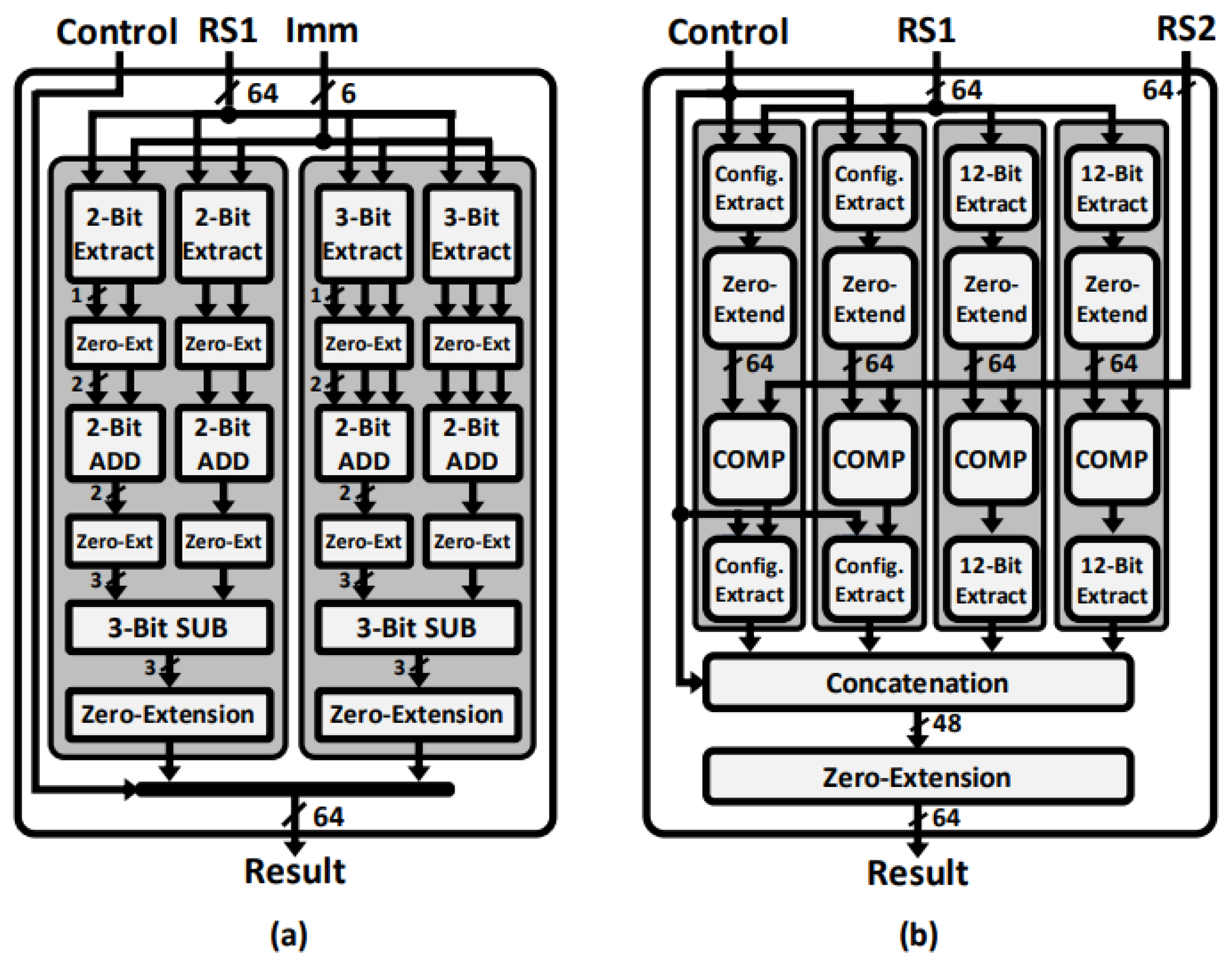
3.2. Proposed Crypto-Processor Microarchitecture
4. Experimental Results
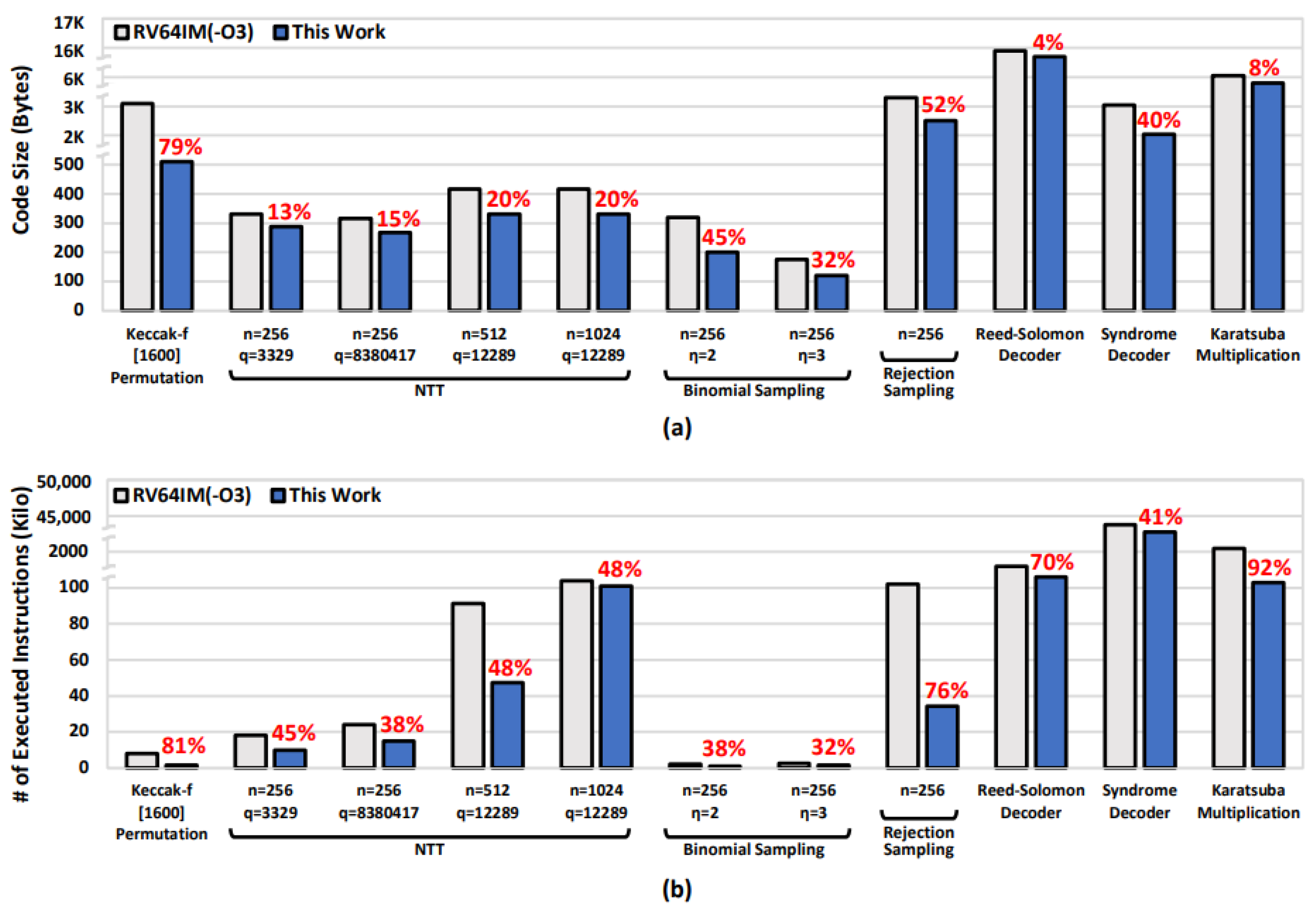
4.1. Performance Analysis
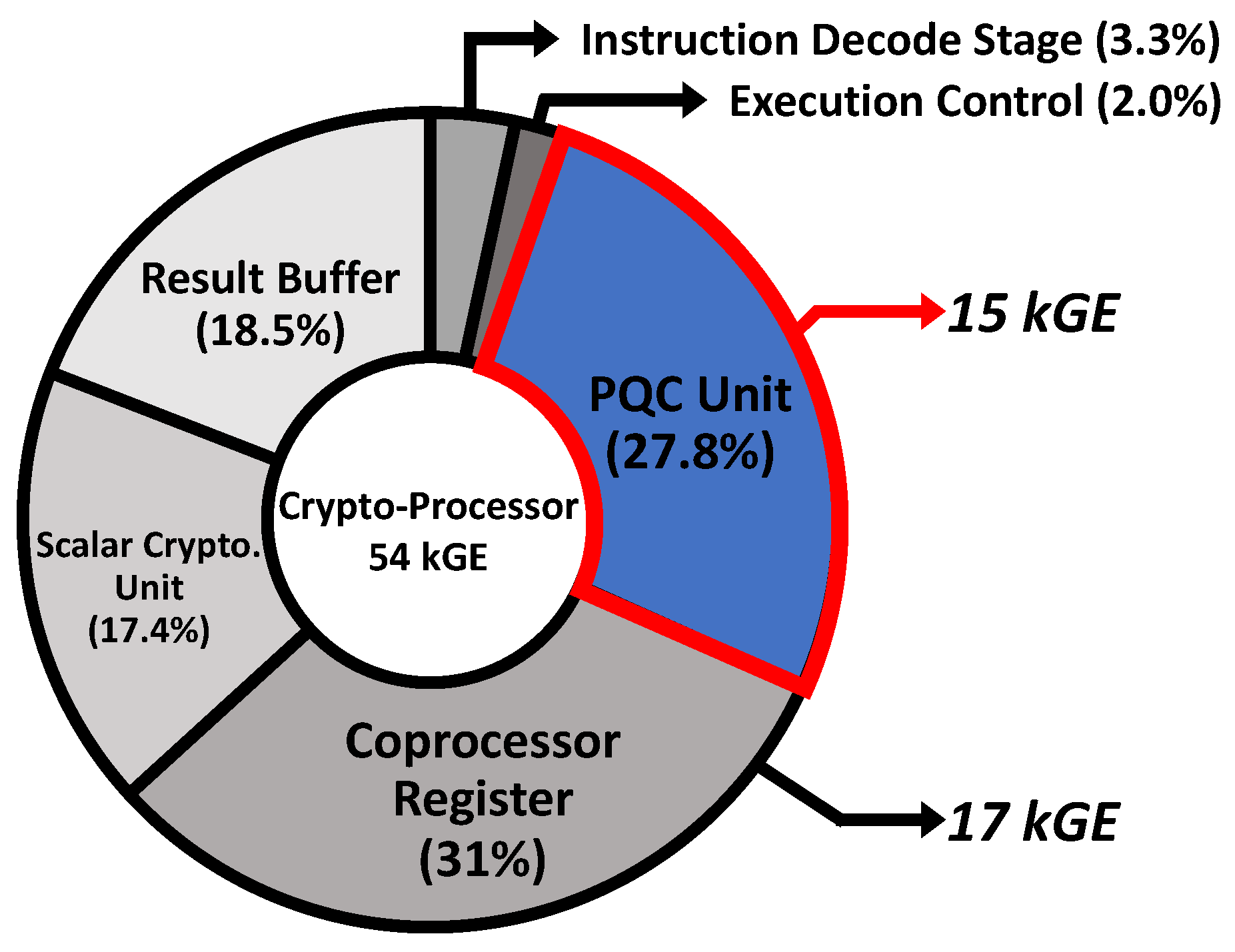
4.2. Hardware Implementation Results
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Diffie, W.; Hellman, M.E. New directions in cryptography. In Secure Communications and Asymmetric Cryptosystems; Routledge: Abingdon, UK, 2019; pp. 143–180. [Google Scholar]
- Miller, V.S. Use of elliptic curves in cryptography. In Proceedings of the Conference on the Theory and Application of Cryptographic Techniques, Lyon, France, 23–27 April 1985; Springer: Berlin/Heidelberg, Germany, 1985; pp. 417–426. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Kumar, M. Post-quantum cryptography Algorithm’s standardization and performance analysis. Array 2022, 15, 100242. [Google Scholar] [CrossRef]
- Dam, D.T.; Tran, T.H.; Hoang, V.P.; Pham, C.K.; Hoang, T.T. A Survey of Post-Quantum Cryptography: Start of a New Race. Cryptography 2023, 7, 40. [Google Scholar] [CrossRef]
- Dang, V.B.; Mohajerani, K.; Gaj, K. High-Speed Hardware Architectures and FPGA Benchmarking of CRYSTALS-Kyber, NTRU, and Saber. IEEE Trans. Comput. 2023, 72, 306–320. [Google Scholar] [CrossRef]
- Nejatollahi, H.; Dutt, N.; Ray, S.; Regazzoni, F.; Banerjee, I.; Cammarota, R. Post-quantum lattice-based cryptography implementations: A survey. ACM Comput. Surv. (CSUR) 2019, 51, 1–41. [Google Scholar] [CrossRef]
- Choquin, L.; Piry, F. Arm Custom Instructions: Enabling Innovation and Greater Flexibility on Arm; Technical Report; ARM: Cambridge, UK, 2020. [Google Scholar]
- Fritzmann, T.; Sharif, U.; Müller-Gritschneder, D.; Reinbrecht, C.; Schlichtmann, U.; Sepulveda, J. Towards reliable and secure post-quantum co-processors based on RISC-V. In Proceedings of the 2019 Design, Automation & Test in Europe Conference & Exhibition (DATE), Florence, Italy, 25–29 March 2019; pp. 1148–1153. [Google Scholar]
- Banerjee, U.; Ukyab, T.S.; Chandrakasan, A.P. Sapphire: A Configurable Crypto-Processor for Post-Quantum Lattice-based Protocols. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2019, 2019, 1140. [Google Scholar] [CrossRef]
- Alkim, E.; Evkan, H.; Lahr, N.; Niederhagen, R.; Petri, R. ISA extensions for finite field arithmetic: Accelerating Kyber and NewHope on RISC-V. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2020, 2020, 219–242. [Google Scholar] [CrossRef]
- Fritzmann, T.; Sigl, G.; Sepúlveda, J. RISQ-V: Tightly coupled RISC-V accelerators for post-quantum cryptography. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2020, 2020, 239–280. [Google Scholar] [CrossRef]
- Nannipieri, P.; Di Matteo, S.; Zulberti, L.; Albicocchi, F.; Saponara, S.; Fanucci, L. A RISC-V Post Quantum Cryptography Instruction Set Extension for Number Theoretic Transform to Speed-Up CRYSTALS Algorithms. IEEE Access 2021, 9, 150798–150808. [Google Scholar] [CrossRef]
- OpenHW Group. CORE-V Extension Interface; Technical report; OpenHW Group: Ottawa, ON, USA, 2022. [Google Scholar]
- Xin, G.; Han, J.; Yin, T.; Zhou, Y.; Yang, J.; Cheng, X.; Zeng, X. VPQC: A domain-specific vector processor for post-quantum cryptography based on RISC-V architecture. IEEE Trans. Circuits Syst. Regul. Pap. 2020, 67, 2672–2684. [Google Scholar] [CrossRef]
- Fernández-Caramés, T.M. From pre-quantum to post-quantum IoT security: A survey on quantum-resistant cryptosystems for the Internet of Things. IEEE Internet Things J. 2019, 7, 6457–6480. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Z.; Ma, Z. Key encapsulation mechanism with explicit rejection in the quantum random oracle model. In Proceedings of the Public-Key Cryptography–PKC 2019: 22nd IACR International Conference on Practice and Theory of Public-Key Cryptography, Beijing, China, 14–17 April 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 618–645. [Google Scholar]
- Soni, D.; Basu, K.; Nabeel, M.; Karri, R. A hardware evaluation study of NIST post-quantum cryptographic signature schemes. In Proceedings of the Second PQC Standardization Conference, NIST, Santa Barbara, CA, USA, 22–24 August 2019. [Google Scholar]
- Alagic, G.; Apon, D.; Cooper, D.; Dang, Q.; Dang, T.; Kelsey, J.; Lichtinger, J.; Liu, Y.; Miller, C.; Moody, D.; et al. Status Report on the Third Round of the NIST Post-Quantum Cryptography Standardization Process; US Department of Commerce, NIST: Gaithersburg, MD, USA, 2022.
- Chuang, Y.L.; Fan, C.I.; Tseng, Y.F. An efficient algorithm for the shortest vector problem. IEEE Access 2018, 6, 61478–61487. [Google Scholar] [CrossRef]
- Regev, O. Lattice-based cryptography. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2016; Springer: Berlin/Heidelberg, Germany, 2006; pp. 131–141. [Google Scholar]
- Khalid, A.; Oder, T.; Valencia, F.; O’Neill, M.; Güneysu, T.; Regazzoni, F. Physical protection of lattice-based cryptography: Challenges and solutions. In Proceedings of the 2018 on Great Lakes Symposium on VLSI, Chicago, IL, USA, 23–25 May 2018; pp. 365–370. [Google Scholar]
- Lyubashevsky, V.; Peikert, C.; Regev, O. On ideal lattices and learning with errors over rings. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, France, 30 May–3 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–23. [Google Scholar]
- Langlois, A.; Stehlé, D. Worst-case to average-case reductions for module lattices. Des. Codes Cryptogr. 2015, 75, 565–599. [Google Scholar] [CrossRef]
- Lamport, L. Constructing Digital Signatures from a One Way Function; Technical Report, Technical Report CSL-98; SRI International: Palo Alto, CA, USA, 1979. [Google Scholar]
- Buchmann, J.; Dahmen, E.; Hülsing, A. XMSS-a practical forward secure signature scheme based on minimal security assumptions. In Proceedings of the International Workshop on Post-Quantum Cryptography, College Park, MD, USA, 28–30 September 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 117–129. [Google Scholar]
- Sun, S.; Zhang, R.; Ma, H. Efficient parallelism of post-quantum signature scheme SPHINCS. IEEE Trans. Parallel Distrib. Syst. 2020, 31, 2542–2555. [Google Scholar] [CrossRef]
- McEliece, R.J. A public-key cryptosystem based on algebraic. Coding Thv 1978, 4244, 114–116. [Google Scholar]
- Berlekamp, E. Goppa codes. IEEE Trans. Inf. Theory 1973, 19, 590–592. [Google Scholar] [CrossRef]
- Dworkin, M.J. SHA-3 Standard: Permutation-Based Hash and Extendable-Output Function; Technical report; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. [Google Scholar]
- Karabulut, E.; Aysu, A. RANTT: A RISC-V architecture extension for the number theoretic transform. In Proceedings of the 2020 30th International Conference on Field-Programmable Logic and Applications (FPL), Gothenburg, Sweden, 31 August–4 September 2020; pp. 26–32. [Google Scholar]
- Cooley, J.W.; Tukey, J.W. An algorithm for the machine calculation of complex Fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Montgomery, P.L. Modular multiplication without trial division. Math. Comput. 1985, 44, 519–521. [Google Scholar] [CrossRef]
- Alkim, E.; Bilgin, Y.A.; Cenk, M.; Gérard, F. Cortex-M4 optimizations for {R, M} LWE schemes. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2020, 2020, 336–357. [Google Scholar] [CrossRef]
- Chen, M.S.; Güneysu, T.; Krausz, M.; Thoma, J.P. Carry-less to bike faster. In Proceedings of the Applied Cryptography and Network Security: 20th International Conference, ACNS 2022, Rome, Italy, 20–23 June 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 833–852. [Google Scholar]
- Schöffel, M.; Feldmann, J.; Wehn, N. Code-based Cryptography in IoT: A HW/SW Co-Design of HQC. arXiv 2023, arXiv:2301.04888. [Google Scholar]
- Waterman, A.; Lee, Y.; Patterson, D.A.; Asanovi, K. The Risc-v Instruction Set Manual. Volume 1: User-Level Isa, Version 2.0; Technical report; Department of Electrical Engineering and Computer Sciences, California University: Berkeley, CA, USA, 2014. [Google Scholar]
- Oder, T.; Speith, J.; Höltgen, K.; Güneysu, T. Towards practical microcontroller implementation of the signature scheme Falcon. In Proceedings of the International Conference on Post-Quantum Cryptography, Chongqing, China, 8–10 May 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 65–80. [Google Scholar]
- Marshall, B. RISC-V Cryptographic Extension Proposals. Volume I: Scalar & Entropy Source Instructions; RISC-V International: Zurich, Switzerland, 2021. [Google Scholar]
- Banerjee, U.; Das, S.; Chandrakasan, A.P. Accelerating post-quantum cryptography using an energy-efficient tls crypto-processor. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020; pp. 1–5. [Google Scholar]
- Soni, D.; Karri, R. Efficient hardware implementation of pqc primitives and pqc algorithms using high-level synthesis. In Proceedings of the 2021 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Tampa, FL, USA, 7–9 July 2021; pp. 296–301. [Google Scholar]
- Zaruba, F.; Benini, L. The Cost of Application-Class Processing: Energy and Performance Analysis of a Linux-Ready 1.7-GHz 64-Bit RISC-V Core in 22-nm FDSOI Technology. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2019, 27, 2629–2640. [Google Scholar] [CrossRef]
- Stoffelen, K. Efficient cryptography on the RISC-V architecture. In Proceedings of the International Conference on Cryptology and Information Security in Latin America, Santiago de, Chile, Chile, 2–4 October 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 323–340. [Google Scholar]
- Li, H.; Mentens, N.; Picek, S. Maximizing the Potential of Custom RISC-V Vector Extensions for Speeding up SHA-3 Hash Functions. In Proceedings of the 2023 Design, Automation & Test in Europe Conference & Exhibition (DATE), Antwerp, Belgium, 17–19 April 2023. [Google Scholar]
- Kannwischer, M.J.; Rijneveld, J.; Schwabe, P.; Stoffelen, K. PQM4: Post-Quantum Crypto Library for the ARM Cortex-M4; GitHub: San Francisco, CA, USA, 2019. [Google Scholar]
- GF2X/GF2X · GITLAB. Available online: https://gitlab.inria.fr/gf2x/gf2x (accessed on 15 November 2023).


| Class | Algorithm Type | Public-Key Encryption/ Key-Establishment | Disigtal Signature |
|---|---|---|---|
| NIST PQC Standard | Latice | CRYSTALS-Kyber | CRYSTALS-Dilithium Falcon |
| Hash | - | SPHINCS+ | |
| NIST PQC Round-4 Candidate | Code | BIKE HQC Classic McEliece | - |
| Isogeny | SIKE | - |
| Type | Encoding Map | |||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | |
| R | Functon 7 | rs2 | rs1 | Function 3 | rd | Opcode | ||||||||||||||||||||||||||
| R4 | rs3 | Func. 2 | rs2 | rs1 | Function 3 | rd | Opcode | |||||||||||||||||||||||||
| Custom1 | Immediate | rs2 | rs1 | Function 3 | rd | Opcode | ||||||||||||||||||||||||||
| Custom2 | Function 7 | - | rs1 | Function 3 | rd | Opcode | ||||||||||||||||||||||||||
| Operation | Instruction | Description |
|---|---|---|
| Keccak-f Permutation | XOR5 | RD = CR[rs1] ⌃CR[rs1+1] ⌃CR[rs1+2] ⌃CR[rs1+3] ⌃CR[rs1+4] |
| ROLX | RD = ROL(RS1, 1) ⌃RS2 | |
| ANDX | RD = CR[rs1] ⌃(∼CR[rs2] & CR[rs3]) | |
| XROL | RD = ROL(RS1 ⌃RS2, Imm) | |
| Montgomery Reduction | MR4 | RD = (RS1 − ((RS1 × ) & 64’hFFFF) ∗ RS2) >> 16 |
| MR4U | RD = (RS1 + ((RS1 × ) & 64’hFFFF) ∗ RS2) >> 16 | |
| MR8 | RD = (RS1 − ((RS1 × ) & 64’hFFFF_FFFF) ∗ RS2) >> 32 | |
| Binomial Sampling | SND2 | RD = {61’b0, ({1’b0, ({1’b0, RS1[Imm]} + {1’b0, RS1[Imm+1]})}) − ({1’b0, ({1’b0, RS1[Imm+2]} + {1’b0, RS1[Imm+3]})})} |
| SND3 | RD = {61’b0, ({1’b0, ({1’b0, RS1[Imm]} + {1’b0, RS1[Imm+1]} + {1’b0, RS1[Imm+2]})}) − ({1’b0, ({1’b0, RS1[Imm+3]} + {1’b0, RS1[Imm+4]} + {1’b0, RS1[Imm+5]})})} | |
| Rejection Sampling | REJH | RD[11:0] = (RS1[11:0] < RS2) ? RS1[11:0] : 12’b0 RD[23:12] = (RS1[23:12] < RS2) ? RS1[23:12] : 12’b0 RD[35:24] = (RS1[35:24] < RS2) ? RS1[35:24] : 12’b0 RD[47:36] = (RS1[47:36] < RS2) ? RS1[47:36] : 12’b0 RD[63:48] = 16’b0 |
| REJ | RD[23:0] = (RS1[22:0] < RS2) ? {1’b0, RS1[22:0]} : 24’b0 RD[47:24] = (RS1[46:24] < RS2) ? {1’b0, RS1[47:24]} : 24’b0 RD[63:48] = 16’b0 | |
| Finite Field Arithmetic | SQR | RD = {1’b0, RS1[31], 1’b0, RS1[30], ... , 1’b0, RS1[1], 1’b0, RS1[0]} |
| CLMUL | RD = (RS2[0] ? (RS1 << 0) : 64’b0) ⌃... ⌃(RS2[63] ? (RS1 << 63) : 64’b0 ) | |
| CLMULH | RD = (RS2[0] ? (RS1 >> 63) : 64’b0) ⌃... ⌃(RS2[63] ? (RS1 >> 0) : 64’b0 ) | |
| Conditional Arithmetic | CON4 | RD = RS1[15] ? RS2 : 64’b0 |
| CON8 | RD = RS1[31] ? RS2 : 64’b0 | |
| CR Access | RDCR | GRP[rd] = CR[rs1] |
| WRCR | CR[rd] = GPR[rs1] |
| Supportin Algorithm | Proposed RISC-V Post-Quantum Cryptography ISA | |||||
|---|---|---|---|---|---|---|
| Keccak-f Permutation | Montgomery Reduction | Sampling | Finite Field Arithmetic | Conditional Arithmetic | CR Access | |
| PKE/ KEM | Kyber | O | O | O | O | |
| BIKE | O | O | O | |||
| HQC | O | O | O | |||
| Classic McEliece | O | O | O | |||
| DS | Dilithium | O | O | O | O | |
| Falcon | O | O | O | O | ||
| SPHINCS+ | O | O | ||||
| RV64IM (-O3) | E31 (RV32IMAC) [44] | Cortex-M4 [44] | Accelerator [45] | This Work |
|---|---|---|---|---|
| 11.722 | 13.774 | 12.969 | 1.8 | 1.632 |
| Parameter (n, q) | Implementation | ||||
|---|---|---|---|---|---|
| RV64IM (-O3) | Accelerator [32] | Accelerator [14] | Cortex-M4F [39] | This Work | |
| (256, 3329) | 25.53 | 43.76 | 18.49 | - | 13.88 |
| (253, 8380417) | 29.50 | 43.76 | 18.55 | - | 15.16 |
| (512, 12289) | 108.20 | 81.06 | 75.90 | 55.20 | |
| (1024, 12289) | 237.74 | 180.24 | 157.70 | 119.98 | |
| Target Algorithm | Parameter | Implementation | ||
| RV64IM (-O3) | Accelerator [13] | This Work | ||
| Binomial Sampling | n = 256, = 2 | 2.46 | - | 1.24 |
| n = 256, = 3 | 3.01 | 2.36 | 2.86 | |
| Rejection Sampling | Parameter | RV64IM (-O3) | Cortex-M4 [46] | This Work |
| n = 256 | 206.36 | 60.43 | 47.36 | |
| Target Algorithm | Implementation | |
|---|---|---|
| RV64IM (-O3) | This Work | |
| Reed-Solomon Decoder (HQC-128) | 861.17 | 300.24 |
| Syndrome Decoder (mceliece348864) | 45,556.83 | 27,830.81 |
| Karatsuba Multiplication | 2311.75 | 305.98 |
| Design | TCHE’20 [13] | IEEE Access’21 [14] | FPL’20 [32] | TCHE’19 [11] | TCAS-I’20 [16] | This Work |
|---|---|---|---|---|---|---|
| Platform | ASIC (65nm) | FPGA (ZCU106) | FPGA (VIRTEX-7) | ASIC (40nm) | ASIC (28nm) | ASIC (28nm) |
| Frequency (MHz) | 45 | 100 | - | 72 | 300 | 150 |
| Gate Counts (kGE) | - | - | 106 e | 37 + | 477 + | |
| Complexity (LUT/FF/DSP/BRAM) | - | 178/0/5/ 377/0/10/ | 417/462/0/ | - | - | - |
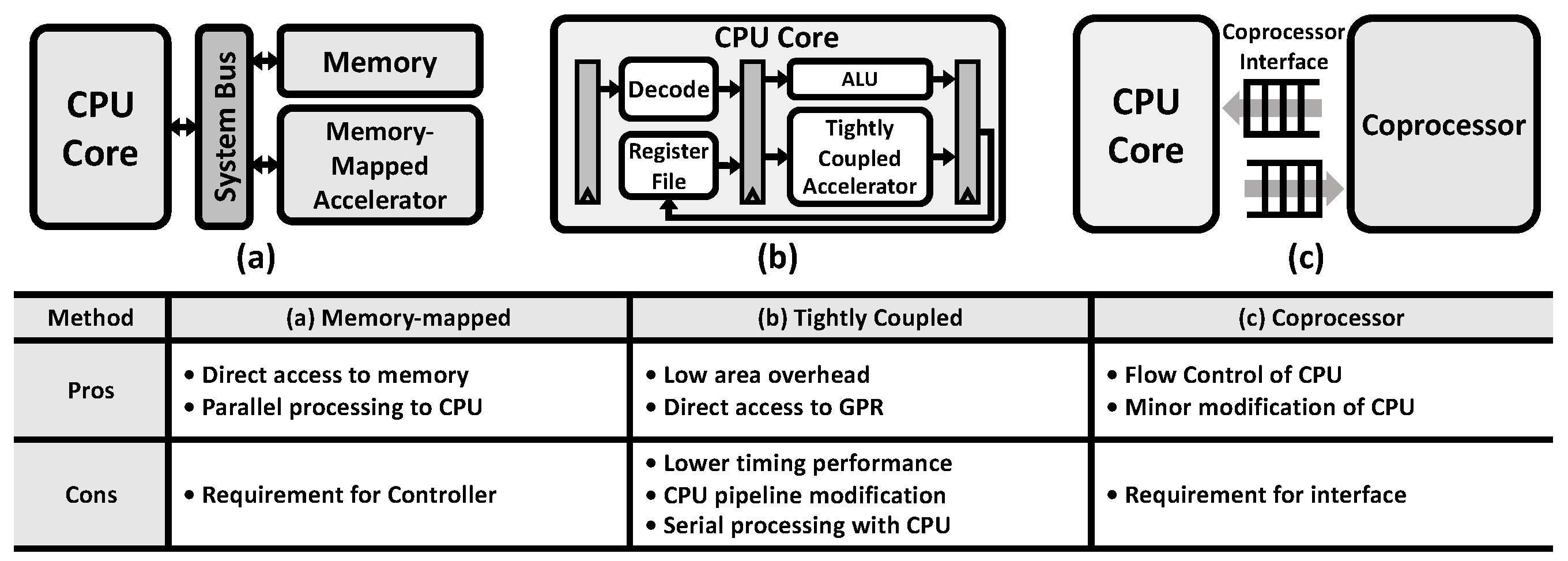
| Accelerator Type | Tightly Coupled | Tightly Coupled | Tightly Coupled | Memory-mapped | Coprocessor | Coprocessor |
| Supported NIST PQC algorithms | Kyber Saber | Kyber Dilithium | Kyber Dilithium Falcon | Kyber Dilithium | Kyber | Kyber Dilithium Falcon SPHINCS+ BIKE HQC Classic McEliece |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Kim, W.; Kim, J.-H. A Programmable Crypto-Processor for National Institute of Standards and Technology Post-Quantum Cryptography Standardization Based on the RISC-V Architecture. Sensors 2023, 23, 9408. https://doi.org/10.3390/s23239408
Lee J, Kim W, Kim J-H. A Programmable Crypto-Processor for National Institute of Standards and Technology Post-Quantum Cryptography Standardization Based on the RISC-V Architecture. Sensors. 2023; 23(23):9408. https://doi.org/10.3390/s23239408
Chicago/Turabian StyleLee, Jihye, Whijin Kim, and Ji-Hoon Kim. 2023. "A Programmable Crypto-Processor for National Institute of Standards and Technology Post-Quantum Cryptography Standardization Based on the RISC-V Architecture" Sensors 23, no. 23: 9408. https://doi.org/10.3390/s23239408
APA StyleLee, J., Kim, W., & Kim, J.-H. (2023). A Programmable Crypto-Processor for National Institute of Standards and Technology Post-Quantum Cryptography Standardization Based on the RISC-V Architecture. Sensors, 23(23), 9408. https://doi.org/10.3390/s23239408





