Second Harmonic Modulation for Ultrasonic Signals Based on the Design of the Phononic Crystal Filter
Abstract
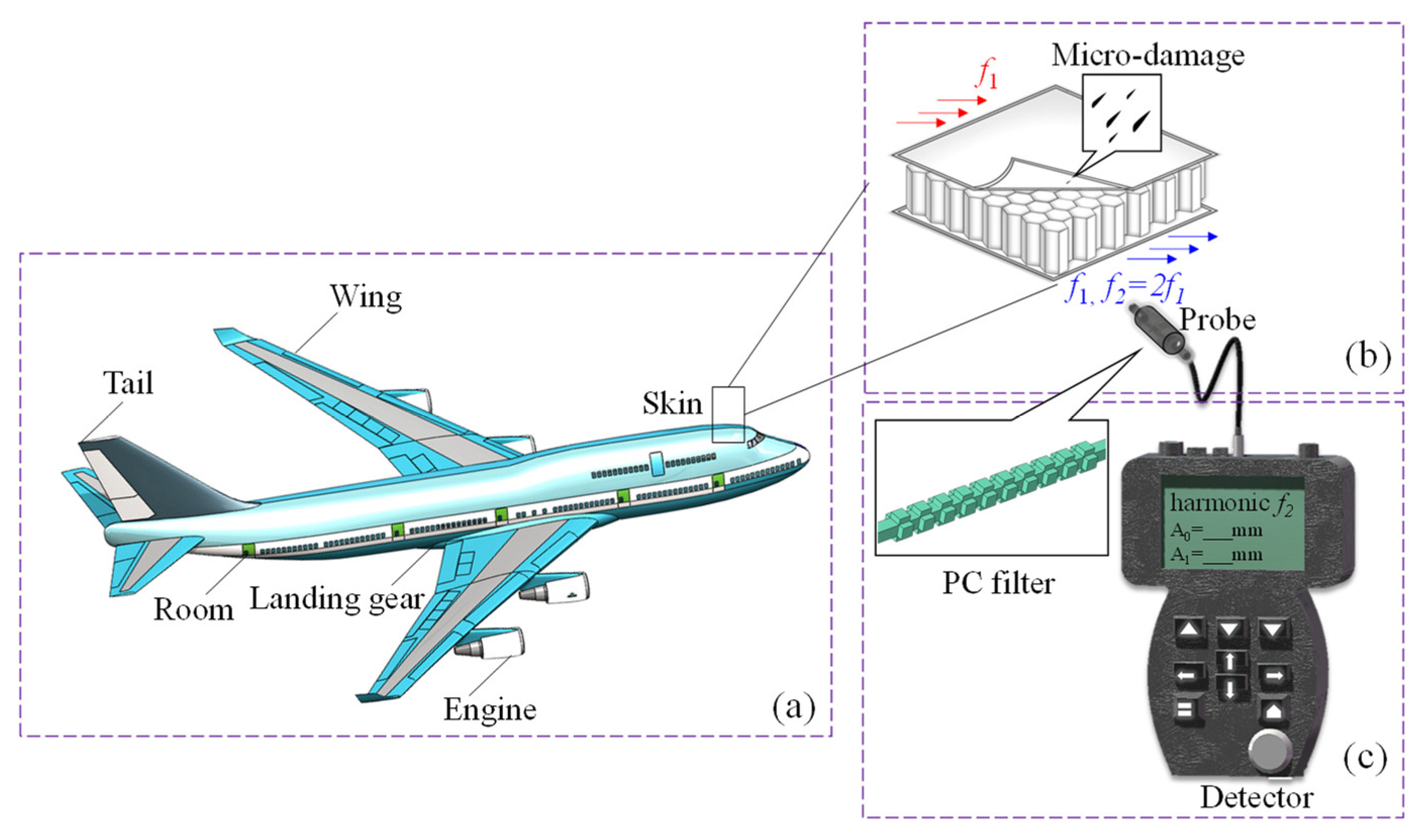
:1. Introduction
2. Design Method of PC Filter
3. Numerical Simulations
3.1. Bandgaps Properties Analysis
- (a)
- Choose the built-in 3D Solid Mechanics module.
- (b)
- Set material properties and boundary conditions. This 3D lattice possesses threefold symmetry in all directions and is made of aluminum. Floquet periodic boundary conditions () are applied in all three symmetric directions, corresponding to the characteristics of the Bragg boundaries, with a wave vector .
- (c)
- Mesh the geometry. The minimum mesh size should be less than 1/10 of the wavelength.
- (d)
- Conduct a frequency sweep analysis to obtain the characteristic frequency curve/band structure of the PC.
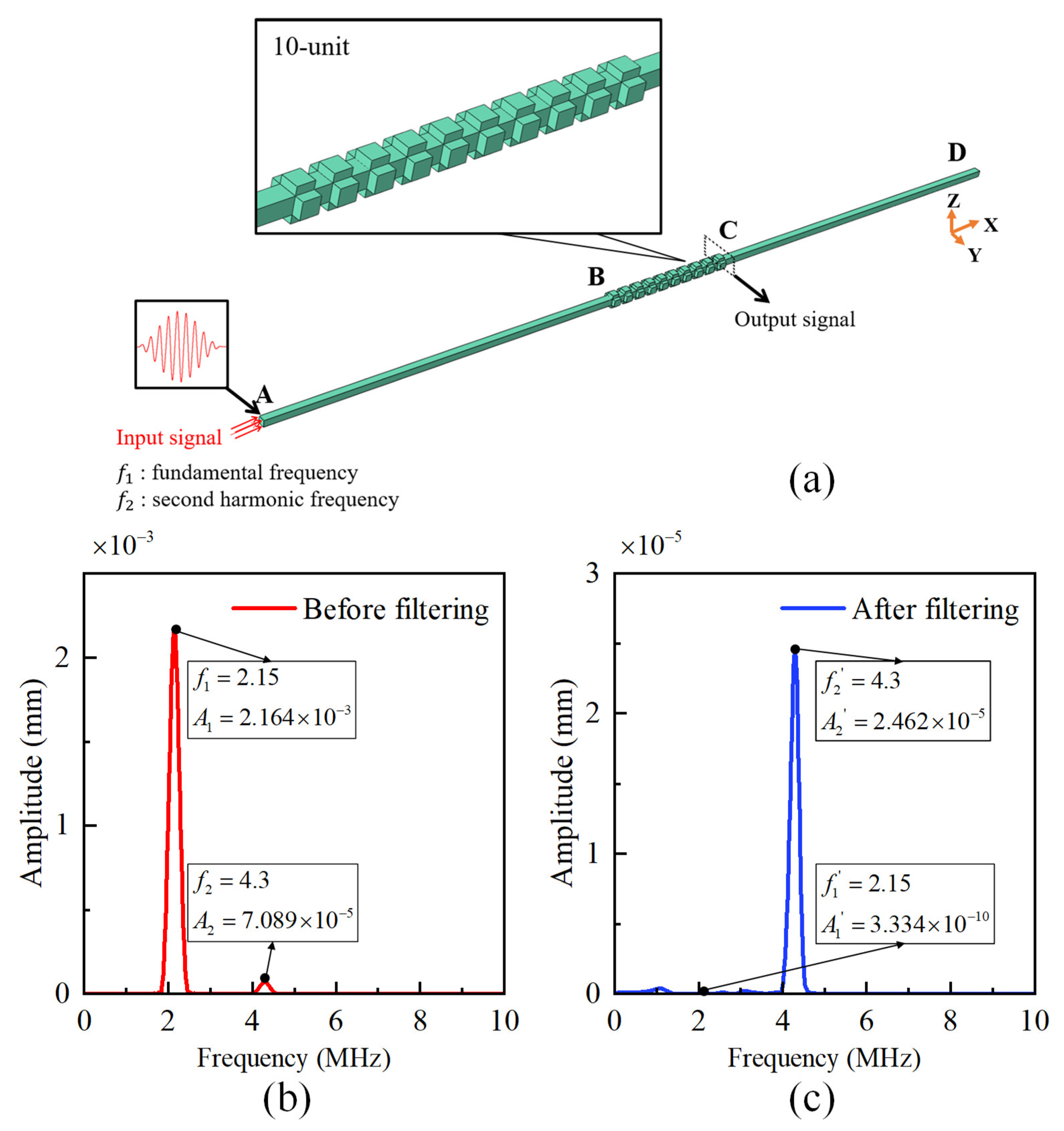
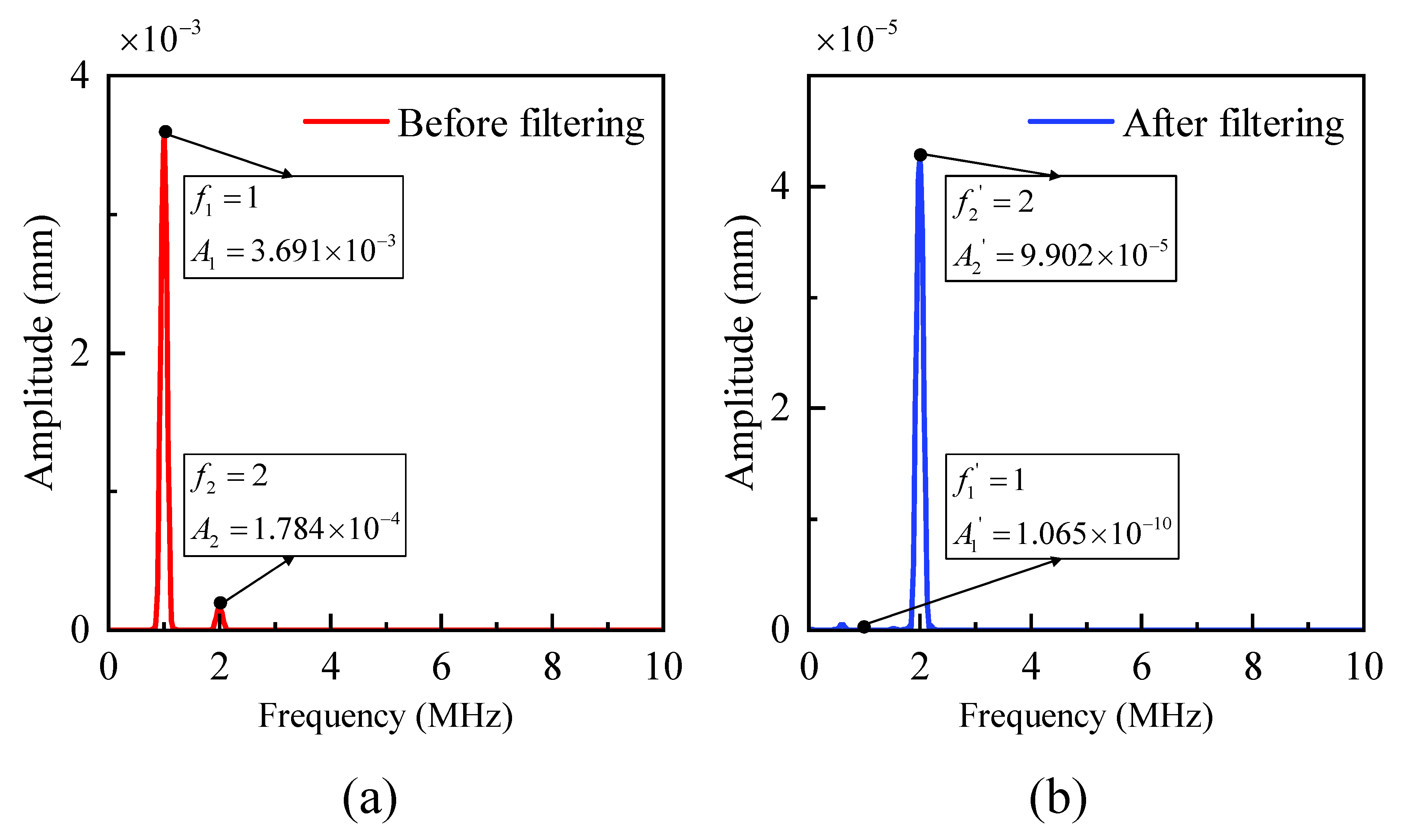
3.2. Filtering Ability Verification
4. Parametric Studies
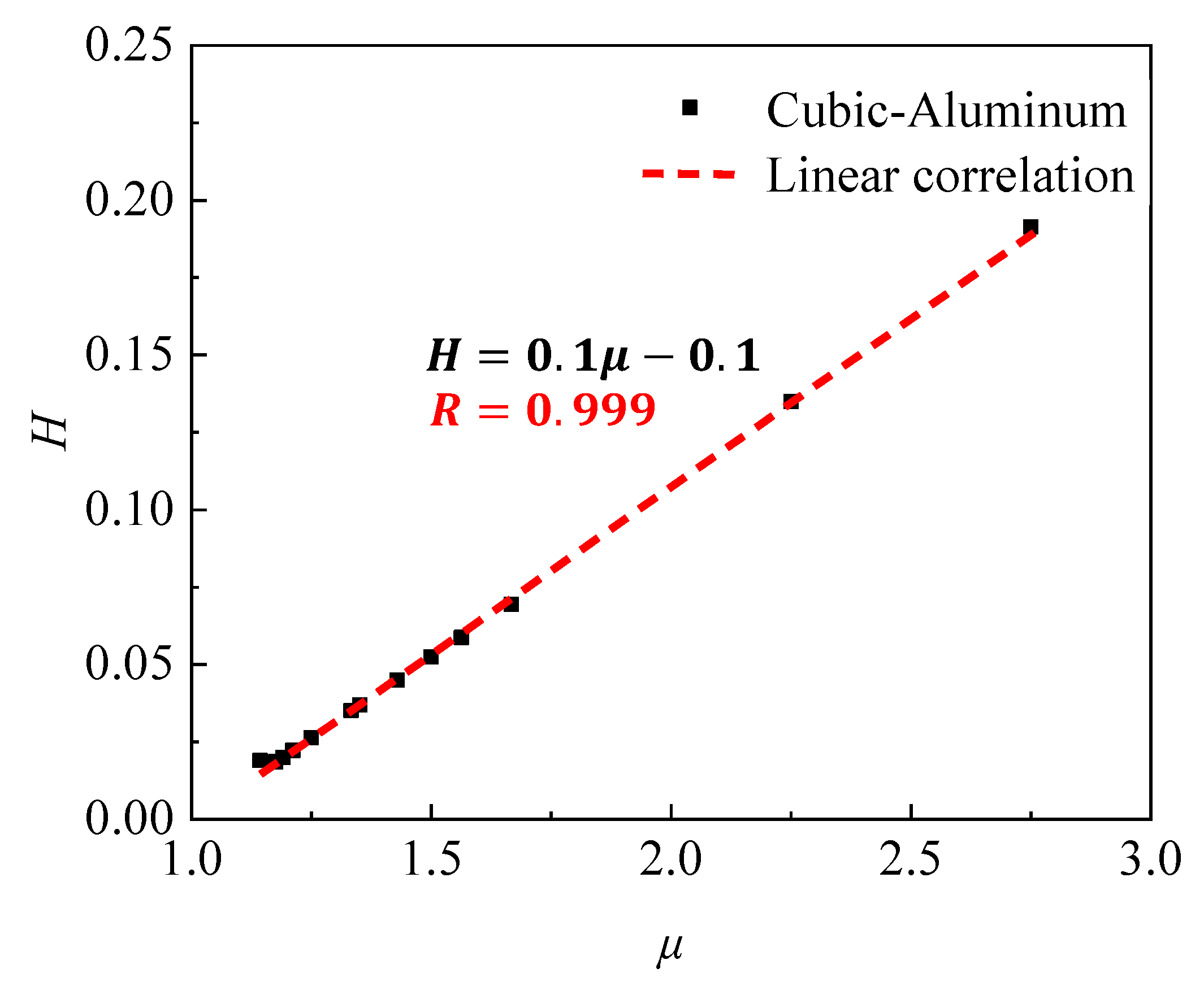
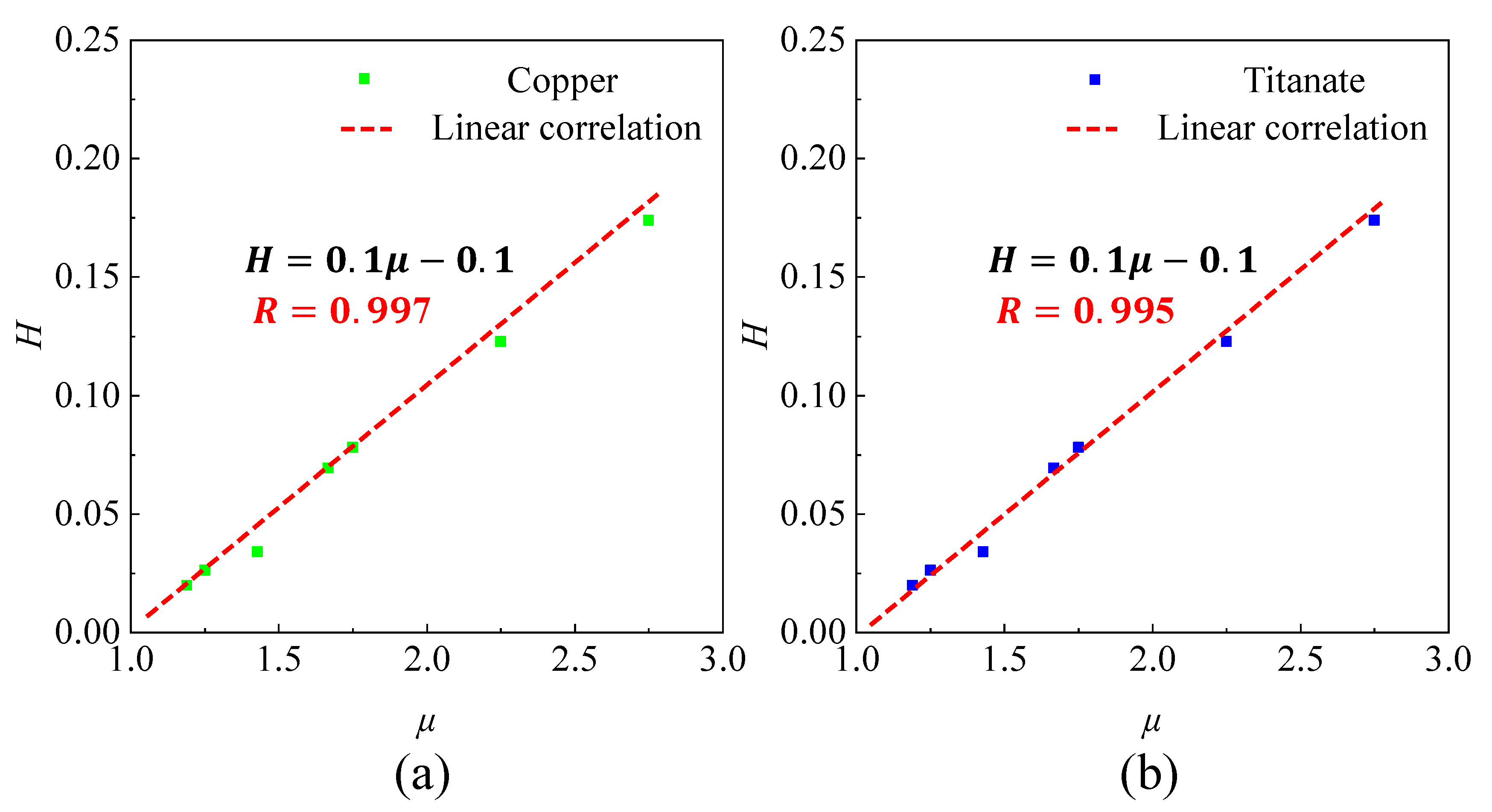
4.1. Mechanism Research
4.2. Other Influencing Factors
4.3. Cases for Design Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Smith, D.R.; Padilla, W.J.; Vier, D.C.; Nemat-Nasser, S.C.; Schultz, S. Composite Medium with Simultaneously Negative Permeability and Permittivity. Phys. Rev. Lett. 2000, 84, 4184–4187. [Google Scholar] [CrossRef] [PubMed]
- Xia, B.; Li, L.; Liu, J.; Yu, D. Acoustic Metamaterial With Fractal Coiling Up Space for Sound Blocking in a Deep Subwavelength Scale. J. Vib. Acoust. 2018, 140, 011011. [Google Scholar] [CrossRef]
- Matlack, K.H.; Bauhofer, A.; Krödel, S.; Palermo, A.; Daraio, C. Composite 3D-Printed Metastructures for Low-Frequency and Broadband Vibration Absorption. Proc. Natl. Acad. Sci. USA 2016, 113, 8386–8390. [Google Scholar] [CrossRef] [PubMed]
- Gao, N.; Zhang, Z.; Deng, J.; Guo, X.; Cheng, B.; Hou, H. Acoustic Metamaterials for Noise Reduction: A Review. Adv. Mater. Technol. 2022, 7, 2100698. [Google Scholar] [CrossRef]
- Kaina, N.; Lemoult, F.; Fink, M.; Lerosey, G. Negative Refractive Index and Acoustic Superlens from Multiple Scattering in Single Negative Metamaterials. Nature 2015, 525, 77–81. [Google Scholar] [CrossRef]
- Kanno, Y.; Tsuruta, K.; Fujimori, K.; Fukano, H.; Nogi, S. Phononic-Crystal Acoustic Lens by Design for Energy-Transmission Devices. Electron. Comm. Jpn. 2014, 97, 22–27. [Google Scholar] [CrossRef]
- Ghoreshi, M.; Bahrami, A. Acoustic Invisibility Cloak Based on Two-Dimensional Solid-Fluid Phononic Crystals. Solid. State Commun. 2022, 342, 114646. [Google Scholar] [CrossRef]
- Kadic, M.; Bückmann, T.; Schittny, R.; Wegener, M. Metamaterials beyond Electromagnetism. Rep. Prog. Phys. 2013, 76, 126501. [Google Scholar] [CrossRef]
- Quinteros, L.; Meruane, V.; Lenz Cardoso, E.; Ruiz, R.O. Phononic Bandgap Optimization in Sandwich Panels Using Cellular Truss Cores. Materials 2021, 14, 5236. [Google Scholar] [CrossRef]
- Han, D.-H.; Zhao, J.-B.; Zhang, G.-J.; Yao, H. Study on Low-Frequency Band Gap Characteristics of a New Helmholtz Type Phononic Crystal. Symmetry 2021, 13, 1379. [Google Scholar] [CrossRef]
- Zhang, P.; Xue, H.; Gao, S. Asymptotic Stability Controller Design of Three Fixed-Wing UAVs Formation with Windy Field. In Proceedings of the 2019 IEEE International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; pp. 1280–1285. [Google Scholar]
- Zhang, P.; To, A.C. Broadband Wave Filtering of Bioinspired Hierarchical Phononic Crystal. Appl. Phys. Lett. 2013, 102, 121910. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-F.; Wang, Y.-Z.; Wu, B.; Chen, W.; Wang, Y.-S. Tunable and Active Phononic Crystals and Metamaterials. Appl. Mech. Rev. 2020, 72, 040801. [Google Scholar] [CrossRef]
- Nguyen, H.; Wu, Q.; Chen, J.; Yu, Y.; Chen, H.; Tracy, S.; Huang, G. A Broadband Acoustic Panel Based on Double-Layer Membrane-Type Metamaterials. Appl. Phys. Lett. 2021, 118, 184101. [Google Scholar] [CrossRef]
- Ash, B.J.; Worsfold, S.R.; Vukusic, P.; Nash, G.R. A Highly Attenuating and Frequency Tailorable Annular Hole Phononic Crystal for Surface Acoustic Waves. Nat. Commun. 2017, 8, 174. [Google Scholar] [CrossRef]
- He, L.; Wen, Z.; Jin, Y.; Torrent, D.; Zhuang, X.; Rabczuk, T. Inverse Design of Topological Metaplates for Flexural Waves with Machine Learning. Mater. Des. 2021, 199, 109390. [Google Scholar] [CrossRef]
- Yang, S.; Zhong, Y.; Yan, S.; Zhang, Z.; Li, X.; Yu, S.-Y.; Lu, M.-H. A Review of Elastic Plate Wave Metamaterials. Chin. Sci. Bull. 2022, 67, 1232–1248. [Google Scholar] [CrossRef]
- Wang, B.; Zhong, S.; Lee, T.-L.; Fancey, K.S.; Mi, J. Non-Destructive Testing and Evaluation of Composite Materials/Structures: A State-of-the-Art Review. Adv. Mech. Eng. 2020, 12, 168781402091376. [Google Scholar] [CrossRef]
- Bayer, P.; Notea, A.; Singher, L. Early Detection of Fatigue Damage through Ultrasonic Non-Destructive Evaluation—Part I: Theory. J. Test. Eval. 1999, 27, 428–431. [Google Scholar]
- Yan, X.; Wang, H.; Fan, X. Research Progress in Nonlinear Ultrasonic Testing for Early Damage in Metal Materials. Materials 2023, 16, 2161. [Google Scholar] [CrossRef]
- Novak, A.; Bentahar, M.; Tournat, V.; El Guerjouma, R.; Simon, L. Nonlinear Acoustic Characterization of Micro-Damaged Materials through Higher Harmonic Resonance Analysis. NDT E Int. 2012, 45, 1–8. [Google Scholar] [CrossRef]
- Gartsev, S.; Zuo, P.; Rjelka, M.; Mayer, A.; Köhler, B. Nonlinear Interaction of Rayleigh Waves in Isotropic Materials: Numerical and Experimental Investigation. Ultrasonics 2022, 122, 106664. [Google Scholar] [CrossRef] [PubMed]
- Pan, Q.; Li, S.; Xu, L.; Zhang, Y.; Chang, M.; Xu, X.; Li, S.; Li, W. Research on Nonlinear Ultrasonic Testing Technology of Microcracks in Metallic Materials. In Proceedings of the 2021 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 8 August 2021; pp. 1362–1367. [Google Scholar]
- Croxford, A.J.; Wilcox, P.D.; Drinkwater, B.W.; Nagy, P.B. The Use of Non-Collinear Mixing for Nonlinear Ultrasonic Detection of Plasticity and Fatigue. J. Acoust. Soc. Am. 2009, 126, EL117–EL122. [Google Scholar] [CrossRef]
- Lv, H.; Zhang, J.; Jiao, J.; Croxford, A. Fatigue Crack Inspection and Characterisation Using Non-Collinear Shear Wave Mixing. Smart Mater. Struct. 2020, 29, 055024. [Google Scholar] [CrossRef]
- Chen, H.; Li, S. Collinear Nonlinear Mixed-Frequency Ultrasound with FEM and Experimental Method for Structural Health Prognosis. Processes 2022, 10, 656. [Google Scholar] [CrossRef]
- Levy, K.; Kim, J.; Jacobs, L. Investigation of the Relationship between Classical and Nonclassical Ultrasound Nonlinearity Parameters and Microstructural Mechanisms in Metals. J. Acoust. Soc. Am. 2020, 148, 2429–2437. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, S.; Zhang, C.; Jin, L.; Yang, Q. Quantitative Testing of Residual Deformation in Plate with Varying Thickness Based on Nonlinear Ultrasound. Mater. Des. 2022, 214, 110402. [Google Scholar] [CrossRef]
- Chakrapani, S.; Barnard, D. Fatigue Damage Evaluation of Carbon Fiber Reinforced Composites Using Nonlinear Resonance Spectroscopy. Ndt E Int. 2020, 116, 110402. [Google Scholar] [CrossRef]
- Gholizadeh, S. A Review of Non-Destructive Testing Methods of Composite Materials. Procedia Struct. Integr. 2016, 1, 50–57. [Google Scholar] [CrossRef]
- Boccardi, S.; Fierro, G.; Meo, M. Nonlinear Ultrasonic Imaging of Damage in Composite Materials Using a Higher Harmonic and Modulated Multi-Path Reciprocal Method. Struct. Health Monit.-Int. J. 2021, 20, 2953–2962. [Google Scholar] [CrossRef]
- Wang, J.S.; Cheng, Y.; Xu, X.D.; Liu, X.J. Laser-Ultrasonic Investigation on Lamb Waves in Two-Dimensional Phononic Crystal Plates. Int. J. Thermophys. 2015, 36, 1195–1201. [Google Scholar] [CrossRef]
- Cheng, C.; Wu, F.G.; Zhang, X.; Yao, Y.W. Phononic Crystal Multi-Channel Low-Frequency Filter Based on Locally Resonant Unit. Acta Phys. Sin. 2014, 63, 024301. [Google Scholar] [CrossRef]
- Dong, H.-W.; Wang, Y.-S.; Zhang, C. Inverse Design of High- Q Wave Filters in Two-Dimensional Phononic Crystals by Topology Optimization. Ultrasonics 2017, 76, 109–124. [Google Scholar] [CrossRef] [PubMed]
- Katunin, A.; Dragan, K.; Dziendzikowski, M. Damage Identification in Aircraft Composite Structures: A Case Study Using Various Non-Destructive Testing Techniques. Compos. Struct. 2015, 127, 1–9. [Google Scholar] [CrossRef]
- Sun, D.; Zhu, W.; Xiang, Y.; Xuan, F.-Z. Advances in nonlinear ultrasonic detection of microcracks. Chin. Sci. Bull. 2022, 67, 597–609. [Google Scholar] [CrossRef]
- Lee, K.Y.; Jeon, W. Hierarchical Phononic Crystals for Filtering Multiple Target Frequencies of Ultrasound. Sci. Rep. 2020, 10, 8070. [Google Scholar] [CrossRef]
- Iglesias Martínez, J.A.; Moughames, J.; Ulliac, G.; Kadic, M.; Laude, V. Three-Dimensional Phononic Crystal with Ultra-Wide Bandgap at Megahertz Frequencies. Appl. Phys. Lett. 2021, 118, 063507. [Google Scholar] [CrossRef]
- Smith, E.J.; Matlack, K.H. Metal Additively Manufactured Phononic Materials as Ultrasonic Filters in Nonlinear Ultrasound Measurements. J. Acoust. Soc. Am. 2021, 149, 3739–3750. [Google Scholar] [CrossRef]
- Liu, T.-W.; Chan, C.-T.; Wu, R.-T. Deep-Learning-Based Acoustic Metamaterial Design for Attenuating Structure-Borne Noise in Auditory Frequency Bands. Materials 2023, 16, 1879. [Google Scholar] [CrossRef]
- Hinuma, Y.; Pizzi, G.; Kumagai, Y.; Oba, F.; Tanaka, I. Band Structure Diagram Paths Based on Crystallography. Comput. Mater. Sci. 2017, 128, 140–184. [Google Scholar] [CrossRef]
- Li, F.; Zhao, Y.; Cao, P.; Hu, N. Mixing of Ultrasonic Lamb Waves in Thin Plates with Quadratic Nonlinearity. Ultrasonics 2018, 87, 33–43. [Google Scholar] [CrossRef] [PubMed]







| Reference | PC Configuration | Working Frequency | Parameter Analysis | Design Method |
|---|---|---|---|---|
| Lee et al. [38] | hierarchical PCs | 20 kHz~10 MHz | - | - |
| Iglesias M. et al. [39] | cubic symmetry | 0.6~7.5 MHz | - | - |
| Elizabeth J. et al. [40] | cubic, beam | 100 kHz~5 MHz | - | - |
| Liu et al. [41] | plate | ~3 kHz | geometry | deep learning method |
| This work | cubic | 1~10 MHz | material/geometry | dimensionless method |
| L/mm | d/mm | Band Gap Center Frequency/MHz | Band Gap Type | Filtering Ability |
|---|---|---|---|---|
| 0.35 | 0.3 | 4.69 | First | × |
| 0.35 | 0.3 | 3.98 | Second | × |
| 0.35 | 0.3 | 1.83 | Third | √ |
| 0.4 | 0.2 | 3.52 | First | × |
| 0.4 | 0.2 | 3.15 | Second | √ |
| 0.45 | 0.2 | 3.69 | First | × |
| 0.45 | 0.2 | 3.34 | Second | × |
| 0.45 | 0.2 | 3.04 | Third | √ |
| 0.5 | 0.25 | 2.81 | First | × |
| 0.5 | 0.25 | 2.52 | Second | √ |
| 0.5 | 0.3 | 2.15 | First | √ |
| 0.5 | 0.3 | 1.28 | Second | × |
| 0.5 | 0.4 | 1.63 | First | √ |
| 0.5 | 0.4 | 1.37 | Second | √ |
| L/mm | d/mm | Fundamental Frequency/MHz | Second Harmonic Frequency/MHz | Adapt to Linear Correlation | Filtering Ability |
|---|---|---|---|---|---|
| 0.4 | 0.2 | 3.5 | 7 | No | × |
| 0.45 | 0.2 | 3.34 | 6.68 | No | × |
| 0.45 | 0.2 | 3.69 | 7.38 | No | × |
| 0.5 | 0.3 | 1.28 | 2.56 | No | × |
| 0.6 | 0.2 | 2.97 | 5.94 | No | × |
| 0.45 | 0.2 | 3.34 | 6.68 | No | × |
| 0.4 | 0.2 | 3.15 | 6.3 | Yes | √ |
| 0.45 | 0.3 | 1.82 | 3.64 | Yes | √ |
| 0.5 | 0.3 | 2.15 | 4.3 | Yes | √ |
| 0.5 | 0.4 | 1.54 | 3.08 | Yes | √ |
| 0.5 | 0.4 | 1.62 | 3.24 | Yes | √ |
| 0.5 | 0.4 | 1.37 | 2.74 | Yes | √ |
| 1 | 0.6 | 1 | 2 | Yes | √ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Zhao, Y.; Cao, P. Second Harmonic Modulation for Ultrasonic Signals Based on the Design of the Phononic Crystal Filter. Sensors 2023, 23, 9227. https://doi.org/10.3390/s23229227
Zhu Y, Zhao Y, Cao P. Second Harmonic Modulation for Ultrasonic Signals Based on the Design of the Phononic Crystal Filter. Sensors. 2023; 23(22):9227. https://doi.org/10.3390/s23229227
Chicago/Turabian StyleZhu, Yue, Youxuan Zhao, and Peng Cao. 2023. "Second Harmonic Modulation for Ultrasonic Signals Based on the Design of the Phononic Crystal Filter" Sensors 23, no. 22: 9227. https://doi.org/10.3390/s23229227
APA StyleZhu, Y., Zhao, Y., & Cao, P. (2023). Second Harmonic Modulation for Ultrasonic Signals Based on the Design of the Phononic Crystal Filter. Sensors, 23(22), 9227. https://doi.org/10.3390/s23229227








