Trajectory-BERT: Trajectory Estimation Based on BERT Trajectory Pre-Training Model and Particle Filter Algorithm
Abstract
:1. Introduction
- The BERT model has been adapted to train sequences of continuous trajectory, and the pre-training model for the BERT trajectory has been acquired;
- For the task scenario, the BERT trajectory pre-training model and the particle filter algorithm are combined to construct a candidate trajectory set for the observed trajectory;
- The BERT trajectory pre-training model is used to calculate the maximum posterior probability of trajectory under trajectory sets and obtain the optimal trajectory estimation.
2. Methodology
2.1. The Task Scenario
2.2. Decision Criteria
| Algorithm 1: Procedure for calculating the maximum a posteriori probability |
| 1: Input an alternative trajectory and compute its prior probability ; 2: The input trajectory sequence is masked point by point and fed into the BERT trajectory pre-training model to calculate the prior probability of trajectory points: ; 3: The prior probability of the entire trajectory is estimated by multiplying the conditional probabilities one by one: ; 4: Calculate the Likelihood: ; 5: Calculate the posterior probability: . |
2.3. Trajectory Pre-Processing
3. Train Model
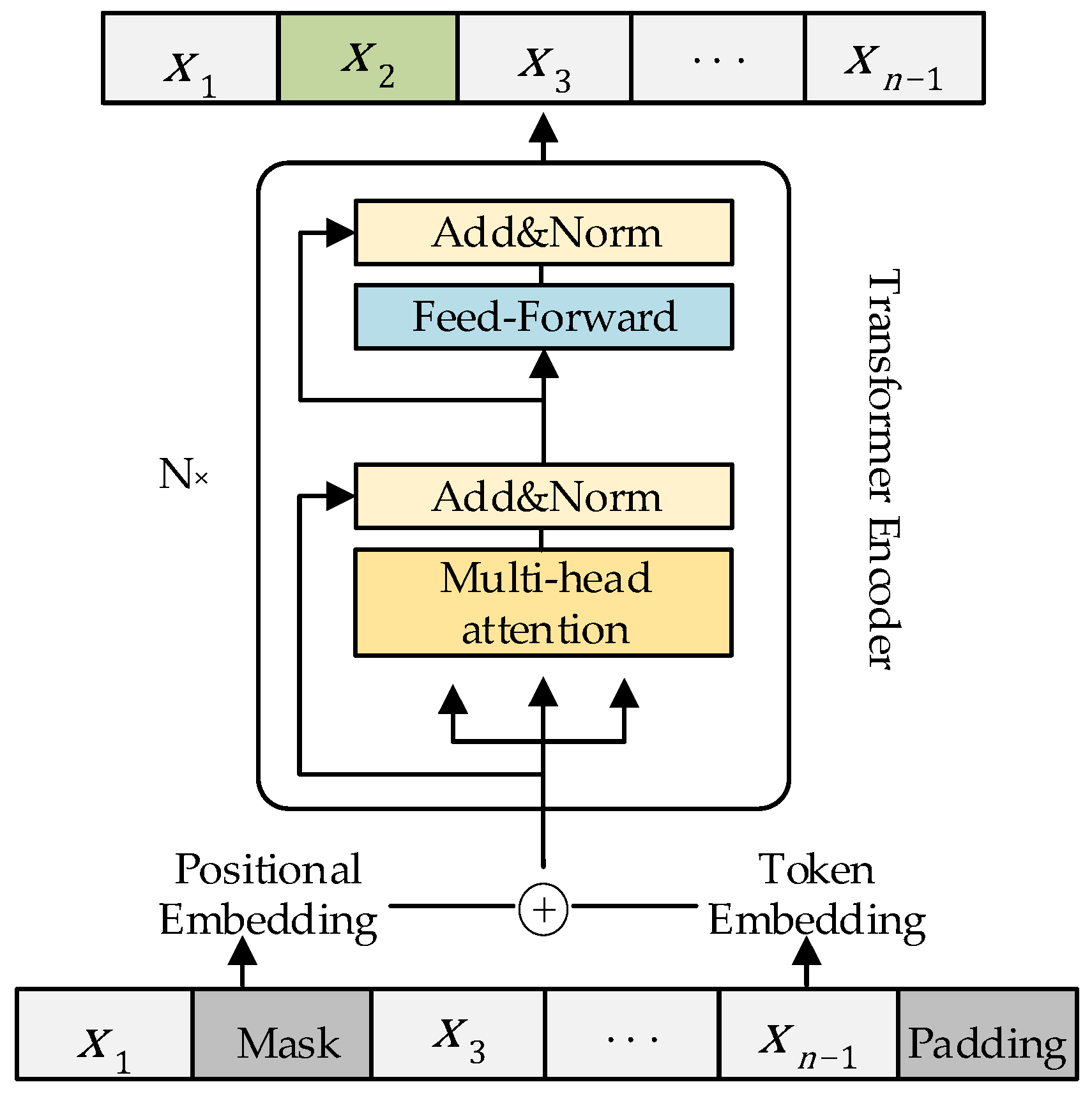
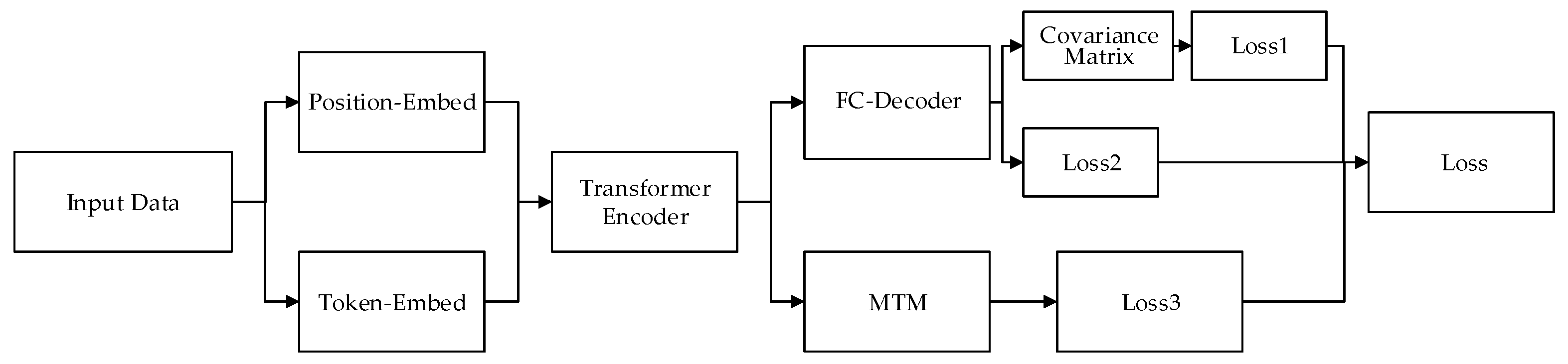
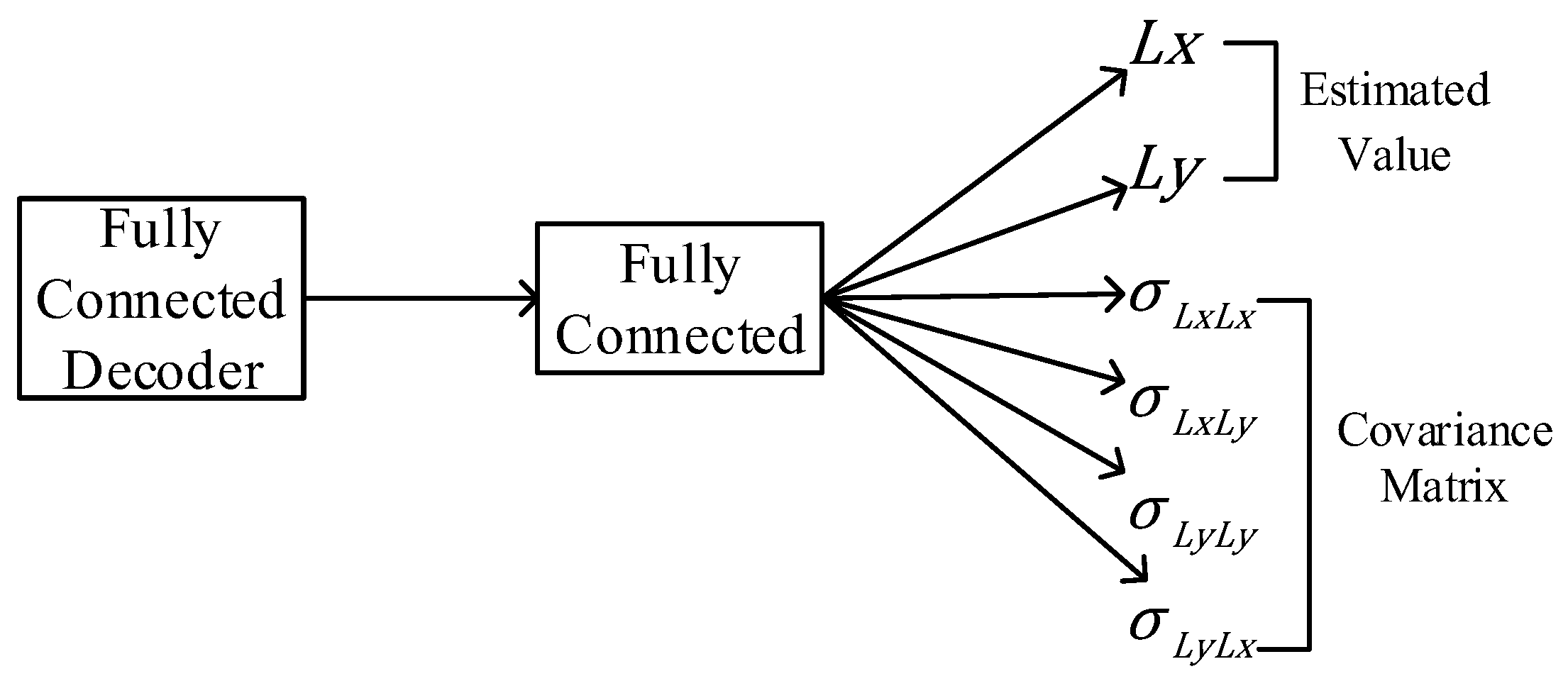
3.1. Model Structure
3.2. Loss Function
4. Set of Alternative Trajectories
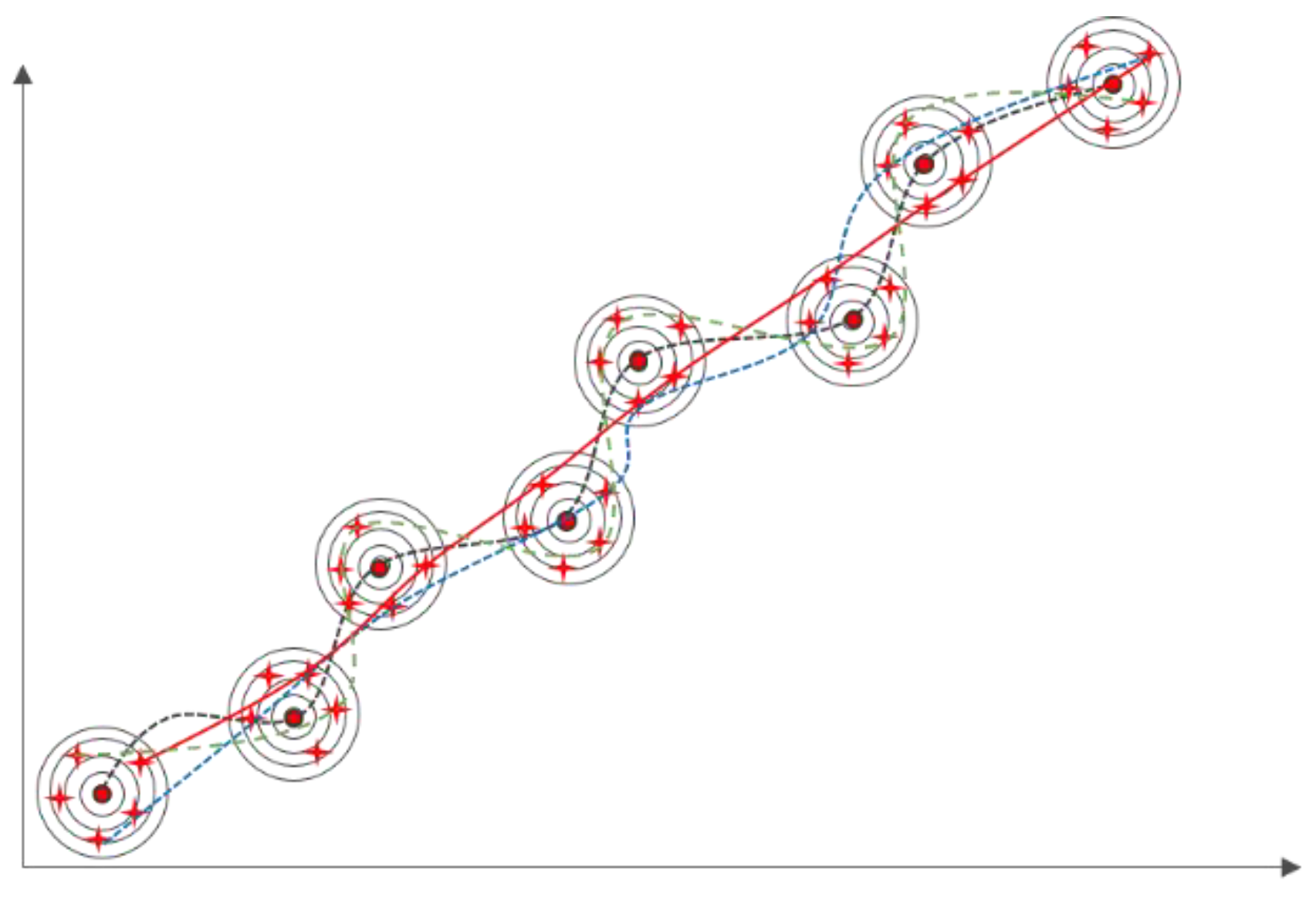
4.1. Particle Filter
| Algorithm 2: Process of traditional particle filter algorithm |
| 1: Setting initial values: ; 2: Generate particles and initial weights, and set the number of generated particles as : ; 3: Prediction step: , ; 4: Update step: the observation is assumed to be , , is the probability density function of the observation noise; 5: Weights are normalized: ; 6: The new particle and the new weight are calculated; 7: Repeat steps 3, 4, and 5 to obtain new particles and weights in a cycle |
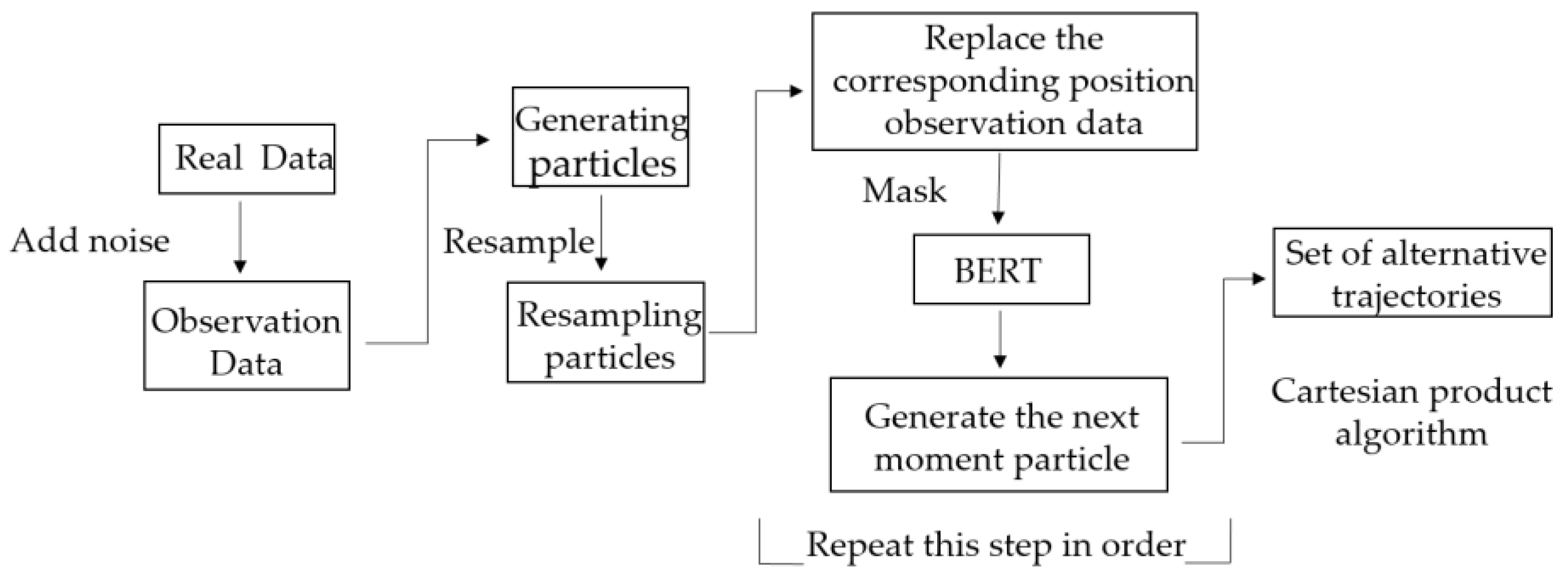
4.2. Construct the Set of Alternative Trajectories
| Algorithm 3: Improved particle filter Algorithm A |
| Trajectory of observation: ; 1: Create the primary particles: ; 2: Obtain m trajectories with varying initial observations: ; 3: Mask the trajectory data: ; 4: The second batch of particles is generated by the BERT trajectory pre-training model: ; 5: Mask the trajectory data: ; 6: The third batch of particles is generated by the BERT trajectory pre-training model: ; 7: Alternate trajectories are obtained by generating particles one by one in order: . |
| Algorithm 4: Improved particle filter Algorithm B |
| Trajectory of Observation: ; 1: Create the primary particles: ; 2: Obtain m trajectories with varying initial observations: ; 3: Mask the trajectory data: ; 4: The second batch of particles is generated by the BERT trajectory pre-training model: ; 5: Mask the trajectory data: ; 6: The third batch of particles is generated by the BERT trajectory pre-training model: ; 7: Alternate trajectories are obtained by generating particles one by one in order: . |
5. Experimental Analysis
5.1. Evaluation Indicators
5.2. Datasets
5.3. Experimental Parameter Settings
5.4. Analysis of Experimental Results
5.4.1. Comparison of Different Loss Functions
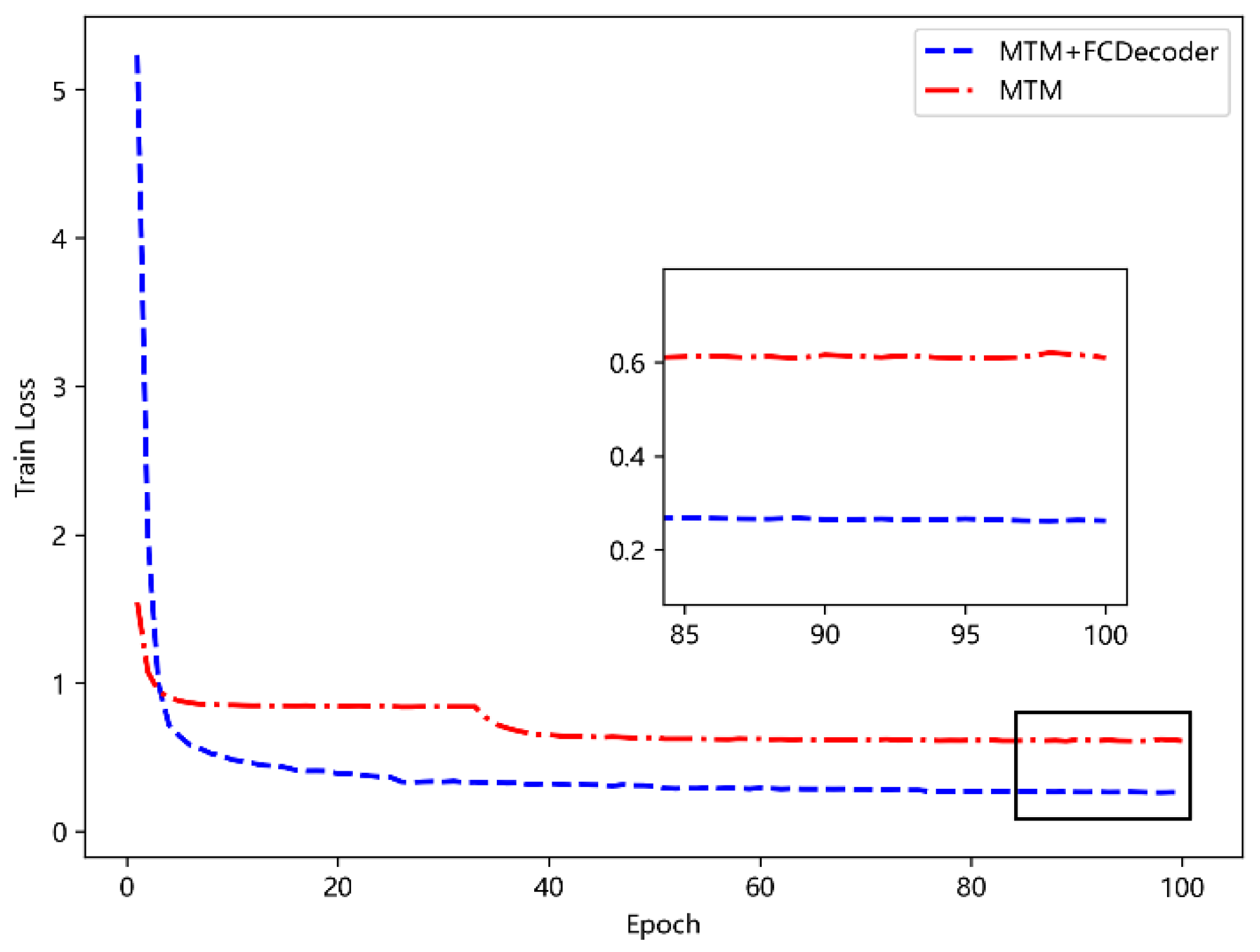
5.4.2. Functional Analysis of the FC-Decode Layer
5.4.3. Effect Analysis of Positional Embedding and Token Embedding
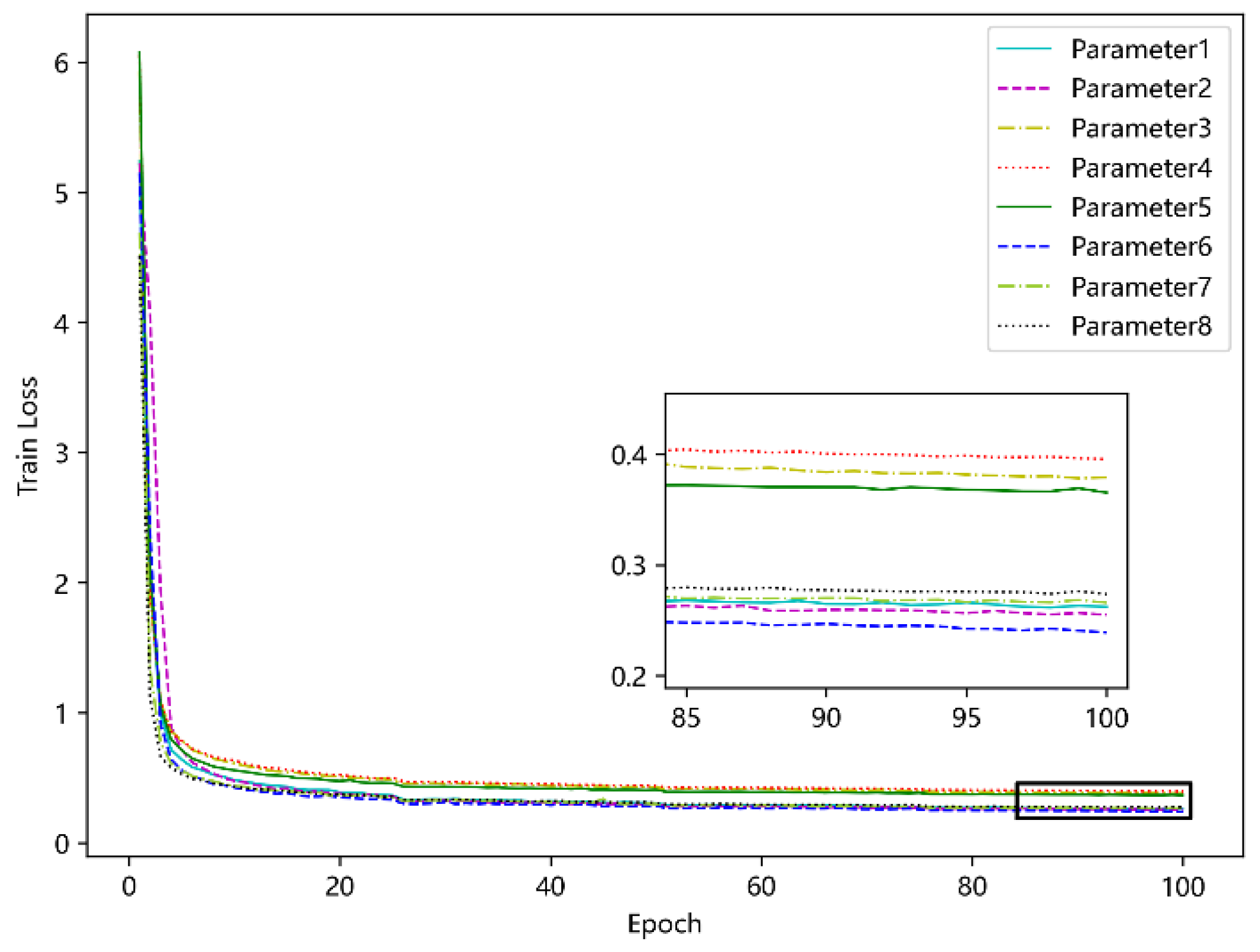
5.4.4. Determine the Optimal Parameters of the Model
5.4.5. Verify the Model Training Effect
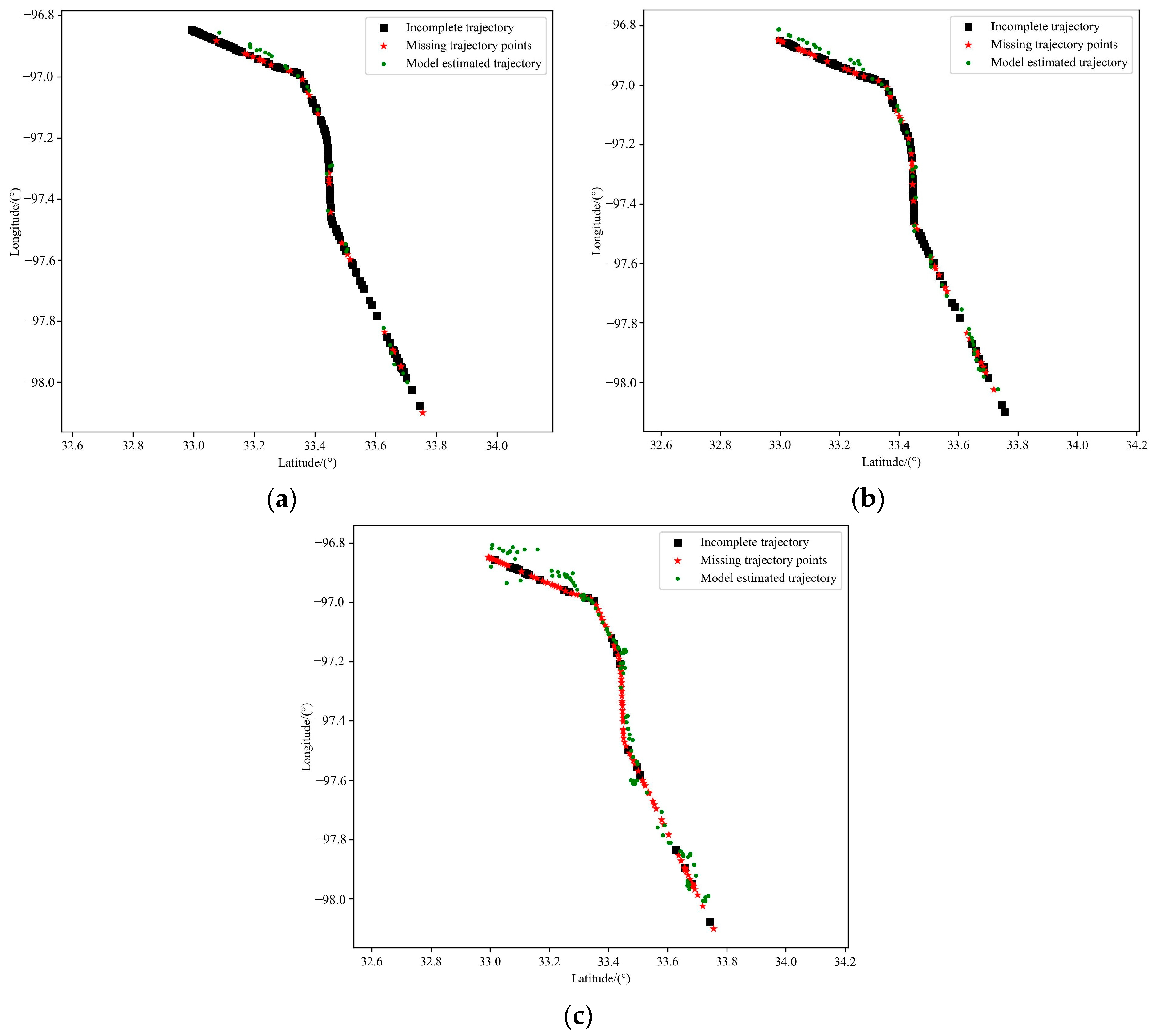
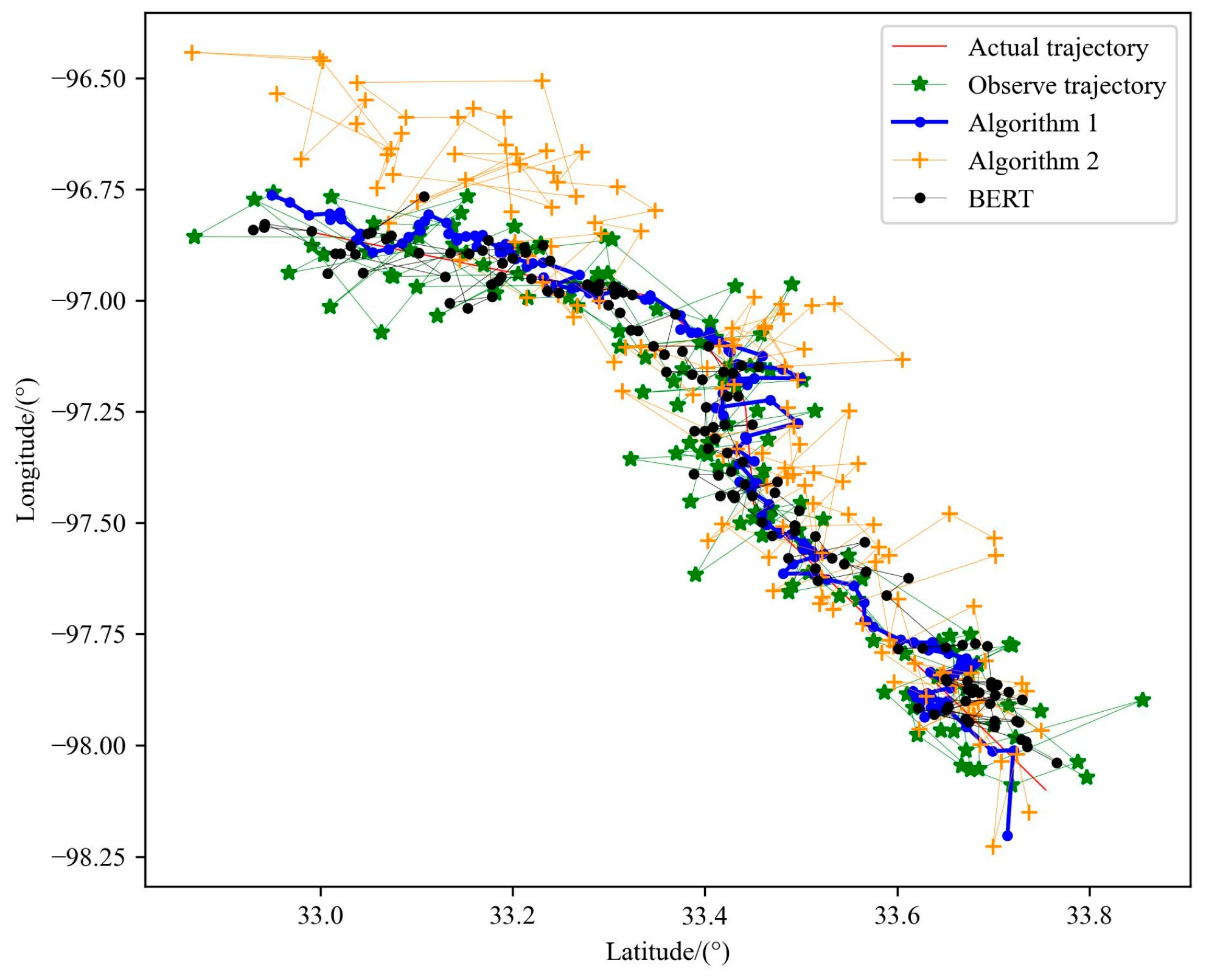
5.4.6. Comparison of Performance of Two Particle Filter Algorithms
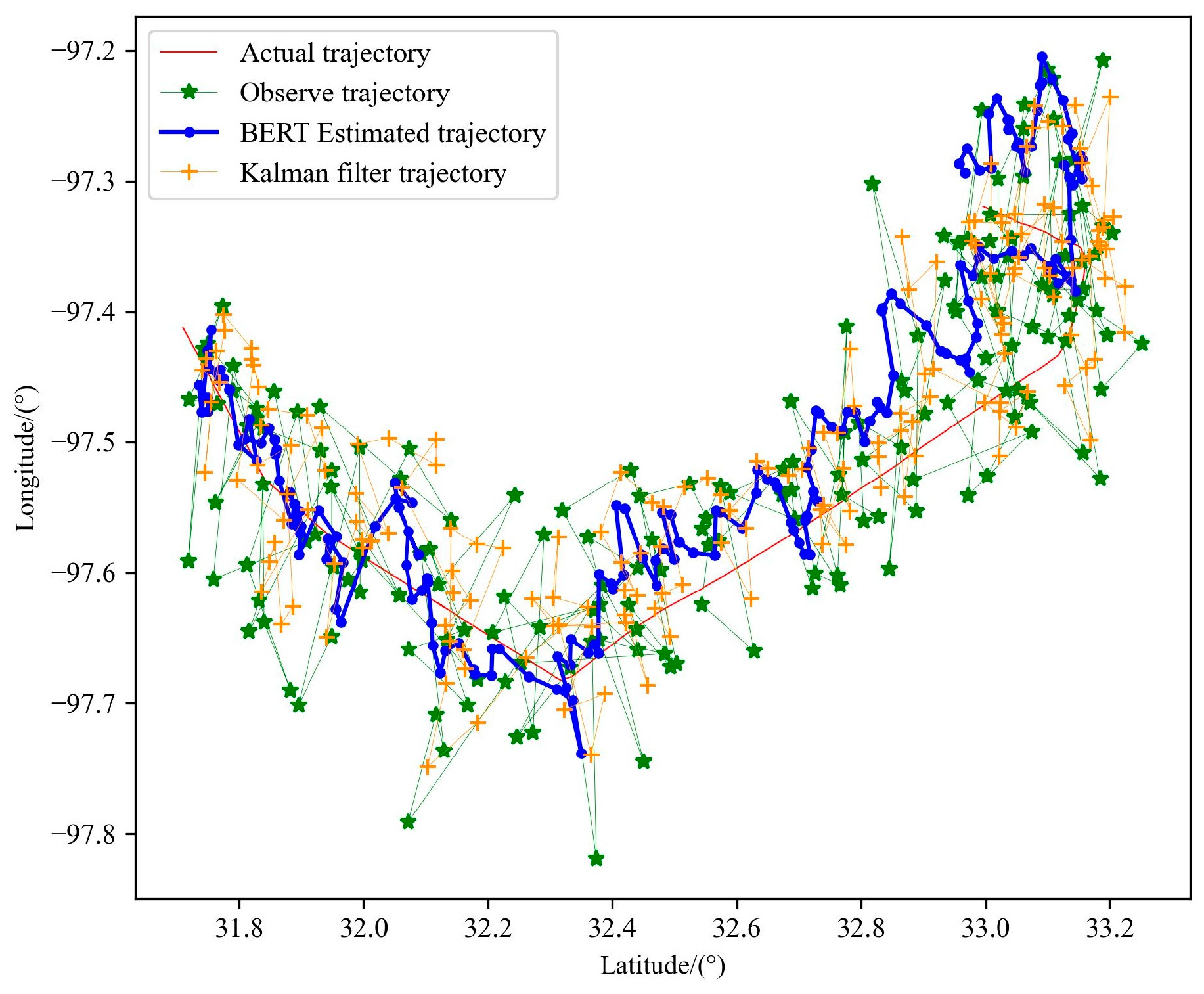
5.4.7. Compare Kalman Filter Algorithms
| Algorithm 5: Kalman filter algorithm process |
| 1: A priori estimate: 2: The covariance of the prior estimate: 3: Calculate Kalman gain: 4: Update the estimate: 5: Update the covariance matrix: |
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schafer, M.; Strohmeier, M.; Lenders, V.; Martinovic, I.; Wilhelm, M. Bringing up OpenSky: A large-scale ADS-B sensor network for research. In Proceedings of the Ipsn-14 International Symposium on Information Processing in Sensor Networks, Berlin, Germany, 15–17 April 2014; pp. 83–94. [Google Scholar]
- Graser, A. An exploratory data analysis protocol for identifying problems in continuous movement data. J. Locat. Based Serv. 2021, 15, 89–117. [Google Scholar] [CrossRef]
- Kontopoulos, I.; Makris, A.; Tserpes, K. A Deep Learning Streaming Methodology for Trajectory Classification. ISPRS Int. J. Geo-Inf. 2021, 10, 250. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Y.; Achuthan, K.; Zhang, X. A ship movement classification based on Automatic Identification System (AIS) data using Convolutional Neural Network. Ocean Eng. 2020, 218, 108182. [Google Scholar] [CrossRef]
- Franco, L.; Placidi, L.; Giuliari, F.; Hasan, I.; Cristani, M.; Galasso, F. Under the hood of transformer networks for trajectory forecasting. Pattern Recognit. 2023, 138, 109372. [Google Scholar] [CrossRef]
- Giuliari, F.; Hasan, I.; Cristani, M.; Galasso, F. Transformer Networks for Trajectory Forecasting. arXiv 2020, arXiv:2003.08111. [Google Scholar]
- Guo, D.; Wu, E.Q.; Wu, Y.; Zhang, J.; Law, R.; Lin, Y. FlightBERT: Binary Encoding Representation for Flight Trajectory Prediction. IEEE Trans. Intell. Transp. Syst. 2022, 24, 1828–1842. [Google Scholar] [CrossRef]
- Gao, C.; Yan, J.; Zhou, S.; Varshney, P.K.; Liu, H. Long short-term memory-based deep recurrent neural networks for target tracking. Inf. Sci. 2019, 502, 279–296. [Google Scholar] [CrossRef]
- Gao, C.; Yan, J.; Zhou, S.; Chen, B.; Liu, H. Long short-term memory-based recurrent neural networks for nonlinear target tracking. Signal Process. 2019, 164, 67–73. [Google Scholar] [CrossRef]
- Zeng, J.; Zhao, Y.; Yu, Y.; Gao, M.; Zhou, W.; Wen, J. BMAM: Complete the missing POI in the incomplete trajectory via mask and bidirectional attention model. EURASIP J. Wirel. Commun. Netw. 2022, 2022, 53. [Google Scholar] [CrossRef]
- Harrison, M. ADS-X the Next Gen Approach for the Next Generation Air Transportation System. In Proceedings of the 25th Digital Avionics Systems Conference, Portland, OR, USA, 15–19 October 2006; pp. 1–8. [Google Scholar]
- Luckenbaugh, G.; Landriau, S.; Dehn, J.; Rudolph, S. Service Oriented Architecture for the Next Generation Air Transportation System. In Proceedings of the Integrated Communications, Navigation and Surveillance Conference, Herndon, VA, USA, 30 April–3 May 2007; pp. 1–9. [Google Scholar]
- Sipe, A.; Moore, J. Air traffic functions in the NextGen and SESAR airspace. In Proceedings of the IEEE/AIAA Digital Avionics Systems Conference, Orlando, FL, USA, 23–29 October 2009; pp. 2.A.6-1–2.A.6-7. [Google Scholar]
- Wang, X.; Jiang, X.; Chen, L.; Wu, Y. KVLMM: A Trajectory Prediction Method Based on a Variable-Order Markov Model with Kernel Smoothing. IEEE Access 2018, 6, 25200–25208. [Google Scholar] [CrossRef]
- Chiou, Y.S.; Wang, C.L.; Yeh, S.C. Reduced-complexity scheme using alpha–beta filtering for location tracking. IET Commun. 2011, 5, 1806–1813. [Google Scholar] [CrossRef]
- Sanchez Pedroche, D.; Amigo, D.; Garcia, J.; Molina, J.M. Architecture for Trajectory-Based Fishing Ship Classification with AIS Data. Sensors 2020, 20, 3782. [Google Scholar] [CrossRef]
- Huang, H.; Hong, F.; Liu, J.; Liu, C.; Feng, Y.; Guo, Z. FVID: Fishing Vessel Type Identification Based on VMS Trajectories. J. Ocean Univ. China 2018, 18, 403–412. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Li, X. Exploring the Context of Locations for Personalized Location Recommendations; AAAI Press: Washington, DC, USA, 2016. [Google Scholar]
- Crivellari, A.; Beinat, E. From Motion Activity to Geo-Embeddings: Generating and Exploring Vector Representations of Locations, Traces and Visitors through Large-Scale Mobility Data. ISPRS Int. J. Geo-Inf. 2019, 8, 134. [Google Scholar] [CrossRef]
- Nawaz, A.; Huang, Z.; Wang, S.; Akbar, A.; AlSalman, H.; Gumaei, A. GPS Trajectory Completion Using End-to-End Bidirectional Convolutional Recurrent Encoder-Decoder Architecture with Attention Mechanism. Sensors 2020, 20, 5143. [Google Scholar] [CrossRef] [PubMed]
- Crivellari, A.; Resch, B.; Shi, Y. TraceBERT-A Feasibility Study on Reconstructing Spatial-Temporal Gaps from Incomplete Motion Trajectories via BERT Training Process on Discrete Location Sequences. Sensors 2022, 22, 1682. [Google Scholar] [CrossRef] [PubMed]
- Musleh, M.; Mokbel, M. A Demonstration of KAMEL: A Scalable BERT-based System for Trajectory Imputation. In Proceedings of the Companion of the 2023 International Conference on Management of Data, Seattle, WA, USA, 18–23 June 2023; pp. 191–194. [Google Scholar]
- Wang, A.; Cho, K. BERT has a Mouth, and It Must Speak: BERT as a Markov Random Field Language Model. arXiv 2019, arXiv:1902.04094. [Google Scholar]
- Goyal, K.; Dyer, C.; Berg-Kirkpatrick, T. Exposing the Implicit Energy Networks behind Masked Language Models via Metropolis—Hastings. arXiv 2021, arXiv:2106.02736. [Google Scholar]
- Yamakoshi, T.; Hawkins, R.D.; Griffiths, T.L. Probing BERT’s priors with serial reproduction chains. arXiv 2022, arXiv:2202.12226. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Wu, Y.; Yu, H.; Du, J.; Liu, B.; Yu, W. An Aircraft Trajectory Prediction Method Based on Trajectory Clustering and a Spatiotemporal Feature Network. Electronics 2022, 11, 3453. [Google Scholar] [CrossRef]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space. arXiv 2013, arXiv:1301.3781. [Google Scholar]





| Parameter | The Numerical |
|---|---|
| Optimizer | Adam |
| Rate of learning | l−3 |
| Weight decline | l−5 |
| Epoch | 100 |
| Batch Size | 1024 |
| Dropout | 0.1 |
| Sequence length | 100 |
| Parameter Setting | Loss | ||||
|---|---|---|---|---|---|
| Input Dimensions | Output Dimensions | Number of Heads | Number of Encoder | ||
| Parameter 1 | 128 | 256 | 4 | 4 | 0.2619 |
| Parameter 2 | 256 | 256 | 4 | 4 | 0.2547 |
| Parameter 3 | 128 | 128 | 4 | 4 | 0.3783 |
| Parameter 4 | 64 | 128 | 4 | 4 | 0.3956 |
| Parameter 5 | 256 | 128 | 4 | 4 | 0.3653 |
| Parameter 6 | 256 | 256 | 2 | 4 | 0.2387 |
| Parameter 7 | 256 | 256 | 4 | 2 | 0.2657 |
| Parameter 8 | 256 | 256 | 2 | 2 | 0.2734 |
| Percentage of Missing Points | Evaluation Indicators | |
|---|---|---|
| MAE | MEDV/km | |
| 20% | 0.00319 | 0.484 |
| 40% | 0.00873 | 1.358 |
| 80% | 0.02123 | 3.391 |
| Parameter | Trajectory Data | MAE | MEDV/km | |
|---|---|---|---|---|
| Number of Particles | Number of Alternative Trajectories | |||
| \ | \ | Observe Trajectory | 0.05115 | 8.183 |
| 15 | 500,000 | Algorithm A Trajectory | 0.02843 | 4.492 |
| 15 | 500,000 | Algorithm B Trajectory | 0.09796 | 15.408 |
| \ | \ | BERT | 0.03015 | 4.860 |
| Parameter | Trajectory Data | MAE | MEDV/km | |
|---|---|---|---|---|
| Number of Particles | Number of Alternative Trajectories | |||
| \ | \ | Observe Trajectory | 0.05342 | 8.301 |
| 15 | 500,000 | Trajectory estimation by BERT | 0.03104 | 4.913 |
| \ | \ | Trajectory estimation by Kalman filter | 0.03522 | 5.529 |
| Parameter | Trajectory Data | MAE | MEDV/km | |
|---|---|---|---|---|
| Number of Particles | Number of Alternative Trajectories | |||
| \ | \ | Observe Trajectory | 0.04665 | 7.390 |
| 15 | 500,000 | Trajectory estimation by BERT | 0.03508 | 5.435 |
| \ | \ | Trajectory estimation by Kalman filter | 0.03887 | 6.267 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Yu, H.; Du, J.; Ge, C. Trajectory-BERT: Trajectory Estimation Based on BERT Trajectory Pre-Training Model and Particle Filter Algorithm. Sensors 2023, 23, 9120. https://doi.org/10.3390/s23229120
Wu Y, Yu H, Du J, Ge C. Trajectory-BERT: Trajectory Estimation Based on BERT Trajectory Pre-Training Model and Particle Filter Algorithm. Sensors. 2023; 23(22):9120. https://doi.org/10.3390/s23229120
Chicago/Turabian StyleWu, You, Hongyi Yu, Jianping Du, and Chenglong Ge. 2023. "Trajectory-BERT: Trajectory Estimation Based on BERT Trajectory Pre-Training Model and Particle Filter Algorithm" Sensors 23, no. 22: 9120. https://doi.org/10.3390/s23229120
APA StyleWu, Y., Yu, H., Du, J., & Ge, C. (2023). Trajectory-BERT: Trajectory Estimation Based on BERT Trajectory Pre-Training Model and Particle Filter Algorithm. Sensors, 23(22), 9120. https://doi.org/10.3390/s23229120








