Robust H-Infinity Tracking Control for a Valve-Controlled Hydraulic Motor System with Uncertain Parameters in the Complex Load Environment
Abstract
1. Introduction
2. Valve-Controlled Hydraulic Motor System Model
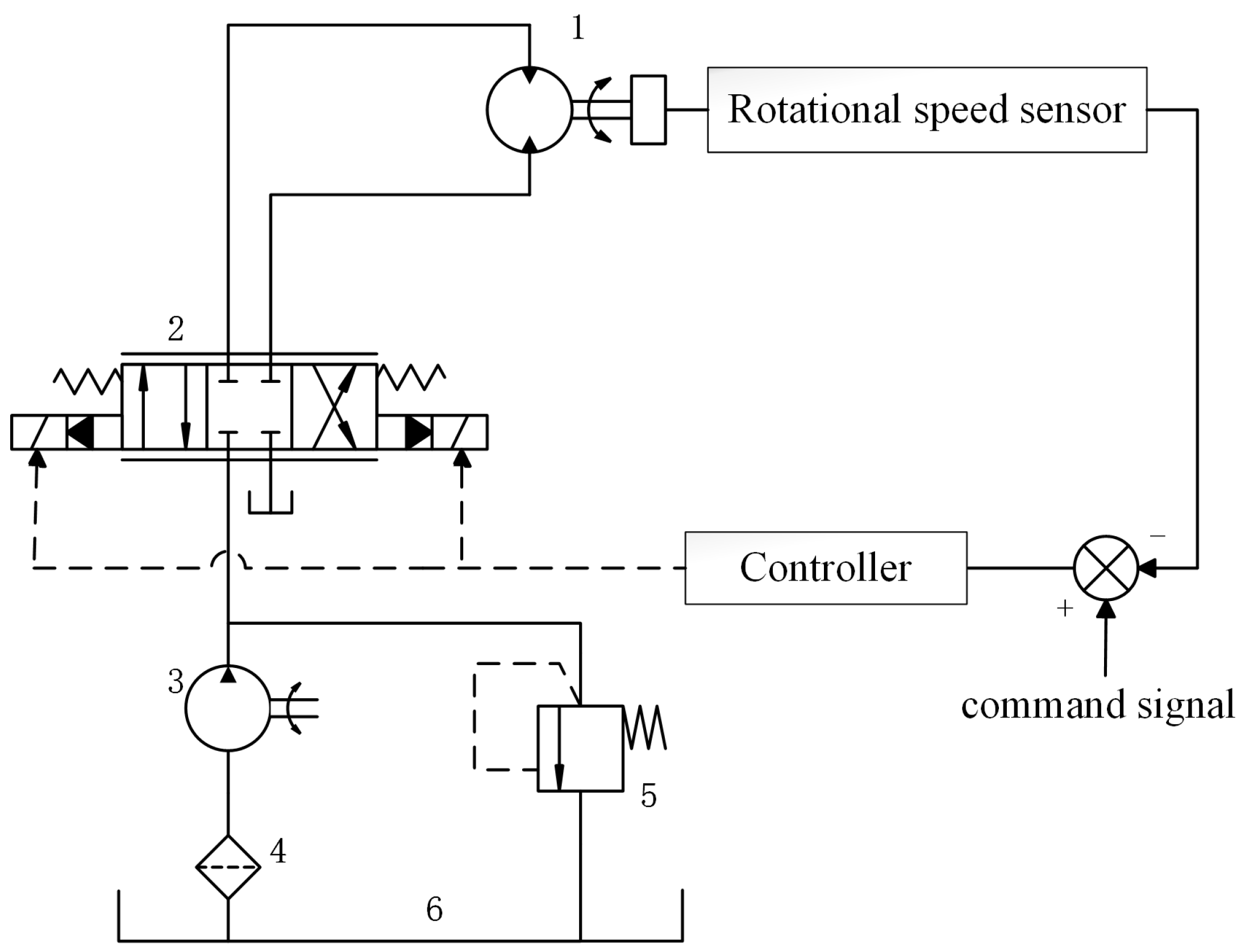
2.1. System Composition
2.2. Dynamic Model
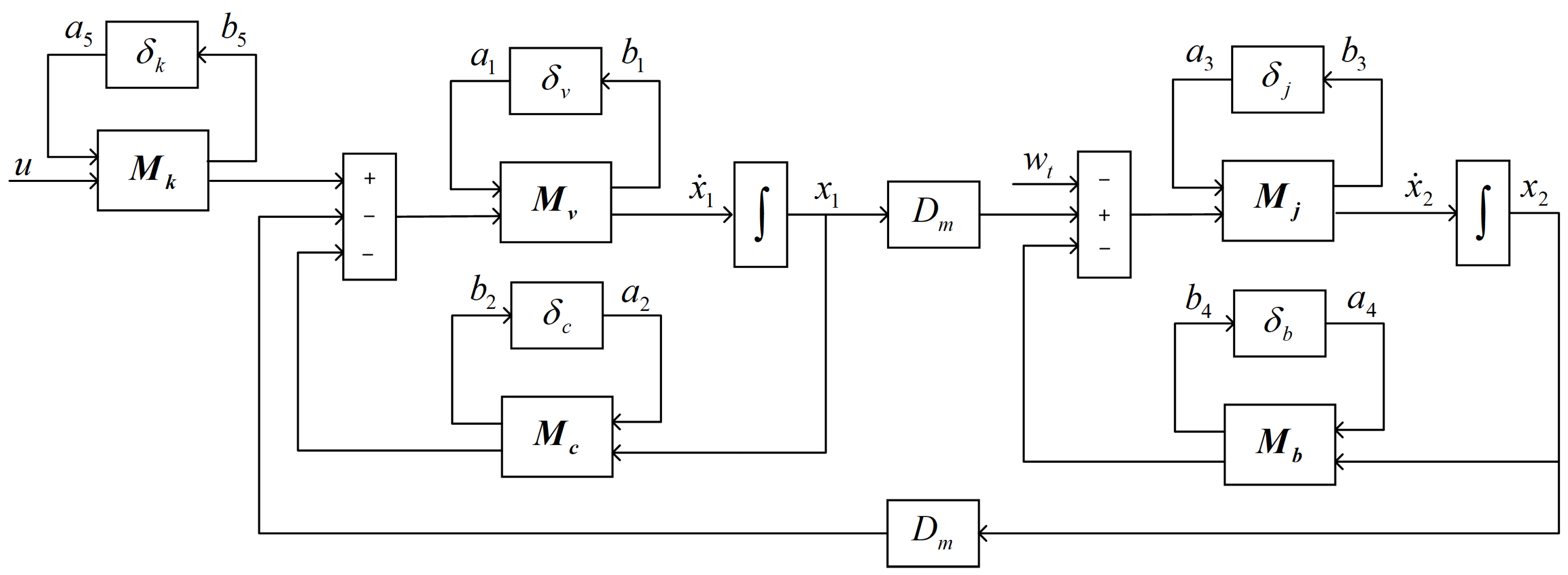
2.3. Model with Uncertainties
3. H-Infinity Tracking Control
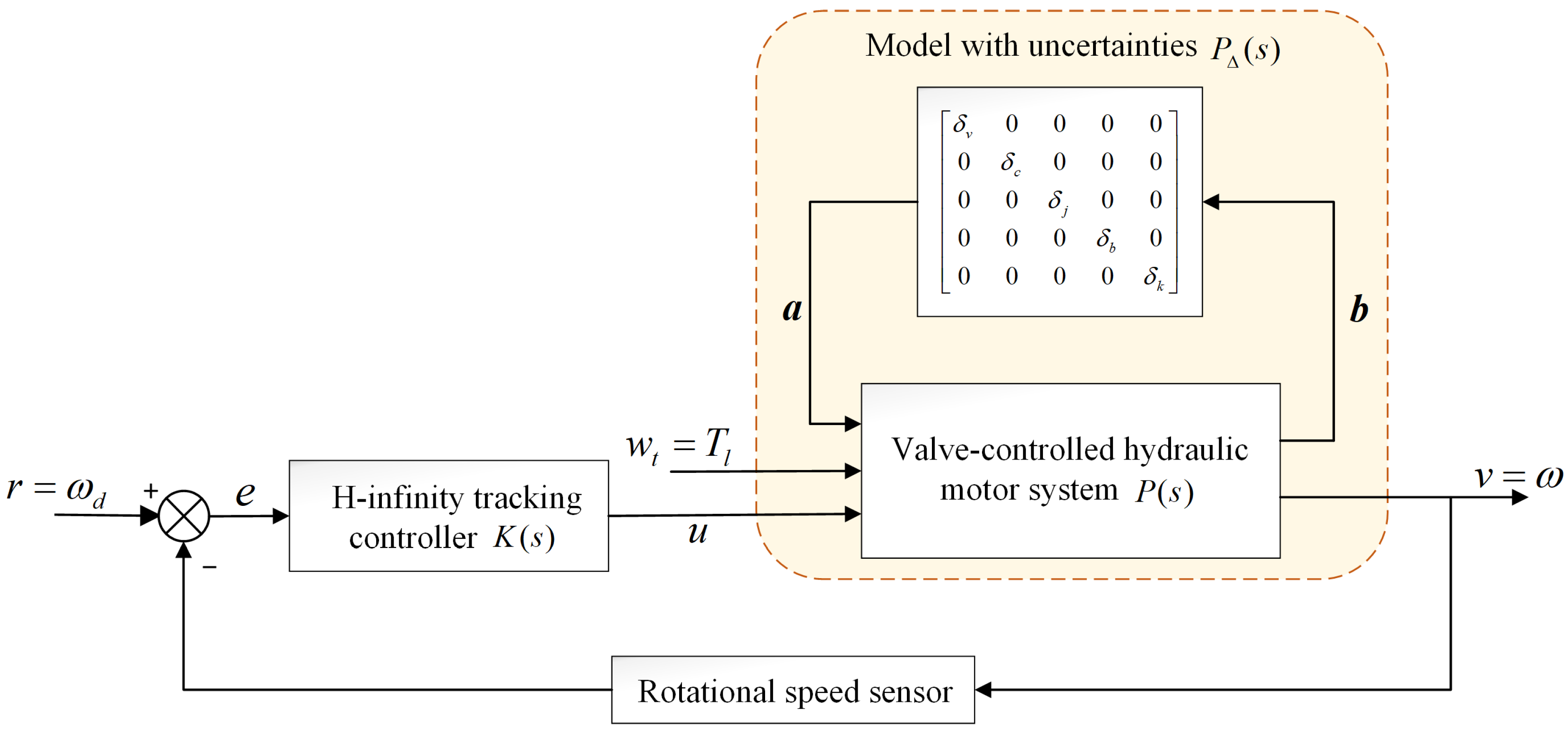
3.1. H-Infinity Control Method with Uncertainty
3.2. Design of H-Infinity Tracking Controller
4. Simulation Results
4.1. Without Load Torque
4.2. Load Torque Abrupt Change
4.3. Single-Frequency Load Torque Condition
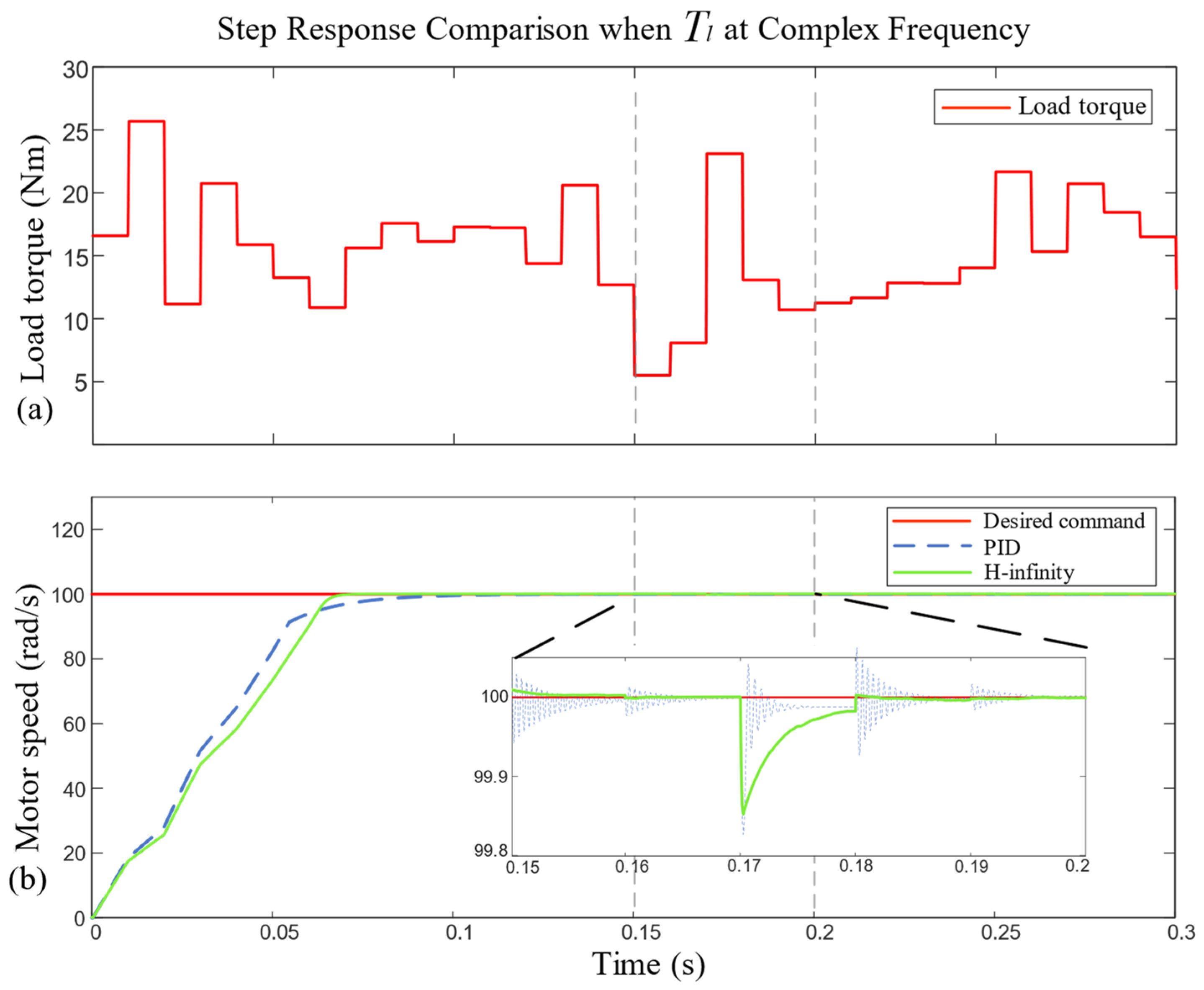
4.4. Complex-Frequency Load Torque Condition
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jelali, M.; Kroll, A. Hydraulic Servo-Systems: Modelling, Identification and Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2002; ISBN 1852336927. [Google Scholar]
- Yao, J. Model-based nonlinear control of hydraulic servo systems: Challenges, developments and perspectives. Front. Mech. Eng. 2018, 13, 179–210. [Google Scholar] [CrossRef]
- Guo, Y.; Cheng, W.; Gong, D.; Zhang, Y.; Zhang, Z.; Xue, G. Adaptively robust rotary speed control of an anchor-hole driller under varied surrounding rock environments. Control Eng. Pract. 2019, 86, 24–36. [Google Scholar] [CrossRef]
- Gu, K.K.; Lin, Q.; Wang, W.J.; Wang, H.Y.; Guo, J.; Liu, Q.Y.; Zhu, M.H. Analysis on the effects of rotational speed of grinding stone on removal behavior of rail material. Wear 2015, 342, 52–59. [Google Scholar] [CrossRef]
- Kim, H.; Choi, Y.; Park, J.; Lee, J.; Kim, J.; Lee, H.; Lee, J.; Suh, J. Active control for rock grinding works of an underwater construction robot consisting of hydraulic rotary and linear actuators. In International Conference on Advanced Engineering Theory and Applications; Springer International Publishing: Cham, Switzerland, 2016; pp. 713–722. [Google Scholar]
- Korchagin, P.A.; Teterina, I.A.; Korchagina, E.A. Road roller operator’s vibroprotection system improvement. J. Phys. Conf. Ser. 2021, 1791, 12012. [Google Scholar] [CrossRef]
- Issabek, Z.; Kadyrov, Z.; Kim, A. Automatic Control System of Asphalt Concrete Milling Process Based on Road Milling Machines. Int. Rev. Mech. Eng. 2021, 15, 394–405. [Google Scholar] [CrossRef]
- Kim, W.; Chen, X.; Lee, Y.; Chung, C.C.; Tomizuka, M. Discrete-time nonlinear damping backstepping control with observers for rejection of low and high frequency disturbances. Mech. Syst. Signal Process. 2018, 104, 436–448. [Google Scholar] [CrossRef]
- Dubonjić, L.; Prodanović, S.; Stojanović, V.; Morato, M.M. PD controller design for a system of a valve controlled hydromotor. Engineering Today 2023, 2. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, C.; Li, J.; Tan, Y. Research on servo valve-controlled hydraulic motor system based on active disturbance rejection control. Meas. Control 2023, 1268509181. [Google Scholar] [CrossRef]
- Hu, Y.; Li, D. An improved active disturbance rejection controller for hydraulic valve-controlled hydraulic motor. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 6037–6042. [Google Scholar]
- Wang, X.; Feng, Y.; Sun, Y. Research on improved active disturbance rejection control of continuous rotary motor electro-hydraulic servo system. J. Cent. South Univ. 2020, 27, 3733–3743. [Google Scholar] [CrossRef]
- Yan, H.; Xu, L.; Dong, L. Finite-Time Sliding Mode Control of the Valve-Controlled Hydraulic System. In Proceedings of the 2018 10th International Conference on Modelling, Identification and Control (ICMIC), Guiyang, China, 2–4 July 2018; pp. 1–5. [Google Scholar]
- Simon, D. Optimal State Estimation: Kalman, H infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006; ISBN 0470045337. [Google Scholar]
- Ali, H.H.; Fales, R.C. A review of flow control methods. Int. J. Dyn. Control 2021, 9, 1847–1854. [Google Scholar] [CrossRef]
- Ackermann, J.; Bartlett, A.; Kaesbauer, D.; Sienel, W.; Steinhauser, R. Robust Control: Systems with Uncertain Physical Parameters; Springer: Berlin/Heidelberg, Germany, 1993; ISBN 0387198431. [Google Scholar]
- Manring, N.D.; Fales, R.C. Hydraulic Control Systems; John Wiley & Sons: Hoboken, NJ, USA, 2019; ISBN 1119416477. [Google Scholar]
- Ali, H.H.; Khafaji, S.O.W.; Al-Bakri, F.F. H∞ LOOP SHAPING CONTROL DESIGN OF THE ROTATIONAL VELOCITY OF A HYDRAULIC MOTOR. Int. J. Mechatron. Appl. Mech. 2021, 10, 72–79. [Google Scholar]
- Yan, X.; Wang, P.; Qing, J.; Wu, S.; Zhao, F. Robust power control design for a small pressurized water reactor using an H infinity mixed sensitivity method. Nucl. Eng. Technol. 2020, 52, 1443–1451. [Google Scholar] [CrossRef]
- Ijaz, S.; Javaid, U.; Ashraf, M.A.; Khan, Y.A. Mixed sensitivity∞ controller design for force tracking control of electro-hydraulic servo system. In Proceedings of the 2018 15th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 9–13 January 2018; pp. 291–297. [Google Scholar]
- Zhou, X.; Xie, W.; Miao, L.; Li, Y.; Zhao, J.; Li, L.; Xu, Y.; Ren, Y. The Simulation Study of Simulink-based Four-way Slide Valve Modeling. In Proceedings of the 2022 9th International Forum on Electrical Engineering and Automation (IFEEA), Zhuhai, China, 4–6 November 2022; pp. 141–144. [Google Scholar]
- Panchenko, A.; Voloshina, A.; Kiurchev, S.; Titova, O.; Onopreychuk, D.; Stefanov, V.; Safoniuk, I.; Pashchenko, V.; Radionov, H.; Golubok, M. Development of the universal model of mechatronic system with a hydraulic drive. J. Enterp. Technol. 2018, 4, 94. [Google Scholar]
- Lu, W.; Zhou, K.; Doyle, J.C. Stabilization of uncertain linear systems: An LFT approach. IEEE T. Automat. Contr. 1996, 41, 50–65. [Google Scholar] [CrossRef][Green Version]
- Zhou, K.; Doyle, J.C. Essentials of Robust Control; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Li, X.; Wang, X.; Wang, Y. Mixed sensitivity H∞ controller design for variable-speed pump-controlled motor system. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; pp. 503–508. [Google Scholar]
- Saini, P.; Thakur, P. H-Infinity Based Robust Temperature Controller Design for a Non-linear Systems. Wireless Pers. Commun. 2022, 126, 305–333. [Google Scholar] [CrossRef]
- Green, M.; Limebeer, D.J. Linear Robust Control; Courier Corporation: Chelmsford, MA, USA, 2012; ISBN 0486488365. [Google Scholar]
- Menezes, E.J.; Araújo, A.M. Wind turbine structural control using H-infinity methods. Eng. Struct. 2023, 286, 116095. [Google Scholar] [CrossRef]
- Servo Valves Pilot Operated: Flow Control Valve with Analog Interface. Available online: https://www.moog.com/literature/ICD/Moog-ServoValves-G761_761Series-Catalog-en.pdf (accessed on 3 September 2023).
- Stanley GR29 Underwater Grinder. Available online: https://www.stanleyinfrastructure.com/sites/default/files/pdf/gr29-uw-specsheet.pdf (accessed on 3 September 2023).
- Kwakernaak, H. Robust control and H∞-optimization—Tutorial paper. Automatica 1993, 29, 255–273. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.; Peng, G.; Chen, Y.; Zhang, Z. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mech. Syst. Signal Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]





| Parameter | Symbol | Value |
|---|---|---|
| Motor displacement | 2.28 × 10−6 (m3/rad) | |
| Total volume of hydraulic system | 1.1 × 10−4 (m3) | |
| Effective bulk modulus | 0.9 × 109 (N/m2) | |
| Total discharge coefficient | 4 × 10−12 (m5/N/s) | |
| Flow gain coefficient | 3.5 × 10−7 (m3/s) | |
| Moment of inertia | 0.01 (kg·m3) | |
| Damping coefficient | 0.02 (N·s·m) | |
| Fuel supply pressure | 1.6 × 107 (Pa) |
| Controller | Rise Time (s) | Steady-State Error (rad/s) |
|---|---|---|
| PID | 0.1 | 0.0078 |
| H-infinity | 0.036 | 0.0068 |
| Controller | Time to Steady-State Recovery (s) | Steady-State Error (rad/s) |
|---|---|---|
| PID | 0.01 | 0.052 |
| H-infinity | 0.01 | 0.02 |
| Controller | Rise Time (s) | Peak-To-Peak Value (rad/s) | Average Steady-State Error (rad/s) |
|---|---|---|---|
| PID | 0.12 | 0.035 | 0.02 |
| H-infinity | 0.059 | 0.012 | 0.012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, K.; Feng, G.; Ding, B. Robust H-Infinity Tracking Control for a Valve-Controlled Hydraulic Motor System with Uncertain Parameters in the Complex Load Environment. Sensors 2023, 23, 9092. https://doi.org/10.3390/s23229092
Lu K, Feng G, Ding B. Robust H-Infinity Tracking Control for a Valve-Controlled Hydraulic Motor System with Uncertain Parameters in the Complex Load Environment. Sensors. 2023; 23(22):9092. https://doi.org/10.3390/s23229092
Chicago/Turabian StyleLu, Kunwei, Guodong Feng, and Beichen Ding. 2023. "Robust H-Infinity Tracking Control for a Valve-Controlled Hydraulic Motor System with Uncertain Parameters in the Complex Load Environment" Sensors 23, no. 22: 9092. https://doi.org/10.3390/s23229092
APA StyleLu, K., Feng, G., & Ding, B. (2023). Robust H-Infinity Tracking Control for a Valve-Controlled Hydraulic Motor System with Uncertain Parameters in the Complex Load Environment. Sensors, 23(22), 9092. https://doi.org/10.3390/s23229092






