Person-Specific Template Matching Using a Dynamic Time Warping Step-Count Algorithm for Multiple Walking Activities
Abstract
:1. Introduction
2. Related Works
3. Materials and Methods
3.1. Background Methods
3.1.1. Dynamic Time Warping (DTW)
3.1.2. DTW Barycentre Averaging (DBA)
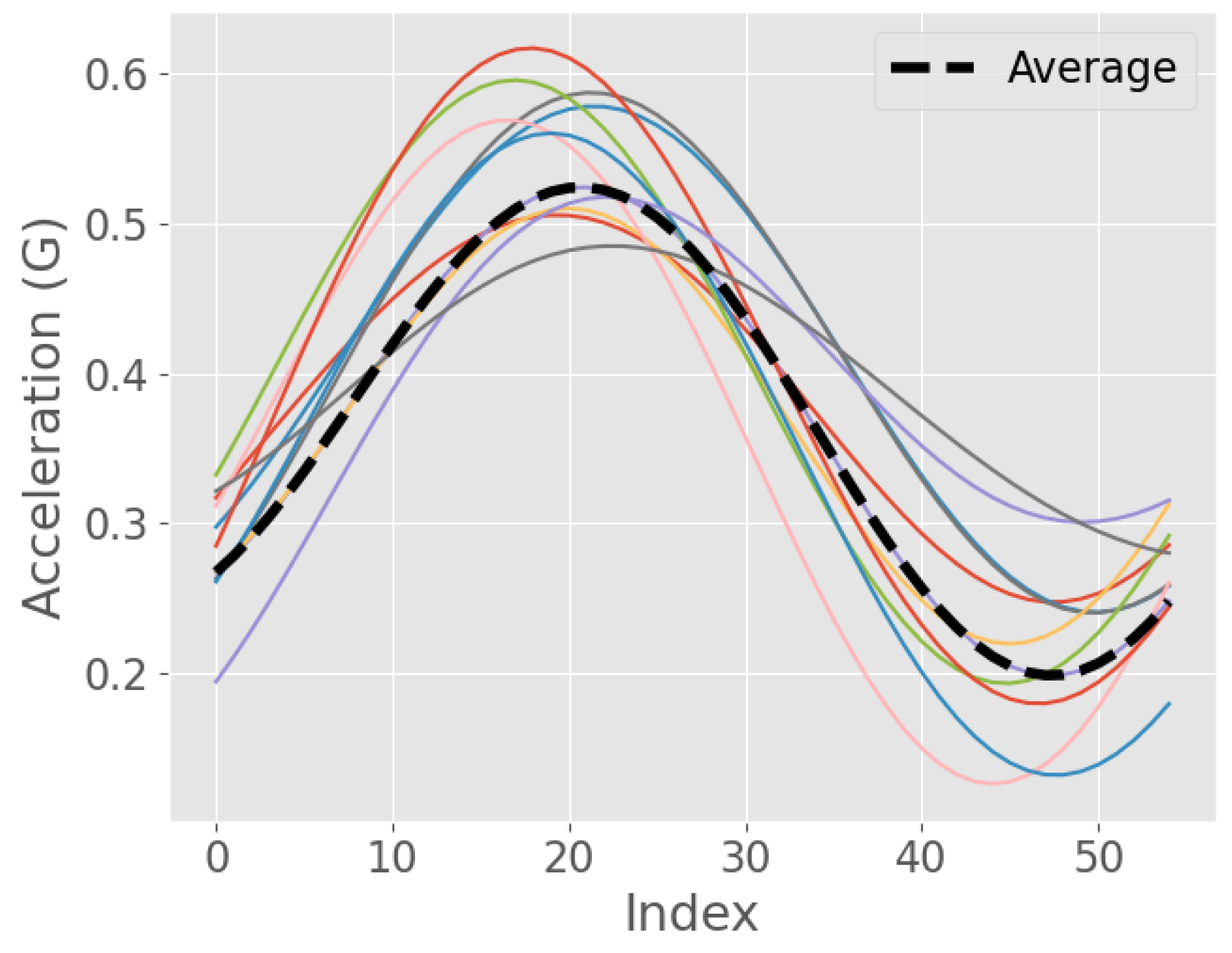
3.2. Algorithm Development
3.3. Signal Preprocessing
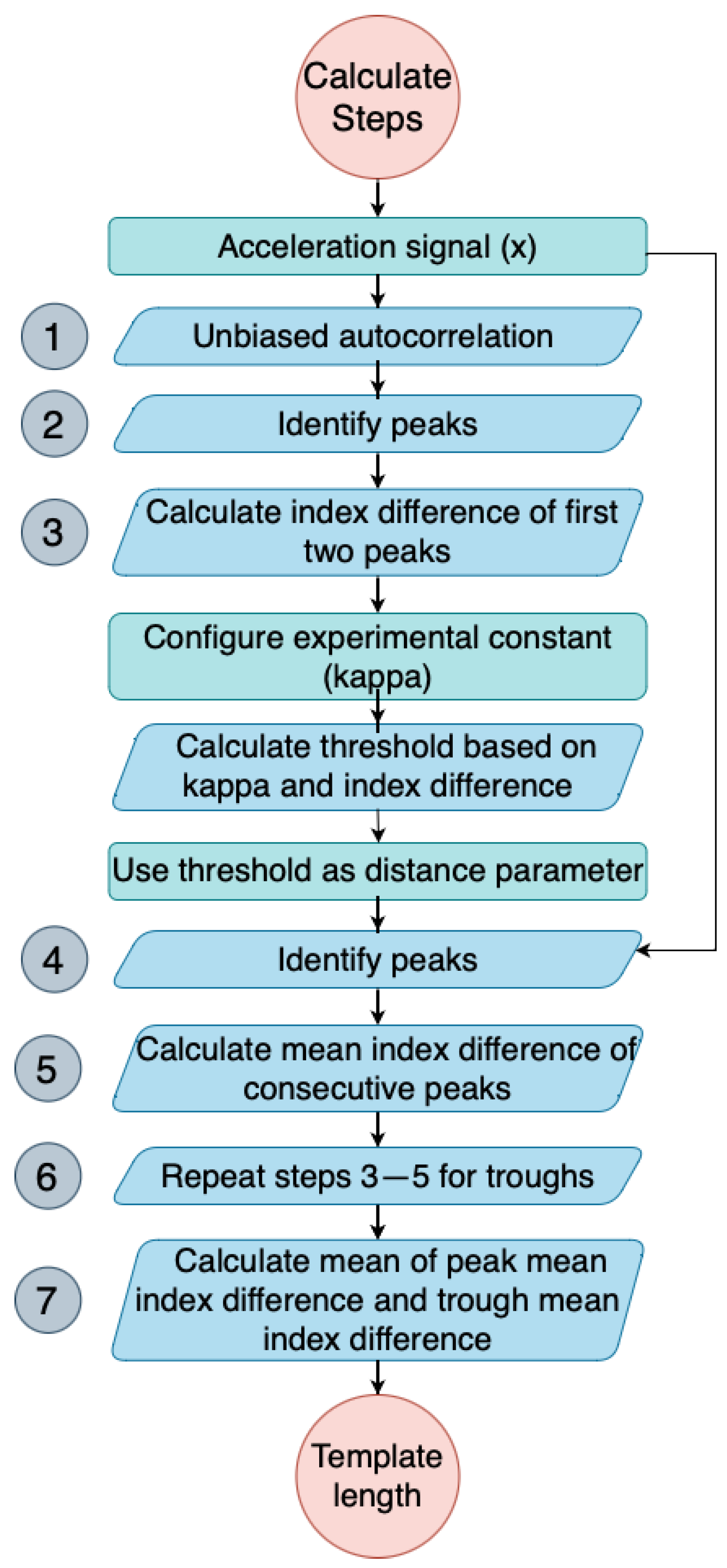
3.3.1. Template Length Calculation
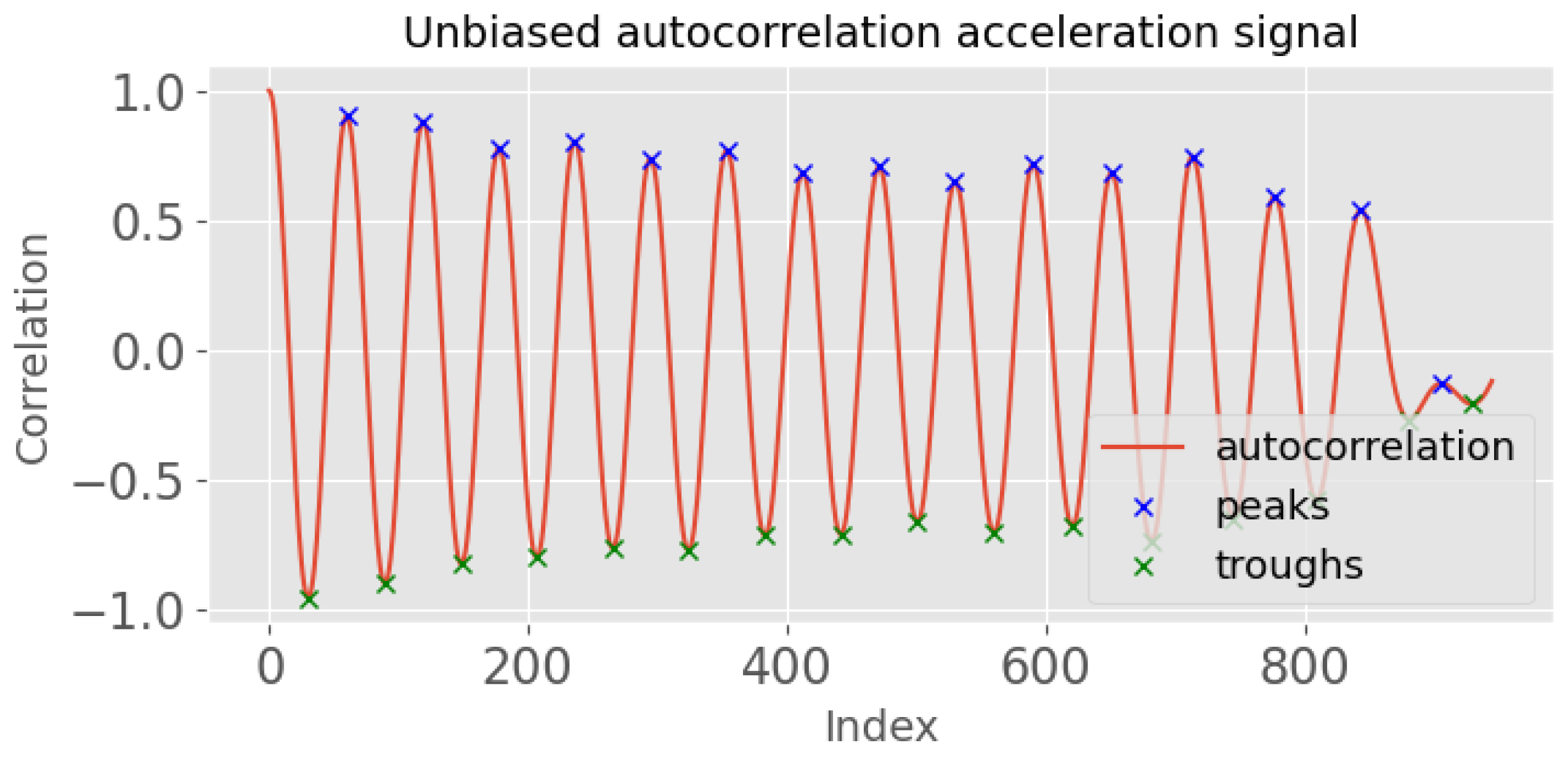
- Obtain the unbiased autocorrelation signal of the input acceleration signal. This autocorrelation signal will be used to identify the periodicity of the signal, which is an important feature in detecting steps.where x is the acceleration signal, N is the length of the signal, and m is the time lag. An example output is shown in Figure 3, where the x-axis is the index for a given time lag (m). By analysing this autocorrelation plot, the periodicity of the signal can be identified by measuring the time difference between the first two prominent peaks, which corresponds to its fundamental period.
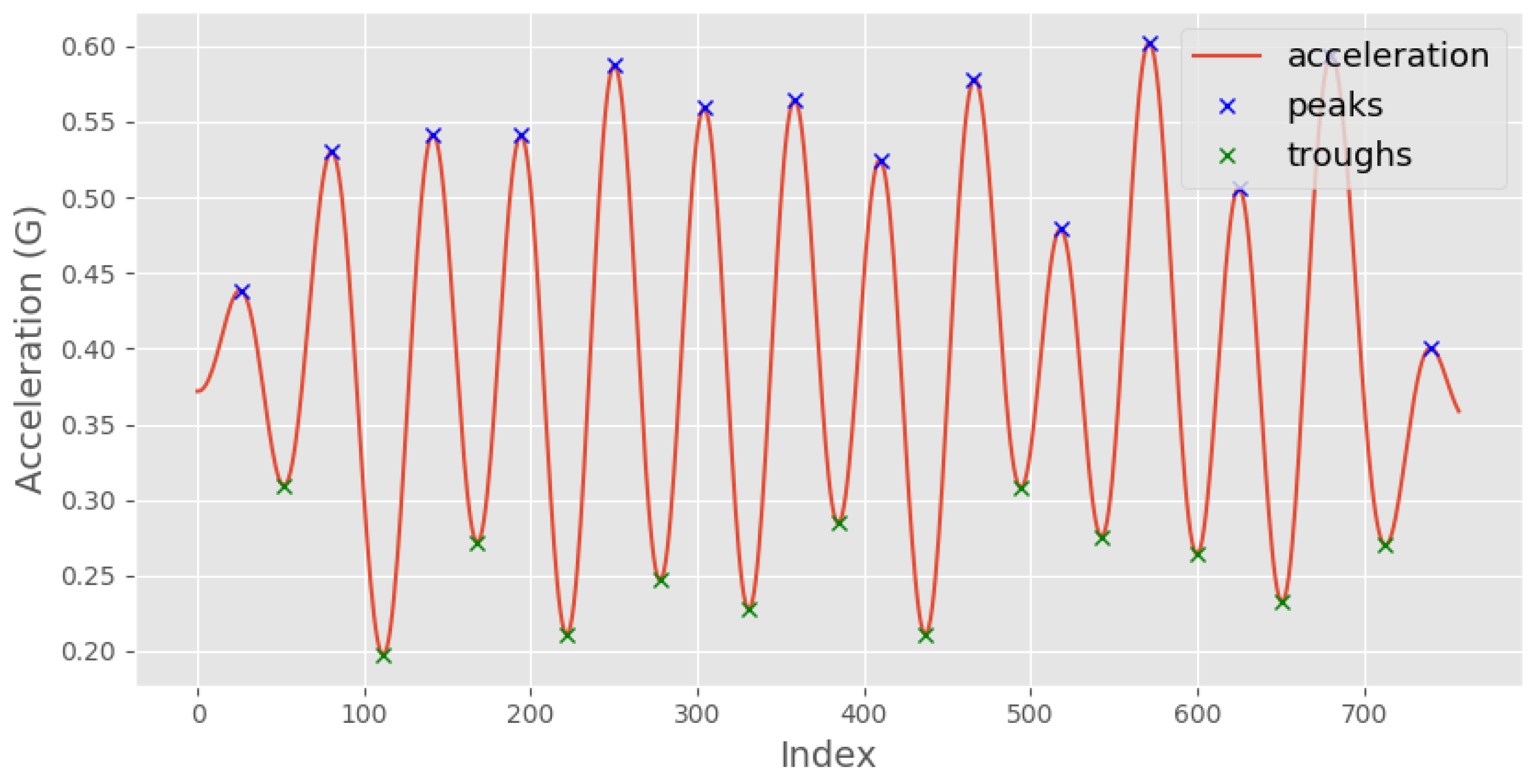
- Identify the peaks of the autocorrelation signal, , using scipy.signal.find_peaks. The peaks correspond to the periodicity of the input signal.
- Calculate the index (time) difference between the first two peaks of the autocorrelation signal (). This time difference provides an estimate of the minimum allowable time between neighbouring peaks in the input signal.
- Calculate the mean time difference between each consecutive pair of peaks in the original acceleration signal (from step 4). This value represents the average time period of the detected steps in the input signal.
- Repeat steps 3–5 for the troughs, which correspond to the negative peaks of the acceleration signal.
- Calculate the template length as the mean of the mean time difference of the peaks and the mean time difference of the troughs. This value represents the average time period of both the positive and negative peaks in the input signal.
3.3.2. Template Signal Generation
3.3.3. Template Matching to Calculate the Number of Steps Undertaken
4. Experiments
4.1. Data Acquisition
4.2. Model Validation
5. Results
5.1. Root-Mean-Square Error
5.2. Testing the StepMatchDTWBA Algorithm on an External Public Dataset
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Phillips, S.M.; Cadmus-Bertram, L.; Rosenberg, D.; Buman, M.P.; Lynch, B.M. Wearable technology and physical activity in chronic disease: Opportunities and challenges. Am. J. Prev. Med. 2018, 54, 144–150. [Google Scholar] [CrossRef]
- Ryu, U.; Ahn, K.; Kim, E.; Kim, M.; Kim, B.; Woo, S.; Chang, Y. Adaptive step detection algorithm for wireless smart step counter. In Proceedings of the International Conference on Information Science and Applications, Pattaya, Thailand, 24–26 June 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Chow, J.J.; Thom, J.M.; Wewege, M.A.; Ward, R.E.; Parmenter, B.J. Accuracy of step count measured by physical activity monitors: The effect of gait speed and anatomical placement site. Gait Posture 2017, 57, 199–203. [Google Scholar] [CrossRef]
- Strath, S.J.; Kaminsky, L.A.; Ainsworth, B.E.; Ekelund, U.; Freedson, P.S.; Gary, R.A.; Richardson, C.R.; Smith, D.T.; Swartz, A.M.; American Heart Association Physical Activity Committee of the Council on Lifestyle and Cardiometabolic Health and Cardiovascular, Exercise, Cardiac Rehabilitation and Prevention Committee of the Council on Clinical Cardiology, and Council. Guide to the assessment of physical activity: Clinical and research applications: A scientific statement from the American Heart Association. Circulation 2013, 128, 2259–2279. [Google Scholar]
- Godfrey, A.; Del Din, S.; Barry, G.; Mathers, J.C.; Rochester, L. Instrumenting gait with an accelerometer: A system and algorithm examination. Med. Eng. Phys. 2015, 37, 400–407. [Google Scholar] [CrossRef]
- Broderick, J.M.; Ryan, J.; O’Donnell, D.M.; Hussey, J. A guide to assessing physical activity using accelerometry in cancer patients. Support. Care Cancer 2014, 22, 1121–1130. [Google Scholar] [CrossRef]
- Ummels, D.; Beekman, E.; Theunissen, K.; Braun, S.; Beurskens, A.J. Counting steps in activities of daily living in people with a chronic disease using nine commercially available fitness trackers: Cross-sectional validity study. JMIR mHealth uHealth 2018, 6, e70. [Google Scholar] [PubMed]
- Walker, R.K.; Hickey, A.M.; Freedson, P.S. Advantages and limitations of wearable activity trackers: Considerations for patients and clinicians. Clin. J. Oncol. Nurs. 2016, 20, 606–610. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-Organero, M.; Ruiz-Blázquez, R. Detecting steps walking at very low speeds combining outlier detection, transition matrices and autoencoders from acceleration patterns. Sensors 2017, 17, 2274. [Google Scholar] [CrossRef]
- Fulk, G.D.; Combs, S.A.; Danks, K.A.; Nirider, C.D.; Raja, B.; Reisman, D.S. Accuracy of 2 activity monitors in detecting steps in people with stroke and traumatic brain injury. Phys. Ther. 2014, 94, 222–229. [Google Scholar] [CrossRef]
- Backhouse, M.R.; Hensor, E.M.A.; White, D.; Keenan, A.M.; Helliwell, P.S.; Redmond, A.C. Concurrent validation of activity monitors in patients with rheumatoid arthritis. Clin. Biomech. 2013, 28, 473–479. [Google Scholar] [CrossRef]
- Chandrasekar, A.; Hensor, E.M.A.; Mackie, S.L.; Backhouse, M.R.; Harris, E. Preliminary concurrent validity of the Fitbit-Zip and ActiGraph activity monitors for measuring steps in people with polymyalgia rheumatica. Gait Posture 2018, 61, 339–345. [Google Scholar] [CrossRef] [PubMed]
- Marschollek, M.; Goevercin, M.; Wolf, K.H.; Song, B.; Gietzelt, M.; Haux, R.; Steinhagen-Thiessen, E. A performance comparison of accelerometry-based step detection algorithms on a large, non-laboratory sample of healthy and mobility-impaired persons. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008. [Google Scholar]
- Capela, N.A.; Lemaire, E.D.; Baddour, N. Feature selection for wearable smartphone-based human activity recognition with able bodied, elderly, and stroke patients. PLoS ONE 2015, 10, e0124414. [Google Scholar]
- Oudre, L.; Barrois-Müller, R.; Moreau, T.; Truong, C.; Vienne-Jumeau, A.; Ricard, D.; Vayatis, N.; Vidal, P.P. Template-based step detection with inertial measurement units. Sensors 2018, 18, 4033. [Google Scholar] [CrossRef]
- Fortune, E.; Lugade, V.; Morrow, M.; Kaufman, K. Validity of using tri-axial accelerometers to measure human movement—Part II: Step counts at a wide range of gait velocities. Med. Eng. Phys. 2014, 36, 659–669. [Google Scholar] [CrossRef]
- Genovese, V.; Mannini, A.; Sabatini, A.M. A smartwatch step counter for slow and intermittent ambulation. IEEE Access 2017, 5, 13028–13037. [Google Scholar] [CrossRef]
- Huang, Y.; Zheng, H.; Nugent, C.; McCullagh, P.; Black, N.; Burns, W.; Tully, M.A.; McDonough, S.M. An orientation free adaptive step detection algorithm using a smart phone in physical activity monitoring. Health Technol. 2012, 2, 249–258. [Google Scholar] [CrossRef]
- Liu, H.; Schultz, T. How Long Are Various Types of Daily Activities? Statistical Analysis of a Multimodal Wearable Sensor-Based Human Activity Dataset. In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022), Online, 9–11 February 2022. [Google Scholar] [CrossRef]
- Xu, C.; He, J.; Zhang, X.; Wang, C.; Duan, S. Detection of freezing of gait using template-matching based approaches. J. Sens. 2017, 2017, 1260734. [Google Scholar] [CrossRef]
- Folgado, D.; Barandas, M.; Antunes, M.; Nunes, M.L.; Liu, H.; Hartmann, Y.; Schultz, T.; Gamboa, H. TSSEARCH: Time Series Subsequence Search Library. SoftwareX 2022, 18, 101049. [Google Scholar] [CrossRef]
- Small, S.R.; Chan, S.; Walmsley, R.; von Fritsch, L.; Acquah, A.; Mertes, G.; Feakins, B.G.; Creagh, A.; Strange, A.; Matthews, C.E.; et al. Development and validation of a machine learning wrist-worn step detection algorithm with deployment in the UK biobank. medRxiv 2023. [Google Scholar] [CrossRef]
- Luu, L.; Pillai, A.; Lea, H.; Buendia, R.; Khan, F.M.; Dennis, G. Accurate step count with generalized and personalized deep learning on accelerometer data. Sensors 2022, 22, 3989. [Google Scholar] [CrossRef]
- Berndt, D.J.; Clifford, J. Using dynamic time warping to find patterns in time series. In Proceedings of the 3rd International Conference on Knowledge Discovery and Data Mining, AAAIWS’94, Seattle, WA, USA, 31 July–1 August 1994; pp. 359–370. [Google Scholar]
- Petitjean, F.; Ketterlin, A.; Gancarski, P. A global averaging method for dynamic time warping, with applications to clustering. Pattern Recognit. 2011, 44, 678–693. [Google Scholar] [CrossRef]
- Kaptein, R.G.; Wezenberg, D.; IJmker, T.; Houdijk, H.; Beek, P.J.; Lamoth, C.J.C.; Daffertshofer, A. Shotgun approaches to gait analysis: Insights & limitations. J. NeuroEng. Rehabil. 2014, 11, 120. [Google Scholar]
- Micó-Amigo, M.E.; Kingma, I.; Ainsworth, E.; Walgaard, S.; Niessen, M.; van Lummel, R.C.; van Dieën, J.H. A novel accelerometry-based algorithm for the detection of step durations over short episodes of gait in healthy elderly. J. NeuroEng. Rehabil. 2016, 13, 38. [Google Scholar] [CrossRef]
- Wang, W.; Guo, Y.; Huang, B.; Zhao, G.; Liu, B.; Wang, L. Analysis of filtering methods for 3D acceleration signals in body sensor network. In Proceedings of the International Symposium on Bioelectronics and Bioinformations 2011, Suzhou, China, 3–5 November 2011; pp. 263–266. [Google Scholar] [CrossRef]
- Mathie, M. Monitoring and Interpreting Human Movement Patterns Using a Triaxial Accelerometer. Doctoral Dissertation, UNSW, Sydney, Australia, 2003. [Google Scholar]
- Antonsson, E.K.; Mann, R.W. The frequency content of gait. J. Biomech. 1985, 18, 39–47. [Google Scholar] [CrossRef]
- Johnston, W.; Judice, P.B.; Molina García, P.; Mühlen, J.M.; Lykke Skovgaard, E.; Stang, J.; Schumann, M.; Cheng, S.; Bloch, W.; Brønd, J.C.; et al. Recommendations for determining the validity of consumer wearable and smartphone step count: Expert statement and checklist of the INTERLIVE network. Br. J. Sport. Med. 2021, 55, 780–793. [Google Scholar] [CrossRef]
- Salzman, B. Gait and balance disorders in older adults. Am. Fam. Phys. 2010, 82, 61–68. [Google Scholar]
- Giavarina, D. Understanding Bland-Altman analysis. Biochem. Medica 2015, 25, 141–151. [Google Scholar] [CrossRef]
- Sasko, B.; Thiem, U.; Christ, M.; Trappe, H.J.; Ritter, O.; Pagonas, N. Size matters: An observational study investigating estimated height as a reference size for calculating tidal volumes if low tidal volume ventilation is required. PLoS ONE 2018, 13, e0199917. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef]
- Pottel, H. Critical review of method comparison studies for the evaluation of estimating glomerular filtration rate equations. Int. J. Nephrol. Kidney Fail. 2015, 1, 1–7. [Google Scholar] [CrossRef]
- Aboy, M.; Crespo, C.; McNames, J.; Bassale, J.; Goldstein, B. Automatic detection algorithm for physiologic pressure signal components. In Proceedings of the Second Joint 24th Annual Conference and the Annual Fall Meeting of the Biomedical Engineering Society, Houston, TX, USA, 23–26 October 2002; Volume 1, pp. 196–197. [Google Scholar] [CrossRef]
- Dirican, A.; Aksoy, S. Step Counting Using Smartphone Accelerometer and Fast Fourier Trransform. J. Eng. Nat. Sci. 2017, 8, 175–182. [Google Scholar]
- Brajdic, A.; Harle, R. Walk detection and step counting on unconstrained smartphones. In Proceedings of the 2013 ACM International Joint Conference on Pervasive and Ubiquitous Computing, UbiComp ’13, Zurich, Switzerland, 8–12 September 2013; Association for Computing Machinery: New York, NY, USA, 2013; pp. 225–234. [Google Scholar] [CrossRef]
- Salvi, D.; Velardo, C.; Brynes, J.; Tarassenko, L. An optimised algorithm for accurate steps counting from smart-phone accelerometry. In Proceedings of the 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 4423–4427. [Google Scholar] [CrossRef]
- Pham, V.T.; Nguyen, D.A.; Dang, N.D.; Pham, H.H.; Tran, V.A.; Sandrasegaran, K.; Tran, D.T. Highly accurate step counting at various walking states using low-cost inertial measurement unit support indoor positioning system. Sensors 2018, 18, 3186. [Google Scholar] [CrossRef]
- Menz, H.B.; Lord, S.R.; Fitzpatrick, R.C. Acceleration patterns of the head and pelvis when walking on level and irregular surfaces. Gait Posture 2003, 18, 35–46. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Zhen, T.; Kong, J.L.; Wang, L.M.; Zhou, X.L.; Voit, E.O. Walking gait phase detection based on acceleration signals using voting-weighted integrated neural network. Complexity 2020, 2020, 4760297. [Google Scholar] [CrossRef]
- Filippou, V.; Redmond, A.C.; Bennion, J.; Backhouse, M.R.; Wong, D. Capturing accelerometer outputs in healthy volunteers under normal and simulated-pathological conditions using ML classifiers. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2020, 2020, 4604–4607. [Google Scholar] [PubMed]

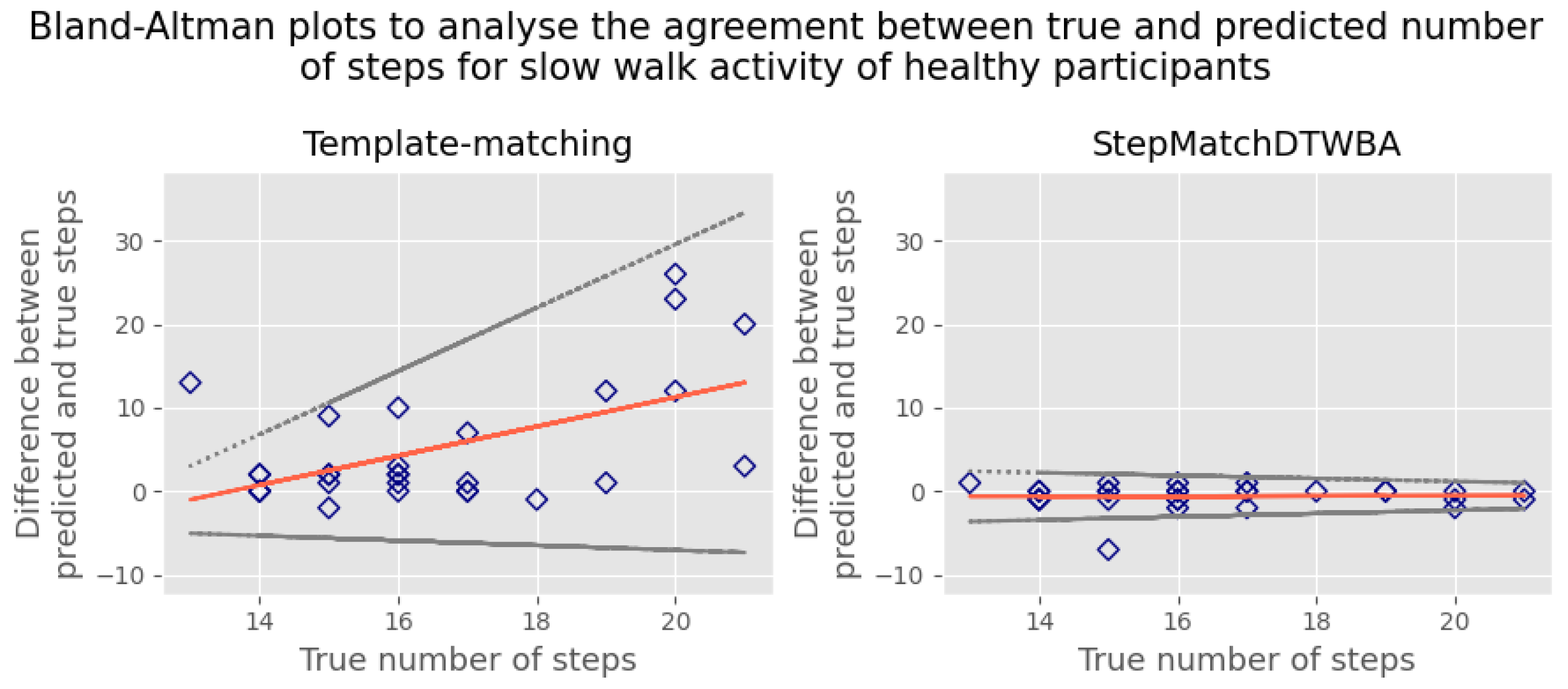
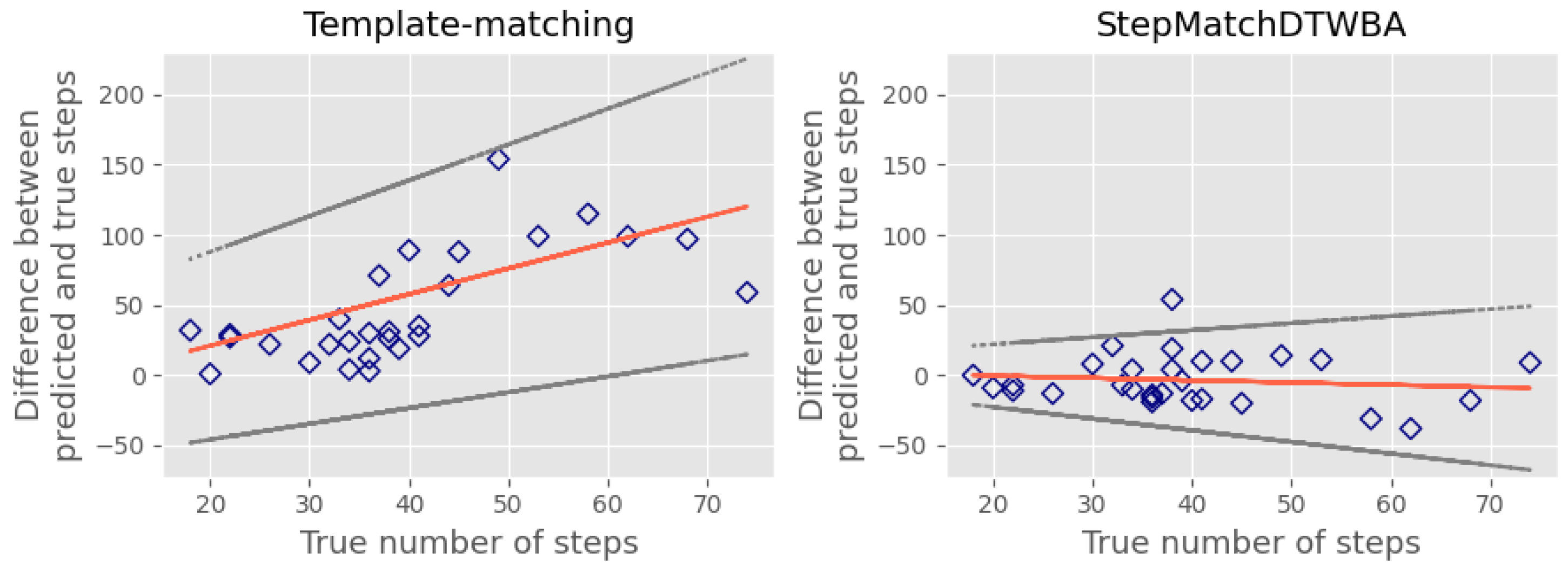
| Activity | Normal | Simulated Pathological |
|---|---|---|
| Slow walk | 0.65 | 0.95 |
| Normal walk | 0.10 | 0.90 |
| Fast walk | 0.10 | 0.75 |
| Upstairs | 0.10 | 1.30 |
| Downstairs | 0.10 | 1.30 |
| All | 0.10 | 1.20 |
| Healthy | Simulated Pathological | |||||||
|---|---|---|---|---|---|---|---|---|
| Activity | Benchmark Peak Detection | StepMatch DTWBA | Template Matching | Thresholding F-Domain * | Benchmark Peak Detection | StepMatch DTWBA | Template Matching | Thresholding F-Domain * |
| Slow walk | 2.81 | 1.59 | 8.99 | 6.61 | 20.80 | 18.31 | 84.07 | 27.68 |
| (2.70, 2.92) | (1.39, 1.77) | (8.34, 9.59) | (6.34, 6.86) | (18.41, 22.94) | (17.22, 19.33) | (76.36, 91.14) | (65.55, 28.78) | |
| Normal walk | 4.03 | 1.00 | 1.35 | 4.09 | 15.94 | 14.04 | 50.87 | 23.13 |
| (3.91, 4.16) | (0.94, 1.06) | (1.28, 1.42) | (3.93, 4.23) | (13.76, 17.87) | (13.32, 14.72) | (47.03, 54.45) | (21.98, 24.22) | |
| Fast walk | 5.07 | 2.35 | 1.74 | 5.85 | 12.64 | 8.91 | 43.02 | 15.81 |
| (4.98, 5.16) | (2.25, 2.45) | (1.63, 1.84) | (5.74, 5.96) | (11.79, 13.44) | (8.47, 9.33) | (38.56, 47.06) | (14.74, 16.80) | |
| Stairs ascent | 4.55 | 2.04 | 1.90 | 5.37 | 10.01 | 7.98 | 42.12 | 38.06 |
| (4.41, 4.69) | (1.93, 2.15) | (1.76, 2.03) | (5.21, 5.52) | (9.43, 10.55) | (7.20, 8.70) | (39.18, 44.88) | (37.03, 39.07) | |
| Stairs descent | 5.16 | 2.57 | 1.11 | 6.36 | 9.07 | 8.74 | 59.22 | 34.63 |
| (4.98, 5.32) | (2.40, 2.74) | (1.08, 1.15) | (6.23, 6.48) | (8.27, 9.80) | (8.19, 9.25) | (56.15, 62.13) | (33.62, 35.61) | |
| Average | 4.32 | 1.91 | 3.02 | 5.66 | 13.69 | 11.60 | 55.86 | 27.86 |
| Position | True Steps | StepMatchDTWBA (Difference) | Pham et al. [41] (Difference) |
|---|---|---|---|
| Hand (1) | 326 | 324 (−2) | 323 (−3) |
| Hand (2) | 340 | 338 (−2) | 332 (−8) |
| Armband (1) | 335 | 331 (−4) | 335 (0) |
| Armband (2) | 343 | 340 (−3) | 335 (−5) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filippou, V.; Backhouse, M.R.; Redmond, A.C.; Wong, D.C. Person-Specific Template Matching Using a Dynamic Time Warping Step-Count Algorithm for Multiple Walking Activities. Sensors 2023, 23, 9061. https://doi.org/10.3390/s23229061
Filippou V, Backhouse MR, Redmond AC, Wong DC. Person-Specific Template Matching Using a Dynamic Time Warping Step-Count Algorithm for Multiple Walking Activities. Sensors. 2023; 23(22):9061. https://doi.org/10.3390/s23229061
Chicago/Turabian StyleFilippou, Valeria, Michael R. Backhouse, Anthony C. Redmond, and David C. Wong. 2023. "Person-Specific Template Matching Using a Dynamic Time Warping Step-Count Algorithm for Multiple Walking Activities" Sensors 23, no. 22: 9061. https://doi.org/10.3390/s23229061
APA StyleFilippou, V., Backhouse, M. R., Redmond, A. C., & Wong, D. C. (2023). Person-Specific Template Matching Using a Dynamic Time Warping Step-Count Algorithm for Multiple Walking Activities. Sensors, 23(22), 9061. https://doi.org/10.3390/s23229061








