The Implementation of Precise Point Positioning (PPP): A Comprehensive Review
Abstract
:1. Introduction
2. Error Sources in PPP
2.1. Ionospheric Delays
2.2. Tropospheric Delays
2.3. Satellite Orbit and Clock Errors
2.4. Code Biases
2.5. Phase Biases
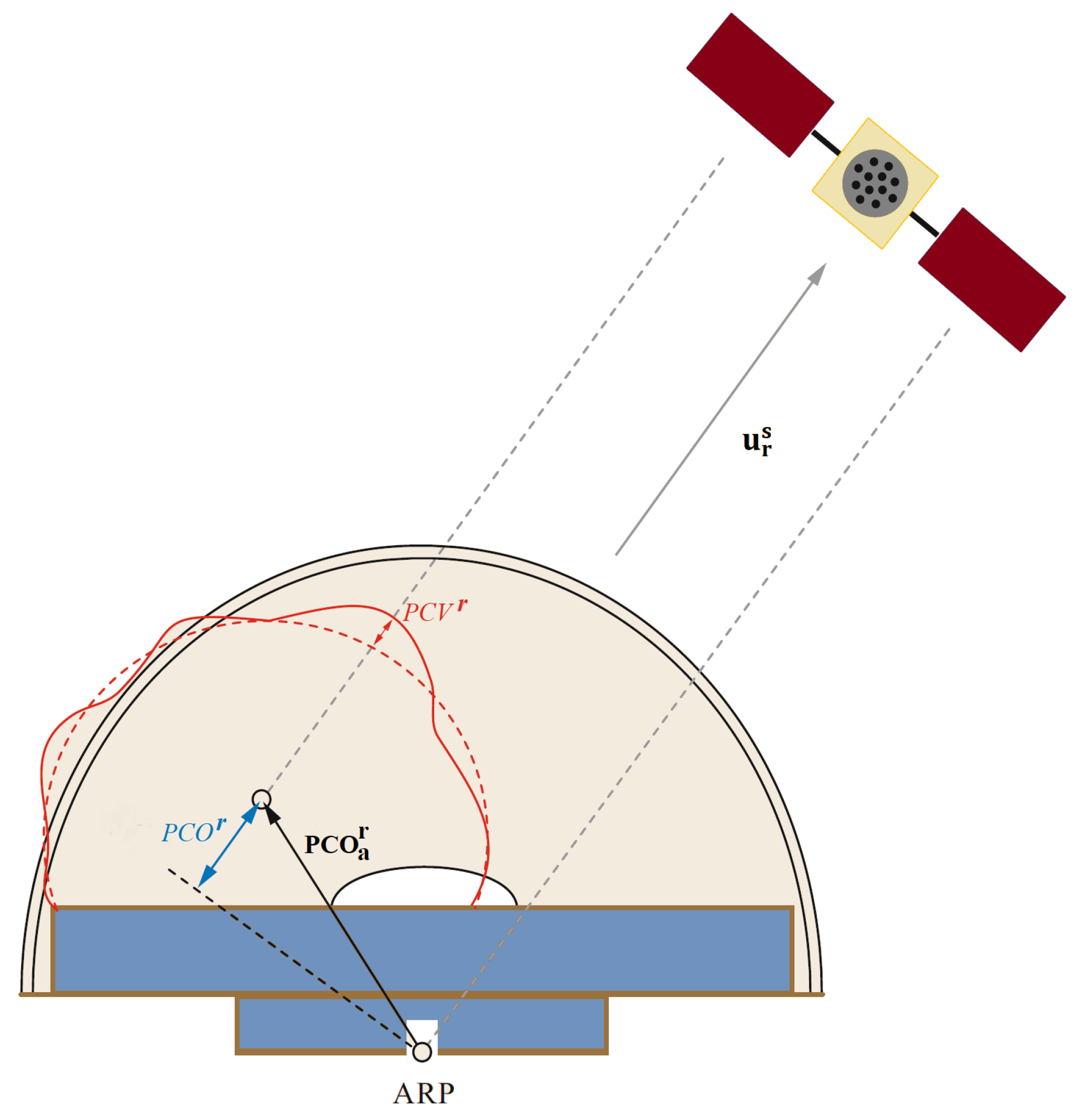
2.6. Antenna Phase Center Effects
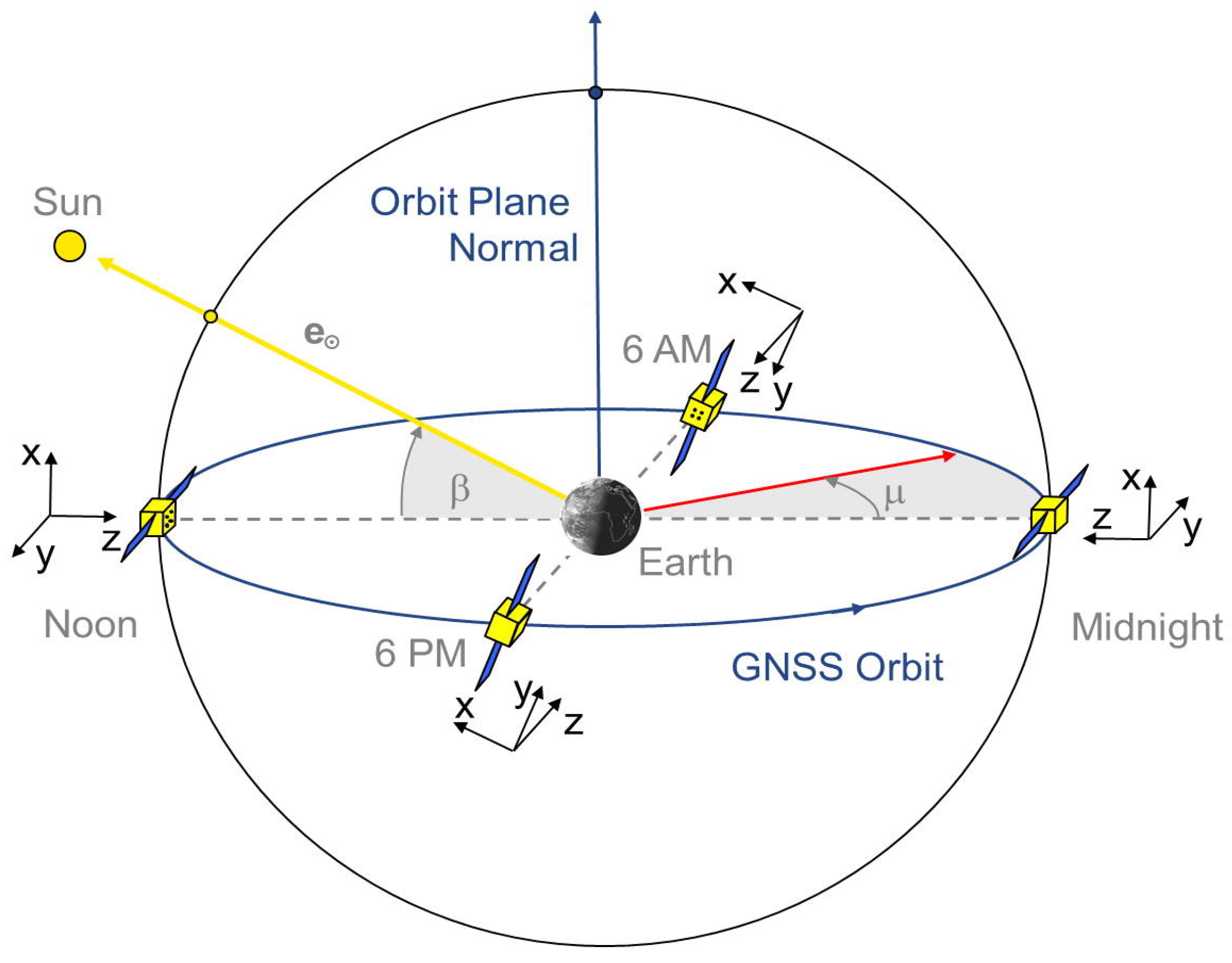
2.6.1. Satellite APC Errors
2.6.2. Receiver APC Errors
2.7. Phase Wind-Up
2.8. Site Displacement Effects
2.8.1. Solid Earth Tides
2.8.2. Polar Tides
2.8.3. Ocean Loading
3. PPP Models
3.1. GNSS Code and Phase Observations
3.1.1. Ionospheric-Free (IF) Code and Phase
3.1.2. Geometric-Free (GF) Code and Phase
3.1.3. Wide-Lane (WL) Phase Observation
3.1.4. Narrow-Lane (NL) Code Observation
3.1.5. Melbourne–Wübbena (MW) Function
3.2. Standard PPP
3.3. Ambiguity-Fixed PPP
3.4. PPP-RTK
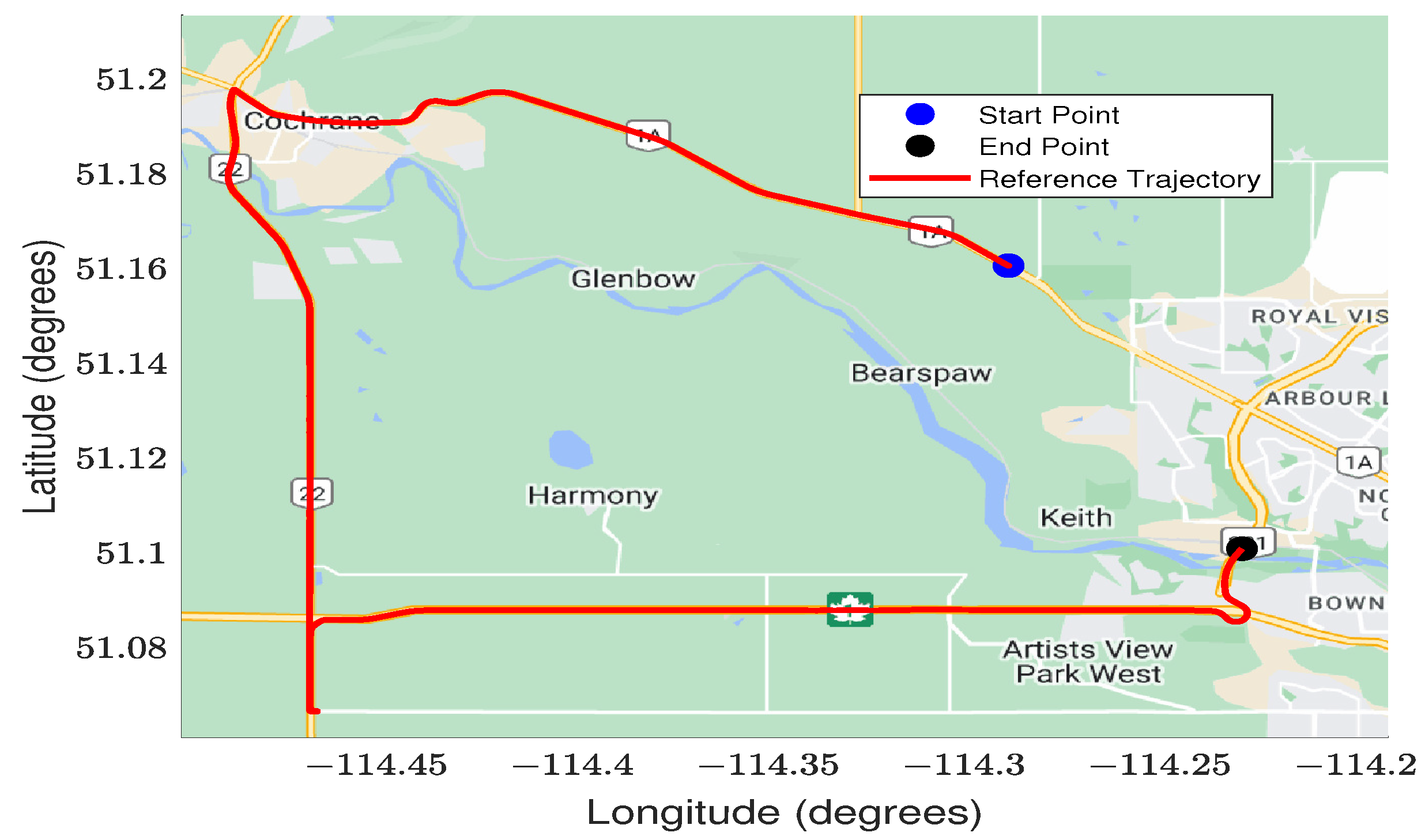
4. Practical Considerations and Experimental Results
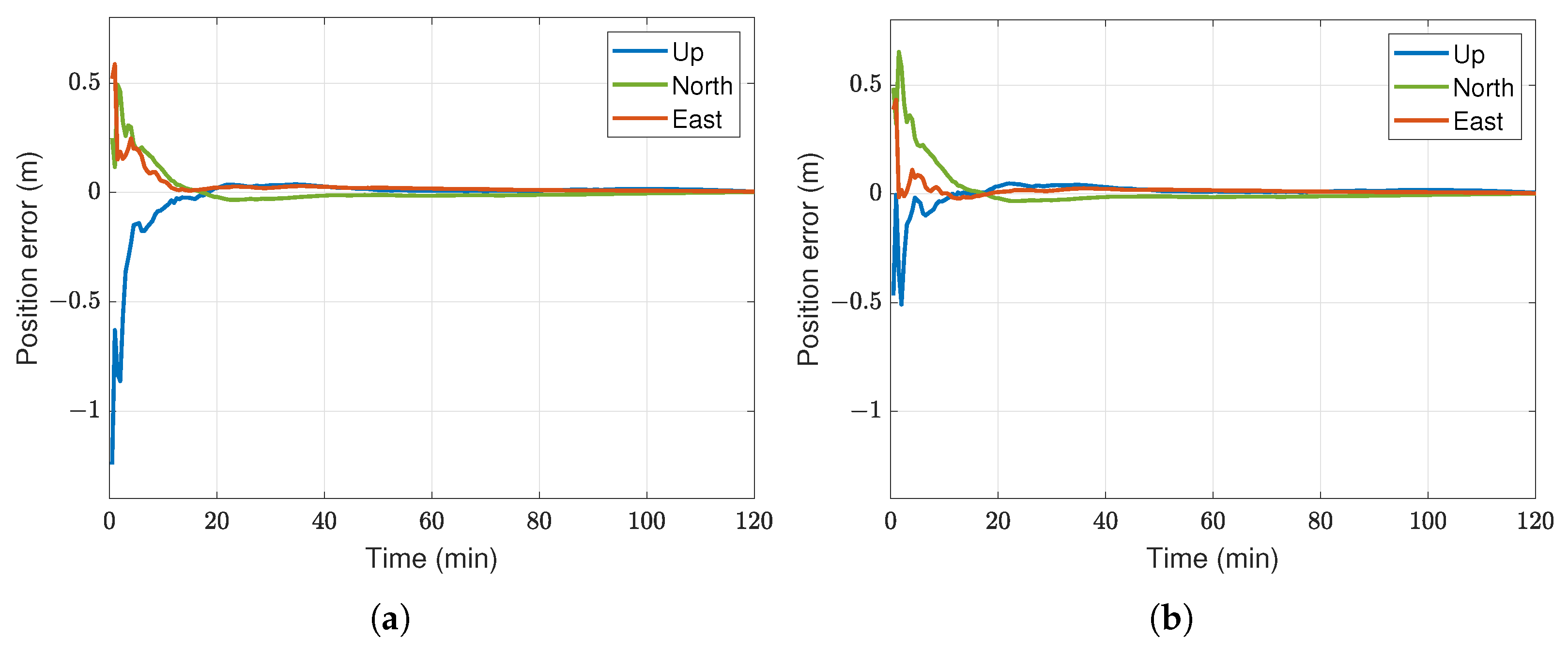
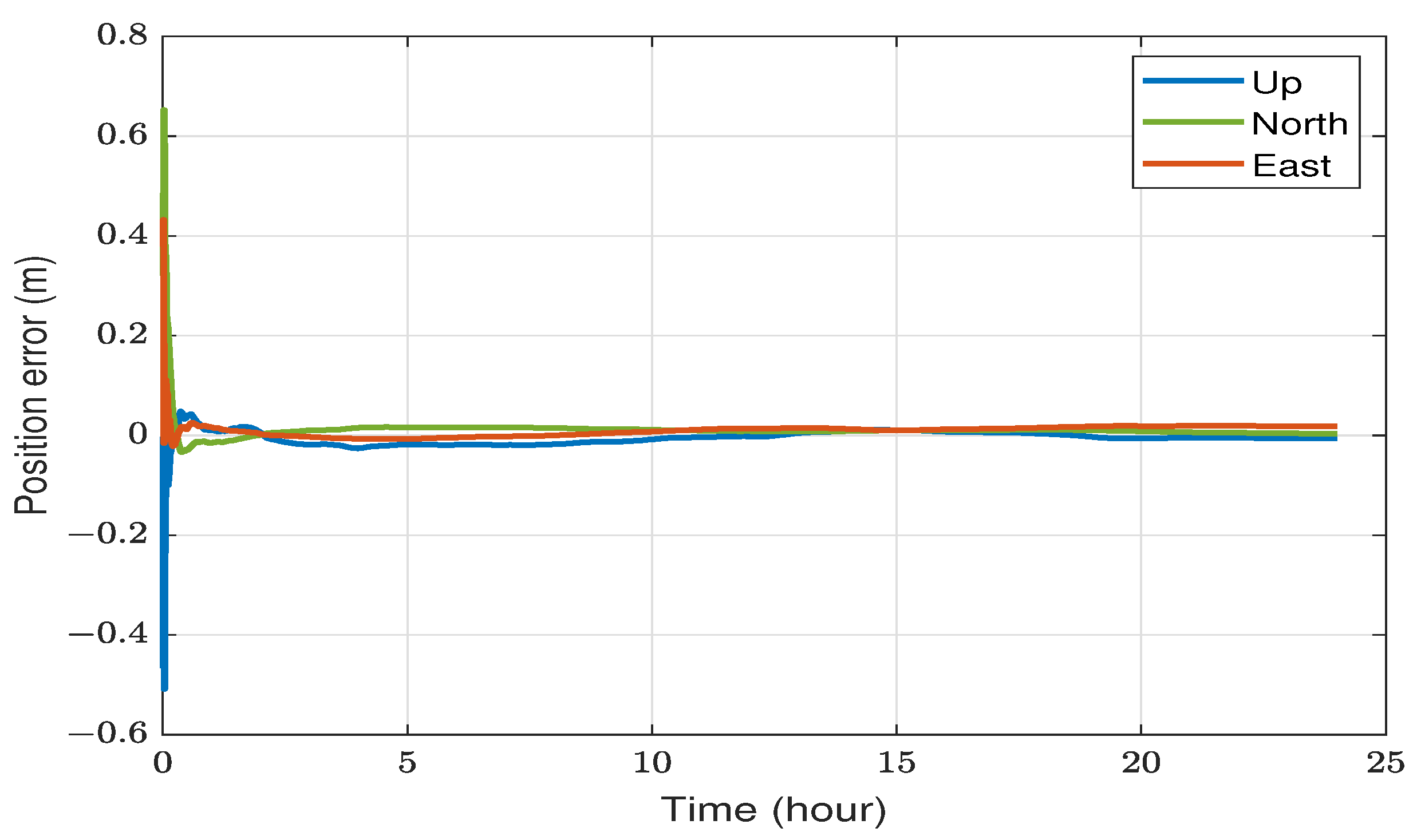
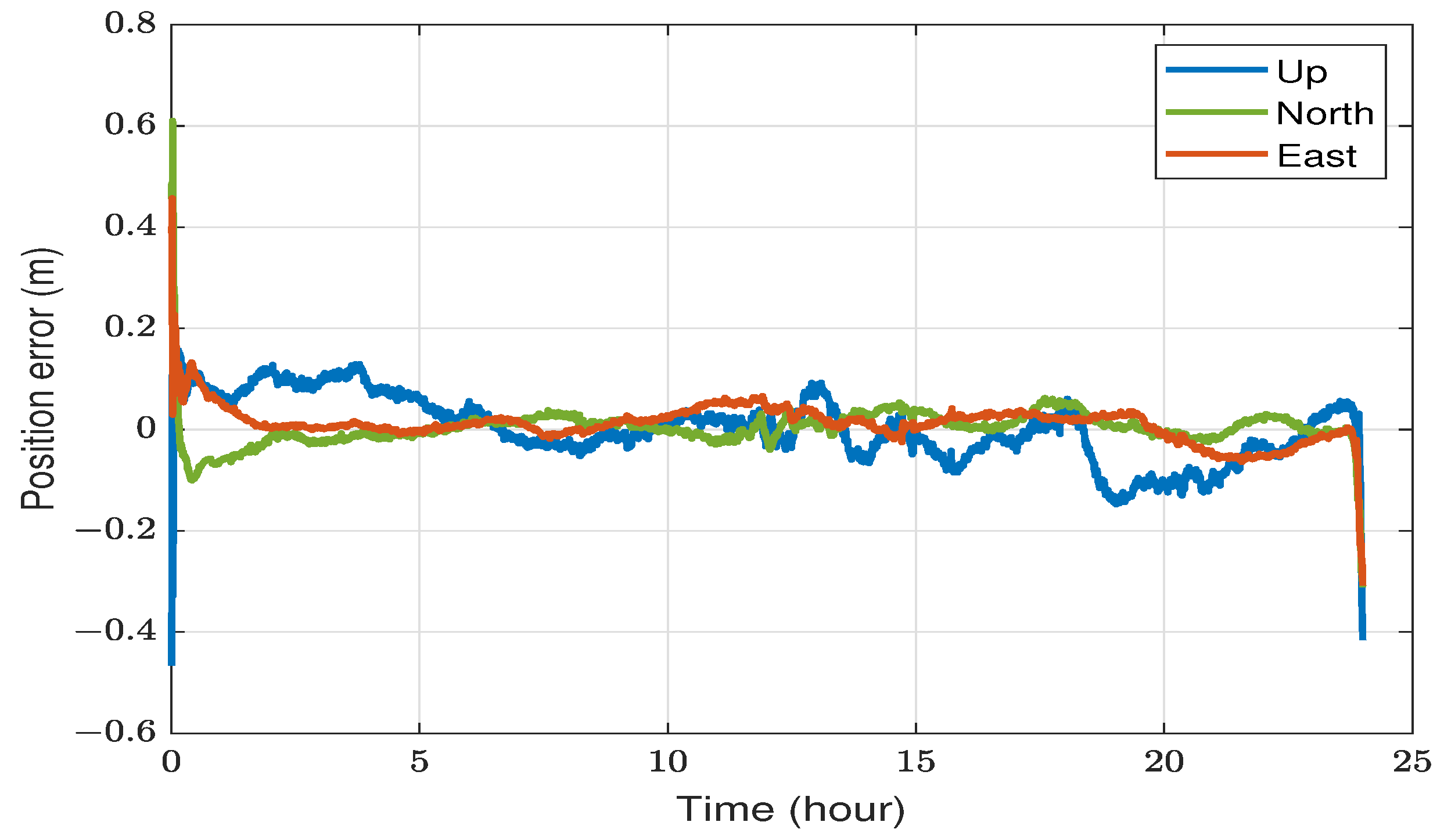
4.1. Static Results
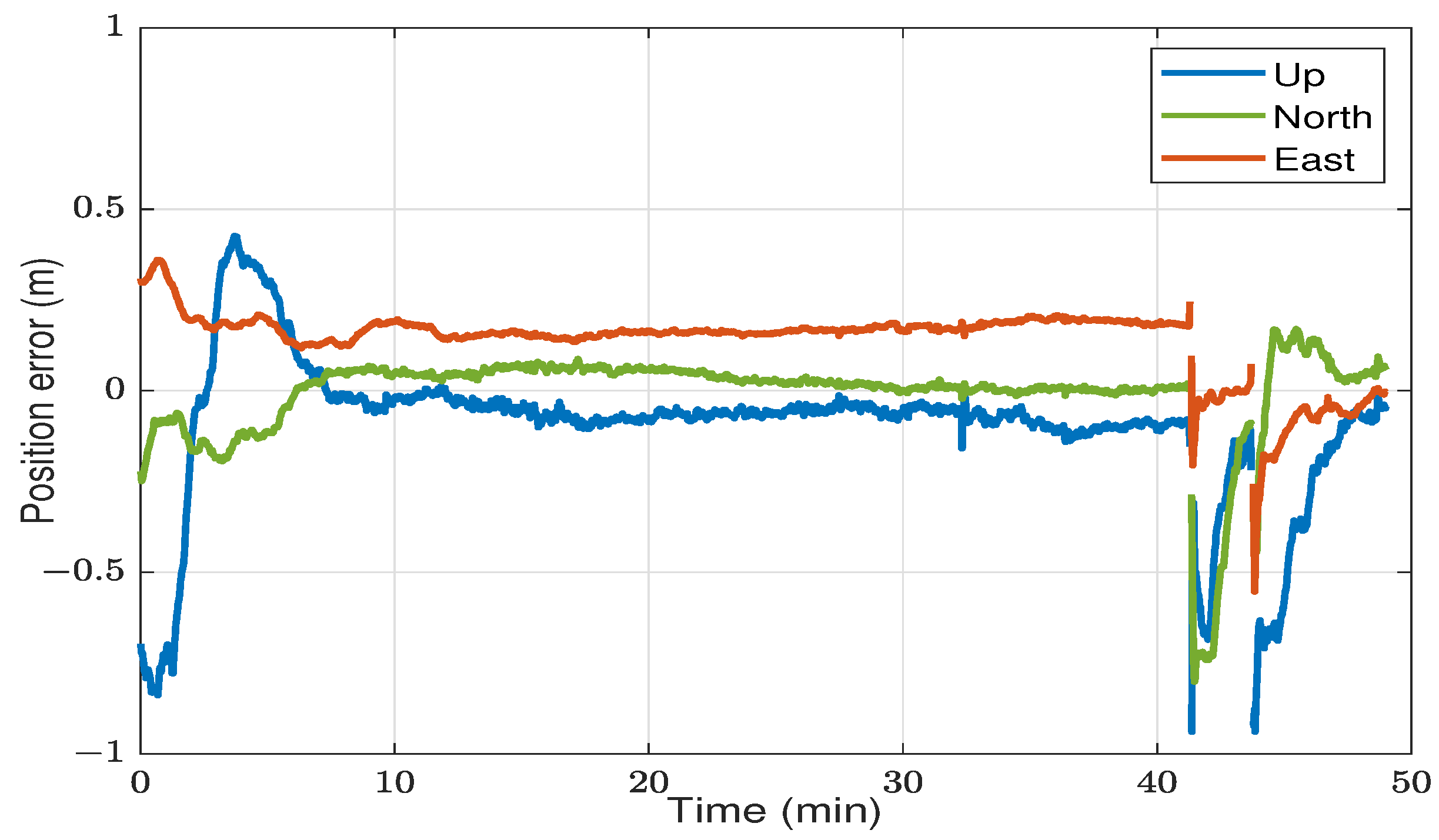
4.2. Kinematic Results
5. PPP Challenges and Solutions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements and Performance Second Edition; Ganga-Jamuna Press: Lincoln, MA, USA, 2006. [Google Scholar]
- Counselman, C.C., III; Shapiro, I.I.; Greenspan, R.L.; Cox, D.B., Jr. Backpack VLBI terminal with subcentimeter capability. In Radio Interferometry Techniques for Geodesy; NASA, Massachusetts Institute of Technology: Cambridge, MA, USA, 1979; pp. 409–414. [Google Scholar]
- Counselman, C.C.; Gourevitch, S.A. Miniature interferometer terminals for earth surveying: Ambiguity and multipath with global positioning system. IEEE Trans. Geosci. Remote Sens. 1981, GE-19, 244–252. [Google Scholar] [CrossRef]
- El-Rabbany, A. Introduction to GPS: The Global Positioning System; Artech House: Norwood, MA, USA, 2002. [Google Scholar]
- Kaplan, E.; Hegarty, C. Understanding GPS: Principles and Applications; Artech House: Norwood, MA, USA, 2006. [Google Scholar]
- Zumberge, J.; Heflin, M.; Jefferson, D.; Watkins, M.; Webb, F.H. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Kouba, J.; Lahaye, F.; Tétreault, P. Precise Point Positioning. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; Chapter 25; pp. 723–751. [Google Scholar] [CrossRef]
- Bisnath, S.; Gao, Y. Precise Point Positioning: A Powerful Technique with a Promising Future; GPS World: Cleveland, OH, USA, 2009; pp. 43–50. [Google Scholar]
- Elsheikh, M.; Noureldin, A.; Korenberg, M. Integration of GNSS Precise Point Positioning and reduced inertial sensor system for lane-level car navigation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 2246–2261. [Google Scholar] [CrossRef]
- Vana, S.; Bisnath, S. Low-Cost, Triple-Frequency, Multi-GNSS PPP and MEMS IMU Integration for Continuous Navigation in Simulated Urban Environments. J. Inst. Navig. 2023, 70, navi.578. [Google Scholar] [CrossRef]
- Elsheikh, M.; Noureldin, A.; El-Sheimy, N.; Korenberg, M. Performance Analysis of MEMS-based RISS/PPP Integrated Positioning for Land Vehicles. In Proceedings of the 2020 IEEE 92nd Vehicular Technology Conference (VTC2020-Fall), IEEE, Virtual, 18 November–16 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- An, X.; Meng, X.; Jiang, W. Multi-constellation GNSS Precise Point Positioning with multi-frequency raw observations and dual-frequency observations of ionospheric-free linear combination. Satell. Navig. 2020, 1, 7. [Google Scholar] [CrossRef]
- Kalinnikov, V.; Ustinov, A.; Zagretdinov, R.; Tertyshnikov, A.; Kosarev, N. The Precise Point Positioning Method (PPP) in environmental monitoring applications. In Proceedings of the 25th International Symposium on Atmospheric and Ocean Optics: Atmospheric Physics, SPIE, Novosibirsk, Russia, 18 December 2019; Volume 11208, pp. 1444–1448. [Google Scholar]
- Fang, R.; Lv, H.; Hu, Z.; Wang, G.; Zheng, J.; Zhou, R.; Xiao, K.; Li, M.; Liu, J. GPS/BDS Precise Point Positioning with B2b products for high-rate seismogeodesy: Application to the 2021 Mw 7.4 Maduo earthquake. Geophys. J. Int. 2022, 231, 2079–2090. [Google Scholar] [CrossRef]
- Takasu, T.; Yasuda, A. Development of the low-cost RTK-GPS receiver with an open source program package RTKLIB. In Proceedings of the International Symposium on GPS/GNSS, International Convention Center, Jeju, Republic of Korea, 22–25 September 2009; Volume 1, pp. 1–6. [Google Scholar]
- Zhou, F.; Dong, D.; Li, W.; Jiang, X.; Wickert, J.; Schuh, H. GAMP: An open-source software of multi-GNSS precise point positioning using undifferenced and uncombined observations. GPS Solut. 2018, 22, 33. [Google Scholar] [CrossRef]
- Bahadur, B.; Nohutcu, M. PPPH: A MATLAB-based software for multi-GNSS precise point positioning analysis. GPS Solut. 2018, 22, 113. [Google Scholar] [CrossRef]
- Chen, C.; Chang, G. PPPLib: An open-source software for Precise Point Positioning using GPS, BeiDou, Galileo, GLONASS, and QZSS with multi-frequency observations. GPS Solut. 2021, 25, 18. [Google Scholar] [CrossRef]
- Glaner, M.F.; Weber, R. An open-source software package for Precise Point Positioning: raPPPid. GPS Solut. 2023, 27, 174. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, A.; Ni, S.; Xiao, G.; Xu, H. PPP-ARISEN: An open-source Precise Point Positioning software with ambiguity resolution for interdisciplinary research of seismology, geodesy and geodynamics. GPS Solut. 2023, 27, 45. [Google Scholar] [CrossRef]
- Elsheikh, M. Integration of GNSS Precise Point Positioning and Inertial Technologies for Land Vehicle Navigation. Ph.D. Thesis, Queen’s University (Canada), Kingston, ON, Canada, 2019. [Google Scholar]
- Karaim, M.; Elsheikh, M.; Noureldin, A. GNSS Error Sources. In Multifunctional Operation and Application of GPS; Rustamov, R.B., Hashimov, A.M., Eds.; IntechOpen: London, UK, 2018; Volume Chapter 4, pp. 69–85. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric time-delay algorithm for single-frequency GPS users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar] [CrossRef]
- Yasyukevich, Y.V.; Zatolokin, D.; Padokhin, A.; Wang, N.; Nava, B.; Li, Z.; Yuan, Y.; Yasyukevich, A.; Chen, C.; Vesnin, A. Klobuchar, NeQuickG, BDGIM, GLONASS, IRI-2016, IRI-2012, IRI-Plas, NeQuick2, and GEMTEC Ionospheric Models: A Comparison in Total Electron Content and Positioning Domains. Sensors 2023, 23, 4773. [Google Scholar] [CrossRef] [PubMed]
- Juan, J.; Hernández-Pajares, M.; Sanz, J.; Ramos-Bosch, P.; Aragon-Angel, A.; Orus, R.; Ochieng, W.; Feng, S.; Jofre, M.; Coutinho, P.; et al. Enhanced Precise Point Positioning for GNSS users. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4213–4222. [Google Scholar] [CrossRef]
- Johnston, G.; Riddell, A.; Hausler, G. The International GNSS Service. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; Chapter 33; pp. 967–982. [Google Scholar] [CrossRef]
- IGS Products Website. Available online: https://www.igs.org/products/ (accessed on 6 August 2023).
- Hobiger, T.; Jakowski, N. Atmospheric Signal Propagation. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; Chapter 6; pp. 66–193. [Google Scholar] [CrossRef]
- Nie, Z.; Yang, H.; Zhou, P.; Gao, Y.; Wang, Z. Quality assessment of CNES real-time ionospheric products. GPS Solut. 2019, 23, 11. [Google Scholar] [CrossRef]
- Schaer, S.; Gurtner, W. IONEX: The IONosphere Map EXchange Format. Version 1.0, 25 Feburary 1998. Available online: https://files.igs.org/pub/data/format/ionex1.pdf (accessed on 6 August 2023).
- Spilker, J.J. Tropospheric Effects on GPS. Glob. Position. Syst. Theory Appl. 1996, 1, 517–546. [Google Scholar]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar]
- Davis, J.; Herring, T.; Shapiro, I.; Rogers, A.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Berg, H. Allgemeine Meteorologie; Dümmlers Verlag Bonn: Bonn, Germany, 1948. [Google Scholar]
- Marini, J.W. Correction of satellite tracking data for an arbitrary tropospheric profile. Radio Sci. 1972, 7, 223–231. [Google Scholar] [CrossRef]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. Solid Earth 2006, 111, B02406. [Google Scholar] [CrossRef]
- Kouba, J. Testing of global pressure/temperature (GPT) model and global mapping function (GMF) in GPS analyses. J. Geod. 2009, 83, 199–208. [Google Scholar] [CrossRef]
- Niell, A. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophys. Res. Solid Earth 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Hilla, S. The Extended Standard Product 3 Orbit Format (SP3-d). 21 Feburary 2016. Available online: http://epncb.eu/ftp/data/format/sp3d.pdf (accessed on 6 August 2023).
- Hoffman-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS—Global Navigation Satellite Systems; Springer: Wien, Austria, 2008. [Google Scholar]
- Xu, G. GPS: Theory, Algorithms and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Ray, J.; Gurtner, W. RINEX Extensions to Handle Clock Information—Version 3.04. 4 July 2017. Available online: https://files.igs.org/pub/data/format/rinex_clock304.txt (accessed on 6 August 2023).
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)–achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Khachikyan, R.; Weber, G.; Langley, R.; Mervart, L.; Hugentobler, U. IGS-MGEX: Preparing the ground for multi-constellation GNSS science. Inside GNSS 2014, 9, 42–49. [Google Scholar]
- Hadas, T.; Bosy, J. IGS RTS precise orbits and clocks verification and quality degradation over time. GPS Solut. 2015, 19, 93–105. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, B.; Yuan, Y.; Li, Z.; Wang, N. Multi-GNSS triple-frequency differential code bias (DCB) determination with Precise Point Positioning (PPP). J. Geod. 2018, 93, 765–784. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A. Code Biases in Multi-GNSS Point Positioning. In Proceedings of the 2013 International Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 28–30 January 2013; pp. 616–628. [Google Scholar]
- Håkansson, M.; Jensen, A.B.; Horemuz, M.; Hedling, G. Review of code and phase biases in multi-GNSS positioning. GPS Solut. 2017, 21, 849–860. [Google Scholar] [CrossRef]
- IS-GPS-200N; NAVSTAR GPS Space Segment/Navigation User Segment Interfaces; Interface Specification IS-GPS-200. Global Positioning System Directorate: El Segundo, CA, USA, 2022.
- Differential Code Biases Products Website. Available online: https://cddis.nasa.gov/archive/gnss/products/bias/ (accessed on 6 August 2023).
- Romero, I. RINEX—The Receiver Independent Exchange Format—Version 4.00. 1 December 2021. Available online: https://files.igs.org/pub/data/format/rinex_4.00.pdf (accessed on 6 August 2023).
- Odijk, D.; Teunissen, P.J. Characterization of between-receiver GPS-Galileo inter-system biases and their effect on mixed ambiguity resolution. GPS Solut. 2013, 17, 521–533. [Google Scholar] [CrossRef]
- Dalla Torre, A.; Caporali, A. An analysis of intersystem biases for multi-GNSS positioning. GPS Solut. 2015, 19, 297–307. [Google Scholar] [CrossRef]
- Rothacher, M.; Schmid, R. ANTEX: The Antenna Exchange Format, Version 1.4. 15 September 2010. Available online: https://files.igs.org/pub/data/format/antex14.txt (accessed on 6 August 2023).
- IGS Antenna Phase Center Calibration Files Archive. Available online: https://files.igs.org/pub/station/general/pcv_archive/ (accessed on 6 August 2023).
- Masoumi, S. Reminder about the Upcoming Switch of the IGS to IGS20/igs20.atx and repro3 Standards (IGS Mail-8274, 15 November 2022). Available online: https://lists.igs.org/pipermail/igsmail/2022/008270.html (accessed on 6 August 2023).
- Montenbruck, O.; Schmid, R.; Mercier, F.; Steigenberger, P.; Noll, C.; Fatkulin, R.; Kogure, S.; Ganeshan, A. GNSS satellite geometry and attitude models. Adv. Space Res. 2015, 56, 1015–1029. [Google Scholar] [CrossRef]
- Folkner, W.M.; Williams, J.G.; Boggs, D.H. The Planetary and Lunar Ephemeris DE 421; Memorandum IOM 343R-08-003; Jet Propulsion Laboratory: Pasadena, CA, USA, 2008. [Google Scholar]
- Meeus, J.H. Astronomical Algorithms; Willmann-Bell, Inc.: Richmond, Virginia, USA, 1991. [Google Scholar]
- Hauschild, A. Basic Observation Equations. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; Volume Chapter 19, pp. 561–582. [Google Scholar] [CrossRef]
- Noureldin, A.; Karamat, T.B.; Georgy, J. Fundamentals of Inertial Navigation, Satellite-Based Positioning and Their Integration; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Wu, J.T.; Wu, S.C.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of antenna orientation on GPS carrier phase. Manuscripta Geod. 1993, 18, 91–98. [Google Scholar]
- Kouba, J.; Héroux, P. Precise Point Positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- McCarthy, D. IERS Conventions; IERS Technical Note No. 3; Observatoire de Paris: Paris, France, 1989. [Google Scholar]
- Petit, G.; Luzum, B. IERS Conventions; IERS Technical Note No. 36; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt, Germany, 2010. [Google Scholar]
- Wahr, J.M. Deformation induced by polar motion. J. Geophys. Res. Solid Earth 1985, 90, 9363–9368. [Google Scholar] [CrossRef]
- Ocean Tide Loading Computation Service (Chalmers University). Available online: http://holt.oso.chalmers.se/loading (accessed on 6 August 2023).
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Li, X.; Huang, J.; Li, X.; Shen, Z.; Han, J.; Li, L.; Wang, B. Review of PPP–RTK: Achievements, challenges, and opportunities. Satell. Navig. 2022, 3, 28. [Google Scholar] [CrossRef]
- Elsheikh, M.; Yang, H.; Nie, Z.; Liu, F.; Gao, Y. Testing and analysis of instant PPP using freely available augmentation corrections. In Proceedings of the 31st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018; pp. 1893–1901. [Google Scholar]
- Knoop, V.L.; de Bakker, P.F.; Tiberius, C.C.; van Arem, B. Lane determination with GPS Precise Point Positioning. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2503–2513. [Google Scholar] [CrossRef]
- Li, P.; Jiang, X.; Zhang, X.; Ge, M.; Schuh, H. GPS+ Galileo+ BeiDou Precise Point Positioning with triple-frequency ambiguity resolution. GPS Solut. 2020, 24, 78. [Google Scholar] [CrossRef]
- Shi, J.; Gao, Y. A comparison of three PPP integer ambiguity resolution methods. GPS Solut. 2014, 18, 519–528. [Google Scholar] [CrossRef]
- Hauschild, A. Combinations of Observations. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 583–604. [Google Scholar] [CrossRef]
- Collins, P.; Bisnath, S.; Lahaye, F.; Héroux, P. Undifferenced GPS ambiguity resolution using the decoupled clock model and ambiguity datum fixing. Navigation 2010, 57, 123–135. [Google Scholar] [CrossRef]
- Odijk, D.; Zhang, B.; Khodabandeh, A.; Odolinski, R.; Teunissen, P.J. On the estimability of parameters in undifferenced, uncombined GNSS network and PPP-RTK user models by means of S-system theory. J. Geod. 2016, 90, 15–44. [Google Scholar] [CrossRef]
- Collins, P. Isolating and estimating undifferenced GPS integer ambiguities. In Proceedings of the 2008 National Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 28–30 January 2008; pp. 720–732. [Google Scholar]
- Laurichesse, D.; Mercier, F.; BERTHIAS, J.P.; Broca, P.; Cerri, L. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. Navigation 2009, 56, 135–149. [Google Scholar] [CrossRef]
- Loyer, S.; Perosanz, F.; Mercier, F.; Capdeville, H.; Marty, J.C. Zero-difference GPS ambiguity resolution at CNES–CLS IGS Analysis Center. J. Geod. 2012, 86, 991–1003. [Google Scholar] [CrossRef]
- Geng, J.; Yang, S.; Guo, J. Assessing IGS GPS/Galileo/BDS-2/BDS-3 phase bias products with PRIDE PPP-AR. Satell. Navig. 2021, 2, 17. [Google Scholar] [CrossRef]
- Teunissen, P.; Khodabandeh, A. Review and principles of PPP-RTK methods. J. Geod. 2015, 89, 217–240. [Google Scholar] [CrossRef]
- Geng, J.; Teferle, F.N.; Meng, X.; Dodson, A. Towards PPP-RTK: Ambiguity resolution in real-time precise point positioning. Adv. Space Res. 2011, 47, 1664–1673. [Google Scholar] [CrossRef]
- Teunissen, P.J. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Teunissen, P.J. Mixed integer estimation and validation for next generation GNSS. In Handbook of Geomathematics; Freeden, W., Nashed, M.Z., Sonar, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1101–1127. [Google Scholar] [CrossRef]
- Wabbena, G.; Schmitz, M.; Bagge, A. PPP-RTK: Precise Point Positioning using state-space representation in RTK networks. In Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2005), Long Beach, CA, USA, 13–16 September 2005; pp. 2584–2594. [Google Scholar]
- Daily Observations of IGS Stations. Available online: https://cddis.nasa.gov/archive/gnss/data/daily/ (accessed on 6 August 2023).
- de Bakker, P.F.; Tiberius, C.C. Real-time multi-GNSS single-frequency Precise Point Positioning. GPS Solut. 2017, 21, 1791–1803. [Google Scholar] [CrossRef]
- Rovira-Garcia, A.; Juan, J.M.; Sanz, J.; Gonzalez-Casado, G. A worldwide ionospheric model for fast Precise Point Positioning. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4596–4604. [Google Scholar] [CrossRef]
- Aggrey, J.; Bisnath, S. Improving GNSS PPP convergence: The case of atmospheric-constrained, multi-GNSS PPP-AR. Sensors 2019, 19, 587. [Google Scholar] [CrossRef]
- Elsheikh, M.; Abdelfatah, W.; Noureldin, A.; Iqbal, U.; Korenberg, M. Low-cost real-time PPP/INS integration for automated land vehicles. Sensors 2019, 19, 4896. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Wang, H.; Zhou, Y.; Shen, Z. Multi-GNSS PPP/INS/Vision/LiDAR tightly integrated system for precise navigation in urban environments. Inf. Fusion 2023, 90, 218–232. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elsheikh, M.; Iqbal, U.; Noureldin, A.; Korenberg, M. The Implementation of Precise Point Positioning (PPP): A Comprehensive Review. Sensors 2023, 23, 8874. https://doi.org/10.3390/s23218874
Elsheikh M, Iqbal U, Noureldin A, Korenberg M. The Implementation of Precise Point Positioning (PPP): A Comprehensive Review. Sensors. 2023; 23(21):8874. https://doi.org/10.3390/s23218874
Chicago/Turabian StyleElsheikh, Mohamed, Umar Iqbal, Aboelmagd Noureldin, and Michael Korenberg. 2023. "The Implementation of Precise Point Positioning (PPP): A Comprehensive Review" Sensors 23, no. 21: 8874. https://doi.org/10.3390/s23218874
APA StyleElsheikh, M., Iqbal, U., Noureldin, A., & Korenberg, M. (2023). The Implementation of Precise Point Positioning (PPP): A Comprehensive Review. Sensors, 23(21), 8874. https://doi.org/10.3390/s23218874









