Research on a Multimodel Fusion Diagnosis Method for Evaporation Ducts in the East China Sea
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Methods
2.2.1. Direct Detection Method
2.2.2. Evaporation Duct Model
- a.
- BYC model
- b.
- NPS model
- c.
- NWA model
- d.
- NRL model
- e.
- LKB model
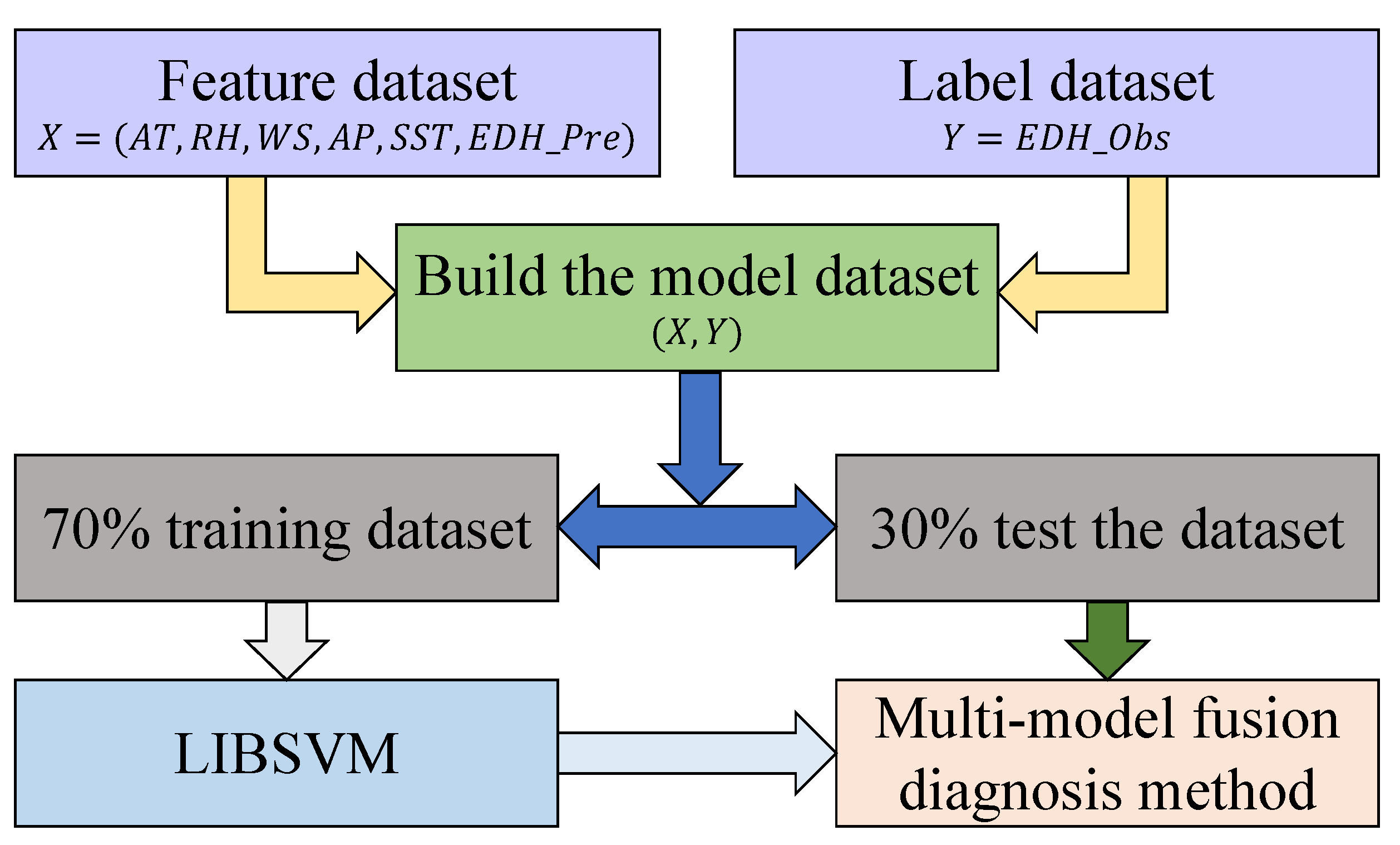
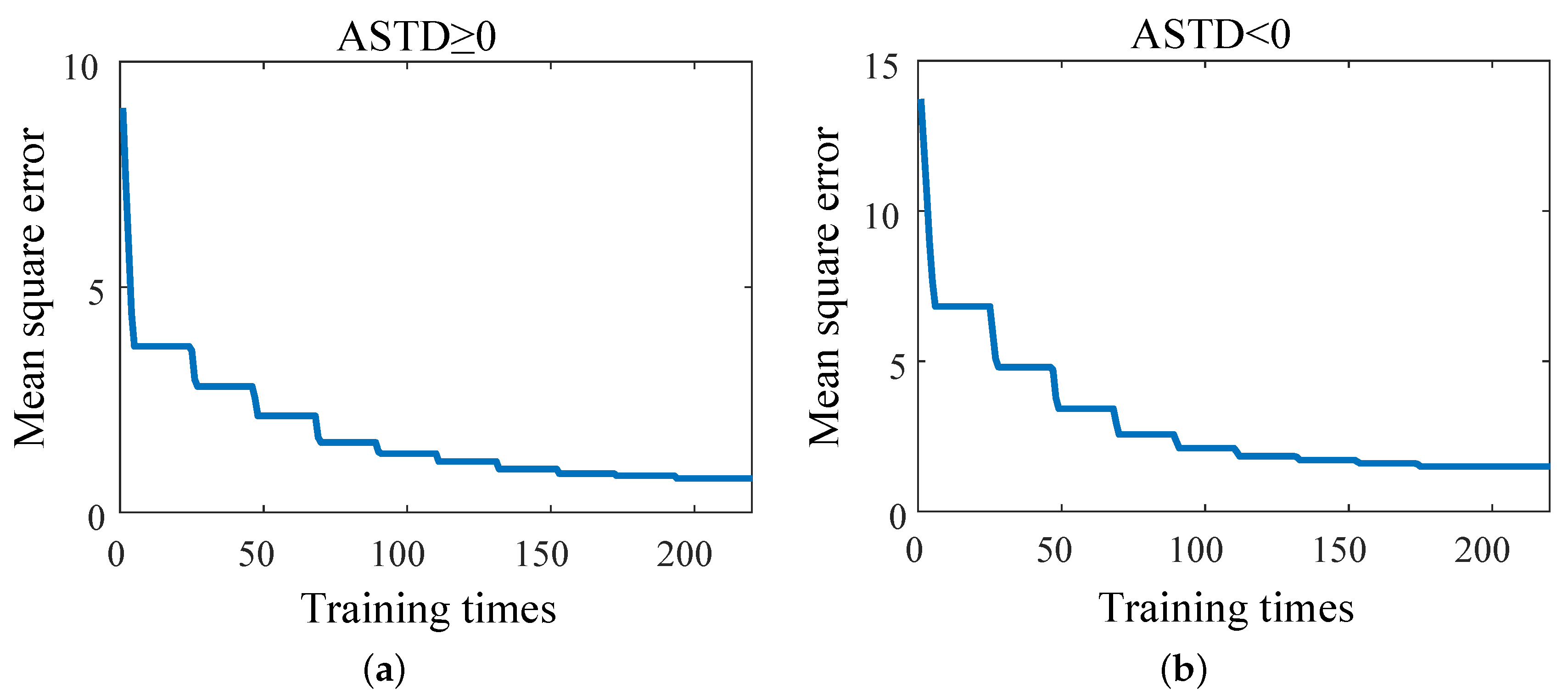
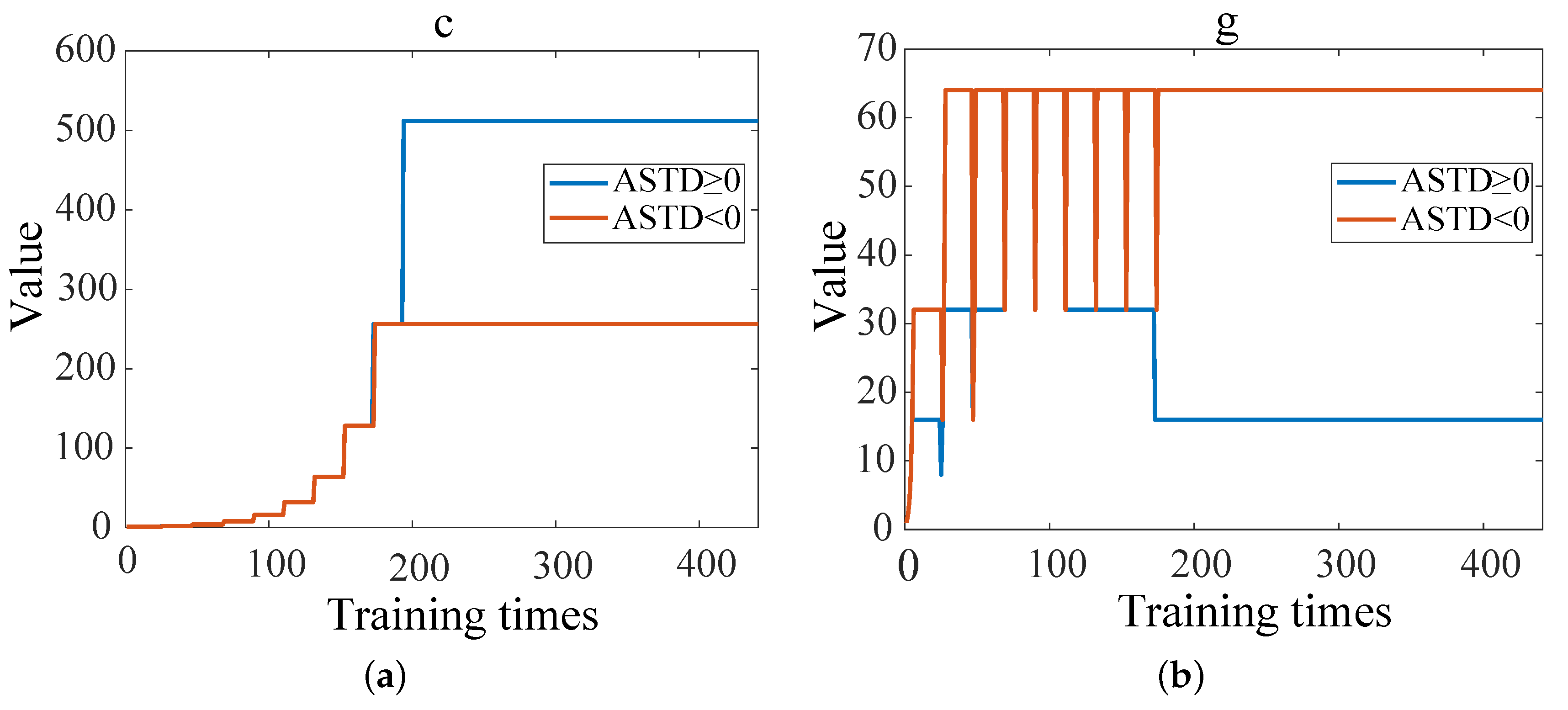
2.2.3. Multimodel Fusion Diagnosis Method
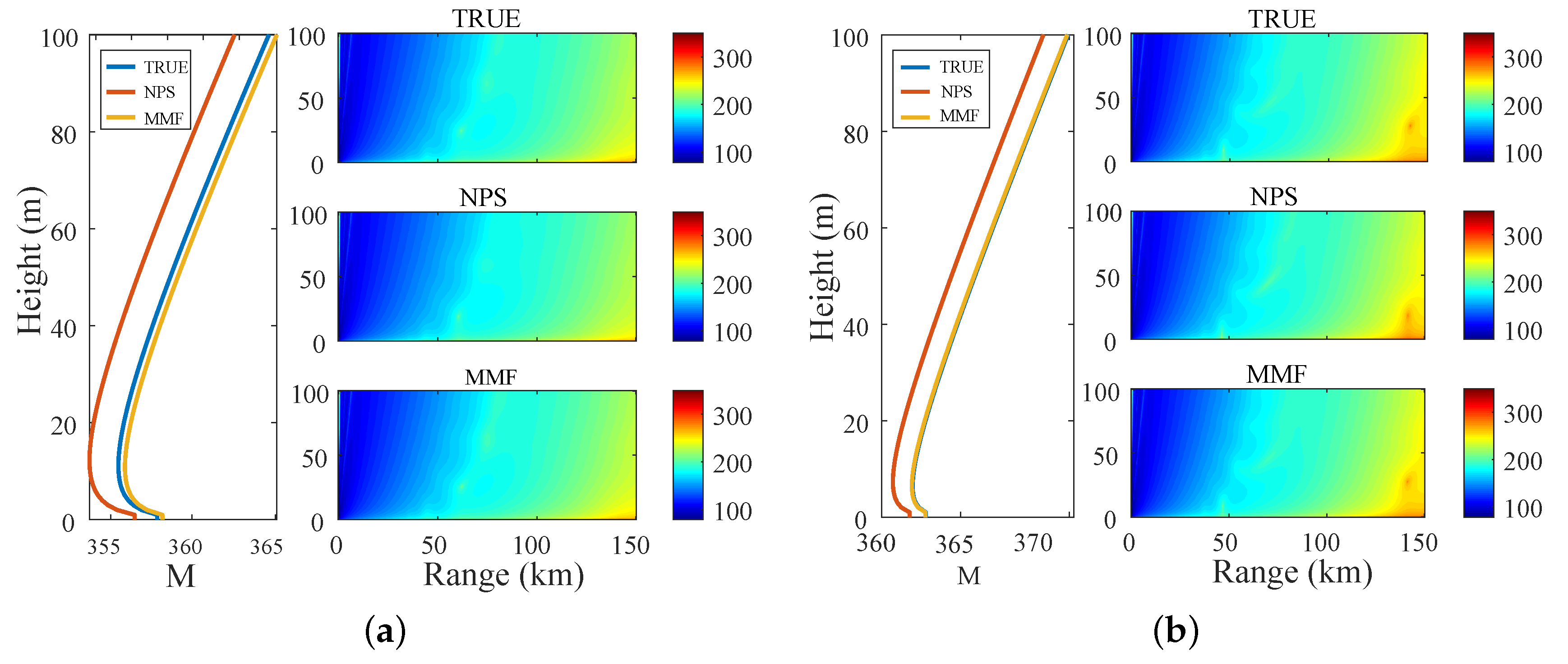
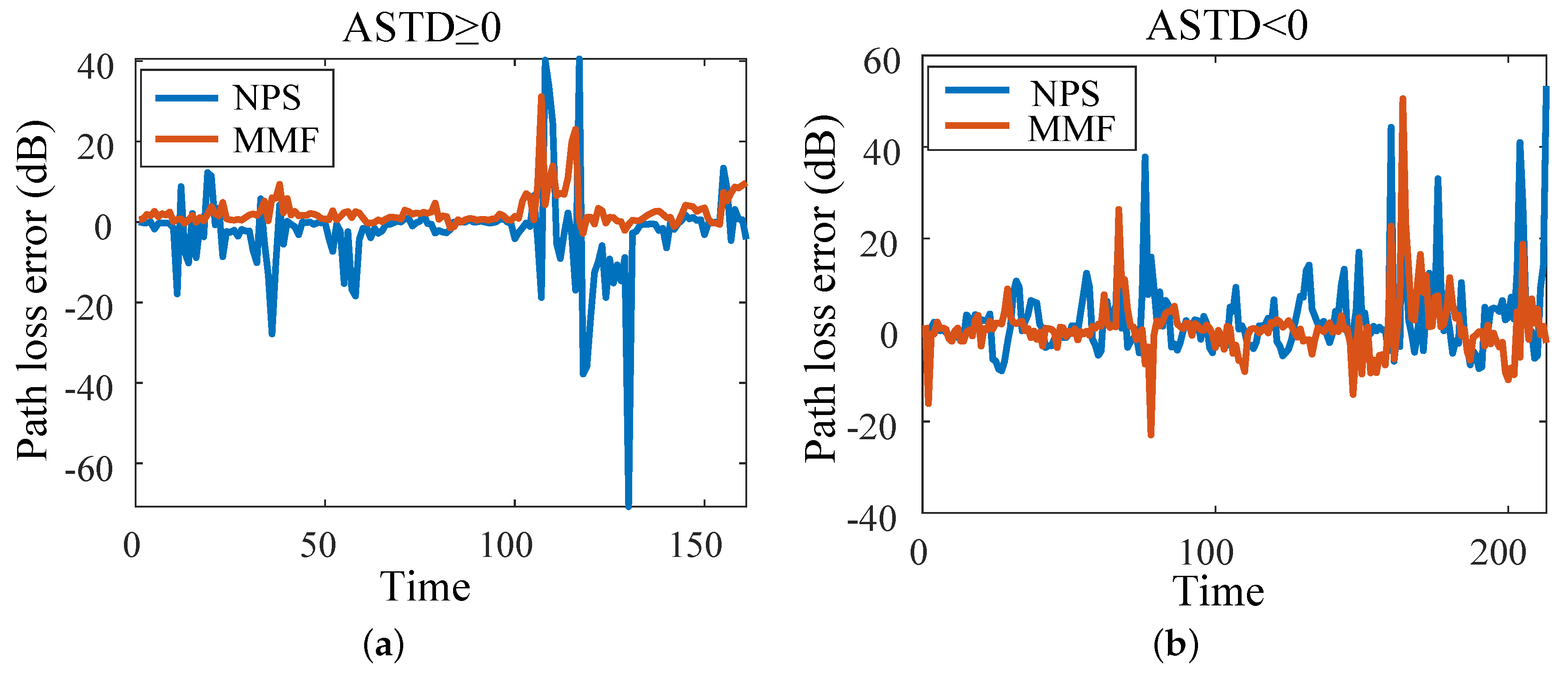
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, X.; Yang, P.; Zhou, F.; Zhou, Z. Comparison of evaporation duct height statistics based on surface bulk measurements over Yongxing Island. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 1306–1310. [Google Scholar] [CrossRef]
- Huang, L.; Zhao, X.; Liu, Y.; Yang, P.; Ding, J.; Zhou, Z. The diurnal variation of the evaporation duct height and its relationship with environmental variables in the south China Sea. IEEE Trans. Antennas Propag. 2022, 70, 10865–10875. [Google Scholar] [CrossRef]
- Chen, Z. Study on Evaporation Duct Model A Considering Turbulence Based on Cosine Similarity. In Proceedings of the 2022 IEEE 10th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 17–19 June 2022; Volume 10, pp. 2538–2541. [Google Scholar]
- Han, J.; Wu, J.J.; Zhu, Q.L.; Wang, H.G.; Zhou, Y.F.; Jiang, M.B.; Zhang, S.B.; Wang, B. Evaporation duct height nowcasting in China’s Yellow Sea based on deep learning. Remote Sens. 2021, 13, 1577. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, S.; Yang, F.; Yang, K. Statistical Analysis of Hybrid Atmospheric Ducts over the Northern South China Sea and Their Influence on Over-the-Horizon Electromagnetic Wave Propagation. J. Mar. Sci. Eng. 2023, 11, 669. [Google Scholar] [CrossRef]
- Ji, H.; Yin, B.; Zhang, J.; Zhang, Y.; Li, Q.; Hou, C. Multiscale Decomposition Prediction of Propagation Loss for EM Waves in Marine Evaporation Duct Using Deep Learning. J. Mar. Sci. Eng. 2022, 11, 51. [Google Scholar] [CrossRef]
- Yang, S.; Li, X.; Wu, C.; He, X.; Zhong, Y. Application of the PJ and NPS evaporation duct models over the South China Sea (SCS) in winter. PLoS ONE 2017, 12, e0172284. [Google Scholar] [CrossRef] [PubMed]
- Chai, X.; Li, J.; Zhao, J.; Wang, W.; Zhao, X. LGB-PHY: An evaporation duct height prediction model based on physically constrained lightGBM algorithm. Remote Sens. 2022, 14, 3448. [Google Scholar] [CrossRef]
- Tang, H.; Zhang, Y.; Wang, H.; Yu, X. Study on Distribution Characteristics of Evaporation Duct for Electromagnetic Wave Propagation. In Proceedings of the 2023 5th International Conference on Electronic Engineering and Informatics (EEI), Wuhan, China, 30 June–2 July 2023; pp. 365–370. [Google Scholar]
- Chai, X.; Li, J.; Zhao, J.; Zhao, X. Application of Machine Learning in the Research of Evaporation Duct Height: A review. J. Phys. Conf. Ser. 2022, 2203, 012079. [Google Scholar] [CrossRef]
- Guo, X.; Kang, S.; Zhang, Y. Comparison of evaporation duct models with meteorology grads tower measurements. In Proceedings of the ISAPE2012, Xi’an, China, 22–26 October 2012; p. 620. [Google Scholar]
- Babin, S.M.; Young, G.S.; Carton, J.A. A new model of the oceanic evaporation duct. J. Appl. Meteorol. Climatol. 1997, 36, 193–204. [Google Scholar] [CrossRef]
- Babin, S.M. A New Model of the Oceanic Evaporation Duct and Its Comparison with Current Models; University of Maryland: College Park, MD, USA, 1996. [Google Scholar]
- Babin, S.M.; Dockery, G.D. LKB-based evaporation duct model comparison with buoy data. J. Appl. Meteorol. Climatol. 2002, 41, 434–446. [Google Scholar] [CrossRef]
- Frederickson, P.A.; Davidson, K.L.; Goroch, A.K. Operational bulk evaporation duct model for MORIAH. Version 2000, 12, 93943–95114. [Google Scholar]
- Frederickson, P.A.; Davidson, K.L.; Newton, A. An operational bulk evaporation duct model. In Proceedings of the Battlespace Atmospheric and Cloud Impacts on Military Operations Conference, Monterey, CA, USA, 9–11 September 2003; p. 1. [Google Scholar]
- Qiu, Z.; Hu, T.; Wang, B.; Zou, J.; Li, Z. Selection optimal method of evaporation duct model based on sensitivity analysis. J. Atmos. Ocean. Technol. 2022, 39, 941–957. [Google Scholar] [CrossRef]
- Zhao, W.; Li, J.; Zhao, J.; Jiang, T.; Zhu, J.; Zhao, D.; Zhao, J. Research on evaporation duct height prediction based on back propagation neural network. IET Microwaves Antennas Propag. 2020, 14, 1547–1554. [Google Scholar] [CrossRef]
- Wesely, M.L. Comments on “Bulk parameterization of air-sea exchanges of heat and water vapor including the molecular constraints at the interface”. J. Atmos. Sci. 1980, 37, 2798–2800. [Google Scholar] [CrossRef]
- Tian, B.; Liu, Q.; Lu, J.; He, X.; Zeng, G.; Teng, L. The influence of seasonal and nonreciprocal evaporation duct on electromagnetic wave propagation in the Gulf of Aden. Results Phys. 2020, 18, 103181. [Google Scholar] [CrossRef]
- Yan, Y.; Lu, B.; Xu, T. Exploring the Relationship between Host Self-Description and Consumer Purchase Behavior Using a Self-Presentation Strategy. Systems 2023, 11, 430. [Google Scholar] [CrossRef]
- Zhao, W.; Li, J.; Zhao, J.; Zhao, D.; Zhu, X. PDD_GBR: Research on evaporation duct height prediction based on gradient boosting regression algorithm. Radio Sci. 2019, 54, 949–962. [Google Scholar] [CrossRef]
- Mai, Y.; Sheng, Z.; Shi, H.; Li, C.; Liu, L.; Liao, Q.; Zhang, W.; Zhou, S. A new diagnostic model and improved prediction algorithm for the heights of evaporation ducts. Front. Earth Sci. 2020, 8, 102. [Google Scholar] [CrossRef]
- Wang, B.; Wu, Z.S.; Zhao, Z.W.; Wang, H.G. A passive technique to monitor evaporation duct height using coastal GNSS-R. IEEE Geosci. Remote Sens. Lett. 2011, 8, 587–591. [Google Scholar] [CrossRef]
- Zhang, M.; Sun, X.; Xu, J. Heavy metal pollution in the East China Sea: A review. Mar. Pollut. Bull. 2020, 159, 111473. [Google Scholar] [CrossRef]
- Qiu, Z.; Zhang, C.; Wang, B.; Hu, T.; Zou, J.; Li, Z.; Chen, S.; Wu, S. Analysis of the accuracy of using ERA5 reanalysis data for diagnosis of evaporation ducts in the East China Sea. Front. Mar. Sci. 2023, 9, 1108600. [Google Scholar] [CrossRef]
- Kang, S.; Zhang, Y.; Wang, H.; Wang, Z. The characteristics and detection of atmospheric duct. Atmos. Ducts Troposphere 2014, 44–68. [Google Scholar]
- Yan, X.; Yang, K.; Ma, Y. Calculation method for evaporation duct profiles based on artificial neural network. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 2274–2278. [Google Scholar] [CrossRef]
- Ai, G.; Sheng, P.; Du, J.; Zheng, Y.; Cai, X.; Wu, H.; Hu, Y.; Hua, Y.; Li, X. Barometric altimetry system as virtual constellation applied in CAPS. Sci. China Ser. G Phys. Mech. Astron. 2009, 52, 376–383. [Google Scholar] [CrossRef]
- Yang, C.; Wang, J.; Shi, Y. A Multi-Dimensional Deep-Learning-Based Evaporation Duct Height Prediction Model Derived from MAGIC Data. Remote Sens. 2022, 14, 5484. [Google Scholar] [CrossRef]
- Jiang, Y.; Yao, X.; Zhang, Y. An Evaporation Duct Height Estimation Algorithm Based on Deep Neural Networks. J. Phys. Conf. Ser. 2022, 2224, 012020. [Google Scholar] [CrossRef]
- Almond, T.; Clarke, J. Consideration of the usefulness of microwave propagation prediction methods on air-to-ground paths. In IEE Proceedings F (Communications, Radar and Signal Processing); IET Digital Library: London, UK, 1983; Volume 130, pp. 649–656. [Google Scholar]

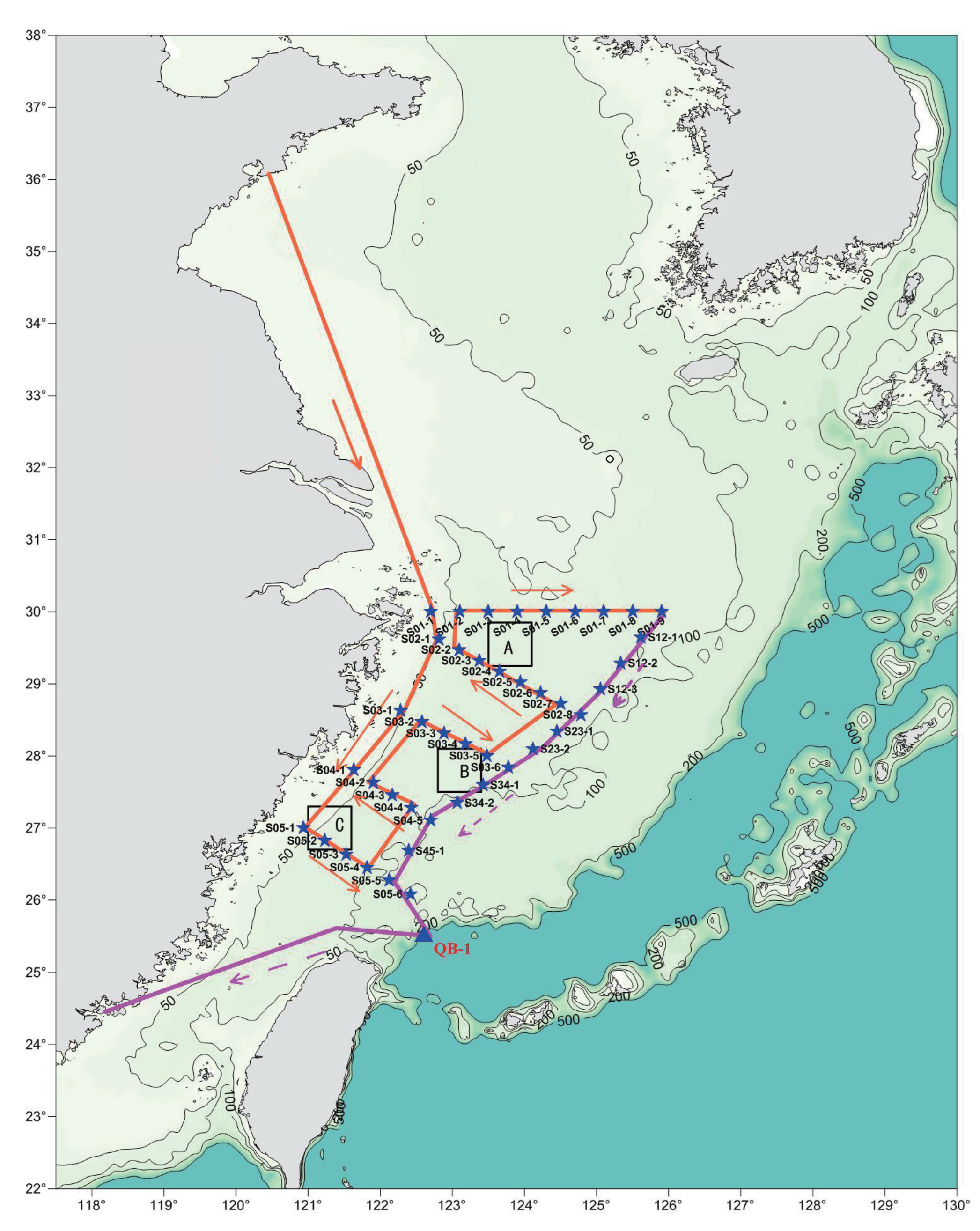

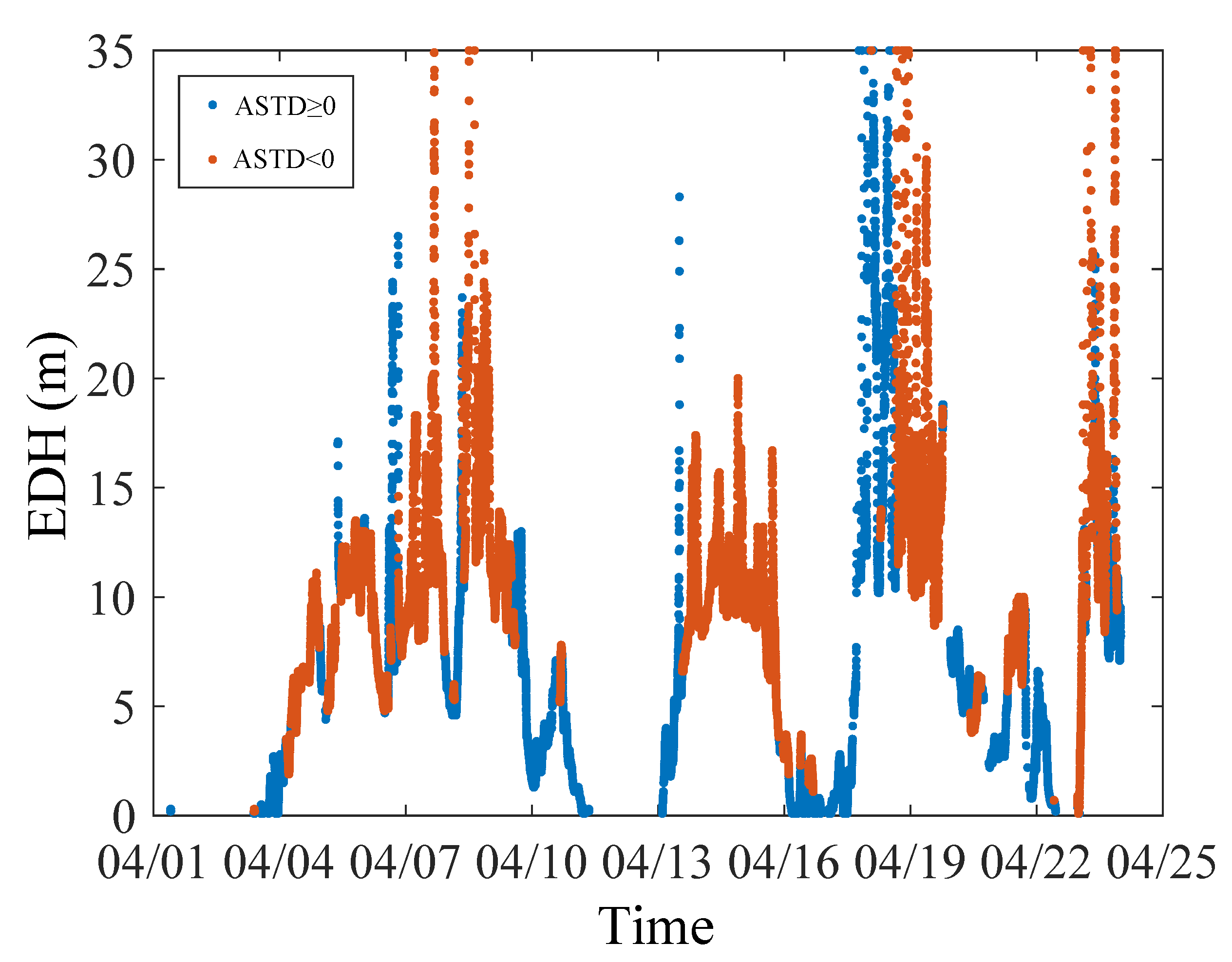
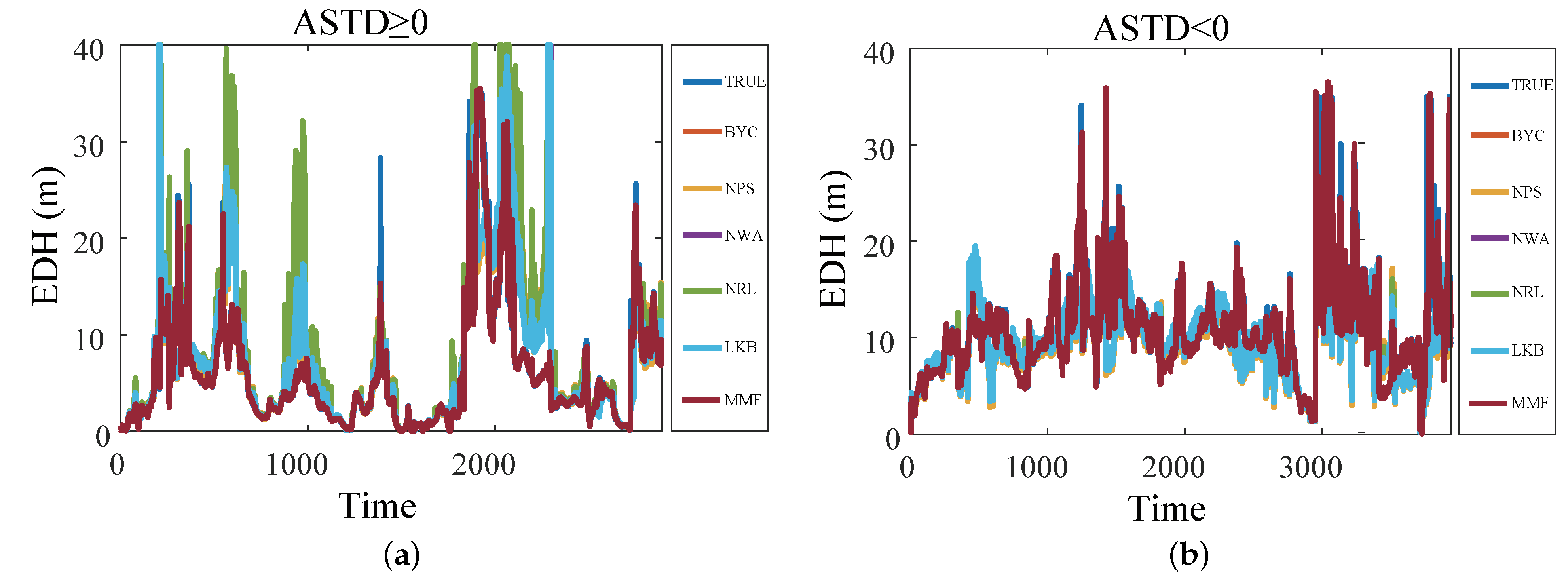

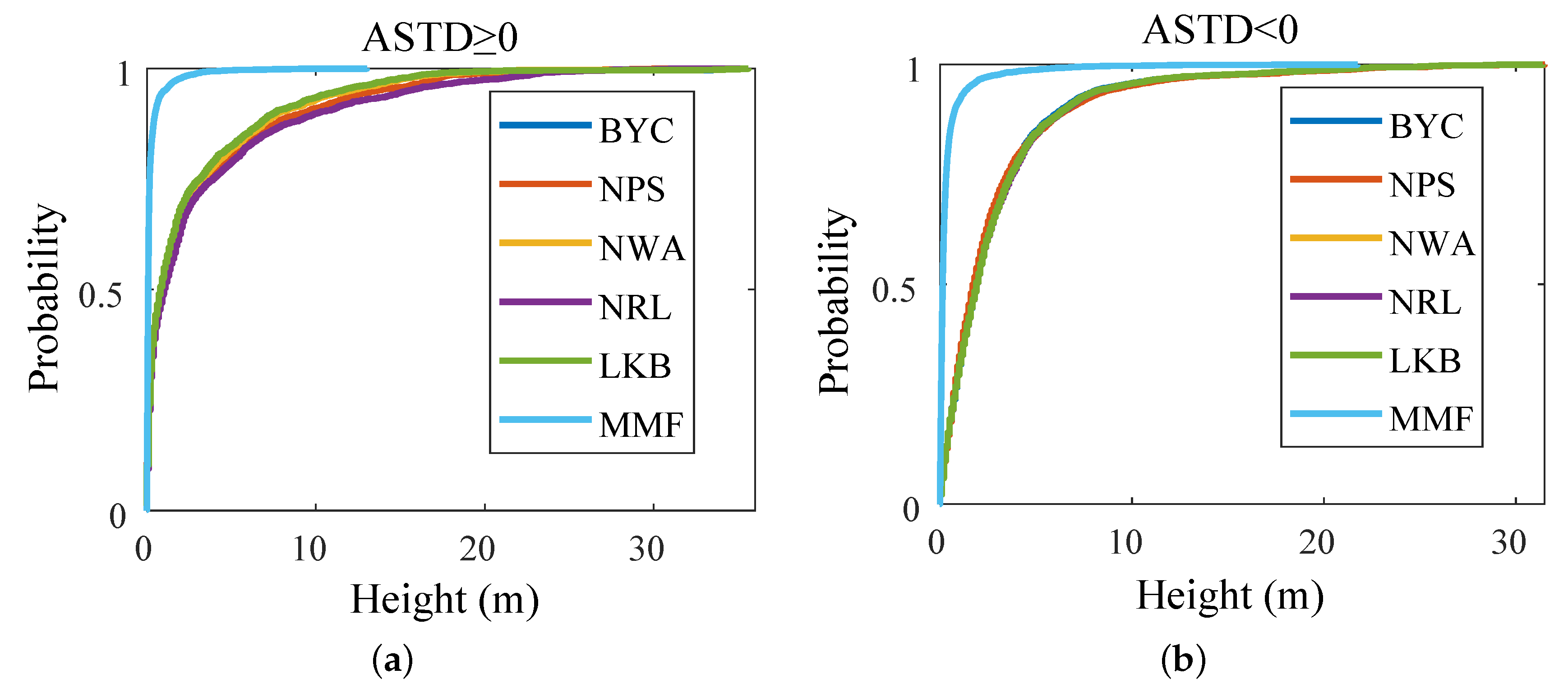
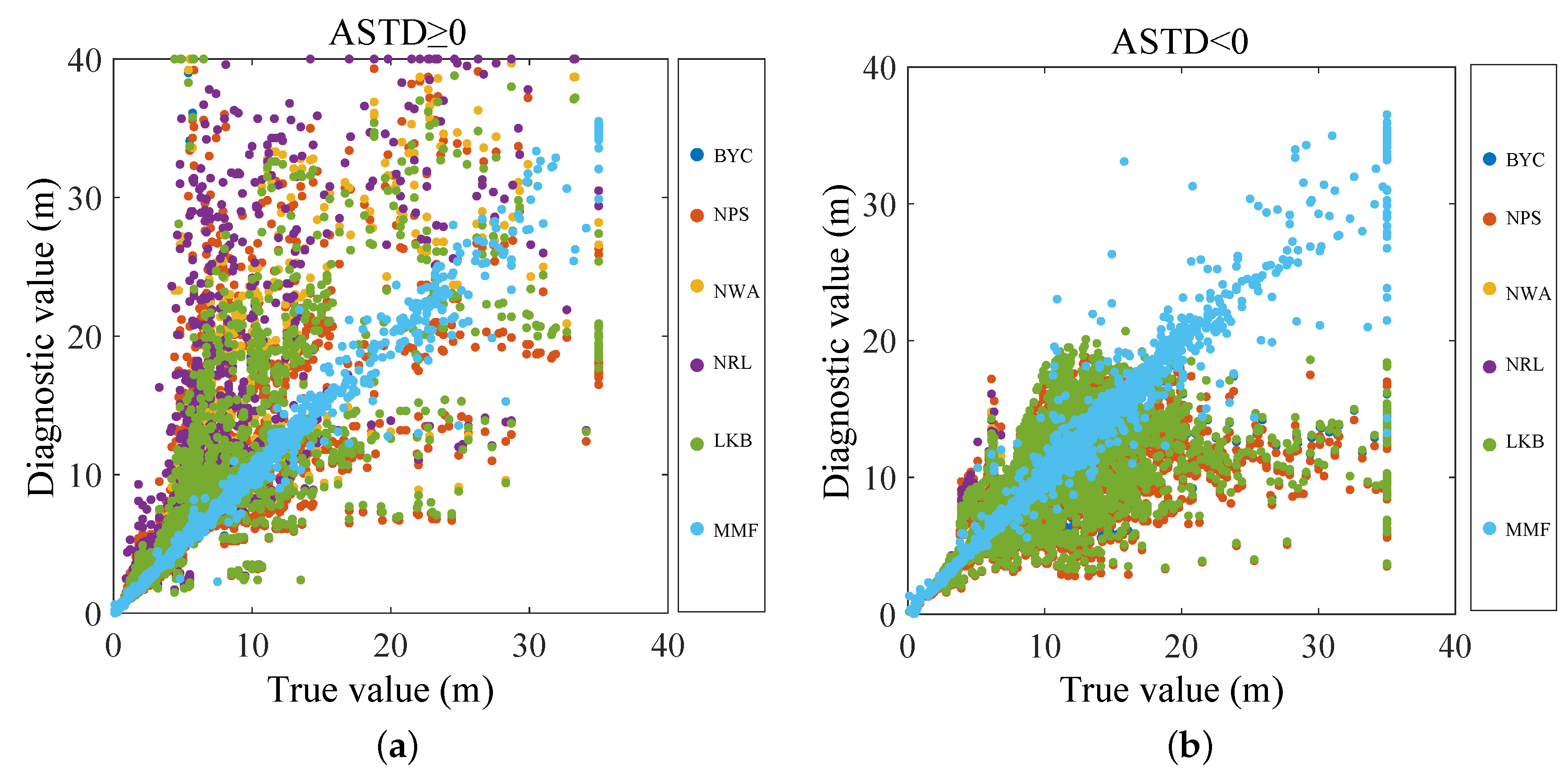

| Sensor | Type | Data | Specification | Location |
|---|---|---|---|---|
| HUMICAP | Vaisala HMP155 | Relative humidity | RH: | Mast 3rd level (22.3 m) |
| 15–25 °C: ±1% RH (0–90% RH) | Mast 1st level (14.8 m) | |||
| −20–40 °C: ±1.7% RH (90–100% RH) | Accommodation deck (8.3 m) | |||
| Air temperature | AT: ±(0.055–0.0057 × AT °C) | Accommodation deck (8.3 m) | ||
| Forecastle deck (6 m) | ||||
| Barometric pressure | Young 61302L | Air pressure | ±0.2 hPa (25 °C), ±0.3 hPa (−40–60 °C) | Compass deck (13.1 m) |
| Weather station | Airmar 150WXS | Wind speed | 5% (10 m/s) | Compass deck (13.1 m) |
| Infrared thermometers | Optris CTLT20 | Sea surface temperature | ±1 °C | Compass deck (13.1 m) |
| Condition | Parameter | Data |
|---|---|---|
| ASTD ≥ 0 | c | 512 |
| g | 16 | |
| ASTD < 0 | c | 256 |
| g | 64 |
| Parameter | Model | Atmospheric Condition | |
|---|---|---|---|
| ASTD ≥ 0 | ASTD < 0 | ||
| RMSE | BYC | 4.93 | 4.75 |
| NPS | 5.48 | 4.86 | |
| NWA | 5.04 | 4.77 | |
| NRL | 6.17 | 4.78 | |
| LKB | 4.93 | 4.77 | |
| MMF | 0.72 | 1.17 | |
| PCC | BYC | 0.76 | 0.51 |
| NPS | 0.72 | 0.51 | |
| NWA | 0.76 | 0.50 | |
| NRL | 0.71 | 0.50 | |
| LKB | 0.76 | 0.50 | |
| MMF | 0.99 | 0.97 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Qiu, Z.; Fan, C.; Song, G.; Wang, B.; Hu, T.; Zou, J.; Li, Z.; Wu, S. Research on a Multimodel Fusion Diagnosis Method for Evaporation Ducts in the East China Sea. Sensors 2023, 23, 8786. https://doi.org/10.3390/s23218786
Zhang C, Qiu Z, Fan C, Song G, Wang B, Hu T, Zou J, Li Z, Wu S. Research on a Multimodel Fusion Diagnosis Method for Evaporation Ducts in the East China Sea. Sensors. 2023; 23(21):8786. https://doi.org/10.3390/s23218786
Chicago/Turabian StyleZhang, Cheng, Zhijin Qiu, Chen Fan, Guoqing Song, Bo Wang, Tong Hu, Jing Zou, Zhiqian Li, and Sheng Wu. 2023. "Research on a Multimodel Fusion Diagnosis Method for Evaporation Ducts in the East China Sea" Sensors 23, no. 21: 8786. https://doi.org/10.3390/s23218786
APA StyleZhang, C., Qiu, Z., Fan, C., Song, G., Wang, B., Hu, T., Zou, J., Li, Z., & Wu, S. (2023). Research on a Multimodel Fusion Diagnosis Method for Evaporation Ducts in the East China Sea. Sensors, 23(21), 8786. https://doi.org/10.3390/s23218786







