Abstract
In the context of Kalman filters, the predicted error covariance matrix and measurement noise covariance matrix are used to represent the uncertainty of state variables and measurement noise, respectively. However, in real-world situations, these matrices may vary with time due to measurement faults. To address this issue in CubeSat attitude estimation, an adaptive extended Kalman filter has been proposed that can dynamically estimate the predicted error covariance matrix and measurement noise covariance matrix using an expectation-maximization approach. Simulation experiments have shown that this algorithm outperforms existing methods in terms of attitude estimation accuracy, particularly in sunlit and shadowed phases of the orbit, with the same filtering parameters and initial conditions.
1. Introduction
Cube satellites (CubeSats) are being developed because they are capable of carrying out missions such as Earth observation, astronomical physics, etc., in place of large satellites [1,2]. Additionally, CubeSats, which are predominant in low Earth orbit (LEO), have been considered to be key enablers in global coverage and connectivity [3]. Furthermore, they use commercial off the shelf (COTS) components, which reduces development and production costs. A CubeSat is a standard cubic satellite with a side of 10 cm and a mass of approximately 1 kg. Large CubeSats can be built using several cubic units, for instance, two-, three- and six-unit CubeSats. CubeSats have increased access to space by providing low launch cost since they are a carried as secondary payloads in the launch vehicle. Although they are relatively cheap to produce and launch, they have limitations in size, weight, and power (SWaP), limiting the size and performance of the subsystems [4].
The attitude determination and control system (ADCS) is one of the satellite subsystems, and its key function is centered around steering the spacecraft to its intended orientation. The ADCS can further be divided into two subsystems: attitude determination and attitude control subsystems. The former uses sensors to compute the rotation of a rigid body about its center of mass (attitude), while the latter uses actuators to reorient the rigid body to the desired rotation. The desired orientation could be nadir pointing to help ground stations to telecommand or sun pointing to maximize power generation. It is evident in Figure 1 that the attitude determination system (ADS) serves as a reference for control.
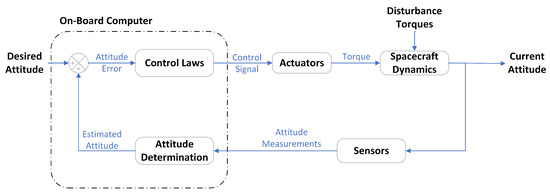
Figure 1.
Attitude determination and control system.
The ADS sensors are broadly categorized into reference and inertial sensors. The reference sensors provide directional measurements of the satellite regarding another celestial object in space, for instance, horizon sensors, sun sensors, etc. [4]. Inertial sensors are used to determine the rate of attitude change of an object about an inertial frame of reference [5]. These sensors typically include gyroscopes, which are used to measure angular velocity. Since the ADS uses COTS components, the sensors are usually categorized by high noise levels, which affect the systems’ accuracy. The accuracy of CubeSat attitude estimation can also be influenced by the accumulated attitude error over time, which is caused by drifts of the inertial sensors used.
The attitude determination or estimation algorithms are used to process sensor measurements to compute the attitude. The computed attitude can take several parameterizations; for instance, it may be described using Euler angles, quaternions, axis angle or directional cosine matrix (DCM) [6,7,8]. However, minimal parameterizations such as Euler angles, Rodriguez parameters and modified Rodriguez parameters (MRPs) are frequently avoided in filter designs for global attitude because they can fall victim to singularities, but they are commonly used to define local error attitudes [9]. The most popular attitude parameterization technique is the quaternion since it encounters no singularity problem.
The attitude determination algorithms or single frame methods use measurement vectors provided by reference sensors to calculate an object’s orientation instantaneously. These deterministic algorithms include triaxial attitude determination (TRIAD), Davenport’s q method, quaternion estimator (QUEST) and single value decomposition (SVD) [10,11]. These deterministic methods have been well defined in [12]; therefore, we will not go into detail here. Attitude estimation algorithms make use of vector measurements, inertial measurements and previous attitude information to provide the current optimal attitude estimate. The estimation process can be divided into filtering of sensor measurements and computation of attitude from sensor observations [13]. As stated in [13,14], the filtering process can be accomplished through various methods, such as particle filtering and derivatives of the Kalman filter.
It is common to couple a magnetometer and a sun sensor to measure attitude in small satellites such as CubeSat because each sensor cannot provide three-axis attitude knowledge independently [15,16,17,18,19]. When one vector is available, the satellite is free to rotate about that vector; thus, at least two vectors are used [15]. When the satellite is in orbit, it passes through regions where the sunlight is blocked by the Earth, referred to as the eclipse phase. For low Earth orbit satellites, they spend about 35 min of their orbital time in this phase [20]. During this region, only one vector is available for computing the satellite’s attitude, resulting in high attitude error. The high attitude error affects attitude control accuracy, and this may result in loss of communication during overpasses. It is possible to use additional auxiliary sensors during this phase, but due to the CubeSat’s limited mass and volume, only minimal components are used.
In an attempt to make the attitude estimation process accurate during both the sun and eclipse phases, several methods have been employed. The authors in [21] propose the use of magnetic field derivatives as the second vector in the QUEST-aided multiplicative EKF architecture to increase the accuracy of attitude estimation during the eclipse phase. Using only magnetometer measurements, the proposed method can estimate rough attitude and angular rate even during eclipse phases; therefore, it can also be used in case of gyroscope failure. In [22], it was found that the SVD-aided EKF outperformed the traditional EKF during the eclipse phase. This improved performance was due to the capability of the SVD-aided EKF to adapt the measurement error covariance matrix () when the ADS lost sensor measurements. During the eclipse phase, when the satellite was in shadow and the reference sensors might not have been providing reliable measurements, the SVD-aided EKF utilized an adaptation rule to update the matrix. This adaptation allowed the filter to effectively account for the loss of sensor measurements and to adjust the covariance matrix accordingly, leading to improved attitude estimation accuracy. This adaptive behavior of the SVD-aided EKF during the eclipse phase was found to be a significant advantage over the traditional EKF, which did not incorporate such an adaptation. As a result, the SVD-aided EKF demonstrated superior performance in terms of attitude estimation accuracy during this challenging phase of the satellite’s orbit, as shown in the research findings by [22]. In contrast, the research revealed that the SVD-aided EKF may exhibit poor performance over a longer period (e.g., over 1000 s) compared to the traditional EKF, particularly during extended eclipse phases. For instance, in the case of low Earth orbit (LEO) CubeSats, the eclipse phase typically lasts for approximately 35 min (2100 s), as shown in [20]. As a result, the SVD-aided EKF may not be well suited for attitude estimation during such prolonged eclipse phases. Another paper [23] proposes a prediction approach for estimating satellite attitude during the eclipse phase and an adaptive scheme that utilizes the SVD-aided EKF to determine the sun phase. However, the study identified that the accuracy of the prediction algorithm was compromised due to the prolonged duration of the eclipse period.
The SVD-aided EKF was developed as an attempt to enhance the performance of the traditional EKF by incorporating measurement noise covariance matrix adaptation. However, it has been observed that the SVD-aided EKF may face limitations in prolonged eclipse phases. In response, further research has been conducted to develop improved approaches that can make the EKF more adaptable to anomalies such as measurement faults during extended eclipse periods. In [24], the authors present a technique for computing satellite attitude estimation using an EKF with singular value decomposition (SVD) assistance. The algorithm also incorporates simultaneous adjustments of the process and measurement covariance utilizing data obtained from magnetometers and sun sensors. When the process noise increases or the spacecraft is in eclipse, SVD-aided adaptive EKF performs better than SVD-aided EKF. The authors in [25] propose a hierarchical and efficient framework for satellite attitude determination that aims to compensate for observation errors in raw attitude data. It includes a simplified adaptive Kalman filtering module, a neural-network-based system error compensation module, and a weighted attitude smoothing module. The performance of the proposed framework, trained with full matrix elements, was found to be comparable to the optimal accuracy when compared with conventional algorithms. Another study in [26] introduces a novel algorithm called adaptive iterated extended Kalman filter (AIEKF) for relative position and attitude estimation, considering model uncertainty in a nonlinear stochastic discrete-time system with unknown disturbance. The AIEKF algorithm employs Gauss–Newton iterative optimization steps for maximum a posteriori (MAP) estimation and incorporates a switch-mode combination technique to achieve adaptability. The mean-square estimation error (MSE) of the state estimate is derived, and it is proven that the AIEKF outperforms the traditional extended Kalman filter (EKF) or iterated extended Kalman filter (IEKF) in terms of MSE.
The structure of the paper is as follows: The attitude estimation and static algorithms are presented in Section 2 in detail. Section 3 provides an introduction to the mathematical models utilized for the presented CubeSat. The proposed filter adaptation method is presented in Section 4. In Section 5, the simulation results of the adaptive EKF algorithm for a hypothetical CubeSat are presented. In Section 6, a brief conclusion is given.
2. Attitude Estimation Algorithms
In this section, we look at the singular value decomposition, extended Kalman filter and their hybrid, as they have been proven to be robust algorithms.
2.1. The SVD Algorithm
The SVD algorithm is a deterministic technique for computing the attitude matrix that minimizes Wahba’s problem [11,27]. An alternative way to simplify the Wahba’s loss function is to use a matrix given as:
where is the non-negative weight, is a set of reference vectors in the reference frame, and is a set of measured vectors in the satellite body frame. The optimal attitude matrix is calculated using and matrices, such that
To examine the rotation angle error, the error covariance matrix is defined as
where , and .
2.2. The Extended Kalman Filter
The extended Kalman filter (EKF) is appropriate for nonlinear state equations; therefore, it can be used as an alternative attitude estimator [28]. Nonlinear discrete time systems can be defined as follows:
where state vector is involved in the system and measurement differential functions denoted by f and h, respectively, y is the expected measurement, and w and v are the process and measurement noises with known covariance, respectively. The EKF consists of two steps: prediction and measurement update, that is,
Prediction step
Measurement Update
The differential function h is deduced from the relationship between reference vectors and the satellite measured vectors, given by
where is the attitude matrix in quaternion form. The measured vector is the expected measurement given a set of references vector; therefore, it is similar to from (5).
2.3. SVD-Aided EKF Algorithm
The SVD-aided EKF reduces the computational cost of the EKF by using rough attitude estimates from the SVD algorithm instead of non-linear measurements [24]. The estimation covariance obtained from the SVD is used as the measurement noise covariance matrix in the filter, which inherently makes it adaptive to noise increments in measurements. In the SVD-aided EKF, the discrete time system is defined as
3. System Model
3.1. System Kinematics
The change in attitude of a satellite is modeled using the kinematics equation, which describes rotational motion despite the cause. The kinematic equation of a satellite using quaternions attitude representation is given by
where and r are the components of the angular velocity provided by the gyroscope [29], and is the scalar component of the quaternion. The kinematic equation is useful when defining the state transition matrix in the extended Kalman filter. In this research, quaternions are employed for attitude computation due to their mathematical advantages, such as singularity avoidance and efficient numerical representation. However, for graphical presentation and visualization, Euler angles are used, as they are more commonly used in aerospace engineering and provide a more intuitive representation of attitude. This choice allows for a clear and easy-to-understand presentation of the results in a familiar format. The computed quaternion is converted to Euler angles using
3.2. Environment Models
3.2.1. International Geomagnetic Reference Field (IGRF)
The IGRF denotes the main geomagnetic field generated by internal sources, primarily inside the core of the Earth [30]. The absence of electric currents on the surface allows for computation of the Earth’s geomagnetic field as the negative gradient of a scalar potential, such that the magnetic field can be expressed as . The potential function is represented by a finite series expansion in terms of Gauss coefficients, and [31]:
Here, are the radial distance from the Earth’s center, geocentric co-latitude, longitude and time, respectively. The variable a is the Earth’s radius. More information about the spherical harmonic coefficients can be found in [30]. The latest version in the series, IGRF-13, extends up to thirteen harmonic degrees.
3.2.2. PSA Sun Position Algorithm
This paper utilizes the PSA algorithm to calculate the solar vector in the inertial frame due to its small computational footprint and high accuracy. It has been established that when applied over a period ranging from 2020 to 2050, the maximum error in angular deviation from the actual solar vector is only 35 arc-sec, with the algorithm maintaining its computational structure and simplicity [32]. The PSA algorithm’s inputs consist of the location’s latitude and longitude, along with the time specified in universal time (UT1), encompassing year, month, day, hours, minutes, and seconds. The sun vector is given by
where and are the zenith and azimuth angles. More information on how these angles are obtained can be found in [32].
3.3. Measurement Model
In this model, we assume that only zero-mean Gaussian white noise can corrupt the sensor measurements. The measurement model for the vector observations can be given as
where is the sun and magnetic field vector observations in the body frame, can either be or modeled in the reference frame, is the Gaussian white noise, and is the attitude matrix expressed in quaternions.
For gyroscopes, the inherent sensor bias introduces errors throughout the attitude determination process; therefore, these errors are also included in the state vector estimate. The gyroscope mathematical model presented in this paper is
where gyroscope noise and bias of a satellite are represented by and , respectively, while the true angular velocity of the satellite relative to the inertial frame is denoted by .
3.4. Coordinate Systems
Several reference frames are used to describe the satellite’s attitude. This paper employs three reference frames, each of which is defined by its fixed element or direction, as well as by the location of its center or origin, that is, satellite body coordinate frame, orbit referenced coordinate frame and Earth centered inertial (ECI) coordinate frame. These coordinate frames have been well explained in [14].
4. Adaptive EKF
During extended eclipse phases, it was noted that the traditional extended Kalman filter (EKF) exhibited superior performance compared to other methods such as the singular value decomposition (SVD)-aided EKF. However, if the accuracy of the process and measurement noise covariance matrices is compromised, the EKF may produce substantial estimation errors, despite outperforming other algorithms in prolonged eclipses. As a result, there is a great need for developing an adaptive EKF that is compatible with inaccurate covariance matrices. Firstly, we discuss how each covariance matrix affects the performance of the extended Kalman filter (EKF). The process noise covariance matrix can cause inaccurate prediction of the error covariance matrix in (7), which directly affects the computation of the Kalman gain as shown in (8). Finally, the optimal estimate and the estimated error covariance matrix are derived from the incorrect and as seen in (9) and (10), respectively. Additionally, it is clear that an imprecise measurement noise covariance matrix can lead to an imprecise Kalman gain, resulting in inadequate state estimation. It is apparent that and directly affect the state estimate as compared to . In this paper, a and adaptive filter is proposed for attitude estimation. The filter performance will be compared to the SVD-aided EKF in the sun and eclipse phases, which performs better than the conventional EKF in attitude estimation.
4.1. Expectation Maximization
There is usually inadequate information for training Bayesian networks; for example, it is difficult to accurately determine noise covariance matrices in a Kalman filter [33]. Such latent parameters can explicitly be estimated using the expectation maximization (EM) algorithm, which is an iterative algorithm used in unsupervised learning. The EM algorithm is an approach used to find the maximum likelihood (ML) estimates of the latent variables in a statistical method. It is used to find the maximum likelihood estimate of the parameters, given the observed data. The algorithm consists of two steps: the expectation step, where the expectation of the log-likelihood function is calculated, given the current estimates of the parameters, and the maximization step (M-step), where the parameters are updated to maximize the expected log-likelihood [34]. The algorithm iterates between these two steps until convergence, at which point the parameters are considered to be the maximum likelihood estimates. The goal of this paper is to use the joint log-likelihood function to estimate inaccurate noise covariance matrices and based on the available measurements (i.e., measurements taken from time 1 to k) and the unknown state vector , that is,
where . The joint log-likelihood function contains the natural logarithm function log and the probability density function p, which depends on the parameter . To obtain an approximate maximum likelihood (ML) solution for the parameter , we employ the expectation maximization (EM) algorithm, which maximizes the joint log-likelihood function, such that
where is the ML estimate of . It is impossible to solve the complete data log-likelihood function due to the unavailable . The EM algorithm addresses the problem by approximating the joint likelihood function in (21) as its minimum variance estimate , such that [35,36]
where is an approximation of at the ith step.
The EM algorithm takes advantage of this property to generate a series of values , where , with the aim of successively improving the accuracy of the maximum likelihood (ML) estimate. The algorithm is summarized in Algorithm 1. During the E-step, the complete data log-likelihood’s expectation is evaluated, which relies on the current estimates and measurements . Following this, the M-step maximizes the computed utilizing an arithmetic technique.
| Algorithm 1 The expectation maximization algorithm |
|
4.1.1. E Step
The EM algorithm approximates the joint likelihood function as its minimum variance estimate as shown in (22). To determine the minimum variance estimate, we compute the joint log likelihood and the second posterior PDF . Firstly, the joint log likelihood in (20) is written as the product of the conditional likelihood, such that
where , since the expected measurement is only dependent on state as shown in (5). The probability distribution of the sensor measurements is typically not dependent on the current state error and measurement noise covariance matrix . This is because the measurements are generally assumed to be independent of both the state error covariance matrix and the measurement noise covariance matrix, which together determine the joint distribution of the state estimates and the measurements [36]. In the EKF model, the predicted PDF is approximated as Gaussian, that is,
The symbol represents the Gaussian probability density function (PDF) with mean vector and covariance matrix ∑, and is obtained using Equation (6). At this stage, is considered inaccurate because of . The likelihood PDF of the measurement model in (7) is given by
The joint log-likelihood function can be computed using (23)–(25). The logarithm of the normal distribution is:
The logarithm of the normal distribution is:
Putting everything together:
where |.| is the determinant operation of a matrix. After determining the joint likelihood in (28), the posterior PDF is computed. At the step, the state vector estimate and corresponding state estimation error covariance matrix have been calculated. From here, the nonlinear measurement function is linearized using the intermediate state estimate , that is,
where is the Jacobian matrix of the measurement function at . The second posterior PDF is approximated as Gaussian by using a measurement update of the EKF, such that
where and are obtained using and , respectively, given as:
To obtain the minimum variance estimate, Equations (28) and (30) are substituted into Equation (22). The resulting expression is
where is the trace of a matrix. Matrices and are given by
represents the squared Mahalanobis distance between the prediction and the observation, and can be seen as an intermediate step in the calculation of the expected value. The measurement is further linearized at such that
From there, can be computed as
4.1.2. M Step
The M-step entails maximizing regarding , such that
At the maximum point, satisfies
Since , (41) becomes a partial derivative problem, that is, and . The partial derivative can be calculated by exploiting (34) as
where and are given by (35) and (36), respectively. Substituting (42) and (43) in (41) yields
therefore, the error and measurement noise covariance matrices are defined as and , respectively.
4.2. and Adaptive EKF
The proposed adaptive extended Kalman filter (EKF) algorithm in Algorithm 2 involves two primary steps: the time update and the iterated measurement update. In the time update, the predicted state vector and the nominal predicted state error covariance matrix are calculated using Equations (6) and (7), respectively. The algorithm requires several inputs, including the initial state vector , state error covariance matrix , measurement covariance matrix , process noise covariance matrix , and the number of iterated measurements N. The prediction step only computes the state vector and error covariance matrix, considering the system model kinematics and the previous state error covariance matrix. The nominal predicted error covariance matrix serves as an appropriate initial value for , as it includes the information on the state transition matrix , process noise covariance matrix , and the previous estimation error covariance matrix . The for loop estimates the optimal state vector , predicted error covariance matrix , and measurement noise covariance matrix in an adaptive manner.
| Algorithm 2 and adaptive EKF for attitude estimation. |
Inputs: Prediction Step:
Measurement update
for
end for
outputs: |
5. Results and Analysis
In the simulations, a CubeSat in a low Earth orbit is considered, with a principal moment of inertia of kg.m. The spacecraft is assumed to be tumbling, and its initial state is arbitrarily chosen as . The orbit parameters, satellite kinematics, and sensor and environmental models are used to validate the proposed algorithm for attitude estimation. In this study, the sun sensor, magnetometer, and gyroscope are used as attitude sensors. The local magnetic vector is computed using the international geomagnetic reference field model, while a sun position algorithm is used to extract the local reference sun vector. The orbit used in this paper is circular with an inclination of 0 at an altitude of 600 km. The simulation epoch is 2021.01.01, UTC 00:00 with a time-step of 1 s.
The first part of this section is devoted to analyzing the performance of SVD-EKF and proposed AEKF using the Big O notation, the second part analyzes the algorithms during sun phase on the orbit. The third part analyzes the performance of the two algorithms during the eclipse phase. The simultaneous and adaptive extended Kalman filter is referred to as AEKF in this study. The evaluation of the estimation accuracy for the measurement noise covariance matrix and predicted error covariance matrix was carried out using the SRNFN and ASRNFN metrics, which were chosen as the error measures. These metrics provide information about the magnitude of the errors in the estimated matrices by measuring the difference between the estimated and reference values, and they are defined as
The predicted error covariance at time k is represented by , while refers to the reference value of the predicted error covariance matrix at that same time. Similarly, the formulas used for calculating SRNFN and ASRNFN for the predicted error covariance matrix are also applied to the measurement noise covariance matrix. The SRNFN is a metric that measures the similarity between two matrices. The SRNFN is widely used in the field of computer vision and image processing as a measure of the similarity between two images [37]. The Averaged Square Root of Normalized Frobenius Norm (ASRNFN) is an extension of the SRNFN, which is used to measure the similarity between multiple matrices. The ASRNFN is calculated as the average of the SRNFN between each pair of matrices [38].
5.1. Complexity of Algorithms
The big notation is a mathematical notation used to analyze and describe the performance or complexity of algorithms. It provides a framework to express how the runtime or resource usage of an algorithm grows as the input size increases. The notation is represented as (f(n)), where “O” stands for order of magnitude and “f(n)” represents a function that describes the algorithm’s growth rate. The function “f(n)” typically represents the number of operations or resource usage as a function of the input size “n”. The purpose of the big notation is to provide a simplified approximation of the algorithm’s complexity, ignoring constant factors and lower-order terms. By analyzing the big O complexity of algorithms, researchers and developers can make informed decisions about algorithm selection, understand the trade-offs between runtime and resources, and identify areas for optimization. It provides a standardized framework for reasoning about algorithmic efficiency and assists in designing more efficient algorithms to effectively solve computational problems.
- SVD-aided EKFThe operations of predicting the state and error covariance matrix involve matrix multiplication, which has a time complexity of , where n is the size of the matrices involved (in this case, 7 × 7 matrices). The computation of involves multiplication and addition operations with matrices and vectors. Assuming that the input vectors have dimensions 3 × 1, the complexity of this section is () or (1). The SVD operation performed on the matrix has a complexity of (), where m and n are the dimensions of matrix B. Since has dimensions 3x3, the complexity is () or (1). In conclusion, the overall complexity of the SVD-aided EKF can be approximated as .
- Proposed adaptive filterThe prediction part of the algorithm is similar to that of the SVD-aided EKF, and therefore, the complexity is (). The loop iterates N−1 times. The operations such as calculating gain involve matrix multiplication, which has a time complexity of (), where n is the size of the matrices involved (in this case, 6 × 7 and 7 × 7 matrices). The remaining operations in the loop, such as matrix additions and subtractions, have a constant time complexity, (1). Overall, the time complexity is given by (N × ()) = ().
Although both the SVD-aided extended Kalman filter (EKF) and the proposed adaptive EKF algorithms have similar complexities in terms of their big O notation, the complexity analysis only provides an approximation of the computational requirements. The actual runtime performance of the algorithms may differ based on various factors, such as the specific implementation details and the size of the input data.
5.2. Sun Phase
Firstly, we compare the performance of the SVD-EKF and the proposed AEKF during sun phases. During the sun phase or normal operation mode, the filter depends on the sun sensor and magnetometer measurements for measurement update. The proposed algorithm is affected by the number of iterated measurements N: the more that is iterated, the more accurate the state estimates; however, this means an increased computational time. For these simulations, . Table 1 shows the root mean square error of the attitude angles for both filters considered in this study. It is evident that both filters perform reasonably well under the sun mode, as all sensor measurements are available.

Table 1.
Comparison of the root mean square errors of the SVD-EKF and proposed algorithm during the sun phase.
Table 2 shows the single-step run time for the two algorithms. It shows that the proposed algorithm has more computational time as compared to the SVD-EKF. Even though the computational load is higher by only a small margin, the accuracy of the proposed algorithm is significant. To demonstrate the efficacy of the proposed algorithm, we calculated the SRNFN and ASRNFN values of the predicted error and measurement noise covariance matrices, which are useful in analyzing the convergence of these matrices. An analysis of the results presented in Figure 2 and Table 3 indicate that the proposed algorithm outperforms the SVD-EKF algorithm, as evidenced by its lower SRNFN and ASRNFN values.

Table 2.
Single-step run execution of the proposed algorithm and SVD-EKF.
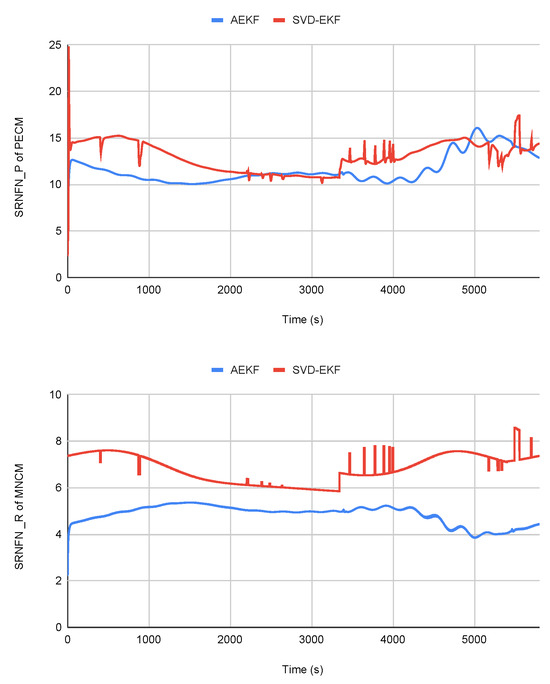
Figure 2.
SRNFN and SRNFN of the two filters during sun phase.

Table 3.
Evaluation of the proposed algorithm and SVD-Aided EKF in sunlit phase using ASRNFN and ASRNFN.
5.3. Eclipse Phase
According to the study in [20], satellites in low Earth orbit are in the eclipse phase for approximately 28 min. During this phase, the attitude-determination system depends solely on magnetometer measurements. Table 4 displays the root mean square error of the SVD-EKF method and AEKF. While the proposed algorithm’s error increased slightly, it still performs significantly better than the SVD-aided EKF. Table 4 confirms that the gyroscope bias increased during the eclipse phase, as compared to the values in Table 1. This increase in bias is likely due to the temperature changes that occur during the eclipse phase. Although modern gyroscopes are designed to minimize temperature-related errors and often include temperature-compensation features, the effects of temperature changes cannot be eliminated. Therefore, it is crucial to consider the potential impact of temperature changes on gyroscope bias when designing and implementing attitude-determination systems for satellites.

Table 4.
Comparison of the root mean square errors of the SVD-EKF and proposed algorithm during eclipse phase.
The inferior estimation accuracy of the SVD-EKF algorithm during the eclipse phase is likely due to the sensitivity of the SVD algorithm, which requires at least two vector measurements to compute attitude. Despite relying solely on magnetometer measurements, the proposed algorithm performs reasonably well. Furthermore, Figure 3 and Table 5 show that the proposed algorithm has a smaller SRNFN and ASRNFN than the SVD-EKF even in the eclipse phase. The noise during the eclipse phase affects the measurements used to estimate the measurement noise and state covariance matrices; therefore, the resulting matrices are less accurate or less precise.
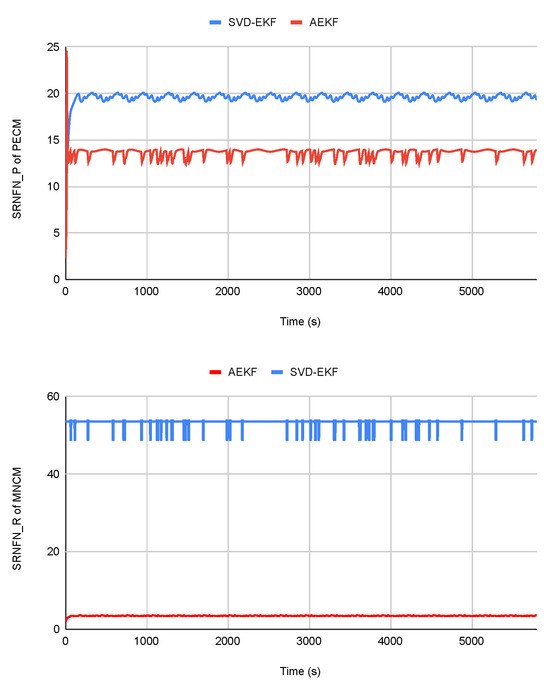
Figure 3.
SRNFN and SRNFN of the two filters during eclipse phase.

Table 5.
Evaluation of the proposed algorithm and SVD-aided EKF in eclipse phase using ASRNFN and ASRNFN.
6. Conclusions
This paper presents the design and numerical analysis of an error and measurement noise covariance matrix-adaptive extended Kalman filter algorithm based on the expectation maximization method. A novel attitude-estimation algorithm was created utilizing an adaptive filter approach. The performance of this newly developed algorithm, as well as a state-of-the-art existing algorithm, was evaluated through application on CubeSat attitude estimation in both the eclipse and sun phases of the orbit. During both phases, the proposed adaptive EKF outperforms the existing algorithm, being the SVD-EKF. The SVD algorithm requires a minimum of two vector measurements and associated reference models to function optimally. However, during the eclipse phase, only magnetometer measurements are available, which causes the performance of the SVD-aided algorithm to deteriorate. Based on the simulation findings outlined in the paper, the proposed algorithm demonstrated significantly improved accuracy in attitude estimation compared to SVD-aided EKF algorithms. However, it was also observed that the proposed algorithm has marginally higher computational complexity.
To ensure the accuracy and reliability of the proposed algorithm in various conditions and applications, it is necessary to conduct rigorous validation and verification through both simulations and real-world tests. This will help to confirm the effectiveness of the algorithm and to identify any potential limitations or areas for improvement. Furthermore, the proposed algorithm can be optimized to improve its performance and to reduce computational complexity. This could involve refining the algorithm’s underlying mathematical models and algorithms, as well as optimizing its implementation and hardware requirements. By doing so, the algorithm could potentially be made more efficient and practical for use in a wider range of systems and applications.
Given the promising outcomes achieved by the proposed algorithm, future research will primarily focus on optimizing the algorithm to significantly decrease its overall complexity. This optimization endeavor will involve a comprehensive exploration of various techniques and methodologies aimed at streamlining the algorithm’s computational demands while maintaining its accuracy and performance. To accomplish this, each component of the algorithm will be meticulously examined to identify potential areas for improvement. Strategies such as algorithmic modifications, efficient data structures, and parallel computing techniques will be employed to alleviate the computational burden. The objective of these efforts is to strike a balance between complexity reduction and algorithmic efficiency, enabling the algorithm to be more practical and applicable in real-world scenarios with limited resources.
Author Contributions
Methodology, K.M.; supervision, O.M. and B.B.; review and editing, T.T.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Botswana International University of Science and Technology, grant number S00387.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Selva, D.; Krejci, D. A survey and assessment of the capabilities of Cubesats for Earth observation. Acta Astronaut. 2012, 74, 50–68. [Google Scholar] [CrossRef]
- Carrara, V.; Kuga, H.K.; Bringhenti, P.M.; de Carvalho, M.J. Attitude determination, control and operating modes for CONASAT Cubesats. In Proceedings of the 24th International Symposium on Space Flight Dynamics (ISSFD), Laurel, MD, USA, 9 May 2014. [Google Scholar]
- Mahmood, N.H.; Böcker, S.; Munari, A.; Clazzer, F.; Moerman, I.; Mikhaylov, K.; Lopez, O.; Park, O.S.; Mercier, E.; Bartz, H.; et al. White paper on critical and massive machine type communication towards 6G. arXiv 2020, arXiv:2004.14146. [Google Scholar]
- Xia, X.; Sun, G.; Zhang, K.; Wu, S.; Wang, T.; Xia, L.; Liu, S. NanoSats/CubeSats ADCS survey. In Proceedings of the 2017 29th Chinese Control And Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 5151–5158. [Google Scholar] [CrossRef]
- Rao, A.S.; Radanovic, M.; Liu, Y.; Hu, S.; Fang, Y.; Khoshelham, K.; Palaniswami, M.; Ngo, T. Real-time monitoring of construction sites: Sensors, methods, and applications. Autom. Constr. 2022, 136, 104099. [Google Scholar] [CrossRef]
- Shuster, M.D. A survey of attitude representations. Navigation 1993, 8, 439–517. [Google Scholar]
- Phillips, W.; Hailey, C.; Gebert, G. Review of attitude representations used for aircraft kinematics. J. Aircr. 2001, 38, 718–737. [Google Scholar] [CrossRef]
- Díaz, E.O. Attitude Representations. In 3D Motion of Rigid Bodies; Springer: Berlin/Heidelberg, Germany, 2019; pp. 185–230. [Google Scholar]
- Parwana, H.; Kothari, M. Quaternions and attitude representation. arXiv 2017, arXiv:1708.08680. [Google Scholar]
- Zhu, X.; Ma, M.; Cheng, D.; Zhou, Z. An optimized triad algorithm for attitude determination. Artif. Satell. 2017, 52, 41. [Google Scholar] [CrossRef][Green Version]
- Hajiyev, C.; Guler, D.C. Review on gyroless attitude determination methods for small satellites. Prog. Aerosp. Sci. 2017, 90, 54–66. [Google Scholar] [CrossRef]
- Cilden Guler, D.; Conguroglu, E.S.; Hajiyev, C. Single-Frame Attitude Determination Methods for Nanosatellites. Metrol. Meas. Syst. 2017, 24, 313–324. [Google Scholar] [CrossRef]
- Crassidis, J.L.; Markley, F.L.; Cheng, Y. Survey of nonlinear attitude estimation methods. J. Guid. Control Dyn. 2007, 30, 12–28. [Google Scholar] [CrossRef]
- Markley, F.L.; Crassidis, J.L. Fundamentals of Spacecraft Attitude Determination and Control; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–486. [Google Scholar] [CrossRef]
- Wertz, J.R. Spacecraft Attitude Determination and Control (Astrophysics and Space Science Library 73), 1978th ed.; Reidel, D., Ed.; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Kuga, H.K.; Carrara, V. Attitude determination with magnetometers and accelerometers to use in satellite simulator. Math. Probl. Eng. 2013, 2013, 401282. [Google Scholar] [CrossRef][Green Version]
- Hajiyev, C.; Cilden, D.; Somov, Y. Gyro-free attitude and rate estimation for a small satellite using SVD and EKF. Aerosp. Sci. Technol. 2016, 55, 324–331. [Google Scholar] [CrossRef]
- Hajiyev, C.; Çilden, D.; Somov, Y. Gyroless attitude and rate estimation of small satellites using singular value decomposition and extended Kalman filter. In Proceedings of the 2015 16th International Carpathian Control Conference (ICCC), Szilvasvarad, Hungary, 27–30 May 2015; pp. 159–164. [Google Scholar]
- Cilden, D.; Hajiyev, C.; Soken, H.E. Attitude and attitude rate estimation for a nanosatellite using SVD and UKF. In Proceedings of the 2015 7th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 16–19 June 2015; pp. 695–700. [Google Scholar]
- Sumanth, R.M. Computation of eclipse time for low-Earth orbiting small satellites. Int. J. Aviat. Aeronaut. Aerosp. 2019, 6. [Google Scholar] [CrossRef]
- Yakupoglu-Altuntas, S.; Esit, M.; Soken, H.E.; Hajiyev, C. Backup Magnetometer-only Attitude Estimation Algorithm for Small Satellites. IEEE Sens. J. 2022, 22, 13544–13551. [Google Scholar] [CrossRef]
- Hajiyev, C.; Cilden-Guler, D.; Somov, Y. Attitude determination of nanosatellites in the sun-eclipse phases. In Proceedings of the 2017 8th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 19–22 June 2017; pp. 397–401. [Google Scholar]
- Hajiyev, C.; Cilden-Guler, D. Gyroless Nanosatellite Attitude Estimation in Loss of Sun Sensor Measurements. IFAC-PapersOnLine 2018, 51, 89–94. [Google Scholar] [CrossRef]
- Hajiyev, C.; Cilden-Guler, D. Satellite attitude estimation using SVD-Aided EKF with simultaneous process and measurement covariance adaptation. Adv. Space Res. 2021, 68, 3875–3890. [Google Scholar] [CrossRef]
- Cao, K.; Li, J.; Song, R.; Li, Y. HE2LM-AD: Hierarchical and efficient attitude determination framework with adaptive error compensation module based on ELM network. ISPRS J. Photogramm. Remote Sens. 2023, 195, 418–431. [Google Scholar] [CrossRef]
- Xiong, K.; Wei, C. Adaptive iterated extended Kalman filter for relative spacecraft attitude and position estimation. Asian J. Control 2018, 20, 1595–1610. [Google Scholar] [CrossRef]
- Markley, F.L. Attitude determination using vector observations and the singular value decomposition. J. Astronaut. Sci. 1988, 36, 245–258. [Google Scholar]
- Lefferts, E.J.; Markley, F.L.; Shuster, M.D. Kalman filtering for spacecraft attitude estimation. J. Guid. Control Dyn. 1982, 5, 417–429. [Google Scholar] [CrossRef]
- Kang, C.W.; Park, C.G. Attitude estimation with accelerometers and gyros using fuzzy tuned Kalman filter. In Proceedings of the 2009 European Control Conference (ECC), Budapest, Hungary, 23–26 August 2009; pp. 3713–3718. [Google Scholar] [CrossRef]
- Alken, P.; Thébault, E.; Beggan, C.D.; Amit, H.; Aubert, J.; Baerenzung, J.; Bondar, T.; Brown, W.; Califf, S.; Chambodut, A.; et al. International geomagnetic reference field: The thirteenth generation. Earth Planets Space 2021, 73, 49. [Google Scholar] [CrossRef]
- Makovec, K.L. A Nonlinear Magnetic Controller for Three-Axis Stability of Nanosatellites. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2001. [Google Scholar]
- Blanco, M.J.; Milidonis, K.; Bonanos, A.M. Updating the PSA sun position algorithm. Sol. Energy 2020, 212, 339–341. [Google Scholar] [CrossRef]
- Do, C.B.; Batzoglou, S. What is the expectation maximization algorithm? Nat. Biotechnol. 2008, 26, 897–899. [Google Scholar] [CrossRef] [PubMed]
- Moon, T.K. The expectation-maximization algorithm. IEEE Signal Process. Mag. 1996, 13, 47–60. [Google Scholar] [CrossRef]
- Schön, T.B.; Wills, A.; Ninness, B. System identification of nonlinear state-space models. Automatica 2011, 47, 39–49. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Xu, B.; Wu, Z.; Chambers, J.A. A new adaptive extended Kalman filter for cooperative localization. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 353–368. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Single image haze removal using dark channel prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 2341–2353. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).