Focusing Coherent Light through Volume Scattering Phantoms via Wavefront Shaping
Abstract
:1. Introduction
2. Fabrication and Characterization of Phantoms with Well-Defined Optical Properties
2.1. Volume Scattering Phantoms
2.2. Characterization of the Scattering and Absorption Coefficients
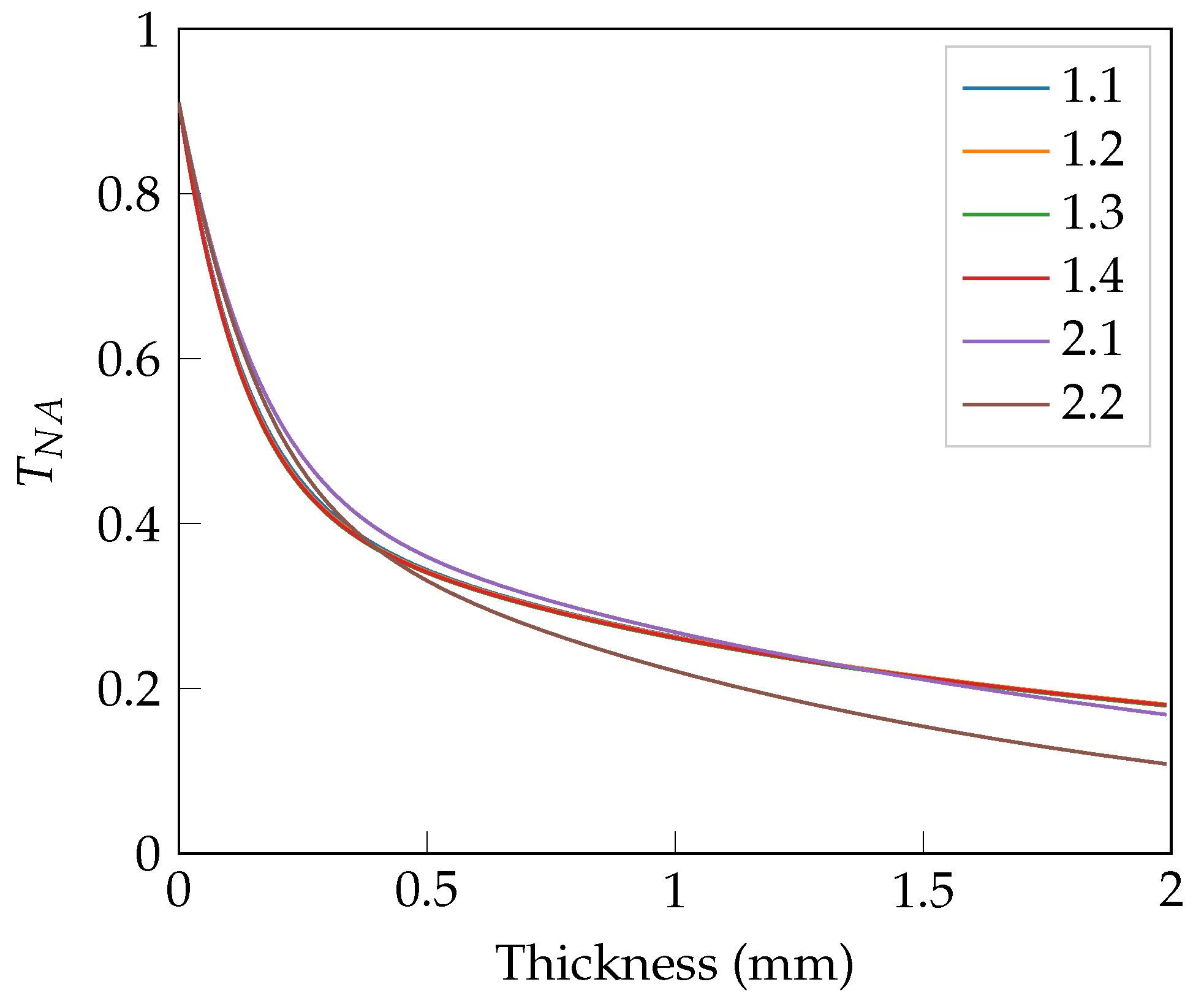
2.3. Calculation of the Angular-Dependent Transmittance via the Hybrid Method
3. Wavefront Shaping Setup
4. Results
4.1. Solely Scattering Phantoms
4.2. Influence of Absorption
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vellekoop, I.M. Feedback-based wavefront shaping. Opt. Express 2015, 23, 12189–12206. [Google Scholar] [CrossRef] [PubMed]
- Vellekoop, I.M.; Mosk, A.P. Focusing coherent light through opaque strongly scattering media. Opt. Lett. 2007, 32, 2309–2311. [Google Scholar] [CrossRef] [PubMed]
- Gigan, S. Optical microscopy aims deep. Nat. Photonics 2017, 11, 14–16. [Google Scholar] [CrossRef]
- Vellekoop, I.M.; Lagendijk, A.; Mosk, A. Exploiting disorder for perfect focusing. Nat. Photonics 2010, 4, 320–322. [Google Scholar] [CrossRef]
- Aulbach, J.; Gjonaj, B.; Johnson, P.M.; Mosk, A.P.; Lagendijk, A. Control of Light Transmission through Opaque Scattering Media in Space and Time. Phys. Rev. Lett. 2011, 106, 103901. [Google Scholar] [CrossRef] [PubMed]
- Ojambati, O.S.; Hosmer-Quint, J.T.; Gorter, K.; Mosk, A.P.; Vos, W.L. Controlling the intensity of light in large areas at the interfaces of a scattering medium. Phys. Rev. A 2016, 94, 043834. [Google Scholar] [CrossRef]
- Cao, H.; Mosk, A.P.; Rotter, S. Shaping the propagation of light in complex media. Nat. Phys. 2020, 18, 994–1007. [Google Scholar] [CrossRef]
- Pogue, B.W.; Patterson, M.S. Review of tissue simulating phantoms for optical spectroscopy, imaging and dosimetry. J. Biomed. Opt. 2006, 4, 041102. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, B.F.; Loitsch, S.; McLaughlin, R.A.; Scolaro, L.; Rigby, P.; Sampson, D.D. Fibrin phantom for use in optical coherence tomography. J. Biomed. Opt. 2010, 15, 030507. [Google Scholar] [CrossRef] [PubMed]
- Biton, N.; Kupferman, J.; Arnon, S. OAM light propagation through tissue. Sci. Rep. 2021, 11, 2407. [Google Scholar] [CrossRef] [PubMed]
- Krauter, P.; Nothelfer, S.; Bodenschatz, N.; Simon, E.; Stocker, S.; Foschum, F.; Kienle, A. Optical phantoms with adjustable subdiffusive scattering parameters. J. Biomed. Opt. 2015, 20, 105008. [Google Scholar] [CrossRef] [PubMed]
- Foschum, F.; Bergmann, F.; Kienle, A. Precise determination of the optical properties of turbid media using an optimized integrating sphere and advanced Monte Carlo simulations. Part 1: Theory. Appl. Opt. 2020, 59, 3203–3215. [Google Scholar] [CrossRef] [PubMed]
- Foschum, F.; Bergmann, F.; Kienle, A. Precise determination of the optical properties of turbid media using an optimized integrating sphere and advanced Monte Carlo simulations. Part 2: Experiments. Appl. Opt. 2020, 59, 3216–3226. [Google Scholar] [CrossRef] [PubMed]
- Case, K.M.; Zweifel, P.F. Linear Transport Theory; Addison-Wesley Publishing Company: Boston, MA, USA, 1967. [Google Scholar]
- Vellekoop, I.M.; Mosk, A.P. Phase control algorithms for focusing light through turbid media. Opt. Commun. 2008, 281, 3071–3080. [Google Scholar] [CrossRef]
- Hua, Y.; Sui, X.; Zhou, S.; Chen, Q.; Gu, G.; Bai, H.; Li, W. A novel method of global optimisation for wavefront shaping based on the differential evolution algorithm. Opt. Commun. 2021, 481, 126541. [Google Scholar] [CrossRef]
- Wu, Z.; Luo, J.; Feng, Y.; Guo, X.; Shen, Y.; Li, Z. Controlling 1550-nm light through a multimode fiber using a Hadamard encoding algorithm. Opt. Express 2019, 27, 5570–5580. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Speckle Phenomena in Optics: Theory and Applications, 2nd ed.; SPIE: Bellingham, WA, USA, 2020; pp. 7–25. [Google Scholar]
- Van Putten, E.; Vellekoop, I.M.; Mosk, A. Spatial amplitude and phase modulation using commercial twisted nematic LCDs. Appl. Opt. 2008, 47, 2076–2081. [Google Scholar] [CrossRef] [PubMed]
- Fuentes, J.; Fernández, E.; Prieto, P.; Artal, P. Interferometric method for phase calibration in liquid crystal spatial light modulators using a self-generated diffraction-grating. Opt. Express 2016, 24, 14159–14171. [Google Scholar] [CrossRef] [PubMed]





| Set.Sample | d (mm) | (mm) | (mm) |
|---|---|---|---|
| 1.1 | 0.395(9) | 3.688(5) | 0.0034(3) |
| 1.2 | 0.947(4) | 3.781(2) | 0.0020(1) |
| 1.3 | 1.514(9) | 3.841(4) | 0.0020(1) |
| 1.4 | 1.987(3) | 3.817(5) | 0.0019(1) |
| 2.1 | 0.901(8) | 2.724(3) | 0.0213(1) |
| 2.2 | 1.045(3) | 2.757(1) | 0.0598(1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fritzsche, N.; Ott, F.; Pink, K.; Kienle, A. Focusing Coherent Light through Volume Scattering Phantoms via Wavefront Shaping. Sensors 2023, 23, 8397. https://doi.org/10.3390/s23208397
Fritzsche N, Ott F, Pink K, Kienle A. Focusing Coherent Light through Volume Scattering Phantoms via Wavefront Shaping. Sensors. 2023; 23(20):8397. https://doi.org/10.3390/s23208397
Chicago/Turabian StyleFritzsche, Niklas, Felix Ott, Karsten Pink, and Alwin Kienle. 2023. "Focusing Coherent Light through Volume Scattering Phantoms via Wavefront Shaping" Sensors 23, no. 20: 8397. https://doi.org/10.3390/s23208397
APA StyleFritzsche, N., Ott, F., Pink, K., & Kienle, A. (2023). Focusing Coherent Light through Volume Scattering Phantoms via Wavefront Shaping. Sensors, 23(20), 8397. https://doi.org/10.3390/s23208397





