Reconstruction of Gap-Free Land Surface Temperature at a 100 m Spatial Resolution from Multidimensional Data: A Case in Wuhan, China
Abstract
1. Introduction
2. Materials and Methods
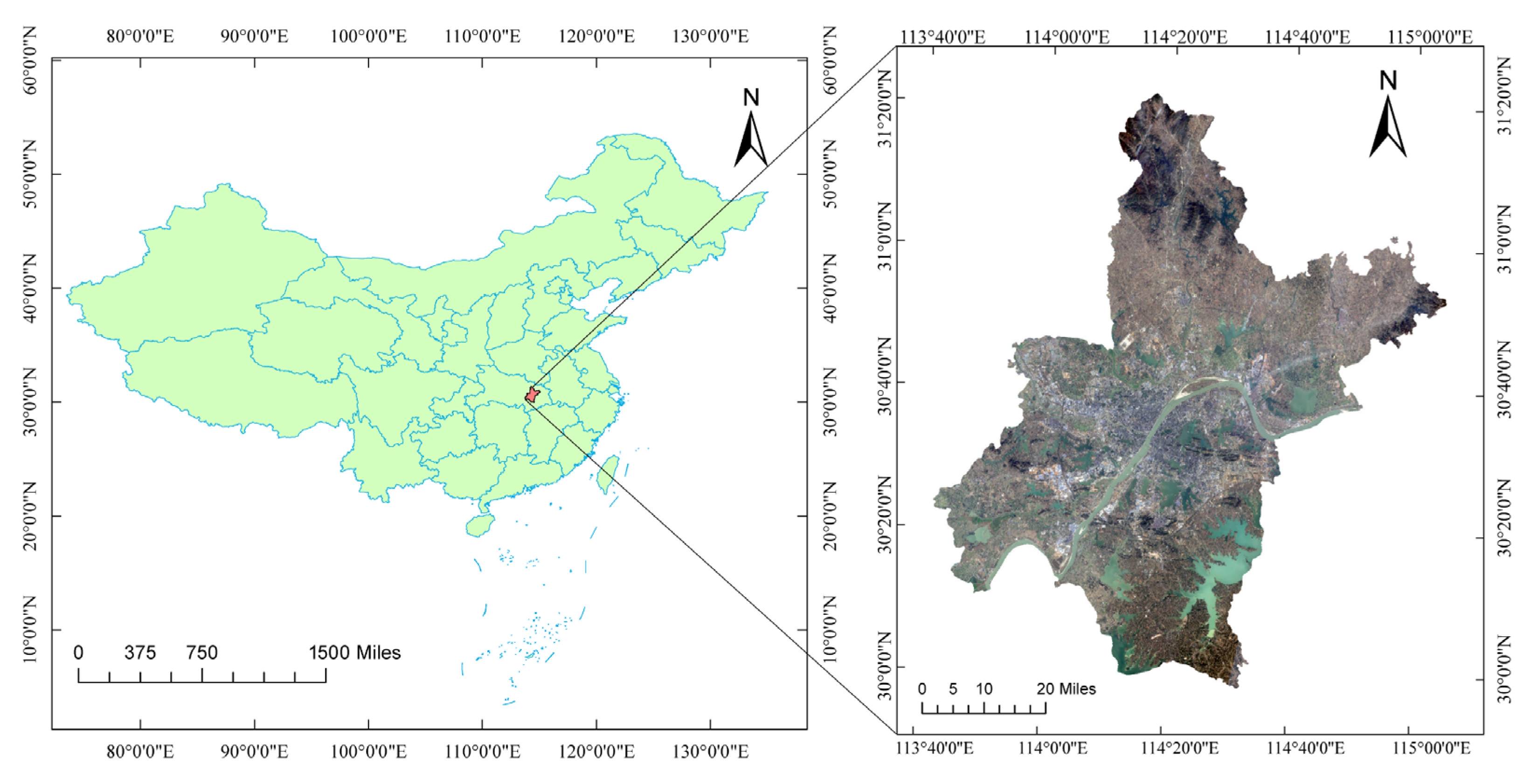
2.1. Study Area
2.2. Data Acquisition and Processing
2.3. Methodology
2.3.1. Spline Interpolation Method
2.3.2. RF Regression Model
2.3.3. The Spatial Feature-Considered Random Forest Regression Model
- Step 1: Obtain the spatial features of the original LST
- 2.
- Step 2: Construction of the stable nonlinear link
- 3.
- Step 3: Processing of residuals
- 4.
- Step 4: Acquire the ultimate gap-free LST
2.4. Cloud Mask for Verification
2.5. The Further Application and Exploration of SFRFR
2.5.1. An Application for Analyzing Urban Thermal Environment Changes
2.5.2. Further Exploration of Model Performance
2.6. Validation Method
3. Results
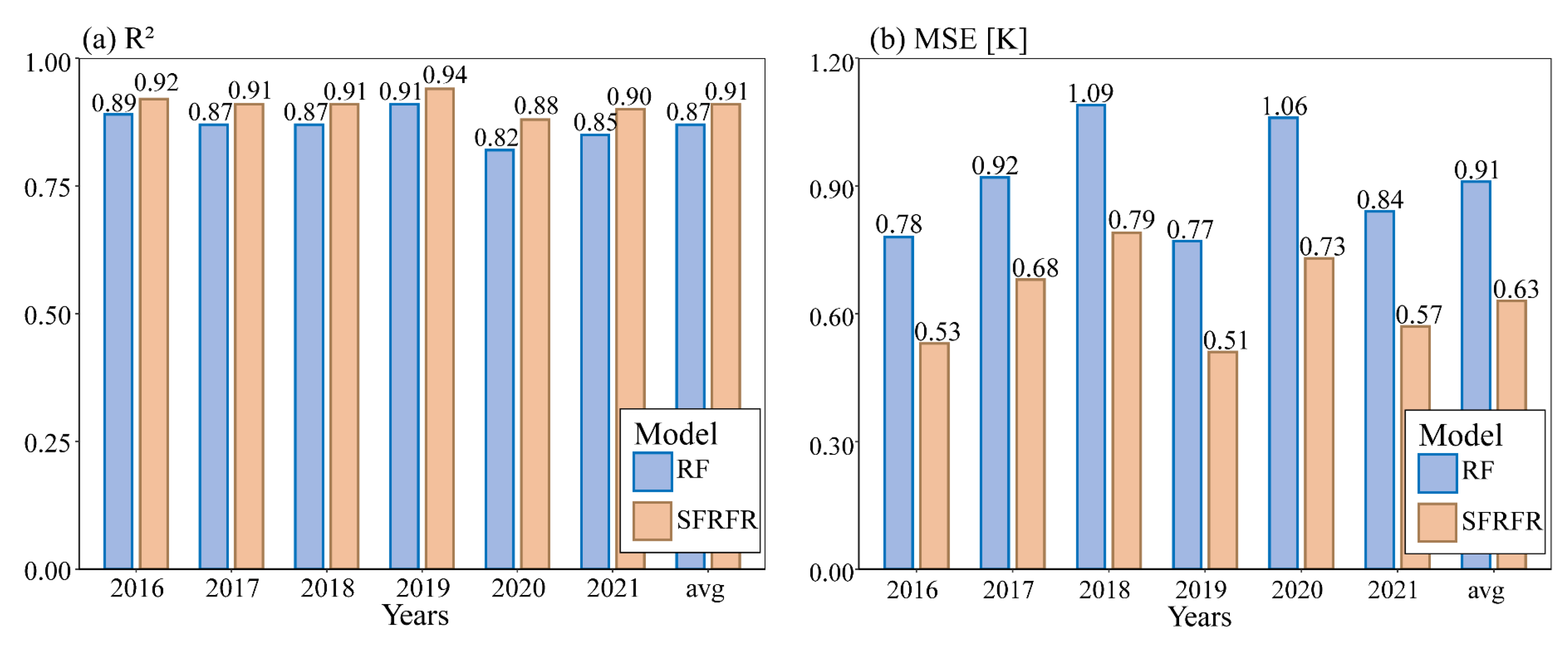
3.1. Results of the Evaluation Metrics
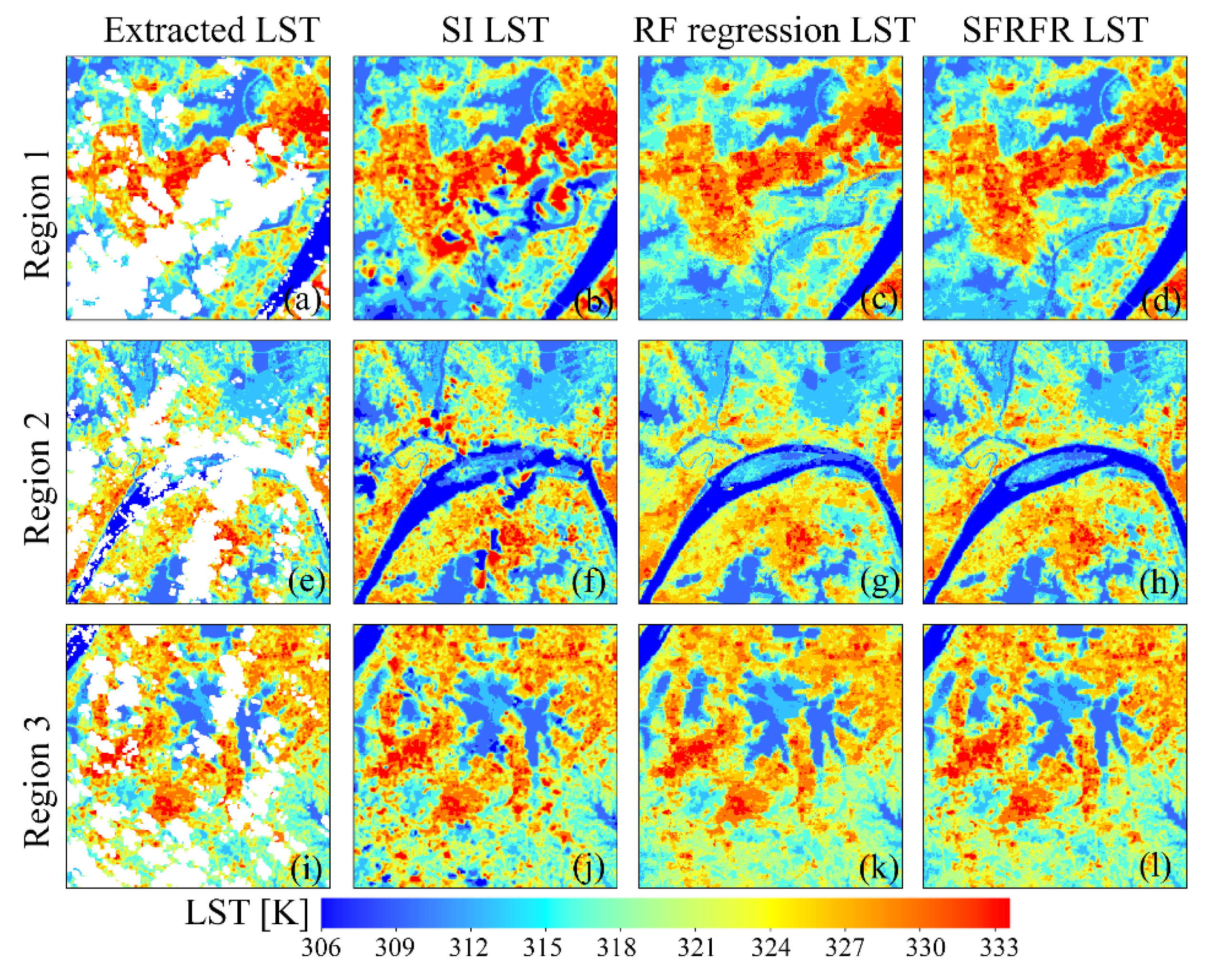
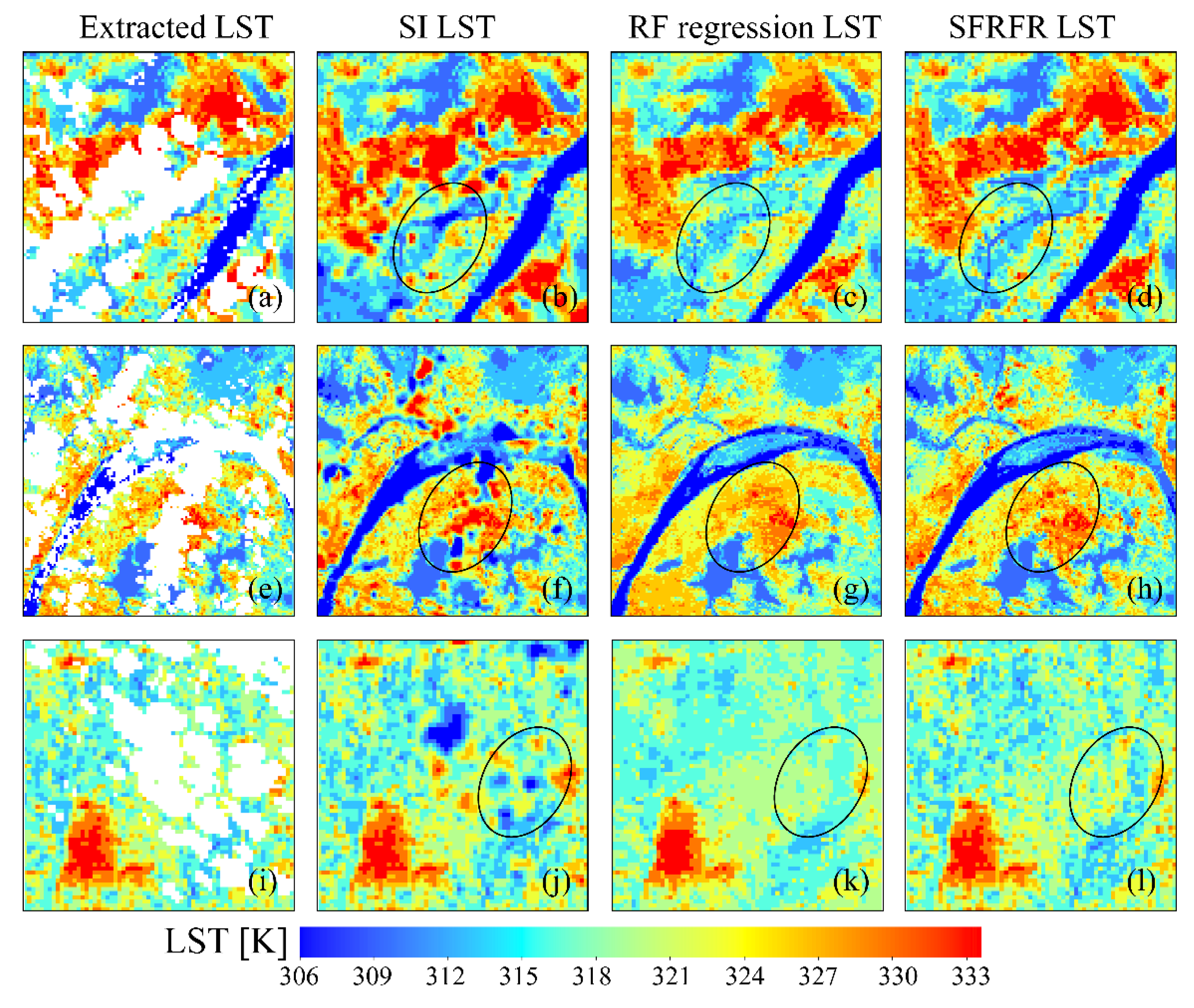
3.2. Performance of the Reconstructed Gap-Free LST
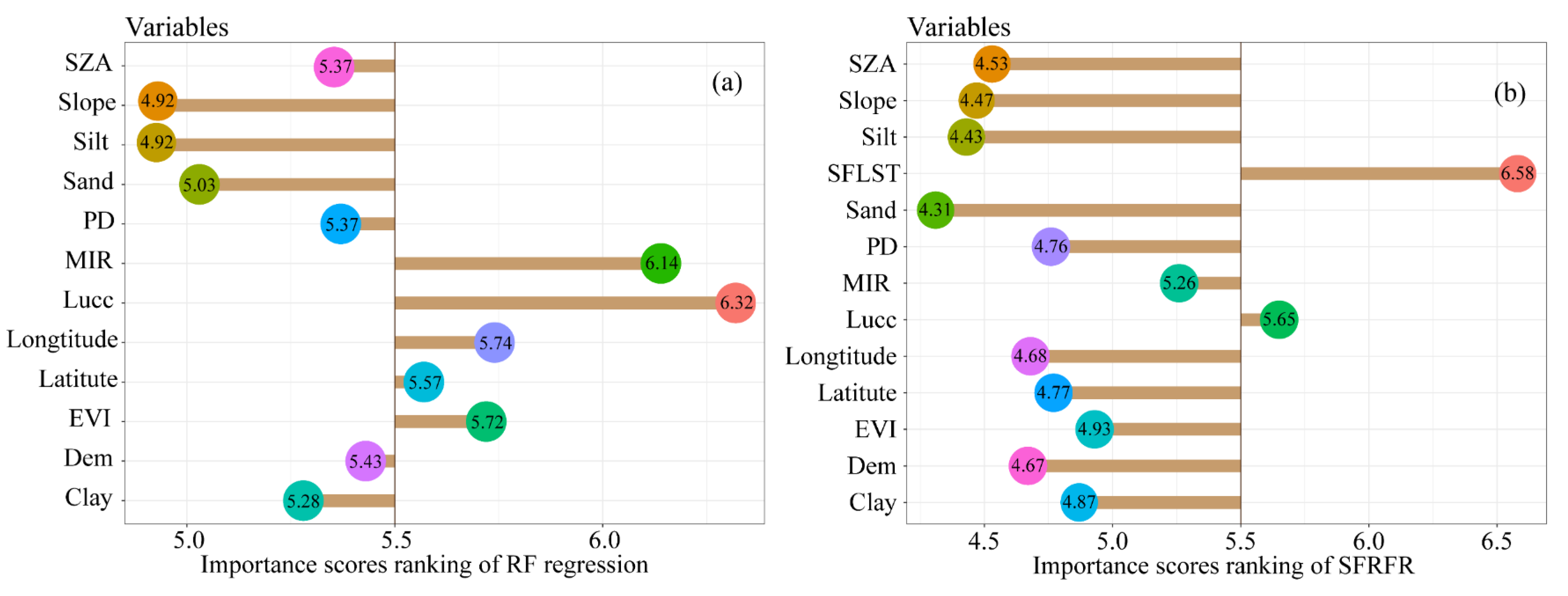
3.3. The Residuals and Importance Scores Ranking
3.4. Performance of Reconstructed Gap-Free LST from 2016 to 2021
3.5. The Results of Reconstructed Landsat-LST at 250 m
4. Discussion
4.1. Advantages of the Proposed Model
4.2. Contributions of Parameters Accounted for in the Model
4.3. Variation in Urban Thermal Emissions from 2016 to 2021 in Wuhan
4.4. The Improvement Gained by the Spatial Feature of the LST
4.5. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luyssaert, S.; Jammet, M.; Stoy, P.C.; Estel, S.; Pongratz, J.; Ceschia, E.; Churkina, G.; Don, A.; Erb, K.; Ferlicoq, M.; et al. Land management and land-cover change have impacts of similar magnitude on surface temperature. Nat. Clim. Change 2014, 4, 389–393. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Farahmand, A.; Melton, F.S.; Teixeira, J.; Anderson, M.C.; Wardlow, B.D.; Hain, C.R. Remote sensing of drought: Progress, challenges and opportunities. RvGeo 2015, 53, 452–480. [Google Scholar] [CrossRef]
- Anderson, M.C.; Kustas, W.P.; Norman, J.M.; Hain, C.R.; Mecikalski, J.R.; Schultz, L.; González-Dugo, M.P.; Cammalleri, C.; d’Urso, G.; Pimstein, A.; et al. Mapping daily evapotranspiration at field to continental scales using geostationary and polar orbiting satellite imagery. Hydrol. Earth Syst. Sci. 2011, 15, 223–239. [Google Scholar] [CrossRef]
- Peng, J.; Ma, J.; Liu, Q.Y.; Liu, Y.X.; Hu, Y.N.; Li, Y.R.; Yue, Y.M. Spatial-temporal change of land surface temperature across 285 cities in China: An urban-rural contrast perspective. Sci. Total Environ. 2018, 635, 487–497. [Google Scholar] [CrossRef]
- Zhong, L.; Su, Z.; Ma, Y.; Salama, M.S.; Sobrino, J.A. Accelerated Changes of Environmental Conditions on the Tibetan Plateau Caused by Climate Change. J. Clim. 2011, 24, 6540–6550. [Google Scholar] [CrossRef]
- Asrar, G.R. Advances in Quantitative Earth Remote Sensing: Past, Present and Future. Sensors 2019, 19, 5399. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Hook, S.J.; Gabell, A.R.; Green, A.A.; Kealy, P.S. A comparison of techniques for extracting emissivity information from thermal infrared data for geologic studies. Remote Sens. Environ. 1992, 42, 123–135. [Google Scholar] [CrossRef]
- Cristóbal, J.; Jiménez-Muñoz, J.; Prakash, A.; Mattar, C.; Skoković, D.; Sobrino, J. An Improved Single-Channel Method to Retrieve Land Surface Temperature from the Landsat-8 Thermal Band. Remote Sens. 2018, 10, 431. [Google Scholar] [CrossRef]
- Zhong, X.K.; Huo, X.; Ren, C.; Labed, J.; Li, Z.L. Retrieving Land Surface Temperature from Hyperspectral Thermal Infrared Data Using a Multi-Channel Method. Sensors 2016, 16, 687. [Google Scholar] [CrossRef]
- Rozenstein, O.; Qin, Z.H.; Derimian, Y.; Karnieli, A. Derivation of Land Surface Temperature for Landsat-8 TIRS Using a Split Window Algorithm. Sensors 2014, 14, 5768–5780. [Google Scholar] [CrossRef] [PubMed]
- Du, C.; Ren, H.; Qin, Q.; Meng, J.; Zhao, S. A Practical Split-Window Algorithm for Estimating Land Surface Temperature from Landsat 8 Data. Remote Sens. 2015, 7, 647–665. [Google Scholar] [CrossRef]
- Fan, X.-M.; Liu, H.-G.; Liu, G.-H.; Li, S.-B. Reconstruction of MODIS land-surface temperature in a flat terrain and fragmented landscape. Int. J. Remote Sens. 2014, 35, 7857–7877. [Google Scholar] [CrossRef]
- Sarafanov, M.; Kazakov, E.; Nikitin, N.O.; Kalyuzhnaya, A.V. A Machine Learning Approach for Remote Sensing Data Gap-Filling with Open-Source Implementation: An Example Regarding Land Surface Temperature, Surface Albedo and NDVI. Remote Sens. 2020, 12, 3865. [Google Scholar] [CrossRef]
- Shen, H.; Li, X.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.; Zhang, L. Missing Information Reconstruction of Remote Sensing Data: A Technical Review. IEEE Trans. Geosci. Remote Sens. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- Maxwell, S.K.; Schmidt, G.L.; Storey, J.C. A multi-scale segmentation approach to filling gaps in Landsat ETM+ SLC-off images. Int. J. Remote Sens. 2007, 28, 5339–5356. [Google Scholar] [CrossRef]
- Romero-Sanchez, M.E.; Ponce-Hernandez, R.; Franklin, S.E.; Aguirre-Salado, C.A. Comparison of data gap-filling methods for Landsat ETM+ SLC-off imagery for monitoring forest degradation in a semi-deciduous tropical forest in Mexico. Int. J. Remote Sens. 2015, 36, 2786–2799. [Google Scholar] [CrossRef]
- Chen, X.; Li, W.; Chen, J.; Rao, Y.; Yamaguchi, Y. A Combination of TsHARP and Thin Plate Spline Interpolation for Spatial Sharpening of Thermal Imagery. Remote Sens. 2014, 6, 2845–2863. [Google Scholar] [CrossRef]
- Liu, H.; Weng, Q. Scaling Effect of Fused ASTER-MODIS Land Surface Temperature in an Urban Environment. Sensors 2018, 18, 4058. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Mitra, P.; Ghosh, S.K. Spatial Interpolation to Predict Missing Attributes in GIS Using Semantic Kriging. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4771–4780. [Google Scholar] [CrossRef]
- Ozelkan, E.; Bagis, S.; Ozelkan, E.C.; Ustundag, B.B.; Yucel, M.; Ormeci, C. Spatial interpolation of climatic variables using land surface temperature and modified inverse distance weighting. Int. J. Remote Sens. 2015, 36, 1000–1025. [Google Scholar] [CrossRef]
- Artusi, A.; Banterle, F.; Chetverikov, D. A Survey of Specularity Removal Methods. Comput. Graph. Forum 2011, 30, 2208–2230. [Google Scholar] [CrossRef]
- Wu, P.; Yin, Z.; Zeng, C.; Duan, S.-B.; Gottsche, F.-M.; Ma, X.; Li, X.; Yang, H.; Shen, H. Spatially Continuous and High-Resolution Land Surface Temperature Product Generation: A review of reconstruction and spatiotemporal fusion techniques. IEEE Trans. Geosci. Remote Sens. 2021, 9, 112–137. [Google Scholar] [CrossRef]
- Xu, Y.; Shen, Y. Reconstruction of the land surface temperature time series using harmonic analysis. Comput. Geosci. 2013, 61, 126–132. [Google Scholar] [CrossRef]
- Yao, R.; Wang, L.; Huang, X.; Sun, L.; Chen, R.; Wu, X.; Zhang, W.; Niu, Z. A Robust Method for Filling the Gaps in MODIS and VIIRS Land Surface Temperature Data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10738–10752. [Google Scholar] [CrossRef]
- Feng, G.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- Li, L.; Zhan, W.; Du, H.; Lai, J.; Wang, C.; Fu, H.; Huang, F.; Liu, Z.; Wang, C.; Li, J.; et al. Long-Term and Fine-Scale Surface Urban Heat Island Dynamics Revealed by Landsat Data Since the 1980s: A Comparison of Four Megacities in China. J. Geophys. Res. Atmos. 2022, 127, e2021JD035598. [Google Scholar] [CrossRef]
- Weng, Q.H.; Fu, P.; Gao, F. Generating daily land surface temperature at Landsat resolution by fusing Landsat and MODIS data. Remote Sens. Environ. 2014, 145, 55–67. [Google Scholar] [CrossRef]
- Bo, H.; Juan, W.; Huihui, S.; Dongjie, F.; KwanKit, W. Generating High Spatiotemporal Resolution Land Surface Temperature for Urban Heat Island Monitoring. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1011–1015. [Google Scholar] [CrossRef]
- Mo, Y.; Xu, Y.; Chen, H.; Zhu, S. A Review of Reconstructing Remotely Sensed Land Surface Temperature under Cloudy Conditions. Remote Sens. 2021, 13, 2838. [Google Scholar] [CrossRef]
- Zhao, W.; Duan, S.-B. Reconstruction of daytime land surface temperatures under cloud-covered conditions using integrated MODIS/Terra land products and MSG geostationary satellite data. Remote Sens. Environ. 2020, 247, 111931. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, W.; Ma, M.; He, K. Gap-Free LST Generation for MODIS/Terra LST Product Using a Random Forest-Based Reconstruction Method. Remote Sens. 2021, 13, 2828. [Google Scholar] [CrossRef]
- Hutengs, C.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Ejiagha, I.R.; Ahmed, M.R.; Dewan, A.; Gupta, A.; Rangelova, E.; Hassan, Q.K. Urban Warming of the Two Most Populated Cities in the Canadian Province of Alberta, and Its Influencing Factors. Sensors 2022, 22, 2894. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.H.; Wang, S.J.; Bai, X.Y.; Tian, Y.C.; Wu, L.H.; Xiao, J.Y.; Chen, F.; Qian, Q.H. Relationship among land surface temperature and LUCC, NDVI in typical karst area. Sci. Rep. 2018, 8, 641. [Google Scholar] [CrossRef]
- Sayão, V.M.; Demattê, J.A.M.; Bedin, L.G.; Nanni, M.R.; Rizzo, R. Satellite land surface temperature and reflectance related with soil attributes. Geoderma 2018, 325, 125–140. [Google Scholar] [CrossRef]
- Sims, D.A.; Rahman, A.F.; Cordova, V.D.; El-Masri, B.Z.; Baldocchi, D.D.; Bolstad, P.V.; Flanagan, L.B.; Goldstein, A.H.; Hollinger, D.Y.; Misson, L.; et al. A new model of gross primary productivity for North American ecosystems based solely on the enhanced vegetation index and land surface temperature from MODIS. Remote Sens. Environ. 2008, 112, 1633–1646. [Google Scholar] [CrossRef]
- Peng, W.; Yuan, X.; Gao, W.; Wang, R.; Chen, W. Assessment of urban cooling effect based on downscaled land surface temperature: A case study for Fukuoka, Japan. Urban Clim. 2021, 36, 100790. [Google Scholar] [CrossRef]
- Loveland, T.R.; Dwyer, J.L. Landsat: Building a strong future. Remote Sens. Environ. 2012, 122, 22–29. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, Z.; Hu, T.; Wang, G.; He, G.; Zhang, Z.; Li, H.; Wu, Z.; Liu, X. An Efficient Framework for Producing Landsat-Based Land Surface Temperature Data Using Google Earth Engine. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 4689–4701. [Google Scholar] [CrossRef]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the MODIS Land-Surface Temperature/Emissivity products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
- Fensholt, R.; Proud, S.R. Evaluation of Earth Observation based global long term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ. 2012, 119, 131–147. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture-climate interactions in a changing climate: A review. Earth Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Wu, H.; Li, W. Downscaling Land Surface Temperatures Using a Random Forest Regression Model with Multitype Predictor Variables. IEEE Access 2019, 7, 21904–21916. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Du, H.Y.; Xu, Y.Q.; Lu, D.B.; Wang, X.Y.; Guo, Z.Y. Temporal and spatial variation relationship and influence factors on surface urban heat island and ozone pollution in the Yangtze River Delta, China. Sci. Total Environ. 2018, 631–632, 921–933. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L. Spatial Downscaling of MODIS Land Surface Temperatures Using Geographically Weighted Regression: Case Study in Northern China. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6458–6469. [Google Scholar] [CrossRef]
- Kartal, S.; Sekertekin, A. Prediction of MODIS land surface temperature using new hybrid models based on spatial interpolation techniques and deep learning models. Environ. Sci. Pollut. Res. 2022, 29, 67115–67134. [Google Scholar] [CrossRef]
- Franke, R. Smooth interpolation of scattered data by local thin plate splines. Comput. Math. Appl. 1982, 8, 273–281. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees (CART). Biometrics 1984, 40, 358. [Google Scholar]
- Tang, K.; Zhu, H.; Ni, P. Spatial Downscaling of Land Surface Temperature over Heterogeneous Regions Using Random Forest Regression Considering Spatial Features. Remote Sens. 2021, 13, 3645. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, F.; Jiang, H.; Hu, H.; Zhong, K.; Jing, W.; Yang, J.; Jia, B. Downscaling Aster Land Surface Temperature over Urban Areas with Machine Learning-Based Area-To-Point Regression Kriging. Remote Sens. 2020, 12, 1082. [Google Scholar] [CrossRef]
- Hu, D.; Meng, Q.; Zhang, L.; Zhang, Y. Spatial quantitative analysis of the potential driving factors of land surface temperature in different “Centers” of polycentric cities: A case study in Tianjin, China. Sci. Total Environ. 2020, 706, 135244. [Google Scholar] [CrossRef]
- Fan, Q.; Song, X.; Shi, Y.; Gao, R. Influencing Factors of Spatial Heterogeneity of Land Surface Temperature in Nanjing, China. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 8341–8349. [Google Scholar] [CrossRef]










| Data | Sources | Spatial Resolution (m) | Time Resolution (d) | Acquisition Date |
|---|---|---|---|---|
| Practical single-channel application land surface temperature (PSC APP LST) | Landsat 8 | 100 | 16 | 26 July 2017 |
| Enhanced vegetation index (EVI) | MOD13Q1 | 250 | 16 | 27 July 2017 |
| Solar zenith angle (SZA) | MOD13Q1 | 250 | 16 | 27 July 2017 |
| Middle-infrared surface reflectance (MIR) | MOD13Q1 | 250 | 16 | 27 July 2017 |
| Land use and land cover change (LUCC) | Zenodo | 30 | 365 | 2017 |
| Population density (PD) | Worldpop | 100 | 365 | 2017 |
| Soil texture (ST) | SoilGrids250m | 250 | / | 2017 |
| Digital elevation model (DEM) | ALOS | 12.5 | / | 2011 |
| Slope | ALOS | 12.5 | / | 2011 |
| Acquisition Date | Source | Sensor | Data Loss (%) |
|---|---|---|---|
| 05 Jun 2016 | Landsat 8 | TIRs | 13.72 |
| 23 July 2016 | Landsat 8 | TIRs | 2.06 |
| 01 Sep 2016 | Landsat 7 | ETM+ | 21.07 |
| 16 Jun 2017 | Landsat 7 | ETM+ | 66.72 |
| 18 July 2017 | Landsat 7 | ETM+ | 39.20 |
| 27 Aug 2017 | Landsat 8 | TIRs | 4.80 |
| 03 Jun 2018 | Landsat 7 | ETM+ | 53.09 |
| 21 July 2018 | Landsat 7 | ETM+ | 23.13 |
| 29 July 2018 | Landsat 8 | TIRs | 10.00 |
| 14 Jun 2019 | Landsat 8 | TIRs | 26.08 |
| 30 Jun 2019 | Landsat 8 | TIRs | 13.19 |
| 17 Aug 2019 | Landsat 8 | TIRs | 3.00 |
| 08 Jun 2020 | Landsat 7 | ETM+ | 28.15 |
| 11 Aug 2020 | Landsat 7 | ETM+ | 63.06 |
| 27 Aug 2020 | Landsat 7 | ETM+ | 29.38 |
| 29 July 2021 | Landsat 7 | ETM+ | 30.51 |
| 06 Aug 2021 | Landsat 8 | TIRs | 39.52 |
| 30 Aug 2021 | Landsat 7 | ETM+ | 30.70 |
| Model | Differences in Quantitative Error Indicators (K) | |||||
|---|---|---|---|---|---|---|
| Min | 1-st Qu | Med | Mean | 3-rd Qu | Max | |
| SFRFR | −7.96 | −0.70 | −0.10 | −0.05 | 0.52 | 11.1 |
| RF regression | −9.81 | −0.76 | −0.13 | −0.05 | 0.55 | 13.5 |
| SI | −51.01 | −1.11 | −0.02 | −0.02 | 1.07 | 47.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Teng, H.; Chen, H.; Han, L.; Chen, L. Reconstruction of Gap-Free Land Surface Temperature at a 100 m Spatial Resolution from Multidimensional Data: A Case in Wuhan, China. Sensors 2023, 23, 913. https://doi.org/10.3390/s23020913
Wu Z, Teng H, Chen H, Han L, Chen L. Reconstruction of Gap-Free Land Surface Temperature at a 100 m Spatial Resolution from Multidimensional Data: A Case in Wuhan, China. Sensors. 2023; 23(2):913. https://doi.org/10.3390/s23020913
Chicago/Turabian StyleWu, Zefeng, Hongfen Teng, Haoxiang Chen, Lingyu Han, and Liangliang Chen. 2023. "Reconstruction of Gap-Free Land Surface Temperature at a 100 m Spatial Resolution from Multidimensional Data: A Case in Wuhan, China" Sensors 23, no. 2: 913. https://doi.org/10.3390/s23020913
APA StyleWu, Z., Teng, H., Chen, H., Han, L., & Chen, L. (2023). Reconstruction of Gap-Free Land Surface Temperature at a 100 m Spatial Resolution from Multidimensional Data: A Case in Wuhan, China. Sensors, 23(2), 913. https://doi.org/10.3390/s23020913




