Acoustic Emission and Artificial Intelligence Procedure for Crack Source Localization
Abstract
1. Introduction
2. Crack Localization: Triangulation Procedure
3. Onset Time Detection
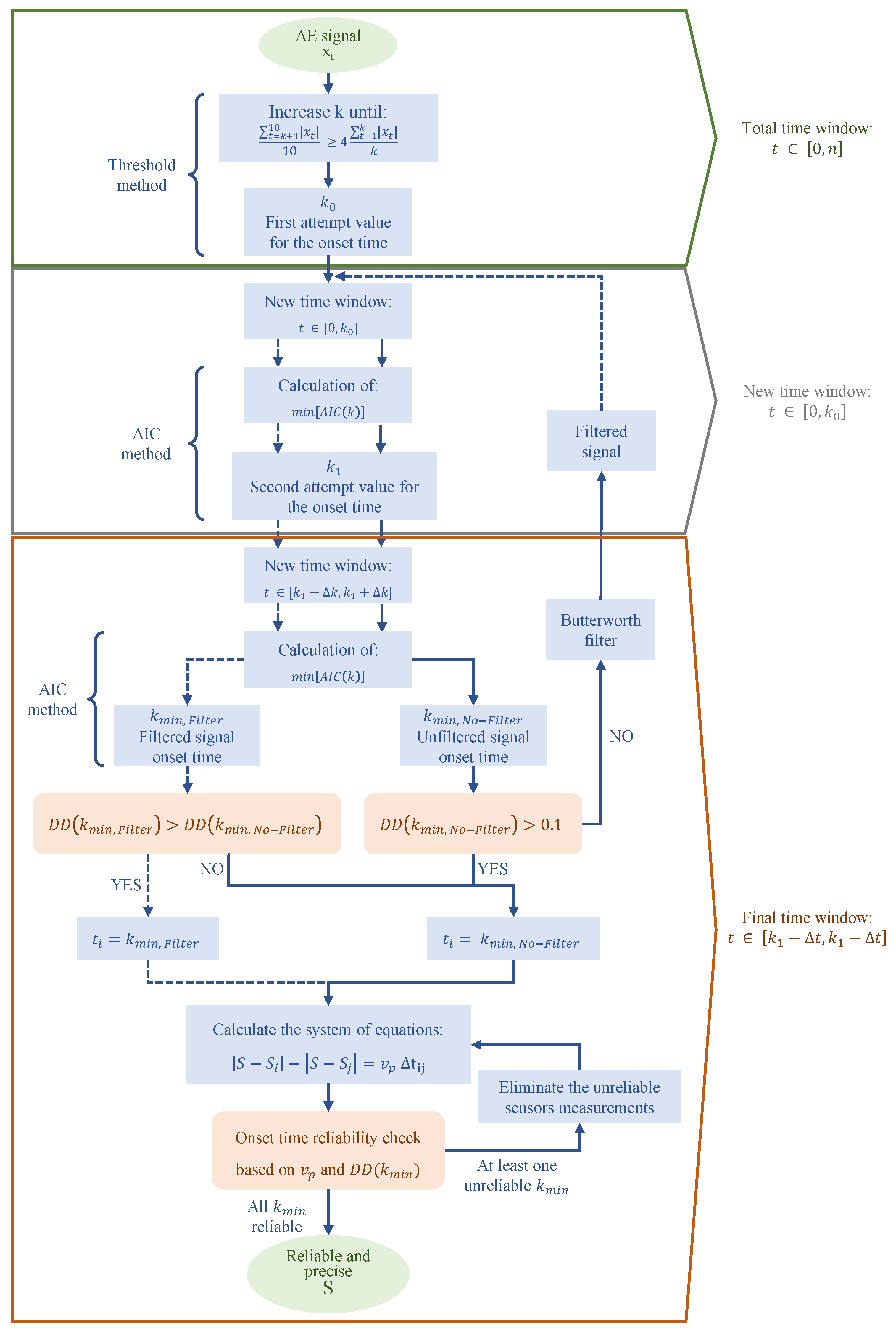
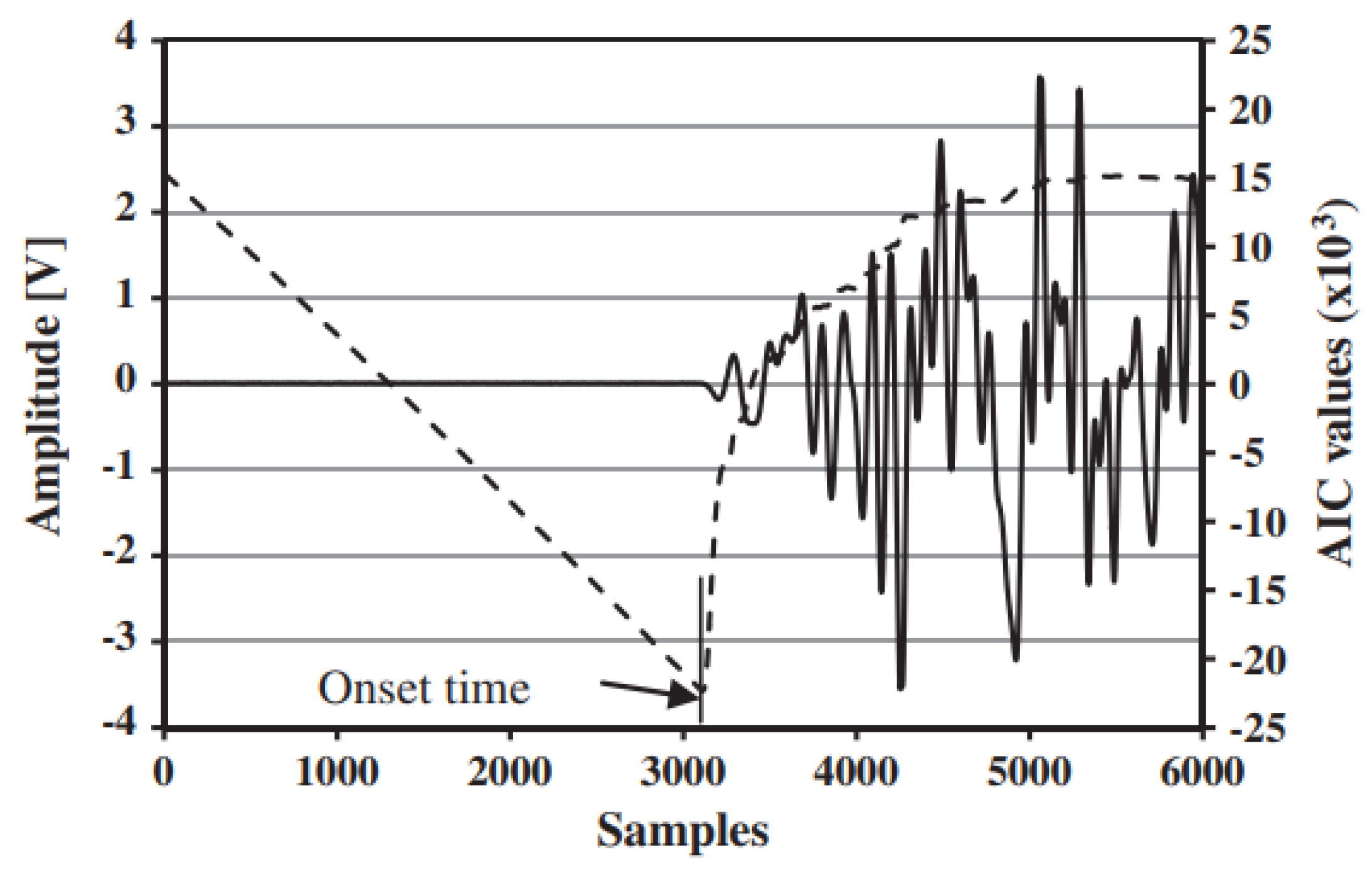
3.1. Improved AIC Picker
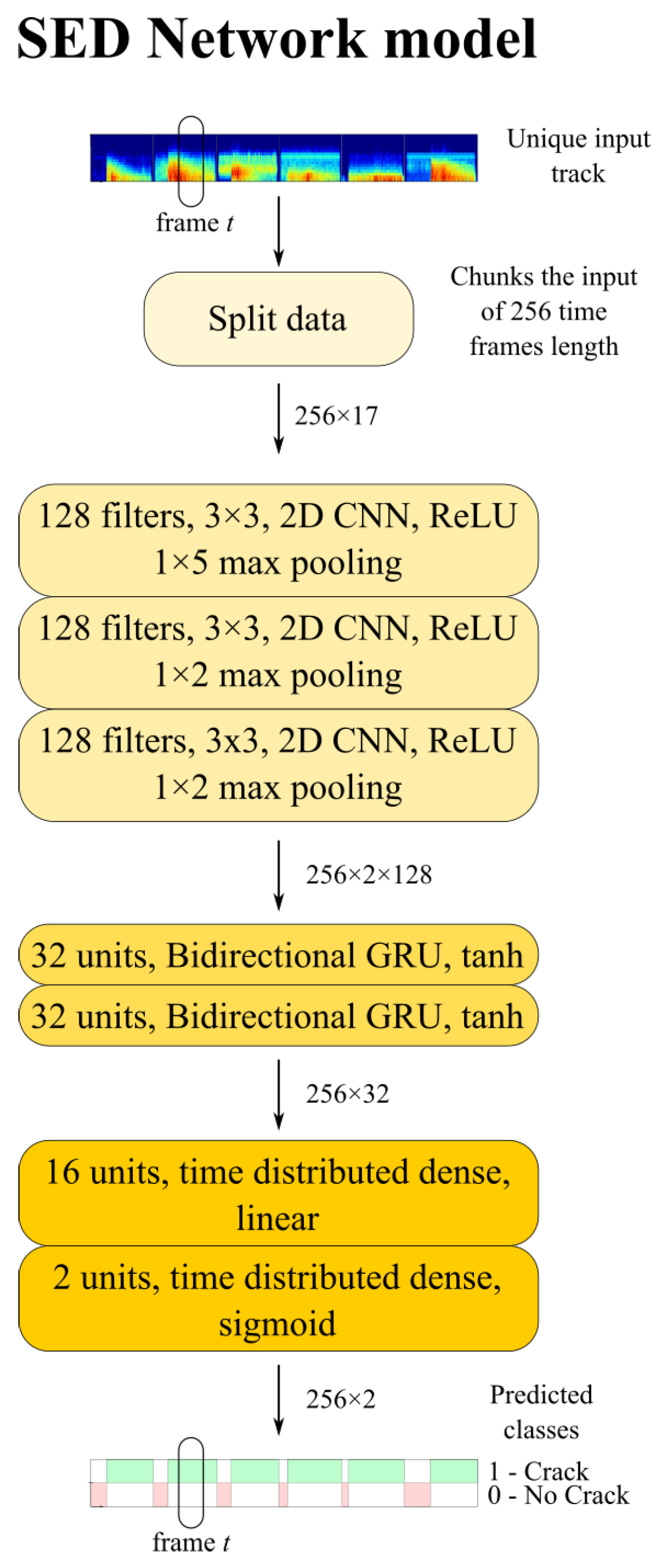
3.2. CRNN for SED
4. SED for Acoustic Emissions Onset Time Detection
4.1. Implemented SED Model Architecture
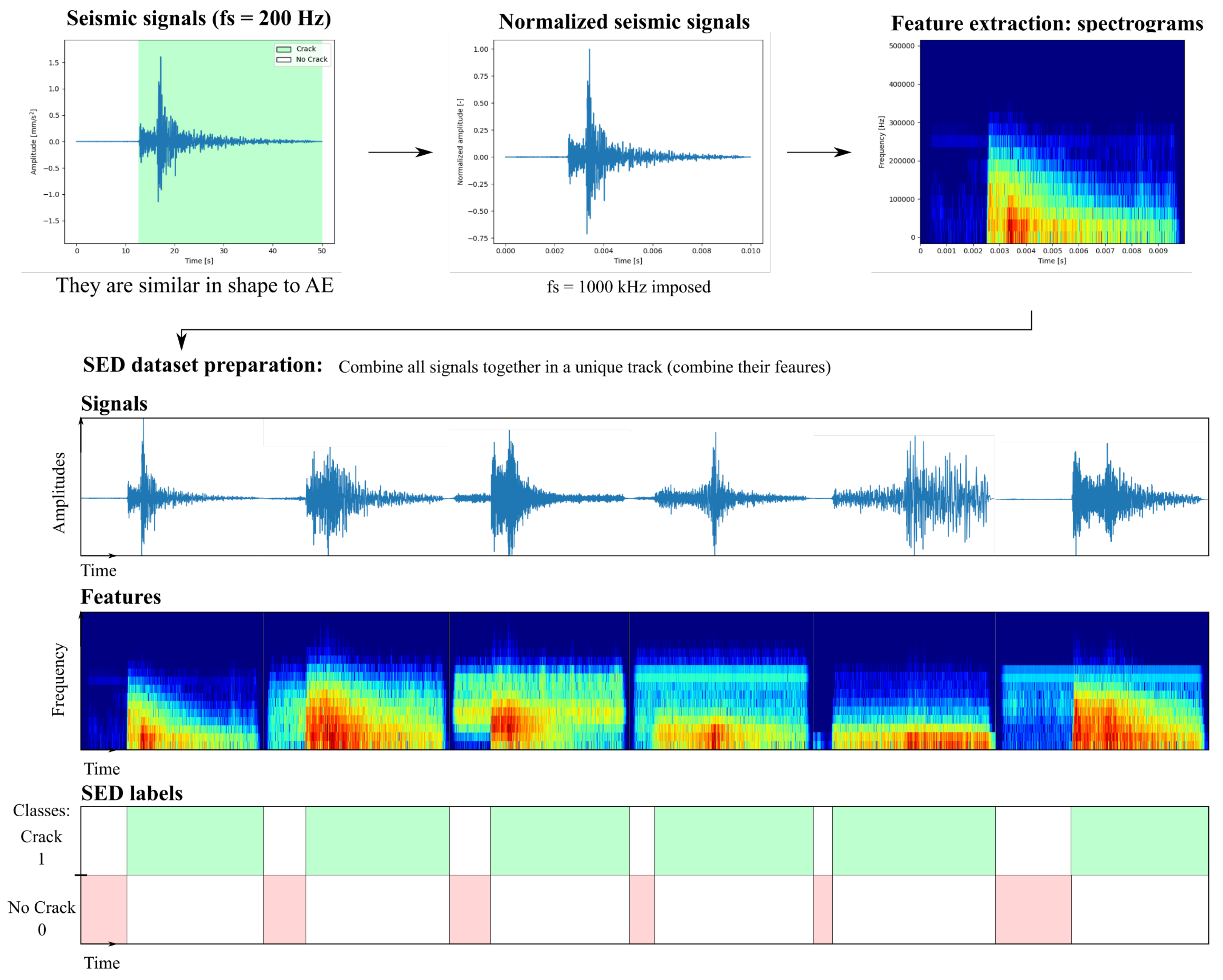
4.2. Datasets Description
5. Results and Discussion
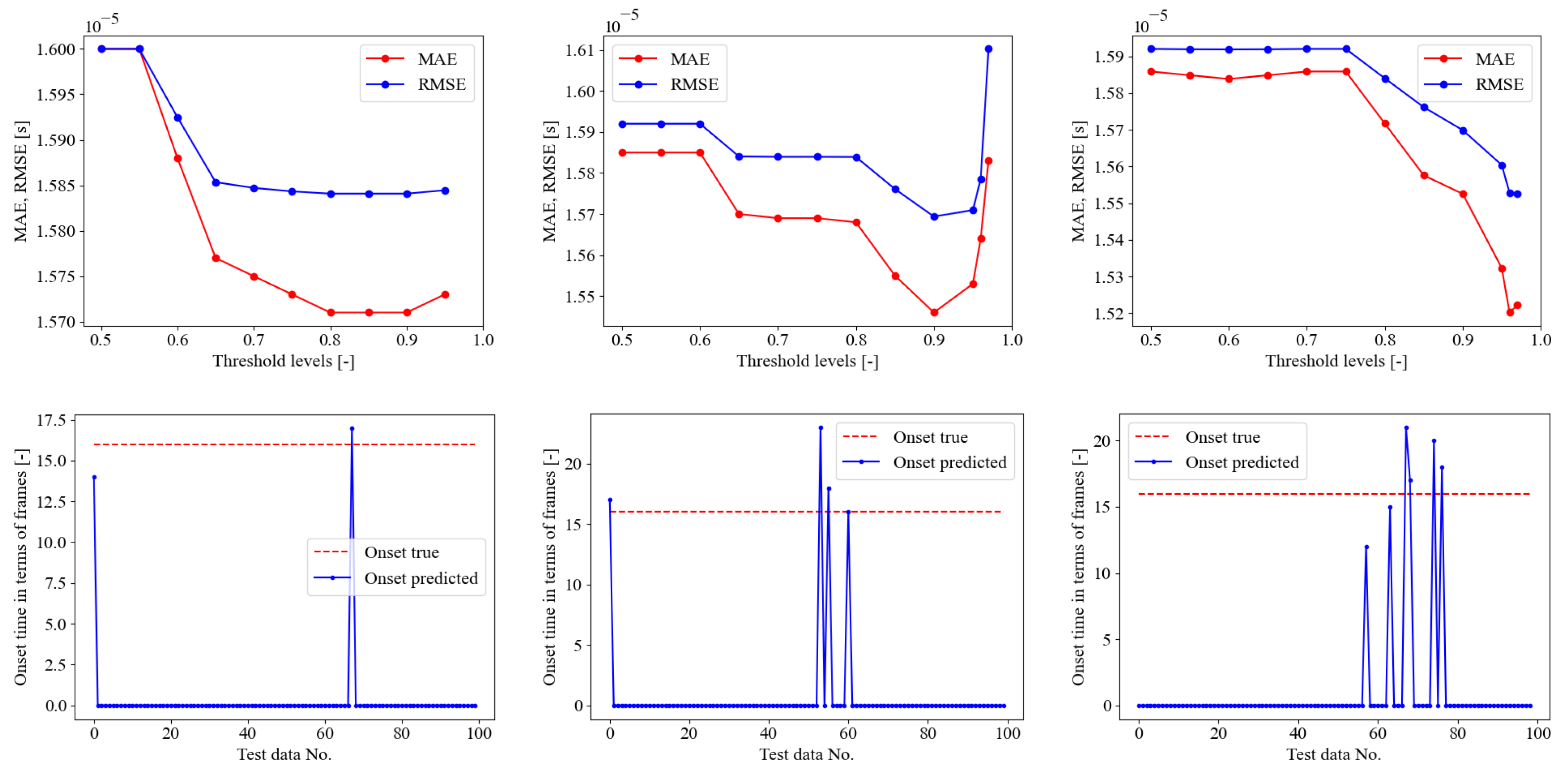
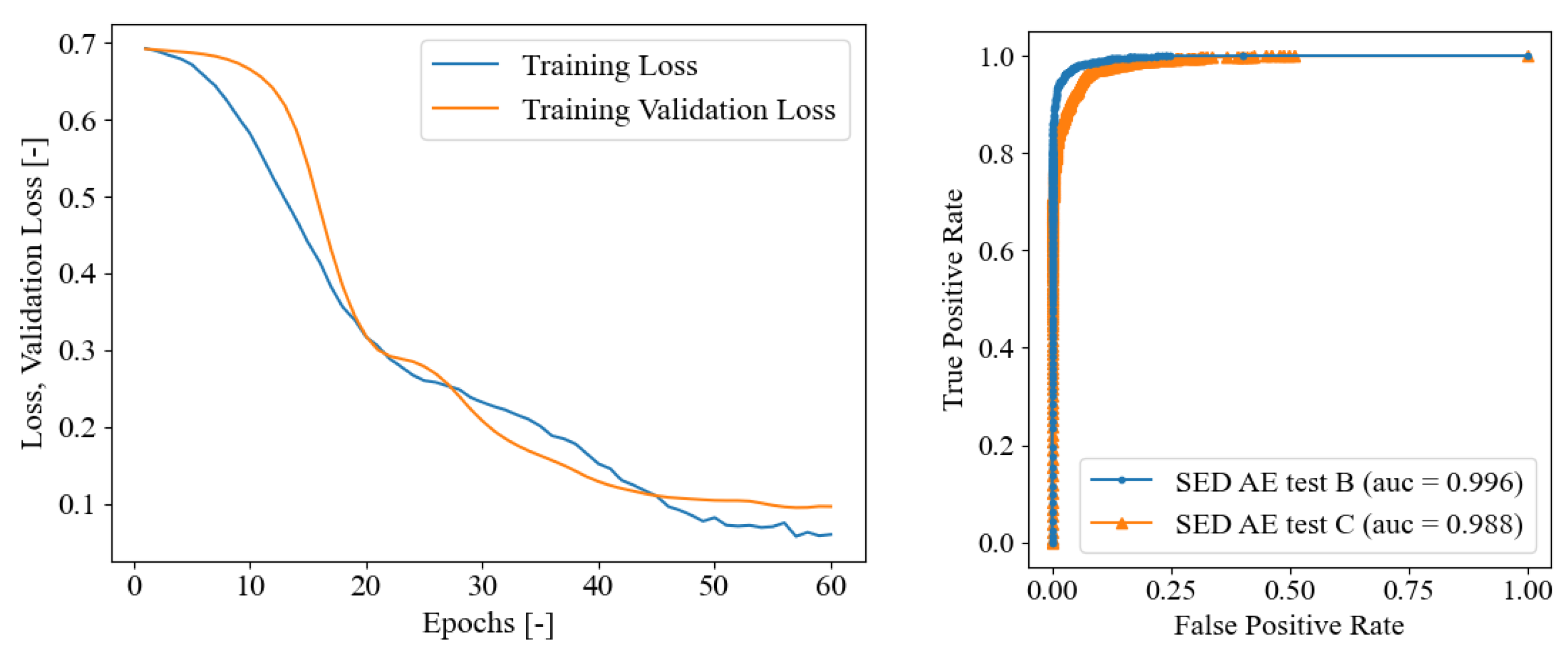
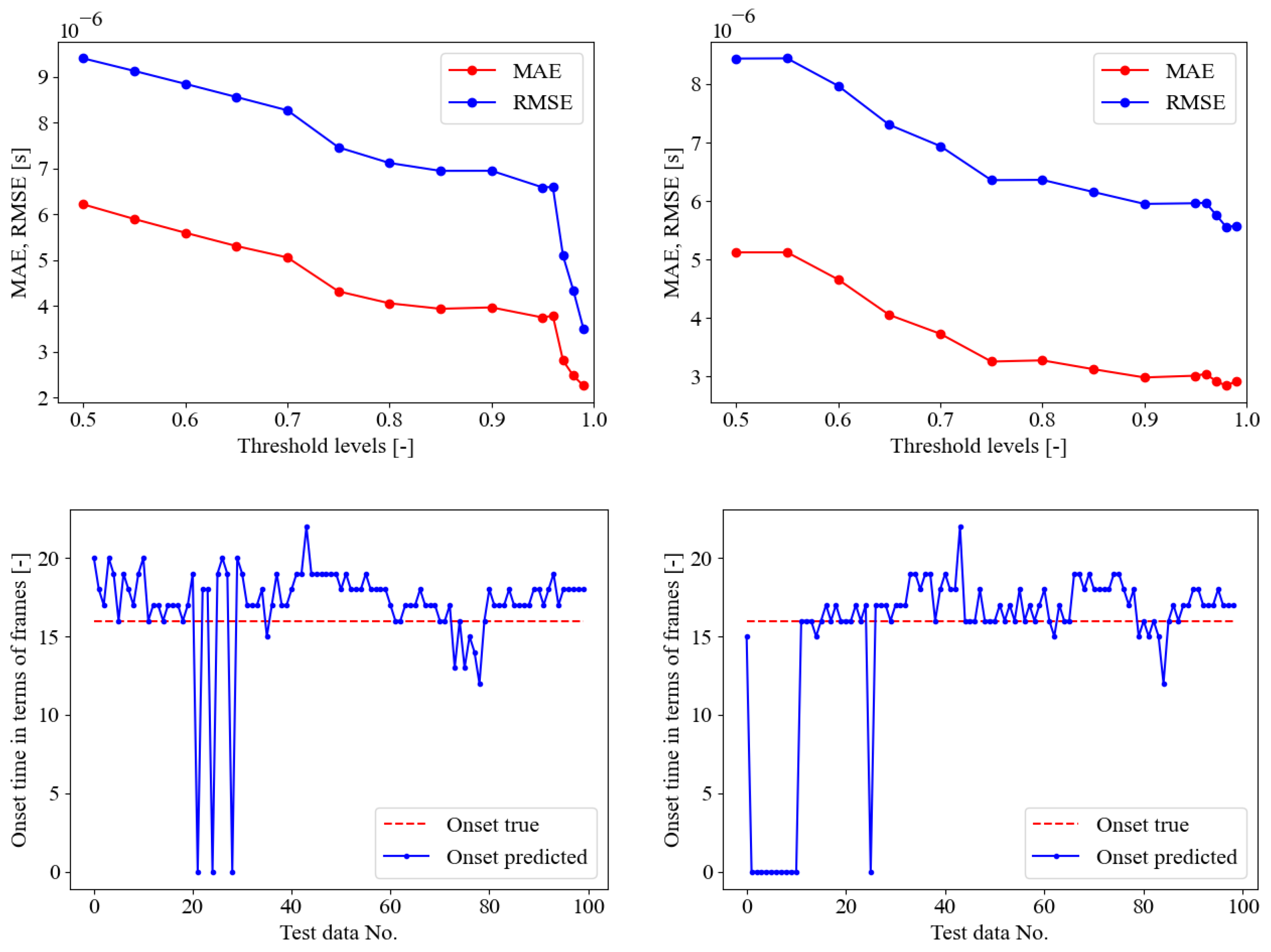
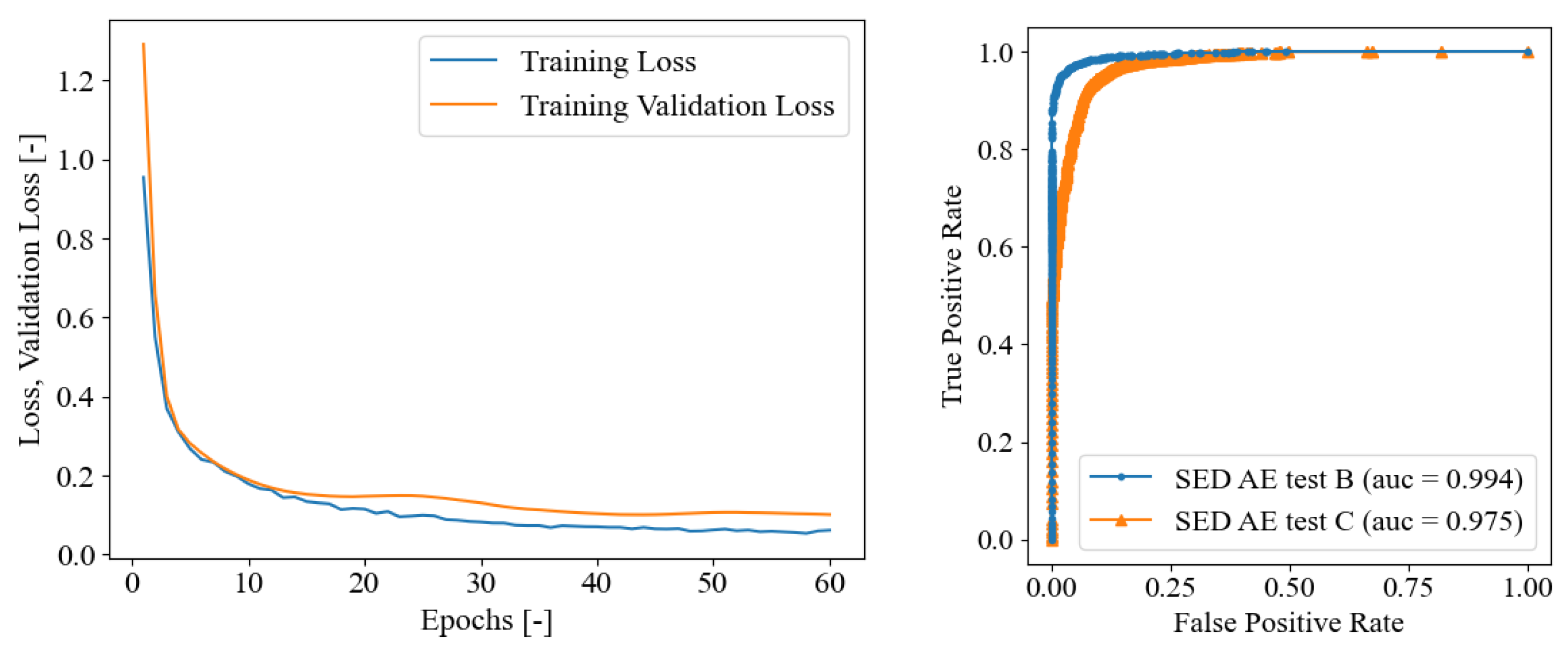
5.1. SED Model Trained on Seismic Data Only
5.2. Training SED Only on AE Dataset
5.3. Fine-Tuning SED on AE Dataset
5.4. Discussion
6. Conclusions and Future Developments
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alaggio, R.; Aloisio, A.; Antonacci, E.; Cirella, R. Two-years static and dynamic monitoring of the Santa Maria di Collemaggio basilica. Constr. Build. Mater. 2021, 268, 121069. [Google Scholar] [CrossRef]
- Aloisio, A.; Antonacci, E.; Fragiacomo, M.; Alaggio, R. The recorded seismic response of the Santa Maria di Collemaggio basilica to low-intensity earthquakes. Int. J. Archit. Herit. 2021, 15, 229–247. [Google Scholar] [CrossRef]
- Clementi, F.; Formisano, A.; Milani, G.; Ubertini, F. Structural health monitoring of architectural heritage: From the past to the future advances. Int. J. Archit. Herit. 2021, 15, 1–4. [Google Scholar] [CrossRef]
- Di Benedetto, M.; Asso, R.; Cucuzza, R.; Rosso, M.; Masera, D.; Marano, G. Concrete Half-Joints: Corrosion Damage Analysis with Numerical Simulation; The International Federation for Structural Concrete: Lausanne, Switzerland, 2021; pp. 297–304. [Google Scholar]
- Rosso, M.M.; Asso, R.; Aloisio, A.; Di Benedetto, M.; Cucuzza, R.; Greco, R. Corrosion effects on the capacity and ductility of concrete half-joint bridges. Constr. Build. Mater. 2022, 360, 129555. [Google Scholar] [CrossRef]
- Rosso, M.M.; Aloisio, A.; Cucuzza, R.; Marano, G.C.; Alaggio, R. Train-Track-Bridge Interaction Analytical Model with Non-proportional Damping: Sensitivity Analysis and Experimental Validation. In Proceedings of the European Workshop on Structural Health Monitoring, Palermo, Italy, 4–7 July 2022; Springer: Berlin/Heidelberg, Germany, 2023; pp. 223–232. [Google Scholar]
- Rosso, M.M.; Cucuzza, R.; Marano, G.C.; Aloisio, A.; Cirrincione, G. Review on deep learning in structural health monitoring. In Bridge Safety, Maintenance, Management, Life-Cycle, Resilience and Sustainability; CRC Press: Boca Raton, FL, USA, 2022; pp. 309–315. [Google Scholar]
- Rosso, M.M.; Marasco, G.; Aiello, S.; Aloisio, A.; Chiaia, B.; Marano, G.C. Convolutional networks and transformers for intelligent road tunnel investigations. Comput. Struct. 2023, 275, 106918. [Google Scholar] [CrossRef]
- Parisi, F.; Mangini, A.; Fanti, M.; Adam, J.M. Automated location of steel truss bridge damage using machine learning and raw strain sensor data. Autom. Constr. 2022, 138, 104249. [Google Scholar] [CrossRef]
- Sony, S.; Gamage, S.; Sadhu, A.; Samarabandu, J. Vibration-based multiclass damage detection and localization using long short-term memory networks. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 35, pp. 436–451. [Google Scholar]
- Grosse, C.U.; Finck, F. Quantitative evaluation of fracture processes in concrete using signal-based acoustic emission techniques. Cem. Concr. Compos. 2006, 28, 330–336. [Google Scholar] [CrossRef]
- Behnia, A.; Chai, H.K.; Shiotani, T. Advanced structural health monitoring of concrete structures with the aid of acoustic emission. Constr. Build. Mater. 2014, 65, 282–302. [Google Scholar] [CrossRef]
- Aggelis, D.G. Classification of cracking mode in concrete by acoustic emission parameters. Mech. Res. Commun. 2011, 38, 153–157. [Google Scholar] [CrossRef]
- Ohtsu, M. Acoustic emission characteristics in concrete and diagnostic applications. J. Acoust. Emiss. 1987, 6, 99–108. [Google Scholar]
- Carpinteri, A.; Lacidogna, G.; Manuello, A. Damage mechanisms interpreted by acoustic emission signal analysis. In Key Engineering Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2007; Volume 347, pp. 577–582. [Google Scholar]
- Ohtsu, M.; Okamoto, T.; Yuyama, S. Moment tensor analysis of acoustic emission for cracking mechanisms in concrete. Struct. J. 1998, 95, 87–95. [Google Scholar]
- Cheng, L.; Xin, H.; Groves, R.M.; Veljkovic, M. Acoustic emission source location using Lamb wave propagation simulation and artificial neural network for I-shaped steel girder. Constr. Build. Mater. 2021, 273, 121706. [Google Scholar] [CrossRef]
- Carpinteri, A.; Lacidogna, G.; Niccolini, G. Critical behaviour in concrete structures and damage localization by acoustic emission. In Key Engineering Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2006; Volume 312, pp. 305–310. [Google Scholar]
- Carpinteri, A.; Lacidogna, G. Structural monitoring and integrity assessment of medieval towers. J. Struct. Eng. 2006, 132, 1681–1690. [Google Scholar] [CrossRef]
- Rocchi, A.; Santecchia, E.; Ciciulla, F.; Mengucci, P.; Barucca, G. Characterization and optimization of level measurement by an ultrasonic sensor system. IEEE Sensors J. 2019, 19, 3077–3084. [Google Scholar] [CrossRef]
- Tong, C.; Kennett, B.L. Automatic seismic event recognition and later phase identification for broadband seismograms. Bull. Seismol. Soc. Am. 1996, 86, 1896–1909. [Google Scholar] [CrossRef]
- Baer, M.; Kradolfer, U. An automatic phase picker for local and teleseismic events. Bull. Seismol. Soc. Am. 1987, 77, 1437–1445. [Google Scholar] [CrossRef]
- Xu, J. P-wave onset detection based on the spectrograms of the AE signals. In Advanced Materials Research; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2011; Volume 250, pp. 3807–3810. [Google Scholar]
- Boschetti, F.; Dentith, M.D.; List, R.D. A fractal-based algorithm for detecting first arrivals on seismic traces. Geophysics 1996, 61, 1095–1102. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extention of the maximum likelihood principle. In Proceedings of the 2nd International Symposium on Information Theory, Tsahkadsor, Armenia, USSR, 2–8 September 1971; Akademiai Kiado: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Carpinteri, A.; Xu, J.; Lacidogna, G.; Manuello, A. Reliable onset time determination and source location of acoustic emissions in concrete structures. Cem. Concr. Compos. 2012, 34, 529–537. [Google Scholar] [CrossRef]
- Entezami, A.; Sarmadi, H.; Mariani, S. An unsupervised learning approach for early damage detection by time series analysis and deep neural network to deal with output-only (big) data. Eng. Proc. 2020, 2, 17. [Google Scholar]
- Flah, M.; Ragab, M.; Lazhari, M.; Nehdi, M. Localization and classification of structural damage using deep learning single-channel signal-based measurement. Autom. Constr. 2022, 139, 104271. [Google Scholar] [CrossRef]
- Dai, H.; MacBeth, C. The application of back-propagation neural network to automatic picking seismic arrivals from single-component recordings. J. Geophys. Res. Solid Earth 1997, 102, 15105–15113. [Google Scholar] [CrossRef]
- Kalafat, S.; Sause, M.G. Acoustic emission source localization by artificial neural networks. Struct. Health Monit. 2015, 14, 633–647. [Google Scholar] [CrossRef]
- Yu, Y.; Samali, B.; Rashidi, M.; Mohammadi, M.; Nguyen, T.N.; Zhang, G. Vision-based concrete crack detection using a hybrid framework considering noise effect. J. Build. Eng. 2022, 61, 105246. [Google Scholar] [CrossRef]
- Yu, Y.; Rashidi, M.; Samali, B.; Mohammadi, M.; Nguyen, T.N.; Zhou, X. Crack detection of concrete structures using deep convolutional neural networks optimized by enhanced chicken swarm algorithm. Struct. Health Monit. 2022, 21, 14759217211053546. [Google Scholar] [CrossRef]
- Modarres, C.; Astorga, N.; Droguett, E.L.; Meruane, V. Convolutional neural networks for automated damage recognition and damage type identification. Struct. Control Health Monit. 2018, 25, e2230. [Google Scholar] [CrossRef]
- Melchiorre, J.; Rosso, M.M.; Cucuzza, R.; Manuello Bertetto, A.; Marano, G.C. Deep acoustic emission detection trained on seismic signals. In Proceedings of the 30th Italian Workshop on Neural Networks (WIRN 2022), Vietri sul Mare, Italy, 7–9 September 2022. [Google Scholar]
- Madarshahian, R.; Soltangharaei, V.; Anay, R.; Caicedo, J.M.; Ziehl, P. Hsu-Nielsen source acoustic emission data on a concrete block. Data Brief 2019, 23, 103813. [Google Scholar] [CrossRef]
- Cuadra, J.; Vanniamparambil, P.; Servansky, D.; Bartoli, I.; Kontsos, A. Acoustic emission source modeling using a data-driven approach. J. Sound Vib. 2015, 341, 222–236. [Google Scholar] [CrossRef]
- Grégoire, D.; Verdon, L.; Lefort, V.; Grassl, P.; Saliba, J.; Regoin, J.P.; Loukili, A.; Pijaudier-Cabot, G. Mesoscale analysis of failure in quasi-brittle materials: Comparison between lattice model and acoustic emission data. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 1639–1664. [Google Scholar] [CrossRef]
- Ernst, R.; Dual, J. Acoustic emission localization in beams based on time reversed dispersion. Ultrasonics 2014, 54, 1522–1533. [Google Scholar] [CrossRef]
- Madarshahian, R.; Ziehl, P.; Caicedo, J.M. Acoustic emission Bayesian source location: Onset time challenge. Mech. Syst. Signal Process. 2019, 123, 483–495. [Google Scholar] [CrossRef]
- Gollob, S.; Kocur, G.K.; Schumacher, T.; Mhamdi, L.; Vogel, T. A novel multi-segment path analysis based on a heterogeneous velocity model for the localization of acoustic emission sources in complex propagation media. Ultrasonics 2017, 74, 48–61. [Google Scholar] [CrossRef] [PubMed]
- Kurz, J.H.; Grosse, C.U.; Reinhardt, H.W. Strategies for reliable automatic onset time picking of acoustic emissions and of ultrasound signals in concrete. Ultrasonics 2005, 43, 538–546. [Google Scholar] [CrossRef]
- Zhang, H.; Thurber, C.; Rowe, C. Automatic P-wave arrival detection and picking with multiscale wavelet analysis for single-component recordings. Bull. Seismol. Soc. Am. 2003, 93, 1904–1912. [Google Scholar] [CrossRef]
- Yokota, T. An automatic measurement of arrival time of seismic waves and its application to an on-line processing system. Bull. Earthq. Res. Inst. Univ. Tokyo 1981, 55, 449–484. [Google Scholar]
- Kitagawa, G.; Akaike, H. A procedure for the modeling of non-stationary time series. Ann. Inst. Stat. Math. 1978, 30, 351–363. [Google Scholar] [CrossRef]
- Maeda, N. A method for reading and checking phase times in autoprocessing system of seismic wave data. Zisin 1985, 38, 365–379. [Google Scholar] [CrossRef]
- Butterworth, S. On the theory of filter amplifiers. Wirel. Eng. 1930, 7, 536–541. [Google Scholar]
- Mesaros, A.; Heittola, T.; Virtanen, T.; Plumbley, M.D. Sound event detection: A tutorial. IEEE Signal Process. Mag. 2021, 38, 67–83. [Google Scholar] [CrossRef]
- Adavanne, S.; Pertilä, P.; Virtanen, T. Sound event detection using spatial features and convolutional recurrent neural network. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 771–775. [Google Scholar]
- Mesaros, A.; Heittola, T.; Benetos, E.; Foster, P.; Lagrange, M.; Virtanen, T.; Plumbley, M.D. Detection and classification of acoustic scenes and events: Outcome of the DCASE 2016 challenge. IEEE/ACM Trans. Audio, Speech, Lang. Process. 2017, 26, 379–393. [Google Scholar] [CrossRef]
- Cakır, E.; Parascandolo, G.; Heittola, T.; Huttunen, H.; Virtanen, T. Convolutional recurrent neural networks for polyphonic sound event detection. IEEE/ACM Trans. Audio, Speech, Lang. Process. 2017, 25, 1291–1303. [Google Scholar] [CrossRef]
- Cakir, E.; Heittola, T.; Huttunen, H.; Virtanen, T. Polyphonic sound event detection using multi label deep neural networks. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; pp. 1–7. [Google Scholar]
- Chen, Y.; Jin, H. Rare Sound Event Detection Using Deep Learning and Data Augmentation. In Proceedings of the Interspeech, Graz, Austria, 15–19 September 12019; pp. 619–623. [Google Scholar]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow; O’Reilly Media, Inc.: Newton, MA, USA, 2022. [Google Scholar]
- Chollet, F. Keras; GitHub: San Francisco, CA, USA, 2015; Available online: https://faroit.com/keras-docs/1.0.1/getting-started/faq/ (accessed on 19 September 2022).
- Rodrigues, G.C.; Braga, R.P. Evaluation of NASA POWER reanalysis products to estimate daily weather variables in a hot summer mediterranean climate. Agronomy 2021, 11, 1207. [Google Scholar] [CrossRef]
- Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Problems in RMSE-based wave model validations. Ocean Model. 2013, 72, 53–58. [Google Scholar] [CrossRef]
- Feilhauer, H.; Asner, G.P.; Martin, R.E.; Schmidtlein, S. Brightness-normalized partial least squares regression for hyperspectral data. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1947–1957. [Google Scholar] [CrossRef]
- Guo, C.; Liu, L.; Zhang, K.; Sun, H.; Zhang, Y.; Li, A.; Bai, Z.; Dong, H.; Li, C. High-throughput estimation of plant height and above-ground biomass of cotton using digital image analysis and Canopeo. Technol. Agron. 2022, 2, 1–10. [Google Scholar]
- Sejdić, E.; Djurović, I.; Jiang, J. Time–frequency feature representation using energy concentration: An overview of recent advances. Digit. Signal Process. 2009, 19, 153–183. [Google Scholar] [CrossRef]
- McFee, B.; Raffel, C.; Liang, D.; Ellis, D.P.; McVicar, M.; Battenberg, E.; Nieto, O. librosa: Audio and music signal analysis in python. In Proceedings of the 14th Python in Science Conference, Austin, TX, USA, 6–12 July 2015; Volume 8, pp. 18–25. [Google Scholar]
- Anitescu, C.; Atroshchenko, E.; Alajlan, N.; Rabczuk, T. Artificial Neural Network Methods for the Solution of Second Order Boundary Value Problems. Comput. Mater. Contin. 2019, 59, 345–359. [Google Scholar] [CrossRef]
- Pullano, S.A.; Bianco, M.G.; Critello, D.C.; Menniti, M.; La Gatta, A.; Fiorillo, A.S. A Recursive algorithm for indoor positioning using pulse-echo ultrasonic signals. Sensors 2020, 20, 5042. [Google Scholar] [CrossRef]
- Hameed, M.M.; AlOmar, M.K.; Baniya, W.J.; AlSaadi, M.A. Incorporation of artificial neural network with principal component analysis and cross-validation technique to predict high-performance concrete compressive strength. Asian J. Civ. Eng. 2021, 22, 1019–1031. [Google Scholar] [CrossRef]
- Brownlee, J. How to Grid Search Hyperparameters for Deep Learning Models in Python with Keras. línea]. Disponible en. 2016. Available online: https://machinelearningmastery.com/grid-search-hyperparameters-deep-learning-models-python-keras (accessed on 19 September 2022).
- Raschka, S.; Mirjalili, V. Python Machine Learning: Machine Learning and Deep Learning with Python, Scikit-Learn, and TensorFlow 2; Packt Publishing Ltd.: Birmingham, UK, 2019. [Google Scholar]
- Pan, S.J.; Tsang, I.W.; Kwok, J.T.; Yang, Q. Domain adaptation via transfer component analysis. IEEE Trans. Neural Netw. 2010, 22, 199–210. [Google Scholar] [CrossRef]
- Long, M.; Cao, Y.; Wang, J.; Jordan, M. Learning transferable features with deep adaptation networks. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 97–105. [Google Scholar]



| Layer (Type) | Output Shape | Param # |
|---|---|---|
| input_2 (InputLayer) | [(None, 1, 256, 17)] | 0 |
| conv2d_3 (Conv2D) | (None, 128, 256, 17) | 1280 |
| batch_normalization_3 (BatchNormalization) | (None, 128, 256, 17) | 512 |
| activation_3 (Activation) | (None, 128, 256, 17) | 0 |
| max_pooling2d_3 (MaxPooling2D) | (None, 128, 256, 4) | 0 |
| dropout_4 (Dropout) | (None, 128, 256, 4) | 0 |
| conv2d_4 (Conv2D) | (None, 128, 256, 4) | 147,584 |
| batch_normalization_4 (BatchNormalization) | (None, 128, 256, 4) | 512 |
| activation_4 (Activation) | (None, 128, 256, 4) | 0 |
| max_pooling2d_4 (MaxPooling2D) | (None, 128, 256, 2) | 0 |
| dropout_5 (Dropout) | (None, 128, 256, 2) | 0 |
| conv2d_5 (Conv2D) | (None, 128, 256, 2) | 147,584 |
| batch_normalization_5 (BatchNormalization) | (None, 128, 256, 2) | 512 |
| activation_5 (Activation) | (None, 128, 256, 2) | 0 |
| max_pooling2d_5 (MaxPooling2D) | (None, 128, 256, 1) | 0 |
| dropout_6 (Dropout) | (None, 128, 256, 1) | 0 |
| permute_1 (Permute) | (None, 256, 128, 1) | 0 |
| reshape_1 (Reshape) | (None, 256, 128) | 0 |
| bidirectional_2 (Bidirectional) | (None, 256, 32) | 31,104 |
| bidirectional_3 (Bidirectional) | (None, 256, 32) | 12,672 |
| time_distributed_2 (TimeDistributed) | (None, 256, 32) | 1056 |
| dropout_7 (Dropout) | (None, 256, 32) | 0 |
| time_distributed_3 (TimeDistributed) | (None, 256, 2) | 66 |
| strong_out (Activation) | (None, 256, 2) | 0 |
| Total params: 342,882 | ||
| Trainable params: 342,114 | ||
| Non-trainable params: 768 |
| Predicted Classes | Threshold: | 96% | ||||||
|---|---|---|---|---|---|---|---|---|
| True Classes | 0 No Crack | 1 Crack | Precision | Recall | F1-Score | MAE | RMSE | NRMSE |
| 0 No Crack | 98.88% | 1.12% | 96.58% | 98.88% | 97.72% | [s] | [s] | [-] |
| 1 Crack | 3.51% | 96.49% | 98.86% | 98.86% | 98.86% | 8.598 × 10−6 | 2.635 × 10−5 | 0.1421 |
| AE—Test A | Predicted Classes | Threshold: | 85% | ||
| True Classes | 0 No Crack | 1 Crack | Precision | Recall | F1-score |
| 0 No Crack | 4.36% | 95.64% | 96.77% | 4.36% | 8.34% |
| 1 Crack | 0.15% | 99.85% | 51.08% | 51.08% | 51.08% |
| AE—Test B | Predicted Classes | Threshold: | 90% | ||
| True Classes | 0 No Crack | 1 Crack | Precision | Recall | F1-score |
| 0 No Crack | 8.02% | 91.98% | 69.31% | 8.02% | 14.37% |
| 1 Crack | 3.55% | 96.45% | 51.19% | 51.19% | 51.19% |
| AE—Test C | Predicted Classes | Threshold: | 96% | ||
| True Classes | 0 No Crack | 1 Crack | Precision | Recall | F1-score |
| 0 No Crack | 9.79% | 90.21% | 71.81% | 9.79% | 17.22% |
| 1 Crack | 3.84% | 96.16% | 51.59% | 51.59% | 51.59% |
| AE—Test B | Predicted Classes | Threshold: | 99% | |||||
| True Classes | 0 No Crack | 1 Crack | Precision | Recall | F1-Score | MAE | RMSE | NRMSE |
| 0 No Crack | 98.93% | 1.07% | 93.39% | 98.93% | 96.08% | [s] | [s] | [-] |
| 1 Crack | 7.00% | 93.00% | 98.86% | 98.86% | 98.86% | 2.260 × 10−6 | 3.501 × 10−6 | 0.2188 |
| AE—Test C | Predicted Classes | Threshold: | 98% | |||||
| True Classes | 0 No Crack | 1 Crack | Precision | Recall | F1-score | MAE | RMSE | NRMSE |
| 0 No Crack | 93.94% | 6.06% | 94.59% | 93.94% | 94.26% | [s] | [s] | [-] |
| 1 Crack | 5.38% | 94.62% | 93.98% | 93.98% | 93.98% | 2.838 × 10−6 | 5.557 × 10−6 | 0.3473 |
| AE—Test B | Predicted Classes | Threshold: | 95% | |||||
| True Classes | 0 No Crack | 1 Crack | Precision | Recall | F1-score | MAE | RMSE | NRMSE |
| 0 No Crack | 98.30% | 1.70% | 94.64% | 98.30% | 96.43% | [s] | [s] | [-] |
| 1 Crack | 5.56% | 94.44% | 98.23% | 98.23% | 98.23% | 1.610 × 10−6 | 3.135 × 10−6 | 0.1960 |
| AE—Test C | Predicted Classes | Threshold: | 97% | |||||
| True Classes | 0 No Crack | 1 Crack | Precision | Recall | F1-score | MAE | RMSE | NRMSE |
| 0 No Crack | 91.29% | 8.71% | 93.33% | 91.29% | 92.30% | [s] | [s] | [-] |
| 1 Crack | 6.52% | 93.48% | 91.47% | 91.47% | 91.47% | 2.657 × 10−6 | 5.482 × 10−6 | 0.3426 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melchiorre, J.; Manuello Bertetto, A.; Rosso, M.M.; Marano, G.C. Acoustic Emission and Artificial Intelligence Procedure for Crack Source Localization. Sensors 2023, 23, 693. https://doi.org/10.3390/s23020693
Melchiorre J, Manuello Bertetto A, Rosso MM, Marano GC. Acoustic Emission and Artificial Intelligence Procedure for Crack Source Localization. Sensors. 2023; 23(2):693. https://doi.org/10.3390/s23020693
Chicago/Turabian StyleMelchiorre, Jonathan, Amedeo Manuello Bertetto, Marco Martino Rosso, and Giuseppe Carlo Marano. 2023. "Acoustic Emission and Artificial Intelligence Procedure for Crack Source Localization" Sensors 23, no. 2: 693. https://doi.org/10.3390/s23020693
APA StyleMelchiorre, J., Manuello Bertetto, A., Rosso, M. M., & Marano, G. C. (2023). Acoustic Emission and Artificial Intelligence Procedure for Crack Source Localization. Sensors, 23(2), 693. https://doi.org/10.3390/s23020693









