Combining Model-Agnostic Meta-Learning and Transfer Learning for Regression
Abstract
1. Introduction
2. Related Work
3. MAML
4. Observation of the Impact of Differences in the Data Distributions between the Meta- and Target Tasks
- Phase distribution gap: Defined as . If or , the phase of the target task lies outside of the phase distribution of the meta-tasks.
- Amplitude distribution gap: Defined as . If or , the amplitude of the target task lies outside of the amplitude distribution of the meta-tasks.
5. Combining MAML and Transfer Learning
- Joint training (JT): As a pretraining step, the model is trained on all meta-tasks together as one large dataset. Then, the model is fine-tuned by using the dataset of the target task for adaptation.
- Training from scratch (TFS): The model parameters are randomly initialized. Then, the model is trained using the dataset of the target task. No pretraining using meta-task datasets is performed.
- Training on everything (TOE): The model is trained using all available data (datasets from both the meta- and target tasks). The pretraining and adaptation processes are not separate.
| Algorithm 1: Ensemble scheme algorithm. |
|
6. Performance Evaluation
6.1. Sinusoidal Regression
6.2. VR Motion Prediction
- Pitch motion in the upward direction;
- Pitch motion in the downward direction;
- Yaw motion in the rightward direction;
- Yaw motion in the leftward direction;
- Roll motion in the clockwise and counterclockwise directions;
- Playing VR Content 1;
- Playing VR Content 2;
- Playing VR Content 3.
6.3. Temperature Forecasting
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AWS | Automatic Weather Station |
| CART | Classification And Regression Trees |
| CNN | Convolutional Neural Network |
| FTML | Follow The Meta-Leader |
| JT | Joint Training |
| KMA | Korea Meteorological Administration |
| LDAPS | Local Data Assimilation and Prediction System |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MAML | Model-Agnostic Meta-Learning |
| MSE | Mean-Squared Error |
| NN | Neural Network |
| TFS | Training From Scratch |
| TOE | Training On Everything |
| VR | Virtual Reality |
References
- Biggs, J.B. The role of metalearning in study processes. Br. J. Educ. Psychol. 1985, 55, 185–212. [Google Scholar] [CrossRef]
- Bengio, Y.; Bengio, S.; Cloutier, J. Learning a synaptic learning rule. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Seattle, WA, USA, 8–12 July 1991; Volume ii, p. 969. [Google Scholar]
- Lake, B.M.; Salakhutdinov, R.; Tenenbaum, J.B. Human-level concept learning through probabilistic program induction. Science 2015, 350, 1332–1338. [Google Scholar] [CrossRef] [PubMed]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; kavukcuoglu, k.; Wierstra, D. Matching Networks for One Shot Learning. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Barcelona, Spain, 5–10 December 2016; Volume 29. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. In Proceedings of the International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; Volume 70, pp. 1126–1135. [Google Scholar]
- Antoniou, A.; Edwards, H.; Storkey, A. How to train your MAML. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Finn, C.; Rajeswaran, A.; Kakade, S.; Levine, S. Online meta-learning. In Proceedings of the International Conference on Machine Learning (ICML), Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 1920–1930. [Google Scholar]
- Vanschoren, J. Meta-learning: A survey. arXiv 2018, arXiv:1810.03548. [Google Scholar]
- Santoro, A.; Bartunov, S.; Botvinick, M.; Wierstra, D.; Lillicrap, T. Meta-Learning with Memory-Augmented Neural Networks. In Proceedings of the International Conference on Machine Learning (ICML), New York, NY, USA, 19–24 June 2016; Volume 48, pp. 1842–1850. [Google Scholar]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese neural networks for one-shot image recognition. In Proceedings of the ICML Deep Learning Workshop, Lille, France, 6–11 July 2015; Volume 2. [Google Scholar]
- Ravi, S.; Larochelle, H. Optimization as a Model for Few-Shot Learning. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Nichol, A.; Achiam, J.; Schulman, J. On First-Order Meta-Learning Algorithms. arXiv 2018, arXiv:1803.02999. [Google Scholar]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic Gradient Descent with Restarts. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Park, E.; Oliva, J.B. Meta-Curvature. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Vuorio, R.; Sun, S.H.; Hu, H.; Lim, J.J. Multimodal Model-Agnostic Meta-Learning via Task-Aware Modulation. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Collins, L.; Mokhtari, A.; Shakkottai, S. Task-Robust Model-Agnostic Meta-Learning. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Online, 6–12 December 2020; Volume 33, pp. 18860–18871. [Google Scholar]
- Fallah, A.; Mokhtari, A.; Ozdaglar, A. Generalization of Model-Agnostic Meta-Learning Algorithms: Recurring and Unseen Tasks. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Online, 6–14 December 2021; Volume 34, pp. 5469–5480. [Google Scholar]
- Fallah, A.; Mokhtari, A.; Ozdaglar, A. Personalized Federated Learning with Theoretical Guarantees: A Model-Agnostic Meta-Learning Approach. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Online, 6–12 December 2020; Volume 33, pp. 3557–3568. [Google Scholar]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. Proc. IEEE 2021, 109, 43–76. [Google Scholar] [CrossRef]
- Agarwal, N.; Sondhi, A.; Chopra, K.; Singh, G. Transfer Learning: Survey and Classification. In Proceedings of the Smart Innovations in Communication and Computational Sciences; Springer: Singapore, 2021; pp. 145–155. [Google Scholar]
- Houlsby, N.; Giurgiu, A.; Jastrzebski, S.; Morrone, B.; De Laroussilhe, Q.; Gesmundo, A.; Attariyan, M.; Gelly, S. Parameter-Efficient Transfer Learning for NLP. In Proceedings of the International Conference on Machine Learning (ICML), Long Beach, CA, USA, 10–15 June 2019; PMLR 97. pp. 2790–2799. [Google Scholar]
- Guo, Y.; Shi, H.; Kumar, A.; Grauman, K.; Rosing, T.; Feris, R. SpotTune: Transfer Learning Through Adaptive Fine-Tuning. In Proceedings of the the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- You, K.; Kou, Z.; Long, M.; Wang, J. Co-Tuning for Transfer Learning. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Online, 6–12 December 2020; Volume 33, pp. 17236–17246. [Google Scholar]
- Sun, Q.; Liu, Y.; Chua, T.S.; Schiele, B. Meta-Transfer Learning for Few-Shot Learning. In Proceedings of the the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Brown, G. Ensemble Learning. Encyclopedia of Machine Learning; Springer: New York, NY, USA, 2010; Volume 312. [Google Scholar]
- Pal, M. Ensemble learning with decision tree for remote sensing classification. World Acad. Sci. Eng. Technol. 2007, 36, 258–260. [Google Scholar]
- Wang, Z.; Wang, Y.; Srinivasan, R.S. A novel ensemble learning approach to support building energy use prediction. Energy Build. 2018, 159, 109–122. [Google Scholar] [CrossRef]
- Merentitis, A.; Debes, C. Many hands make light work-on ensemble learning techniques for data fusion in remote sensing. IEEE Geosci. Remote Sens. Mag. 2015, 3, 86–99. [Google Scholar] [CrossRef]
- Divina, F.; Gilson, A.; Goméz-Vela, F.; García Torres, M.; Torres, J.F. Stacking ensemble learning for short-term electricity consumption forecasting. Energies 2018, 11, 949. [Google Scholar] [CrossRef]
- Webb, G.I.; Zheng, Z. Multistrategy ensemble learning: Reducing error by combining ensemble learning techniques. IEEE Trans. Knowl. Data Eng. 2004, 16, 980–991. [Google Scholar] [CrossRef]
- XGBoost. Available online: https://xgboost.readthedocs.io/en/stable/ (accessed on 18 November 2022).
- Bayesian Optimization Package. Available online: https://github.com/fmfn/BayesianOptimization (accessed on 18 November 2022).
- Nyamtiga, B.W.; Hermawan, A.A.; Luckyarno, Y.F.; Kim, T.W.; Jung, D.Y.; Kwak, J.S.; Yun, J.H. Edge-Computing-Assisted Virtual Reality Computation Offloading: An Empirical Study. IEEE Access 2022, 10, 95892–95907. [Google Scholar] [CrossRef]
- Nguyen, T.C.; Yun, J.H. Predictive Tile Selection for 360-Degree VR Video Streaming in Bandwidth-Limited Networks. IEEE Commun. Lett. 2018, 22, 1858–1861. [Google Scholar] [CrossRef]
- Cho, D.; Yoo, C.; Im, J.; Cha, D.H. Comparative assessment of various machine learning-based bias correction methods for numerical weather prediction model forecasts of extreme air temperatures in urban areas. Earth Space Sci. 2020, 7, e2019EA000740. [Google Scholar] [CrossRef]










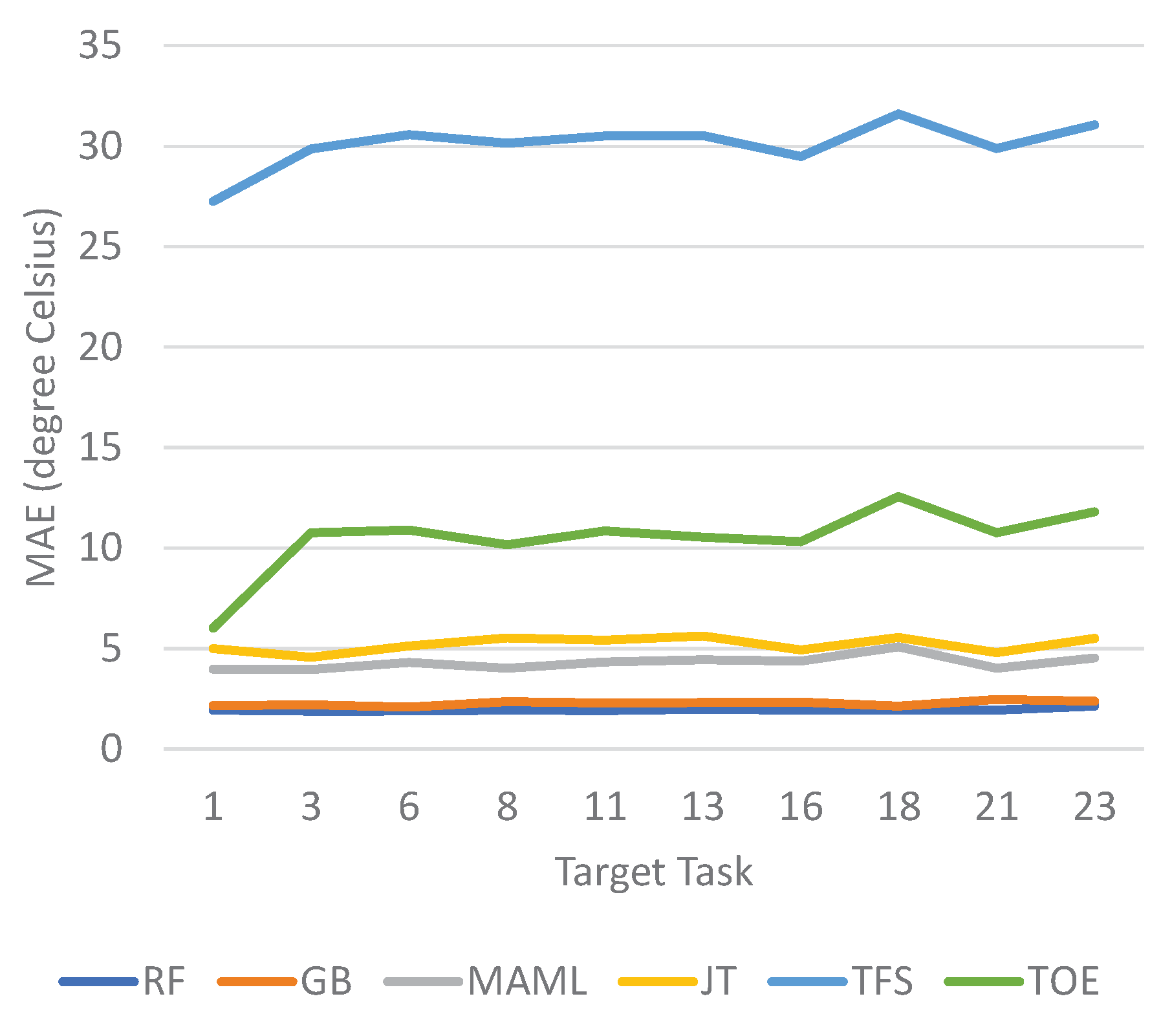
| ine Setting | Meta-Task Amplitude and Phase Distributions | Target-Task Amplitude and Phase |
| ine M(2.5, 0.25)-T(1, 0) | [1, 5]; [0, 0.5] | 1/5; 0 |
| M(2.5, 0.25)-T(1, 0.25) | [1, 5]; [0, 0.5] | 1/5; 0.25 |
| M(2.5, 0.25)-T(1, 0.75) | [1, 5]; [0, 0.5] | 1/5; 0.75 |
| M(2.5, 0.125)-T(1, 0.125) | [1, 5]; [0, 0.25] | 1/5; 0.125 |
| M(2.5, 0.125)-T(1, 0.75) | [1, 5]; [0, 0.25] | 1/5; 0.75 |
| M(2.5, 0.125)-T(1, 1) | [1, 5]; [0, 0.25] | 1/5; |
| ine |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Satrya, W.F.; Yun, J.-H. Combining Model-Agnostic Meta-Learning and Transfer Learning for Regression. Sensors 2023, 23, 583. https://doi.org/10.3390/s23020583
Satrya WF, Yun J-H. Combining Model-Agnostic Meta-Learning and Transfer Learning for Regression. Sensors. 2023; 23(2):583. https://doi.org/10.3390/s23020583
Chicago/Turabian StyleSatrya, Wahyu Fadli, and Ji-Hoon Yun. 2023. "Combining Model-Agnostic Meta-Learning and Transfer Learning for Regression" Sensors 23, no. 2: 583. https://doi.org/10.3390/s23020583
APA StyleSatrya, W. F., & Yun, J.-H. (2023). Combining Model-Agnostic Meta-Learning and Transfer Learning for Regression. Sensors, 23(2), 583. https://doi.org/10.3390/s23020583








