Mechanical Determinants of Sprinting and Change of Direction in Elite Female Field Hockey Players
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Design
2.2.1. Speed-Acceleration Evaluation 30 m
2.2.2. Deceleration
2.2.3. Agility Test
2.2.4. Horizontal Force Velocity Profile
2.2.5. Statistical Analysis
3. Results
3.1. Descriptive Values
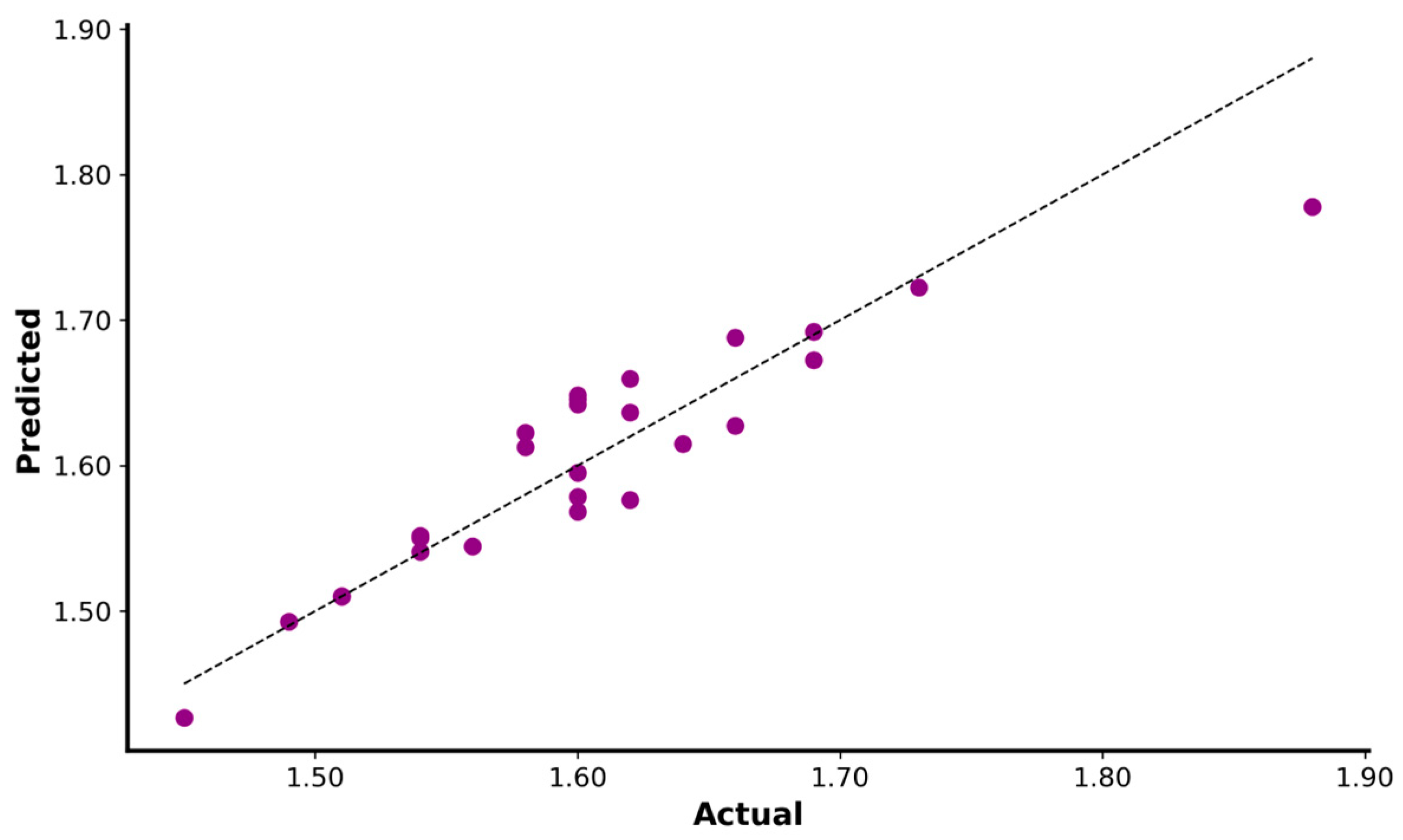
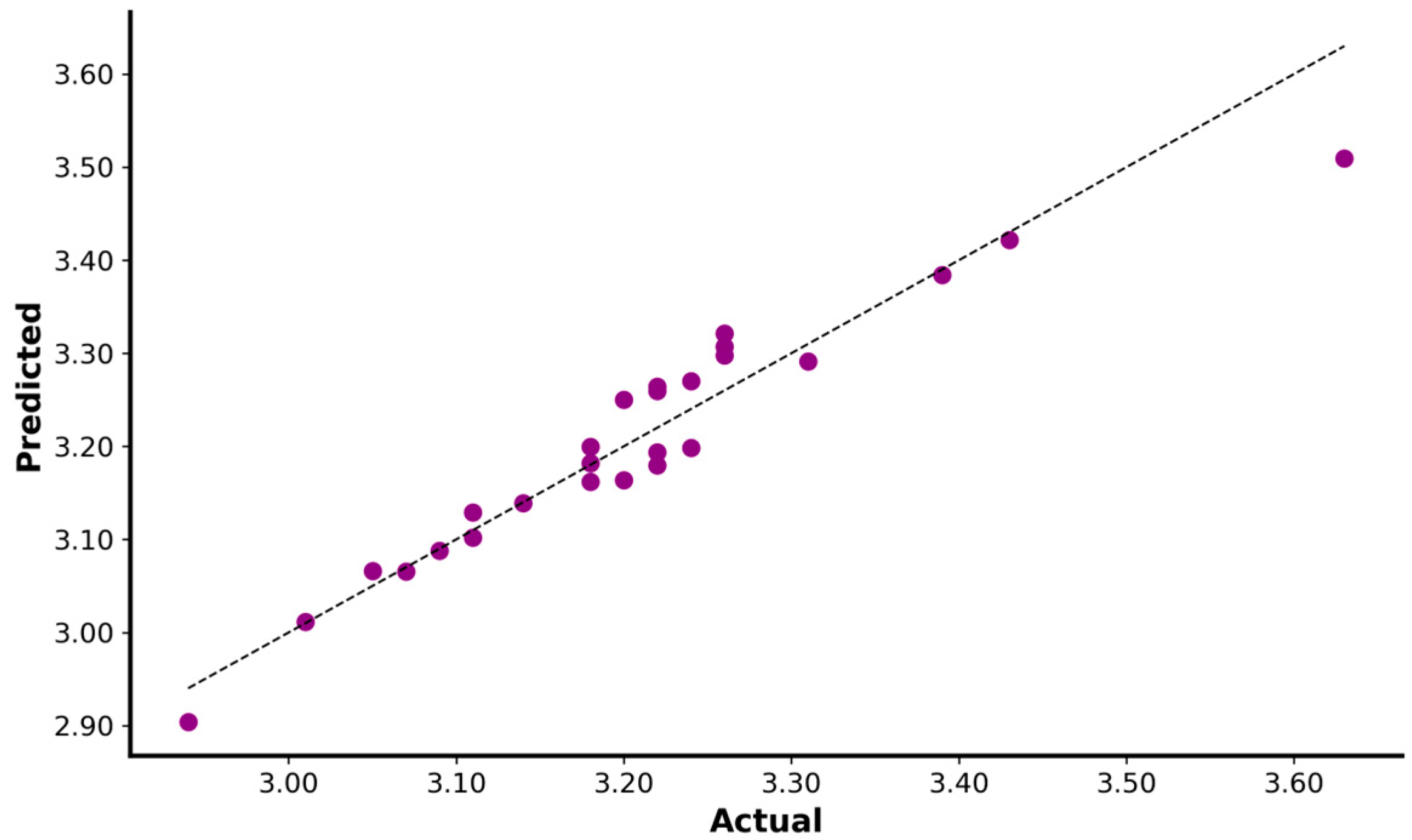
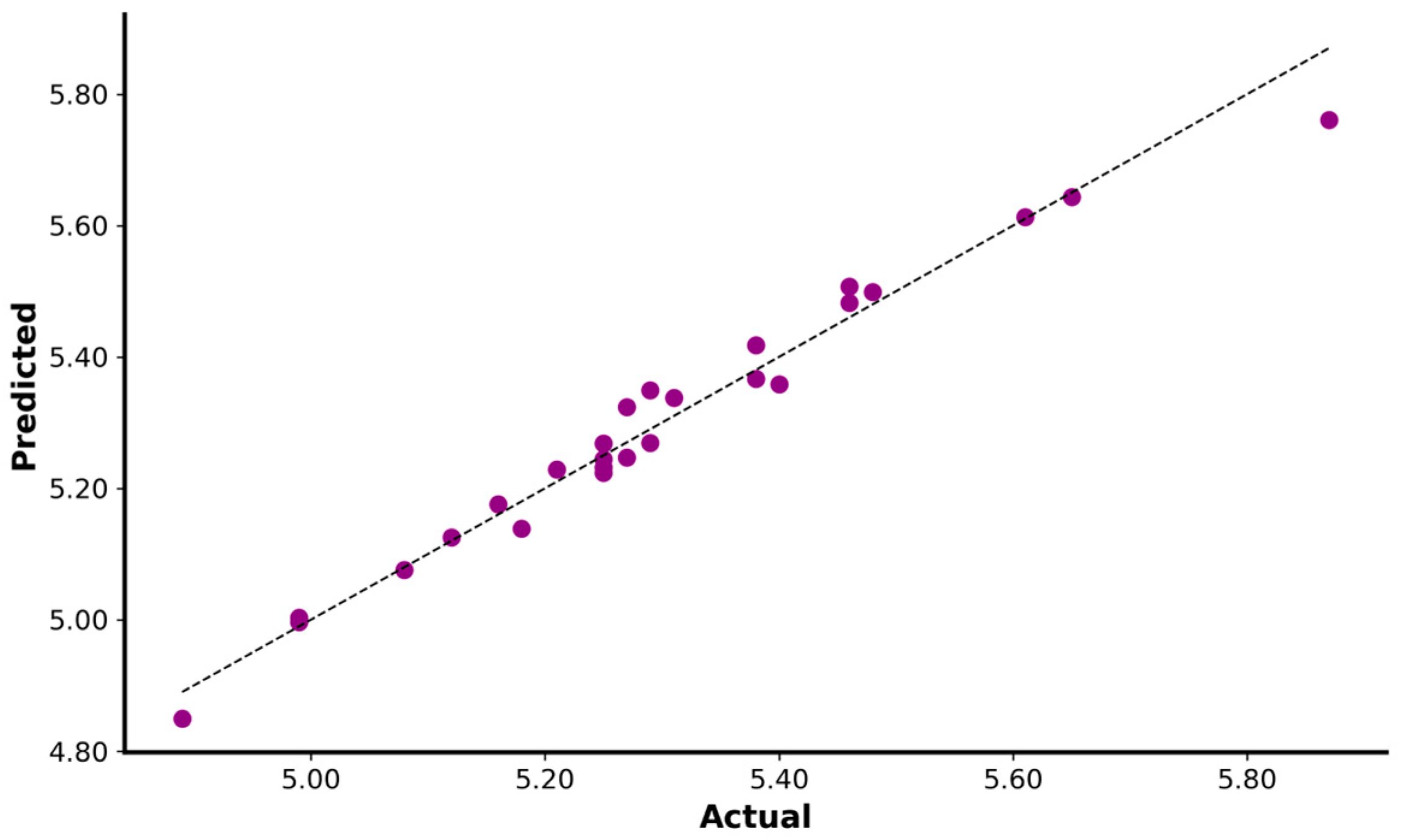
3.1.1. Sprint Variables
3.1.2. Deceleration and Change of Direction
3.1.3. Mechanical Variables
3.2. Mechanical Variables Determining Sprint and Change of Direction Performance
3.2.1. Five Meter Sprint Performance
3.2.2. Fifteen Meter Sprint Performance
3.2.3. Thirty Meter Sprint Performance
3.2.4. Change of Direction
4. Discussion
4.1. Descriptive Values
4.2. Mechanical Variables
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Houtmeyers, K.C.; Jaspers, A.; Figueiredo, P. Managing the training process in elite sports: From descriptive to prescriptive data analytics. Int. J. Sports Physiol. Perform. 2021, 16, 1719–1723. [Google Scholar] [CrossRef] [PubMed]
- West, S.W.; Clubb, J.; Torres-Ronda, L.; Howells, D.; Leng, E.; Vescovi, J.D. More than a Metric: How Training Load is Used in Elite Sport for Athlete Management. Int. J. Sports Med. 2021, 42, 300–306. [Google Scholar] [CrossRef] [PubMed]
- Cerda-Kohler, H.; Aedo-Muñoz, E.; Solar-Altamirano, I. Lineamientos Unidad de Ciencias Aplicadas al Deporte, 1st ed.; Instituto Nacional de Deportes; 2022. Available online: https://www.researchgate.net/publication/359047294_Lineamientos_Unidad_de_Ciencias_Aplicadas_al_Deporte_2022-2028_El_que_el_como_y_el_por_que_hacemos_lo_que_hacemos (accessed on 28 August 2023).
- McGuinness, A.; Malone, S.; Petrakos, G.; Collins, K. The Physical and Physiological Demands of Elite International Female Field Hockey Players During Competitive Match Play. J. Strength Cond. Res. 2019, 33, 3105–3113. [Google Scholar] [CrossRef] [PubMed]
- Laursen, P.; Buchheit, M. Science and Application of High-Intensity Interval Training: Solutions to the Programming Puzzle, 1st ed.; Human Kinetics: Champaign, IL, USA, 2019; Available online: https://www.human-kinetics.co.uk/9781492552123/science-and-application-of-high-intensity-interval-training/ (accessed on 28 August 2023).
- Cormie, P.; McGuigan, M.; Newton, R. Developing maximal neuromuscular power: Part 1—Biological basis of maximal power production. Sports Med. 2011, 41, 17–38. [Google Scholar] [CrossRef] [PubMed]
- Spiteri, T.; Newton, R.U.; Binetti, M.; Hart, N.H.; Sheppard, J.M.; Nimphius, S. Mechanical determinants of faster change of direction and agility performance in basquetball athletes. J. Strength Cond. Res. 2015, 29, 2205–2214. [Google Scholar] [CrossRef]
- Young, W.; Rayner, R.; Talpey, S. It’s Time to Change Direction on Agility Research: A Call to Action. Sports Med. 2021, 7, 12. [Google Scholar] [CrossRef]
- Brughelli, M.; Cronin, J.; Levin, G. Understanding Change of Direction Ability in Sport: A Review of Resistance Training Studies. Sports Med. 2008, 38, 1045–1060. [Google Scholar] [CrossRef]
- Spencer, M.; Lawrence, S.; Rechichi, C.; Bishop, D.; Dawson, B.; Goodman, C. Time-motion analysis of elite field hockey, with special reference to repeated-sprint activity. J. Sports Sci. 2004, 22, 843–850. [Google Scholar] [CrossRef]
- Spencer, M.; Bishop, D.; Dawson, B.; Goodman, C. Physiological and Metabolic Responses of Repeated-Sprint Activities Specific to Field-Based Team Sports. Sports Med. 2005, 35, 1025–1044. [Google Scholar] [CrossRef]
- Gabbett, T. GPS Analisys of elite women’s field hockey training and competition. J. Strength Cond. Res. 2010, 25, 1321–1324. [Google Scholar] [CrossRef]
- McGuinness, A.; Malone, S.; Hughes, B.; Collins, K.; Passmore, D. Physical activity and physiological profiles of elite international female field hockey players across the quarters of competitive match play. J. Strength Cond. Res. 2019, 33, 2513–2522. [Google Scholar] [CrossRef] [PubMed]
- Buchheit, M.; Samozino, P.; Glynn, J.; Ben, M.; Haddad, H.; Mendez-Villanueva, A.; Morin, J.B. Mechanical determinants of acceleration and maximal sprinting speed in highly trained young soccer players. J. Sports Sci. 2014, 32, 1906–1913. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-Reyes, P.; García-Ramos, A.; Cuadrado-Peñafiel, V. Differences in sprint mechanical force-velocity profile between trained soccer and futsal players. Int. J. Sports Physiol. Perform. 2018, 14, 478–485. [Google Scholar] [CrossRef]
- Vanwanseele, B.; Aeles, J. Mechanical determinants of sprint performance in elite and sub-elite field hockey players. In Proceedings of the International Conference on Biomechanics in Sports, Tsukuba, Japan, 18–22 July 2016. [Google Scholar]
- Samozino, P.; Rabita, G.; Dorel, S.; Slawinski, N.; Peyrot, N.; Saez de Villarreal, E.; Morin, J.B. A simple method for measuring power, force, velocity properties, and mechanical effectiveness in sprint running. Scand. J. Med. Sci. Sports 2016, 26, 648–658. [Google Scholar] [CrossRef] [PubMed]
- Devismes, M.; Aeles, J.; Philips, J.; Vanwanseele, B. Sprint force-velocity profiles in soccer players: Impact of sex and playing level. Sports Biomech. 2021, 20, 947–957. [Google Scholar] [CrossRef]
- Stavridis, I.; Smilios, I.; Tsopanidou, A.; Economou, T.; Paradisis, G. Differences in the Force Velocity Mechanical Profile and the Effectiveness of Force Application During Sprint-Acceleration Between Sprinters and Hurdlers. Front. Sports Act. Living 2019, 1, 26. [Google Scholar] [CrossRef]
- Perez, J.; Guilhem, G.; Brocherie, F. Truncated Estimation of Skating Force-Velocity Profiling When Using High-Speed Video-Based Methods Compared to Radar-Derived Processing. Front. Bioeng. Biotechnol. 2021, 9, 661744. [Google Scholar] [CrossRef]
- Stenroth, L.; Vartiainen, P.; Karjalainen, P. Force-velocity profiling in ice hockey skating: Reliability and validity of a simple, low-cost field method. Sports Biomech. 2020, 22, 874–889. [Google Scholar] [CrossRef]
- Baena-Raya, A.; Soriano-Maldonado, A.; Conceição, F.; Jiménez-Reyes, P.; Rodríguez-Pérez, M. Association of the vertical and horizontal force-velocity profile and acceleration with change of direction ability in various sports. Eur. J. Sport Sci. 2021, 21, 1659–1667. [Google Scholar] [CrossRef]
- Lythe, J.; Kilding, A.E. Physical demands and physiological responses during elite field hockey. Int. J. Sports Med. 2011, 32, 523–528. [Google Scholar] [CrossRef]
- Buglione, A.; Ruscello, B.; Milia, R.; Migliaccio, G.M.; Granatelli, G.; D’Ottavio, S. Physical and Physiological demands of elite and sub-elite Field Hockey players. Int. J. Perform. Anal. Sport 2013, 13, 872–884. [Google Scholar] [CrossRef]
- Harper, D.J.; Morin, J.B.; Carling, C.; Kiely, J. Measuring maximal horizontal deceleration ability using radar technology: Reliability and sensitivity of kinematic and kinetic variables. Sports Biomech. 2020, 22, 1192–1208. [Google Scholar] [CrossRef] [PubMed]
- Harper, D.J.; Cohen, D.D.; Carling, C.; Kiely, J. Can countermovement jump neuromuscular performance qualities differentiate maximal horizontal deceleration ability in team sport athletes? Sports 2020, 8, 76. [Google Scholar] [CrossRef]
- Mendiguchia, J.; Edouard, P.; Samozino, P.; Brughelli, M.; Cross, M.; Gill, N.; Morin, J.B. Field monitoring of sprinting power–force–velocity profile before, during and after hamstring injury: Two case reports. J. Sports Sci. 2016, 34, 535–541. [Google Scholar] [CrossRef] [PubMed]
- Mendiguchia, J.; Samozino, P.; Martinez-Ruiz, E.; Schmikli, S.; Morin, J.B.; Mendez-Villanueva, A. Progression of mechanical properties during on-field sprint running after returning to sports from a hamstring muscle injury in soccer players. Int. J. Sports Med. 2014, 35, 690–695. [Google Scholar] [CrossRef] [PubMed]
- Morin, J.B.; Samozino, P. Interpreting Power-Force-Velocity Profiles for Individualized and Specific Training. Int. J. Sports Physiol. Perform. 2016, 11, 267–272. [Google Scholar] [CrossRef]
- Simperingham, K.; Cronin, J.; Ross, A. Advances in Sprint Acceleration Profiling for Field-Based Team-Sport Athletes: Utility, Reliability, Validity and Limitations. Sports Med. 2016, 46, 1619–1645. [Google Scholar] [CrossRef]
- Jia, Y.; Guo, L.; Wang, X. Real-time control systems. In Transportation Cyber-Physical Systems; Elsevier: Amsterdam, The Netherlands, 2018; pp. 81–113. [Google Scholar] [CrossRef]
- Jiménez-Reyes, P.; Samozino, P.; García-Ramos, A.; Cuadrado-Peñafiel, V.; Brughelli, M.; Morin, J.B. Relationship between vertical and horizontal force-velocity-power profiles in various sports and levels of practice. PeerJ 2018, 6, e5937. [Google Scholar] [CrossRef]
- Castagna, C.; Impellizzeri, F.M.; Bizzini, M.; Weston, M.; Manzi, V. Applicability of a change of direction ability field test in soccer assistant referees. J. Strength Cond. Res. 2011, 25, 860–866. [Google Scholar] [CrossRef]
- Morin, J.B.; Samozino, P.; Spreadsheet for Sprint Acceleration Force-Velocity-Power Profiling. Sport Science. 2017. Available online: https://jbmorin.net/2017/12/13/aspreadsheet-for-sprint-acceleration-force-velocity-powerprofiling/ (accessed on 5 November 2022).
- Simperingham, K.D.; Cronin, J.B.; Pearson, S.N.; Ross, A. Reliability of horizontal force–velocity–power profiling during short sprint-running accelerations using radar technology. Sports Biomech. 2019, 18, 88–99. [Google Scholar] [CrossRef]
- Vatcheva, K.; Lee, M.; McCormick, J.; Rahbar, M. Multicollinearity in Regression Analyses Conducted in Epidemiologic Studies. Epidemiology 2016, 6, 227. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, N. Detecting Multicollinearity in Regression Analysis. Am. J. Appl. Math. Stat. 2020, 8, 39–42. [Google Scholar] [CrossRef]
- Eertink, J.; Heymans, M.; Zwezerijnen, G.; Zijlstra, J.; de Vet, H.; Boellaard, R. External validation: A simulation study to compare cross-validation versus holdout or external testing to assess the performance of clinical prediction models using PET data from DLBCL patients. EJNMMI Res. 2022, 12, 58. [Google Scholar] [CrossRef] [PubMed]
- Geroldinger, A.; Lusa, L.; Nold, M.; Heinze, G. Leave-one-out cross-validation, penalization, and differential bias of some prediction model performance measures—A simulation study. Diagn. Progn. Res. 2023, 7, 9. [Google Scholar] [CrossRef] [PubMed]
- Kipp, K.; Warmenhoven, J. Applications of regularized regression models in sports biomechanics research. Sports Biomech. 2022, 1–19. [Google Scholar] [CrossRef]
- Przednowek, K.; Iskra, J.; Maszczyk, A.; Nawrocka, M. Regression shrinkage and neural models in predicting the results of 400-metres hurdles races. Biol. Sport 2016, 33, 415–421. [Google Scholar] [CrossRef]
- Sleivert, G.; Taingahue, M. The relationship between maximal jump-squat power and sprint acceleration in athletes. Eur. J. Appl. Physiol. 2004, 91, 46–52. [Google Scholar] [CrossRef]
- Vescovi, J.D. Impact of maximum speed on sprint performance during high-level youth female field hockey matches: Female athletes in motion (FAiM) study. Int. J. Sports Physiol. Perform. 2014, 9, 621–626. [Google Scholar] [CrossRef]
- González-Frutos, P.; Aguilar-Navarro, M.; Morencos, E.; Mallo, J.; Veiga, S. Relationships between strength and step frequency with fatigue index in repeated sprint ability. Int. J. Environ. Res. Public Health 2022, 19, 196. [Google Scholar] [CrossRef]
- Samozino, P.; Peyrot, N.; Edouard, P.; Nagahara, R.; Jimenez-Reyes, P.; Vanwanseele, B.; Morin, J. Optimal mechanical force-velocity profile for sprint acceleration performance. Scand. J. Med. Sci. Sports 2022, 32, 559–575. [Google Scholar] [CrossRef]
- Hicks, D.; Drummond, C.; Williams, K.; Van den Tillaar, R. Investigating Vertical and Horizontal Force-Velocity Profiles in Club-Level Field Hockey Athletes: Do Mechanical Characteristics Transfer Between Orientation of Movement? Int. J. Strength Cond. 2023, 3, 1–14. [Google Scholar] [CrossRef]
- Haugen, T.; Breitschädel, F.; Seiler, S. Sprint mechanical variables in elite athletes: Are force-velocity profiles sport specific or individual? PLoS ONE 2019, 14, e215551. [Google Scholar] [CrossRef] [PubMed]
- FIFA. Pruebas de Condición Física para los Árbitros; Ferecación Internacional de Fútbol Asociación (FIFA): Zürich, Switzerland, 2020. [Google Scholar]
- Weston, M.; Helsen, W.; MacMahon, C.; Kirkendall, D. The Impact of Specific High-Intensity Training Sessions on Football Referees’ Fitness Levels. Am. J. Sports Med. 2004, 32, 56–61. [Google Scholar] [CrossRef] [PubMed]
- Harper, D.J.; Cohen, D.D.; Rhodes, D.; Carling, C.; Kiely, J. Drop jump neuromuscular performance qualities associated with maximal horizontal deceleration ability in team sport athletes. Eur. J. Sport Sci. 2022, 22, 1005–1016. [Google Scholar] [CrossRef] [PubMed]
- Burgos-Jara, C.; Cerda-Kohler, H.; Aedo-Muñoz, E.; Miarka, B. Eccentric Resistance Training: A Methodological Proposal of Eccentric Muscle Exercise Classification Based on Exercise Complexity, Training Objectives, Methods, and Intensity. Appl. Sci. 2023, 13, 7969. [Google Scholar] [CrossRef]
- McBurnie, A.J.; Harper, D.J.; Jones, P.A.; Dos’Santos, T. Deceleration Training in Team Sports: Another Potential ‘Vaccine’ for Sports-Related Injury? Sports Med. 2022, 52, 1–12. [Google Scholar] [CrossRef]
- Brughelli, M.; Samozino, P. Mechanical Determinants of Sprinting Acceleration in Rugby Athletes. In Proceedings of the 23 Annual Congress of the European College of Sport Science, Dublin, Ireland, 4–7 July 2018; Available online: https://www.researchgate.net/publication/326252262 (accessed on 17 June 2023).
- Morin, J.B.; Bourdin, M.; Edouard, P.; Peyrot, N.; Samozino, P.; Lacour, J.R. Mechanical determinants of 100-m sprint running performance. Eur. J. Appl. Physiol. 2012, 112, 3921–3930. [Google Scholar] [CrossRef]
- Weyand, P.G.; Sandell, R.F.; Prime, D.N.; Bundle, M.W. The biological limits to running speed are imposed from the ground up. J. Appl. Physiol. 2010, 108, 950–961. [Google Scholar] [CrossRef]
- Hunter, J.P.; Marshall, R.N.; McNair, P.J. Relationships between ground reaction force impulse and kinematics of sprint-running acceleration. J. Appl. Biomech. 2005, 21, 31–43. [Google Scholar] [CrossRef]
- Morin, J.; Edouard, P.; Samozino, P. Technical ability of force application as a determinant factor of sprint performance. Med. Sci. Sports Exerc. 2011, 43, 1680–1688. [Google Scholar] [CrossRef]
- Spiteri, T.; Cochrane, J.L.; Hart, N.H.; Haff, G.G.; Nimphius, S. Effect of strength on plant foot kinetics and kinematics during a change of direction task. Eur. J. Sport Sci. 2013, 13, 646–652. [Google Scholar] [CrossRef] [PubMed]
- Nygaard, H.; Guldteig, H.; Van den Tillaar, R. Effect of Different Physical Training Forms on Change of Direction Ability: A Systematic Review and Meta-analysis. Sports Med. 2019, 5, 53. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Dellal, A.; Chamari, K.; Igonin, P.H.; Martin, C.; Hautier, C. The influence of short sprint performance, acceleration, and deceleration mechanical properties on change of direction ability in soccer players—A cross-sectional study. Front. Physiol. 2022, 13, 1027811. [Google Scholar] [CrossRef]
- Harper, D.J.; McBurnie, A.J.; Santos, T.D.; Eriksrud, O.; Evans, M.; Cohen, D.D. Biomechanical and Neuromuscular Performance Requirements of Horizontal Deceleration: A Review with Implications for Random Intermittent Multi-Directional Sports. Sports Med. 2022, 52, 2321–2354. [Google Scholar] [CrossRef]
- Van der Kruk, E.; Reijne, M. Accuracy of human motion capture systems for sport applications; state-of-the-art review. Eur. J. Sport Sci. 2018, 18, 806–819. [Google Scholar] [CrossRef] [PubMed]
- Knudson, D. Letter to editor regarding ‘the correlation of force-velocity-power relationship of a whole-body movement with 20 m and 60 m sprint’. Sport Biomech. 2021. [Google Scholar] [CrossRef] [PubMed]
- Haugen, T.; Seiler, S.; Sandbakk, Ø.; Tønnessen, E. The Training and Development of Elite Sprint Performance: An Integration of Scientific and Best Practice Literature. Sports Med. Open 2019, 5, 44. [Google Scholar] [CrossRef]
| Body Mass (kg) | Height (cm) | Age (Years Old) | |
|---|---|---|---|
| Defenders (8) | 64.8 ± 6.8 | 166.1 ± 2.1 | 27.0 ± 3.7 |
| Midfields (11) | 62.3 ± 5.0 | 166.2 ±4.5 | 24.8 ± 4.6 |
| Forwards (7) | 61.4 ± 2.7 | 166.4 ± 4.3 | 24.7 ± 4.3 |
| Total (26) | 63.1 ± 5.3 | 166.2 ± 4.1 | 25.38 ± 4.2 |
| Q25 | Median | Q75 | |
|---|---|---|---|
| 5-m (s) | 1.55 | 1.60 | 1.65 |
| 15-m (s) | 3.11 | 3.21 | 3.26 |
| 30-m (s) | 5.18 | 5.27 | 5.42 |
| F0 (N/kg) | 5.34 | 5.72 | 6.05 |
| V0 (m/s) | 7.5 | 7.97 | 8.34 |
| Pmax (W/kg) | 10.61 | 11.51 | 12.01 |
| FV profile (N/s/m) | −0.79 | −0.73 | −0.67 |
| RF max (%) | 41.28 | 43.4 | 44.83 |
| DRF (%/s/m) | −7.33 | −6.85 | −0.62 |
| Deceleration (m/s2) | 3.00 | 3.29 | 3.69 |
| CODA (s) | 9.01 | 9.23 | 9.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bustamante-Garrido, A.; Izquierdo, M.; Miarka, B.; Cuartero-Navarrete, A.; Pérez-Contreras, J.; Aedo-Muñoz, E.; Cerda-Kohler, H. Mechanical Determinants of Sprinting and Change of Direction in Elite Female Field Hockey Players. Sensors 2023, 23, 7663. https://doi.org/10.3390/s23187663
Bustamante-Garrido A, Izquierdo M, Miarka B, Cuartero-Navarrete A, Pérez-Contreras J, Aedo-Muñoz E, Cerda-Kohler H. Mechanical Determinants of Sprinting and Change of Direction in Elite Female Field Hockey Players. Sensors. 2023; 23(18):7663. https://doi.org/10.3390/s23187663
Chicago/Turabian StyleBustamante-Garrido, Alejandro, Mikel Izquierdo, Bianca Miarka, Ariel Cuartero-Navarrete, Jorge Pérez-Contreras, Esteban Aedo-Muñoz, and Hugo Cerda-Kohler. 2023. "Mechanical Determinants of Sprinting and Change of Direction in Elite Female Field Hockey Players" Sensors 23, no. 18: 7663. https://doi.org/10.3390/s23187663
APA StyleBustamante-Garrido, A., Izquierdo, M., Miarka, B., Cuartero-Navarrete, A., Pérez-Contreras, J., Aedo-Muñoz, E., & Cerda-Kohler, H. (2023). Mechanical Determinants of Sprinting and Change of Direction in Elite Female Field Hockey Players. Sensors, 23(18), 7663. https://doi.org/10.3390/s23187663









