Verification of the Mode Decomposition Technique for Closely Distributed Modal Systems in the State Space Domain
Abstract
1. Introduction
2. State Space Mode Decomposition
3. Experimental Validation of the New Mode Decomposition Method
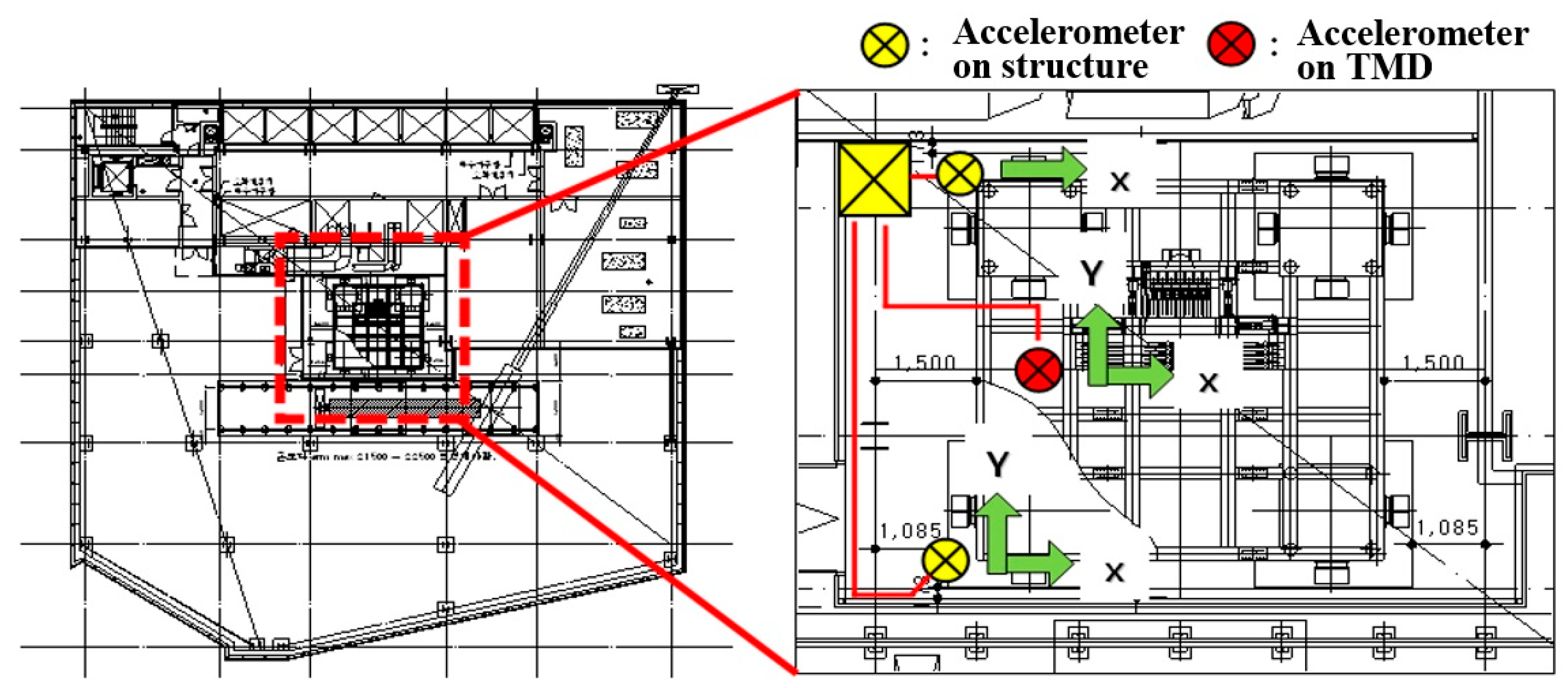
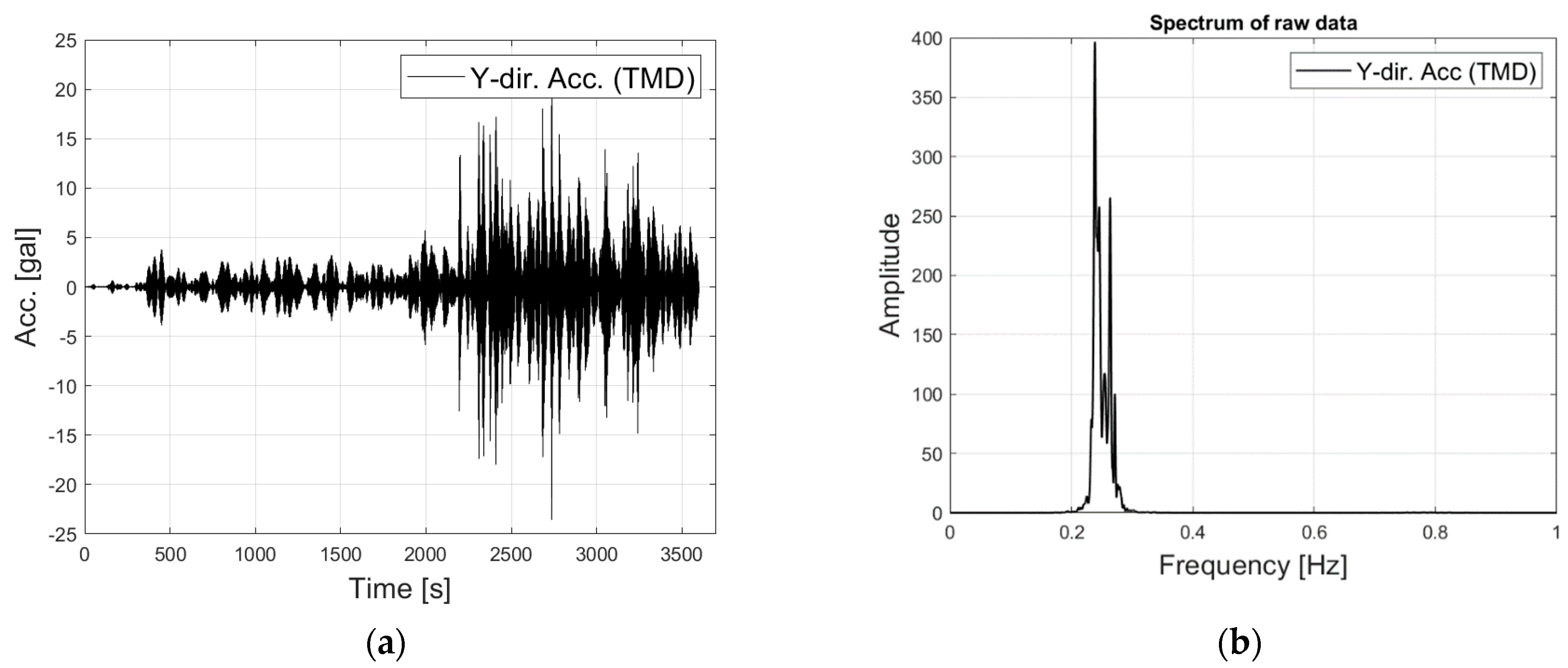
3.1. Benchmark Structure and Data Acquisition
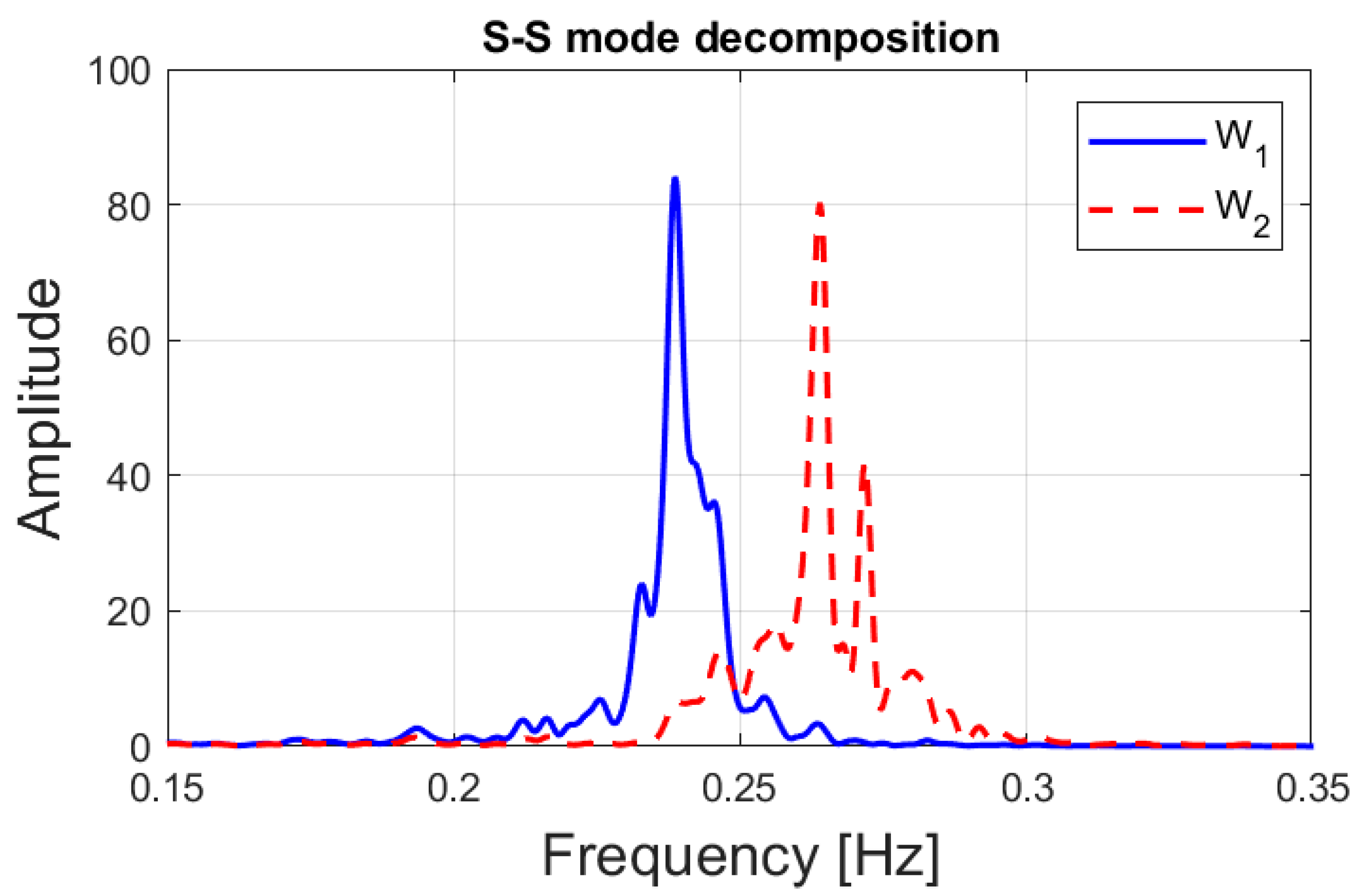
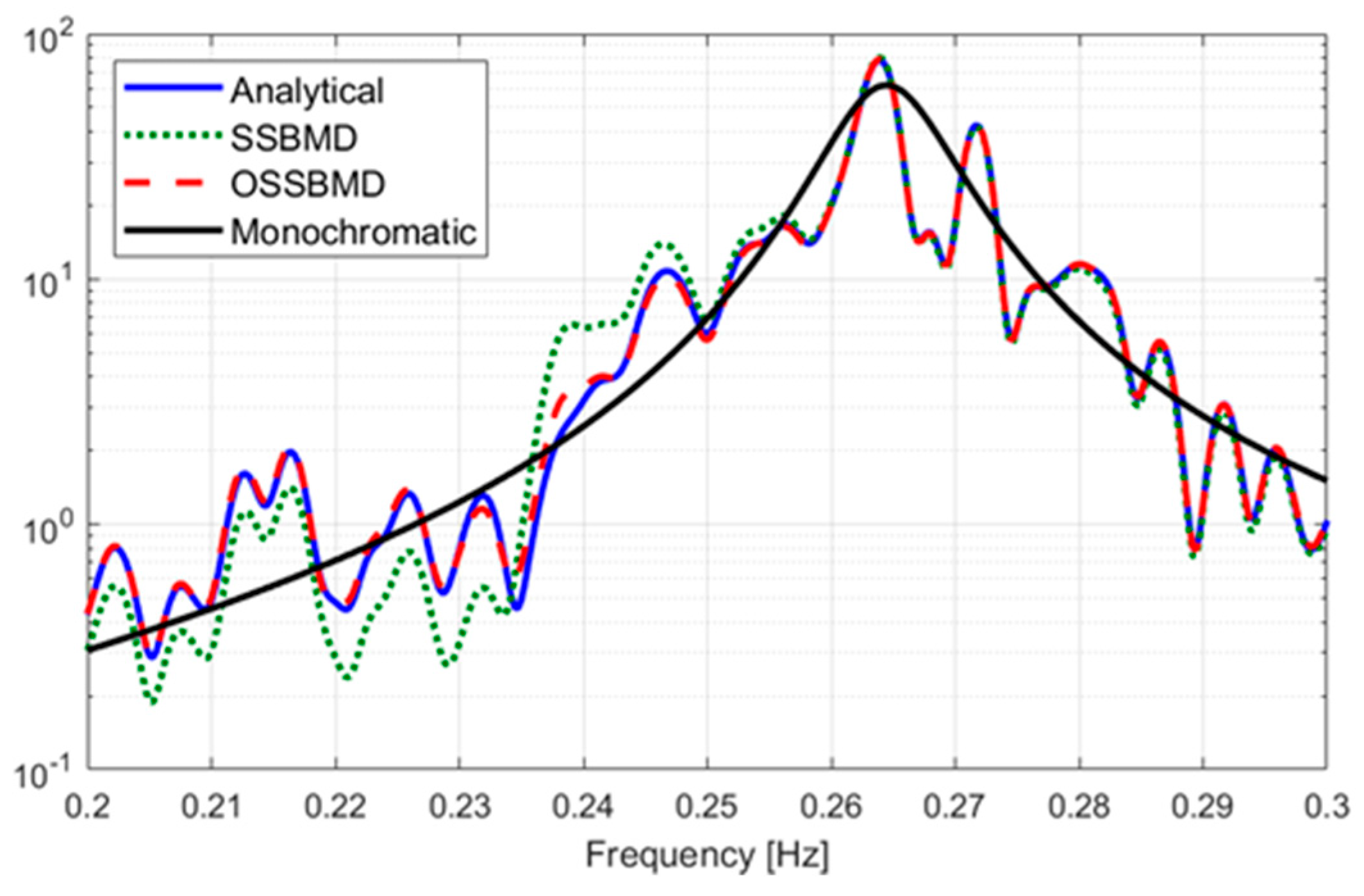
3.2. Validation of the Proposed Mode Decomposition Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Al-Hussein, A.; Haldar, A. Unscented Kalman filter with unknown input and weighted global iteration for health assessment of large structural systems. Struct. Control Health Monit. 2016, 23, 156–175. [Google Scholar] [CrossRef]
- Barbosh, M.; Sadhu, A.; Vogrig, M. Multisensor-based hybrid empirical mode decomposition method towards system identification of structures. Struct. Control Health Monit. 2018, 25, e2147. [Google Scholar] [CrossRef]
- Cruz, C.; Miranda, E. Evaluation of damping ratios for the seismic analysis of tall buildings. J. Struct. Eng. 2017, 143, 04016144. [Google Scholar] [CrossRef]
- Hwang, J.; Kwon, D.; Kareem, A. Estimation of structural modal parameters under winds using a virtual dynamic shaker. J. Eng. Mech. 2018, 144, 04018007. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441–445. [Google Scholar] [CrossRef]
- Brincker, R.; Ventura, C.; Andersen, P. Damping estimation by frequency domain decomposition. In Proceedings of the 19th Int’l Modal Analysis Conference (IMAC), Hyatt Orlando, FL, USA, 5–8 February 2001; pp. 698–703. [Google Scholar]
- Lamarche, C.; Paultre, P.; Proulx, J.; Mousseau, S. Assessment of the frequency domain decomposition technique by forced-vibration tests of a full-scale structure. Earthq. Eng. Struct. Dyn. 2008, 37, 487–494. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, T.; Tamura, Y. A frequency–spatial domain decomposition (FSDD) method for operational modal analysis. Mech. Syst. Sig. Process. 2010, 24, 1227–1239. [Google Scholar] [CrossRef]
- Le, T.; Argoul, P. Modal identification using the frequency scale domain decomposition technique of ambient vibration responses. J. Sound Vib. 2016, 384, 325–338. [Google Scholar] [CrossRef]
- Kim, D.; Oh, B.; Park, H.; Shim, H.; Kim, J. Modal identification for high-rise building structures using orthogonality of filtered response vectors. Comput.-Aided Civ. Infrastruct. Eng. 2017, 32, 1064–1084. [Google Scholar] [CrossRef]
- Balachandran, B.; Smith, S.W.; Pappa, R.S. On Identification of Nonlinear Interactions in Structures. J. Guid. Control Dyn. 1994, 17, 257–262. [Google Scholar] [CrossRef]
- Juan, J.N.; Pappa, R.S. An Eigensystem realization algorithm for modal parameter identification and model reduction. J. Guid. Control Dyn. 1985, 8, 620–627. [Google Scholar] [CrossRef]
- Andersen, M.S.; Niels, N.S. Modal decomposition of the pressure field on a bridge deck under vortex shedding using POD, DMD and ERA with correlation functions as Markov parameters. J. Wind Eng. Ind. Aerodyn. 2021, 215, 104699. [Google Scholar] [CrossRef]
- Li, B.; Au, S. An expectation-maximization algorithm for Bayesian operational modal analysis with multiple (possibly close) modes. Mech. Syst. Signal Process. 2019, 132, 490–511. [Google Scholar] [CrossRef]
- Van Overschee, P.; De Moor, B. Subspace Identification for Linear Systems. Springer: New York, NY, USA, 1996. [Google Scholar]
- Kerschen, G.; Poncelet, F.; Golinval, J. Physical interpretation of independent component analysis in structural dynamics. Mech. Syst. Signal Process. 2007, 21, 1561–1575. [Google Scholar] [CrossRef]
- Poncelet, F.; Kerschen, G.; Golinval, J.; Verhelst, D. Output only modal analysis using blind source separation techniques. Mech. Syst. Signal Process. 2007, 21, 2335–2358. [Google Scholar] [CrossRef]
- Sadhu, A.; Hazra, B.; Narasimhan, S. Blind identification of earthquake-excited structures. Smart Mater. Struct. 2012, 21, 045019. [Google Scholar] [CrossRef]
- Bell, A.; Sejnowski, T. Edges are independent components of natural scenes. In Advances in Neural Information Processing System; MIT Press: London, UK, 1996; Volume 9. [Google Scholar]
- Hyvaerinen, A.; Karhunen, J.; Oja, E. Independent Component Analysis; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Roberts, S.; Everson, R. Independent Component Analysis: Principles and Practice; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Brewick, P.T.; Smyth, A.W. On the application of blind source separation for damping estimation of bridges under traffic loading. J. Sound Vib. 2014, 333, 7333–7351. [Google Scholar] [CrossRef]
- Guo, Y. Nonstationary System Identification Techniques. Ph.D. Thesis, Department of Civil and Environmental Engineering and Earth Sciences, University of Notre Dame, Notre Dame, IN, USA, 2015. [Google Scholar]
- Guo, Y.; Kareem, A. System identification through nonstationary data using time-frequency blind source separation. J. Sound Vib. 2016, 371, 110–131. [Google Scholar] [CrossRef]
- Kareem, A.; Kijewski, T.; Tamura, Y. Mitigation of motions of tall buildings with specific examples of recent applications. Wind Struct. 1999, 2, 201–251. [Google Scholar] [CrossRef]
- Hwang, J.S.; Kwon, D.K.; Kareem, A. Frequency Domain State Space-Based Mode Decomposition Framework. J. Eng. Mech. ASCE 2019, 7, 04019051. [Google Scholar] [CrossRef]
- Hwang, J.S.; Kim, H. Mode decomposition of structures with closely distributed modes and nonclassical damping. Struct. Contr. Health Monit. 2017, 25, e2065. [Google Scholar] [CrossRef]
- McNeil, S. A Modal Identification Algorithm Combining Blind Source Separation and State Space Realization. J. Signal Inf. Process. 2013, 4, 173–185. [Google Scholar] [CrossRef]





| Type | Item | Value | ||
|---|---|---|---|---|
| Structure | Modal mass | 13,453 ton | ||
| Natural frequency | 0.25 Hz | |||
| Damping ratio | 0.78% | |||
| TMD | Moving mass of TMD | 160 ton | ||
| Natural frequency | 0.252 Hz (suboptimally tuned) | |||
| Damping ratio | 4.1% | |||
| System Matrix A | 0 | 0 | 1.0000 | 0 |
| 0 | 0 | 0 | 1.0000 | |
| −2.4972 | 0.0298 | −0.0260 | 0.0015 | |
| 2.5070 | −2.5070 | 0.1298 | −0.1298 | |
| Complex eigenvalue | 1st mode | 2nd mode | ||
| −0.0313 + 1.4963i | −0.0313 − 1.4963i | −0.0467 + 1.6612i | −0.0467 − 1.6612i | |
| Complex eigenmatrix | 1st mode | 2nd mode | ||
| 0.0163 − 0.0602i | 0.0163 + 0.0602i | 0.0183 + 0.0506i | 0.0183 − 0.0506i | |
| −0.0115 − 0.5519i | −0.0115 + 0.5519i | −0.0144 − 0.5126i | −0.0144 + 0.5126i | |
| 0.0896 + 0.0263i | 0.0896 − 0.0263i | −0.0850 + 0.0280i | −0.0850 − 0.0280i | |
| 0.8262 + 0.0000i | 0.8262 + 0.0000i | 0.8522 + 0.0000i | 0.8522 + 0.0000i | |
| Real eigenmatrix (normalized) | 0.0181 | 0.023 | −0.1083 | 0.0982 |
| −0.0277 | −0.0336 | −0.993 | −0.9937 | |
| 0.1084 | −0.0982 | 0.0473 | 0.0542 | |
| 0.9936 | 0.9943 | 0 | 0 | |
| Demixing matrix (normalized) | −0.0332 | 0.0332 | −0.9947 | 0.9936 |
| 0.0509 | −0.0509 | −0.0994 | −0.1071 | |
| 0.9931 | −0.9925 | −0.0206 | 0.0264 | |
| 0.1006 | 0.1062 | 0.0176 | −0.024 | |
| Mode Decomposition | Demixing Matrix | Correlation Coefficient | ||||||
|---|---|---|---|---|---|---|---|---|
| SSBMD ) | 0.0546 | 0.2509 | −0.9879 | 0.9889 | ||||
| 0.1415 | −0.0878 | −0.1138 | −0.1252 | 0.9968 | 0.9792 | 0.9954 | 0.9984 | |
| 0.9825 | −0.9570 | 0.0874 | 0.0718 | |||||
| 0.1078 | 0.1160 | 0.0589 | −0.0351 | |||||
| OSSBMD ) | 0.0533 | 0.1160 | −0.9914 | 0.9915 | ||||
| 0.1325 | −0.0495 | −0.0769 | −0.1030 | 0.9959 | 0.9975 | 0.9983 | 0.9989 | |
| 0.9854 | −0.9856 | 0.0786 | 0.0705 | |||||
| 0.0928 | 0.1124 | 0.0706 | −0.0357 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noh, J.; Hwang, J.-S. Verification of the Mode Decomposition Technique for Closely Distributed Modal Systems in the State Space Domain. Sensors 2023, 23, 7123. https://doi.org/10.3390/s23167123
Noh J, Hwang J-S. Verification of the Mode Decomposition Technique for Closely Distributed Modal Systems in the State Space Domain. Sensors. 2023; 23(16):7123. https://doi.org/10.3390/s23167123
Chicago/Turabian StyleNoh, Jungtae, and Jae-Seung Hwang. 2023. "Verification of the Mode Decomposition Technique for Closely Distributed Modal Systems in the State Space Domain" Sensors 23, no. 16: 7123. https://doi.org/10.3390/s23167123
APA StyleNoh, J., & Hwang, J.-S. (2023). Verification of the Mode Decomposition Technique for Closely Distributed Modal Systems in the State Space Domain. Sensors, 23(16), 7123. https://doi.org/10.3390/s23167123










