Advanced Stiffness Sensing through the Pincer Grasping of Soft Pneumatic Grippers
Abstract
1. Introduction
2. Materials and Methods
2.1. Fundamentals of Stiffness Measurement
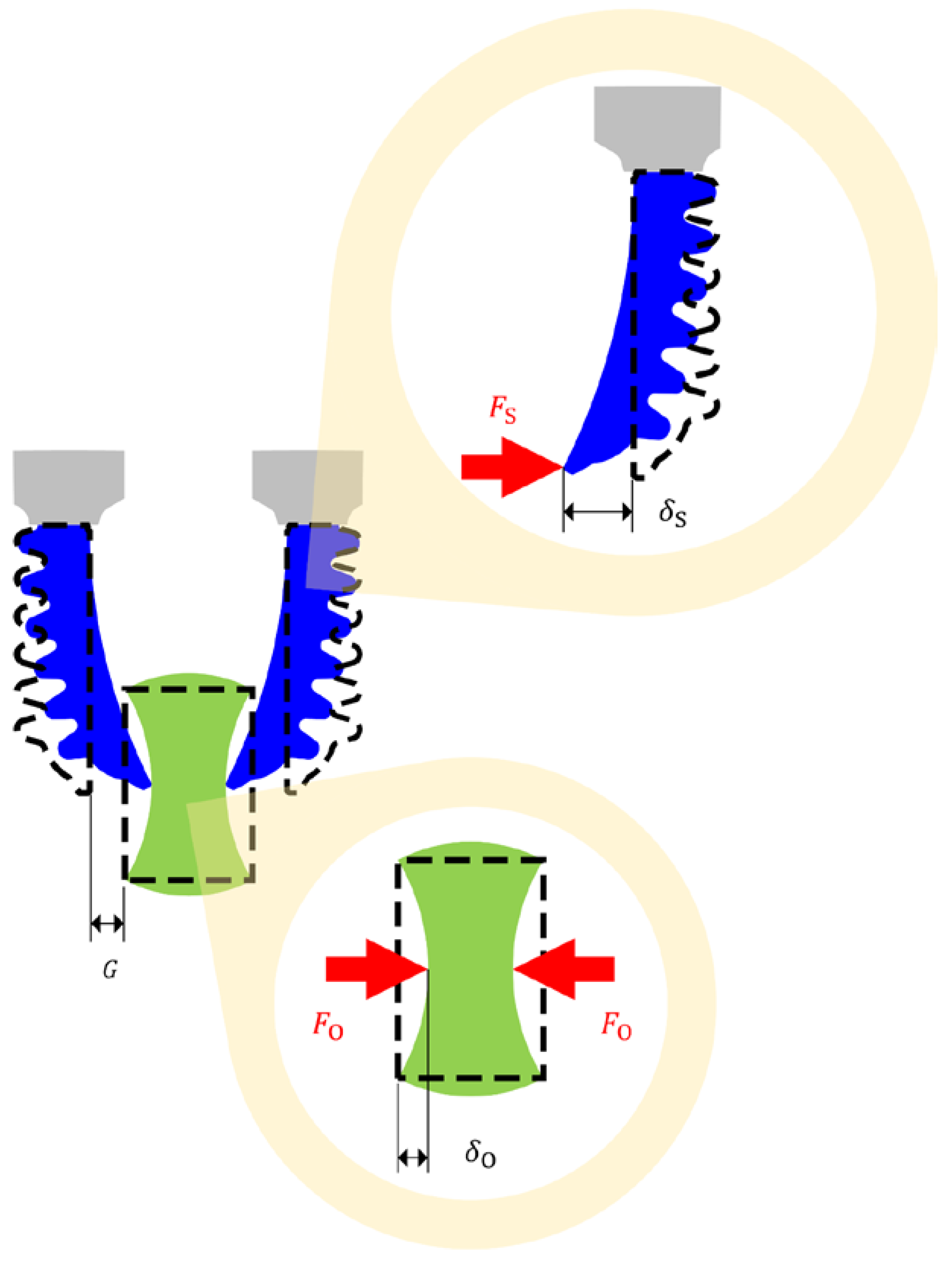
2.2. SPG Pincer Grasping
2.3. SPA Modeling
2.4. Stiffness Sensing through SPG Pincer Grasping
2.5. Validation
3. Results and Discussion
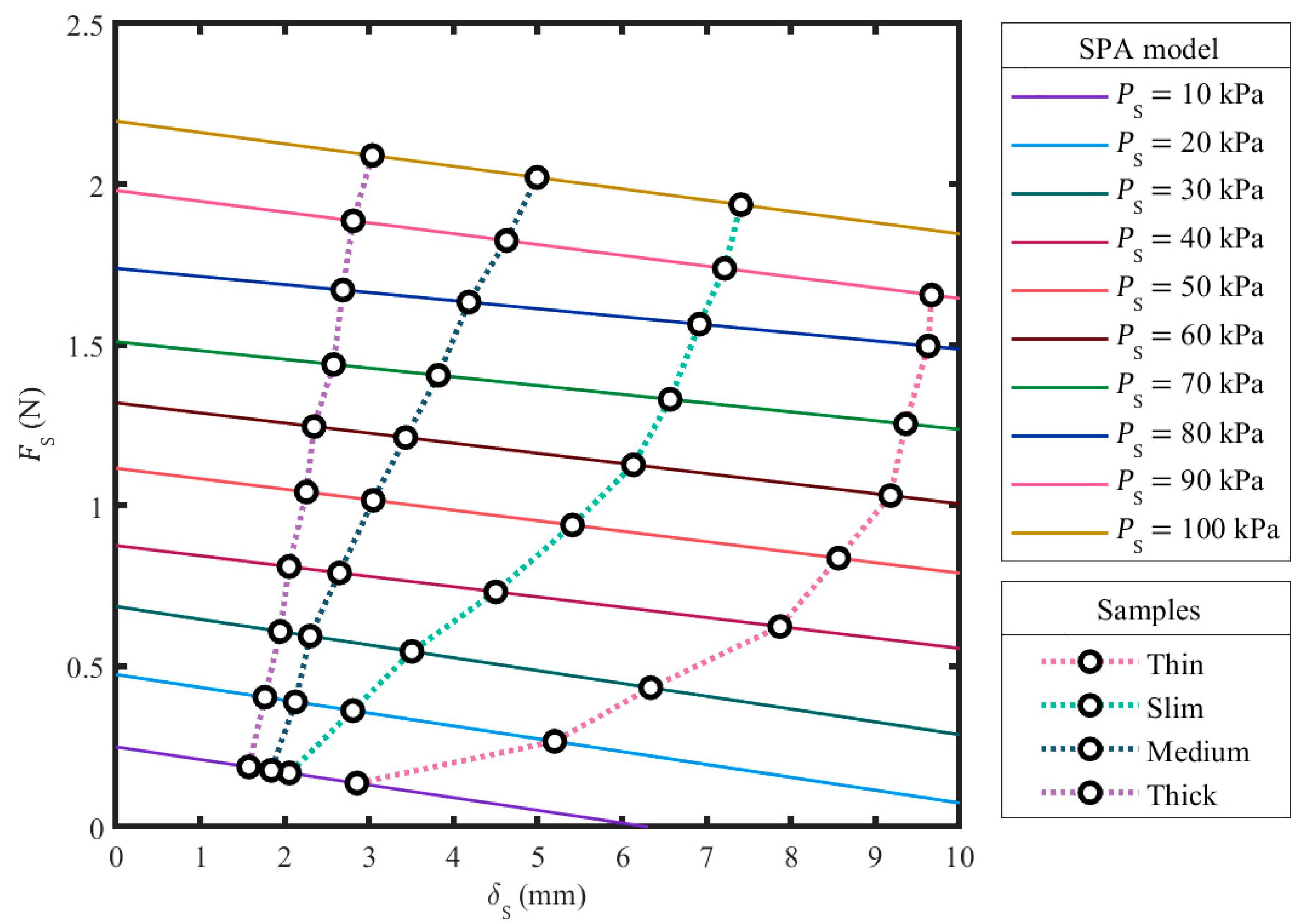
3.1. SPA Modeling
3.2. Stiffness Sensing through SPG Pincer Grasping
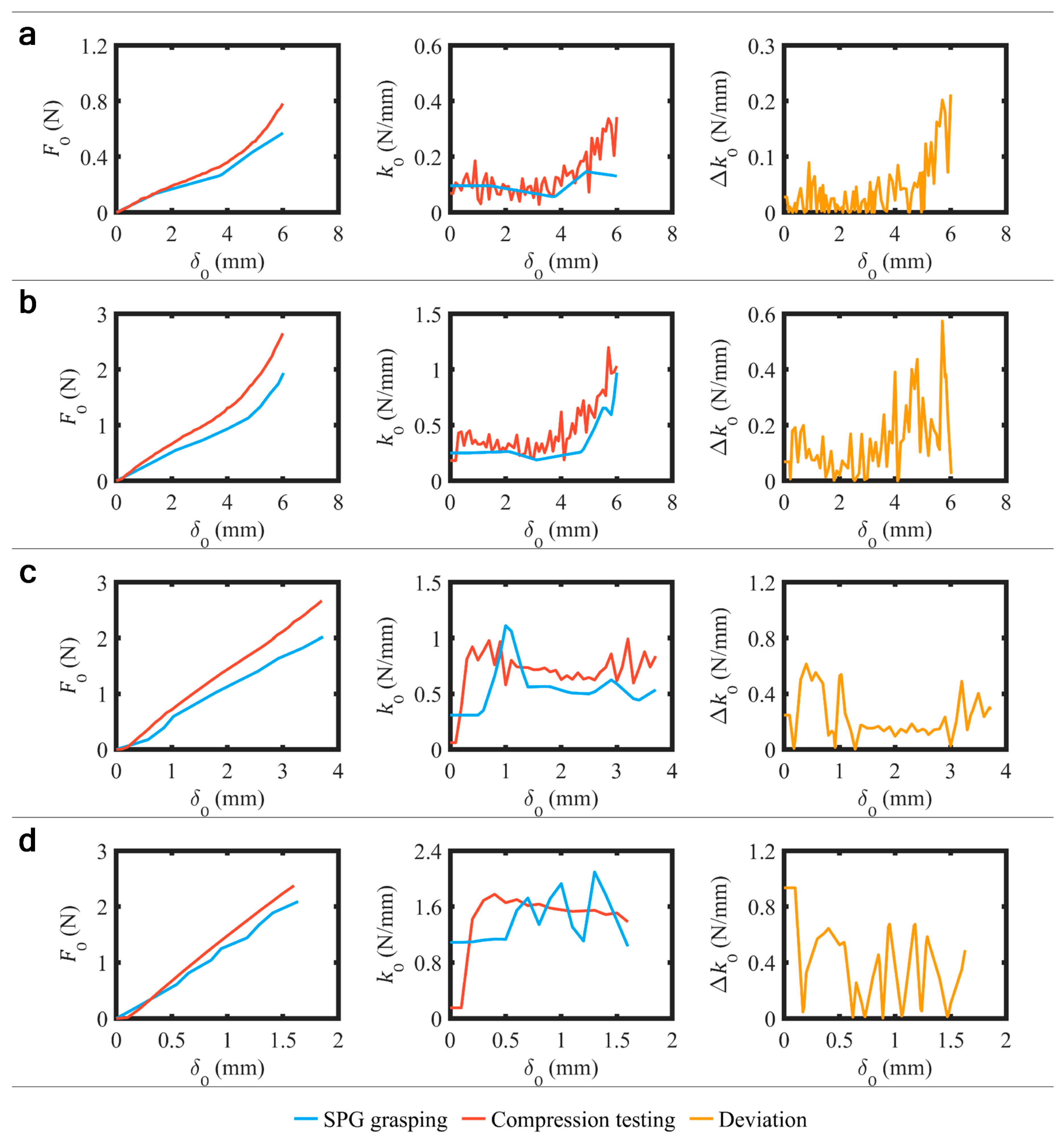
3.3. Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tsai, R.Y. A New Technique for Fully Autonomous and Efficient 3D Robotics Hand/Eye Calibration. IEEE Trans. Robot. Autom. 1989, 5, 345–358. [Google Scholar] [CrossRef]
- Levine, S.; Pastor, P.; Krizhevsky, A.; Ibarz, J.; Quillen, D. Learning hand-eye coordination for robotic grasping with deep learning and large-scale data collection. Int. J. Robot. Res. 2018, 37, 421–436. [Google Scholar] [CrossRef]
- Piazza, C.; Grioli, G.; Catalano, M.G.; Bicchi, A. A Century of Robotic Hands. Annu. Rev. Control Robot. Auton. Syst. 2019, 2, 1–32. [Google Scholar] [CrossRef]
- Marwan, Q.M.; Chua, S.C.; Kwek, L.C. Comprehensive Review on Reaching and Grasping of Objects in Robotics. Robotica 2021, 39, 1849–1882. [Google Scholar] [CrossRef]
- Han, L.; Trinkle, J.C.; Li, Z.X. Grasp analysis as linear matrix inequality problems. IEEE Trans. Robot. Autom. 2000, 16, 663–674. [Google Scholar] [CrossRef]
- Miller, A.T.; Allen, P.K. Graspit: A versatile simulator for robotic grasping. IEEE Robot. Autom. Mag. 2004, 11, 110–122. [Google Scholar] [CrossRef]
- Bohg, J.; Morales, A.; Asfour, T.; Kragic, D. Data-driven grasp synthesis-A survey. IEEE Trans. Robot. 2014, 30, 289–309. [Google Scholar] [CrossRef]
- Zhang, B.; Xie, Y.; Zhou, J.; Wang, K.; Zhang, Z. State-of-the-art robotic grippers, grasping and control strategies, as well as their applications in agricultural robots: A review. Comput. Electron. Agric. 2020, 177, 105694. [Google Scholar] [CrossRef]
- Monkman, G.J.; Hesse, S.; Steinmann, R.; Schunk, H. Robot Grippers; Wiley-VCH: Weinheim, Germany, 2006. [Google Scholar]
- Yang, Y.; Chen, Y.; Li, Y.; Chen, M.Z.Q.; Wei, Y. Bioinspired robotic fingers based on pneumatic actuator and 3D printing of smart material. Soft Robot. 2017, 4, 147–162. [Google Scholar] [CrossRef]
- Santina, C.D.; Arapi, V.; Averta, G.; Damiani, F.; Fiore, G.; Settimi, A.; Catalano, M.G.; Bacciu, D.; Bicchi, A.; Bianchi, M. Learning from humans how to grasp: A data-driven architecture for autonomous grasping with anthropomorphic soft hands. IEEE Robot. Autom. Lett. 2019, 4, 1533–1540. [Google Scholar] [CrossRef]
- Wang, H.; Abu-Dakka, F.J.; Le Nguyen, T.; Kyrki, V.; Xu, H. A Novel Soft Robotic Hand Design with Human-Inspired Soft Palm: Achieving a Great Diversity of Grasps. IEEE Robot. Autom. Mag. 2021, 28, 37–49. [Google Scholar] [CrossRef]
- Yoon, D.; Kim, K. Fully Passive Robotic Finger for Human-Inspired Adaptive Grasping in Environmental Constraints. IEEE/ASME Trans. Mechatron. 2022, 27, 3841–3852. [Google Scholar] [CrossRef]
- Johansson, R.S.; Flanagan, J.R. Coding and use of tactile signals from the fingertips in object manipulation tasks. Nat. Rev. Neurosci. 2009, 10, 345–359. [Google Scholar] [CrossRef] [PubMed]
- Feix, T.; Bullock, I.M.; Dollar, A.M. Analysis of human grasping behavior: Object characteristics and grasp type. IEEE Trans. Haptics 2014, 7, 311–323. [Google Scholar] [CrossRef]
- Lederman, S.J.; Klatzky, R.L. Haptic classification of common objects: Knowledge-driven exploration. Cogn. Psychol. 1990, 22, 421–459. [Google Scholar] [CrossRef]
- De-An, Z.; Jidong, L.; Wei, J.; Ying, Z.; Yu, C. Design and control of an apple harvesting robot. Biosyst. Eng. 2011, 110, 112–122. [Google Scholar] [CrossRef]
- Shaukat, A.; Gao, Y.; Kuo, J.A.; Bowen, B.A.; Mort, P.E. Visual classification of waste material for nuclear decommissioning. Robot. Auton. Syst. 2016, 75, 365–378. [Google Scholar] [CrossRef]
- Zhou, X.; Xu, X.; Liang, W.; Zeng, Z.; Shimizu, S.; Yang, L.T.; Jin, Q. Intelligent Small Object Detection for Digital Twin in Smart Manufacturing with Industrial Cyber-Physical Systems. IEEE Trans. Ind. Inform. 2022, 18, 1377–1386. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, D.; Lee, D.J. Automatic fabric defect detection with a wide-and-compact network. Neurocomputing 2019, 329, 329–338. [Google Scholar] [CrossRef]
- Czerniawski, T.; Nahangi, M.; Haas, C.; Walbridge, S. Pipe spool recognition in cluttered point clouds using a curvature-based shape descriptor. Autom. Constr. 2016, 71, 346–358. [Google Scholar] [CrossRef]
- Phanomchoeng, G.; Rajamani, R. Real-time estimation of rollover index for tripped rollovers with a novel unknown inputs nonlinear observer. In Proceedings of the American Control Conference, Montreal, QC, Canada, 27–29 June 2012; pp. 2090–2095. [Google Scholar]
- Phanomchoeng, G.; Chantranuwathana, S.; Charunyakorn, P. On-line Ladle Lining Temperature Estimation by Using Bounded Jacobian Nonlinear Observer. J. Iron Steel Res. Int. 2016, 23, 792–799. [Google Scholar] [CrossRef]
- Park, J.; Moon, W. A hybrid-type micro-gripper with an integrated force sensor. Microsyst. Technol. 2003, 9, 511–519. [Google Scholar] [CrossRef]
- Almassri, A.M.; Wan Hasan, W.Z.; Ahmad, S.A.; Ishak, A.J.; Ghazali, A.M.; Talib, D.N.; Wada, C. Pressure sensor: State of the art, design, and application for robotic hand. J. Sens. 2015, 2015, 846487. [Google Scholar] [CrossRef]
- Kappassov, Z.; Corrales, J.A.; Perdereau, V. Tactile sensing in dexterous robot hands—Review. Robot. Auton. Syst. 2015, 74, 195–220. [Google Scholar] [CrossRef]
- Kim, D.E.; Li, A.; Dau, M.N.; Kim, H.H.; Chung, W.Y. Deep learning-based smith predictor design for a remote grasping control system. J. Mech. Sci. Technol. 2022, 36, 2533–2545. [Google Scholar] [CrossRef]
- Calandra, R.; Owens, A.; Jayaraman, D.; Lin, J.; Yuan, W.; Malik, J.; Adelson, E.H.; Levine, S. More than a feeling: Learning to grasp and regrasp using vision and touch. IEEE Robot. Autom. Lett. 2018, 3, 3300–3307. [Google Scholar] [CrossRef]
- Girão, P.S.; Ramos, P.M.P.; Postolache, O.; Miguel Dias Pereira, J. Tactile sensors for robotic applications. Meas. J. Int. Meas. Confed. 2013, 46, 1257–1271. [Google Scholar] [CrossRef]
- Kim, G.S. Development of a three-axis gripper force sensor and the intelligent gripper using it. Sens. Actuators A Phys. 2007, 137, 213–222. [Google Scholar] [CrossRef]
- Romano, J.M.; Hsiao, K.; Niemeyer, G.; Chitta, S.; Kuchenbecker, K.J. Human-inspired robotic grasp control with tactile sensing. IEEE Trans. Robot. 2011, 27, 1067–1079. [Google Scholar] [CrossRef]
- Spiers, A.J.; Liarokapis, M.V.; Calli, B.; Dollar, A.M. Single-Grasp Object Classification and Feature Extraction with Simple Robot Hands and Tactile Sensors. IEEE Trans. Haptics 2016, 9, 207–220. [Google Scholar] [CrossRef]
- Spiers, A.J.; Morgan, A.S.; Srinivasan, K.; Calli, B.; Dollar, A.M. Using a Variable-Friction Robot Hand to Determine Proprioceptive Features for Object Classification during Within-Hand-Manipulation. IEEE Trans. Haptics 2020, 13, 600–610. [Google Scholar] [CrossRef] [PubMed]
- Ilievski, F.; Mazzeo, A.D.; Shepherd, R.F.; Chen, X.; Whitesides, G.M. Soft robotics for chemists. Angew. Chem. Int. Ed. 2011, 50, 1890–1895. [Google Scholar] [CrossRef] [PubMed]
- Bao, G.; Fang, H.; Chen, L.; Wan, Y.; Xu, F.; Yang, Q.; Zhang, L. Soft robotics: Academic insights and perspectives through bibliometric analysis. Soft Robot. 2018, 5, 229–241. [Google Scholar] [CrossRef] [PubMed]
- Boyraz, P.; Runge, G.; Raatz, A. An overview of novel actuators for soft robotics. Actuators 2018, 7, 48. [Google Scholar] [CrossRef]
- Bone, G.M.; Lambert, A.; Edwards, M. Automated modeling and robotic grasping of unknown three-dimensional objects. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 292–298. [Google Scholar]
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Thuruthel, T.G.; Ansari, Y.; Falotico, E.; Laschi, C. Control Strategies for Soft Robotic Manipulators: A Survey. Soft Robot. 2018, 5, 149–163. [Google Scholar] [CrossRef]
- Gorissen, B.; Reynaerts, D.; Konishi, S.; Yoshida, K.; Kim, J.W.; De Volder, M. Elastic Inflatable Actuators for Soft Robotic Applications. Adv. Mater. 2017, 29, 1604977. [Google Scholar] [CrossRef]
- Shintake, J.; Cacucciolo, V.; Floreano, D.; Shea, H. Soft Robotic Grippers. Adv. Mater. 2018, 30, 1707035. [Google Scholar] [CrossRef]
- Hughes, J.; Culha, U.; Giardina, F.; Guenther, F.; Rosendo, A.; Iida, F. Soft manipulators and grippers: A review. Front. Robot. AI 2016, 3, 69. [Google Scholar] [CrossRef]
- Hines, L.; Petersen, K.; Lum, G.Z.; Sitti, M. Soft Actuators for Small-Scale Robotics. Adv. Mater. 2017, 29, 1603483. [Google Scholar] [CrossRef]
- Polygerinos, P.; Correll, N.; Morin, S.A.; Mosadegh, B.; Onal, C.D.; Petersen, K.; Cianchetti, M.; Tolley, M.T.; Shepherd, R.F. Soft Robotics: Review of Fluid-Driven Intrinsically Soft Devices; Manufacturing, Sensing, Control, and Applications in Human-Robot Interaction. Adv. Eng. Mater. 2017, 19, 1700016. [Google Scholar] [CrossRef]
- Lipson, H. Challenges and Opportunities for Design, Simulation, and Fabrication of Soft Robots. Soft Robot. 2014, 1, 21–27. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X.; Huang, Y.; Cao, L.; Liu, J. A review of soft manipulator research, applications, and opportunities. J. Field Robot. 2022, 39, 281–311. [Google Scholar] [CrossRef]
- Su, H.; Hou, X.; Zhang, X.; Qi, W.; Cai, S.; Xiong, X.; Guo, J. Pneumatic Soft Robots: Challenges and Benefits. Actuators 2022, 11, 92. [Google Scholar] [CrossRef]
- Udupa, G.; Sreedharan, P.; Dinesh, P.S.; Kim, D. Asymmetric bellow flexible pneumatic actuator for miniature robotic soft gripper. J. Robot. 2014, 2014, 902625. [Google Scholar] [CrossRef]
- Yang, H.; Chen, Y.; Sun, Y.; Hao, L. A novel pneumatic soft sensor for measuring contact force and curvature of a soft gripper. Sens. Actuators A Phys. 2017, 266, 318–327. [Google Scholar] [CrossRef]
- Lotfiani, A.; Yi, X.; Shao, Z.; Zhao, H.; Parkestani, A.N. Analytical modeling and optimization of a corrugated soft pneumatic finger considering the performance of pinch and power grasps. Extrem. Mech. Lett. 2021, 44, 101215. [Google Scholar] [CrossRef]
- Alici, G.; Canty, T.; Mutlu, R.; Hu, W.; Sencadas, V. Modeling and Experimental Evaluation of Bending Behavior of Soft Pneumatic Actuators Made of Discrete Actuation Chambers. Soft Robot. 2018, 5, 24–35. [Google Scholar] [CrossRef]
- Homberg, B.S.; Katzschmann, R.K.; Dogar, M.R.; Rus, D. Haptic identification of objects using a modular soft robotic gripper. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; pp. 1698–1705. [Google Scholar]
- Chen, Y.; Guo, S.; Li, C.; Yang, H.; Hao, L. Size recognition and adaptive grasping using an integration of actuating and sensing soft pneumatic gripper. Robot. Auton. Syst. 2018, 104, 14–24. [Google Scholar] [CrossRef]
- Sankar, S.; Balamurugan, D.; Brown, A.; Ding, K.; Xu, X.; Low, J.H.; Yeow, C.H.; Thakor, N. Texture Discrimination with a Soft Biomimetic Finger Using a Flexible Neuromorphic Tactile Sensor Array That Provides Sensory Feedback. Soft Robot. 2021, 8, 577–587. [Google Scholar] [CrossRef]
- Smerd, R.; Winkler, S.; Salisbury, C.; Worswick, M.; Lloyd, D.; Finn, M. High strain rate tensile testing of automotive aluminum alloy sheet. Int. J. Impact Eng. 2005, 32, 541–560. [Google Scholar] [CrossRef]
- Kallio, M.; Lindroos, T.; Aalto, S.; Järvinen, E.; Kärnä, T.; Meinander, T. Dynamic compression testing of a tunable spring element consisting of a magnetorheological elastomer. Smart Mater. Struct. 2007, 16, 506–514. [Google Scholar] [CrossRef]
- Shi, J.; Woodruff, J.Z.; Umbanhowar, P.B.; Lynch, K.M. Dynamic In-Hand Sliding Manipulation. IEEE Trans. Robot. 2017, 33, 778–795. [Google Scholar] [CrossRef]
- Tamamoto, T.; Takeuchi, K.; Koganezawa, K. Development of gripper to achieve envelope grasping with underactuated mechanism using differential gear. J. Robot. Mechatron. 2018, 30, 855–862. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, Q.; Cai, D.; Chen, C.; Zhang, J.; Duan, W. Theoretical modelling of soft robotic gripper with bioinspired fibrillar adhesives. Mech. Adv. Mater. Struct. 2020, 29, 2250–2266. [Google Scholar] [CrossRef]
- Subhedar, M.S.; Mankar, V.H. Image steganography using redundant discrete wavelet transform and QR factorization. Comput. Electr. Eng. 2016, 54, 406–422. [Google Scholar] [CrossRef]
- Park, S.; Hwang, D. Softness-Adaptive Pinch-Grasp Strategy Using Fingertip Tactile Information of Robot Hand. IEEE Robot. Autom. Lett. 2021, 6, 6370–6377. [Google Scholar] [CrossRef]
- Kruachottikul, P.; Cooharojananone, N.; Phanomchoeng, G.; Chavarnakul, T.; Kovitanggoon, K.; Trakulwaranont, D.; Atchariyachanvanich, K. Bridge Sub Structure Defect Inspection Assistance by using Deep Learning. In Proceedings of the 2019 IEEE 10th International Conference on Awareness Science and Technology, iCAST 2019, Morioka, Japan, 25 October 2019. [Google Scholar]
- Kruachottikul, P.; Cooharojananone, N.; Phanomchoeng, G.; Chavarnakul, T.; Kovitanggoon, K.; Trakulwaranont, D. Deep learning-based visual defect-inspection system for reinforced concrete bridge substructure: A case of Thailand’s department of highways. J. Civ. Struct. Health Monit. 2021, 11, 949–965. [Google Scholar] [CrossRef]
- Dadashzadeh, M.; Abbaspour-Gilandeh, Y.; Mesri-Gundoshmian, T.; Sabzi, S.; Hernández-Hernández, J.L.; Hernández-Hernández, M.; Ignacio Arribas, J. Weed classification for site-specific weed management using an automated stereo computer-vision machine-learning system in rice fields. Plants 2020, 9, 559. [Google Scholar] [CrossRef]
- Ermilov, A.A.; Baranya, S.; Török, G.T. Image-based bed material mapping of a large river. Water 2020, 12, 916. [Google Scholar] [CrossRef]
- Zhang, M.; Hu, X.; Yao, J.; Zhao, L.; Li, J.; Gong, J. Line-based geometric consensus rectification and calibration from single distorted manhattan image. IEEE Access 2019, 7, 156400–156412. [Google Scholar] [CrossRef]
- Li, J.; Bennett, B.L.; Karam, L.J.; Pettinato, J.S. Stereo Vision Based Automated Solder Ball Height and Substrate Coplanarity Inspection. IEEE Trans. Autom. Sci. Eng. 2016, 13, 757–771. [Google Scholar] [CrossRef]
- Choi, I.O.; Park, S.H.; Kang, K.B.; Lee, S.H.; Kim, K.T. Efficient parameter estimation for cone-shaped target based on distributed radar networks. IEEE Sens. J. 2019, 19, 9736–9747. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sithiwichankit, C.; Chancharoen, R. Advanced Stiffness Sensing through the Pincer Grasping of Soft Pneumatic Grippers. Sensors 2023, 23, 6094. https://doi.org/10.3390/s23136094
Sithiwichankit C, Chancharoen R. Advanced Stiffness Sensing through the Pincer Grasping of Soft Pneumatic Grippers. Sensors. 2023; 23(13):6094. https://doi.org/10.3390/s23136094
Chicago/Turabian StyleSithiwichankit, Chaiwuth, and Ratchatin Chancharoen. 2023. "Advanced Stiffness Sensing through the Pincer Grasping of Soft Pneumatic Grippers" Sensors 23, no. 13: 6094. https://doi.org/10.3390/s23136094
APA StyleSithiwichankit, C., & Chancharoen, R. (2023). Advanced Stiffness Sensing through the Pincer Grasping of Soft Pneumatic Grippers. Sensors, 23(13), 6094. https://doi.org/10.3390/s23136094





