Multimode Optical Interconnects on Silicon Interposer Enable Confidential Hardware-to-Hardware Communication
Abstract
1. Introduction
2. Fabrication of OTSVs on Silicon Interposer and Its Performance
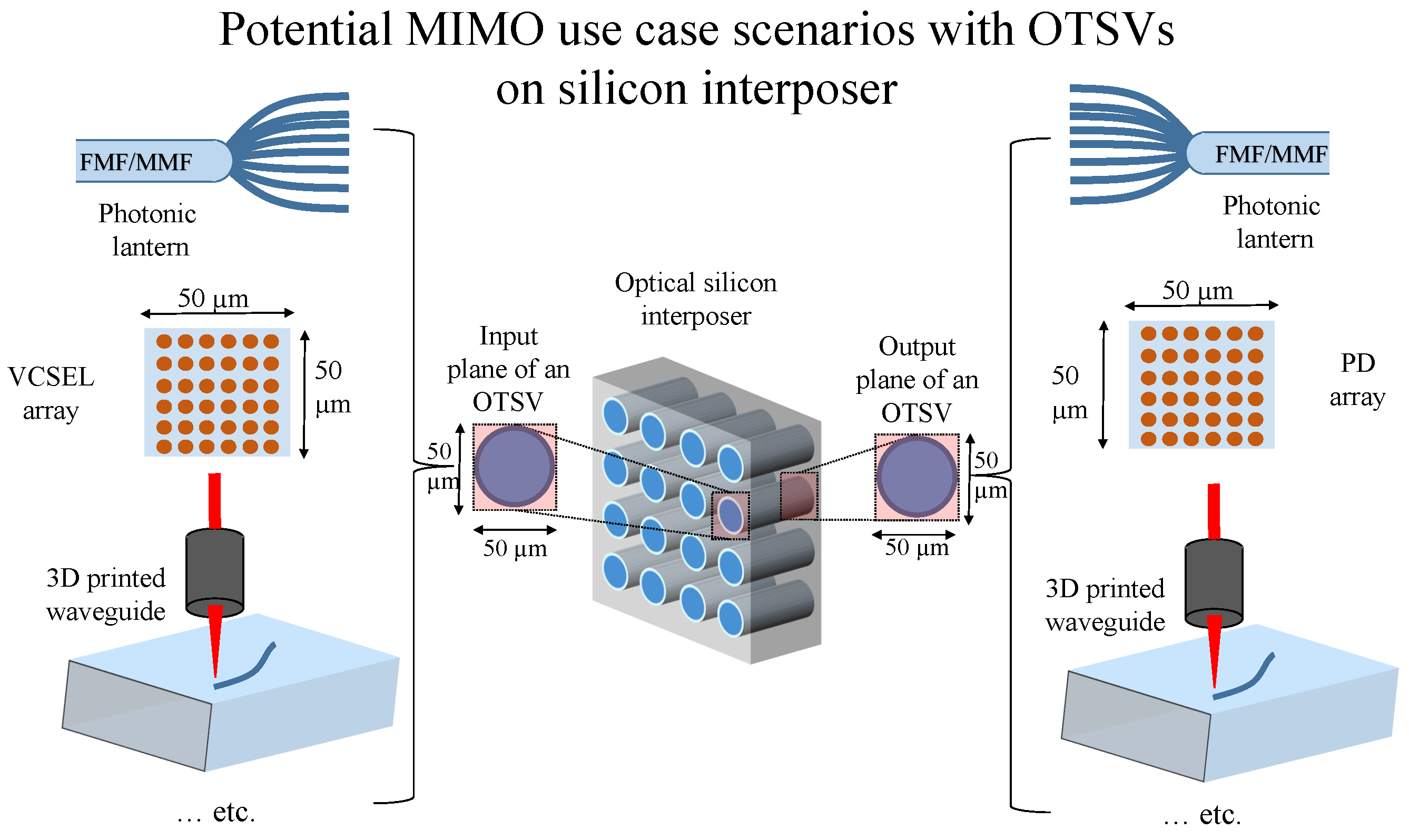
3. Application Scenarios
4. Experimental Procedure
5. Results and Discussion
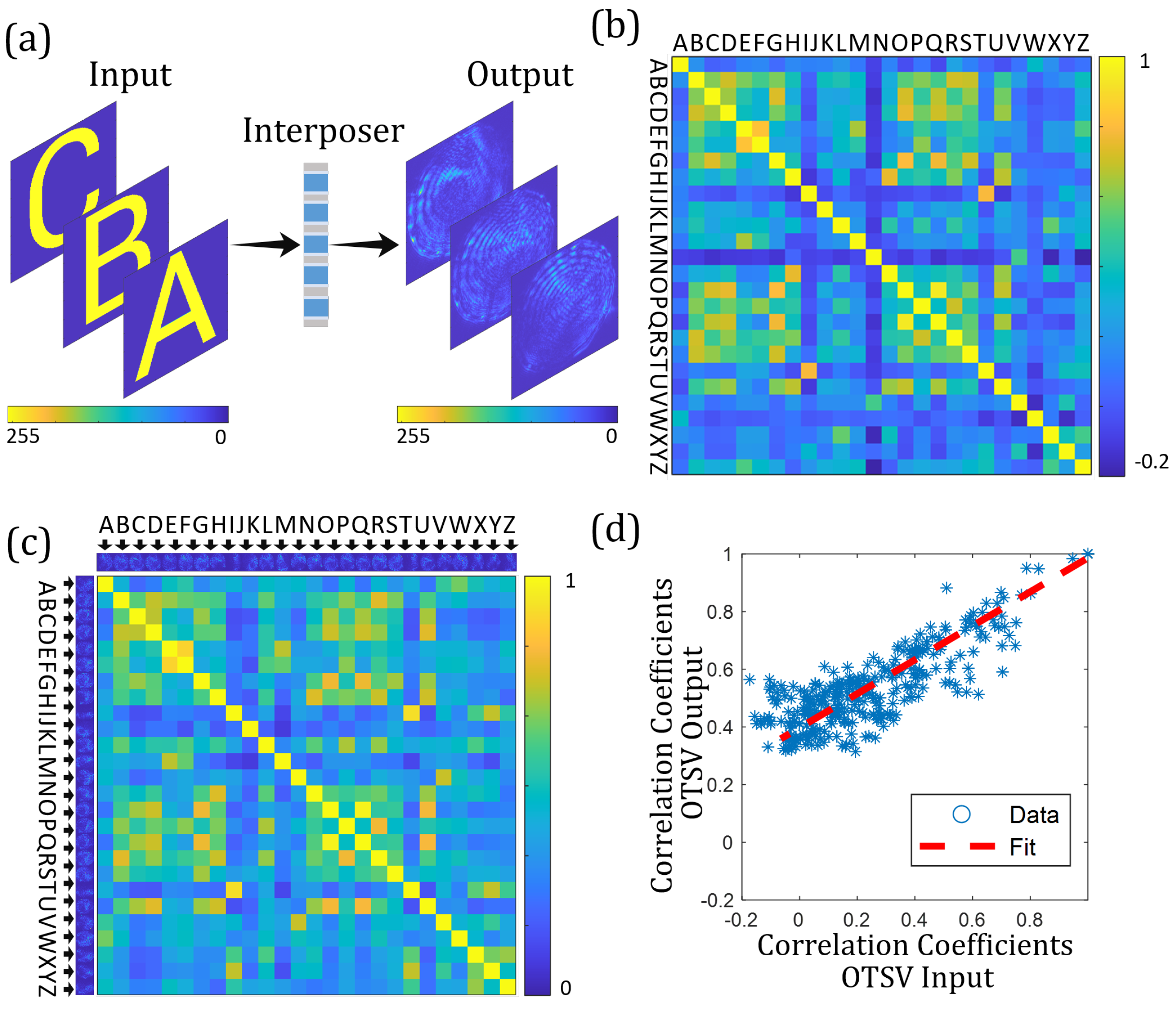
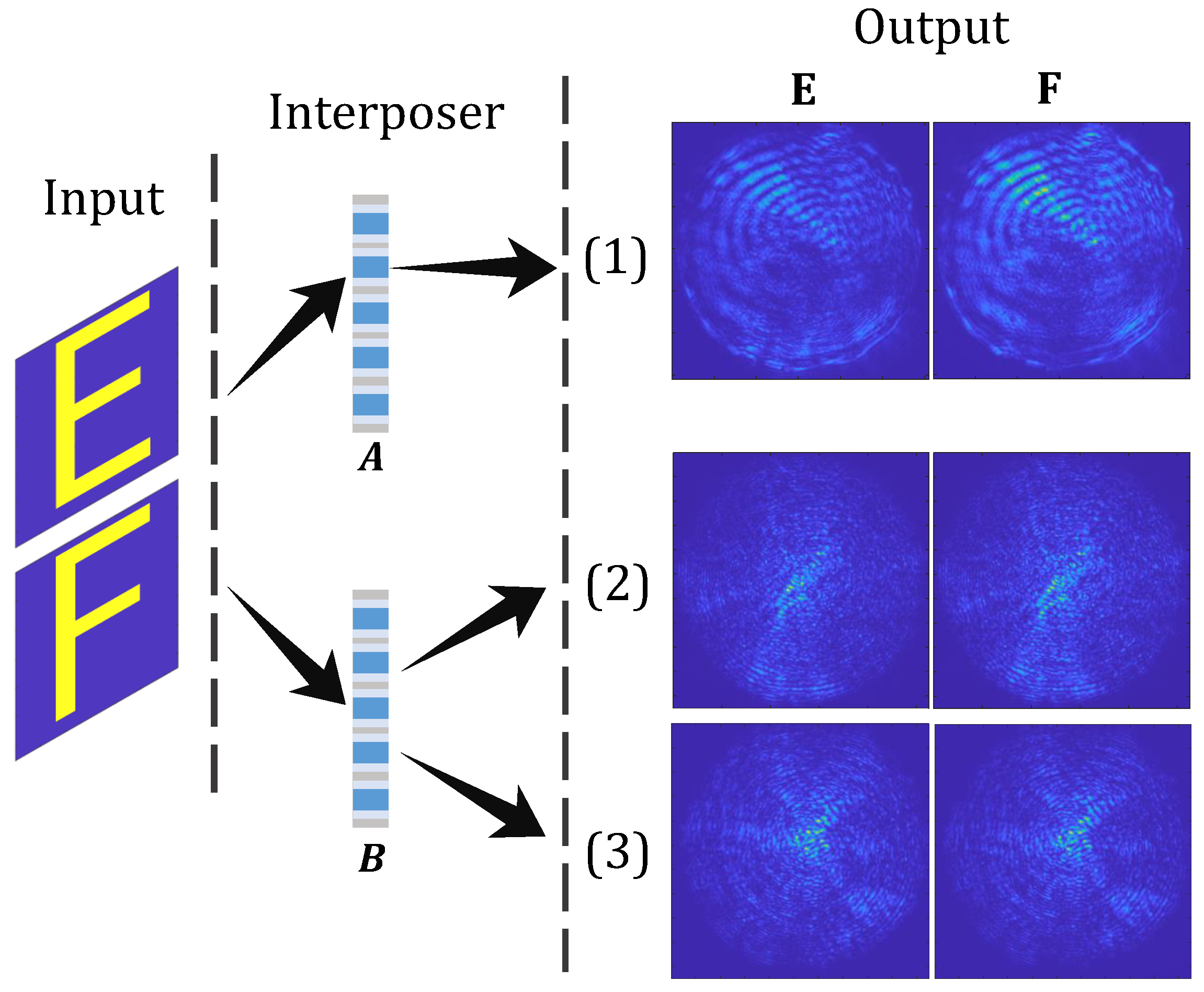
5.1. Non-Orthogonal Input Base: Alphabetic Letters
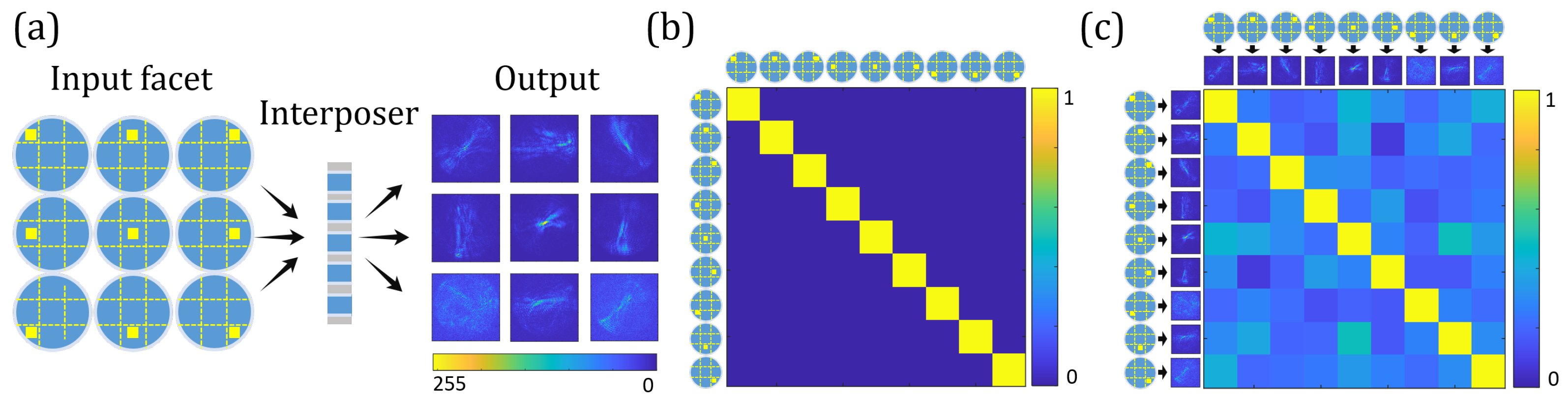
5.2. Orthogonal Input Base: Focal Points
5.3. Comparison of Different OTSV Samples
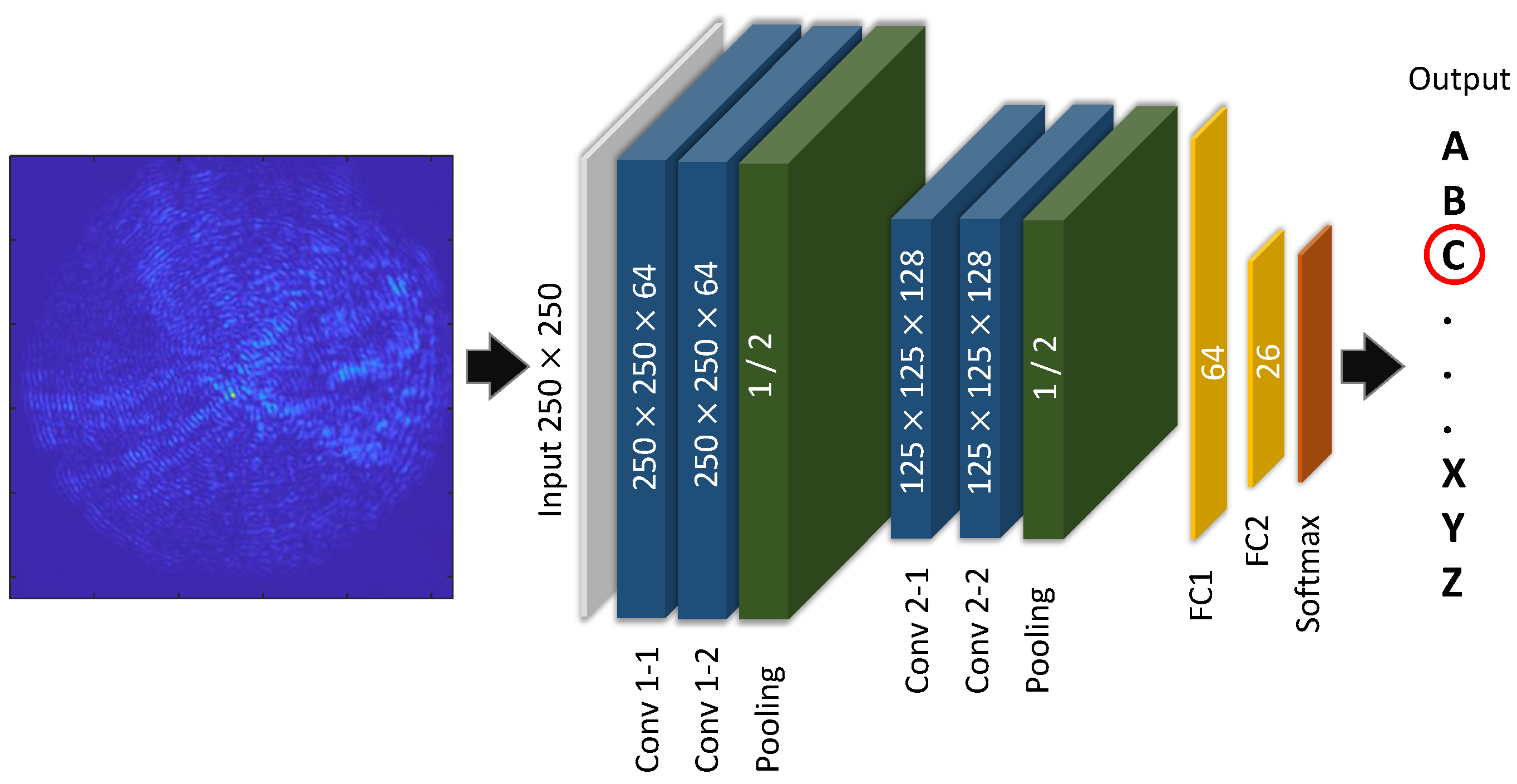
5.4. Recognition of the Speckle Patterns through a Deep Neural Network
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pflaum, A.A.; Gölzer, P. The IoT and digital transformation: Toward the data-driven enterprise. IEEE Pervasive Comput. 2018, 17, 87–91. [Google Scholar] [CrossRef]
- Zeadally, S.; Jabeur, N. Cyber-Physical System Design with Sensor Networking Technologies; Institution of Engineering and Technology: London, UK, 2016. [Google Scholar]
- Elfadel, A.; Fettweis, G. 3D Stacked Chips; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Alguliyev, R.; Imamverdiyev, Y.; Sukhostat, L. Cyber-physical systems and their security issues. Comput. Ind. 2018, 100, 212–223. [Google Scholar] [CrossRef]
- Shearon, C. The New Standard for Cyber Security. In Proceedings of the 2020 Pan Pacific Microelectronics Symposium (Pan Pacific), Kohala Coast, HI, USA, 10–13 February 2020; pp. 1–9. [Google Scholar]
- Shaneman, K.; Gray, S. Optical network security: Technical analysis of fiber tapping mechanisms and methods for detection & prevention. In Proceedings of the IEEE MILCOM 2004. Military Communications Conference, 2004, Monterey, CA, USA, 31 October–3 November 2004; Volume 2, pp. 711–716. [Google Scholar]
- Medard, M.; Marquis, D.; Barry, R.A.; Finn, S.G. Security issues in all-optical networks. IEEE Netw. 1997, 11, 42–48. [Google Scholar] [CrossRef]
- Song, E.C.; Soljanin, E.; Cuff, P.; Poor, H.V.; Guan, K. Rate-distortion-based physical layer secrecy with applications to multimode fiber. IEEE Trans. Commun. 2014, 62, 1080–1090. [Google Scholar] [CrossRef]
- Guan, K.; Cho, J.; Winzer, P.J. Physical layer security in fiber-optic MIMO-SDM systems: An overview. Opt. Commun. 2018, 408, 31–41. [Google Scholar] [CrossRef]
- Li, K.; Yan, P.G.; Cai, Q.Y. Quantum computing and the security of public key cryptography. Fundam. Res. 2021, 1, 85–87. [Google Scholar] [CrossRef]
- Halak, B.; Yilmaz, Y.; Shiu, D. Comparative Analysis of Energy Costs of Asymmetric vs Symmetric Encryption-Based Security Applications. IEEE Access 2022, 10, 76707–76719. [Google Scholar] [CrossRef]
- Gao, Y.; Al-Sarawi, S.F.; Abbott, D. Physical unclonable functions. Nat. Electron. 2020, 3, 81–91. [Google Scholar] [CrossRef]
- Pappu, R.; Recht, B.; Taylor, J.; Gershenfeld, N. Physical one-way functions. Science 2002, 297, 2026–2030. [Google Scholar] [CrossRef] [PubMed]
- Goorden, S.A.; Horstmann, M.; Mosk, A.P.; Škorić, B.; Pinkse, P.W. Quantum-secure authentication of a physical unclonable key. Optica 2014, 1, 421–424. [Google Scholar] [CrossRef]
- Hiller, M.; Kürzinger, L.; Sigl, G.; Müelich, S.; Puchinger, S.; Bossert, M. Low-area Reed decoding in a generalized concatenated code construction for PUFs. In Proceedings of the 2015 IEEE Computer Society Annual Symposium on VLSI, Montpellier, France, 8–10 July 2015; pp. 143–148. [Google Scholar]
- Wyner, A.D. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Mahdavifar, H.; Vardy, A. Achieving the secrecy capacity of wiretap channels using polar codes. IEEE Trans. Inf. Theory 2011, 57, 6428–6443. [Google Scholar] [CrossRef]
- Liu, R.; Trappe, W. Securing Wireless Communications at the Physical Layer; Springer: Berlin/Heidelberg, Germany, 2010; Volume 7. [Google Scholar]
- Shiu, Y.S.; Chang, S.Y.; Wu, H.C.; Huang, S.C.H.; Chen, H.H. Physical layer security in wireless networks: A tutorial. IEEE Wirel. Commun. 2011, 18, 66–74. [Google Scholar] [CrossRef]
- Besser, K.L.; Jorswieck, E.A. Bounds on the secrecy outage probability for dependent fading channels. IEEE Trans. Commun. 2020, 69, 443–456. [Google Scholar] [CrossRef]
- Vellekoop, I.M.; Lagendijk, A.; Mosk, A. Exploiting disorder for perfect focusing. Nat. Photonics 2010, 4, 320–322. [Google Scholar] [CrossRef]
- Yu, S.; Qiu, C.W.; Chong, Y.; Torquato, S.; Park, N. Engineered disorder in photonics. Nat. Rev. Mater. 2021, 6, 226–243. [Google Scholar] [CrossRef]
- Cao, H.; Eliezer, Y. Harnessing disorder for photonic device applications. Appl. Phys. Rev. 2022, 9, 011309. [Google Scholar] [CrossRef]
- Guan, K.; Tulino, A.M.; Winzer, P.J.; Soljanin, E. Secrecy capacities in space-division multiplexed fiber optic communication systems. IEEE Trans. Inf. Forensics Secur. 2015, 10, 1325–1335. [Google Scholar] [CrossRef]
- Rothe, S.; Koukourakis, N.; Radner, H.; Lonnstrom, A.; Jorswieck, E.; Czarske, J.W. Physical layer security in multimode fiber optical networks. Sci. Rep. 2020, 10, 2740. [Google Scholar] [CrossRef]
- Rothe, S.; Besser, K.L.; Krause, D.; Kuschmierz, R.; Koukourakis, N.; Jorswieck, E.; Czarske, J.W. Securing Data in Multimode Fibers by Exploiting Mode-Dependent Light Propagation Effects. Research 2023, 6, 0065. [Google Scholar] [CrossRef]
- Townsend, P.D. Quantum cryptography on multiuser optical fibre networks. Nature 1997, 385, 47–49. [Google Scholar] [CrossRef]
- Charania, S.; Neumann, N.; Killge, S.; Winkler, F.; Al-Husseini, Z.; Szilagyi, L.; Henker, R.; Ellinger, F.; Plettemeier, D.; Bartha, J.W. Design, Fabrication, and Comparison of 3D Multimode Optical Interconnects on Silicon Interposer. J. Light. Technol. 2020, 38, 3454–3460. [Google Scholar] [CrossRef]
- Borhani, N.; Kakkava, E.; Moser, C.; Psaltis, D. Learning to see through multimode fibers. Optica 2018, 5, 960–966. [Google Scholar] [CrossRef]
- Ramalingam, S.; Liu, H.; Kim, M.; Ang, B.; Kwon, W.S.; Lee, T.; Wu, S.; Chang, J.; Wu, E.; Wu, X.; et al. A New Class of High-Capacity, Resource-Rich Field-Programmable Gate Arrays Enabled by Three- Dimensional Integration Chip-Stacked Silicon Interconnect Technology. In 3D Integration in VLSI Circuits; CRC Press: Boca Raton, FL, USA, 2018; Chapter 3. [Google Scholar] [CrossRef]
- The Most Cost-Effective Integrator (TSV Interposer) for 3D IC Integration System-in-Package (SiP), Vol. ASME 2011 Pacific Rim Technical Conference and Exhibition on Packaging and Integration of Electronic and Photonic Systems, MEMS and NEMS: Volume 1, International Electronic Packaging Technical Conference and Exhibition, 2011. Available online: https://asmedigitalcollection.asme.org/InterPACK/proceedings-pdf/InterPACK2011/44618/53/4597366/53_1.pdf (accessed on 27 July 2022).
- Killge, S.; Charania, S.; Richter, K.; Neumann, N.; Al-Husseini, Z.; Plettemeier, D.; Bartha, J.W. Realization of optical multimode TSV waveguides for Si-Interposer in 3D-chip-stacks. In Proceedings of the Micro-Structured and Specialty Optical Fibres V; Kalli, K., Kanka, J., Mendez, A., Peterka, P., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2017; Volume 10232, p. 102320T. [Google Scholar]
- Neumann, N.; Charania, S.; Killge, S.; al Husseini, Z.; Henker, R.; Ellinger, F.; Bartha, J.; Plettemeier, D. Modeling and characterization of optical TSVs. In Proceedings of the Optical Fibers and Their Applications 2017; Dorosz, J., Romaniuk, R.S., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2017; Volume 10325, pp. 169–176. [Google Scholar]
- Charania, S.; Lüngen, S.; Al-Husseini, Z.; Killge, S.; Nieweglowski, K.; Neumann, N.; Plettemeier, D.; Bock, K.; Bartha, J.W. Micro structured coupling elements for 3D silicon optical interposer. In Proceedings of the Integrated Optics: Physics and Simulations III, Prague, Czech Republic, 24–25 April 2017; Cheben, P., Čtyroký, J., Molina-Fernández, I., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2017; Volume 10242, pp. 176–185. [Google Scholar]
- Lüngen, S.; Charania, S.; Tiedje, T.; Nieweglowski, K.; Killge, S.; Lorenz, L.; Bartha, J.; Bock, K. 3D Optical Coupling Techniques on Polymer Waveguides for Wafer and Board Level Integration. In Proceedings of the 2017 IEEE 67th Electronic Components and Technology Conference (ECTC), Orlando, FL, USA, 30 May–2 June 2017; pp. 1612–1618. [Google Scholar]
- Leon-Saval, S.G.; Argyros, A.; Bland-Hawthorn, J. Photonic lanterns: A study of light propagation in multimode to single-mode converters. Opt. Express 2010, 18, 8430–8439. [Google Scholar]
- Birks, T.A.; Gris-Sánchez, I.; Yerolatsitis, S.; Leon-Saval, S.G.; Thomson, R.R. The photonic lantern. Adv. Opt. Photon. 2015, 7, 107–167. [Google Scholar]
- Lee, W.H. Binary synthetic holograms. Appl. Opt. 1974, 13, 1677–1682. [Google Scholar]
- Rothe, S.; Radner, H.; Koukourakis, N.; Czarske, J.W. Transmission matrix measurement of multimode optical fibers by mode-selective excitation using one spatial light modulator. Appl. Sci. 2019, 9, 195. [Google Scholar] [CrossRef]
- Pohle, D.; Rothe, S.; Barbosa, F.; Ferreira, F.; Koukourakis, N.; Czarske, J. Intelligent self calibration tool for adaptive mode multiplexers using multiplane light conversion. J. Eur. Opt. Soc.-Rapid Publ. 2023, 19, 29. [Google Scholar]
- Wu, J.; Wang, T.; Uckermann, O.; Galli, R.; Schackert, G.; Cao, L.; Czarske, J.; Kuschmierz, R. Learned end-to-end high-resolution lensless fiber imaging towards real-time cancer diagnosis. Sci. Rep. 2022, 12, 18846. [Google Scholar]
- Rothe, S.; Zhang, Q.; Koukourakis, N.; Czarske, J. Intensity-Only Mode Decomposition on Multimode Fibers Using a Densely Connected Convolutional Network. J. Light. Technol. 2021, 39, 1672–1679. [Google Scholar]
- Zhang, Q.; Rothe, S.; Koukourakis, N.; Czarske, J. Learning the matrix of few-mode fibers for high-fidelity spatial mode transmission. APL Photonics 2022, 7, 066104. [Google Scholar]
- Sun, J.; Wu, J.; Koukourakis, N.; Cao, L.; Kuschmierz, R.; Czarske, J. Real-time complex light field generation through a multi-core fiber with deep learning. Sci. Rep. 2022, 12, 7732. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Lin, X.; Rivenson, Y.; Yardimci, N.T.; Veli, M.; Luo, Y.; Jarrahi, M.; Ozcan, A. All-optical machine learning using diffractive deep neural networks. Science 2018, 361, 1004–1008. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Charania, S.; Rothe, S.; Koukourakis, N.; Neumann, N.; Plettemeier, D.; Czarske, J.W. Multimode Optical Interconnects on Silicon Interposer Enable Confidential Hardware-to-Hardware Communication. Sensors 2023, 23, 6076. https://doi.org/10.3390/s23136076
Zhang Q, Charania S, Rothe S, Koukourakis N, Neumann N, Plettemeier D, Czarske JW. Multimode Optical Interconnects on Silicon Interposer Enable Confidential Hardware-to-Hardware Communication. Sensors. 2023; 23(13):6076. https://doi.org/10.3390/s23136076
Chicago/Turabian StyleZhang, Qian, Sujay Charania, Stefan Rothe, Nektarios Koukourakis, Niels Neumann, Dirk Plettemeier, and Juergen W. Czarske. 2023. "Multimode Optical Interconnects on Silicon Interposer Enable Confidential Hardware-to-Hardware Communication" Sensors 23, no. 13: 6076. https://doi.org/10.3390/s23136076
APA StyleZhang, Q., Charania, S., Rothe, S., Koukourakis, N., Neumann, N., Plettemeier, D., & Czarske, J. W. (2023). Multimode Optical Interconnects on Silicon Interposer Enable Confidential Hardware-to-Hardware Communication. Sensors, 23(13), 6076. https://doi.org/10.3390/s23136076









