Risk-Aware Distributionally Robust Optimization for Mobile Edge Computation Task Offloading in the Space–Air–Ground Integrated Network
Abstract
1. Introduction
- •
- We investigate the task offloading decision model in the SAGIN environment. The task offloading model consists of two stages: the first stage involves the task offloading decision, while the second stage focuses on edge–cloud collaboration and cloud resource allocation.
- •
- A fuzzy set of computational resources for edge computing nodes was constructed, considering CVaR. Then, based on the theory of Lagrange duality, the model is transformed into a semidefinite programming form, and the RaDROO algorithm is proposed to solve the task offloading problem with distributional robustness under risk awareness.
- •
- We conducted simulation experiments from two aspects. On one hand, we adjusted certain parameters of the proposed model to obtain the optimal values for those parameters. On the other hand, we fixed the parameters and compared them with the state-of-the-art algorithms in different computation and network environments. The experimental results demonstrate that our proposed model and algorithm have better results than the state-of-the-art methods in terms of usability, robustness, and risk.
2. Related Work
2.1. SAGIN Architecture
- −
- Cross-platform efficiency: Through the integration and collaborative operations achieved by SAGIN, different tasks can be offloaded and migrated between different platforms, thereby improving the efficiency of task execution.
- −
- Increased flexibility through edge–cloud collaboration: In the SAGIN network, tasks can be dynamically allocated and scheduled, allowing them to be offloaded to the most suitable platforms based on their computational requirements. This improves resource utilization.
2.2. Traditional Computation Offloading
2.3. Uncertain-Aware Computation Offloading
2.4. Risk-Aware Computation Offloading
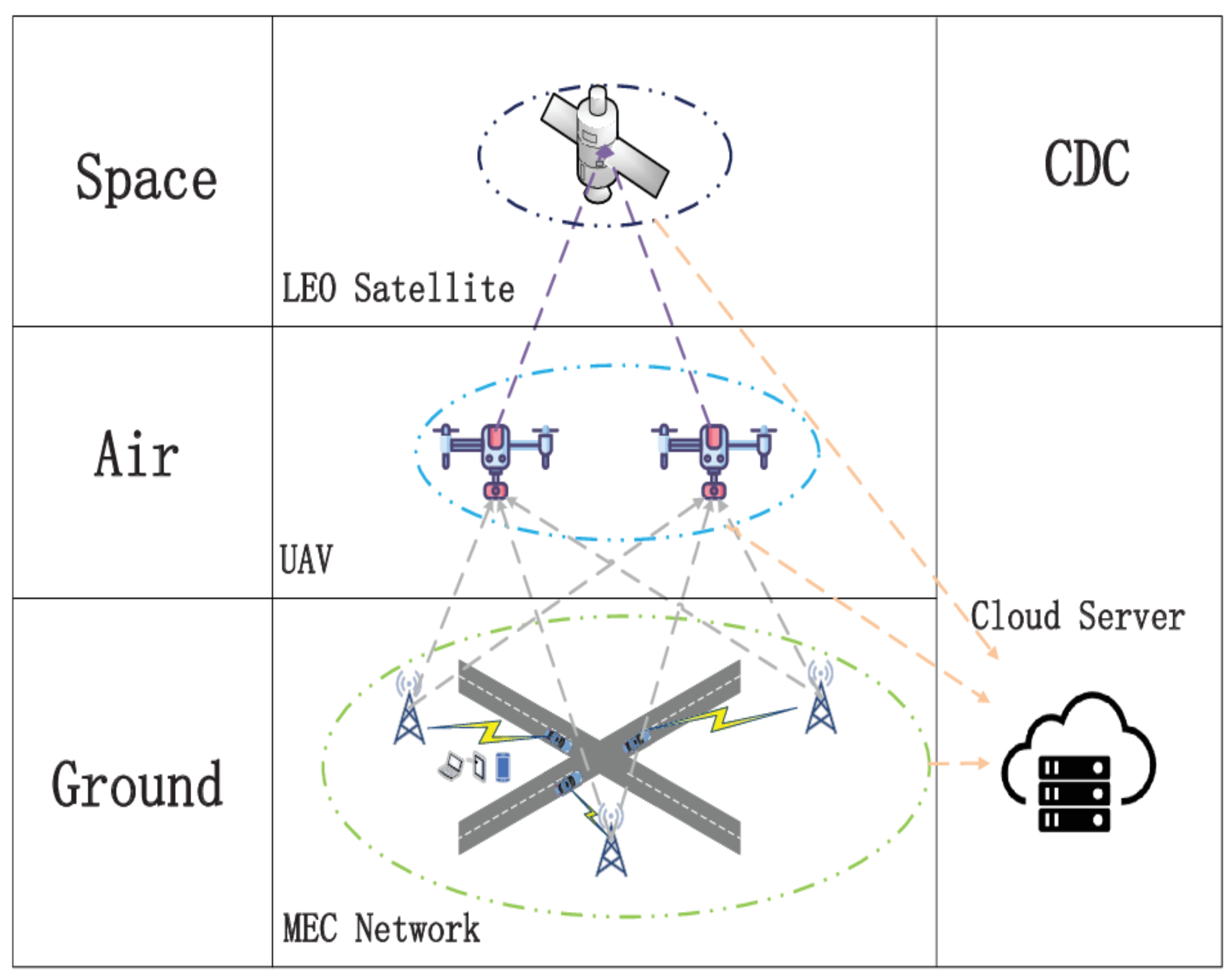
3. Network Architecture and System Model
3.1. SAGIN Architecture and Channel Models
3.2. Computation Task Offloading Model
3.3. Computing Resources Using a Fussy Set Model
4. Risk-Aware Distributionally Robust Optimization Task Offloading Algorithm Design
4.1. Network Architecture and System Model
4.2. Transform from DRO to SDP
4.3. RADROO-MILP Algorithm
| Algorithm 1 Cost-based MILP algorithms for the DRO task offloading problem. |
|
4.4. Complexity Analysis
5. Performance Evaluation
5.1. Simulation Setup
- (1)
- Channel State Information (CSI)
- (2)
- ECNs Information
- (3)
- Comparison Algorithm
- •
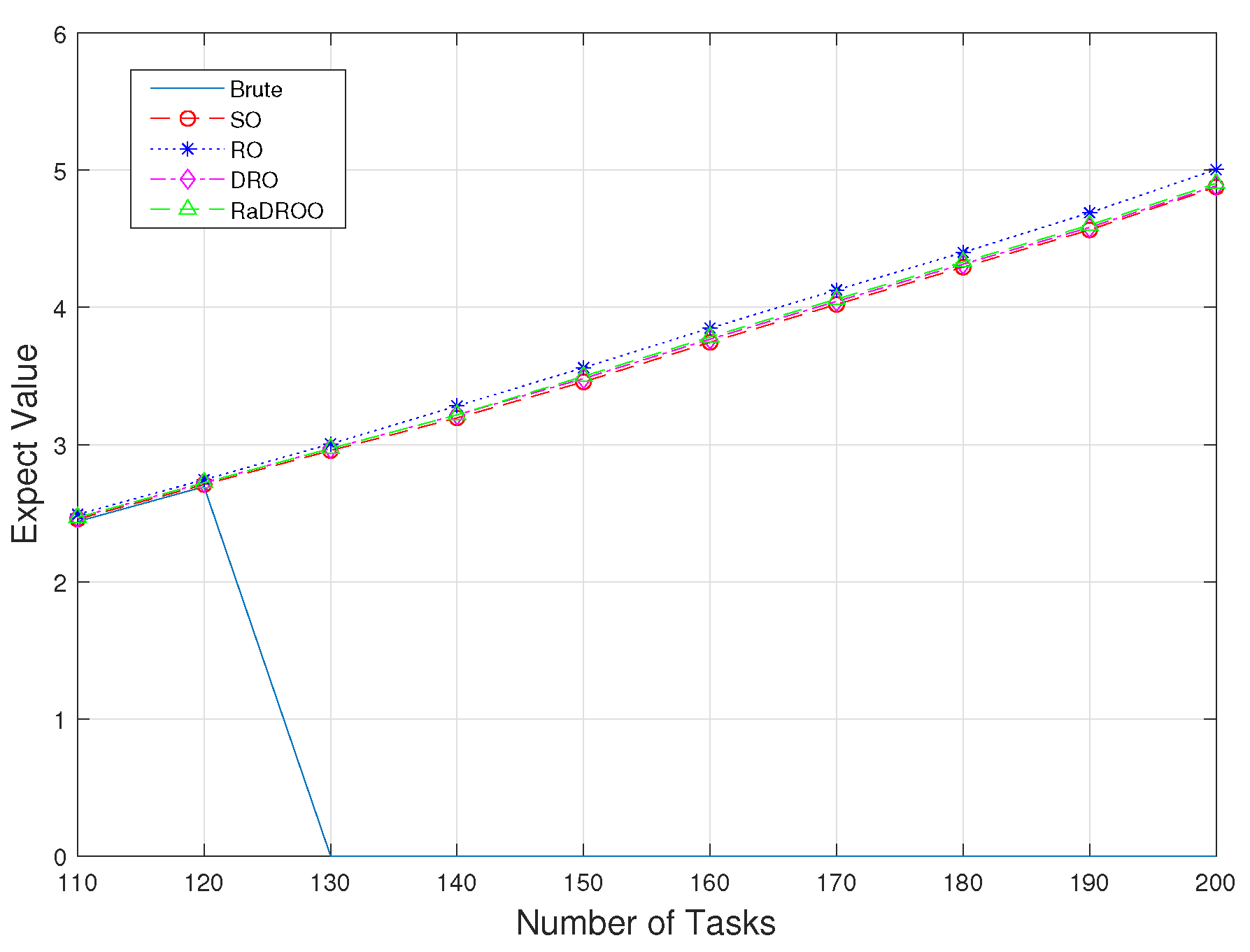
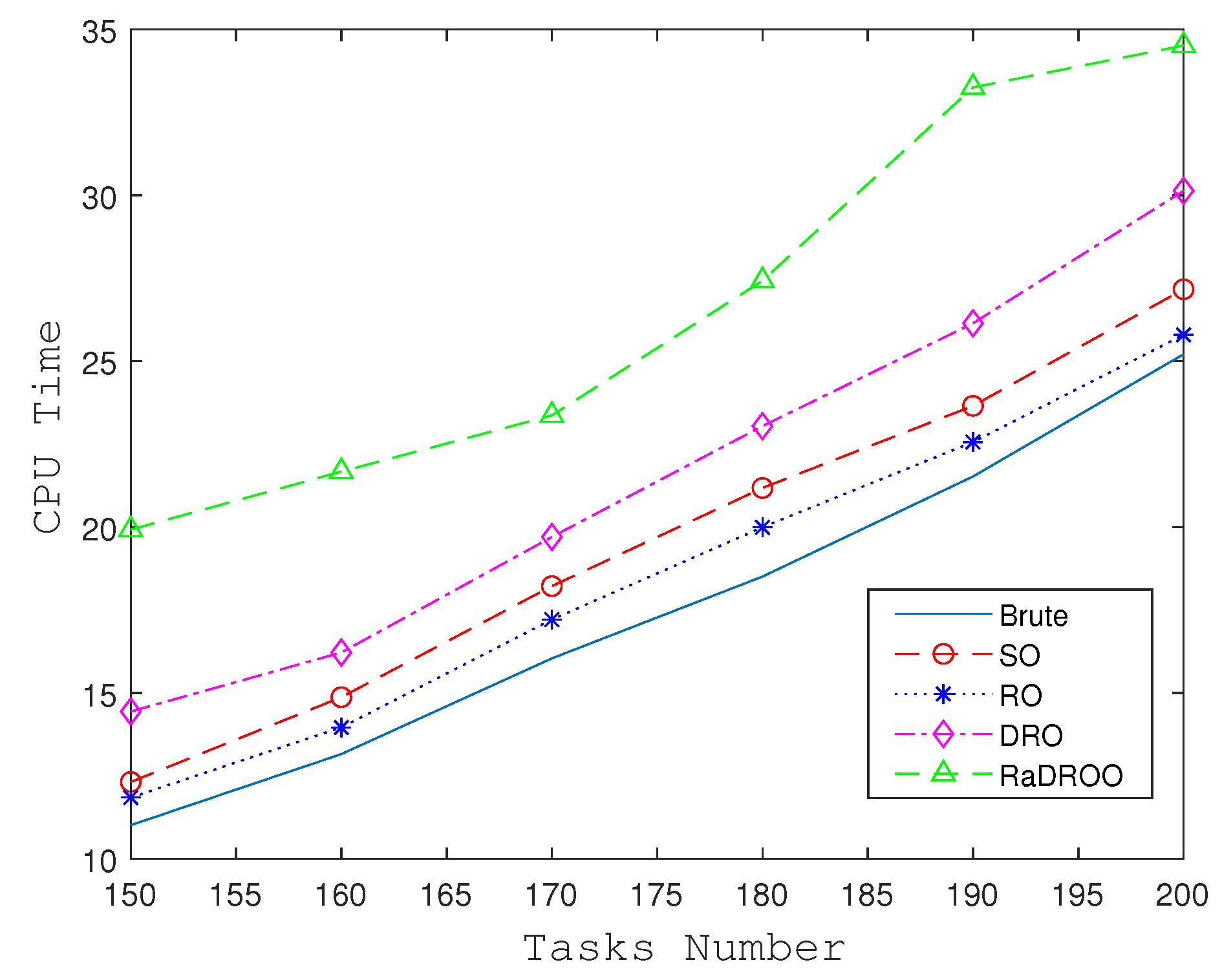
- The Brute-Force algorithm does not take into account any uncertainty or potential computational overflow of tasks to the extent that it may eventually result in the inability to obtain an optimal solution.
- •
- In RO, only the uncertainty of computational resources of ECNs is considered and their possible worst-case scenarios are experimentally selected to ensure their robustness.
- •
- In SO, the fuzzy set is constructed based on the historical data of the computational resources of the given ECNs; thus, we obtain their means and variances.
- •
- In DRO [5], the mean value in the range of the uncertainty set is obtained, and its optimal robust result is obtained by the min–max theory, which guarantees both robustness and practicality. However, there is also a drawback, namely that it is an uncertainty set constructed from historical data, which does not guarantee the stability of the uncertainty set and does not consider its risk.
- •
- In RaDROO, in addition to what the DRO considers, it complements certain deficiencies that it possesses. It considers CVaR, choosing only the part as the benchmark, while using as a weight with the original part. That is to say, it selectively aggravates the proportion of the worse part of the results within the final result in order to guarantee its risk resistance.
5.2. Experiments
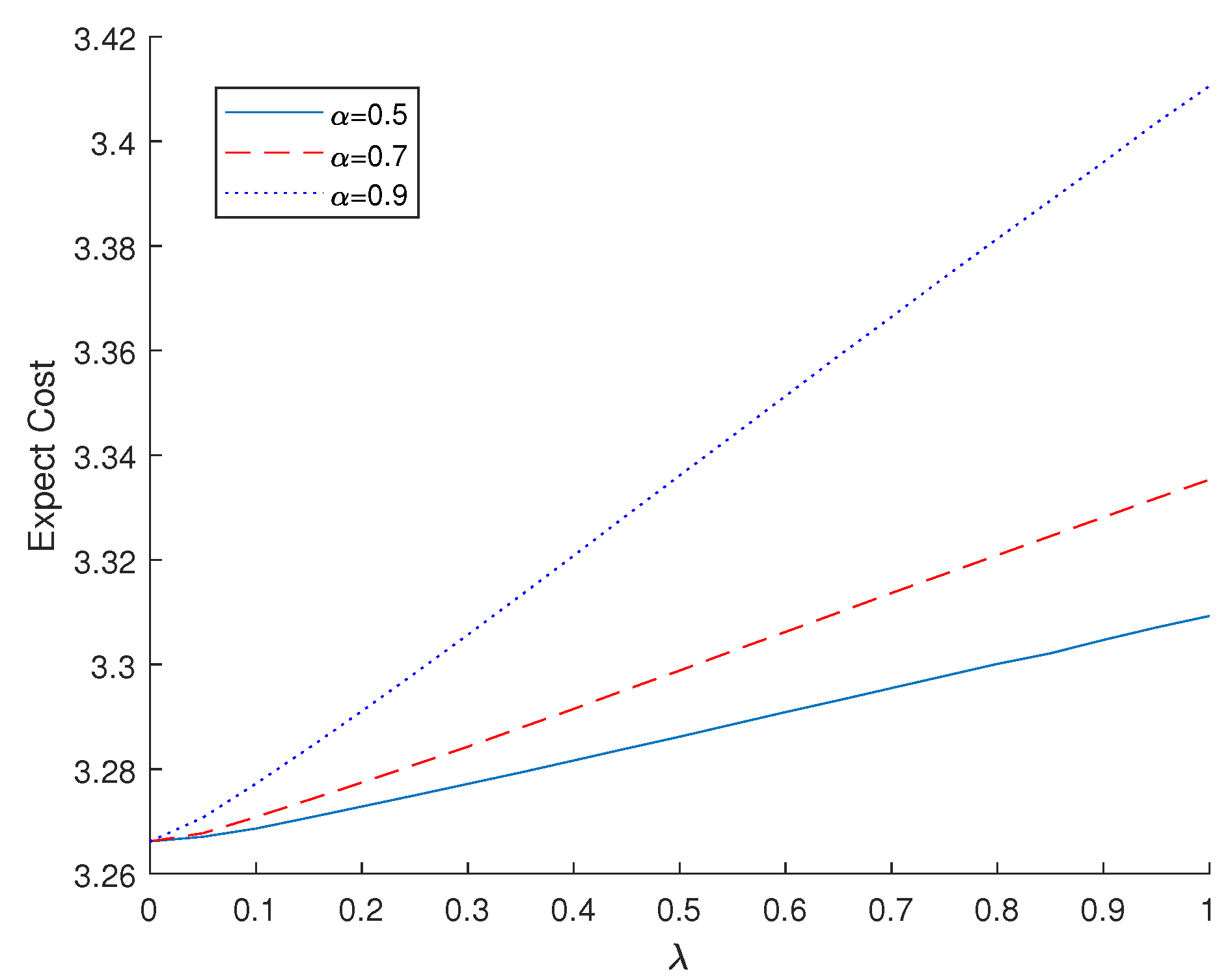
5.2.1. RaDROO Algorithm
5.2.2. Comparison with Other Algorithms
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Zhao, F.; Lu, Y.; Chen, X. Dynamic Task Offloading for Mobile Edge Computing with Hybrid Energy Supply. Tsinghua Sci. Technol. 2023, 28, 421–432. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, G.; Wang, J. Research on Cloud-Edge-End Collaborative Computing Offloading Strategy in the Internet of Vehicles Based on the M-TSA Algorithm. Sensors 2023, 23, 4682. [Google Scholar] [CrossRef]
- Liu, J.; Shi, Y.; Fadlullah, Z.M.; Kato, N. Space-air-ground integrated network: A survey. IEEE Commun. Surv. Tutorials 2018, 20, 2714–2741. [Google Scholar] [CrossRef]
- Qu, Y.; Dai, H.; Wu, F.; Lu, D.; Dong, C.; Tang, S.; Chen, G. Robust offloading scheduling for mobile edge computing. IEEE Trans. Mob. Comput. 2020, I, 2581–2595. [Google Scholar] [CrossRef]
- Chen, Y.; Ai, B.; Niu, Y.; Zhang, H.; Han, Z. Energy-constrained computation offloading in space-air-ground integrated networks using distributionally robust optimization. IEEE Trans. Veh. Technol. 2021, 70, 12113–12125. [Google Scholar] [CrossRef]
- Ma, W.; Mashayekhy, L. Quality-aware video offloading in mobile edge computing: A data-driven two-stage stochastic optimization. In Proceedings of the 2021 IEEE 14th International Conference on Cloud Computing (CLOUD), Chicago, IL, USA, 5–10 September 2021; pp. 594–599. [Google Scholar]
- Chen, M.; Guo, S.; Liu, K.; Liao, X.; Xiao, B. Robust computation offloading and resource scheduling in cloudlet-based mobile cloud computing. IEEE Trans. Mob. Comput. 2020, 20, 2025–2040. [Google Scholar] [CrossRef]
- Wang, H.; Xu, H.; Huang, H.; Chen, M.; Chen, S. Robust task offloading in dynamic edge computing. IEEE Trans. Mob. Comput. 2021, 22, 500–514. [Google Scholar] [CrossRef]
- Wu, Z.; Li, B.; Fei, Z.; Zheng, Z.; Han, Z. Energy-efficient robust computation offloading for fog-iot systems. IEEE Trans. Veh. Technol. 2020, 69, 4417–4425. [Google Scholar] [CrossRef]
- Rahimian, H.; Mehrotra, S. Distributionally robust optimization: A review. arXiv 2019, arXiv:1908.05659. [Google Scholar]
- Ling, A.; Sun, J.; Xiu, N.; Yang, X. Robust two-stage stochastic linear optimization with risk aversion. Eur. J. Oper. Res. 2017, 256, 215–229. [Google Scholar] [CrossRef]
- Bai, Y.; Chen, L.; Song, L.; Xu, J. Risk-aware edge computation offloading using bayesian stackelberg game. IEEE Trans. Netw. Serv. Manag. 2020, 17, 1000–1012. [Google Scholar] [CrossRef]
- Maleki, E.F.; Mashayekhy, L.; Nabavinejad, S.M. Mobility-aware computation offloading in edge computing using machine learning. IEEE Trans. Mob. Comput. 2021, 22, 328–340. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, W. Mean-cvar models for fuzzy portfolio selection. In Proceedings of the 2010 International Conference on Intelligent System Design and Engineering Application, Changsha, China, 13–14 October 2010; pp. 928–930. [Google Scholar]
- Schultz, R.; Neise, F. Algorithms for mean-risk stochastic integer programs in energy. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006. [Google Scholar]
- Albuquerque, M.; Ayyagari, A.; Dorsett, M.A.; Foster, M.S. Global information grid (gig) edge network interface architecture. In Proceedings of the MILCOM 2007—IEEE Military Communications Conference, Orlando, FL, USA, 29–31 October 2007; pp. 1–7. [Google Scholar]
- Yu, S.; Gong, X.; Shi, Q.; Wang, X.; Chen, X. Ec-sagins: Edge-computing-enhanced space–air–ground-integrated networks for internet of vehicles. IEEE Internet Things J. 2021, 9, 5742–5754. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, X.; Sun, M.; Zhang, P. Terminal cooperative interdependent computing task offloading for 6g. IEEE Trans. Netw. Sci. Eng. 2022, 9, 2846–2856. [Google Scholar] [CrossRef]
- Yan, J.; Bi, S.; Zhang, Y.J.; Tao, M. Optimal task offloading and resource allocation in mobile-edge computing with inter-user task dependency. IEEE Trans. Wirel. Commun. 2019, 19, 235–250. [Google Scholar] [CrossRef]
- Yang, Y.; Chang, X.; Jia, Z.; Han, Z.; Han, Z. Towards 6g joint haps-mec-cloud 3c resource allocation for delay-aware computation offloading. In Proceedings of the 2020 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom), Exeter, UK, 17–19 December 2020; pp. 175–182. [Google Scholar]
- Li, Z.; Peng, E. Software-defined optimal computation task scheduling in vehicular edge networking. Sensors 2021, 21, 955. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Z.; Dai, X.; Jiang, H.; Wang, D.; Chen, H.; Yang, L.; Zeng, F. Vehicular task offloading via heat-aware mec cooperation using game-theoretic method. IEEE Internet Things J. 2019, 7, 2038–2052. [Google Scholar] [CrossRef]
- Dai, Y.; Xu, D.; Maharjan, S.; Zhang, Y. Joint load balancing and offloading in vehicular edge computing and networks. IEEE Internet Things J. 2018, 6, 4377–4387. [Google Scholar] [CrossRef]
- Chouhan, S. Energy optimal partial computation offloading framework for mobile devices in multi-access edge computing. In Proceedings of the 2019 International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 19–21 September 2019; pp. 1–6. [Google Scholar]
- Wang, F.; Xu, J.; Cui, S. Optimal energy allocation and task offloading policy for wireless powered mobile edge computing systems. IEEE Trans. Wirel. Commun. 2020, 19, 2443–2459. [Google Scholar] [CrossRef]
- Hmimz, Y.; Chanyour, T.; El Ghmary, M.; Malik, M.O.C. Energy efficient and devices priority aware computation offloading to a mobile edge computing server. In Proceedings of the 2019 5th International Conference on Optimization and Applications (ICOA), Kenitra, Morocco, 25–26 April 2019; pp. 1–6. [Google Scholar]
- Wang, Y.; Wu, L.; Yuan, X.; Liu, X.; Li, X. An energy-efficient and deadline-aware task offloading strategy based on channel constraint for mobile cloud workflows. IEEE Access 2019, 7, 69858–69872. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, S.; Chen, Z.; Han, T.; Qian, Z.; Xiao, M.; Chen, N.; Wu, J.; Lu, S. Towards revenue-driven multi-user online task offloading in edge computing. IEEE Trans. Parallel Distrib. Syst. 2021, 33, 1185–1198. [Google Scholar] [CrossRef]
- Wang, D.; Tian, X.; Cui, H.; Liu, Z. Reinforcement learning-based joint task offloading and migration schemes optimization in mobility-aware mec network. China Commun. 2020, 17, 31–44. [Google Scholar] [CrossRef]
- Samanta, A.; Chang, Z. Adaptive service offloading for revenue maximization in mobile edge computing with delay-constraint. IEEE Internet Things J. 2019, 6, 3864–3872. [Google Scholar] [CrossRef]
- Bi, J.; Zhang, K.; Yuan, H.; Hu, Q. Energy-aware task offloading with genetic particle swarm optimization in hybrid edge computing. In Proceedings of the 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Melbourne, Australia, 17–20 October 2021; pp. 3194–3199. [Google Scholar]
- Li, S.; Ge, H.; Chen, X.; Liu, L.; Gong, H.; Tang, R. Computation offloading strategy for improved particle swarm optimization in mobile edge computing. In Proceedings of the 2021 IEEE 6th International Conference on Cloud Computing and Big Data Analytics (ICCCBDA), Chengdu, China, 24–26 April 2021; pp. 375–381. [Google Scholar]
- Tout, H.; Mourad, A.; Kara, N.; Talhi, C. Multi-persona mobility: Joint cost-effective and resource-aware mobile-edge computation offloading. IEEE/ACM Trans. Netw. 2021, 29, 1408–1421. [Google Scholar] [CrossRef]
- Tang, F.; Kawamoto, Y.; Kato, N.; Liu, J. Future intelligent and secure vehicular network toward 6g: Machine-learning approaches. Proc. IEEE 2019, 108, 292–307. [Google Scholar] [CrossRef]
- Apostolopoulos, P.A.; Tsiropoulou, E.E.; Papavassiliou, S. Risk-aware data offloading in multi-server multi-access edge computing environment. IEEE/ACM Trans. Netw. 2020, 28, 1405–1418. [Google Scholar] [CrossRef]
- Pan, S.; Zhang, Z.; Xue, T.; Hu, G. Enhancing availability for the mec service: Cvar-based computation offloading. In Proceedings of the 2020 IEEE 26th International Conference on Parallel and Distributed Systems (ICPADS), Hong Kong, China, 2–4 December 2020; pp. 342–347. [Google Scholar]
- Vatalaro, F.; Corazza, G.E.; Caini, C.; Ferrarelli, C. Analysis of leo, meo, and geo global mobile satellite systems in the presence of interference and fading. IEEE J. Sel. Areas Commun. 1995, 13, 291–300. [Google Scholar] [CrossRef]
- Qi, F.; Mang, G.; Zhang, S.; Liu, L. A multi-layer architecture for space-air-ground network and iot services. In Proceedings of the 2021 International Wireless Communications and Mobile Computing (IWCMC), 2021 International Wireless Communications and Mobile Computing (IWCMC), Harbin City, China, 28 June–2 July 2021; pp. 1809–1813. [Google Scholar]
- Delage, E.; Ye, Y. Distributionally robust optimization under moment uncertainty with application to data-driven problems. Oper. Res. 2010, 58, 595–612. [Google Scholar] [CrossRef]


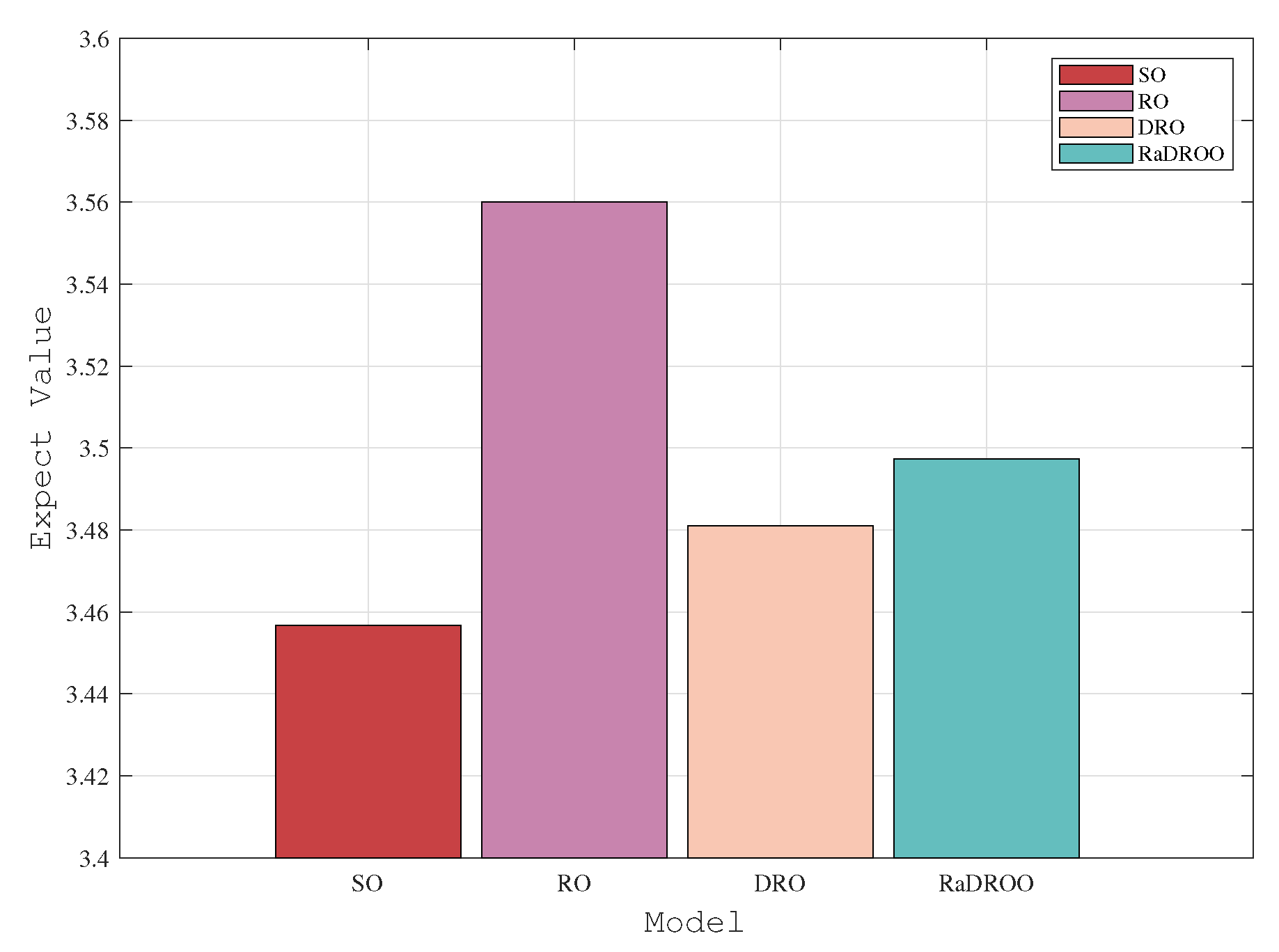
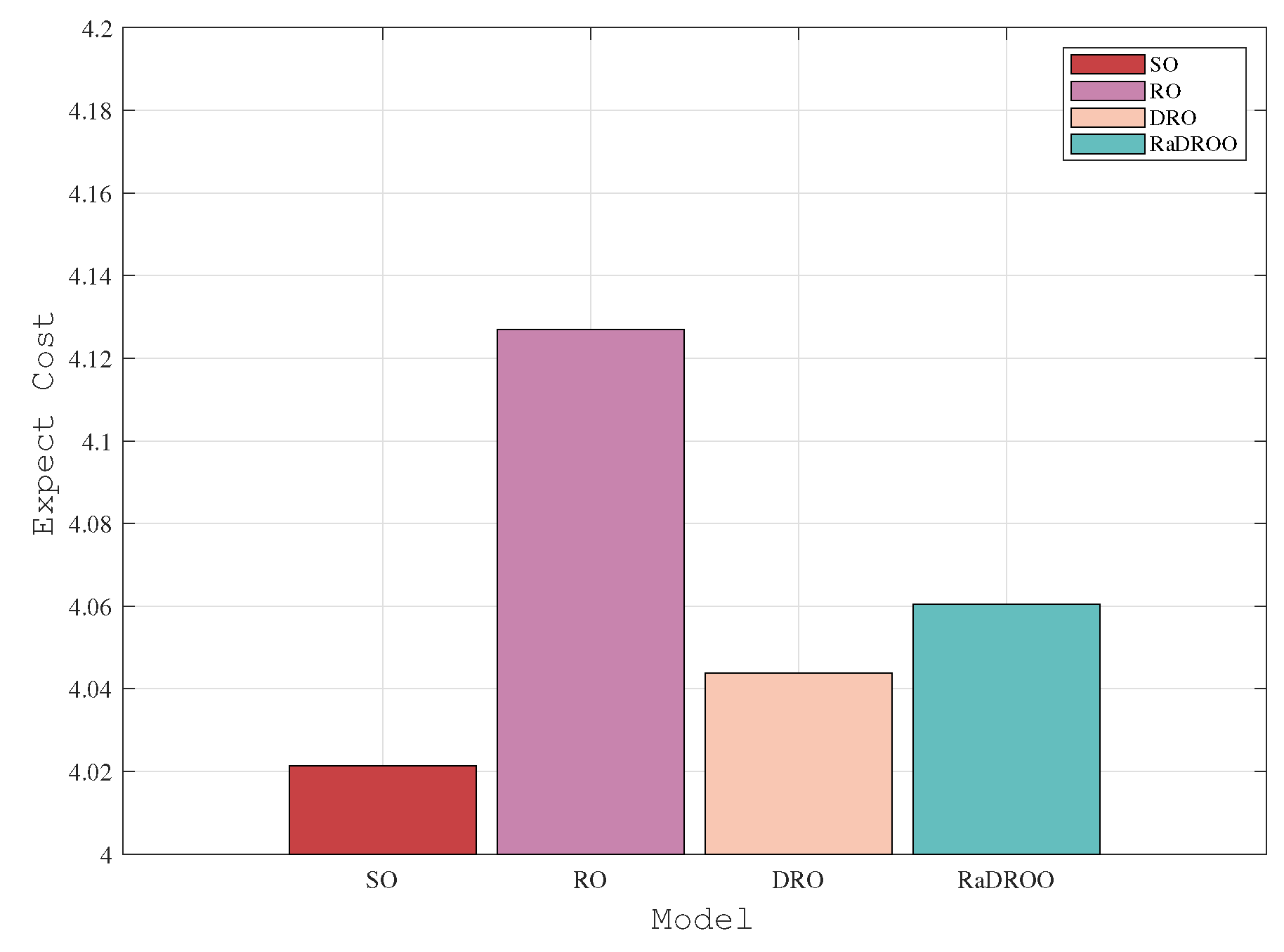
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Chen, P. Risk-Aware Distributionally Robust Optimization for Mobile Edge Computation Task Offloading in the Space–Air–Ground Integrated Network. Sensors 2023, 23, 5729. https://doi.org/10.3390/s23125729
Li Z, Chen P. Risk-Aware Distributionally Robust Optimization for Mobile Edge Computation Task Offloading in the Space–Air–Ground Integrated Network. Sensors. 2023; 23(12):5729. https://doi.org/10.3390/s23125729
Chicago/Turabian StyleLi, Zhiyuan, and Pinrun Chen. 2023. "Risk-Aware Distributionally Robust Optimization for Mobile Edge Computation Task Offloading in the Space–Air–Ground Integrated Network" Sensors 23, no. 12: 5729. https://doi.org/10.3390/s23125729
APA StyleLi, Z., & Chen, P. (2023). Risk-Aware Distributionally Robust Optimization for Mobile Edge Computation Task Offloading in the Space–Air–Ground Integrated Network. Sensors, 23(12), 5729. https://doi.org/10.3390/s23125729







