Shape Discrimination of Individual Aerosol Particles Using Light Scattering
Abstract
1. Introduction
2. Experimental Methods
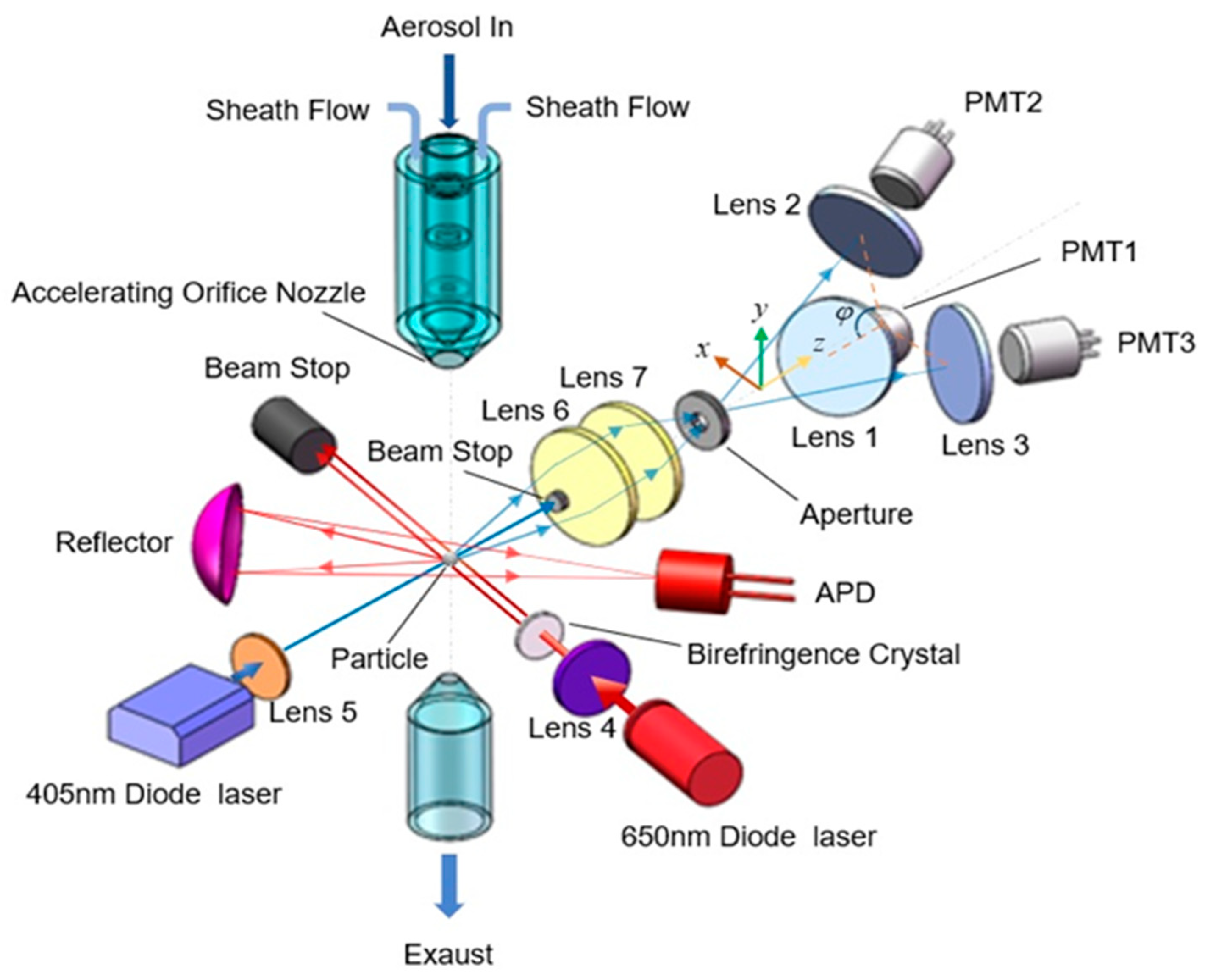
2.1. Experimental Setup
2.2. Calculation Method of Scattered Light
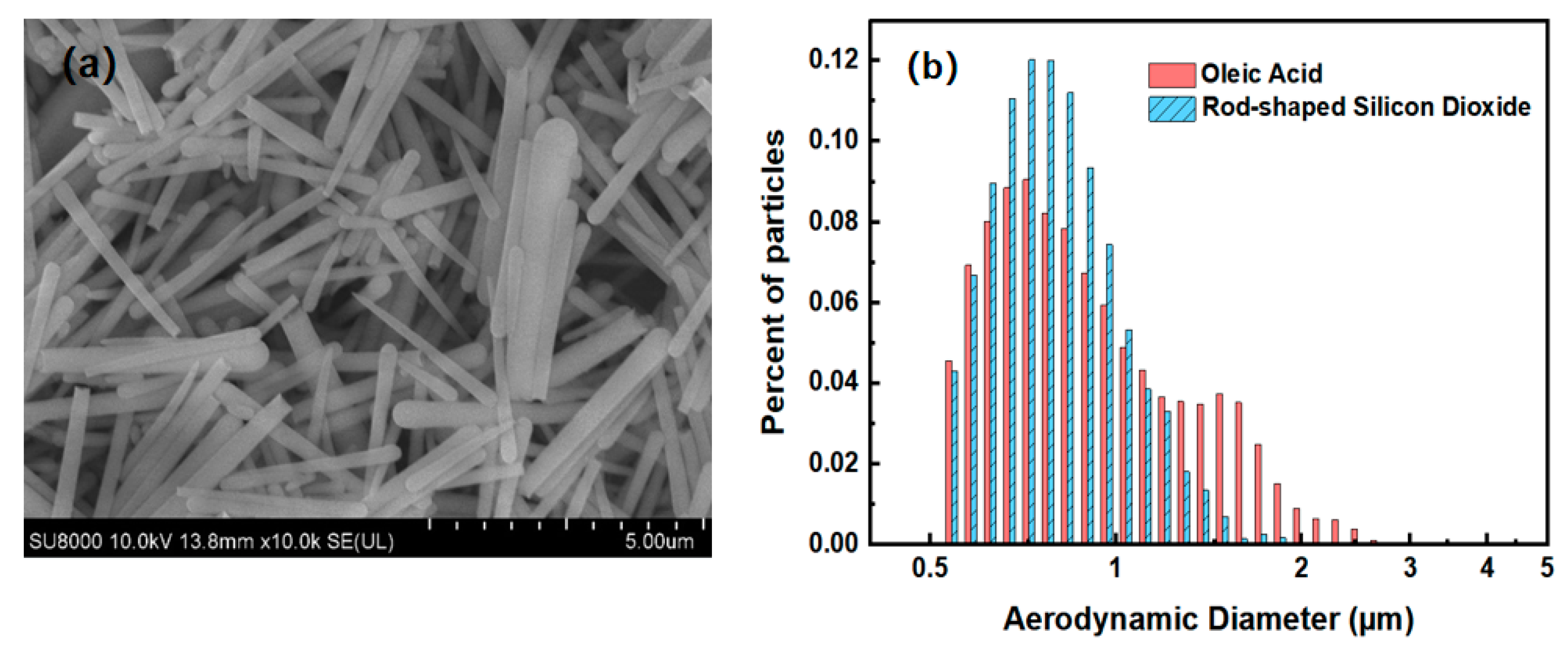
2.3. Sample Generation
3. Results and Discussion
3.1. Extraction and Correction of the Spectral Signal
3.1.1. Signal Extraction
3.1.2. Correction of Light Intensity
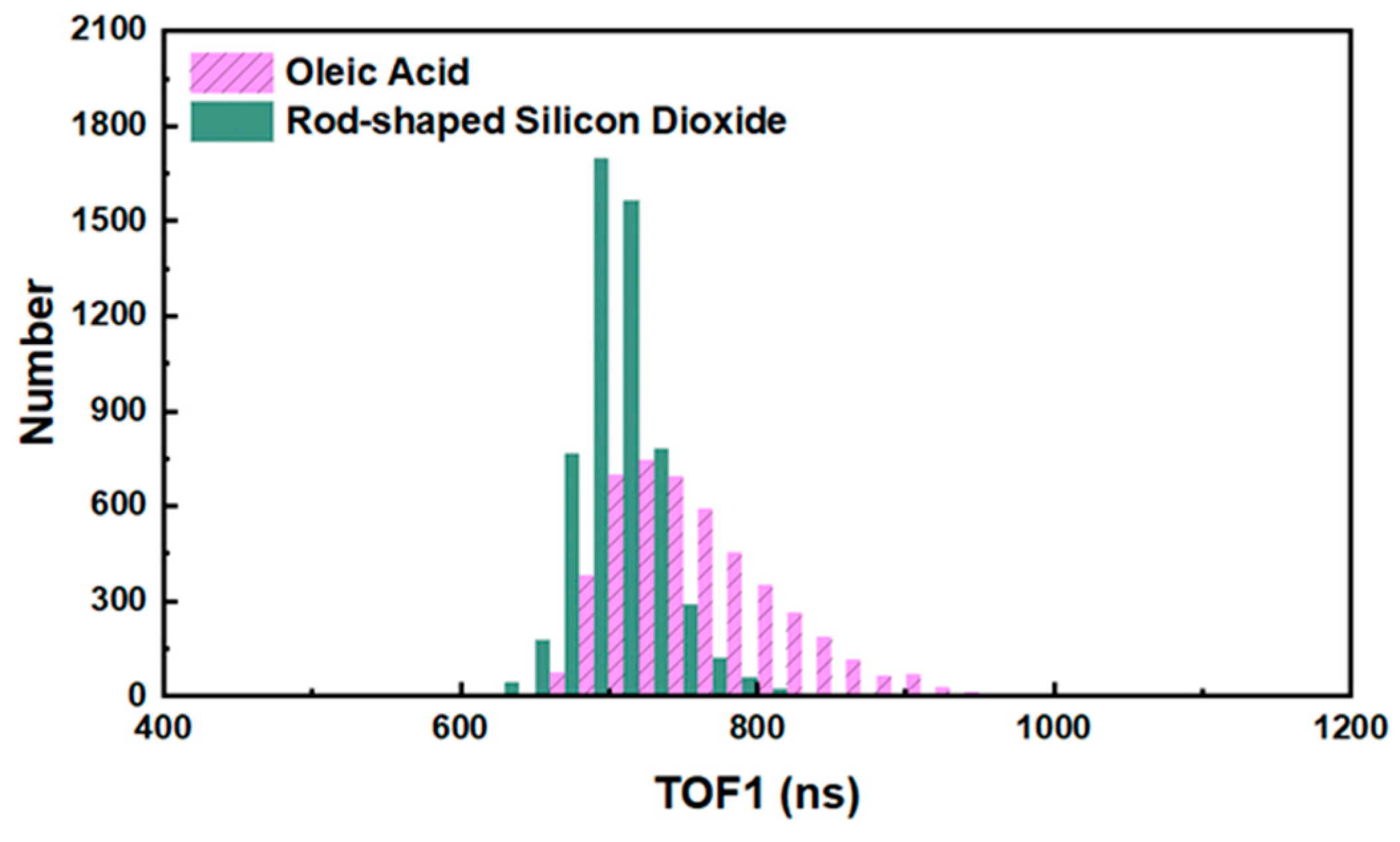
3.2. Screen the Time-of-Flight
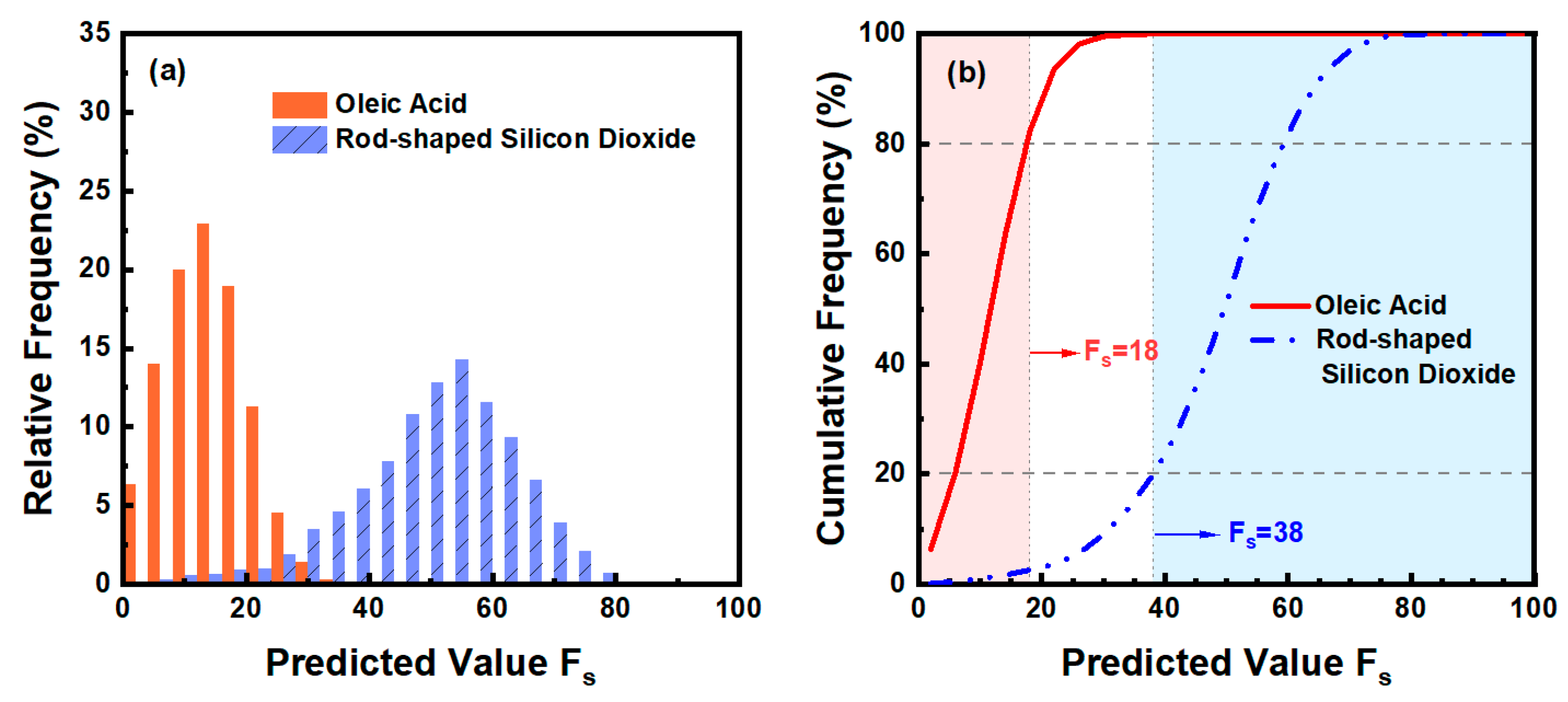
3.3. Modeling and Analysis
3.4. Group by Particle Size
3.5. Preliminary Laboratory Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, X.; Zhao, W.; Fang, B.; Zhou, J.; Wang, S.; Zhang, W.; Venables, D.S.; Chen, W. Three-wavelength cavity-enhanced albedometer for measuring wavelength-dependent optical properties and single-scattering albedo of aerosols. Opt. Express 2018, 26, 33484–33500. [Google Scholar] [CrossRef] [PubMed]
- Stopford, C.; Kaye, P.H.; Greenaway, R.S.; Hirst, E.; Ulanowski, Z.; Stanley, W.R. Real-time detection of airborne asbestos by light scattering from magnetically re-aligned fibers. Opt. Express 2013, 21, 11356–11367. [Google Scholar] [CrossRef]
- Cao, X.; Roy, G.; Bernier, R. Lidar polarization discrimination of bioaerosols. Opt. Eng. 2010, 49, 116201. [Google Scholar] [CrossRef]
- Pan, Y.-L.; Aptowicz, K.B.; Chang, R.K.; Hart, M.; Eversole, J.D. Characterizing and monitoring respiratory aerosols by light scattering. Opt. Lett. 2003, 28, 589–591. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.-L.; Wang, C.; Beresnev, L.A.; Yuffa, A.J.; Videen, G.; Ligon, D.; Santarpia, J.L. Measurement of back-scattering patterns from single laser trapped aerosol particles in air. Appl. Opt. 2017, 56, B1–B4. [Google Scholar] [CrossRef]
- Kaye, P.H.; Aptowicz, K.; Chang, R.K.; Foot, V.; Videen, G. Angularly Resolved Elastic Scattering from Airborne Particles In Optics of Biological Particles; Springer: Berlin/Heidelberg, Germany, 2007; Volume 238. [Google Scholar]
- Kaye, P.H.; Alexander-Buckley, K.; Hirst, E.; Saunders, S.; Clark, J.M. A real-time monitoring system for airborne particle shape and size analysis. J. Geophys. Res. Atmos. 1996, 101, 19215–19221. [Google Scholar] [CrossRef]
- Pan, Y.-L.; Berg, M.J.; Zhang, S.S.-M.; Noh, H.; Cao, H.; Chang, R.K.; Videen, G. Measurement and autocorrelation analysis of two-dimensional light-scattering patterns from living cells for label-free classification. Cytom. Part A 2011, 79, 284–292. [Google Scholar] [CrossRef]
- Aptowicz, K.B.; Pinnick, R.G.; Hill, S.C.; Pan, Y.L.; Chang, R.K. Optical scattering patterns from single urban aerosol particles at Adelphi, Maryland, USA: A classification relating to particle morphologies. J. Geophys. Res. Atmos. 2006, 111, D12212. [Google Scholar] [CrossRef]
- Bi, L.; Lin, W.; Liu, D.; Zhang, K. Assessing the depolarization capabilities of nonspherical particles in a super-ellipsoidal shape space. Opt. Express 2018, 26, 1726–1742. [Google Scholar] [CrossRef] [PubMed]
- Grynko, Y.; Shkuratov, Y.; Förstner, J. Light scattering by randomly irregular dielectric particles larger than the wavelength. Opt. Lett. 2013, 38, 5153–5156. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.; Huang, L.; Zhou, G.; Han, J.; Zeng, A.; Zhao, Y.; Huang, H. Computation and analysis of light scattering by monodisperse biological aerosols. Chin. J. Lasers 2010, 37, 2592–2598. [Google Scholar] [CrossRef]
- Liu, L.; Mishchenko, M.I. Scattering and radiative properties of morphologically complex carbonaceous aerosols: A systematic systematic modeling study. Remote Sens. 2018, 10, 1634. [Google Scholar] [CrossRef]
- Allen, J.; Husar, R.B. Aerosol Particle Size and Shape Measurements through Asymmetric Light Scattering. In Collied and Interface Science; Academic Press: Cambridge, MA, USA, 1976; pp. 141–153. [Google Scholar]
- Diehl, S.R.; Smith, D.T.; Sydor, M. Analysis of suspended solids by single-particle scattering. Appl. Opt. 1979, 18, 1653–1658. [Google Scholar] [CrossRef]
- Gucker, F.T.; Egan, J.J. Measurement of the angular variation of light scattered from single aerosol droplets. J. Colloid Sci. 1961, 16, 68–84. [Google Scholar] [CrossRef]
- Kaye, P.H.; Hirst, E.; Clark, J.M.; Micheli, F. Airborne particle-shape and size classification from spatial light-scattering profiles. J. Aerosol Sci. 1992, 23, 597–611. [Google Scholar] [CrossRef]
- Hirst, E.; Kaye, P.H.; Greenaway, R.S.; Field, P.; Johnson, D.W. Discrimination of micrometre-sized ice and super-cooled droplets in mixed-phase cloud. Atmos. Environ. 2001, 35, 33–47. [Google Scholar] [CrossRef]
- Sivaprakasam, V.; Czege, J.; Eversole, J.D. Wavelength Resolved Polarized Elastic Scatter Measurements from Micron Sized Single Particles. In Proceedings of the Chemical, Biological, Radiological, Nuclear, and Explosives (CBRNE) Sensing XIV, Baltimore, MD, USA, 29 May 2013. [Google Scholar]
- Redding, B.; Pan, Y.L.; Wang, C.J.; Cao, H. Polarization-resolved near-backscattering of airborne aggregates composed of different primary particles. Opt. Lett. 2014, 39, 4076–4079. [Google Scholar] [CrossRef]
- Richardson, J.M.; Aldridge, J.C.; Milstein, B.A. Polarimetric lidar signatures for remote detection of biological warfare agents. In Proceedings of the SPIE Defense and Security Symposium, Orlando, FL, USA, 31 March 2008; pp. 1–11. [Google Scholar]
- Zubko, E.; Shkuratov, Y.; Hart, M.; Eversole, J.; Videen, G. Backscattering and negative polarization of agglomerate particles. Opt. Lett. 2003, 28, 1504–1506. [Google Scholar] [CrossRef]
- Dong, Q.; Huang, Z.; Li, W.; Li, Z.; Song, X.; Liu, W.; Wang, T.; Bi, J.; Shi, J. Polarization lidar measurements of dust optical properties at the junction of the Taklimakan Desert–Tibetan Plateau. Remote Sens. 2022, 14, 558. [Google Scholar] [CrossRef]
- Yong, W.; Ran, L. Differentiation of suspended particles by polarized light scattering at 120°. Opt. Express 2018, 26, 22419–22431. [Google Scholar] [CrossRef]
- Li, D.; Chen, F.; Zeng, N.; Qiu, Z.; He, H.; He, Y.; Ma, H. Study on polarization scattering applied in aerosol recognition in the air. Opt. Express 2019, 27, A581–A595. [Google Scholar] [CrossRef] [PubMed]
- Holm, R.L.; Caldow, R.; Hairston, P.P.; Quant, F.R.; Sem, G.J. An enhanced time-of-flight spectrometer that measures aerodynamic size plus light-scattering intensity. J. Aerosol Sci. 1997, 28, S11–S12. [Google Scholar] [CrossRef]
- Han, Y.; Ding, L.; Wang, Y.; Zheng, H.; Fang, L. Polarized light illuminated scattering characteristics of single airborne particle. J. Quant. Spectrosc. Radiat. Transf. 2021, 266, 107568. [Google Scholar] [CrossRef]
- Heyder, J.; Gebhart, J. Optimization of response functions of light scattering onstruments for size evaluation of aerosol particles. Appl. Opt. 1979, 18, 705–711. [Google Scholar] [CrossRef] [PubMed]
- Kuijk, A.; Blaaderen, A.v.; Imhof, A. Synthesis of monodisperse, rodlike silica colloids with tunable aspect ratio. J. Am. Chem. Soc. 2011, 133, 2346–2349. [Google Scholar] [CrossRef]
- Dick, W.D.; Ziemann, P.J.; Huang, P.F.; McMurry, P.H. Optical shape fraction measurements of submicrometre laboratory and atmospheric aerosols. Meas. Sci. Technol. 1998, 9, 183–196. [Google Scholar] [CrossRef]
- Lee, S.-Y.; Jeong, T.-Y.; Jung, S.; Yee, K.-J. Refractive index dispersion of hexagonal boron nitride in the visible and near-infrared. Phys. Status Solidi (B) 2019, 256, 1800417. [Google Scholar] [CrossRef]
- Hirst, E.; Kaye, P.H.; Buckley, K.M.; Saunders, S.J. A method for investigating the orientational behavior of fibrous particles in gaseous flow. Part. Part. Syst. Charact. 1995, 12, 3–9. [Google Scholar] [CrossRef]
- Barone, T.L.; Hesse, E.; Seaman, C.E.; Baran, A.J.; Beck, T.W.; Harris, M.L.; Jaques, P.A.; Lee, T.; Mischler, S.E. Calibration of the cloud and aerosol spectrometer for coal dust composition and morphology. Adv. Powder Technol. 2019, 30, 1805–1814. [Google Scholar] [CrossRef]









| Evaluation Index | ncomp = 1 | ncomp = 2 | ncomp = 3 | ncomp = 4 | ncomp = 5 |
|---|---|---|---|---|---|
| PCTVAR of X | 0.3954 | 0.6165 | 0.7575 | 0.8659 | 0.9131 |
| PCTVAR of Y | 0.4506 | 0.6390 | 0.6759 | 0.6864 | 0.6889 |
| Evaluation Index | ncomp = 1 | ncomp = 2 |
|---|---|---|
| AUC | 0.9825 | 0.9828 |
| PCTVAR of X | 0.7511 | 0.999 |
| PCTVAR of Y | 0.7226 | 0.724 |
| Evaluation Index | D1 | D2 | D3 |
|---|---|---|---|
| AUC | 0.9950 | 0.9905 | 0.9787 |
| PCTVAR of X | 0.9991 | 0.9990 | 0.9856 |
| PCTVAR of Y | 0.8515 | 0.7938 | 0.7029 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Ding, L.; Wang, Y.; Zheng, H.; Fang, L. Shape Discrimination of Individual Aerosol Particles Using Light Scattering. Sensors 2023, 23, 5464. https://doi.org/10.3390/s23125464
Han Y, Ding L, Wang Y, Zheng H, Fang L. Shape Discrimination of Individual Aerosol Particles Using Light Scattering. Sensors. 2023; 23(12):5464. https://doi.org/10.3390/s23125464
Chicago/Turabian StyleHan, Yan, Lei Ding, Yingping Wang, Haiyang Zheng, and Li Fang. 2023. "Shape Discrimination of Individual Aerosol Particles Using Light Scattering" Sensors 23, no. 12: 5464. https://doi.org/10.3390/s23125464
APA StyleHan, Y., Ding, L., Wang, Y., Zheng, H., & Fang, L. (2023). Shape Discrimination of Individual Aerosol Particles Using Light Scattering. Sensors, 23(12), 5464. https://doi.org/10.3390/s23125464





