Broadband Vibration-Based Energy Harvesting for Wireless Sensor Applications Using Frequency Upconversion
Abstract
1. Introduction
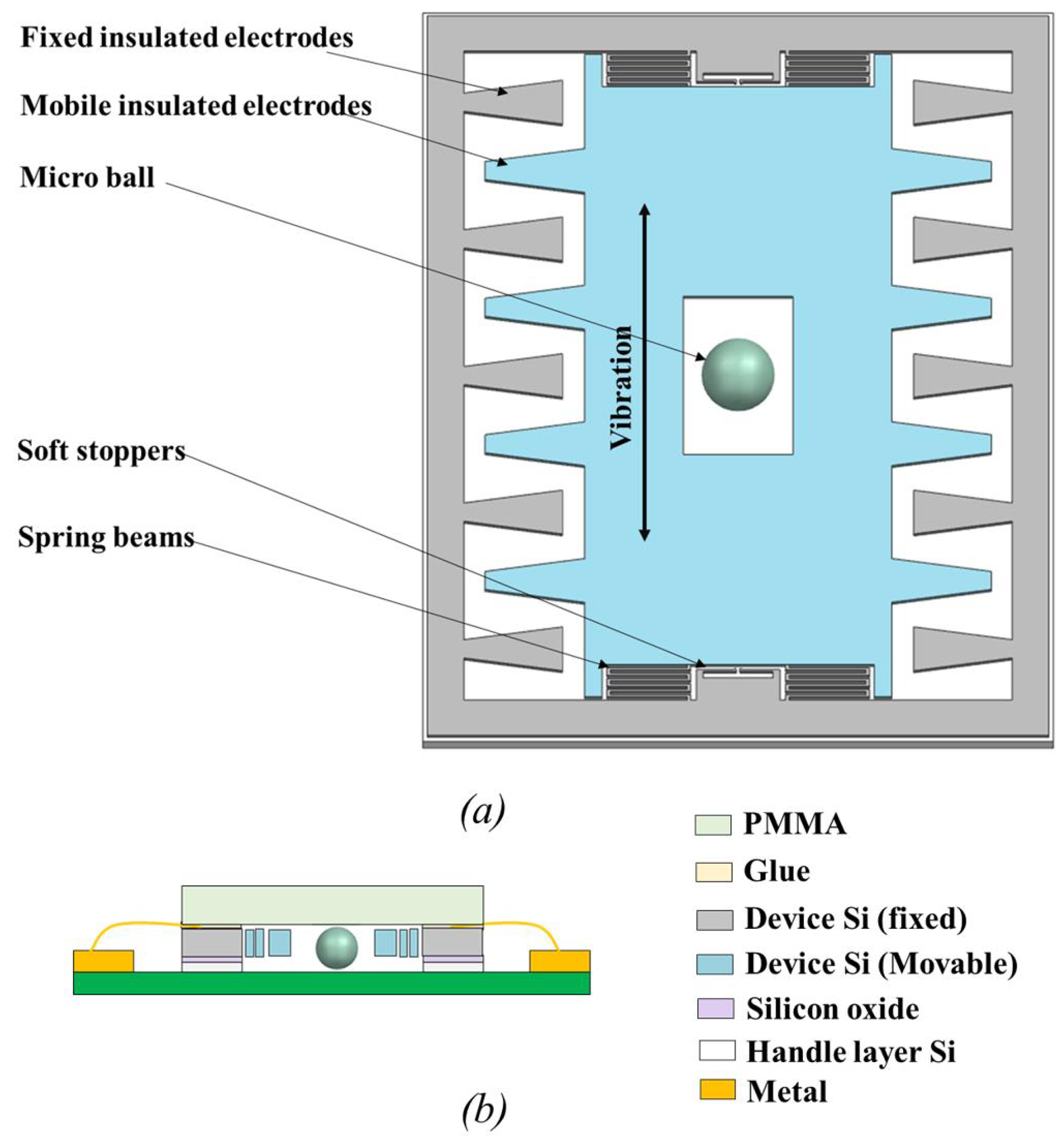
2. Device Description
2.1. Design Concept
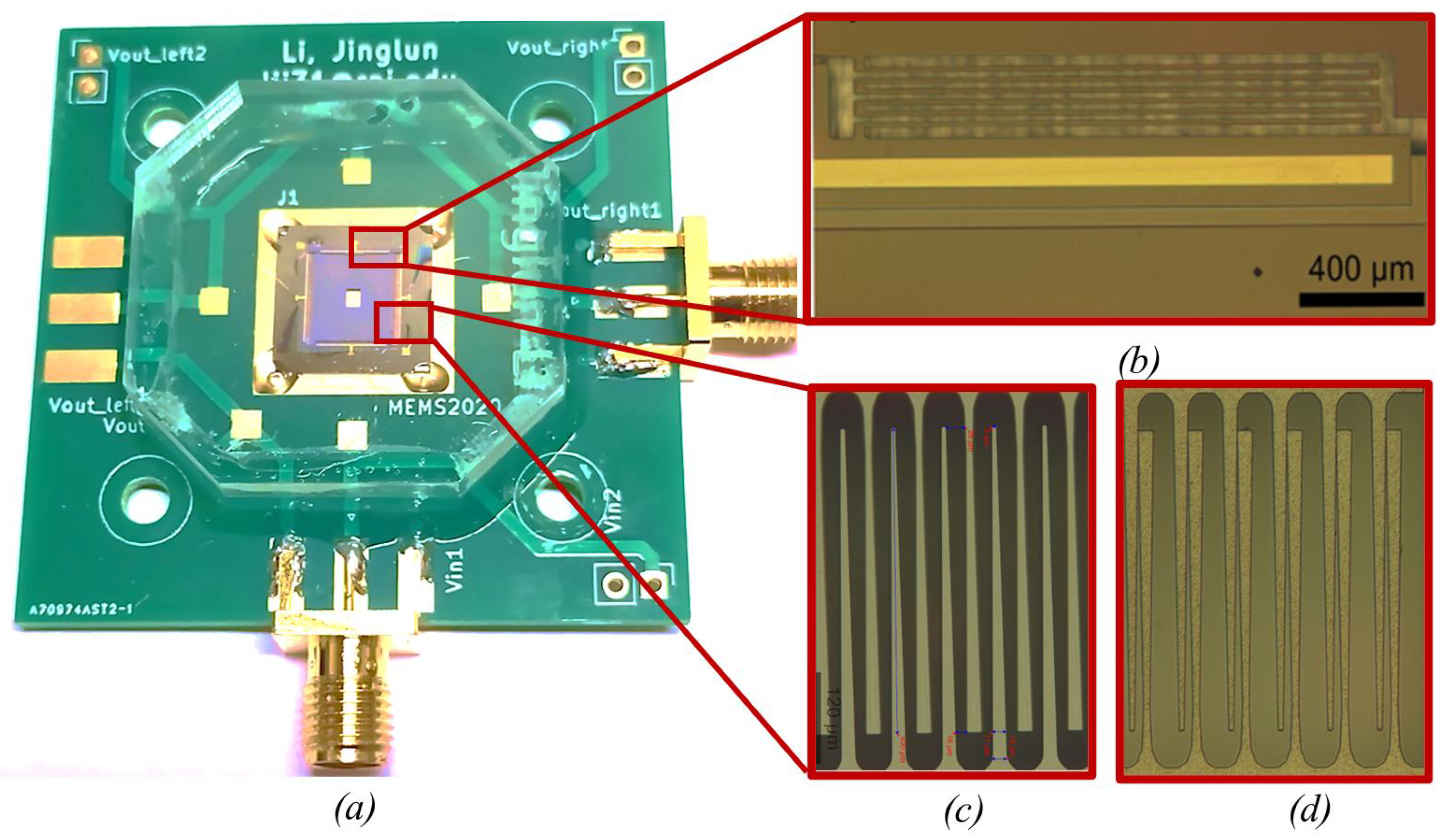
2.2. Device Fabrication and Packaging Process
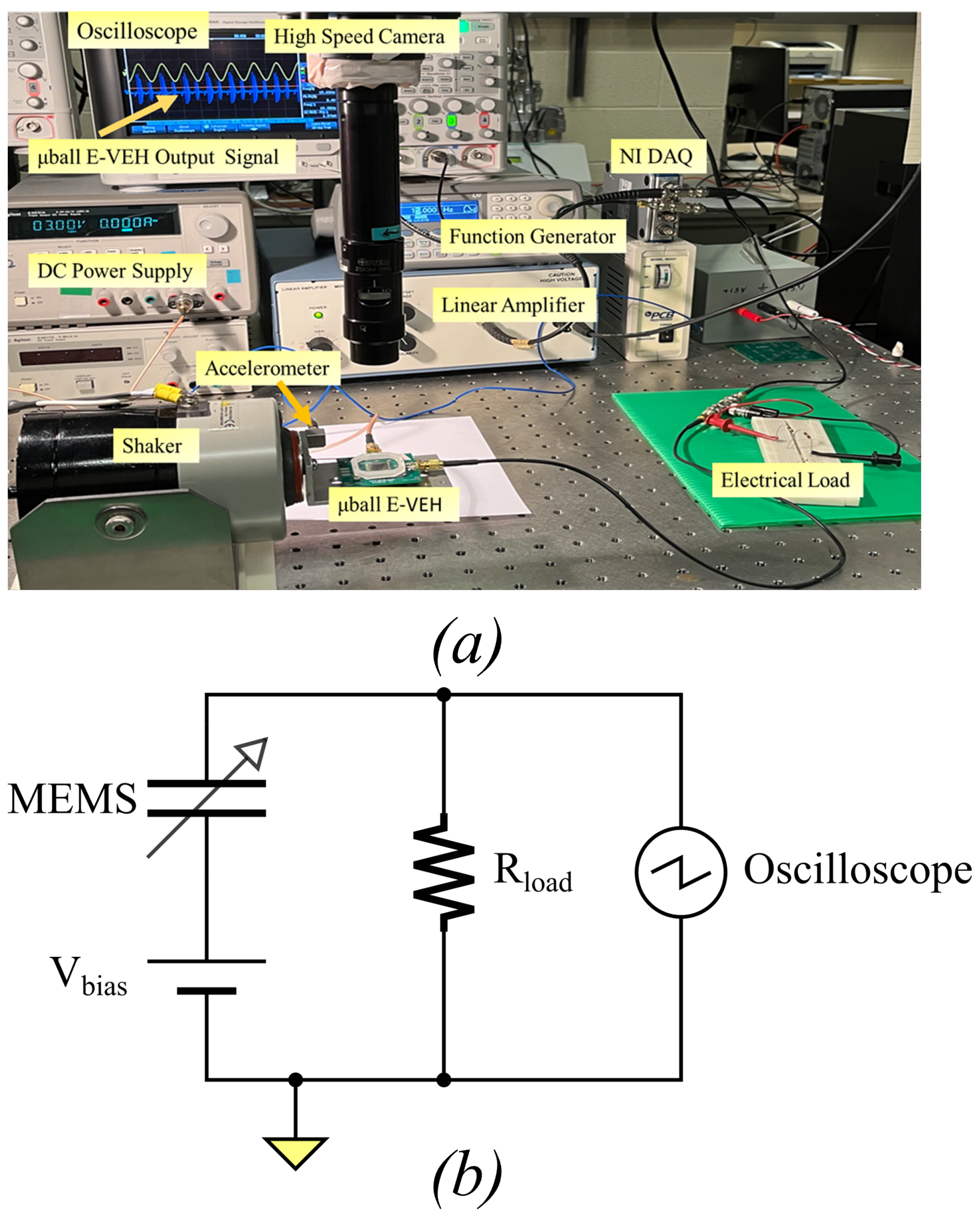
3. Experimental Setup
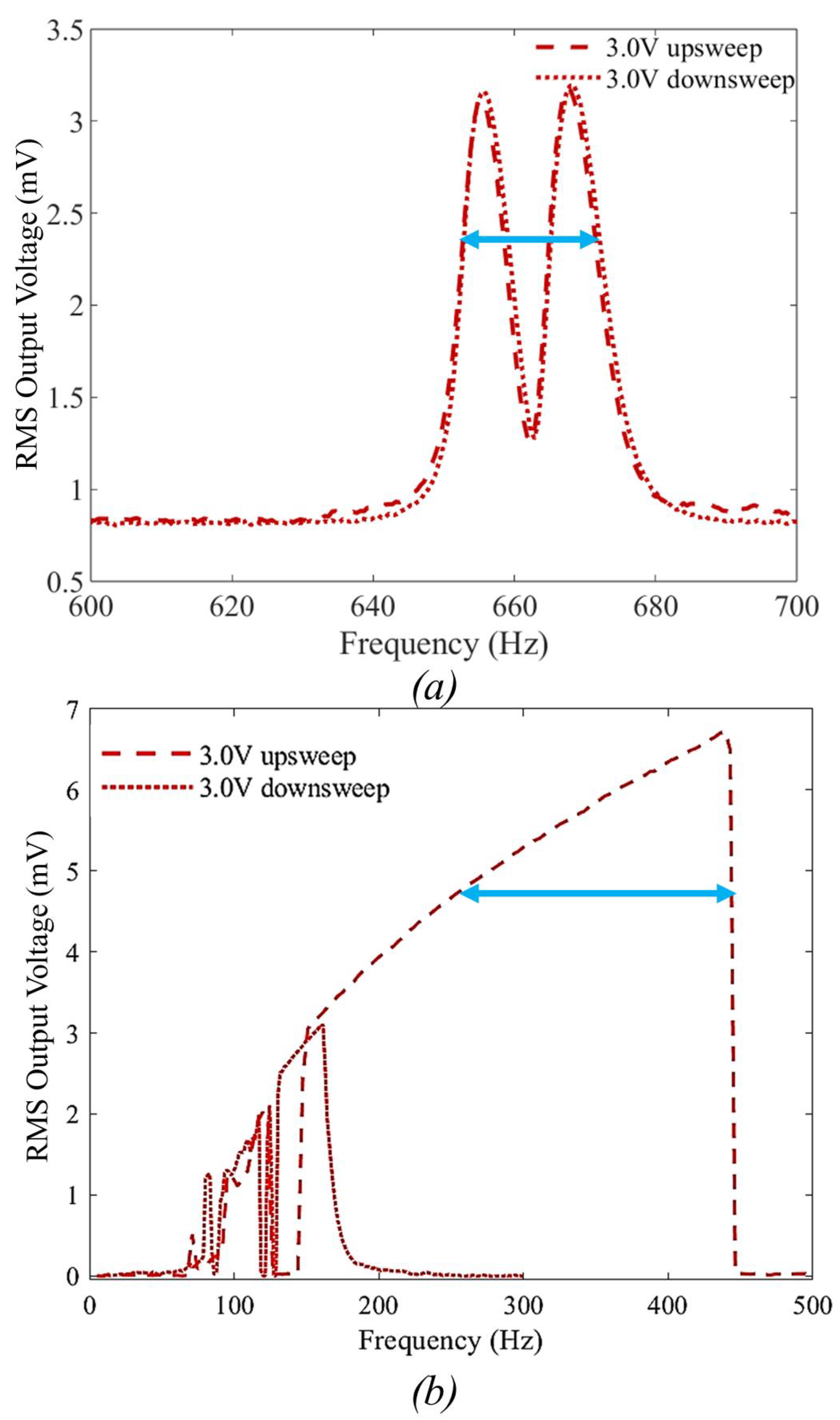
4. Results
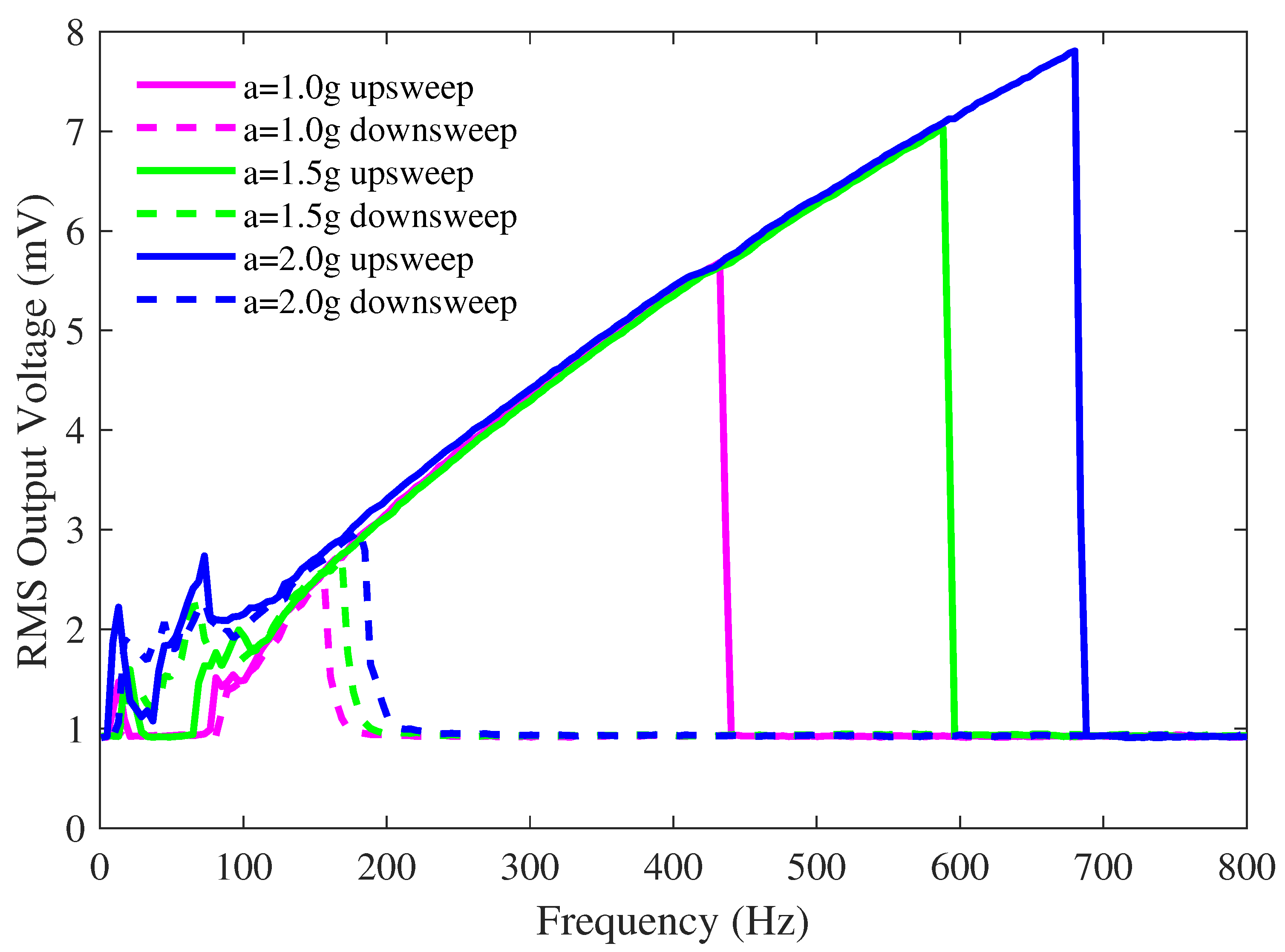
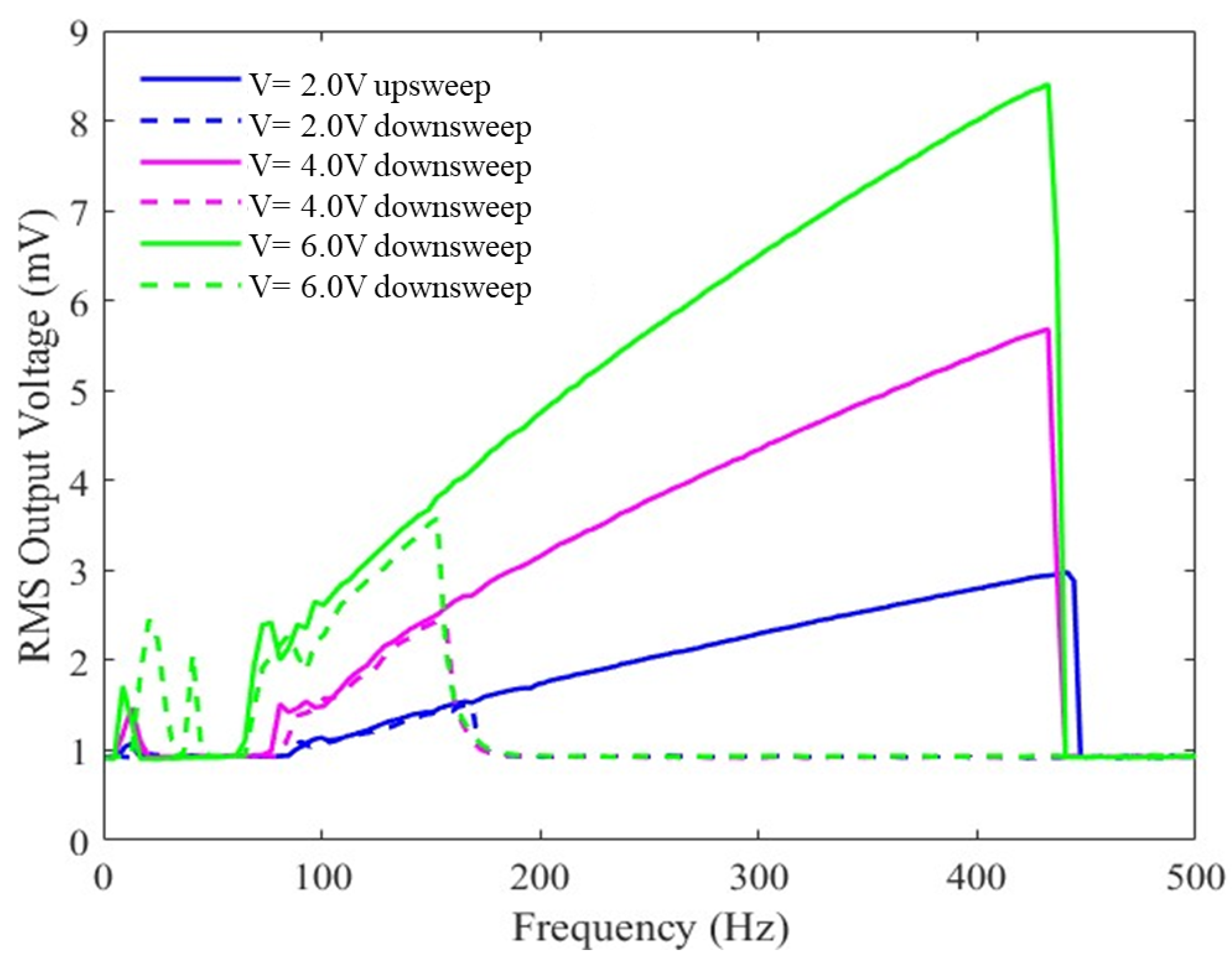
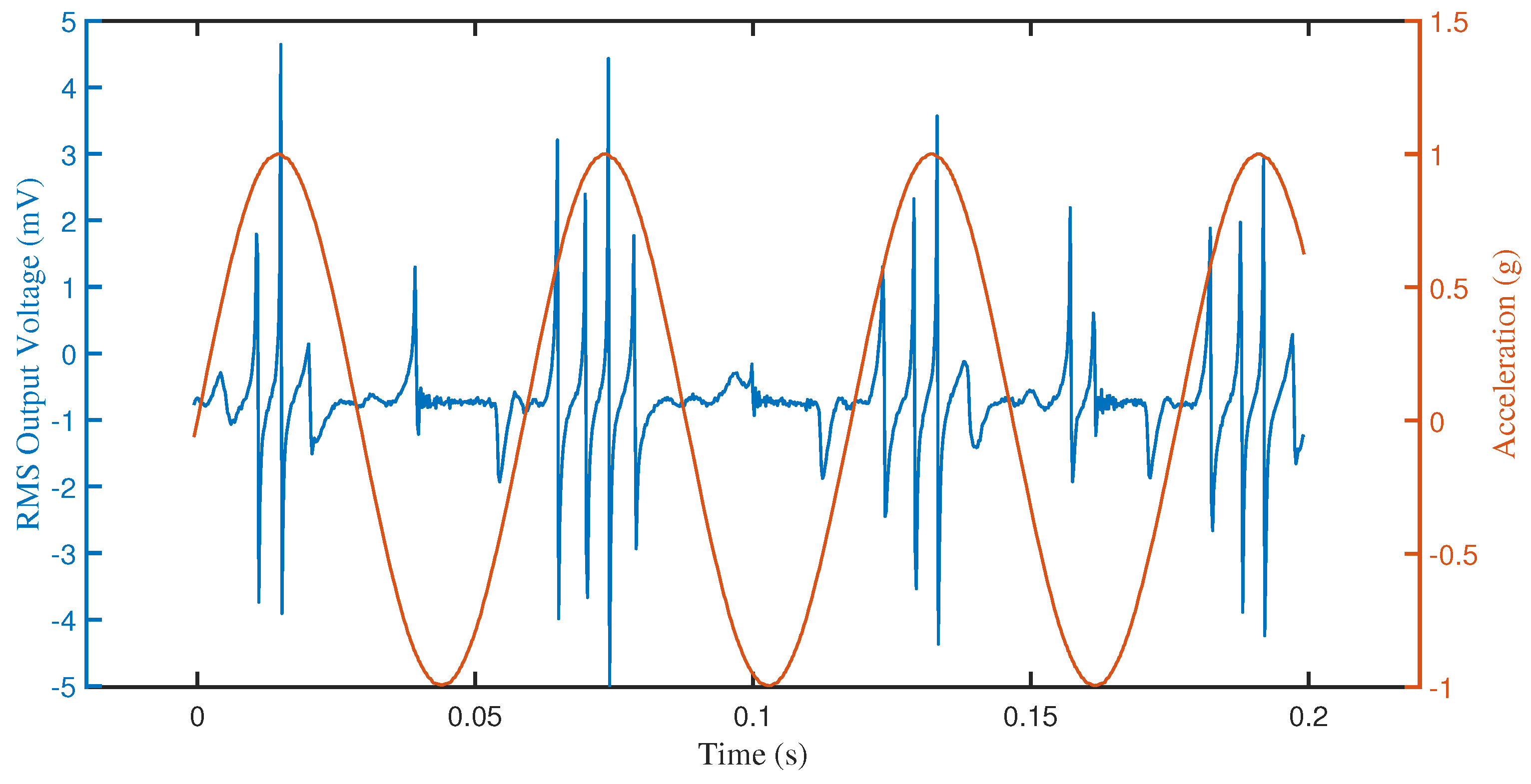
4.1. Device Response without a Microball
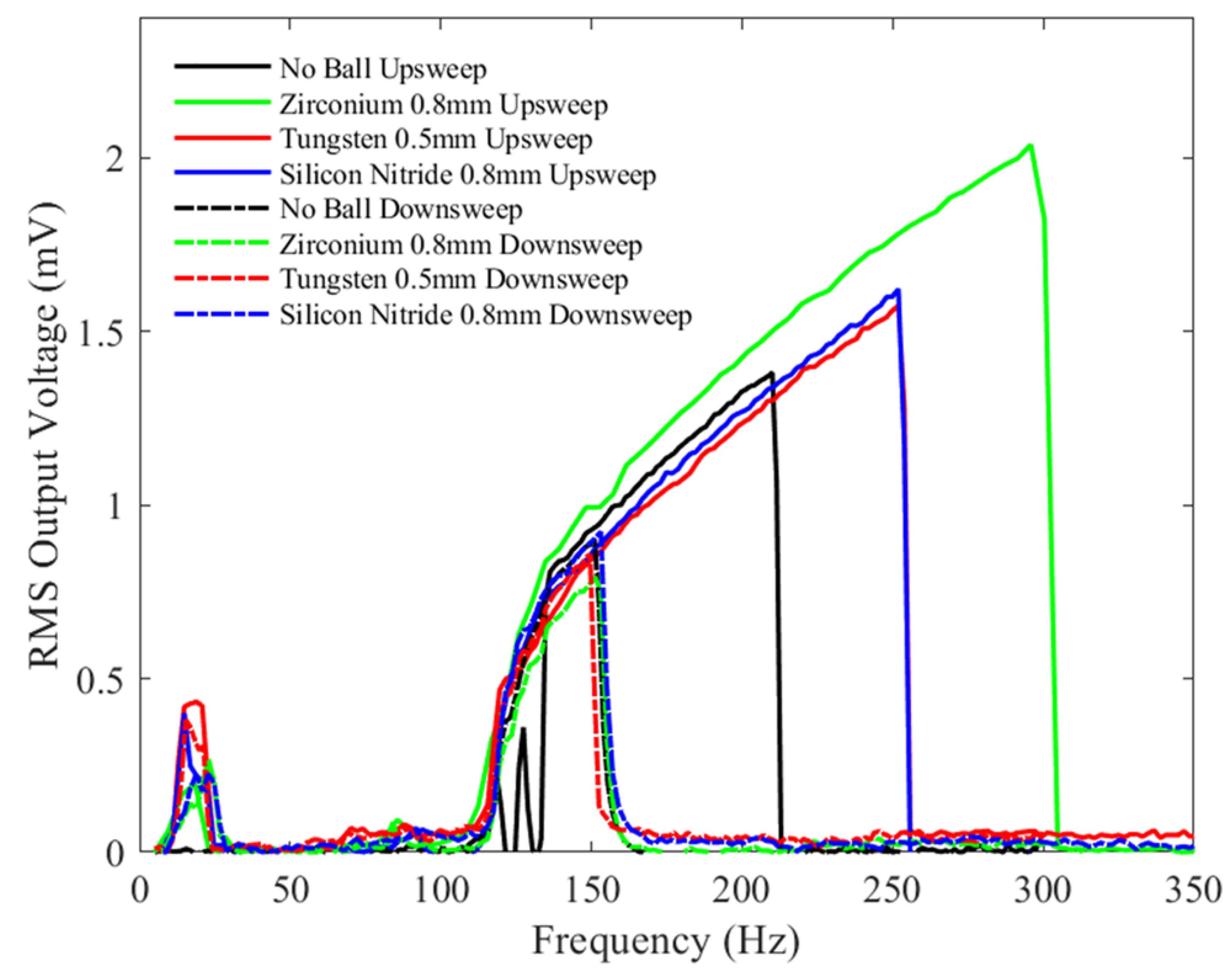
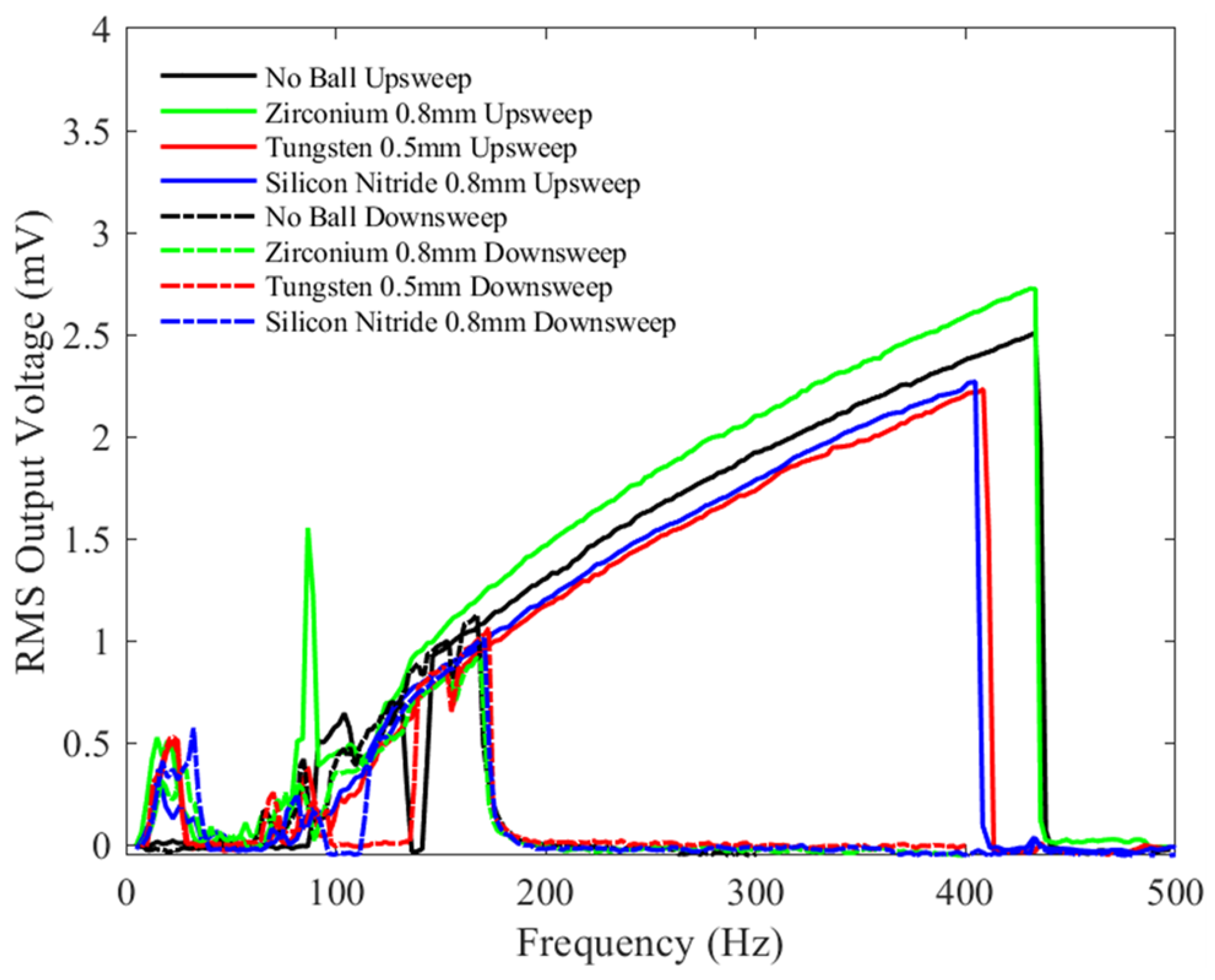
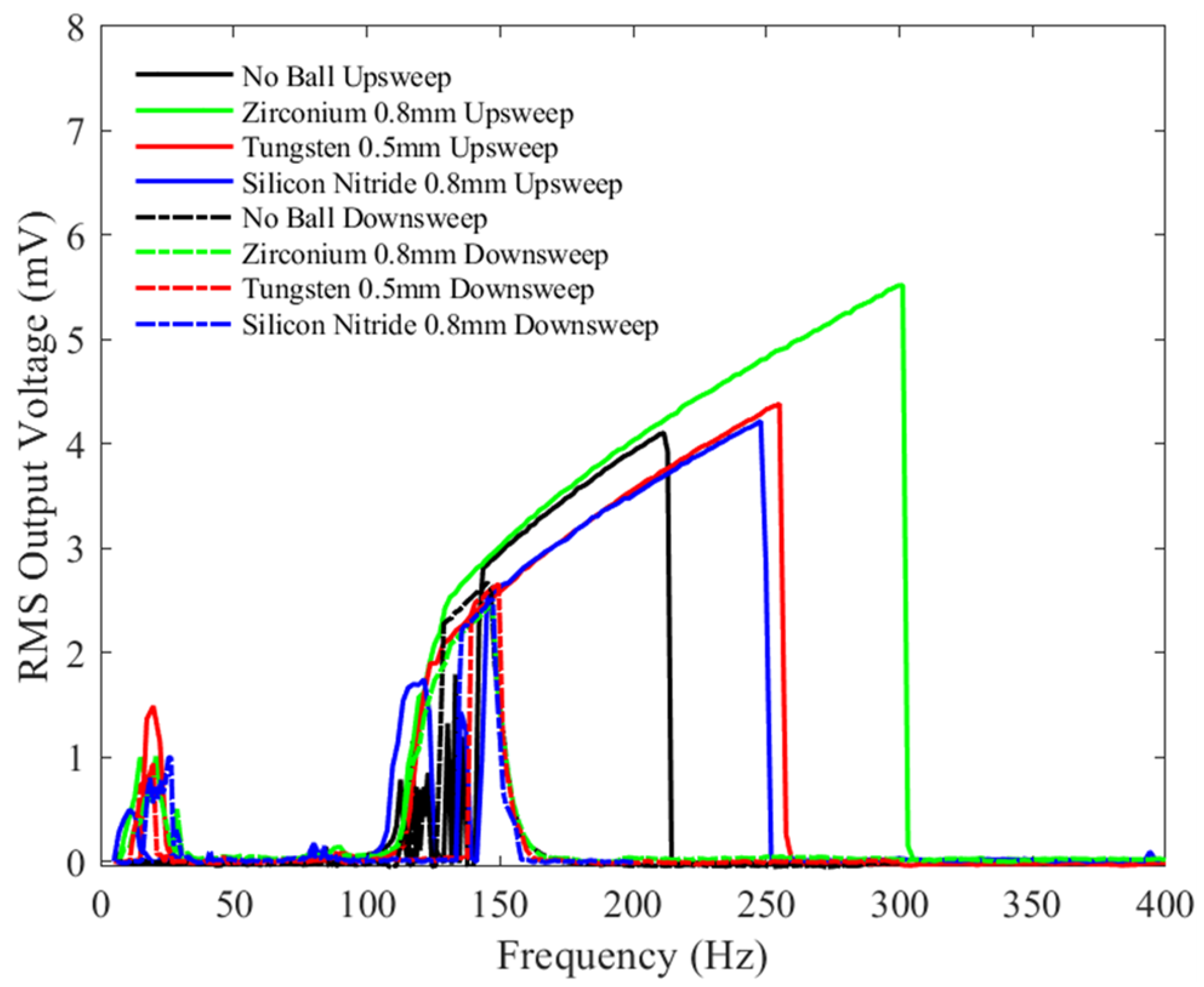
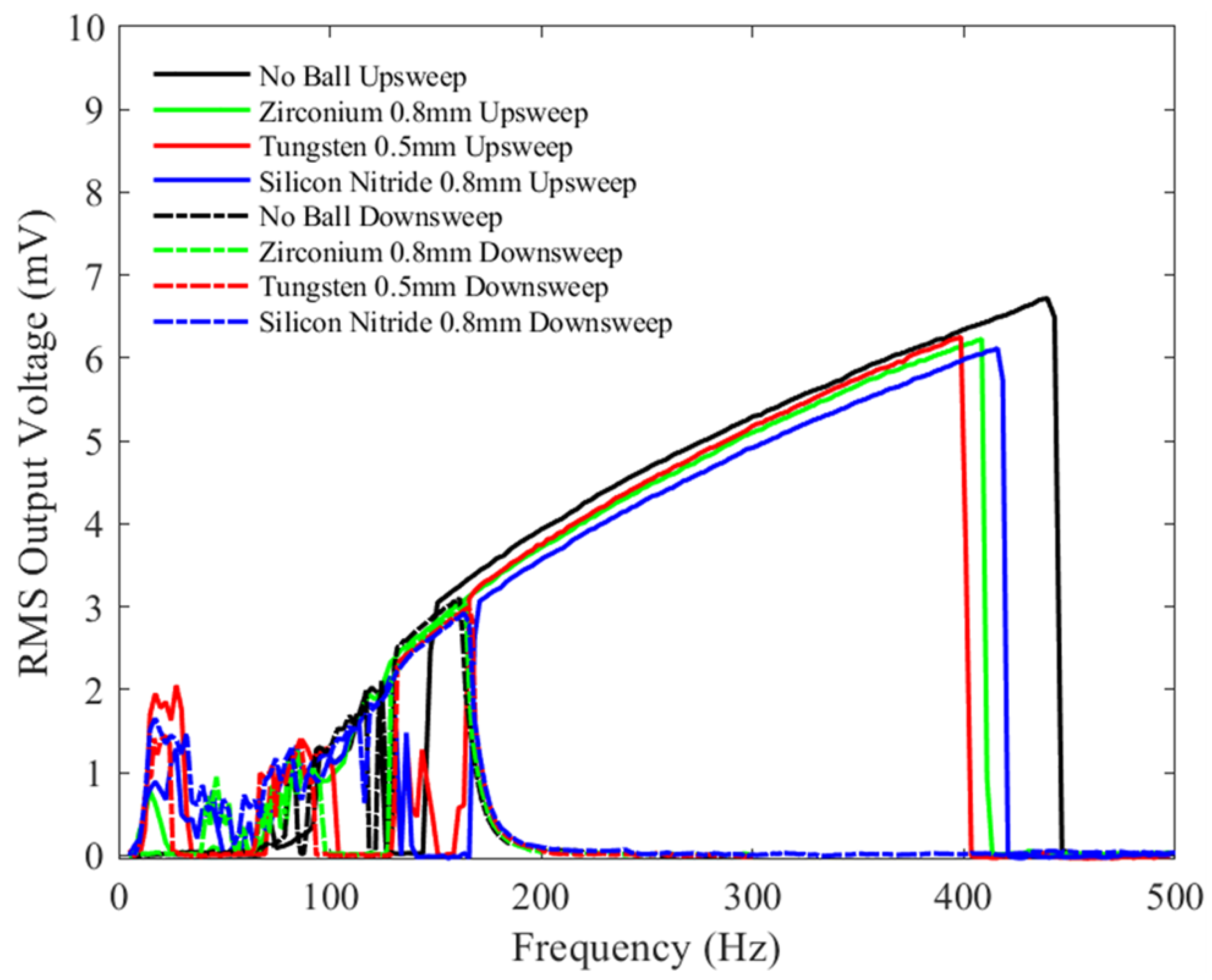
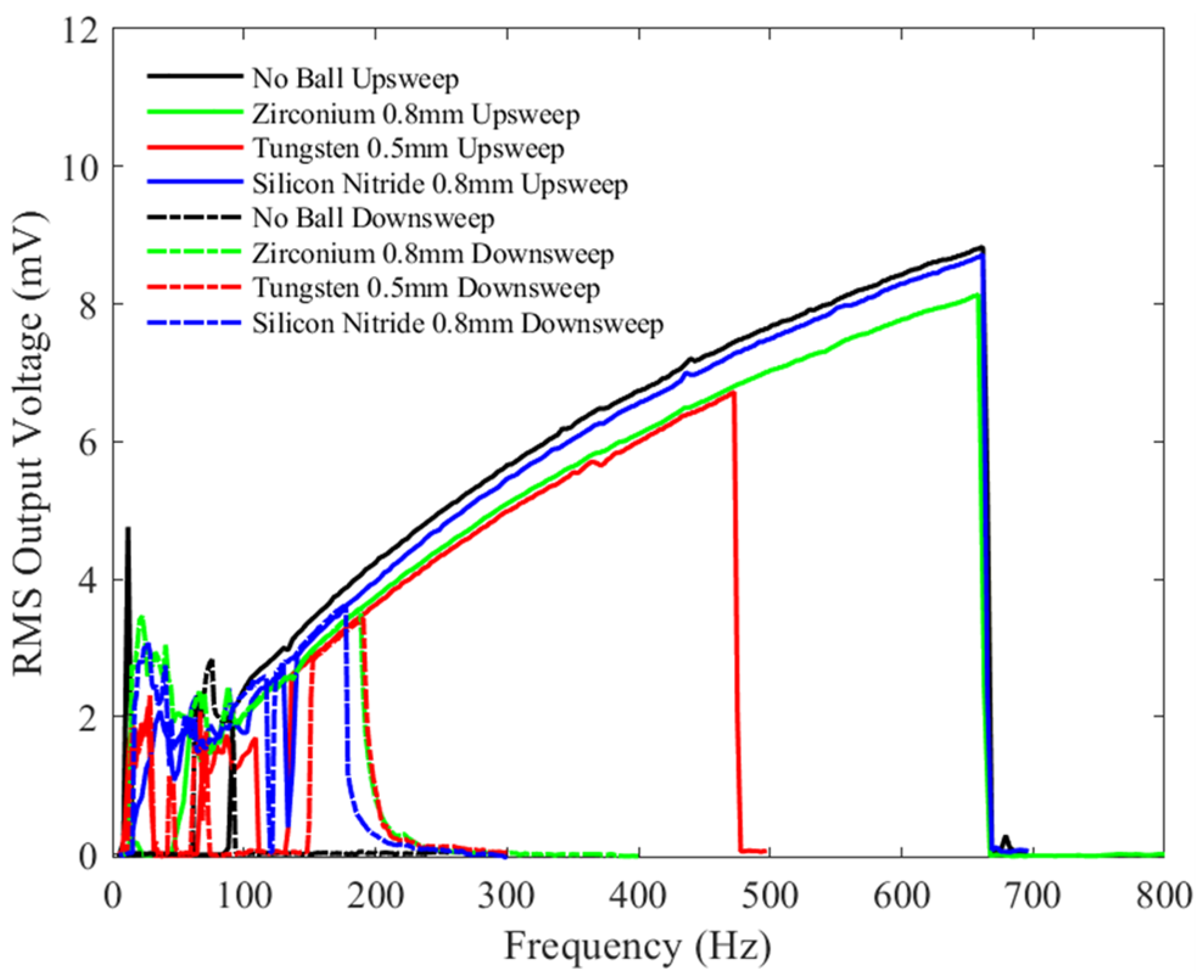
4.2. Device Behavior with Microballs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oxaal, J. Design, Simulation, Fabrication, and Characterization of MEMS Vibration Energy Harvesters. Ph.D. Thesis, Department of Mechanical, Aerospace, and Nuclear Engineering Rensselaer Polytechnic Institute, Troy, NY, USA, 2015. [Google Scholar]
- Oxaal, J.; Hella, M.; Borca-Tasciuc, D.A. Electrostatic MEMS vibration energy harvester for HVAC applications with impact-based frequency up-conversion. J. Micromech. Microeng. 2016, 26, 124012. [Google Scholar] [CrossRef]
- Li, J.; Chang, K.W.; Yang, C.H.; Shiesh, S.C.; Lee, G.B. Rapid and sensitive measurement of glycated hemoglobin for diabetes monitoring by using a two-aptamer assay on an integrated microfluidic system. In Proceedings of the MicroTAS 2014, San Antonio, TX, USA, 26–30 October 2014; pp. 1951–1953. [Google Scholar]
- Li, J.; Chang, K.W.; Wang, C.H.; Yang, C.H.; Shiesh, S.C.; Lee, G.B. On-chip, aptamer-based sandwich assay for detection of glycated hemoglobins via magnetic beads. Biosens. Bioelectron. 2016, 79, 887–893. [Google Scholar] [CrossRef]
- Chang, K.; Li, J.; Yang, C.; Shiesh, S.; Lee, G. Measurement of glycated hemoglobin using an aptamer/antibody assay on an integrated microfluidic system. In Proceedings of the International Conference on Nano/Micro Engineered and Molecular Systems, NEMS 2014, Waikiki Beach, HI, USA, 13–16 April 2014; pp. 647–650. [Google Scholar] [CrossRef]
- Yuan, P.; Wu, J.Y.; Ogletree, D.F.; Urban, J.J.; Dames, C.; Ma, Y. Adapting the electron beam from SEM as a quantitative heating source for nanoscale thermal metrology. Nano Lett. 2020, 20, 3019–3029. [Google Scholar] [CrossRef]
- Ren, Z.; Yuan, J.; Su, X.; Mangla, S.; Nam, C.Y.; Lu, M.; Tenney, S.; Shi, Y. Electro-thermal modeling and experimental validation for multilayered metallic microstructures. Microsyst. Technol. 2020, 27, 2041–2048. [Google Scholar] [CrossRef]
- Chang, K.W.; Li, J.; Yang, C.H.; Shiesh, S.C.; Lee, G.B. An integrated microfluidic system for measurement of glycated hemoglobin Levels by using an aptamer–antibody assay on magnetic beads. Biosens. Bioelectron. 2015, 68, 397–403. [Google Scholar] [CrossRef] [PubMed]
- Dong, S.; Duan, S.; Yang, Q.; Zhang, J.; Li, G.; Tao, R. MEMS-based smart gas metering for Internet of Things. IEEE Internet Things J. 2017, 4, 1296–1303. [Google Scholar] [CrossRef]
- Bishop, D.J.; Giles, C.R.; Austin, G.P. The Lucent LambdaRouter: MEMS technology of the future here today. IEEE Commun. Mag. 2002, 40, 75–79. [Google Scholar] [CrossRef]
- Hopfield, J.J. Artificial neural networks. IEEE Circuits Syst. Mag. 1988, 4, 3–10. [Google Scholar] [CrossRef]
- Chuang, W.C.; Lee, H.L.; Chang, P.Z.; Hu, Y.C. Review on the modeling of electrostatic MEMS. Sensors 2010, 10, 6149–6171. [Google Scholar] [CrossRef]
- Halvorsen, E. Energy harvesters driven by broadband random vibrations. J. Microelectromech. Syst. 2008, 17, 1061–1071. [Google Scholar] [CrossRef]
- Li, J. Electrostatic MEMS Energy Harvesting for Sensor Powering. Ph.D. Thesis, Dept. of Mechanical, Aerospace, and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY, USA, 2021. [Google Scholar]
- Gubbi, J.; Buyya, R.; Marusic, S.; Palaniswami, M. Internet of Things (IoT): A vision, architectural elements, and future directions. Future Gener. Comput. Syst. 2013, 29, 1645–1660. [Google Scholar] [CrossRef]
- Ouro-Koura, H.; Sotoudeh, Z.; Tichy, J.; Borca-Tasciuc, D.A. Effectiveness of Energy Transfer versus Mixing Entropy in Coupled Mechanical–Electrical Oscillators. Energies 2022, 15, 6105. [Google Scholar] [CrossRef]
- Li, J.; Ouro-Koura, H.; Arnow, H.; Nowbahari, A.; Galarza, M.; Obispo, M.; Tong, X.; Azadmehr, M.; Hella, M.M.; Tichy, J.A.; et al. A Novel Comb Design for Enhanced Power and Bandwidth in Electrostatic Mems Energy Converters. In Proceedings of the 2023 IEEE 36th International Conference on Micro Electro Mechanical Systems (MEMS), Munich, Germany, 15–19 January 2023; pp. 728–731. [Google Scholar] [CrossRef]
- Espinosa, H.D.; Zhu, Y.; Moldovan, N. Design and Operation of a MEMS-Based Material Testing System for Nanomechanical Characterization. J. Microelectromech. Syst. 2007, 16, 1219–1231. [Google Scholar] [CrossRef]
- Basset, P.; Galayko, D.; Cottone, F.; Guillemet, R.; Blokhina, E.; Marty, F.; Bourouina, T. Electrostatic vibration energy harvester with combined effect of electrical nonlinearities and mechanical impact. J. Micromech. Microeng. 2014, 24, 035001. [Google Scholar] [CrossRef]
- Eddy, D.S.; Sparks, D.R. Application of MEMS technology in automotive sensors and actuators. Proc. IEEE 1998, 86, 1747–1755. [Google Scholar] [CrossRef]
- André, N.; Rue, B.; Scheen, G.; Flandre, D.; Francis, L.A.; Raskin, J.P. Out-of-plane MEMS-based mechanical airflow sensor co-integrated in SOI CMOS technology. Sens. Actuators A 2014, 206, 67–74. [Google Scholar] [CrossRef]
- Han, D.; Yun, K.S. Piezoelectric energy harvester using mechanical frequency up conversion for operation at low-level accelerations and low-frequency vibration. Microsyst. Technol. 2015, 21, 1669–1676. [Google Scholar] [CrossRef]
- Ferrari, M.; Ferrari, V.; Guizzetti, M.; Marioli, D.; Taroni, A. Piezoelectric multifrequency energy converter for power harvesting in autonomous microsystems. Sens. Actuator A Phys. 2008, 142, 329–335. [Google Scholar] [CrossRef]
- Zorlu, Ö.; Topal, E.T.; Külah, H. A Vibration-Based Electromagnetic Energy Harvester Using Mechanical Frequency Up-Conversion Method. IEEE Sens. J. 2011, 11, 481–488. [Google Scholar] [CrossRef]
- Khan, F.; Sassani, F.; Stoeber, B. Copper foil-type vibration-based electromagnetic energy harvester. J. Micromech. Microeng. 2010, 20, 125006. [Google Scholar] [CrossRef]
- Beeby, S.P.; Torah, R.N.; Tudor, M.J.; Glynne-Jones, P.; O’Donnell, T.; Saha, C.R.; Roy, S. A micro electromagnetic generator for vibration energy harvesting. J. Micromech. Microeng. 2007, 17, 1257. [Google Scholar] [CrossRef]
- Szarka, G.D.; Burrow, S.G.; Proynov, P.P.; Stark, B.H. Maximum power transfer tracking for ultralow-power electromagnetic energy harvesters. IEEE Trans. Power Electron. 2014, 29, 201–212. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, N.; Arnold, D.P. Modeling of magnetic vibrational energy harvesters using equivalent circuit representations. J. Micromech. Microeng. 2007, 17, 2328. [Google Scholar] [CrossRef]
- Chiu, Y.; Lee, Y.C. Flat and robust out-of-plane vibrational electret energy harvester. J. Micromech. Microeng. 2013, 23, 015012. [Google Scholar] [CrossRef]
- Janphuang, P.; Lockhart, R.A.; Isarakorn, D.; Henein, S.; Briand, D.; de Rooij, N.F. Harvesting energy from a rotating gear using an AFM-like MEMS piezoelectric frequency up-converting energy harvester. J. Microelectromech. Syst. 2014, 24, 742–754. [Google Scholar] [CrossRef]
- Li, J.; Xu, C.; Tichy, J.; Borca-Tasciuc, D.A. A 1D model for design and predicting dynamic behavior of out-of-plane MEMS. J. Micromech. Microeng. 2018, 28, 085021. [Google Scholar] [CrossRef]
- Li, J.; Tong, X.; Oxaal, J.; Liu, Z.; Hella, M.; Borca-Tasciuc, D.A. Investigation of parallel-connected MEMS electrostatic energy harvesters for enhancing output power over a wide frequency range. J. Micromech. Microeng. 2019, 29, 094001. [Google Scholar] [CrossRef]
- Li, J.; Tichy, J.; Borca-Tasciuc, D.A. A predictive model for electrostatic energy harvesters with impact-based frequency up-conversion. J. Micromech. Microeng. 2020, 30, 125012. [Google Scholar] [CrossRef]
- Soliman, M.S.M.; Abdel-Rahman, E.M.; El-Saadany, E.F.; Mansour, R.R. A wideband vibration-based energy harvester. J. Micromech. Microeng. 2008, 18, 115021. [Google Scholar] [CrossRef]
- Kempitiya, A.; Borca-Tasciuc, D.A.; Hella, M.M. Low-power ASIC for microwatt electrostatic energy harvesters. IEEE Trans. Ind. Electron. 2012, 60, 5639–5647. [Google Scholar] [CrossRef]
- Basset, P.; Galayko, D.; Paracha, A.M.; Marty, F.; Dudka, A.; Bourouina, T. A batch-fabricated and electret-free silicon electrostatic vibration energy harvester. J. Micromech. Microeng. 2009, 19, 115025. [Google Scholar] [CrossRef]
- Lu, Y.; Juillard, J.; Cottone, F.; Galayko, D.; Basset, P. An Impact-Coupled MEMS Electrostatic Kinetic Energy Harvester and Its Predictive Model Taking Nonlinear Air Damping Effect Into Account. J. Microelectromech. Syst. 2018, 27, 1041–1053. [Google Scholar] [CrossRef]
- Lu, Y.; Cottone, F.; Boisseau, S.; Marty, F.; Galayko, D.; Basset, P. A nonlinear MEMS electrostatic kinetic energy harvester for human-powered biomedical devices. Appl. Phys. Lett. 2015, 107, 253902. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.K.; Rabaey, J. A study of low level vibrations as a power source for wireless sensor nodes. Comput. Commun. 2003, 26, 1131–1144. [Google Scholar] [CrossRef]
- Cowen, A.; Hames, G.; Monk, D.; Wilcenski, S.; Hardy, B. SOIMUMPs Design Handbook; Memscap Inc.: Durham, NC, USA, 2011; pp. 2002–2011. [Google Scholar]
- Kaur, S.; Halvorsen, E. Parameter sensitivity of an in-plane gap closing electrostatic energy harvester with end-stop impacts. J. Intell. Mater. Syst. Struct. 2017, 28, 1640–1650. [Google Scholar] [CrossRef]
- Oxaal, J.; Foster, D.; Hella, M.; Borca-Tasciuc, D.A. Investigation of gap-closing interdigitated capacitors for electrostatic vibration energy harvesting. J. Micromech. Microeng. 2015, 25, 105010. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Total device area | |
| Thickness of the silicon layer | |
| Minimum electrode width | |
| Maximum electrode width | |
| Electrodes overlap length | |
| Electrode length | |
| Nominal gap between the electrodes (narrowest point) | |
| Nominal gap between the electrodes (wide point) | |
| Number of electrode pairs | 80 |
| Size of the cavity housing the ball | |
| Thickness of the parylene film | |
| Length of the silicon shuttle mass | |
| Width of the silicon shuttle mass |
| Material | Diameter | Mass |
|---|---|---|
| Tungsten Carbide | ||
| Tungsten Carbide | ||
| Zirconium Dioxide | ||
| Silicon Nitride |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Ouro-Koura, H.; Arnow, H.; Nowbahari, A.; Galarza, M.; Obispo, M.; Tong, X.; Azadmehr, M.; Halvorsen, E.; Hella, M.M.; et al. Broadband Vibration-Based Energy Harvesting for Wireless Sensor Applications Using Frequency Upconversion. Sensors 2023, 23, 5296. https://doi.org/10.3390/s23115296
Li J, Ouro-Koura H, Arnow H, Nowbahari A, Galarza M, Obispo M, Tong X, Azadmehr M, Halvorsen E, Hella MM, et al. Broadband Vibration-Based Energy Harvesting for Wireless Sensor Applications Using Frequency Upconversion. Sensors. 2023; 23(11):5296. https://doi.org/10.3390/s23115296
Chicago/Turabian StyleLi, Jinglun, Habilou Ouro-Koura, Hannah Arnow, Arian Nowbahari, Matthew Galarza, Meg Obispo, Xing Tong, Mehdi Azadmehr, Einar Halvorsen, Mona M. Hella, and et al. 2023. "Broadband Vibration-Based Energy Harvesting for Wireless Sensor Applications Using Frequency Upconversion" Sensors 23, no. 11: 5296. https://doi.org/10.3390/s23115296
APA StyleLi, J., Ouro-Koura, H., Arnow, H., Nowbahari, A., Galarza, M., Obispo, M., Tong, X., Azadmehr, M., Halvorsen, E., Hella, M. M., Tichy, J. A., & Borca-Tasciuc, D.-A. (2023). Broadband Vibration-Based Energy Harvesting for Wireless Sensor Applications Using Frequency Upconversion. Sensors, 23(11), 5296. https://doi.org/10.3390/s23115296









