A Coherent Wideband Acoustic Source Localization Using a Uniform Circular Array
Abstract
1. Introduction
2. Array Manifold Interpolation
2.1. Signal Model
2.2. The Array Manifold Interpolation Method
3. The Proposed Method
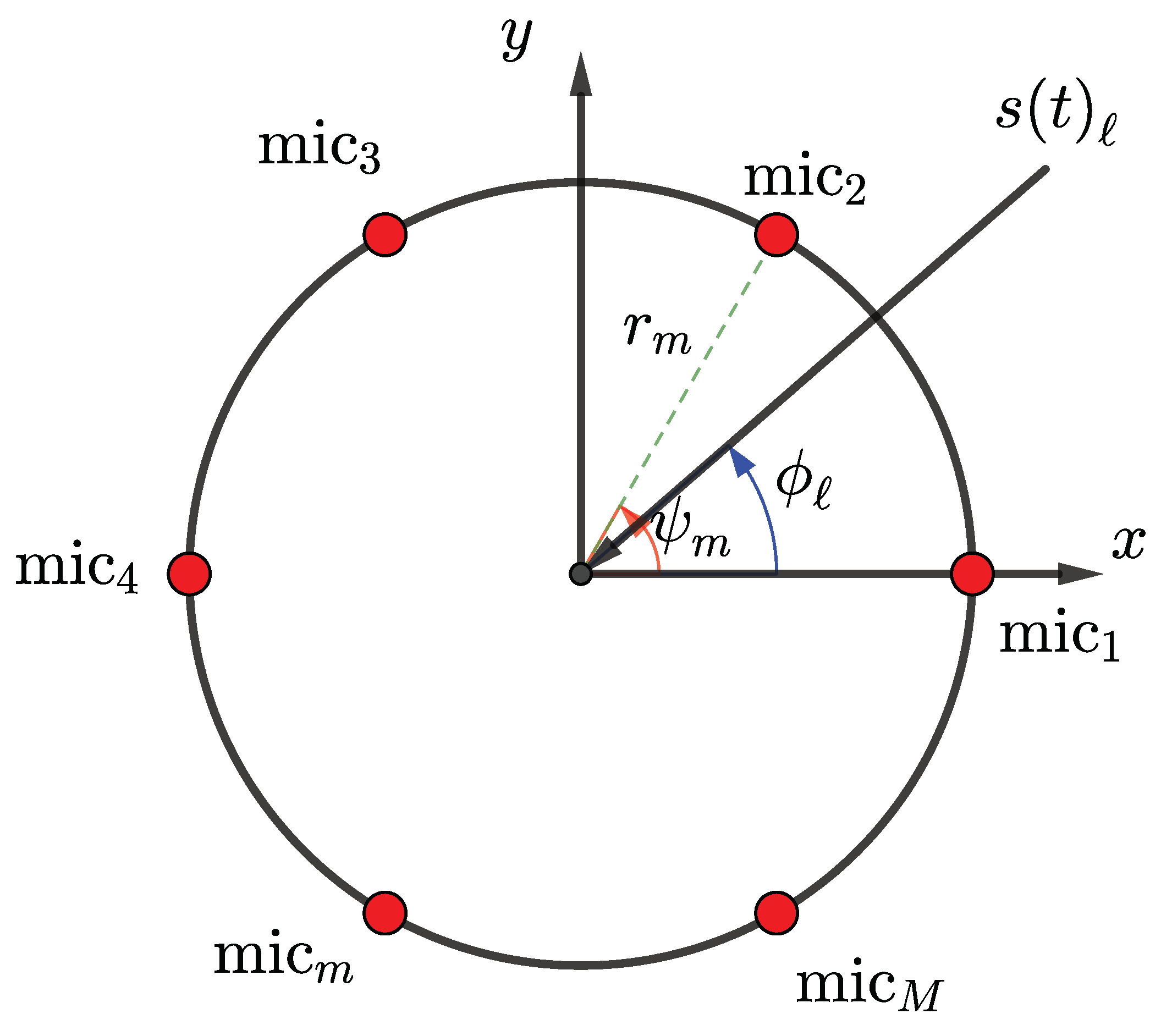
3.1. For the Uniform Circular Array
3.2. The Proposed Focusing Matrix
3.3. Approximation Error
3.4. Computational Complexity
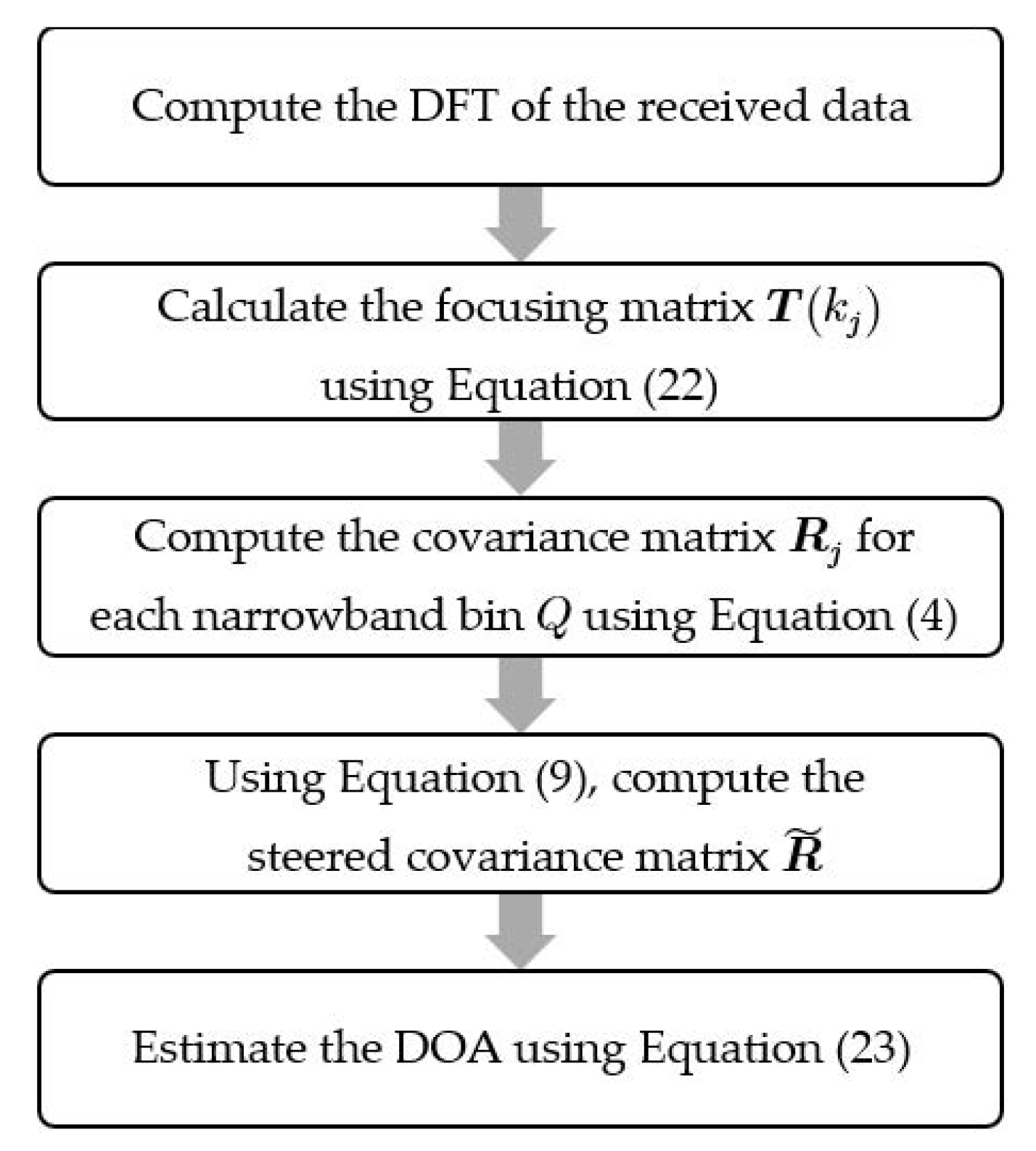
3.5. Direction of Arrival Estimation
4. Monte Carlo Simulations to Test the Efficacy of the Proposed Method
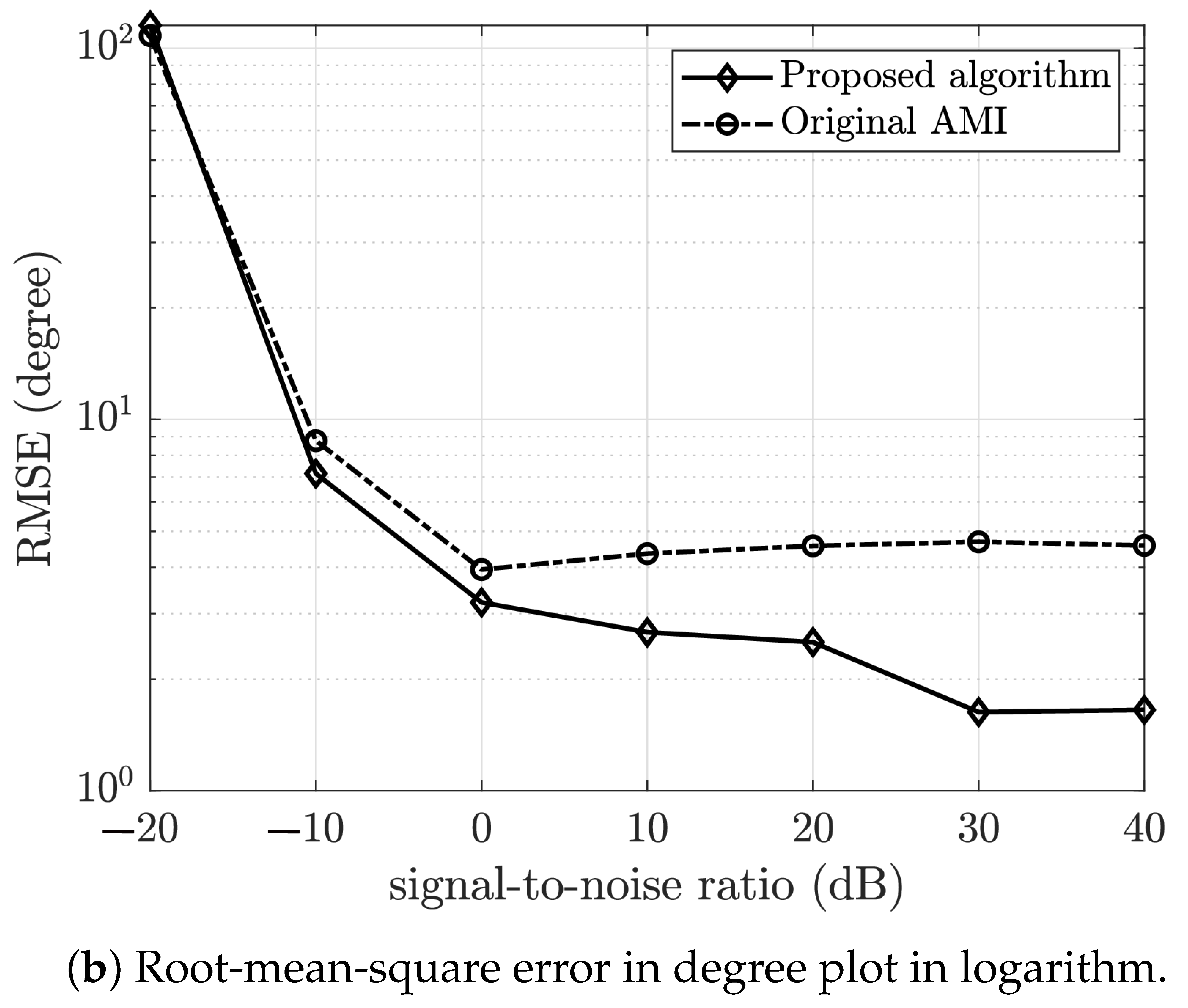
4.1. Root-Mean-Square Performance
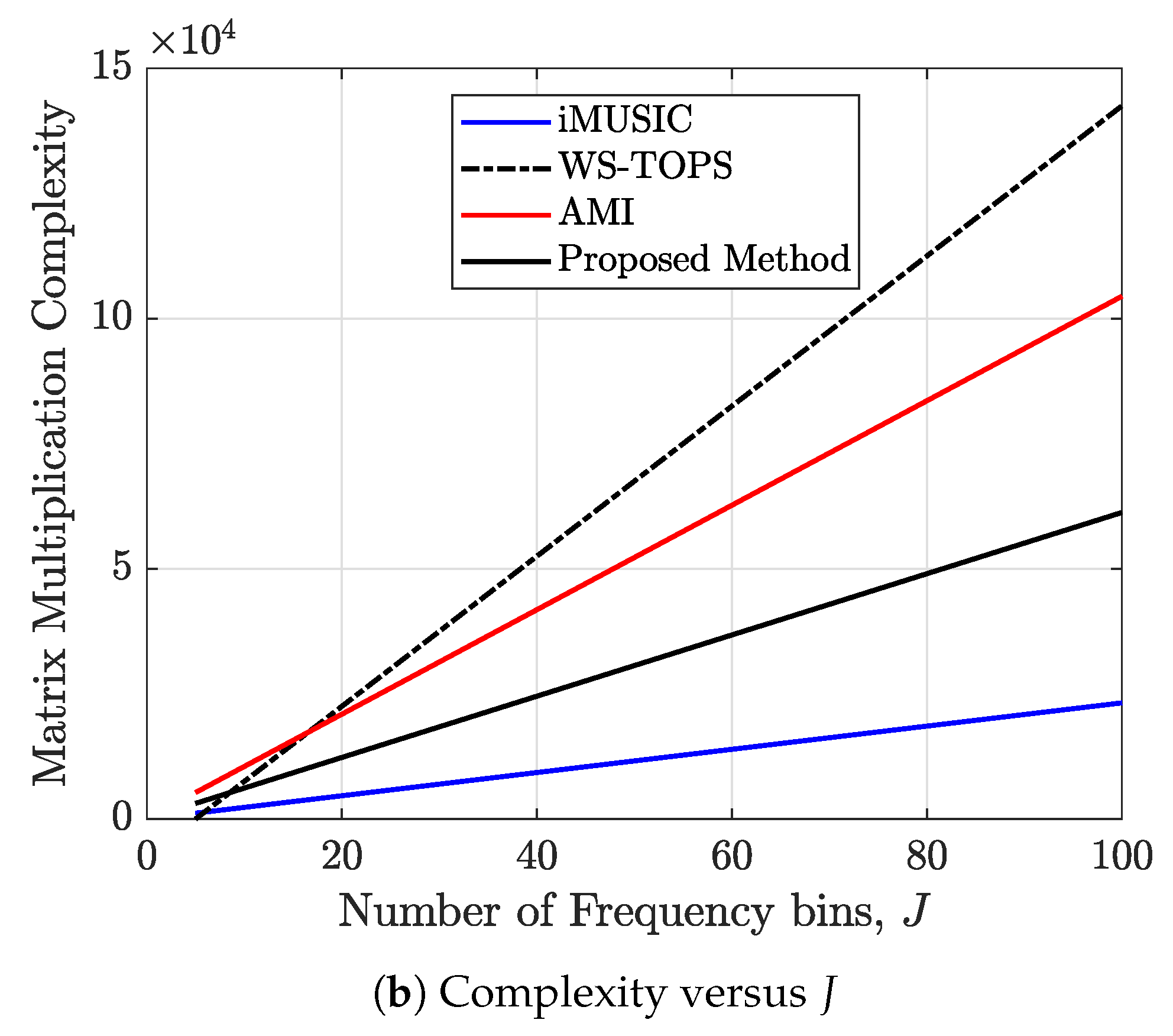
4.2. Computational Efficiency of the Proposed Algorithm
5. Experimental Evaluation
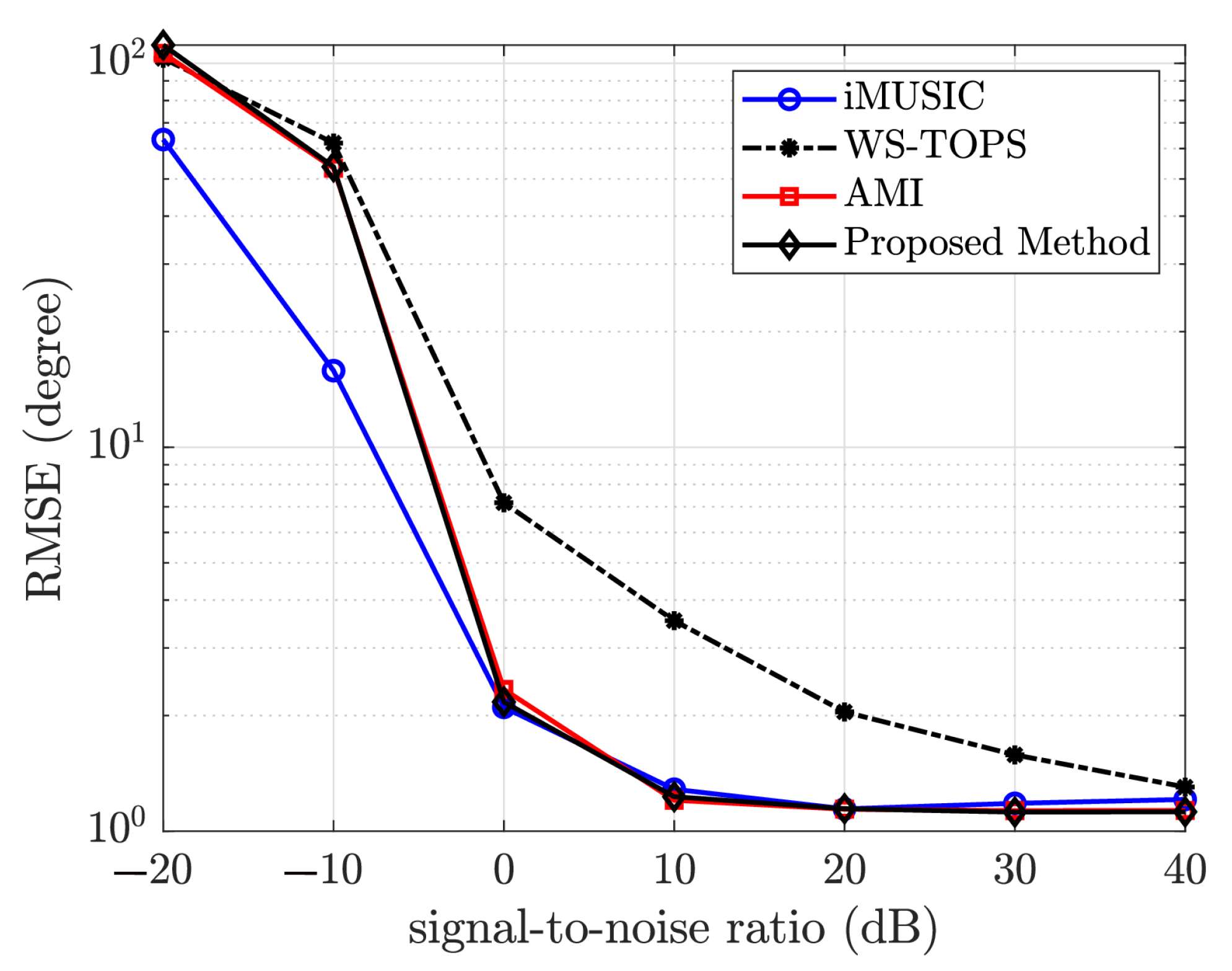
5.1. Root-Mean-Square Error Performance versus Signal-to-Noise Ratio
5.2. Performance by Central Processing Frequency
5.3. Performance for Different Types of Sources
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dehghan Firoozabadi, A.; Irarrazaval, P.; Adasme, P.; Zabala-Blanco, D.; Játiva, P.P.; Azurdia-Meza, C. 3D Multiple Sound Source Localization by Proposed T-Shaped Circular Distributed Microphone Arrays in Combination with GEVD and Adaptive GCC-PHAT/ML Algorithms. Sensors 2022, 22, 1011. [Google Scholar] [CrossRef]
- Zhang, C.; Florêncio, D.; Ba, D.E.; Zhang, Z. Maximum likelihood sound source localization and beamforming for directional microphone arrays in distributed meetings. IEEE Trans. Multimed. 2008, 10, 538–548. [Google Scholar] [CrossRef]
- Rascon, C.; Meza, I. Localization of sound sources in robotics: A review. Robot. Auton. Syst. 2017, 96, 184–210. [Google Scholar] [CrossRef]
- Deleforge, A.; Di Carlo, D.; Strauss, M.; Serizel, R.; Marcenaro, L. Audio-based search and rescue with a drone: Highlights from the IEEE signal processing cup 2019 student competition [SP competitions]. IEEE Signal Process. Mag. 2019, 36, 138–144. [Google Scholar] [CrossRef]
- Roseveare, N.J.; Azimi-Sadjadi, M.R. Robust beamforming algorithms for acoustic tracking of ground vehicles. In Proceedings of the Unattended Ground, Sea, and Air Sensor Technologies and Applications VIII, Kissimmee, FL, USA, 17–20 April 2006; Carapezza, E.M., Ed.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2006; Volume 6231, pp. 51–62. [Google Scholar] [CrossRef]
- Ribeiro, F.; Florencio, D.; Ba, D.; Zhang, C. Geometrically Constrained Room Modeling With Compact Microphone Arrays. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1449–1460. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple Emitter Location and Signal Parameter Estimation. IEEE Trans. Antennas Propag. 1986, AP-34, 276–280. [Google Scholar] [CrossRef]
- Vallet, P.; Mestre, X.; Loubaton, P. Performance Analysis of an Improved MUSIC DoA Estimator. IEEE Trans. Signal Process. 2015, 63, 6407–6422. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT—Estimation of Signal Parameters Via Rotational Invariance Techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Ferguson, B.G. Minimum variance distortionless response beamforming of acoustic array data. J. Acoust. Soc. Am. 1998, 104, 947–954. [Google Scholar] [CrossRef]
- Kiong, T.S.; Salem, S.B.; Paw, J.K.S.; Sankar, K.P.; Darzi, S. Minimum Variance Distortionless Response Beamformer with Enhanced Nulling Level Control via Dynamic Mutated Artificial Immune System. Sci. World J. 2014, 2014, 164053. [Google Scholar] [CrossRef]
- Knapp, C.; Carter, G. The generalized correlation method for estimation of time delay. IEEE Trans. Acoust. Speech Signal Process. 1976, 24, 320–327. [Google Scholar] [CrossRef]
- Gombots, S.; Nowak, J. Sound source localization—State of the art and new inverse scheme. Elektrotechnik Und Informationstechnik 2021, 138, 229–243. [Google Scholar] [CrossRef]
- Su, G.; Morf, M. The signal subspace approach for multiple wide-band emitter location. IEEE Trans. Acoust. Speech Signal Process. 1983, 31, 1502–1522. [Google Scholar] [CrossRef]
- Yoon, Y.S.; Kaplan, L.; McClellan, J. TOPS: New DOA estimator for wideband signals. IEEE Trans. Signal Process. 2006, 54, 1977–1989. [Google Scholar] [CrossRef]
- Yu, H.; Liu, J.; Huang, Z.; Zhou, Y.; Xu, X. A New Method for Wideband DOA Estimation. In Proceedings of the 2007 International Conference on Wireless Communications, Networking and Mobile Computing, Shanghai, China, 21–25 September 2007; pp. 598–601. [Google Scholar] [CrossRef]
- Hayashi, H.; Ohtsuki, T. DOA estimation for wideband signals based on weighted Squared TOPS. EURASIP J. Wirel. Commun. Netw. 2016, 2016, 243. [Google Scholar] [CrossRef]
- Pham, T.; Sadler, B. Adaptive wideband aeroacoustic array processing. In Proceedings of the 8th Workshop on Statistical Signal and Array Processing, Corfu, Greece, 24–26 June 1996; pp. 295–298. [Google Scholar] [CrossRef]
- Wang, H.; Kaveh, M. Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 823–831. [Google Scholar] [CrossRef]
- Valaee, S.; Champagne, B.; Kabal, P. Localization of wideband signals using least-squares and total least-squares approaches. IEEE Trans. Signal Process. 1999, 47, 1213–1222. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, Y.; Wang, Z. Low complexity subspace fitting method for wideband signal location. In Proceedings of the 2008 5th IFIP International Conference on Wireless and Optical Communications Networks (WOCN’08), Surabaya, Indonesia, 5–7 May 2008; pp. 1–4. [Google Scholar] [CrossRef]
- Xu, W.; Chen, B.; Hu, Y.; Li, J. A Novel Wide-Band Directional MUSIC Algorithm Using the Strength Proportion. Sensors 2023, 23, 4562. [Google Scholar] [CrossRef] [PubMed]
- Doron, M.; Doron, E.; Weiss, A. Coherent wide-band processing for arbitrary array geometry. IEEE Trans. Signal Process. 1993, 41, 414–417. [Google Scholar] [CrossRef]
- Zhao, D.; Deng, Z.; Tan, W. Low-Complexity DOA Estimation for Uniform Circular Arrays with Directional Sensors Using Reconfigurable Steering Vectors. Circuits Syst. Signal Process. 2023, 42, 1685–1706. [Google Scholar] [CrossRef]
- Anand, G.; Koul, A.; Gurugopinath, S.; Nagesha, P. Residual Data Vector Method of Underwater Acoustic Source Localization by a Three-Dimensional Array. In Proceedings of the OCEANS 2022-Chennai, Chennai, India, 21–24 February 2022; pp. 1–6. [Google Scholar]
- Suksiri, B.; Fukumoto, M. A computationally efficient wideband direction-of-arrival estimation method for l-shaped microphone arrays. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions With Formulas, Graphs, and Mathematical Tables; United States Department of Commerce, National Bureau of Standards: Washington, DC, USA, 1972.
- Karatsuba, E.A. Calculation of Bessel Functions via the Summation of Series. Numer. Anal. Appl. 2019, 12, 372–387. [Google Scholar] [CrossRef]
- Harvey, D.; van Der Hoeven, J. Integer multiplication in time O(n log n). Ann. Math. 2021, 193, 563–617. [Google Scholar] [CrossRef]
- Salman, T.; Badawy, A.; Elfouly, T.M.; Mohamed, A.; Khattab, T. Estimating the number of sources: An efficient maximization approach. In Proceedings of the 2015 International Wireless Communications and Mobile Computing Conference (IWCMC), Dubrovnik, Croatia, 24–28 August 2015; pp. 199–204. [Google Scholar] [CrossRef]
- Williams, D. Detection: Determining the Number of Sources. In Digital Signal Processing Handbook; Madisetti, V.K., Williams, D.B., Eds.; CRC Press LLC: Boca Raton, FL, USA, 1999. [Google Scholar]
- MiniDSP. UMA-8 USB Mic Array—V2.0. Available online: https://www.minidsp.com/products/usb-audio-interface/uma-8-microphone-array (accessed on 24 October 2022).






| Method | Matrix Multiplication |
|---|---|
| iMUSIC | |
| WS-TOPS | |
| AMI | |
| Proposed Method |
| Method | Eigen Decomposition | Singular-Value Decomposition |
|---|---|---|
| iMUSIC | not required | |
| WS-TOPS | ||
| AMI | not required | |
| Proposed Method | not required |
| Source | Original AMI | Proposed Algorithm |
|---|---|---|
| Car engine | 2.9969 | |
| water fall | 0.6235 | |
| Hovering drone | 1.8102 | |
| Electric fan | 2.3723 | |
| Train engine | 1.2502 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, M.; Nnonyelu, C.J.; Lundgren, J.; Thungström, G.; Sjöström, M. A Coherent Wideband Acoustic Source Localization Using a Uniform Circular Array. Sensors 2023, 23, 5061. https://doi.org/10.3390/s23115061
Jiang M, Nnonyelu CJ, Lundgren J, Thungström G, Sjöström M. A Coherent Wideband Acoustic Source Localization Using a Uniform Circular Array. Sensors. 2023; 23(11):5061. https://doi.org/10.3390/s23115061
Chicago/Turabian StyleJiang, Meng, Chibuzo Joseph Nnonyelu, Jan Lundgren, Göran Thungström, and Mårten Sjöström. 2023. "A Coherent Wideband Acoustic Source Localization Using a Uniform Circular Array" Sensors 23, no. 11: 5061. https://doi.org/10.3390/s23115061
APA StyleJiang, M., Nnonyelu, C. J., Lundgren, J., Thungström, G., & Sjöström, M. (2023). A Coherent Wideband Acoustic Source Localization Using a Uniform Circular Array. Sensors, 23(11), 5061. https://doi.org/10.3390/s23115061








