Unsupervised Anomaly Detection for Cars CAN Sensors Time Series Using Small Recurrent and Convolutional Neural Networks
Abstract
1. Introduction and Related Work
2. Car Time Series Extracted from the CAN Bus
2.1. The Data and the Car
2.2. Our Dataset
2.3. Labels
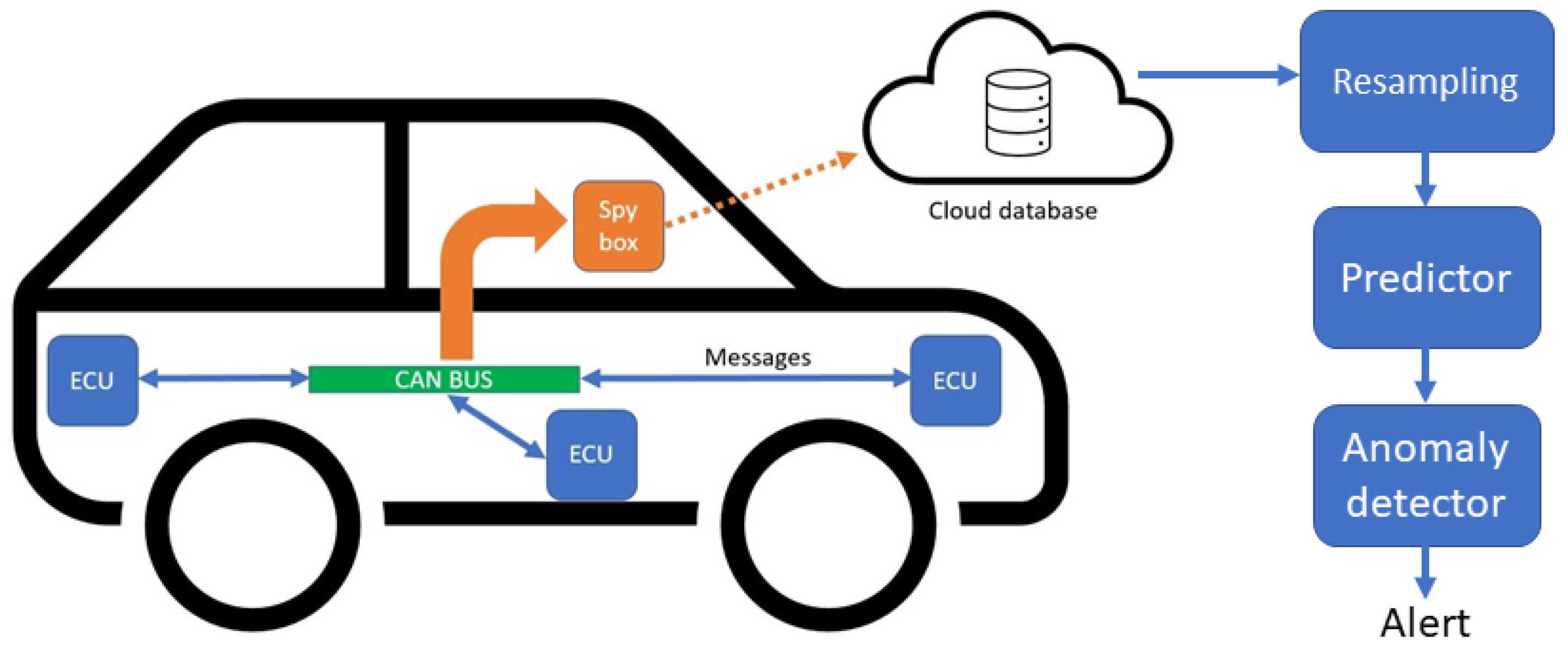
3. System Model and Problem Formulation
3.1. System Model
3.2. Unsupervised Anomaly Detection
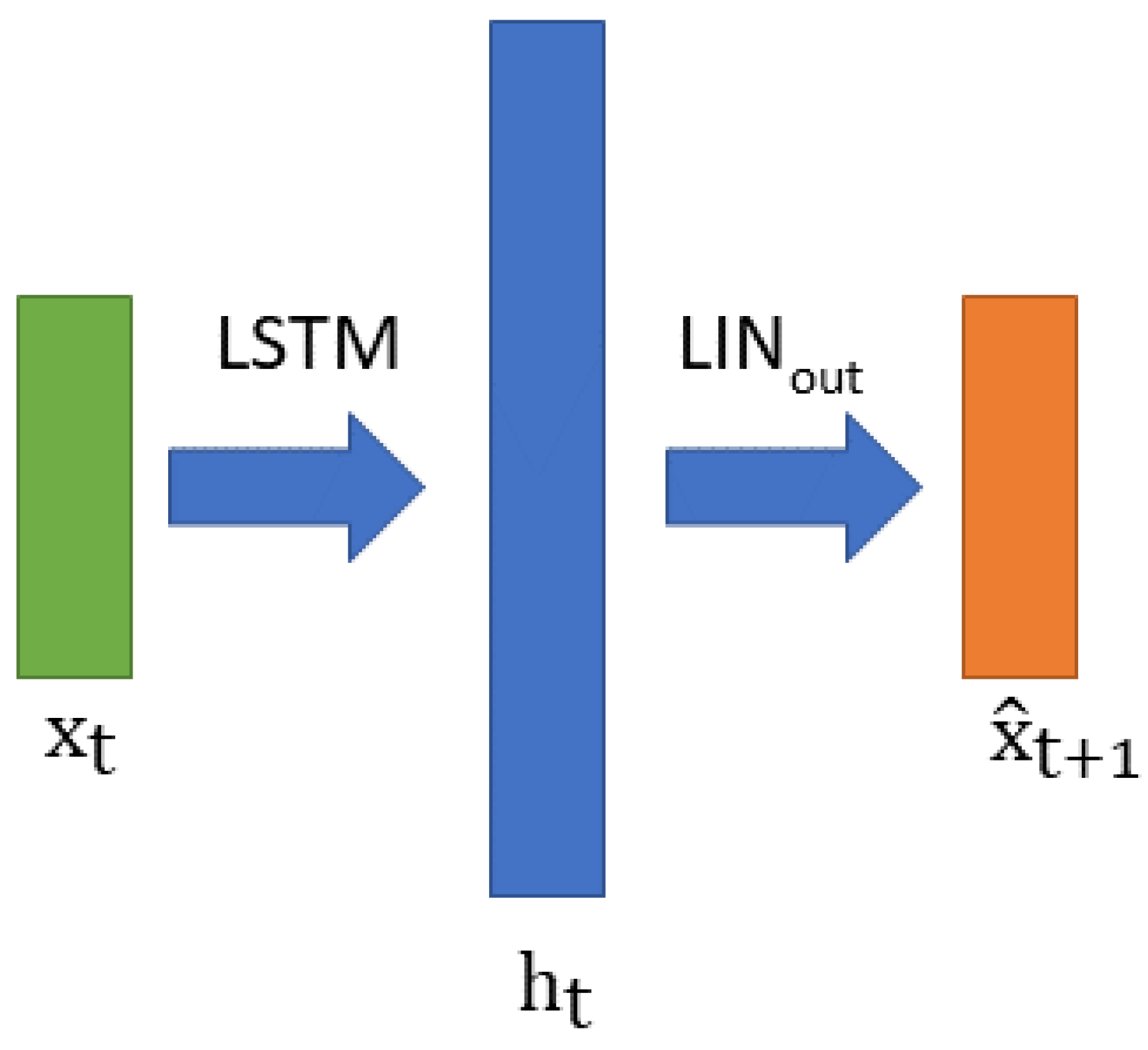
3.3. LSTM Predictor
3.4. CNN Predictor
3.5. GRU Predictor
3.6. Anomaly Detection
4. Results
4.1. Evaluation with Labels (Oil Pressure Failure)
4.2. LSTM Computation Costs Comparison
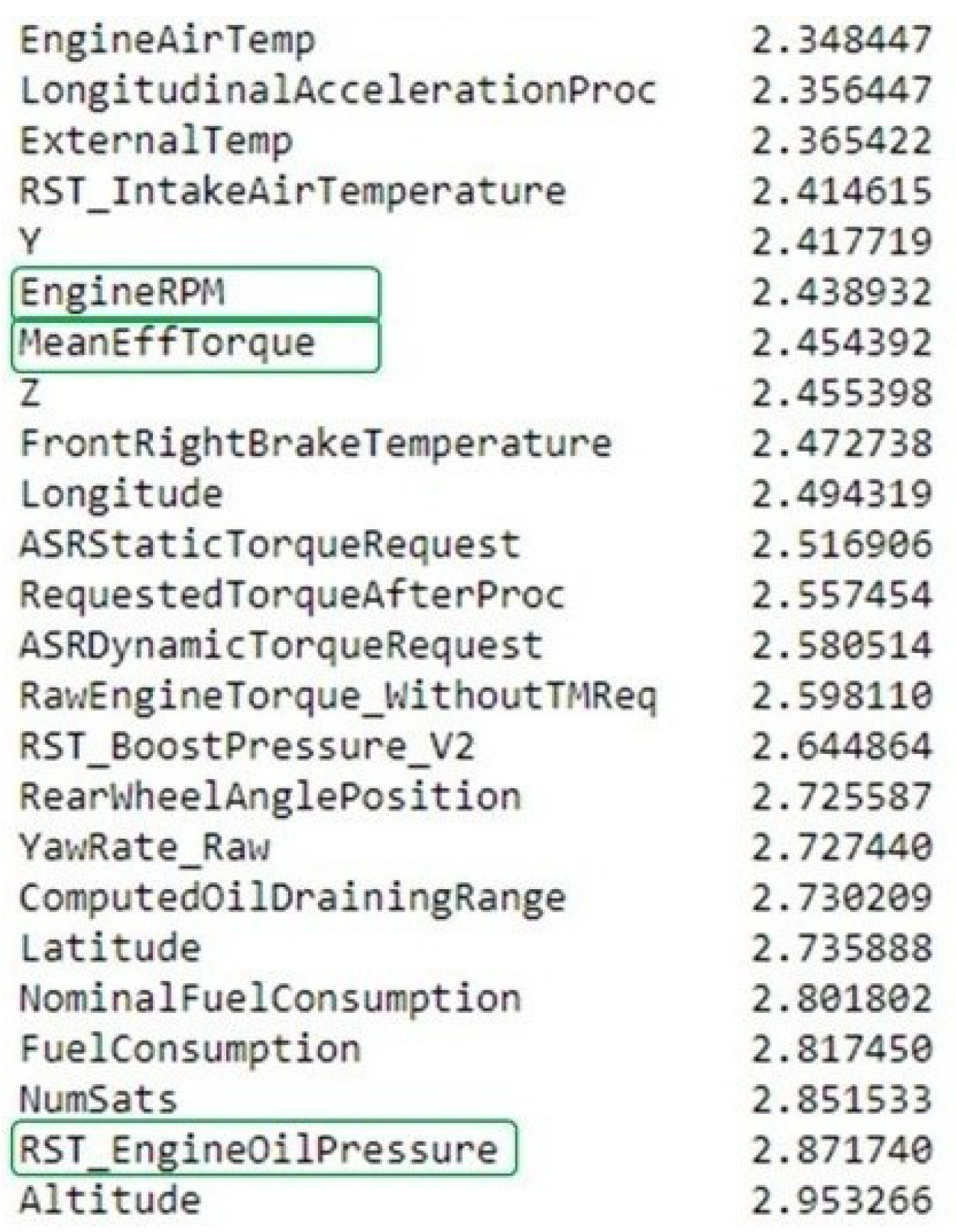
4.3. Correlation of Variables with Labels
5. Discussion and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41, 15. [Google Scholar] [CrossRef]
- Shaukat, K.; Alam, T.M.; Luo, S.; Shabbir, S.; Hameed, I.A.; Li, J.; Abbas, S.K.; Javed, U. A review of time-series anomaly detection techniques: A step to future perspectives. In Advances in Information and Communication, Proceedings of the 2021 Future of Information and Communication Conference (FICC), Vancouver, BC, Canada, 29–30 April 2021; Springer: Berlin/Heidelberg, Germany, 2021; Volume 1, pp. 865–877. [Google Scholar]
- Guha, S.; Mishra, N.; Roy, G.; Schrijvers, O. Robust random cut forest based anomaly detection on streams. In Proceedings of the 33rd International Conference on International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Kejariwal, A. Introducing Practical and Robust Anomaly Detection in a Time Series. Twitter Engineering Blog. Web, 15. 2015. Available online: https://blog.twitter.com/engineering/en_us/a/2015/introducing-practical-and-robust-anomaly-detection-in-a-time-series (accessed on 12 January 2022).
- Stanway, A. Etsy Skyline. Online Code Repos. 2013. Available online: https://github.com/etsy.skyline (accessed on 12 January 2022).
- Laptev, N.; Amizadeh, S.; Flint, I. Generic and scalable framework for automated time-series anomaly detection. In Proceedings of the ACM SIGKDD International Conference, Sydney, NSW, Australia, 10–13 August 2015; pp. 1939–1947. [Google Scholar]
- Ahmad, S.; Lavin, A.; Purdy, S.; Agha, Z. Unsupervised real-time anomaly detection for streaming data. Neurocomputing 2017, 262, 134–147. [Google Scholar] [CrossRef]
- Widanage, C.; Li, J.; Tyagi, S.; Teja, R.; Peng, B.; Kamburugamuve, S.; Baum, D.; Smith, D.; Qiu, J.; Koskey, J. Anomaly detection over streaming data: Indy500 case study. In Proceedings of the 2019 IEEE 12th International Conference on Cloud Computing (CLOUD), Milan, Italy, 8–13 July 2019; pp. 9–16. [Google Scholar]
- Maciąg, P.S.; Kryszkiewicz, M.; Bembenik, R.; Lobo, J.L.; Del Ser, J. Unsupervised anomaly detection in stream data with online evolving spiking neural networks. Neural Netw. 2021, 139, 118–139. [Google Scholar] [CrossRef] [PubMed]
- Munir, M.; Siddiqui, S.; Dengel, A.; Ahmed, S. DeepAnT: A Deep Learning Approach for Unsupervised Anomaly Detection in Time Series. IEEE Access 2019, 7, 1991–2005. [Google Scholar] [CrossRef]
- Ren, H.; Xu, B.; Wang, Y.; Yi, C.; Huang, C.; Kou, X.; Xing, T.; Yang, M.; Tong, J.; Zhang, Q. Time-series anomaly detection service at microsoft. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 3009–3017. [Google Scholar]
- Zhao, H.; Wang, Y.; Duan, J.; Huang, C.; Cao, D.; Tong, Y.; Xu, B.; Bai, J.; Tong, J.; Zhang, Q. Multivariate time-series anomaly detection via graph attention network. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; pp. 841–850. [Google Scholar]
- Geiger, A.; Liu, D.; Alnegheimish, S.; Cuesta-Infante, A.; Veeramachaneni, K. Tadgan: Time series anomaly detection using generative adversarial networks. In Proceedings of the 2020 IEEE International Conference on Big Data (Big Data), Atlanta, GA, USA, 10–13 December 2020; pp. 33–43. [Google Scholar]
- Längkvist, M.; Karlsson, L.; Loutfi, A. A review of unsupervised feature learning and deep learning for time-series modeling. Pattern Recognit. Lett. 2014, 42, 11–24. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory; MIT Press: Cambridge, MA, USA, 1997; Volume 9, pp. 1735–1780. [Google Scholar]
- Bontemps, L.; McDermott, J.; Le-Khac, N. Collective anomaly detection based on long short-term memory recurrent neural networks. In Proceedings of the International Conference of Future Data and Security Engineering, Can Tho City, Vietnam, 23–25 November 2016. [Google Scholar]
- Malhotra, P.; Vig, L.; Shroff, G.; Agarwal, P. Long Short Term Memory Networks for Anomaly Detection in Time Series. In Proceedings of the European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Bruges, Belgium, 22–24 April 2015. [Google Scholar]
- Filonov, P.; Lavrentyev, A.; Vorontsov, A. Multivariate industrial time series with cyber-attack simulation: Fault detection using an lstm-based predictive data model. arXiv 2016, arXiv:1612.06676. [Google Scholar]
- Chauhan, S.; Vig, L. Anomaly detection in ECG time signals via deep long short-term memory networks. In Proceedings of the International Conference on Data Science and Advanced Analytics (DSAA), Paris, France, 19–21 October 2015. [Google Scholar]
- Cherdo, Y.; De Kerret, P.; Pawlak, R. Training lstm for unsupervised anomaly detection without a priori knowledge. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 4297–4301. [Google Scholar]
- Hundman, K.; Constantinou, V.; Laporte, C.; Colwell, I.; Soderstrom, T. Detecting spacecraft anomalies using lstms and nonparametric dynamic thresholding. In Proceedings of the 24th ACM SIGKDD International Conference on KNOWLEDGE Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 387–395. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Meyer, P.; Häckel, T.; Korf, F.; Schmidt, T.C. Network anomaly detection in cars based on time-sensitive ingress control. In Proceedings of the 2020 IEEE 92nd Vehicular Technology Conference (VTC2020-Fall), Victoria, BC, Canada, 18 November–16 December 2020; pp. 1–5. [Google Scholar]
- Rajbahadur, G.K.; Malton, A.J.; Walenstein, A.; Hassan, A.E. A survey of anomaly detection for connected vehicle cybersecurity and safety. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 421–426. [Google Scholar]
- Zhou, A.; Li, Z.; Shen, Y. Anomaly detection of CAN bus messages using a deep neural network for autonomous vehicles. Appl. Sci. 2019, 9, 3174. [Google Scholar] [CrossRef]
- Sun, H.; Chen, M.; Weng, J.; Liu, Z.; Geng, G. Anomaly detection for in-vehicle network using CNN-LSTM with attention mechanism. IEEE Trans. Veh. Technol. 2021, 70, 10880–10893. [Google Scholar] [CrossRef]
- Boumiza, S.; Braham, R. An anomaly detector for CAN bus networks in autonomous cars based on neural networks. In Proceedings of the 2019 International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Barcelona, Spain, 21–23 October 2019; pp. 1–6. [Google Scholar]
- Wang, Y.; Masoud, N.; Khojandi, A. Real-time sensor anomaly detection and recovery in connected automated vehicle sensors. IEEE Trans. Intell. Transp. Syst. 2020, 22, 1411–1421. [Google Scholar] [CrossRef]
- Narayanan, S.N.; Mittal, S.; Joshi, A. OBD_SecureAlert: An anomaly detection system for vehicles. In Proceedings of the 2016 IEEE International Conference on Smart Computing (SMARTCOMP), St. Louis, MO, USA, 18–20 May 2016; pp. 1–6. [Google Scholar]
- Bogdoll, D.; Nitsche, M.; Zöllner, J.M. Anomaly detection in autonomous driving: A survey. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 4488–4499. [Google Scholar]
- Pereira, P.J.; Coelho, G.; Ribeiro, A.; Matos, L.M.; Nunes, E.C.; Ferreira, A.; Pilastri, A.; Cortez, P. Using deep autoencoders for in-vehicle audio anomaly detection. Procedia Comput. Sci. 2021, 192, 298–307. [Google Scholar] [CrossRef]
- Yahoo! Webscope Research. S5—A Labeled Anomaly Detection Dataset, Version 1.0(16M). Available online: https://webscope.sandbox.yahoo.com/catalog.php?datatype=s&did=70 (accessed on 12 January 2022).
- Lavin, A.; Ahmad, S. Evaluating Real-Time Anomaly Detection Algorithms–The Numenta Anomaly Benchmark. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015; pp. 38–44. [Google Scholar]
- Karagiannidis, G.K.; Lioumpas, A.S. An improved approximation for the Gaussian Q-function. IEEE Commun. Lett. 2007, 11, 644–646. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]




| Model | A1 | A2 | A3 | A4 | Mean |
|---|---|---|---|---|---|
| Hierarchical Temporal Memory (HTM) [33] | |||||
| Online evolving Spiking Neural Network (OeSNN-UAD) [9] | |||||
| Deep learning-based Anomaly detection approach for Time-series (DeepAnT) using a Long Short Term Memory (LSTM) [10] | |||||
| Deep learning-based Anomaly detection approach for Time-series (DeepAnT) using a Convolutional Neural Network (CNN) [10] | |||||
| Time-series Anomaly Detection using Generative Adversarial Networks (TadGAN) [13] | |||||
| Long Short Term Memory (LSTM) (ours) | 1 |
| Model | f1 | TPR | FPR | MSE | MACS | #Parameters | |
|---|---|---|---|---|---|---|---|
| CNN (8-8) | 5 s | 102,240 | 10,564 | ||||
| CNN (16-16) | 5 s | 211,392 | 21,812 | ||||
| CNN (32-32) | 5 s | 0 | 450,432 | 46,612 | |||
| GRU (50-50) | 5 s | 40,600 | 39,984 | ||||
| GRU (100-100) | 5 s | 126,200 | 124,884 | ||||
| GRU (150-150) | 5 s | 256,800 | 254,784 | ||||
| LSTM (50-50) | 5 s | 52,600 | 51,884 | ||||
| LSTM (100-100) | 5 s | 165,200 | 163,684 | ||||
| LSTM (150-150) | 5 s | 337,800 | 335,484 | ||||
| CNN (8-8) | 30 s | 102,240 | 10,564 | ||||
| CNN (16-16) | 30 s | 0 | 211,392 | 21,812 | |||
| CNN (32-32) | 30 s | 0 | 450,432 | 46,612 | |||
| GRU (50-50) | 30 s | 0 | 40,600 | 39,984 | |||
| GRU (100-100) | 30 s | 126,200 | 124,884 | ||||
| GRU (150-150) | 30 s | 0 | 256,800 | 254,784 | |||
| LSTM (50-50) | 30 s | 52,600 | 51,884 | ||||
| LSTM (100-100) | 30 s | 0 | 165,200 | 163,684 | |||
| LSTM (150-150) | 30 s | 0 | 337,800 | 335,484 | |||
| CNN (8-8) | 60 s | 102,240 | 10,564 | ||||
| CNN (16-16) | 60 s | 0 | 211,392 | 21,812 | |||
| CNN (32-32) | 60 s | 0 | 450,432 | 46,612 | |||
| GRU (50-50) | 60 s | 0 | 40,600 | 39,984 | |||
| GRU (100-100) | 60 s | 126,200 | 124,884 | ||||
| GRU (150-150) | 60 s | 0 | 256,800 | 254,784 | |||
| LSTM (50-50) | 60 s | 52,600 | 51,884 | ||||
| LSTM (100-100) | 60 s | 0 | 165,200 | 163,684 | |||
| LSTM (150-150) | 60 s | 0 | 337,800 | 335,484 |
| TPR | FPR | TNR | FNR | |
|---|---|---|---|---|
| 5 s | ||||
| 30 s | ||||
| 60 s |
| Model | TPR | FPR | TNR | FNR |
|---|---|---|---|---|
| LSTM (10) | ||||
| LSTM (50) | ||||
| LSTM (10-10) | ||||
| LSTM (50-50) |
| Model | Test MSE | PLR | MACS | #Parameters |
|---|---|---|---|---|
| LSTM (10) | K | K | ||
| LSTM (50) | K | K | ||
| LSTM (10-10) | K | K | ||
| LSTM (50-50) | 14 | K | K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cherdo, Y.; Miramond, B.; Pegatoquet, A.; Vallauri, A. Unsupervised Anomaly Detection for Cars CAN Sensors Time Series Using Small Recurrent and Convolutional Neural Networks. Sensors 2023, 23, 5013. https://doi.org/10.3390/s23115013
Cherdo Y, Miramond B, Pegatoquet A, Vallauri A. Unsupervised Anomaly Detection for Cars CAN Sensors Time Series Using Small Recurrent and Convolutional Neural Networks. Sensors. 2023; 23(11):5013. https://doi.org/10.3390/s23115013
Chicago/Turabian StyleCherdo, Yann, Benoit Miramond, Alain Pegatoquet, and Alain Vallauri. 2023. "Unsupervised Anomaly Detection for Cars CAN Sensors Time Series Using Small Recurrent and Convolutional Neural Networks" Sensors 23, no. 11: 5013. https://doi.org/10.3390/s23115013
APA StyleCherdo, Y., Miramond, B., Pegatoquet, A., & Vallauri, A. (2023). Unsupervised Anomaly Detection for Cars CAN Sensors Time Series Using Small Recurrent and Convolutional Neural Networks. Sensors, 23(11), 5013. https://doi.org/10.3390/s23115013







