EM and SAGE Algorithms for DOA Estimation in the Presence of Unknown Uniform Noise
Abstract
1. Introduction
- We propose a new MEM algorithm applicable to the unknown uniform noise assumption.
- We improve these EM-type algorithms to ensure the stability when the powers of sources are not equal.
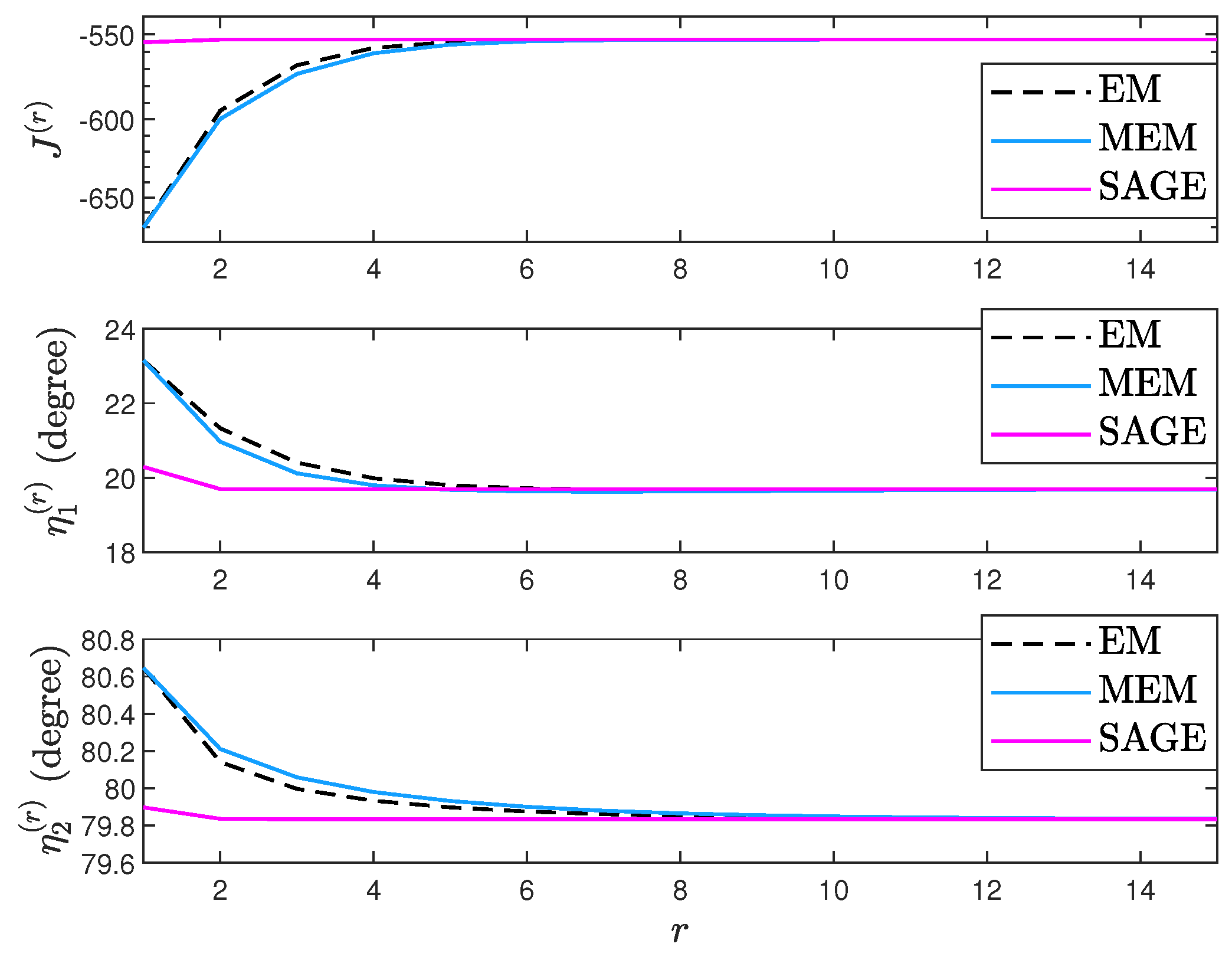
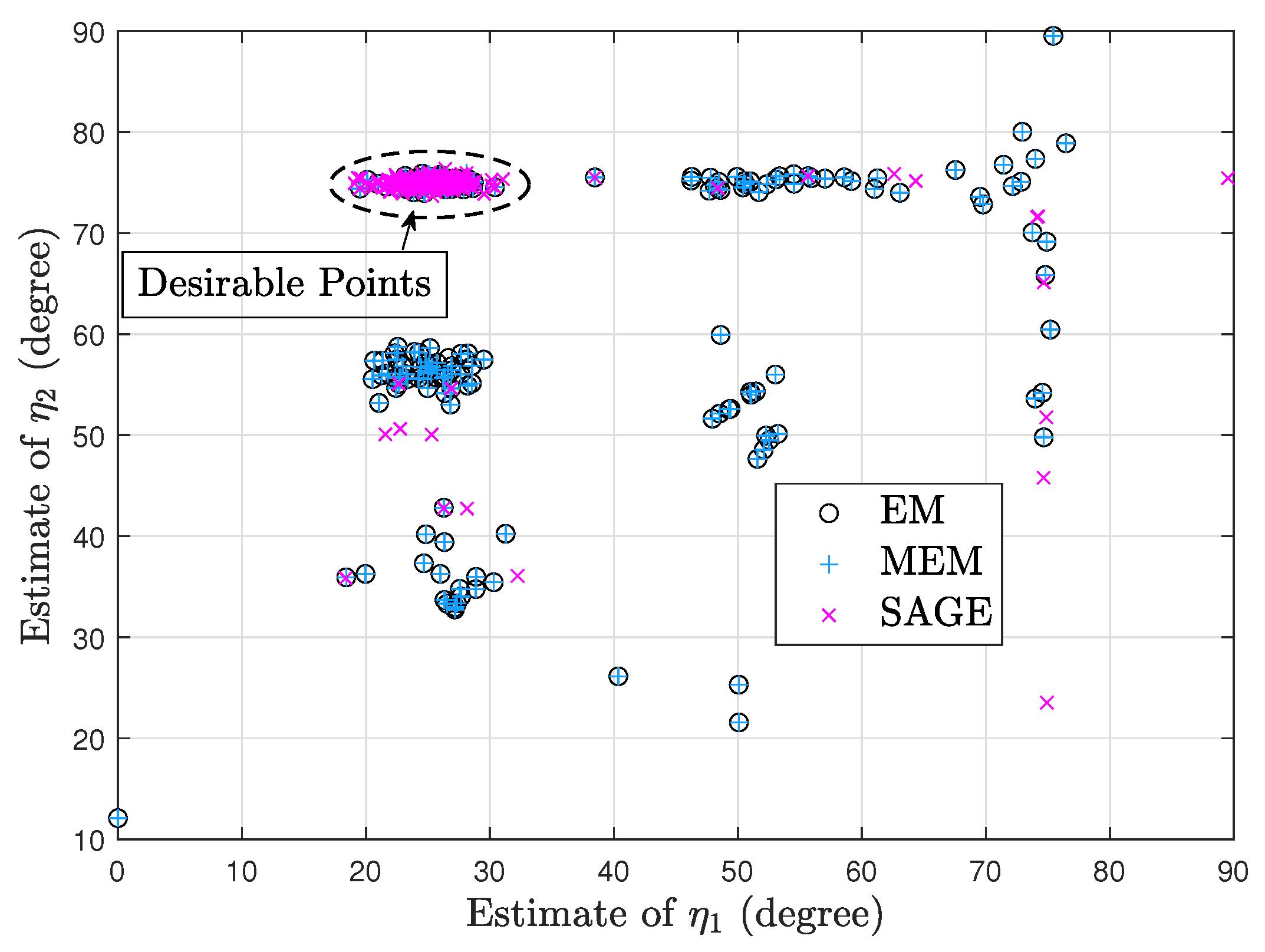
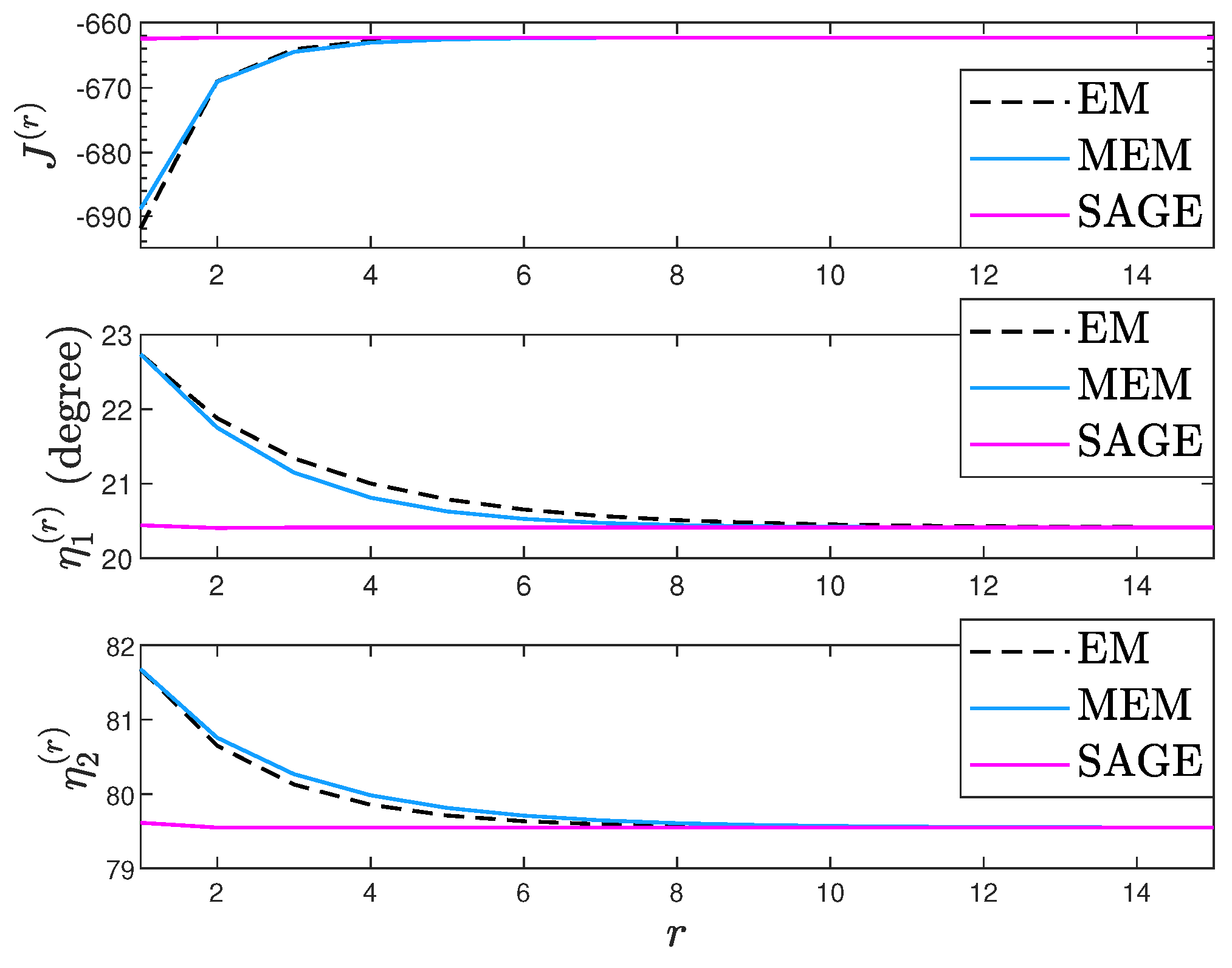
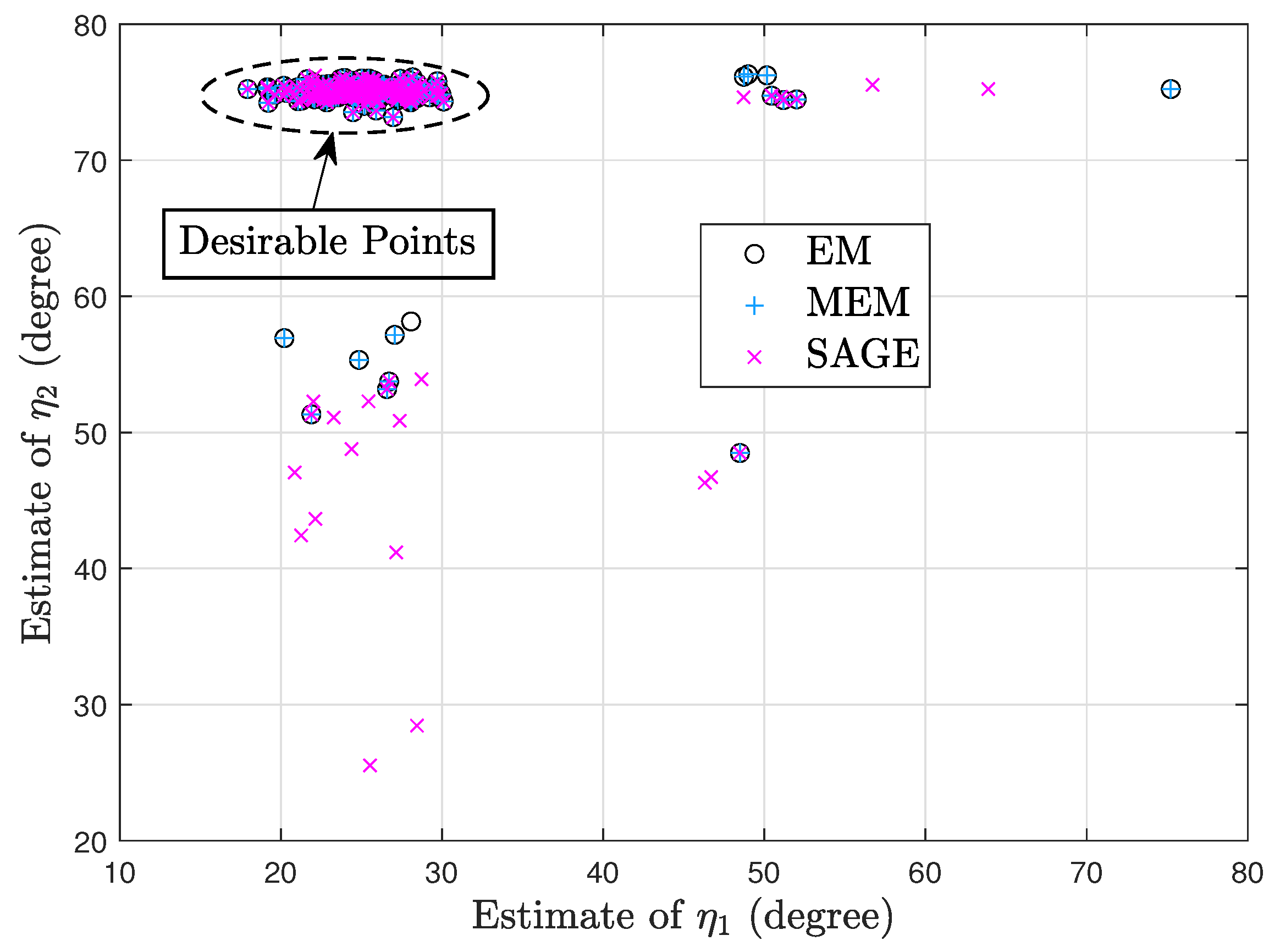
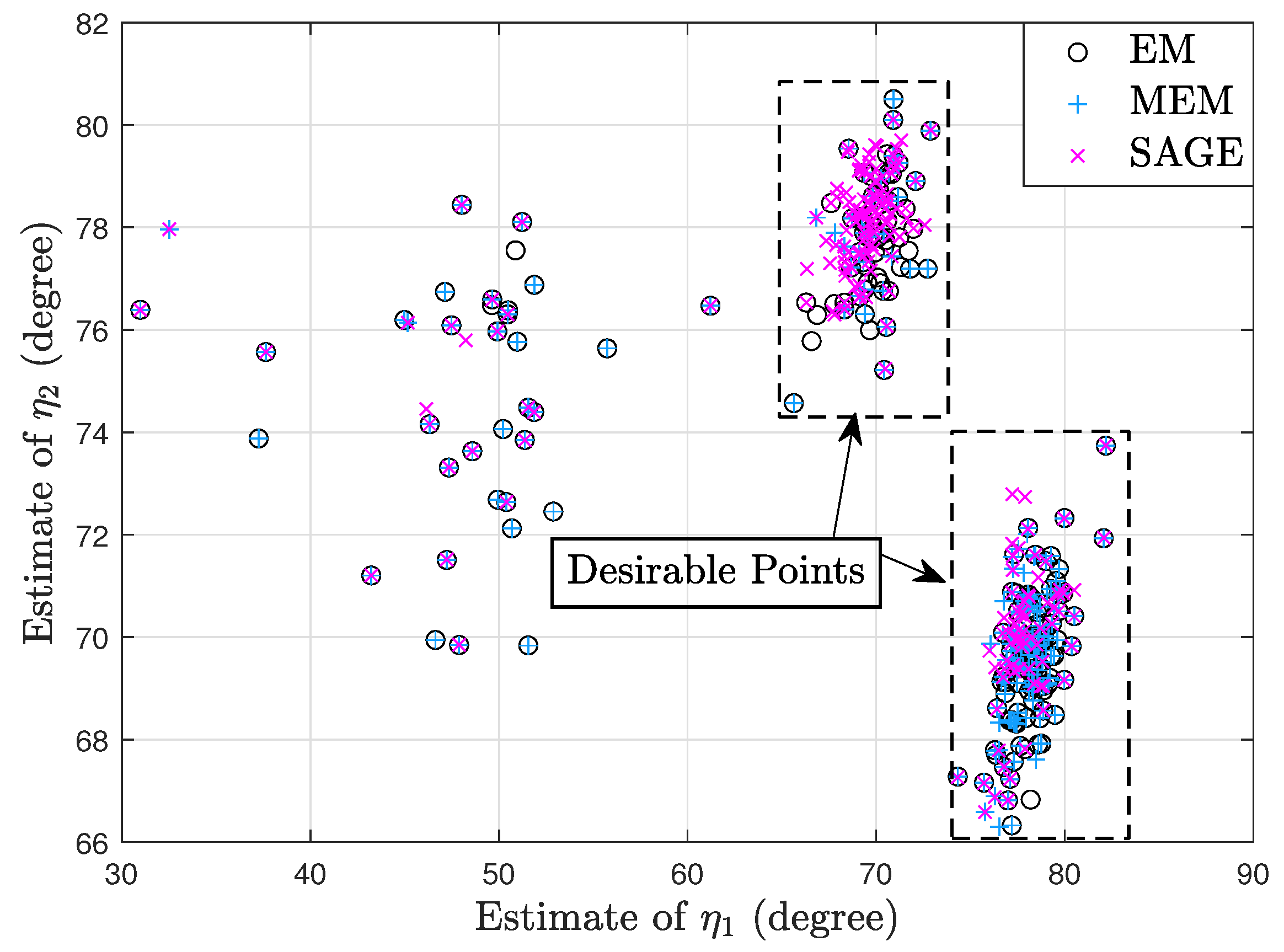
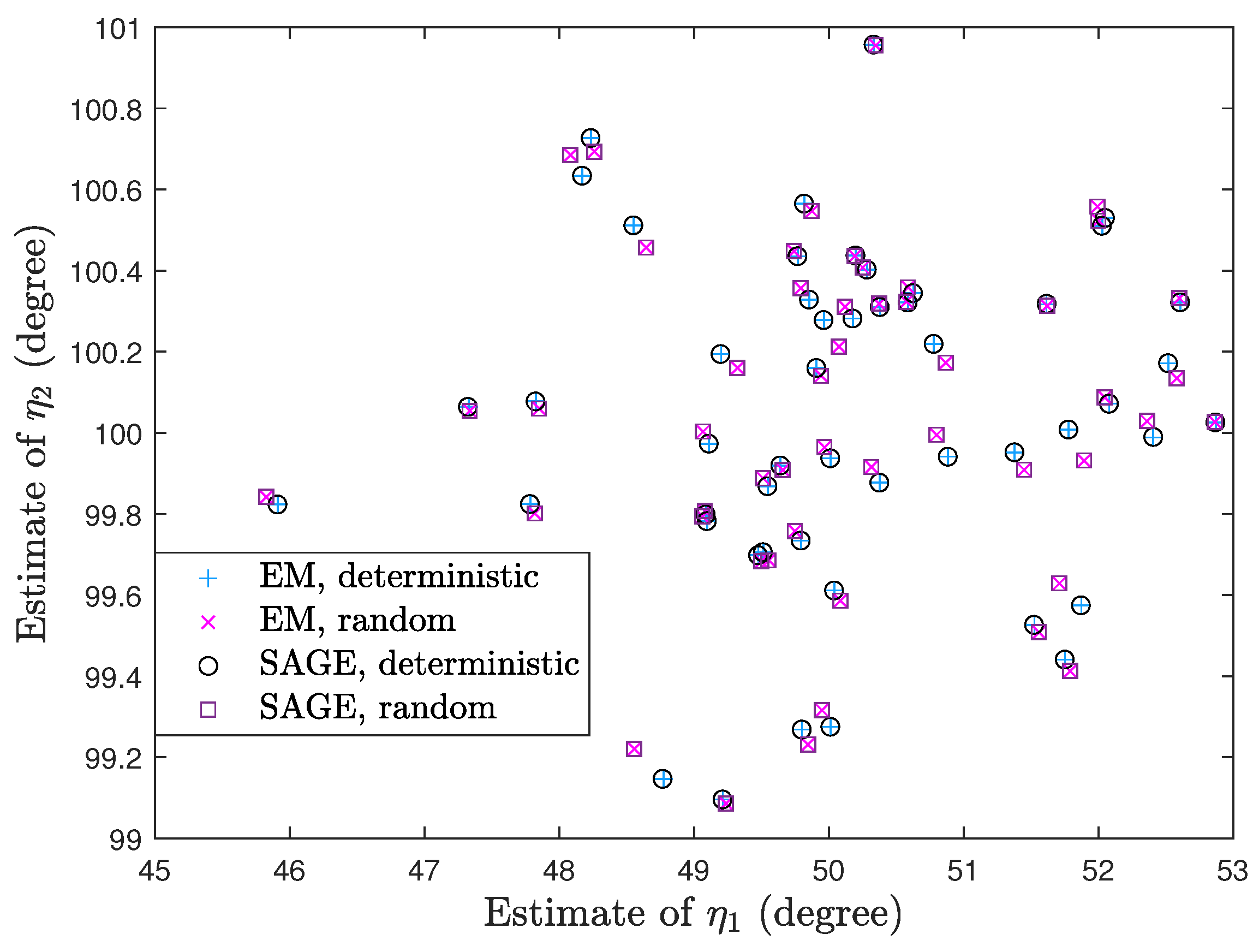
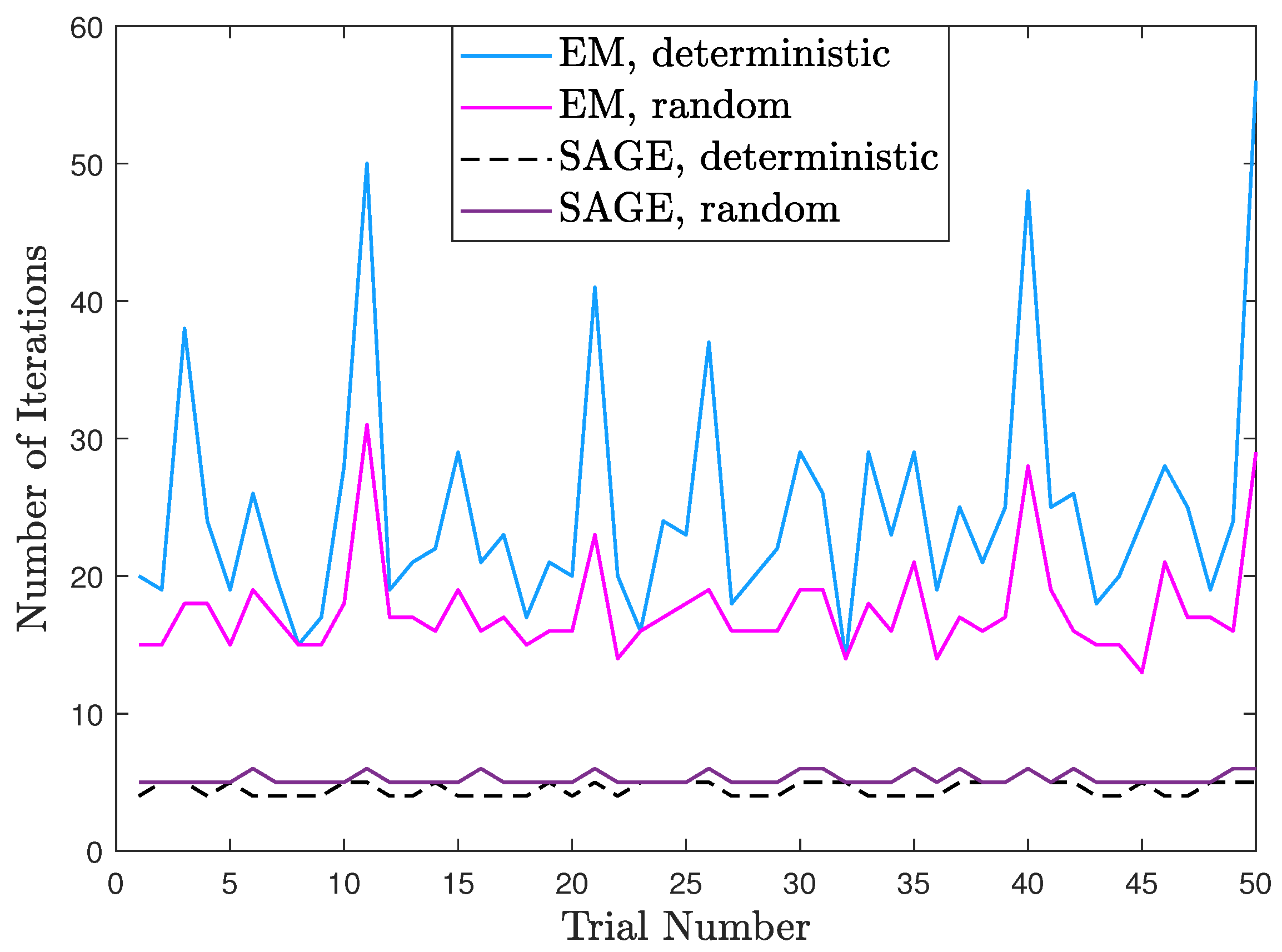
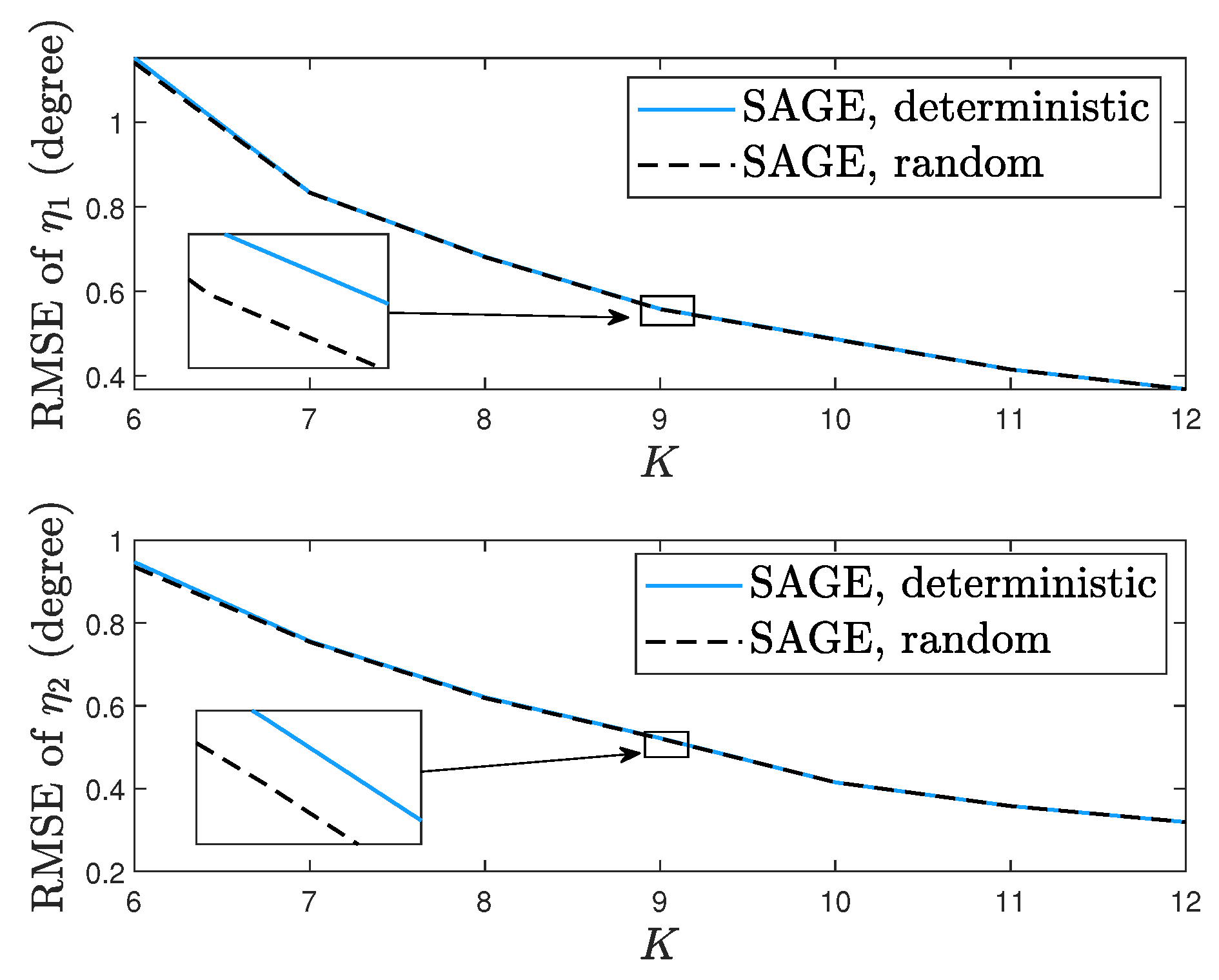
- Via simulation we show that the EM algorithm has similar convergence with the MEM algorithm and the SAGE algorithm outperforms the EM and MEM algorithms for the deterministic signal model. However, the SAGE algorithm cannot always outperform the EM and MEM algorithms for the random signal model.
- Via simulation we show that processing the same snapshots from the random signal model, the SAGE algorithm for the deterministic signal model can require the fewest iterations and computations.
2. Signal Model and Problem Statement
2.1. Deterministic Signal Model
2.2. Random Signal Model
3. EM Algorithm
3.1. Deterministic Signal Model
3.1.1. E-Step
3.1.2. M-Step
3.2. Random Signal Model
3.2.1. E-Step
3.2.2. M-Step
- First CM-step: Estimate but hold fixed. Then, problem (19) can be decomposed into the G parallel subproblems
- is obtained bywhere and if .
4. MEM Algorithm
4.1. Deterministic Signal Model
4.1.1. E-Step
4.1.2. M-Step
4.2. Random Signal Model
4.2.1. E-Step
4.2.2. M-Step
5. SAGE Algorithm
5.1. Deterministic Signal Model
5.1.1. E-Step
5.1.2. M-Step
5.2. Random Signal Model
5.2.1. E-Step
5.2.2. M-Step
- Second CM-step: Estimate but hold and fixed. Then, problem (64) is simplified towhere . We obtain bywhere and if .
6. Properties of the Proposed EM, MEM, and SAGE Algorithms
6.1. Convergence Point
6.2. Complexity and Stability
| Algorithm 1 Gradient ascent with backtracking line search |
|
7. Simulation Results
7.1. Deterministic Signal Model
7.2. Random Signal Model
7.3. Deterministic and Random Signal Models
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Godara, L.C. Application of antenna arrays to mobile communications. II. Beam-forming and direction-of-arrival considerations. Proc. IEEE 1997, 85, 1195–1245. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–38. [Google Scholar]
- Meng, X.; Dyk, D.V. The EM algorithm–an old folk-song sung to a fast new tune. J. R. Stat. Soc. Ser. B (Methodol.) 1997, 59, 511–567. [Google Scholar] [CrossRef]
- Feder, M.; Weinstein, E. Parameter estimation of superimposed signals using the EM algorithm. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 477–489. [Google Scholar] [CrossRef]
- Miller, M.I.; Fuhrmann, D.R. Maximum-likelihood narrow-band direction finding and the EM algorithm. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1560–1577. [Google Scholar] [CrossRef]
- Fessler, J.A.; Hero, A.O. Space-alternating generalized expectation-maximization algorithm. IEEE Trans. Signal Process. 1994, 42, 2664–2677. [Google Scholar] [CrossRef]
- Chung, P.; Bohme, J.F. Comparative convergence analysis of EM and SAGE algorithms in DOA estimation. IEEE Trans. Signal Process. 2001, 49, 2940–2949. [Google Scholar] [CrossRef]
- Gong, M.-Y.; Lyu, B. Alternating maximization and the EM algorithm in maximum-likelihood direction finding. IEEE Trans. Veh. Technol. 2021, 70, 9634–9645. [Google Scholar] [CrossRef]
- Ziskind, I.; Wax, M. Maximum likelihood localization of multiple sources by alternating projection. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1553–1560. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 720–741. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. Performance study of conditional and unconditional direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1783–1795. [Google Scholar] [CrossRef]
- Liao, B.; Chan, S.; Huang, L.; Guo, C. Iterative methods for subspace and DOA estimation in nonuniform noise. IEEE Trans. Signal Process. 2016, 64, 3008–3020. [Google Scholar] [CrossRef]
- Liao, B.; Huang, L.; Guo, C.; So, H.C. New approaches to direction-of-arrival estimation with sensor arrays in unknown nonuniform noise. IEEE Sens. J. 2016, 16, 8982–8989. [Google Scholar] [CrossRef]
- Esfandiari, M.; Vorobyov, S.A.; Alibani, S.; Karimi, M. Non-iterative subspace-based DOA estimation in the presence of nonuniform noise. IEEE Signal Process. Lett. 2019, 26, 848–852. [Google Scholar] [CrossRef]
- Esfandiari, M.; Vorobyov, S.A. A novel angular estimation method in the presence of nonuniform noise. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Singapore, 22–27 May 2022. [Google Scholar]
- Yang, J.; Yang, Y.; Lu, J.; Yang, L. Iterative methods for DOA estimation of correlated sources in spatially colored noise fields. Signal Process. 2021, 185, 108100. [Google Scholar] [CrossRef]
- Selva, J. Efficient computation of ML DOA estimates under unknown nonuniform sensor noise powers. Signal Process. 2023, 205, 108879. [Google Scholar] [CrossRef]
- Pesavento, M.; Gershman, A.B. Maximum-likelihood direction-of-arrival estimation in the presence of unknown nonuniform noise. IEEE Trans. Signal Process. 2001, 49, 1310–1324. [Google Scholar] [CrossRef]
- Chen, C.E.; Lorenzelli, F.; Hudson, R.E.; Yao, K. Stochastic maximum-likelihood DOA estimation in the presence of unknown nonuniform noise. IEEE Trans. Signal Process. 2008, 56, 3038–3044. [Google Scholar] [CrossRef]
- Meng, M.; Rubin, D.B. Maximum likelihood estimation via the ECM algorithm: A general framework. Biometrika 1993, 80, 267–278. [Google Scholar] [CrossRef]
- Chung, P.; Bohme, J.F. DOA estimation using fast EM and SAGE algorithms. Signal Process. 2002, 82, 1753–1762. [Google Scholar] [CrossRef]
- Rhodes, I.B. A tutorial introduction to estimation and filtering. IEEE Trans. Autom. Control 1971, 16, 688–706. [Google Scholar] [CrossRef]
- Jaffer, A.G. Maximum likelihood direction finding of stochastic sources: A separable solution. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing (ICASSP), New York, NY, USA, 11–14 April 1988. [Google Scholar]
- Stoica, P.; Nehorai, A. On the concentrated stochastic likelihood function in array signal processing. Circuits Syst. Signal Process. 1995, 14, 669–674. [Google Scholar] [CrossRef]
- Jeff Wu, C.F. On the convergence properties of the EM algorithm. Ann. Stat. 1983, 11, 95–103. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization, 1st ed.; Cambridge University Press: New York, NY, USA, 2004; pp. 463–466. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, M.-Y.; Lyu, B. EM and SAGE Algorithms for DOA Estimation in the Presence of Unknown Uniform Noise. Sensors 2023, 23, 4811. https://doi.org/10.3390/s23104811
Gong M-Y, Lyu B. EM and SAGE Algorithms for DOA Estimation in the Presence of Unknown Uniform Noise. Sensors. 2023; 23(10):4811. https://doi.org/10.3390/s23104811
Chicago/Turabian StyleGong, Ming-Yan, and Bin Lyu. 2023. "EM and SAGE Algorithms for DOA Estimation in the Presence of Unknown Uniform Noise" Sensors 23, no. 10: 4811. https://doi.org/10.3390/s23104811
APA StyleGong, M.-Y., & Lyu, B. (2023). EM and SAGE Algorithms for DOA Estimation in the Presence of Unknown Uniform Noise. Sensors, 23(10), 4811. https://doi.org/10.3390/s23104811







