Understanding Seepage in Levees and Exploring the Applicability of Using an Optical-Fiber Distributed Temperature System and Smoothing Technique as a Monitoring Method
Abstract
1. Introduction
2. Experiment and Analysis Methods
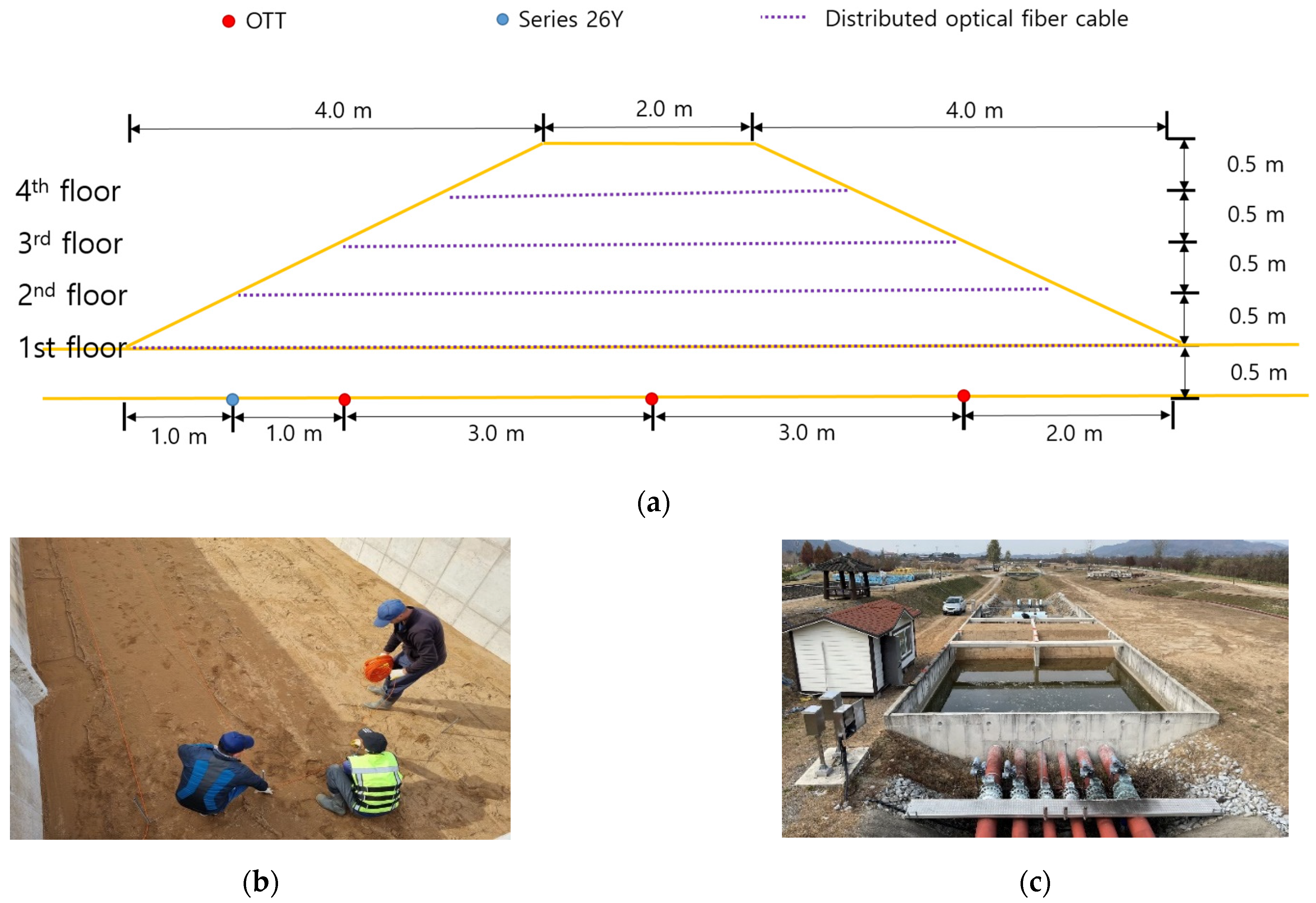
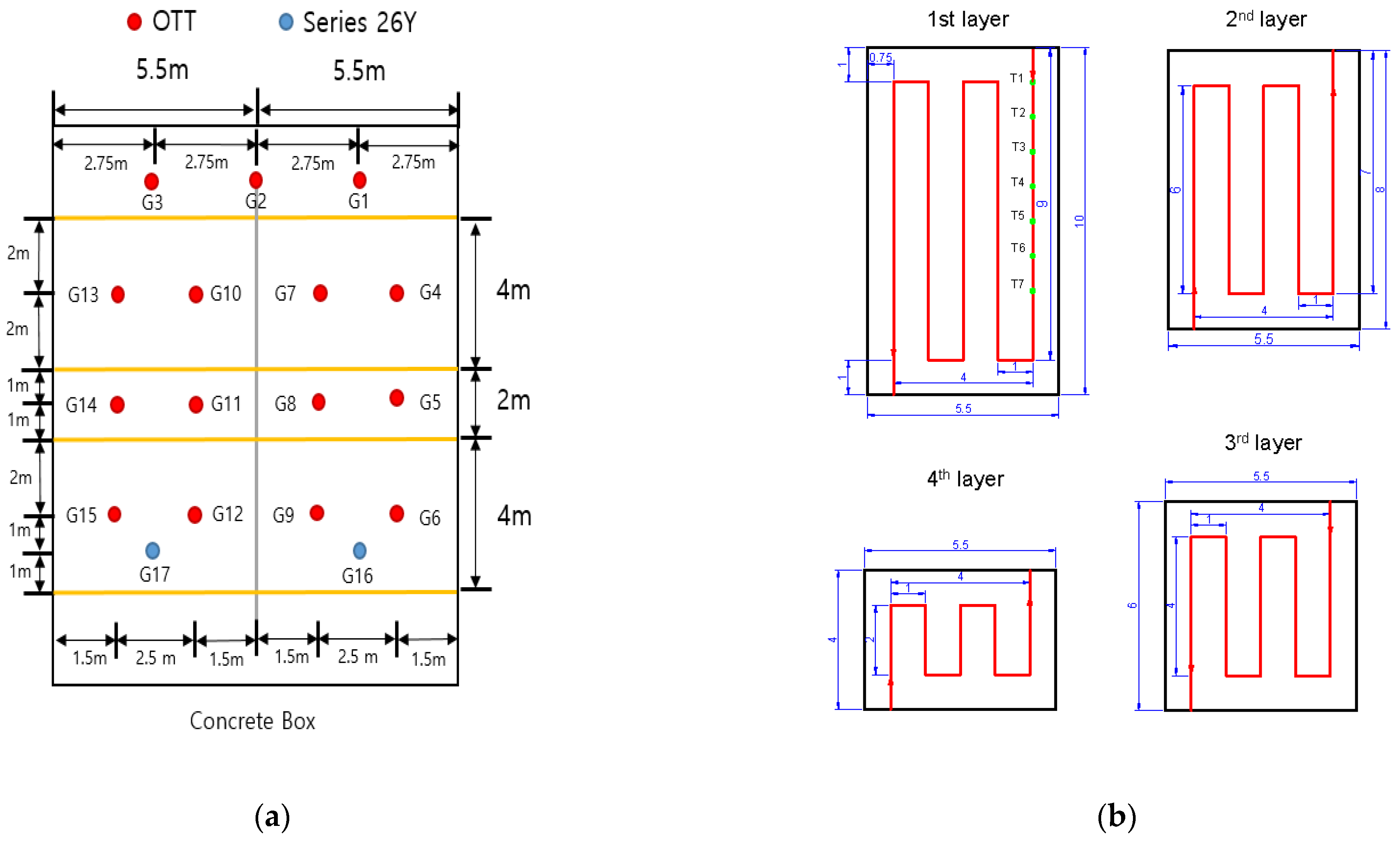
2.1. Experimental Conditions and Methods
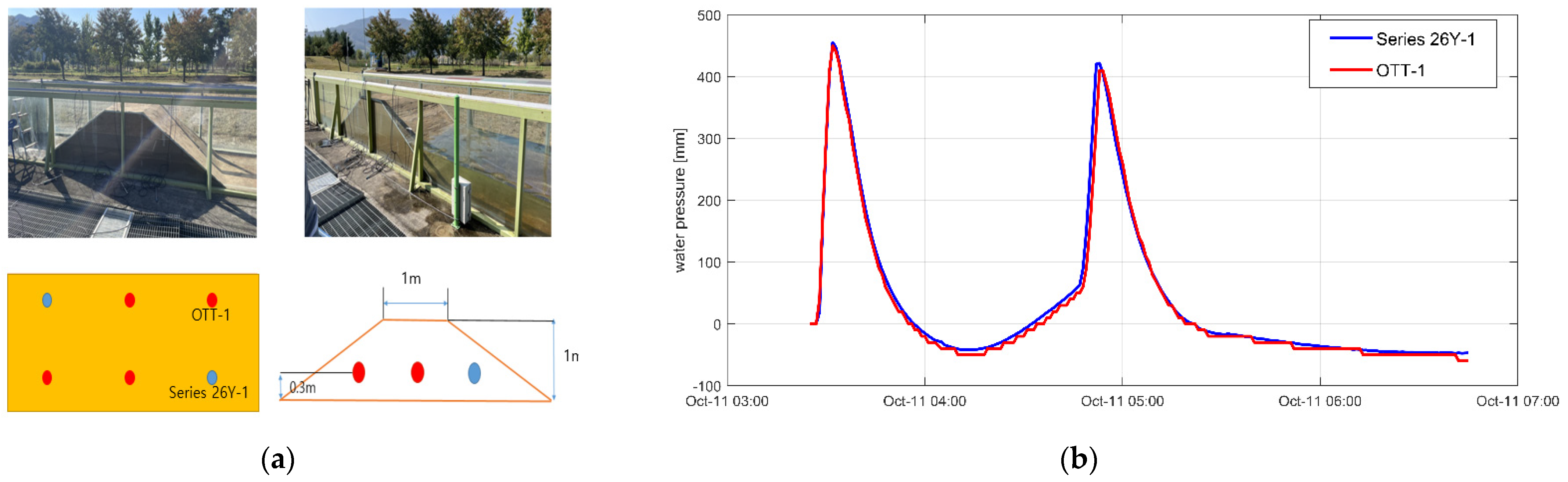
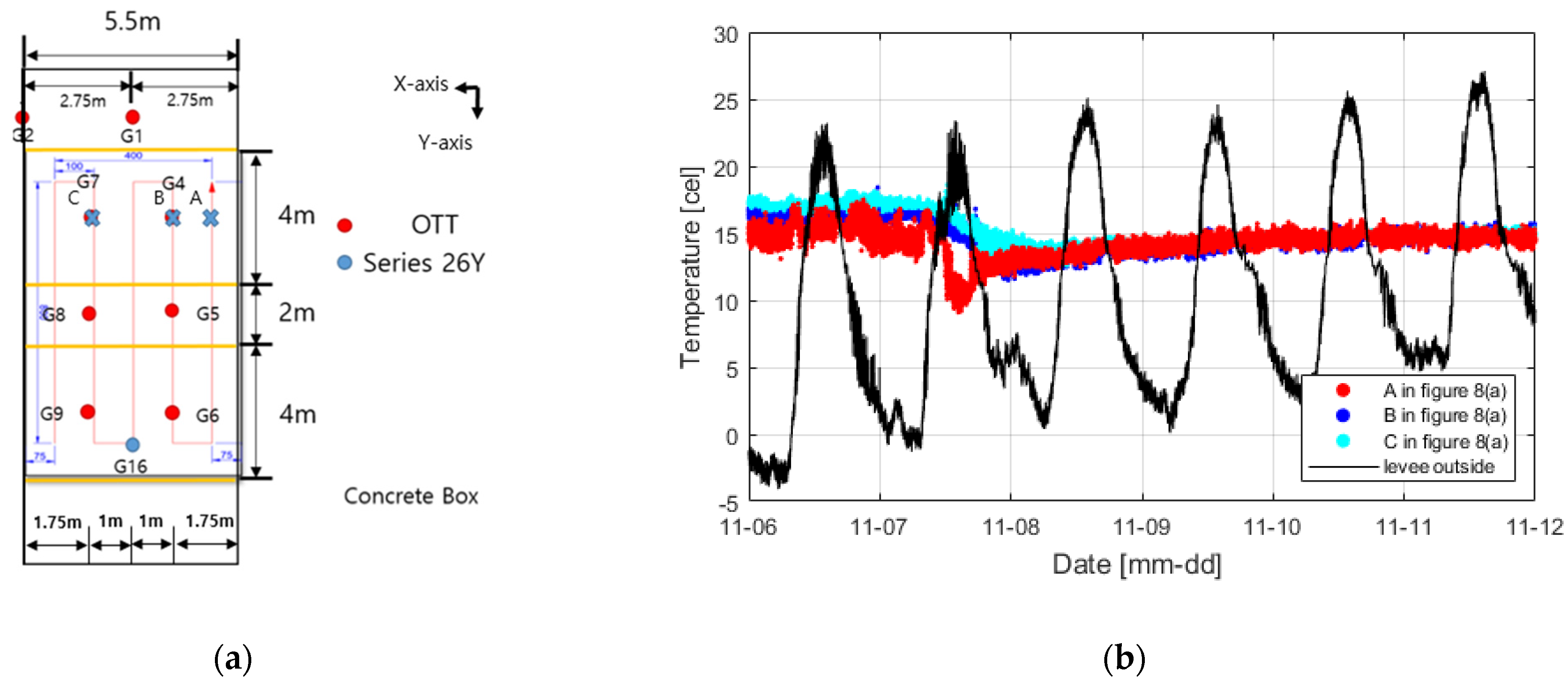
2.2. Measurement Method
3. Results
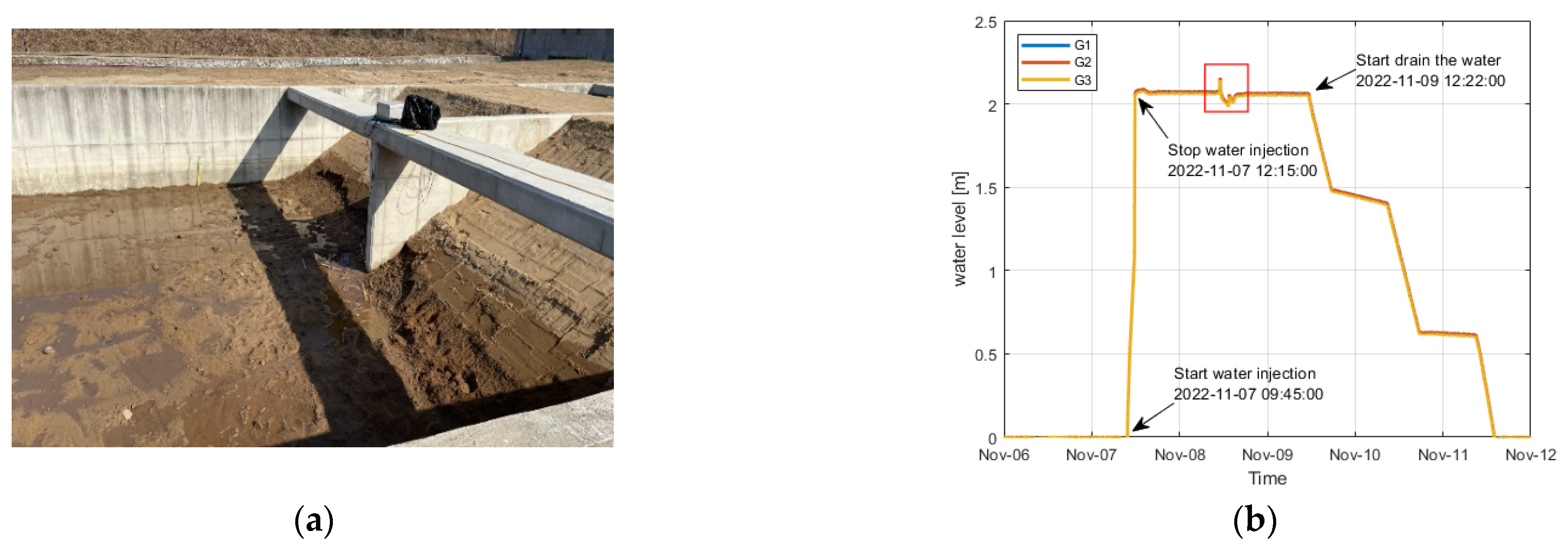
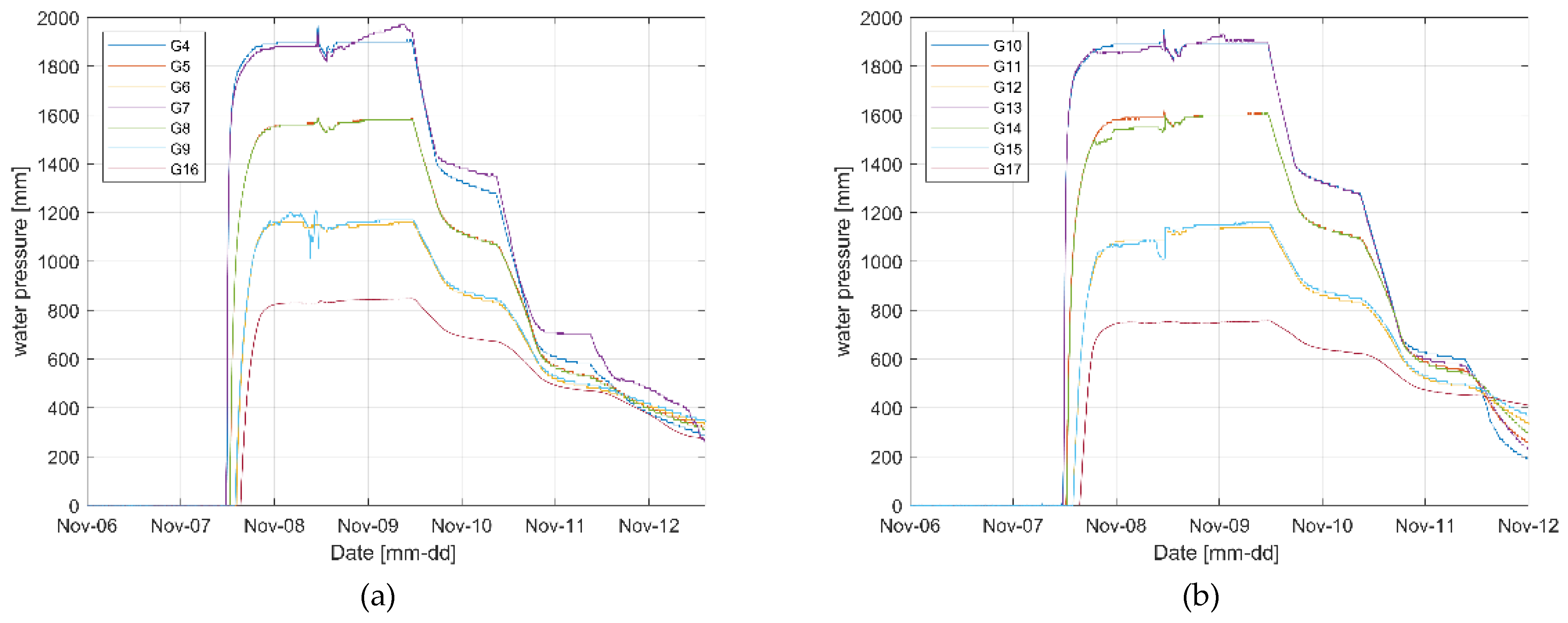
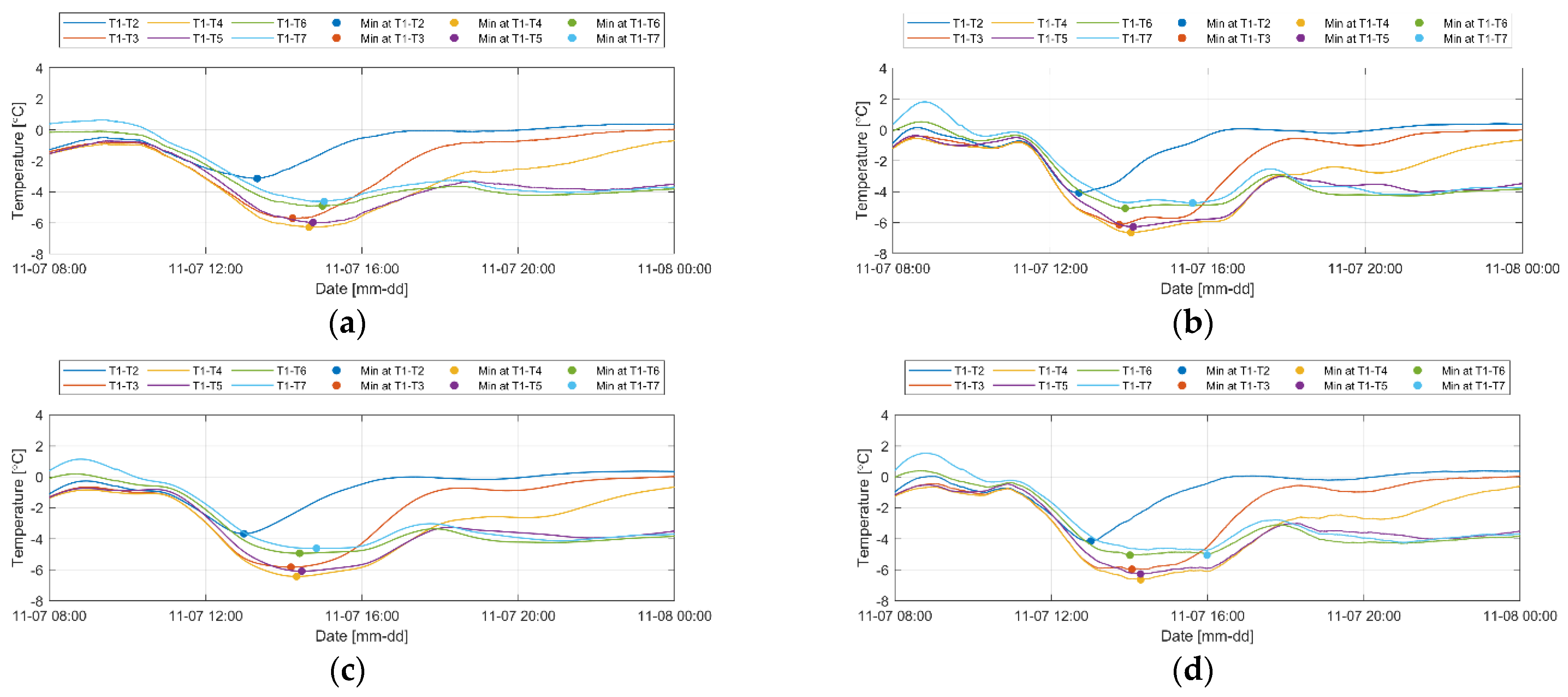
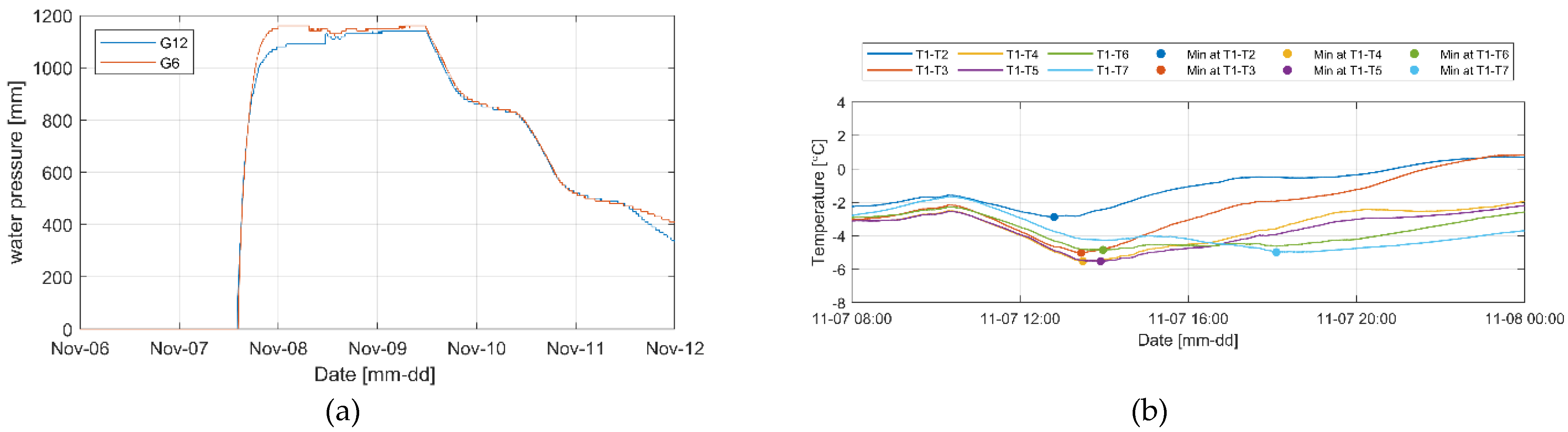
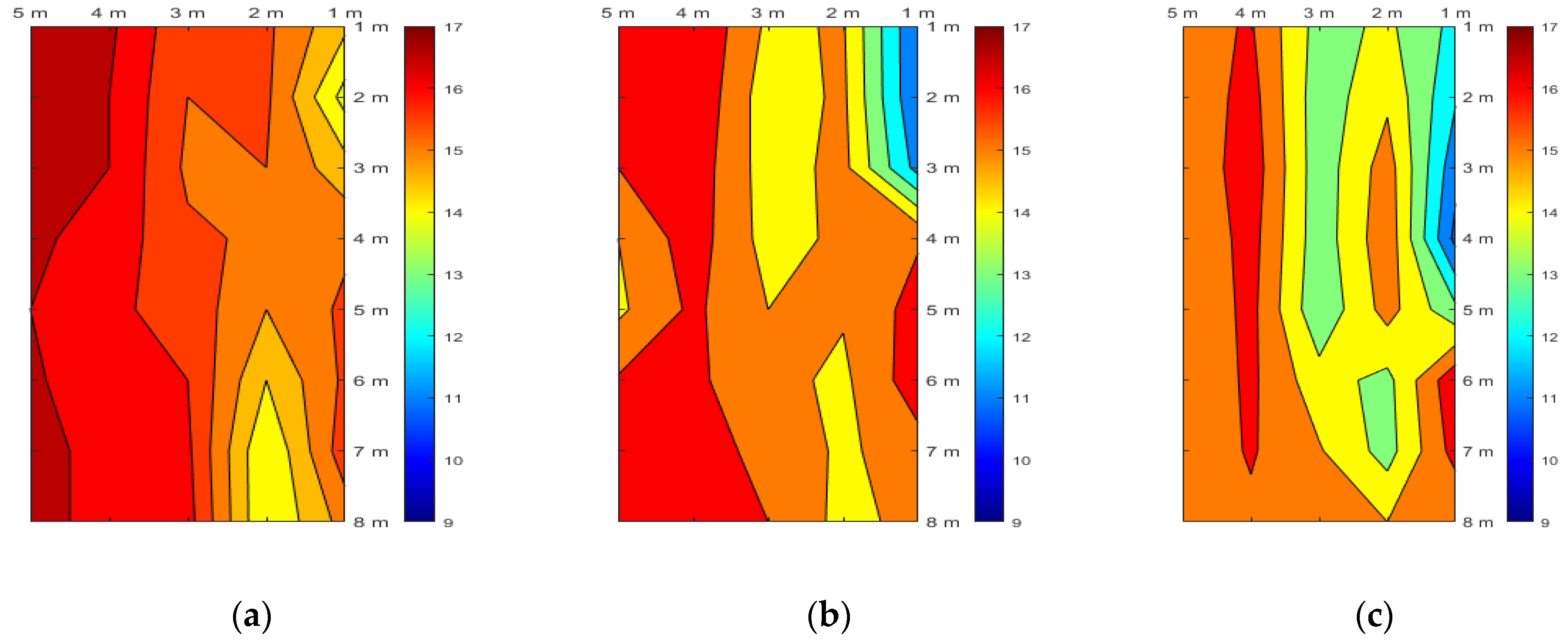
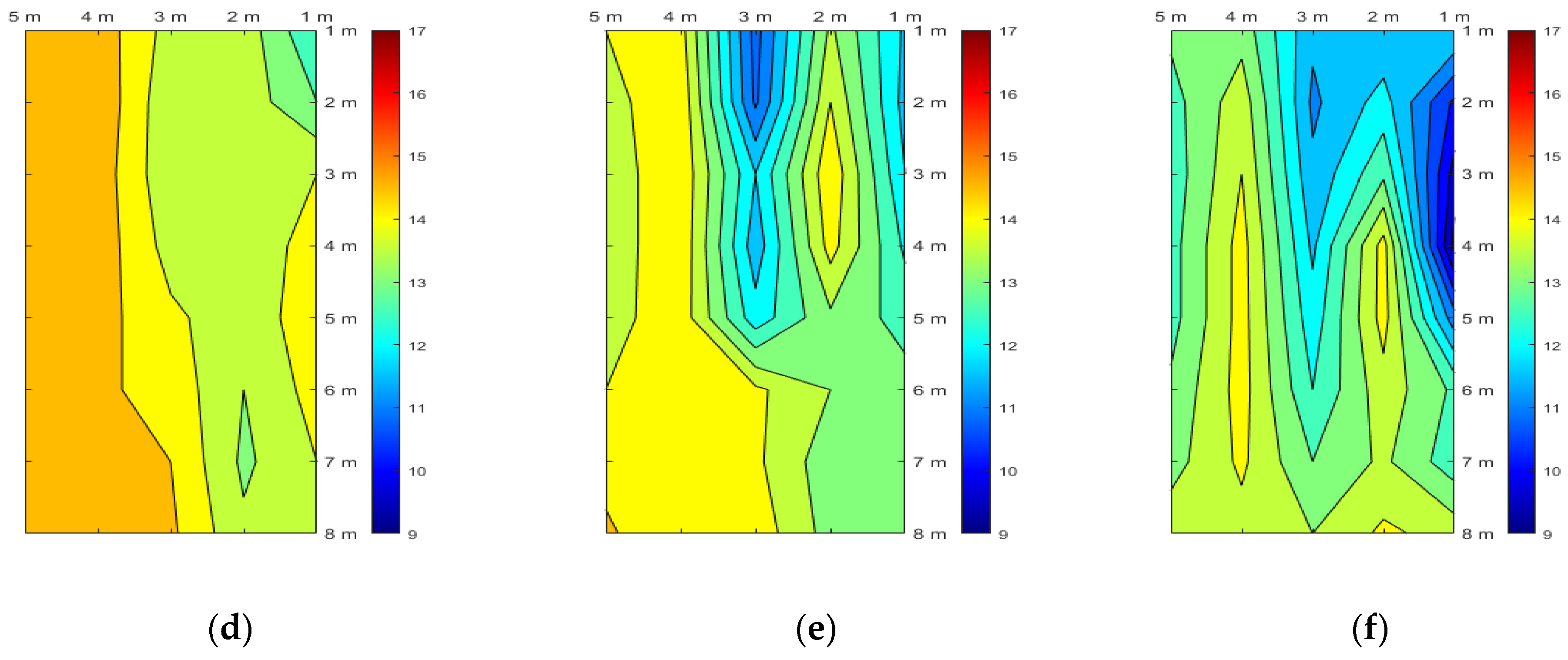
3.1. Experimental Results
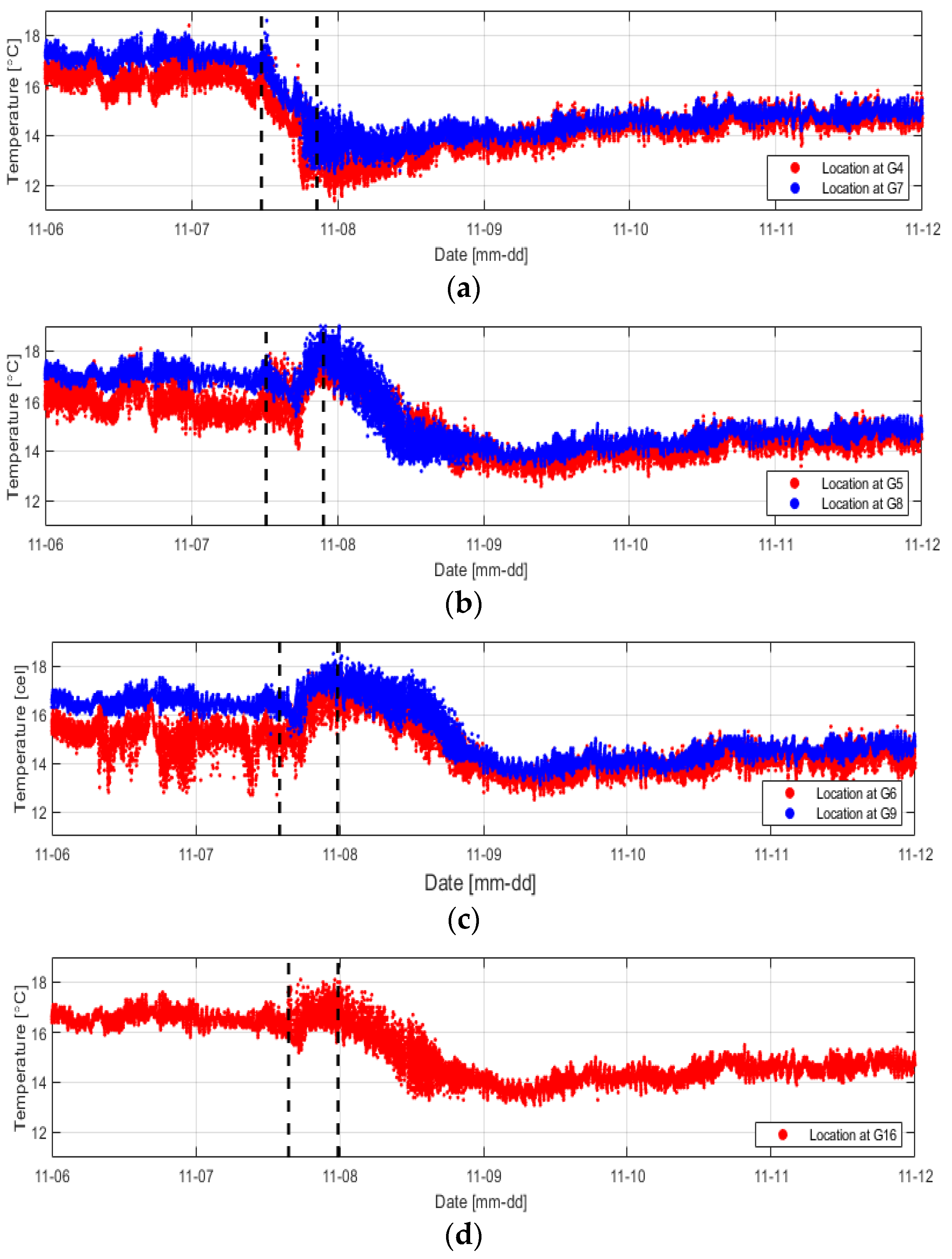
3.2. Temperature
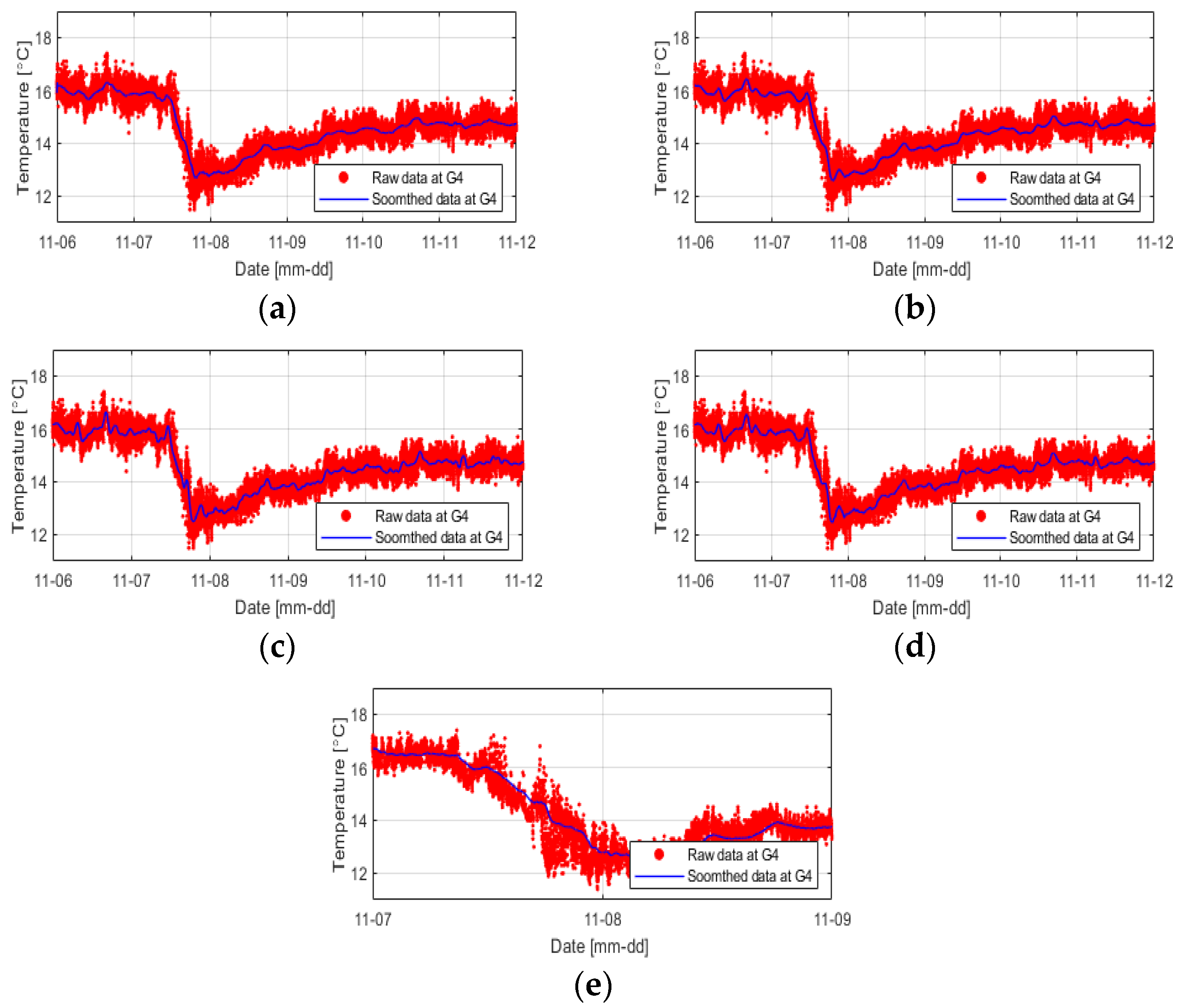
3.3. Data Processing
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Costa, J.E. Floods from Dam Failures; Open-File Rep. No. 85-560; United States Geological Survey: Denver, CO, USA, 1985; p. 54. [Google Scholar]
- ASCE Task Committee on Dam/Levee Breaching. Earthen embankment breaching. J. Hydraul. Eng. 2011, 137, 1549–1564. [Google Scholar] [CrossRef]
- Kang, W.; Ko, D.; Kang, J. Erosion resistance performance of surface-reinforced levees using novel biopolymers investigated via real-scale overtopping experiments. Water 2021, 13, 2482. [Google Scholar] [CrossRef]
- Hui, R.; Jachens, E.; Lund, J. Risk-based planning analysis for a single levee. Water Resour. Res. 2016, 52, 2513–2528. [Google Scholar] [CrossRef]
- Jadid, R.; Montoya, B.M.; Bennett, V.; Gabr, M.A. Effect of repeated rise and fall of water level on seepage-induced deformation and related stability analysis of Princeville levee. Eng. Geol. 2020, 266, 105458. [Google Scholar] [CrossRef]
- Bonaccorsi, B.; Moramarco, T.; Noto, L.V.; Barbetta, S. A multilayer soil approach for seepage process analysis in earthen levees. J. Flood Risk Manag. 2022, 15, e12801. [Google Scholar] [CrossRef]
- Fox, G.A.; Wilson, G.V.; Periketi, R.K.; Cullum, R.F. Sediment transport model for seepage erosion of streambank sediment. J. Hydrol. Eng. 2006, 11, 603–611. [Google Scholar] [CrossRef]
- Nardi, L.; Rinaldi, M.; Solari, L. An experimental investigation on mass failures occurring in a riverbank composed of sandy gravel. Geomorphology 2012, 163, 56–69. [Google Scholar] [CrossRef]
- Michelazzo, G.; Paris, E.; Solari, L. On the vulnerability of river levees induced by seepage. J. Flood Risk Manag. 2018, 11, S677–S686. [Google Scholar] [CrossRef]
- Cola, S.; Girardi, V.; Bersan, S.; Simonini, P.; Schenato, L.; De Polo, F. An optical fiber-based monitoring system to study the seepage flow below the landside toe of a river levee. J. Civ. Struct. Health Monit. 2021, 11, 691–705. [Google Scholar] [CrossRef]
- Bersan, S.; Koelewijn, A.R.; Simonini, P. Effectiveness of distributed temperature measurements for early detection of piping in river embankments. Hydrol. Earth Syst. Sci. 2018, 22, 1491–1508. [Google Scholar] [CrossRef]
- Tresoldi, G.; Arosio, D.; Hojat, A.; Longoni, L.; Papini, M.; Zanzi, L. Long-term hydrogeophysical monitoring of the internal conditions of river levees. Eng. Geol. 2019, 259, 105139. [Google Scholar] [CrossRef]
- Ghafoori, Y.; Maček, M.; Vidmar, A.; Říha, J.; Kryžanowski, A. Analysis of seepage in a laboratory scaled model using passive optical fiber distributed temperature sensor. Water 2020, 12, 367. [Google Scholar] [CrossRef]
- Kappelmeyer, O. The use of near surface temperature measurements for discovering anomalies due to causes at depths. Geophys. Prospect. 1957, 5, 239–258. [Google Scholar] [CrossRef]
- Sourbeer, J.J.; Loheide, S.P. Obstacles to long-term soil moisture monitoring with heated distributed temperature sensing. Hydrol. Process. 2016, 30, 1017–1035. [Google Scholar] [CrossRef]
- Schenato, L. A review of distributed fibre optic sensors for geo-hydrological applications. Appl. Sci. 2017, 7, 896. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, D.; Liu, H.; Sun, Q.; Sun, Z.; Zhang, X.; Wang, W. Design of distributed Raman temperature sensing system based on single-mode optical fiber. Front. Optoelectron. China 2009, 2, 215–218. [Google Scholar] [CrossRef]
- Ouni, S.; Bouhamed, M.; Nasrallah, S.B.; Mammou, A.B.; Ksentini, A. Application of moving average and Savitzky-Golay filtering to DTS data for monitoring soil thermal properties. Int. J. Geosynth. Ground Eng. 2019, 5. [Google Scholar] [CrossRef]
- Lee, C.K.; Kim, Y.S.; Gu, M.M.; Kim, B.G. Real time temperature monitoring system using optic fiber sensor. J. Korea Soc. Comput. Inf. 2010, 15, 209–216. [Google Scholar] [CrossRef]
- Ahn, M.; Bae, I.; Ji, U.; Kang, J. Large-scale levee monitoring experiment using fiberoptic sensor and distributed temperature sensing system. Ecol. Resilient Infrastruct. 2020, 7, 181–188. [Google Scholar]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Apperl, B.; Bernhardt, M.; Schulz, K. Towards improved field application of using distributed temperature sensing for soil moisture estimation: A laboratory experiment. Sensors 2019, 20, 29. [Google Scholar] [CrossRef] [PubMed]
- Cleveland, W.S.; Devlin, S.J. Locally weighted regression: An approach to regression analysis by local fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
- Brown, R.G. Smoothing, Forecasting and Prediction of Discrete Time Series; Prentice Hall: Hoboken, NJ, USA, 1963. [Google Scholar]





| Levee 1 | Levee 2 | ||||
|---|---|---|---|---|---|
| Sensor Number | Distance [m] | Time [mm/dd hh:mm] | Sensor Number | Distance [m] | Time [mm/dd hh:mm] |
| G4 | 2 m | 11/07 11:30 to 11/07 20:37 | G10 | 2 m | 11/07 11:41 to 11/07 20:44 |
| G5 | 5 m | 11/07 12:18 to 11/07 21:33 | G11 | 5 m | 11/07 12:42 to 11/07 21:43 |
| G6 | 8 m | 11/08 14:00 to 11/07 22:40 | G12 | 8 m | 11/08 14:18 to 11/08 22:35 |
| G7 | 2 m | 11/07 11:36 to 11/07 19:45 | G13 | 2 m | 11/07 11:31 to 11/07 20:30 |
| G8 | 5 m | 11/07 12:28 to 11/07 22:34 | G14 | 5 m | 11/07 12:36 to 11/07 22:54 |
| G9 | 8 m | 11/07 13:59 to 11/07 23:11 | G15 | 8 m | 11/07 13:55 to 11/07 23:34 |
| G16 | 9 m | 11/07 15:32 to 11/08 22:45 | G17 | 9 m | 11/07 15:21 to 11/08 23:39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, W. Understanding Seepage in Levees and Exploring the Applicability of Using an Optical-Fiber Distributed Temperature System and Smoothing Technique as a Monitoring Method. Sensors 2023, 23, 4780. https://doi.org/10.3390/s23104780
Kang W. Understanding Seepage in Levees and Exploring the Applicability of Using an Optical-Fiber Distributed Temperature System and Smoothing Technique as a Monitoring Method. Sensors. 2023; 23(10):4780. https://doi.org/10.3390/s23104780
Chicago/Turabian StyleKang, Woochul. 2023. "Understanding Seepage in Levees and Exploring the Applicability of Using an Optical-Fiber Distributed Temperature System and Smoothing Technique as a Monitoring Method" Sensors 23, no. 10: 4780. https://doi.org/10.3390/s23104780
APA StyleKang, W. (2023). Understanding Seepage in Levees and Exploring the Applicability of Using an Optical-Fiber Distributed Temperature System and Smoothing Technique as a Monitoring Method. Sensors, 23(10), 4780. https://doi.org/10.3390/s23104780






