Tool Wear Condition Monitoring Method Based on Deep Learning with Force Signals
Abstract
1. Introduction
2. Research Methods
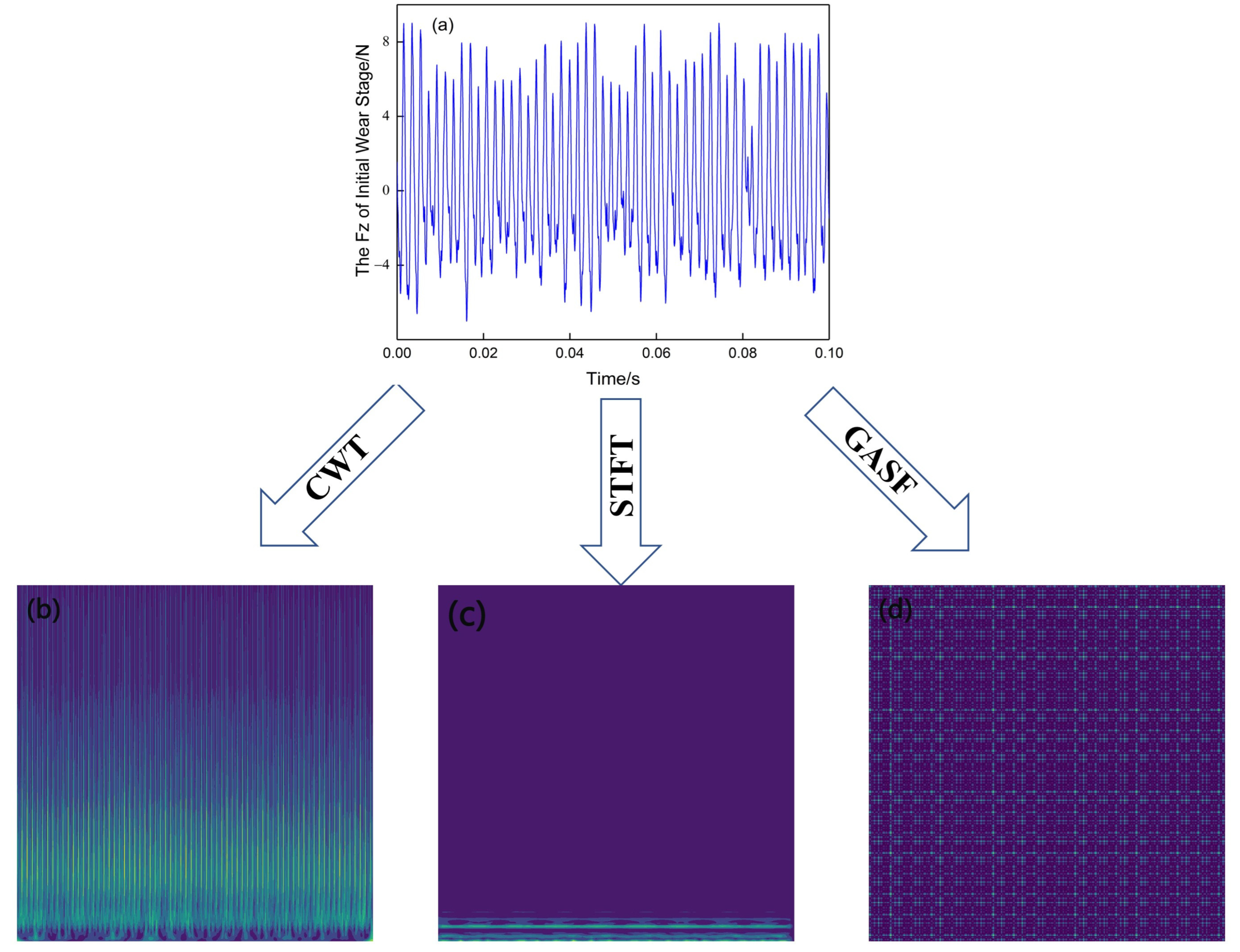
2.1. Continuous Wavelet Transform (CWT)
2.2. Short-Time Fourier Transform (STFT)
2.3. Gramian Angular Summation Field (GASF)
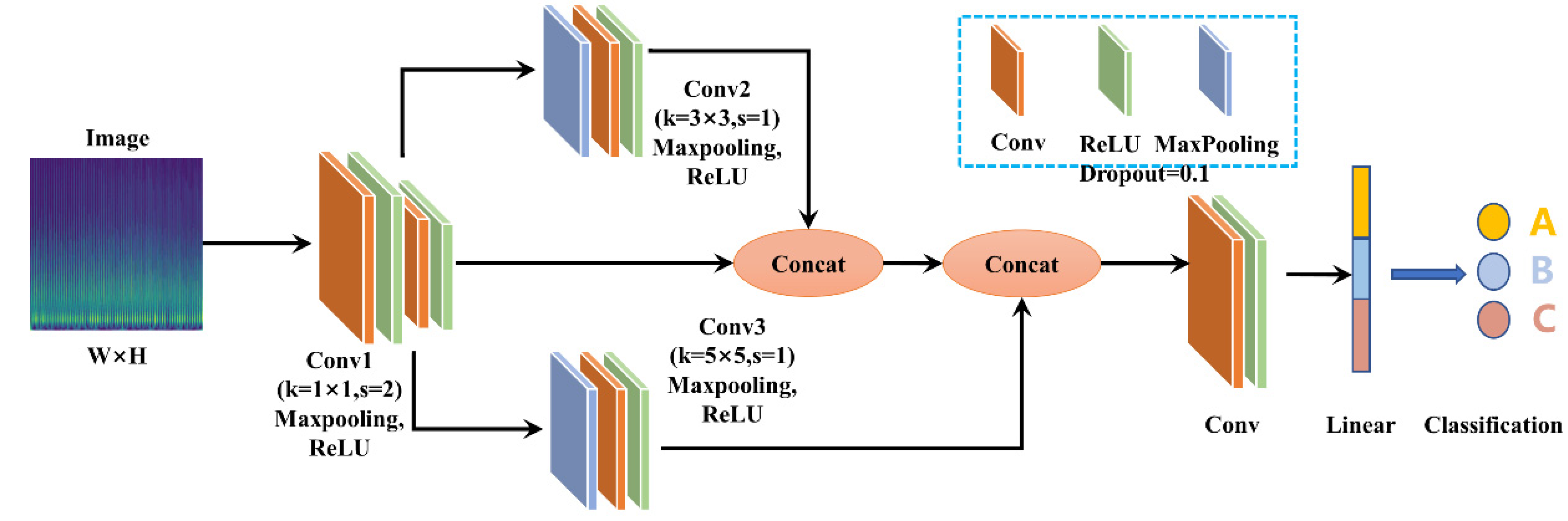
2.4. The CNN Model with Multiscale Feature Pyramid
3. Force Signal to Image
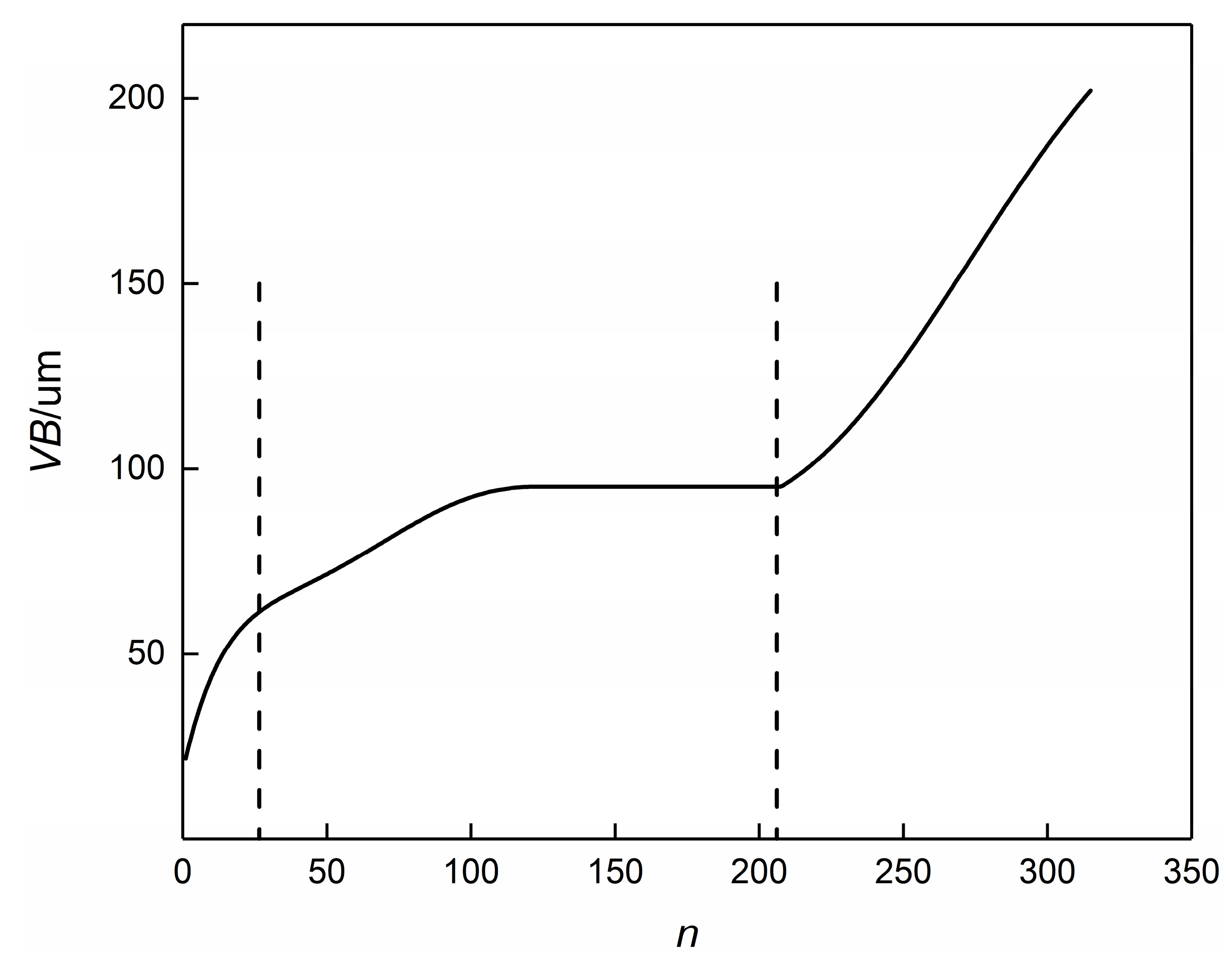
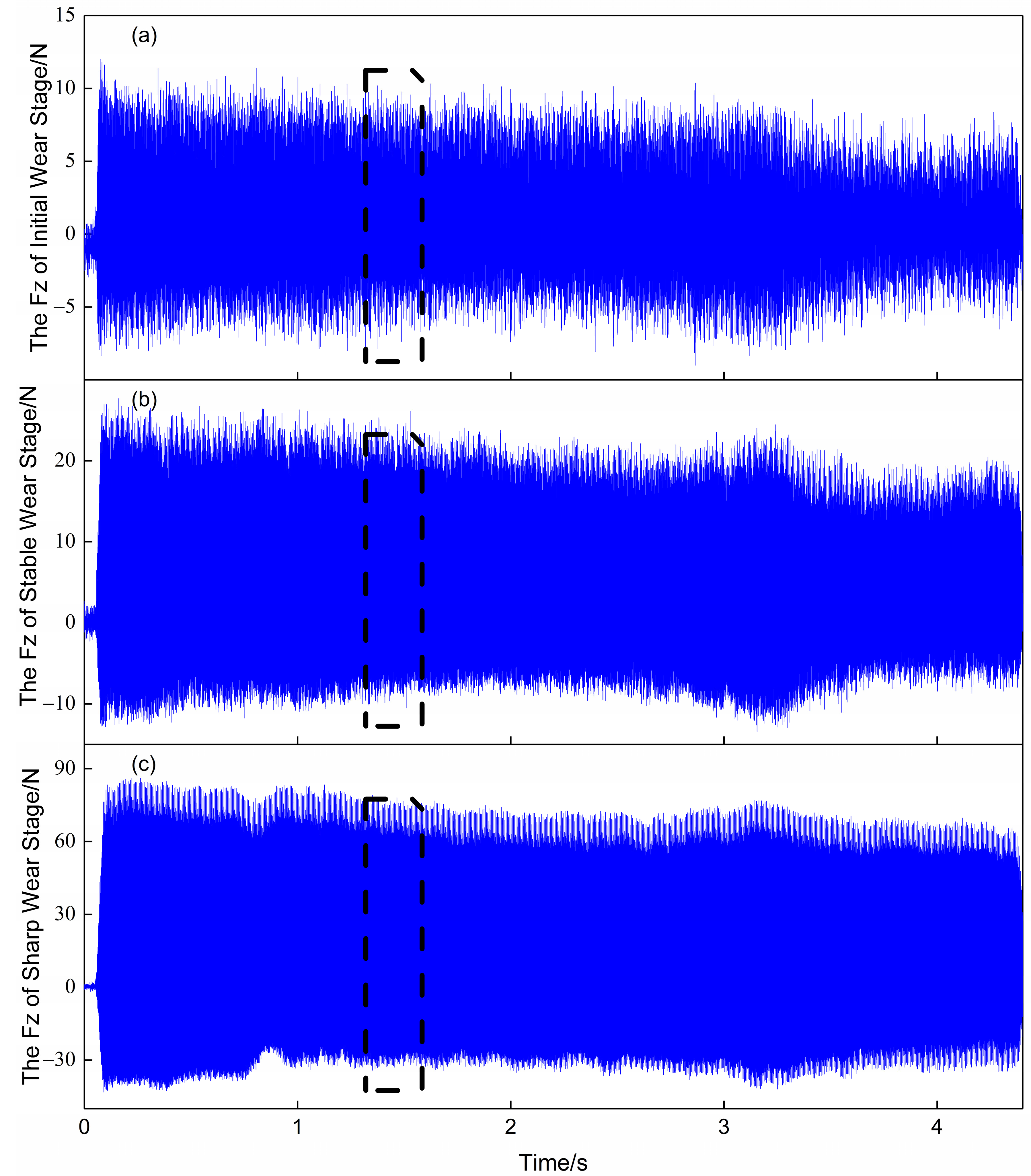
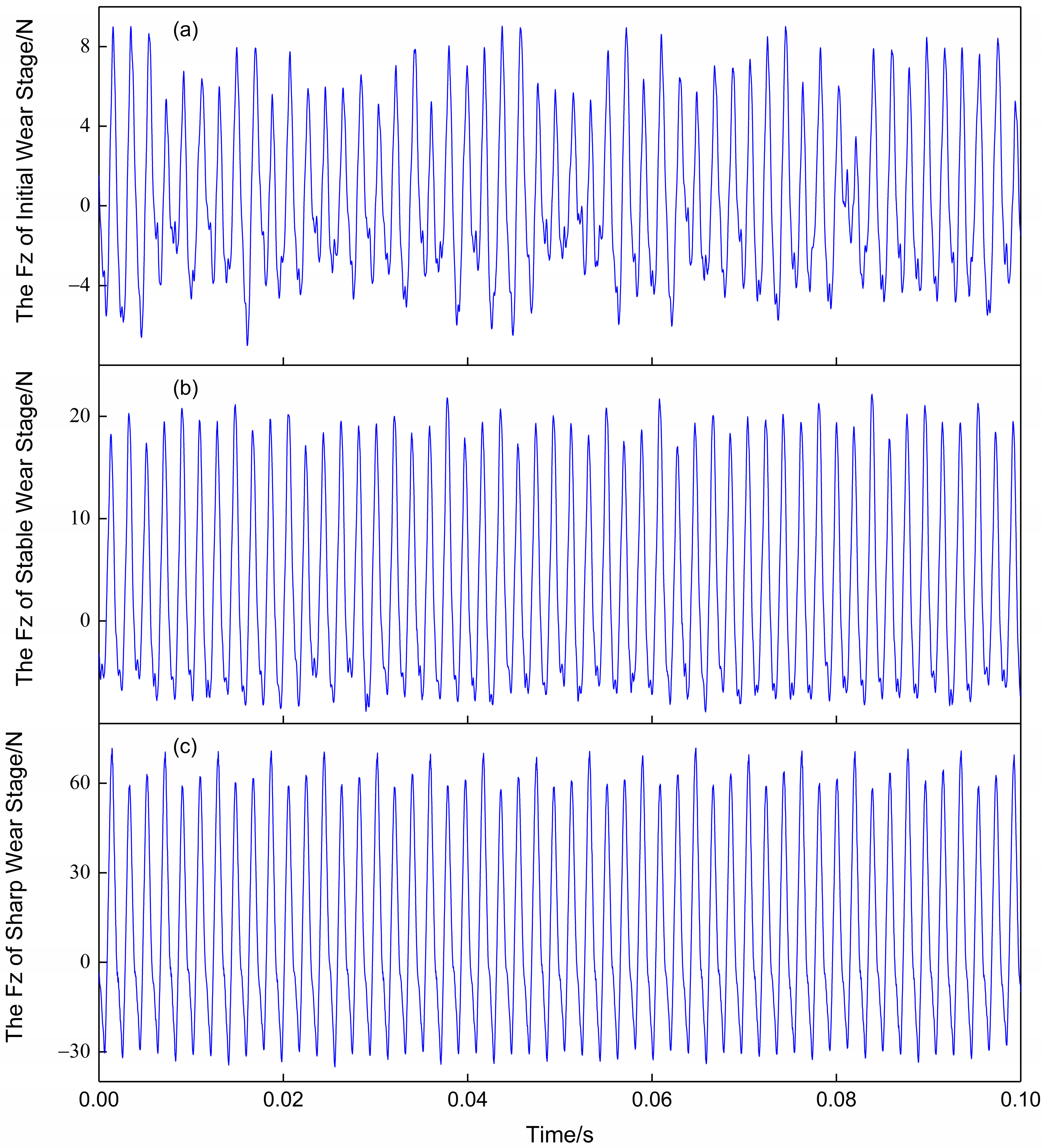
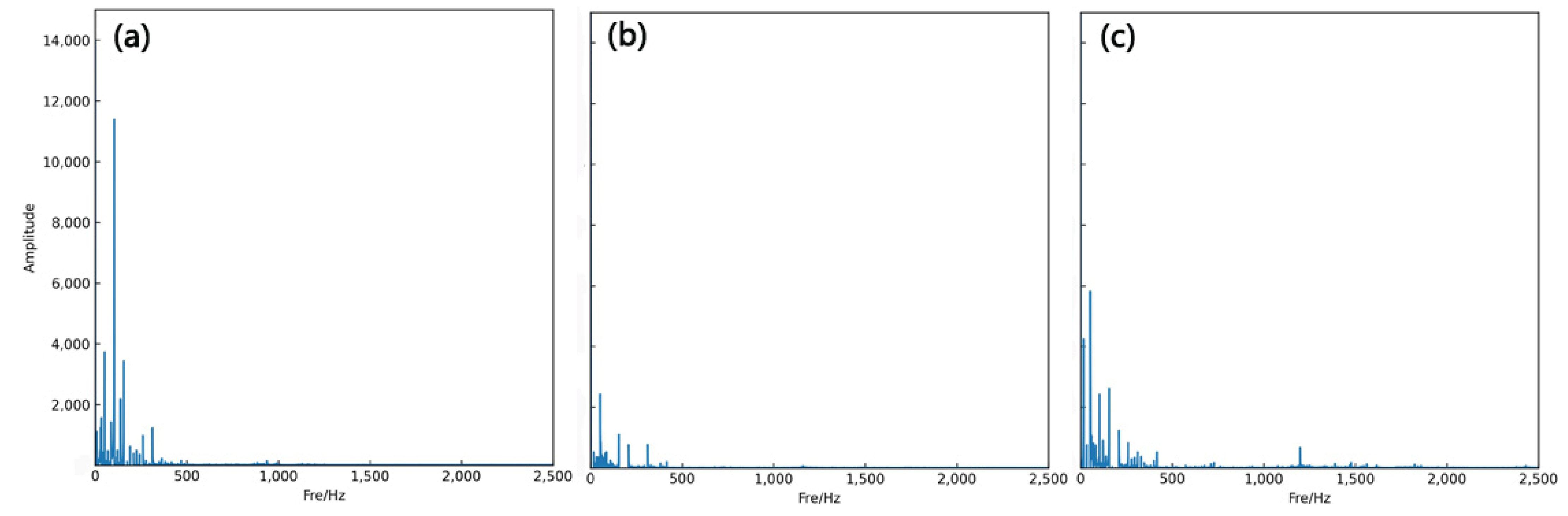
3.1. Force Signal Description
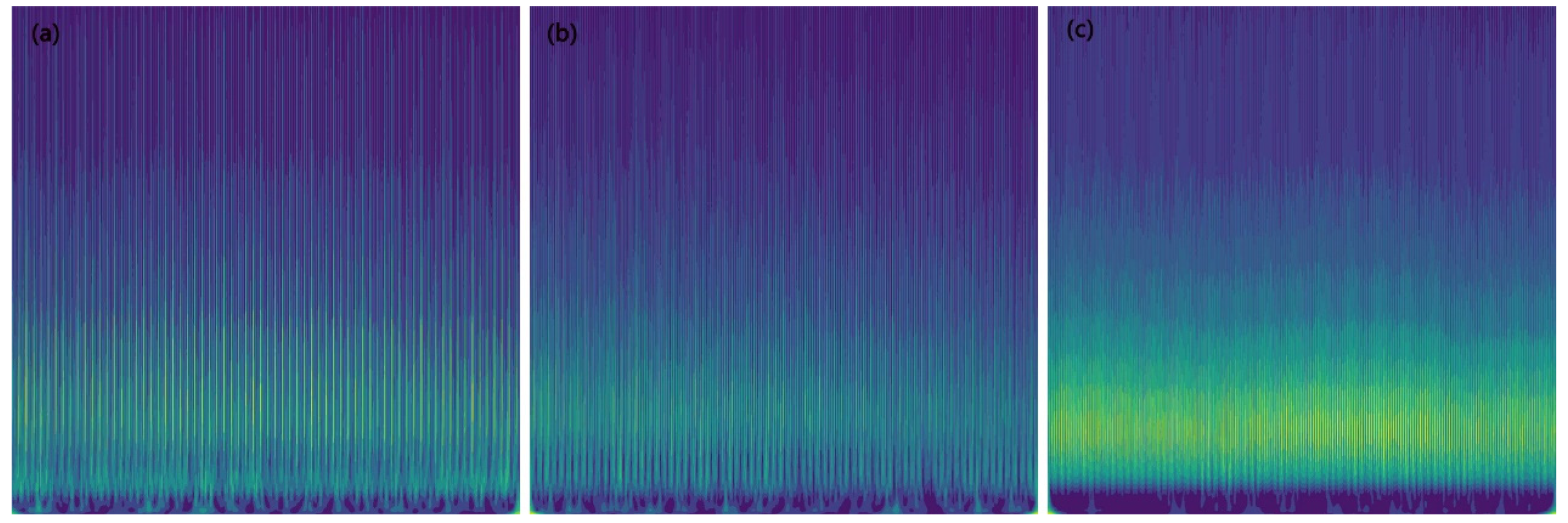
3.2. Force Signal to Image
4. Analysis Procedure
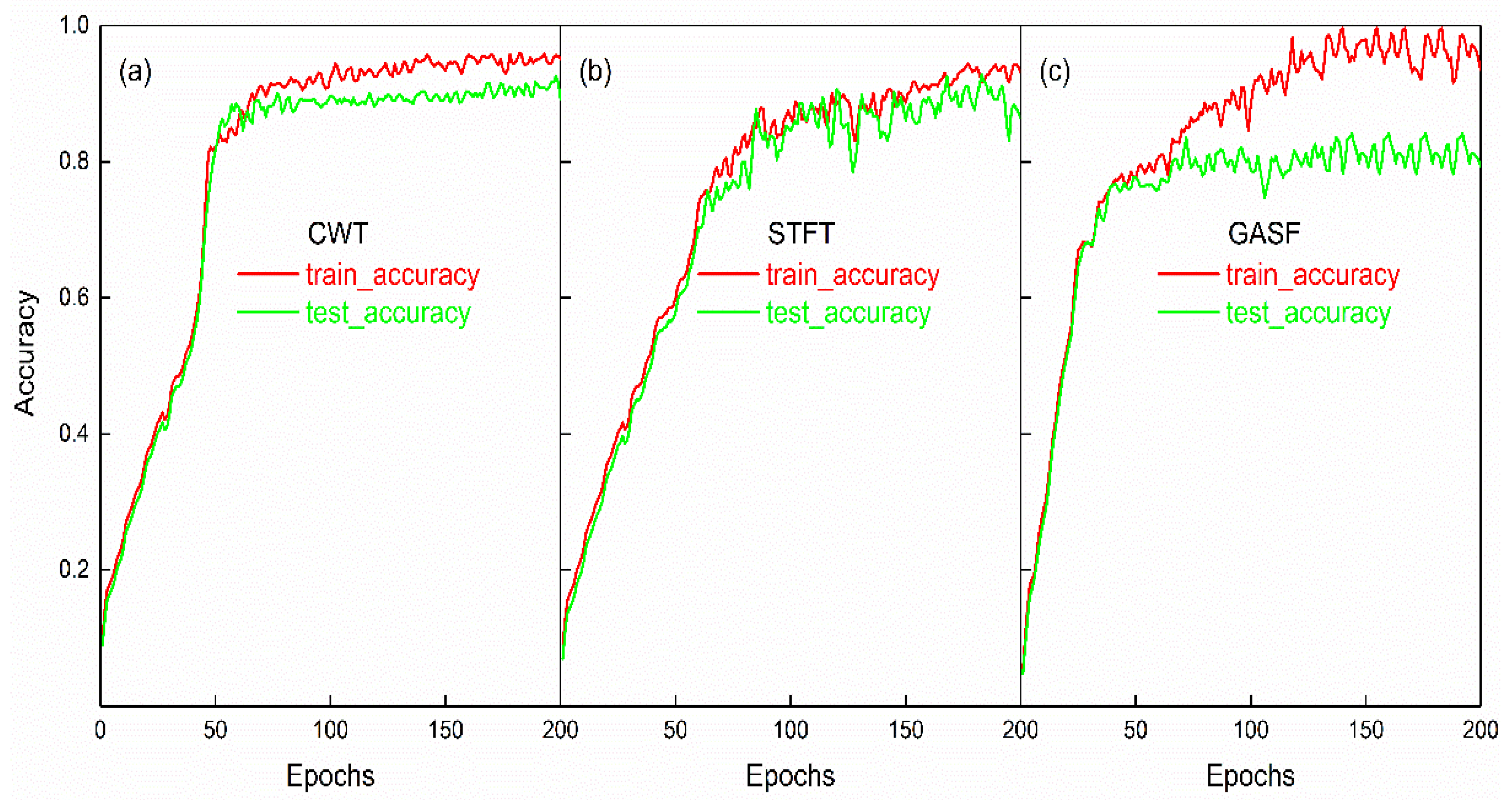
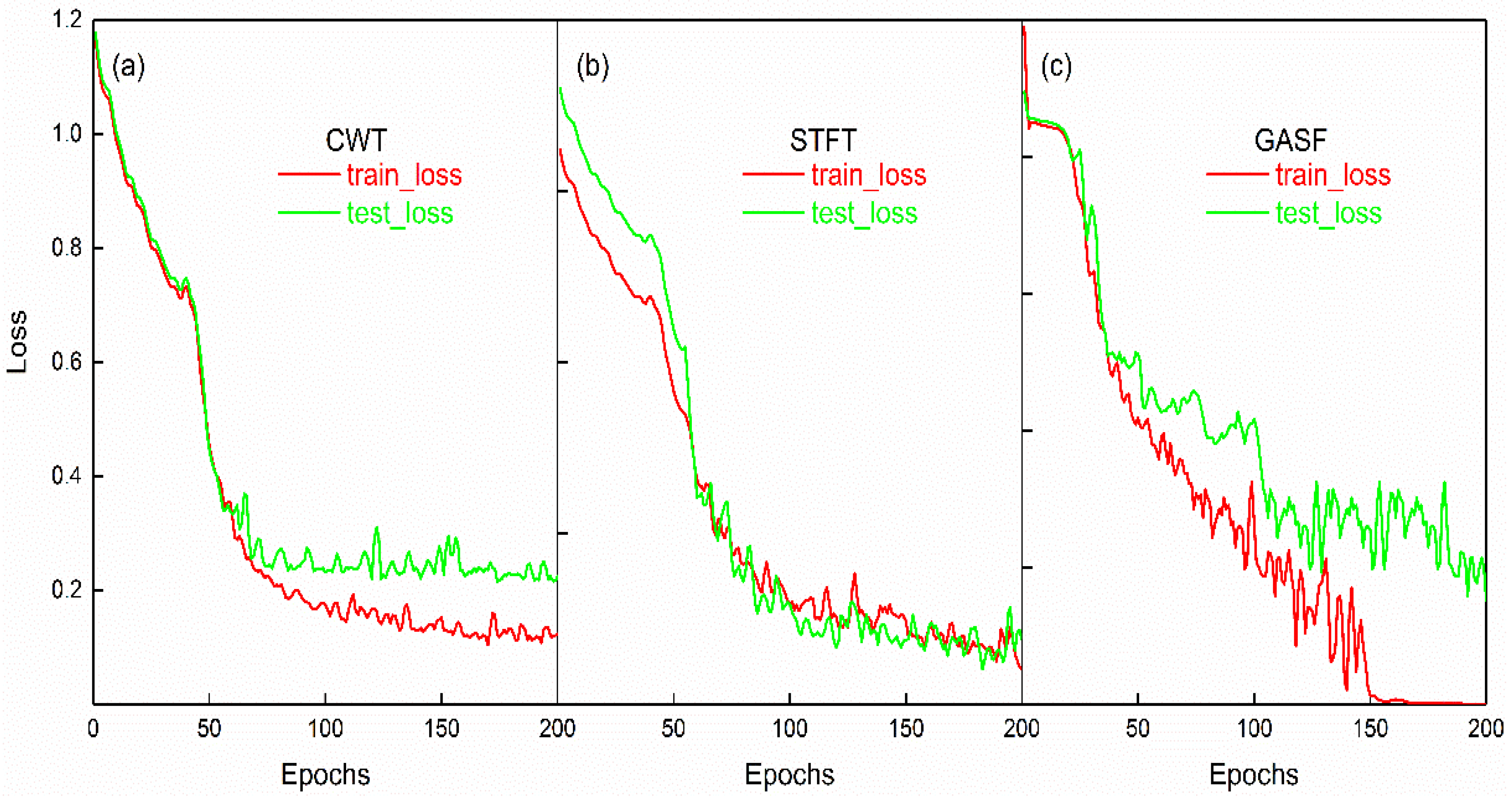
4.1. Results and Analysis of the Datasets
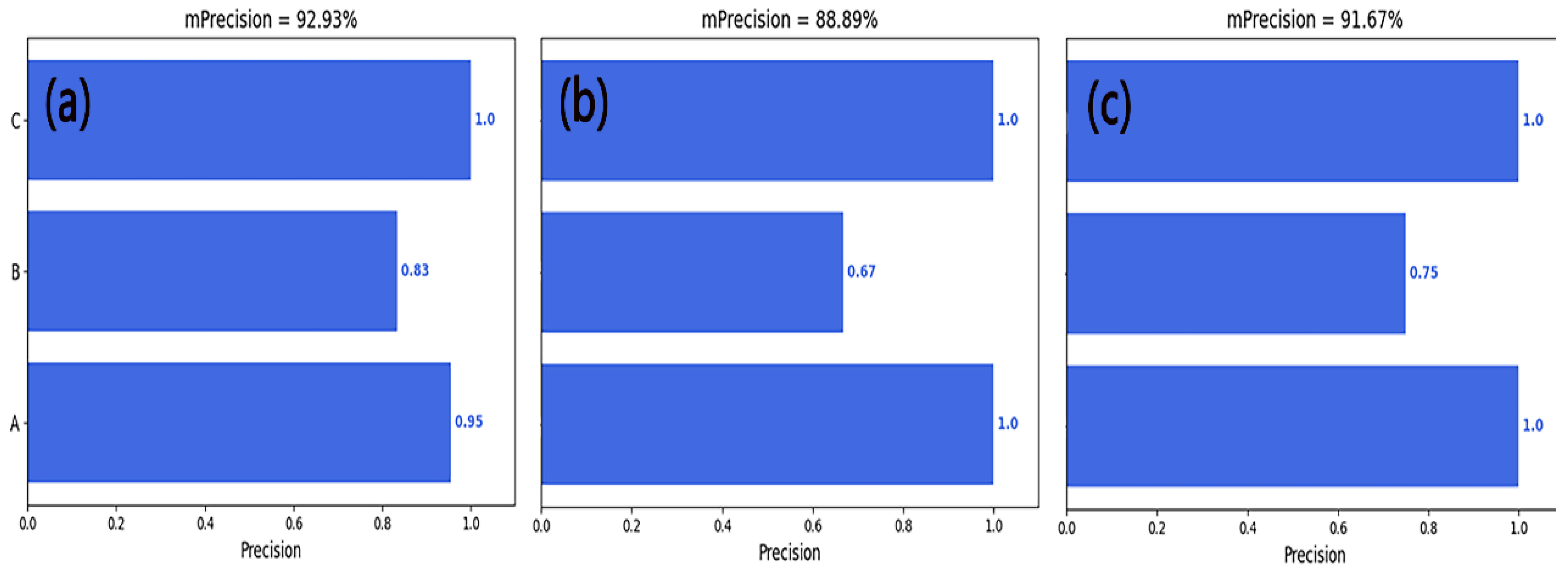
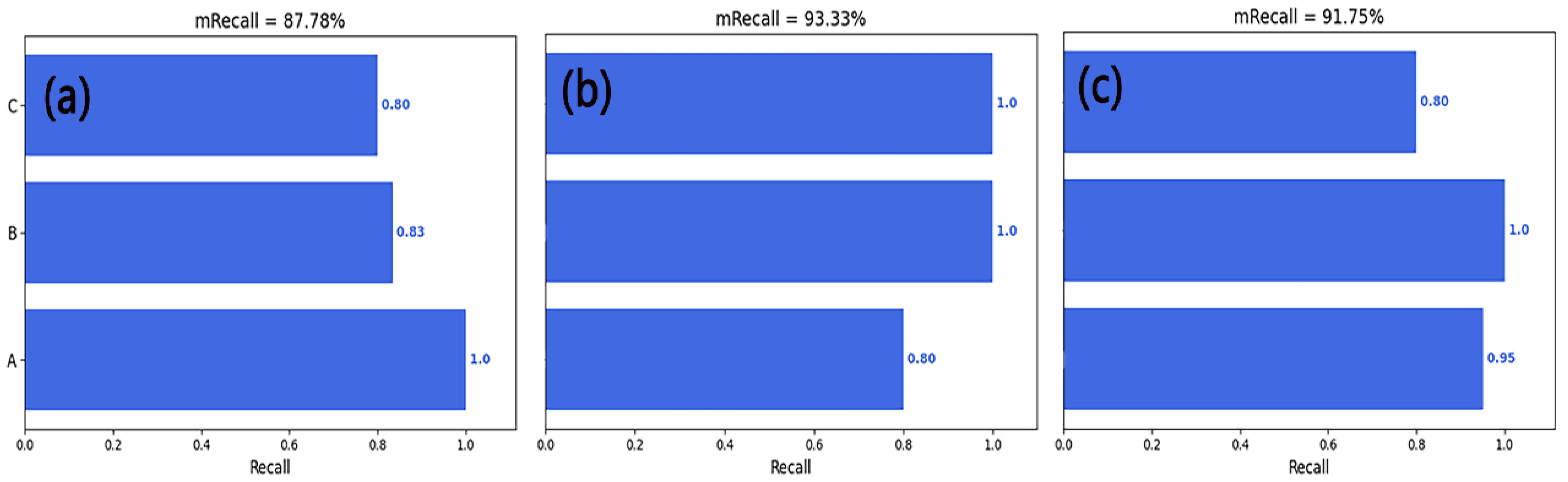
4.2. Precision and Recall
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- del Olmo, A.; López de Lacalle, L.N.; de Pissón, G.M.; Pérez-Salinas, C.; Ealo, J.A.; Sastoque, L.; Fernandes, M.H. Tool wear monitoring of high-speed broaching process with carbide tools to reduce production errors. Mech. Syst. Sign. Process. 2022, 172, 109003. [Google Scholar] [CrossRef]
- Zhou, Y.Q.; Sun, B.T.; Sun, W.F. A tool condition monitoring method based on two–layer angle kernel extreme learning machine and binary differential evolution for milling. Measurement 2020, 166, 108186. [Google Scholar] [CrossRef]
- Rivero, A.; López de Lacalle, L.N.; Penalva, M.L. Tool wear detection in dry high-speed milling based upon the analysis of machine internal signals. Mechatronics 2008, 18, 627–633.4. [Google Scholar] [CrossRef]
- Fong, K.M.; Wang, X.; Kamaruddin, S.; Ismadi, M.Z. Investigation on universal tool wear measurement technique using image-based cross–correlation analysis. Measurement 2021, 169, 108489. [Google Scholar] [CrossRef]
- Jee, W.K.; Ratnam, M.M.; Ahmad, Z.A. Detection of chipping in ceramic cutting inserts from workpiece profile during turning using fast Fourier transform (FFT) and continuous wavelet transform (CWT). Precis. Eng. 2017, 47, 406–423. [Google Scholar]
- Dutta, S.; Datta, A.; Chakladar, N.D.; Pal, S.K.; Mukhopadhyay, S.; Sen, R. Detection of tool condition from the turned surface images using an accurate grey level co-occurrence technique. Precis. Eng. 2012, 36, 458–466. [Google Scholar] [CrossRef]
- López de Lacalle, L.N.; Lamikiz, A.; Sánchez, J.A.; de Bustos, I.F. Simultaneous measurement of forces and machine tool position for diagnostic of machining tests. IEEE Trans. Instrum. Meas. 2005, 54, 2329–2335. [Google Scholar] [CrossRef]
- Yang, X.; Yuan, R.; Lv, Y.; Li, L.; Song, H. A novel multivariate cutting force-based tool wear monitoring method using one-dimensional convolutional neural network. Sensors 2022, 22, 8343. [Google Scholar] [CrossRef]
- Bhuiyan, M.S.H.; Choudhury, I.A.; Dahari, M.; Nukman, Y.; Dawal, S.Z. Application of acoustic emission sensor to investigate the frequency of tool wear and plastic deformation in tool condition monitoring. Measurement 2016, 92, 208–217. [Google Scholar] [CrossRef]
- Yuan, R.; Lv, Y.; Wang, T.; Li, S.; Li, H.W.X. Looseness monitoring of multiple MI bolt joints using multivariate intrinsic multiscale entropy analysis and Lorentz signal-enhanced piezoelectric active sensing. Struct. Health Monit. 2022, 21, 2851–2873. [Google Scholar] [CrossRef]
- Yuan, R.; Liu, L.B.; Yang, Z.Q.; Zhang, Y.R. Tool wear condition monitoring by combining variational mode decomposition and ensemble learning. Sensors 2020, 20, 6113. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Li, J.; Lu, Y. An integrated wireless vibration sensing tool holder for milling tool condition monitoring. Int. J. Adv. Manuf. Technol. 2018, 95, 2885–2896. [Google Scholar] [CrossRef]
- Li, Z.; Liu, R.; Wu, D. Data-driven smart manufacturing: Tool wear monitoring with audio signals and machine learning. J. Manuf. Process. 2019, 48, 66–76. [Google Scholar] [CrossRef]
- Lei, Z.; Zhou, Y.; Sun, B.; Sun, W. An intrinsic timescale decomposition- based kernel extreme learning machine method to detect tool wear conditions in the milling process. Int. J. Adv. Manuf. Technol. 2020, 106, 1203–1212. [Google Scholar] [CrossRef]
- Lin, J.; Bhattacharyya, D.; Kecman, V. Multiple regression and neural networks analyses in composites machining. Compos. Sci. Technol. 2003, 63, 539–548. [Google Scholar] [CrossRef]
- Da Silva, R.H.L.; Da Silva, M.B.; Hassui, A. A probabilistic neural network applied in monitoring tool wear in the end milling operation via acoustic emission and cutting power signals. Mach. Sci. Technol. 2016, 20, 386–405. [Google Scholar] [CrossRef]
- Gomes, M.C.; Brito, L.C.; da Silva, M.B.; Duarte, M.A.V. Tool wear monitoring in micromilling using support vector machine with vibration and sound sensors. Precis. Eng. 2021, 67, 137–151. [Google Scholar] [CrossRef]
- Wu, D.; Jennings, C.; Terpenny, J.; Gao, R.X.; Kumara, S. A comparative study on machine learning algorithms for smart manufacturing: Tool wear prediction using random forests. ASME J. Manuf. Sci. Eng. 2017, 139, 071018. [Google Scholar] [CrossRef]
- Zhu, K.P.; Wong, Y.S.; Hong, G.S. Multi-category micro-milling tool wear monitoring with continuous hidden Markov models. Mech. Syst. Signal Pr. 2009, 23, 547–560. [Google Scholar] [CrossRef]
- Ma, J.; Luo, D.; Liao, X.; Zhang, Z.; Huang, Y.I.; Lu, J. Tool wear mechanism and prediction in milling TC18 titanium alloy using deep learning. Measurement 2021, 173, 108554. [Google Scholar] [CrossRef]
- Chang, W.-Y.; Wu, S.-J.; Hsu, J.-W. Investigated iterative convergences of neural network for prediction turning tool wear. Int. J. Adv. Manuf. Technol. 2020, 106, 2939–2948. [Google Scholar] [CrossRef]
- Wang, J.J.; Yan, J.X.; Li, C.; Gao, R.X.; Zhao, R. Deep heterogeneous GRU model for predictive analytics in smart manufacturing: Application to tool wear prediction. Comput. Ind. 2019, 111, 1–14. [Google Scholar] [CrossRef]
- Li, Z.X.; Liu, X.H.; Incecik, A.; Gupta, M.K.; Krolczyk, G.M.; Gardoni, P. A novel ensemble deep learning model for cutting tool wear monitoring using audio sensors. J. Manuf. Process. 2022, 79, 233–249. [Google Scholar] [CrossRef]
- Zhou, Y.Q.; Zhi, G.F.; Chen, W.; Qian, Q.J.; He, D.D.; Sun, B.T.; Sun, W.F. A new tool wear condition monitoring method based on deep learning under small samples. Measurement 2022, 189, 110622. [Google Scholar] [CrossRef]
- Tran, M.Q.; Liu, M.K.; Tran, Q.V. Milling chatter detection using scalogram and deep convolutional neural network. Int. J. Adv. Manuf. Technol. 2020, 107, 1505–1516. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q. Deep learning-based remaining useful life estimation of bearings using multi–scale feature extraction. Reliab. Eng. Syst. Safe. 2019, 182, 208–218. [Google Scholar] [CrossRef]
- Peng, R.; Liu, J.; Fu, X.; Liu, C.; Zhao, L. Application of machine vision method in tool wear monitoring. Int. J. Adv. Manuf. Technol. 2021, 116, 1357–1372. [Google Scholar] [CrossRef]
- Dai, Y.Q.; Zhu, K.P. A machine vision system for micro-milling tool condition monitoring. Precis. Eng. 2018, 52, 183–191. [Google Scholar] [CrossRef]
- Ong, P.; Lee, W.K.; Lau, R.J.T. Tool condition monitoring in CNC end milling using wavelet neural network based on machine vision. Int. J. Adv. Manuf. Technol. 2019, 104, 1369–1379. [Google Scholar] [CrossRef]
- Berger, B.S.; Minis, I.; Harley, J.; Rokni, M.; Papadopoulos, M. Wavelet based cutting state identification. J. Sound Vib. 1998, 213, 813–827. [Google Scholar] [CrossRef]
- Najmi, A.H.; Sadowsky, J. The continuous wavelet transform and variable resolution time-frequency analysis. Johns Hopkins Apl. Technical. Diges. 1997, 18, 134–140. [Google Scholar]
- Chen, Y.; Li, H.Z.; Jing, X.B.; Hou, L.; Bu, X.J. Intelligend chatter detction using image features and support vector machine. Int. J. Adv. Manuf. Technol. 2019, 102, 1433–1442. [Google Scholar] [CrossRef]
- Arellano, G.M.; Terrazas, G.; Ratchev, S. Tool wear classification using time series imaging and deep learning. Int. J. Adv. Manuf. Technol. 2019, 104, 3647–3662. [Google Scholar] [CrossRef]
- The Prognostics and Health Management Society. 2010 PHM Society Conference Data Challenge. Available online: https://www.phmsociety.org/competition/phm/10 (accessed on 7 May 2023).

| Parameter | Image Size | Learning Rate | Dropout | Batch Size | Optimizer | Loss Function |
|---|---|---|---|---|---|---|
| Value | 128 × 128 × 3 | 0.001 | 0.1 | 4 | SGDM | CrossEntrophy |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Qi, X.; Wang, T.; He, Y. Tool Wear Condition Monitoring Method Based on Deep Learning with Force Signals. Sensors 2023, 23, 4595. https://doi.org/10.3390/s23104595
Zhang Y, Qi X, Wang T, He Y. Tool Wear Condition Monitoring Method Based on Deep Learning with Force Signals. Sensors. 2023; 23(10):4595. https://doi.org/10.3390/s23104595
Chicago/Turabian StyleZhang, Yaping, Xiaozhi Qi, Tao Wang, and Yuanhang He. 2023. "Tool Wear Condition Monitoring Method Based on Deep Learning with Force Signals" Sensors 23, no. 10: 4595. https://doi.org/10.3390/s23104595
APA StyleZhang, Y., Qi, X., Wang, T., & He, Y. (2023). Tool Wear Condition Monitoring Method Based on Deep Learning with Force Signals. Sensors, 23(10), 4595. https://doi.org/10.3390/s23104595








