1. Introduction
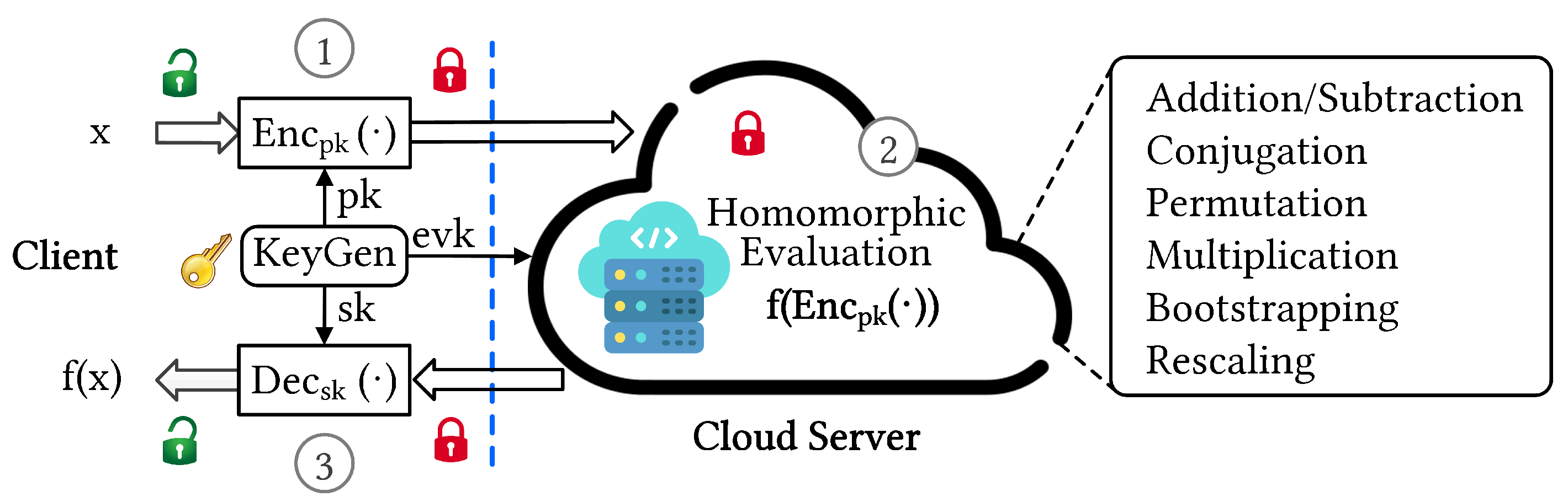
With the explosion of the Internet-of-Things-based data and the widespread use of machine learning (ML) as a cloud-based service, securing private user data during ML inferences has become a pressing concern for cloud-service providers. Fully homomorphic encryption (FHE) is a promising solution for preserving sensitive information in cloud computing because it provides strong defense mechanisms and enables the direct computation on encrypted data (ciphertext) while preserving confidentiality [
1,
2]. However, the requirement for high degrees of security leads to complex parameter settings, resulting in expensive computation on large ciphertext, which limits the practical realization of FHE-based applications. Cloud-side analytics can be resource-intensive and time-consuming, making it necessary to develop cryptographic accelerators to facilitate the deployment of real-world applications. Cryptographic accelerators are designed to reduce the computational overhead of homomorphic functions, thus enabling faster and more efficient computation on encrypted data. The development of such accelerators is crucial to unlock the full potential of FHE-based solutions, make it more accessible to a wider range of users and supporting the secure processing of sensitive data in real-world settings.
Figure 1 illustrates an end-to-end FHE-based cryptosystem with primary homomorphic operations performed in the cloud server.
FHE cryptographic protocols typically involve integer- and lattice-based schemes. The most efficient lattice-based schemes rely on the ring learning with errors (RLWE) problem, which provides strong security guarantees and the desired performance [
3]. In RLWE-based FHE protocols, the input messages are encrypted by adding noise, and the generated ciphertexts are composed of two polynomial rings. The growth of noise through homomorphic computations limits the circuit depth, and the selection of FHE parameters must balance the security requirements with computational complexity [
4]. Parameter selection primarily involves polynomial degree
N, and modulo integer
Q with at least 128-bit security is typically required to guard against unpredictable attacks [
5]. To support multiplicative depth,
N increases proportionally. High-circuit-depth FHE schemes inevitably have the drawback of large ciphertexts, which leads to expensive computations, high-bandwidth data movement, and large storage-space requirements.
Primary homomorphic operations involve addition, multiplication, and permutation of ciphertexts. Homomorphic multiplication between ciphertexts is often computationally expensive because of the convolution of polynomial coefficients.
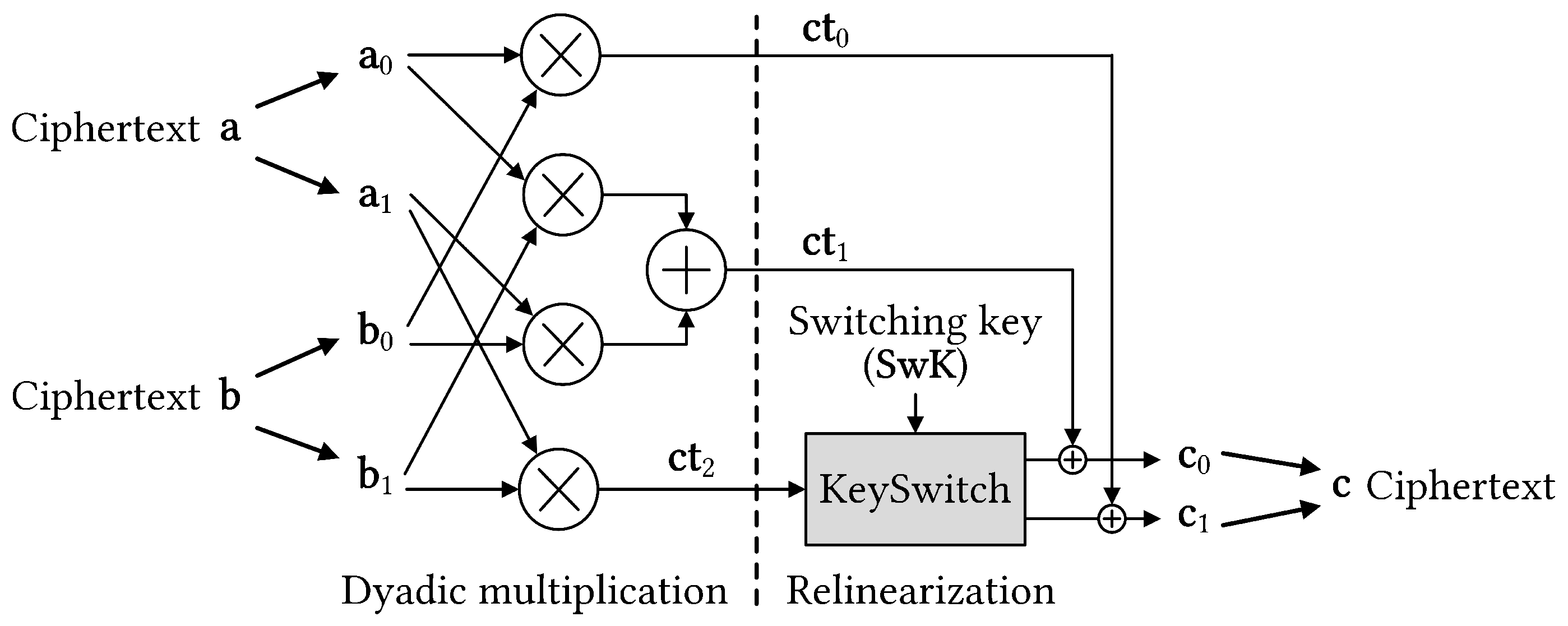
Figure 2 shows a general diagram of the multiplication between two ciphertexts that dominates homomorphic operations. Initially, ciphertext consists of two component polynomials. The ciphertext multiplication results in a tuple of polynomials, making further computation challenging. Thus, an operation is required to revert the ciphertext to its original form. An expensive operation known as key switching is required to relinearize the ciphertext. However, key switching is computationally intensive with number theoretic transform (NTT) and inverse NTT (INTT) operations being dominant. Therefore, developing key switching hardware accelerators is significant for speeding up homomorphic multiplication and realizing FHE-based applications.
1.1. Related Works
While FHE holds potential, its primary limitation is inefficiency, which stems from two factors: complex polynomial operations and time-consuming ciphertext management. To tackle the computational and memory demands of homomorphic functions, various optimization and acceleration efforts are underway.
Table 1 presents FHE accelerators, highlighting the hardware utilized and features of the accelerators. Initially, FHE acceleration depended on general hardware features. However, CPUs lack the capacity to effectively harness FHE’s inherent parallelism [
6]. GPU-based implementations tap into this parallelism, but GPU’s extensive floating-point units remain underused as FHE tasks mainly involve integer operations [
7,
8,
9]. Furthermore, neither CPUs nor GPUs offer sufficient main memory bandwidth to cope with FHE workload’s data-intensive nature.
To enhance FHE scheme performance, researchers have been exploring custom hardware accelerators using ASIC and FPGA technologies. ASIC solutions [
10,
11,
12,
13] show promise, as they surpass CPU/GPU implementations and bridge the performance gap between plaintext and ciphertext computations. However, to accommodate large on-chip memory, expensive advanced technology nodes such as 7 nm or 12 nm are required for ASIC implementations. Furthermore, designing and fabricating these ASIC proposals demand significant engineering time and high non-recurring costs. Since FHE algorithms are not standardized and continue to evolve, any changes would necessitate major ASIC redesign efforts. Conversely, FPGA solutions are more cost-effective than ASICs, offer rapid prototyping and design updates, and are better equipped to adapt to future FHE algorithm modifications.
Several studies have proposed FPGA-accelerated architecture designs for FHE [
14,
15,
16,
17,
18,
19]. Notably, Riazi et al. introduced HEAX, a hardware architecture that accelerates CKKS-based HE on Intel FPGA platforms and supports low parameter sets [
14]. However, the architecture faces high input/output and memory interface bandwidths, as well as costly internal memory, making it difficult to place and route multiple cores on the target FPGA platform. Han et al. proposed coxHE, an FPGA acceleration framework for FHE kernels using the high-level synthesis (HLS) design flow [
16]. Targeting key switching operations, coxHE examined data dependence to minimize interdependence between data, maximizing parallel computation and algorithm acceleration. Mert et al. proposed Medha, a programmable instruction-set architecture that accelerates cloud-side RNS-CKKS operations [
17]. Medha featured seven residue polynomial arithmetic units (RPAU), memory-conservative design, and support for multiple parameter sets using a single hardware accelerator with a divide-and-conquer technique. However, these three FPGA-based implementations only support small parameter sets, insufficient for bootstrapping. Recently, Yang et al. proposed Poseidon, an FPGA-based FHE accelerator supporting bootstrapping on the modern Xilinx U280 FPGA [
18]. Poseidon employed several optimization techniques to enhance resource efficiency. Similarly, Agrawal et al. presented FAB, an FPGA-accelerated design that balances memory and computing consumption for large homomorphic parameter bootstrapping [
19]. FAB accelerates CKKS bootstrapping using a carefully designed datapath for key switching, taking full advantage of on-chip 43 MB on-chip storage. However, the design’s extensive parallelism consumes numerous logic elements, especially with larger parameter sets. Additionally, inefficient scheduling can result in redundant resource consumption and complex workflow synchronization, leading to suboptimal performance. In this work, we adopt a pipelined KeySwitch design to simplify scheduling and target high-throughput implementation. Our design method leverages FPGA fabric’s programmable logic elements and enhances on-chip memory utilization.
1.2. Our Main Contributions
This study presents a comprehensive hardware architecture for the KeySwitch accelerator design, which operates in a highly pipelined manner to speed up CKKS-based FHE schemes. Built on compact NTT and INTT engines [
20], the KeySwitch module efficiently employs on-chip resources. Importantly, our design approach significantly reduces internal memory consumption, allowing on-chip memory to hold temporary data. The design executes subfunctions concurrently in a pipelined and parallel manner to boost throughput. We demonstrate an example design supporting a three-level parameter set. The proposed KeySwitch module was evaluated on the Xilinx UltraScale+ XCU250 FPGA platform, and we provide an in-depth discussion of the design methodology and area breakdown for better understanding of key operations. Compared to the most related study, our KeySwitch module achieves a 1.6x higher throughput rate and superior hardware efficiency.
The remainder of this paper is organized as follows:
Section 2 provides an overview of the underlying operations of RLWE-based HE schemes.
Section 3 describes the key switching algorithm in detail, and
Section 4 presents the design of our KeySwitch module.
Section 5 presents the experimental results, compares our approach with related works, and discusses our findings. Finally,
Section 6 concludes the study.
2. Background
CKKS-based HE schemes have been extensively studied to perform meaningful computations on encrypted data of real and complex numbers. In the encrypted data domain, the ciphertext often consists of two N-degree polynomials, and each coefficient is an integer modulo Q. Therefore, the underlying homomorphic operations in RLWE-based HE schemes share similarities, enabling the development of a single hardware accelerator that can support multiple HE instances. Our study primarily focuses on accelerating CKKS-based homomorphic encryption; however, the operations described at the ciphertext level have a broad applicability to almost all lattice-based homomorphic encryption schemes.
2.1. Residue Number System
The Chinese remainder theorem (CRT) enables a polynomial in
to be represented as an RNS decomposition with smaller pairwise coprimes such that
[
21]. This enables polynomial
in
to be represented in RNS channels as a set of polynomial components. For instance, considering an RNS representation with three pairwise co-prime moduli
, the polynomial
can be represented as a set of three polynomials:
, where each
is a polynomial in
. This technique can significantly reduce the magnitude of coefficients and improve the performance of arithmetic operations in HE.
We denote the polynomial component in a ring field
/
as follows:
Thus, arithmetic operations on large integer coefficients can be performed for each smaller modulus without any loss of precision.
2.2. Gadget Decomposition
Let
q be the modulus and
be a gadget vector. A gadget decomposition [
22], denoted by
, maps an integer
into a vector
and
(mod
q). By extending the domain of the gadget decomposition
from
to
, we can apply it to a polynomial
in
by mapping each coefficient
to a vector
and then replacing
with
in the polynomial expression (
with
). This extension was proposed by [
23].
RNS representation can also be integrated with prime decomposition, as exemplified in [
24]. An element
can be represented in RNS form as
. The inverse mapping, which allows the retrieval of the original element
from its RNS form, is defined by the formula
(mod
Q), where
[
14].
2.3. Key Generation
The client begins by generating a secret key , which is a polynomial in . Then, they generate a uniformly random polynomial from and an error or noise polynomial from a distribution . The corresponding public key is generated as , where is obtained by taking the inner product of and a fixed vector , and adding the error polynomial , that is, .
Let
be a different key: We sample
and
. Using the gadget vector
, we compute
(mod
Q) and return a switching key (
SwK) as
, in which
is a vector of polynomials
[
23].
2.4. Encryption and Decryption
CKKS encodes a vector of maximal
real values into a plaintext polynomial
of
N coefficients, modulo
q. Using the generated public key
, the client encrypts an input message and produces a noisy ciphertext
as follows:
where
is another uniformly random vector and
and
are other noise vectors. After homomorphic computations on ciphertexts, the client obtains the results in the encrypted form
and uses the secret key to recover the desired information. Decryption is performed using
with a small error.
2.5. Homomorphic Operations
Homomorphic addition: Taking ciphertexts
and
for example, their homomorphic addition is computed by coefficient-wise adding their co-pair of RNS-element polynomials:
Homomorphic multiplication: For ciphertexts
and
, their homomorphic multiplication is performed by multiplications between their RNS elements:
This dyadic multiplication produces a special ciphertext of
for a different secret key (that is,
). Subsequently, key switching is performed to relinearize the quadratic form of homomorphic multiplication results and obtain a linear ciphertext of the original form.
Key switching: RLWE ciphertexts can be transformed from one secret key to another using key switching computation with
SwK. This method enables the transformation of a ciphertext decryptable by
into a new ciphertext under a different secret key
with an additional error
. The
SwK is considered a
d encryption of
under different secret keys
, that is,
(mod
Q) [
23].
Key switching () return (mod Q) where , . In detail:
- →
, where .
- →
.
3. Key Switching Algorithm
Algorithm 1 provides a detailed description of the homomorphic multiplication with a key switching operation, which is a crucial building block of the SEAL HE library [
6]. One remarkable feature of homomorphic multiplication is that NTT is a linear transformation, and optimized HE implementations typically store polynomials in the NTT form across operations instead of their coefficient form. Therefore, the first phase of homomorphic multiplication involves dyadic multiplication. However, the use of the Karatsuba algorithm, a fast multiplication technique, can reduce the total number of coefficient-wise multiplications from four to three. Dyadic multiplication produces a tuple of polynomials (
,
,
), where
is a special ciphertext that encrypts the square of the secret key; that is, (
). To recombine the homomorphic products and obtain a linear ciphertext in the form (
), key switching is required to make
decryptable with the original secret key. The homomorphic multiplication is computed using the following equation, which involves key switching using
SwK:
Key switching is a computationally intensive operation that typically dominates the cost of homomorphic multiplication. The key switching operation requires two inputs: the polynomial component and key switching key matrix SwK. The polynomial component is represented in RNS form as residue polynomials, whereas the key switching key matrix is a tensor of matrices of residue polynomials. RNS decomposition was used to enable fast key switching with a highly parallel and pipelined implementation.
Algorithm 1 shows that key switching involves
l INTT and
NTT operations for increasing the modulus, and two INTTs and two
l NTTs for modulus switching. Thus, key switching dominates the homomorphic multiplication process in terms of the computational cost. However, at
l-depth level, the main costs are memory expense and data movement. To illustrate the efficient utilization of the on-chip resources on the FPGA platform, we used a parameter set of five modulo primes as a running example. The implementation results indicate that the proposed approach maximizes the utilization of hardware resources.
| Algorithm 1 Homomorphic multiplication algorithm with a key switching operation [6] |
Input: and , where Output:
- 1:
/* Dyadic multiplication */ - 2:
for to l do - 3:
- 4:
- 5:
- 6:
end for - 7:
/* Key switching */ - 8:
for to ldo ▹ Modulus raising - 9:
INTT - 10:
for to l do - 11:
if then - 12:
Mod - 13:
NTT - 14:
else - 15:
- 16:
end if - 17:
(mod ) - 18:
(mod ) - 19:
end for - 20:
Mod - 21:
NTT - 22:
(mod ) - 23:
(mod ) - 24:
end for - 25:
for to 1 do ▹ Modulus switching - 26:
INTT - 27:
for to l do - 28:
Mod - 29:
NTT - 30:
(mod ) - 31:
(mod ) - 32:
end for - 33:
end for - 34:
return
|
4. KeySwitch Hardware Architecture
Figure 3 illustrates the pipelined architecture of the KeySwitch module with an initial depth of
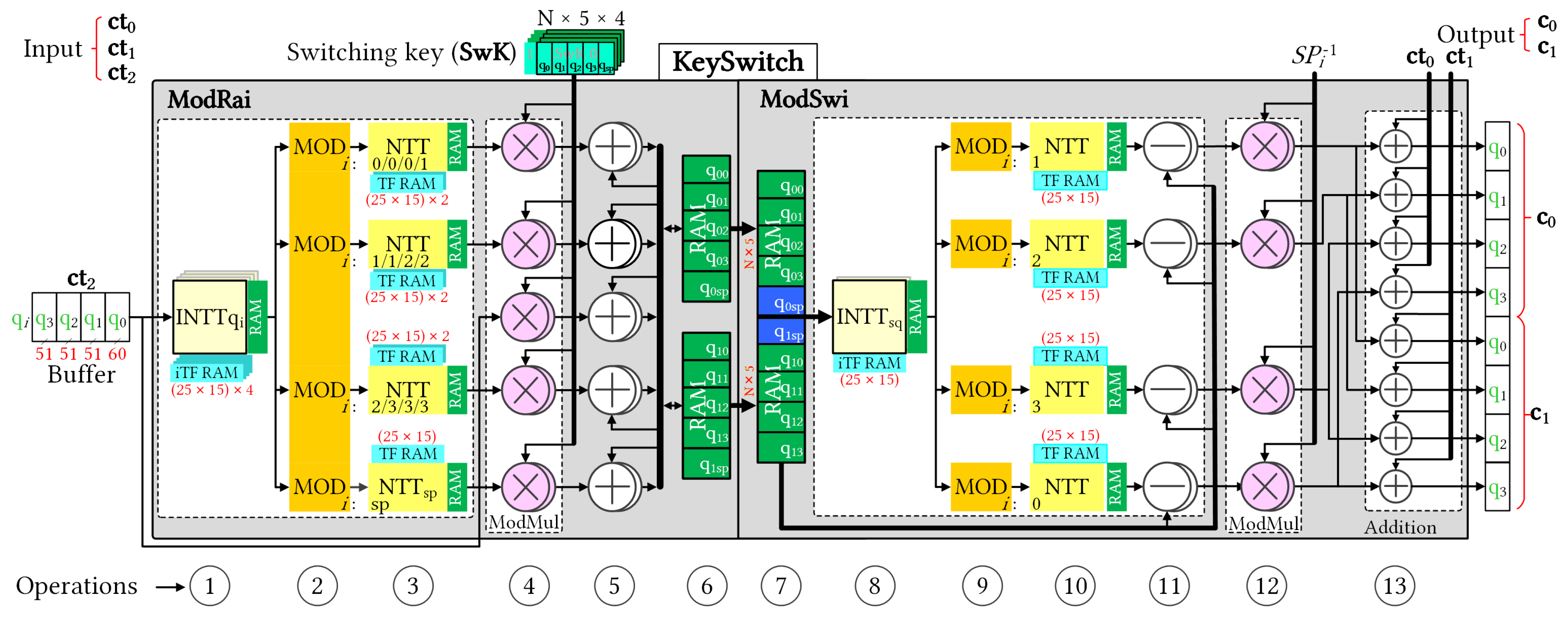
. The KeySwitch module consumes the third component of the dyadic multiplication result and generates relinearized ciphertext. The KeySwitch design was divided in two functional modules with a pipelined connection: ModRai and ModSwi. Two modules have similar structures, and we numbered the sequential operations for clarity. The numbering makes it easier to track the description of their operations.
Key switching operation is computationally intensive, with NTT and INTT operations being dominant. In an FHE setting, ciphertext polynomials are represented in the NTT form by default to reduce the number of NTT/INTT conversions. However, this format is not compatible with the rescaling operation that occurs during moduli switching. Therefore, the key switching process involves performing NTT and INTT operations before and after rescaling, respectively. Consequently, the primary computational costs associated with key switching are for the NTT and INTT operations. Conventionally, the NTT and INTT units consume a large amount of internal memory to store precomputed TFs. In this study, the proposed KeySwitch module employs in-place NTT and INTT hardware designs that aim to reduce the on-chip memory usage [
20]. In particular, each NTT and INTT unit stores several TF bases of the associated modulus and utilizes built-in twiddle factor generator (TFG) to twiddle all other factors. Based on the design method of [
20] and the exploration of the key switching execution, we designed different NTT modules for associated moduli through pipeline stages. By adopting this approach, the proposed KeySwitch module utilizes hardware resources more efficiently.
In the ModRai module, the first INTT operation transforms a sequence of (
) input polynomials into the associated modulus (op ①). The next stage involves performing MOD operations on the previous INTT results for the (
) moduli. Because operations on individual (
) moduli are independent of RNS decomposition, we can perform (
) MODs in parallel (op ②) to efficiently pipeline the computation. Modular multiplication (ModMul) also requires the original input polynomial, which reduces the number of MODs on (
) moduli to (
) MODs at a time.
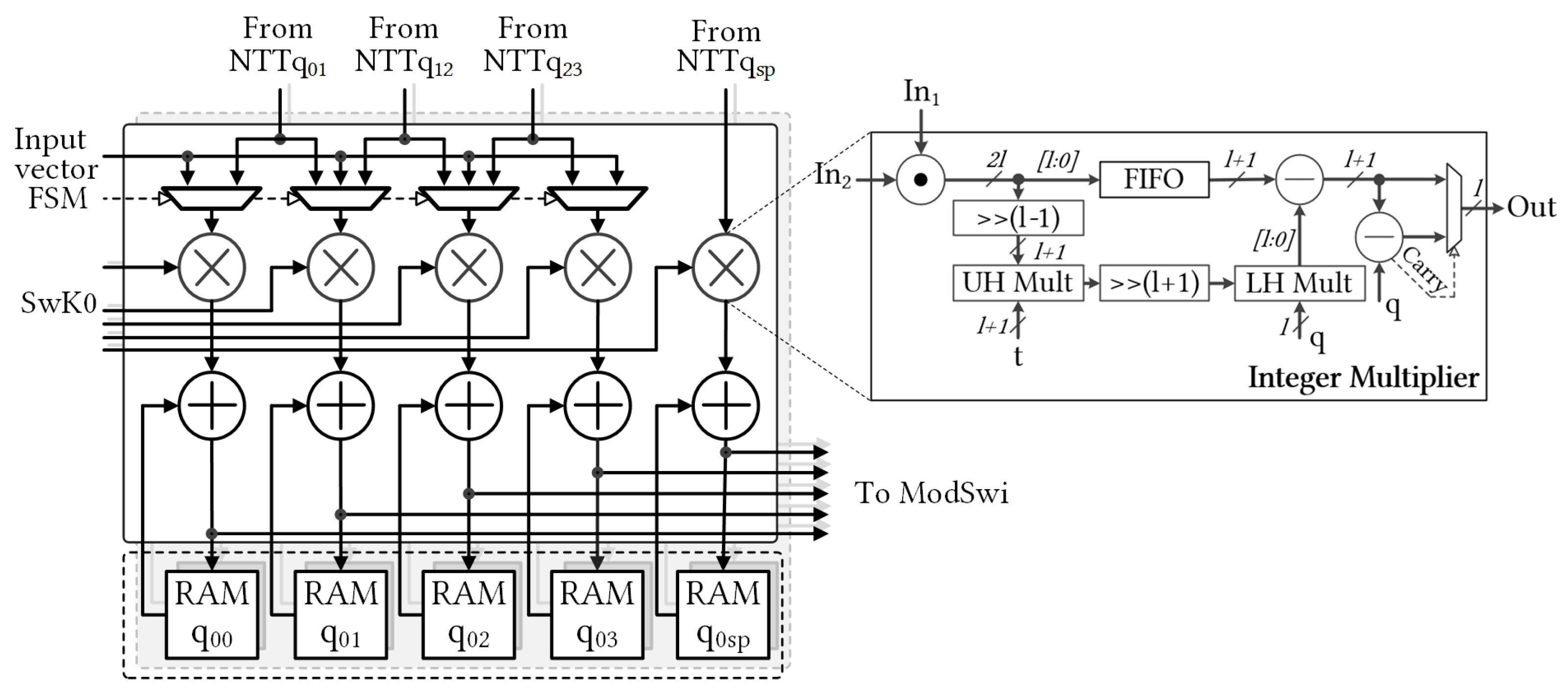
Figure 4 shows selectable MOD outputs. Subsequently, the (
) NTT modules must run in parallel for subsequent NTT computations (op ③). Once the NTT computations are complete, the ModMul module performs modular multiplications with the
SwK using Algorithm 1. To simultaneously generate two relinearized vectors, we deployed
(
) ModMul modules (op ④). After the ModMul product, the results were stored in the following memory banks (ops ⑤ and ⑥, respectively). We used two Ultra RAM (URAM), large-scale, high-speed memory element, banks to store two polynomials with five RNS components. After accumulating (
) polynomials in URAMs, the ModRai module transferred the temporary data to the ModSwi module memory and continued accumulating with the next polynomials. Cooperation after NTT was indicated as MAR, and its detailed structure is shown in
Figure 5.
The ModSwi module performed the second part of the key switching operation after (
) iterations. In this step, temporary data from ModRai were received and stored in RAM banks (op ⑦). The following INTT unit transformed only the two polynomials with the associated special modulus
(op ⑧). The ModSwi module then performed the flooring operation with (
) MR units and (
) NTT computations (ops ⑨ and ⑩, respectively). For the ModMul operation of the 51-bit modulus, the coefficients were compared with half of
, and the subtraction with the residue of
modulo
was then determined [
6]. At the end of the flooring, subtraction with ModRai outputs and subsequent multiplication by the inverse value of the special prime were performed for two polynomials of RNS components in parallel (ops ⑪ and ⑫, respectively). Op ⑬ added the remaining two components of the homomorphic multiplication results to the outputs of the flooring operation, and generated the relinearized ciphertext simultaneously. The output of the key switching operation consisted of two polynomials of RNS components, which are referred to as
c and
c of the key-switched ciphertext
c.
The pipeline timing for the key switching operation is shown in
Figure 6, where each pipeline stage comprises a series of consecutive operations separated by a few cycles. Each square block represents the approximate delay of the one-polynomial NTT computation. The ModRai unit can increase the modulus in a highly pipelined manner, with the results stored in the RAM until all input moduli are transformed (op ⑥). Subsequently, the ModSwi module performs the modulus switching operation only for two polynomials with the associated special modulus. In a pipelined operation, modulus switching has a timing delay of two square blocks. However, the delay gap between consecutive key switching operations depends on the number of modulo primes, which affects the accumulation latency in the ModRai module.
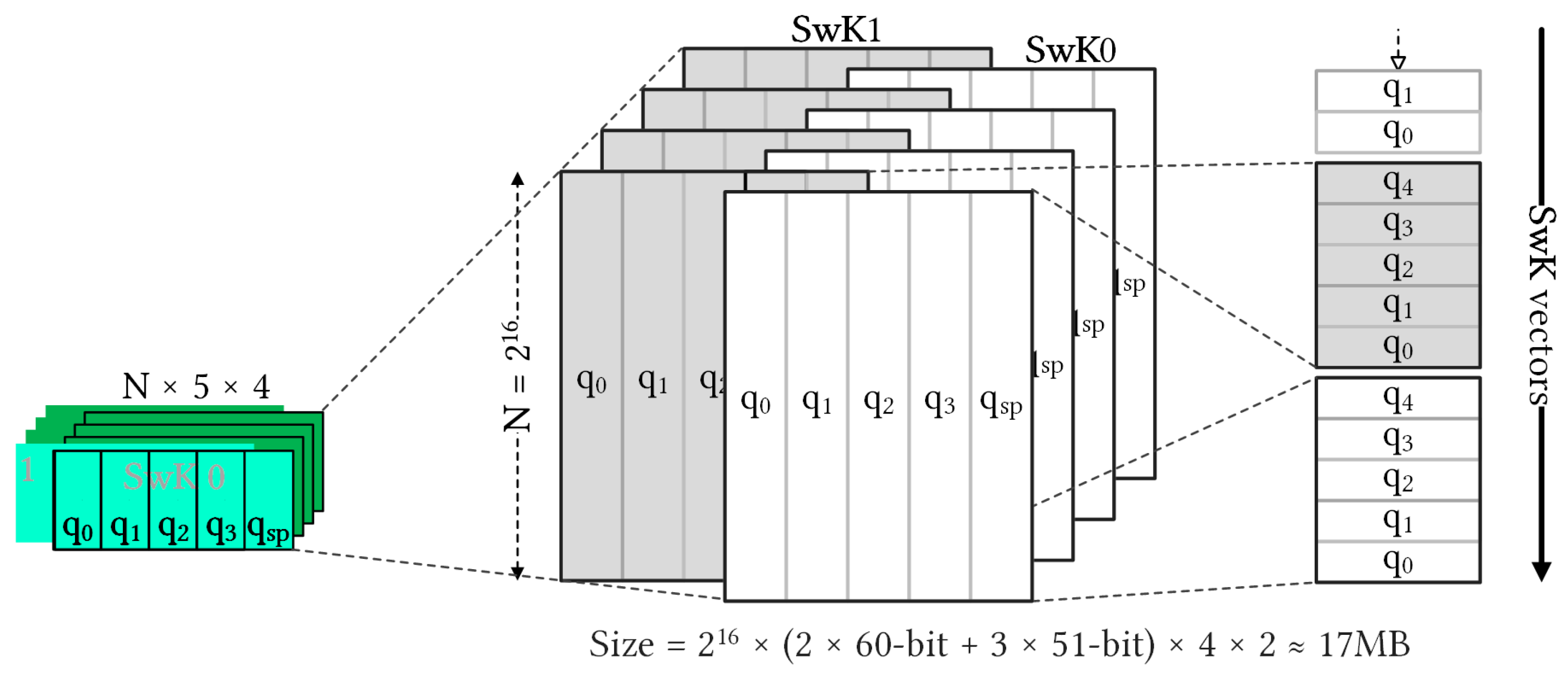
In this configuration of KeySwitch with
and
K,
Figure 7 shows the tensor form of
SwK. In the RNS domain, the component polynomials are 480 KB (
) for
and
with
and 408 KB (
) for
of
. Each ciphertext polynomial size is 1704 KB (
), and each ciphertext size is 3408 KB. The
SwK matrix dominated, accounting for 17,472 KB (
). The same
SwK matrices for all homomorphic multiplication operations at a specific level can be reused. However, these matrices are often too large to be stored in the on-chip memory, leading to a significant data movement overhead and a bottleneck in the overall performance of the cryptosystem. Thus, reducing data movement between the on-chip and external memory is critical for improving the efficiency of the system.