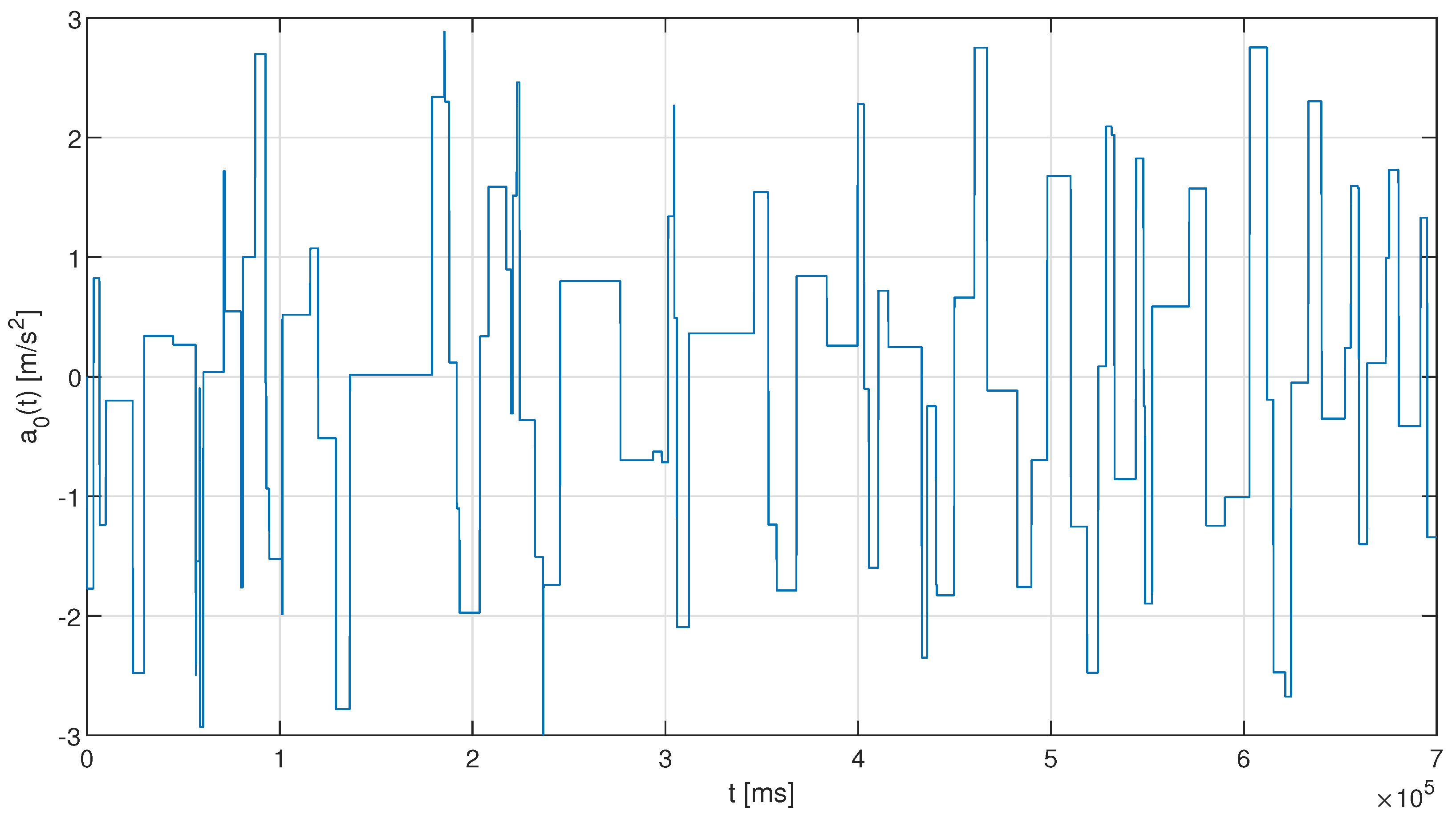1. Introduction
One of the main concerns related to the rapid development of advanced contemporary cars is to increase the safety and the efficiency of road traffic, while maintaining the comfort level of the passengers. Various solutions have been proposed towards the realization of these paradigms, just to mention the Anti-lock Braking Systems (ABS), Electronic Stability Program (ESP), Anti-Slip Regulation (ASR), but also lane assist systems, pre-collision assist, or the Adaptive Cruise Control (ACC) system. With so many functions introduced, cars become more and more automated, where many aspects are now controlled by the on-board computer. This brings us closer to the realization of the idea of autonomous cars, where the full car control will be realized by the on-board systems.
One of the vital use cases for autonomous vehicles, aiming at increasing road efficiency, is vehicles platooning, where a group of vehicles forms a convoy led by the platoon leader. The use of a platoon provides various gains, including an increase in road capacity [
1], a reduction in fuel consumption [
2], and, consequently, lower CO
emissions [
3]. However, in order to benefit from platooning, the inter-vehicle distances in a convoy need to be relatively small, which requires the use of a precise autonomous controller. Several solutions aiming at automatic vehicle control in platooning scenario have been proposed, such as the Cooperative Adaptive Cruise Control (CACC) [
4,
5], or its modifications called platoon controllers [
6,
7]. With such a controller, each vehicle is supposed to follow the pre-defined behavior (e.g., maintaining the targeted inter-vehicle spacing) by controlling its speed and acceleration. In any case, the CACC or the platoon controller requires the use of wireless communications to exchange information between vehicles, as the data retrieved with on-board sensors are insufficient to maintain the required level of safety. It has been shown that reliable communications within the platoon can lead to a significant reduction in inter-car distances [
8].
While Vehicle-to-Vehicle (V2V) and Vehicle-to-Everything (V2X) communication is a key enabling technology in platooning, it is tightly coupled with vehicle dynamics control. Any errors in the exchange of information in the platoon may significantly affect the platooning operations, thus jeopardising the road safety [
9]. The platoon controller should achieve string stability, ensuring the attenuation of the spacing errors between vehicles as they propagate downstream along the platoon. Furthermore, to maintain the short inter-vehicle gaps, a short response time of the control system is required, which is challenging, as continuous-time provisioning of vehicular data to the platoon controller is practically not possible. Typically, sampled-data control is used, where the data packets containing the needed information are available only at discrete time instants. Thus, to enable the short response time of the control system, the frequent periodic dissemination of information using wireless communication is typically assumed [
10]. However, the existing periodic communication mechanisms usually do not account for the constrained amount of wireless communication resources when designing and evaluating the controller. It has been shown in [
9] that, due to the limited availability of resources, both with the Dedicated Short-Range Communications (DSRC) and the Cellular-V2X (C-V2X) packet drops may occur in unfavorable scenarios with heavy road traffic. Thus, the efficient use of resources, allowing for the maximization of the number of communicating vehicles, is of high importance. With the efficient scheduling of data transmissions between the intercommunicating platoon vehicles, the scarce communication resources can be used economically. However, such efficient and reliable scheduling, and dissemination of data is a very challenging task, as reducing the frequency of intra-platoon transmissions might result in degradation of the platoon control performance.
Accounting for the problem of constrained wireless resources, in this paper, we investigate the idea of adaptive adjustment of the rate of intra-platoon transmissions while maintaining the required safety level of autonomous platooning. Our aim is to reduce the use of wireless resources with the constraint on the minimum distance kept between the platoon vehicles, while using a fixed controller design proposed in [
6]. We extend the idea of event-triggered scheduling introduced in [
11], by planning the transmission of each platoon vehicle, taking into account the predicted evolution of the inter-vehicle distances depending on the introduced latency of the disseminated information. We formulate the optimization problem and propose a heuristic solution based on exhaustive search that allows for the selection of the transmission intervals while keeping the inter-vehicle distances above the predefined threshold. We evaluate this proposal in simulations implemented with MATLAB, comparing the consumption of resources and the ability to fulfill the minimum distance constraint with a conventional transmission scheme that uses a fixed-period transmission. We show that it is possible to maintain a safe platoon operation while reducing the use of wireless resources compared to a fixed-period approach, by taking into account the design and parameters of the autonomous controller used in platoon vehicles.
The main contributions of this paper can be summarized as follows:
We formulate the optimization problem, focusing on the minimization of the use of resources, with the constraint on the fraction of time where violations of the minimum inter-vehicle distance were experienced.
We derive a recursive formula for the calculation of the distance error and the relative velocity between the platoon leader and the first follower, as well as for the acceleration of the first follower calculated according to the control strategy proposed in [
6].
We propose a heuristic solution to find the maximum period and the initial delay of transmission for each platoon vehicle, accounting for the constraint on the minimum distance. We use prediction of evolution of the distance error between two subsequent platoon vehicles over time, taking into account the availability of a predefined set of possible transmission periods and initial delays.
We evaluate the proposed approach in simulations, showing that it is possible to reduce the use of resources compared to a fixed-period transmission scheme.
The paper is structured as follows. In
Section 2, a short overview of the existing solutions, focusing on platooning control, with communication imperfections or constraints, is given. In
Section 3, we present the considered system model and the considered platoon controller.
Section 4 introduces the formulation of the optimization problem with the constraint on the minimum inter-vehicle distance violations. This section also presents a recursive formula for the calculation of the evolution of the distance error and the relative velocity between the platoon leader and the first follower, based on the changes of leader acceleration. It is followed by a presentation of the proposed heuristic solution in
Section 5, employing the prediction of the distance error evolution over time when selecting the transmission period and initial delay. Subsequently, the results of numerical simulation are presented in
Section 6, comparing the proposed heuristic approach with a conventional fixed-period transmission. Finally, the discussion of the observations concludes this work in
Section 7.
2. Related Work
The area of autonomous platooning supported by wireless communications has gained a significant focus in the literature in recent years. Many works have been published that can be mostly categorized into one of the following two areas:
Design and performance analysis of the inter-vehicle communication network, including the study on the efficient exchange of information within the platoon [
12], interference mitigation [
13,
14], or the transmission delay analysis [
15].
Design and stability analysis of platoon control strategies [
5,
6,
16,
17].
However, the main limitation of these works is that they focus only on one area of platoon control, neglecting the impact of varying performance of the other one. The communication-centric works typically abstract the control system (assuming that platoon stability can be maintained), while the control-centric works assume a deterministic performance and behavior from the communication network.
Several works can be found that consider the impact of wireless communications performance on the control system design. Such an approach is considered in [
18], accounting for the latency in the distribution of information between vehicles, which is derived using queuing theory. Similarly, in [
19], the authors propose a graceful degradation mechanism for platooning control, switching from CACC to ACC when a failure in wireless communications is experienced. The fallback mechanism for switching between CACC and ACC is also considered in [
20]. The main disadvantage of these works is the limited model of wireless communications, accounting only for the delay in acquiring information or random packet drops.
A more communication-oriented co-design approach can be found in [
21], where the transmission scheduling based on most regular binary sequences and priority-based platoon control is proposed. However, the proposed transmission scheduling assumes static allocation once the proper patterns are found, thus not accounting for the random nature of the channel access that is typically experienced in wireless communications. A scheduling design for C-V2X communications in platoons is proposed in [
22], with the aim being to minimize the tracking error of the inter-vehicle distance, velocity, and acceleration. Along with the scheduling mechanism, a platoon controller coefficients adaptation is considered to fulfill the optimization objective. Similarly, a co-design based on multi-hop communications and distributed controller parameters adaptation is proposed in [
23]. A different control design is considered in [
24], where an age-of-information-based communications scheduling is proposed for an infrastructure-based networked estimator and platoon controller.
While the solutions mentioned above aim to consider jointly the platoon control and the communication model, typically, they consider a very simplified mechanism of services providing data packets to be transmitted in regular intervals. As such a periodic model is typically assumed e.g., for the Cooperative Awareness Messages (CAMs) in V2X communications, it might not be a correct one for the platooning scenario. Typically, the platoon controller will require exchanges of information on a quasi-periodic basis, depending on the occurrence of certain events (e.g., sudden deceleration, detecting obstacles, etc.). Such an approach is considered in [
10,
25], where a co-design of event-triggered scheduling of communications and platoon control is proposed. However, both works focus mostly on the control design, abstracting the wireless communications model.
An event- or scenario-based adaptation of control mechanisms is also considered in [
26], where a multi-layer model predictive control for platooning is proposed, which makes use of the Dynamic Congestion Control (DCC) mechanism to adapt the messaging rate. However, the proposed adaptation relies only on a set of fixed configurations, which are selected based on the estimated channel load. In order to account for the changes of vehicles’ motion parameters with the platoon control, event-based message generation rules can be considered, which rely on observed changes of the ego or of surrounding vehicles. Such generation rules for the cooperative perception mechanism are discussed in [
27], with the application of a similar approach in platooning scenario being presented in [
28], where specific service profiles are considered for message generation.
Following the idea of an event-triggered scheduling of communications and the need to address specific features of wireless communications, such as the use of scheduling grants in C-V2X, we consider in this work an event-based design of quasi-periodic scheduling of transmissions, where the interval between the transmission of subsequent messages for a platoon vehicle is dynamically selected based on the road situation.
3. System Model
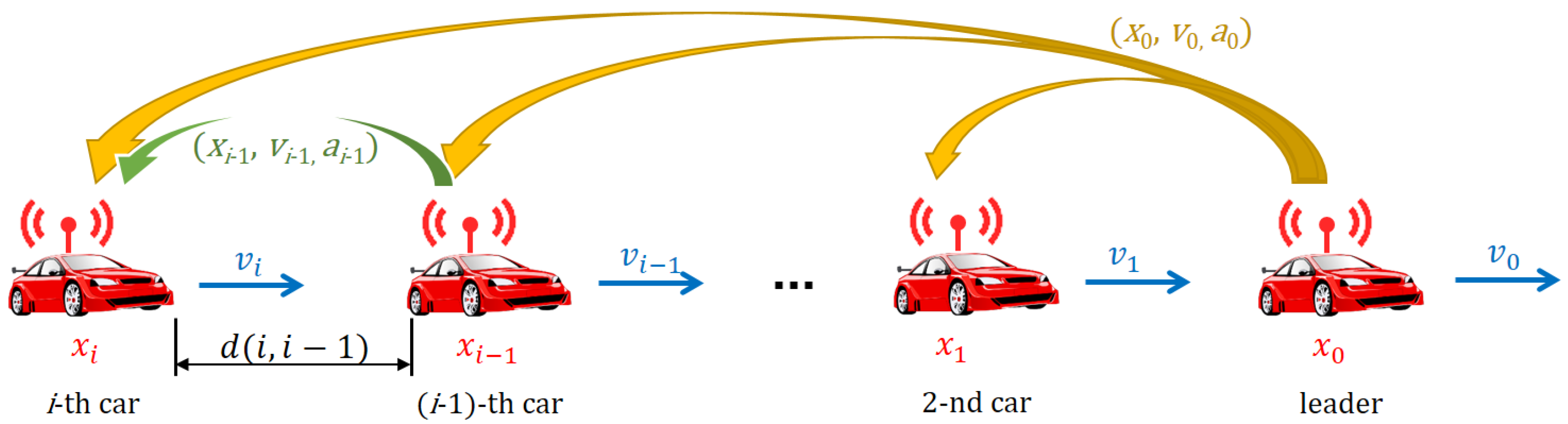
Let us assume a motorway scenario where a platoon of
N vehicles (led by the so-called leader vehicle) drives in a coordinated way, with the longitudinal motion being controlled using the autonomous platoon controller, as shown in
Figure 1. The system model can be then described in a discrete way, with the time step of
, using the following formulas.
where:
is the system state vector at time
, defined as:
where
,
, and
stand for the longitudinal position, velocity, and acceleration of vehicle
i, respectively.
is the state transition matrix, representing the position, velocity. and acceleration changes according to the accelerated motion law:
is the controller actions vector (acceleration changes).
is the disturbances vector. In this work, we focus only on a case where the acceleration disturbance (acceleration change due to external reasons) may occur only to the leader vehicle, so: . A more general scenario with acceleration disturbances being applied also to other platoon vehicles is left for future study.
Figure 1.
Considered platooning scenario using the autonomous leader-predecessor-follower controller and communications model.
Figure 1.
Considered platooning scenario using the autonomous leader-predecessor-follower controller and communications model.
We assume that all platoon vehicles employ a CACC platoon controller proposed in [
6], where a leader-predecessor-follower model is considered. Therefore, each platoon vehicle, except for the leader, updates its acceleration based on the mobility information received from both the platoon leader and its predecessor. The controller actions
are then calculated according to the formula:
with
and
denoting the minimum and maximum acceleration constraints, respectively, and
representing the autonomous controller-calculated acceleration:
where
are the controller coefficients (constants). Furthermore, we assume an ideal engine model, applying immediately the requested acceleration (the impacts of engine imperfections and their modeling are studied e.g., in [
29]). The first term in (
5), i.e.,
represents the impact of the inter-vehicle distance error. The second and third terms represent the influence of the velocity difference vs. the preceding and the leader vehicle, respectively. Similarly, the fourth and fifth terms indicate the impact of the preceding and leader vehicles’ accelerations.
Such a controller definition assumes that the updates are applied in a continuous manner. However, in a realistic platooning scenario, the information on the mobility of the platoon leader or the preceding car needs to be transmitted using wireless communication, and is updated only when a new intra-platoon message is received. Therefore, we assume that the controller actions are made in an event-based manner, whenever a new message updating the mobility parameters is received.
In this work, we consider a general communication scheme based on the quasi-periodic exchange of information, where the interval between subsequent messages may be selected dynamically based on detected events and vehicles’ motion parameters, as shown in
Figure 2.
Each vehicle, upon the detection of any event resulting in a change of motion parameters, selects the initial latency
of the first transmitted message and the interval between any following messages
. The communication pattern (resources used) for each vehicle is then specified with (
6).
The specific V2V communication interface is out of the scope of this paper; however, one can consider both the DSRC or C-V2X being applied, as both are suitable in the provisioning of such information exchange. DSRC is well suited to event-based transmission, and typically, assuming limited range communications within the platoon, it experiences small latency [
30]. On the other hand, the introduced delay may vary for consecutive packets, due to the channel access method used. C-V2X is much more predictable in terms of latency, as it uses a grant mechanism, where the sub-channels available for transmission are allocated in advance for a specific period; however, it is less suitable for handling event-based messaging, thus introducing greater delays.
For the considered scenario, we assume that each vehicle is equipped with an emergency braking mechanism that becomes activated if the distance to the preceding vehicle is below a certain threshold .
4. Problem Formulation
Contrary to other works, rather than optimizing the controller while knowing the communications performance, we aim to minimize the amount of resources used for intra-platoon communications. In particular, we focus on the minimization of the total number of transmissions while maintaining the safe operation of the platoon using a known controller, understood as keeping the time of the emergency braking activation below a predefined level
. More specifically, we assume that emergency braking is activated when the distance between two subsequent vehicles is below a specified threshold distance
. Thus, the optimization problem in terms of the information update period (
) and the initial latency (
) can be described as:
subject to:
where
is the indicator function, defined as:
Here,
T is the observation interval (so with the discrete model, we sum over
samples),
is the acceptable fraction of emergency braking events, and
is the distance error between two subsequent platoon vehicles at time
t, defined as
. The key element impacting upon the selection of resources is then the safety constraint defined in (
8). However, the exact solution to (
8) is nontrivial, due to the mutual dependencies between the accelerations of the consecutive platoon vehicles introduced by the controller, and the possibility of different latency introduced by the individual platoon vehicles. Such a dependency model between the acceleration disturbance
and the distance error for the first pair of vehicles in the platoon
has been found, assuming an information update at every time step
, following the rationale presented in
Appendix A, along with the formulas for the velocity difference in the first pair
and the acceleration of the first follower
. Such relations as functions of the information update period (
) can be expressed as:
where the corresponding
coefficients are calculated recursively as follows.
with
,
,
,
,
.
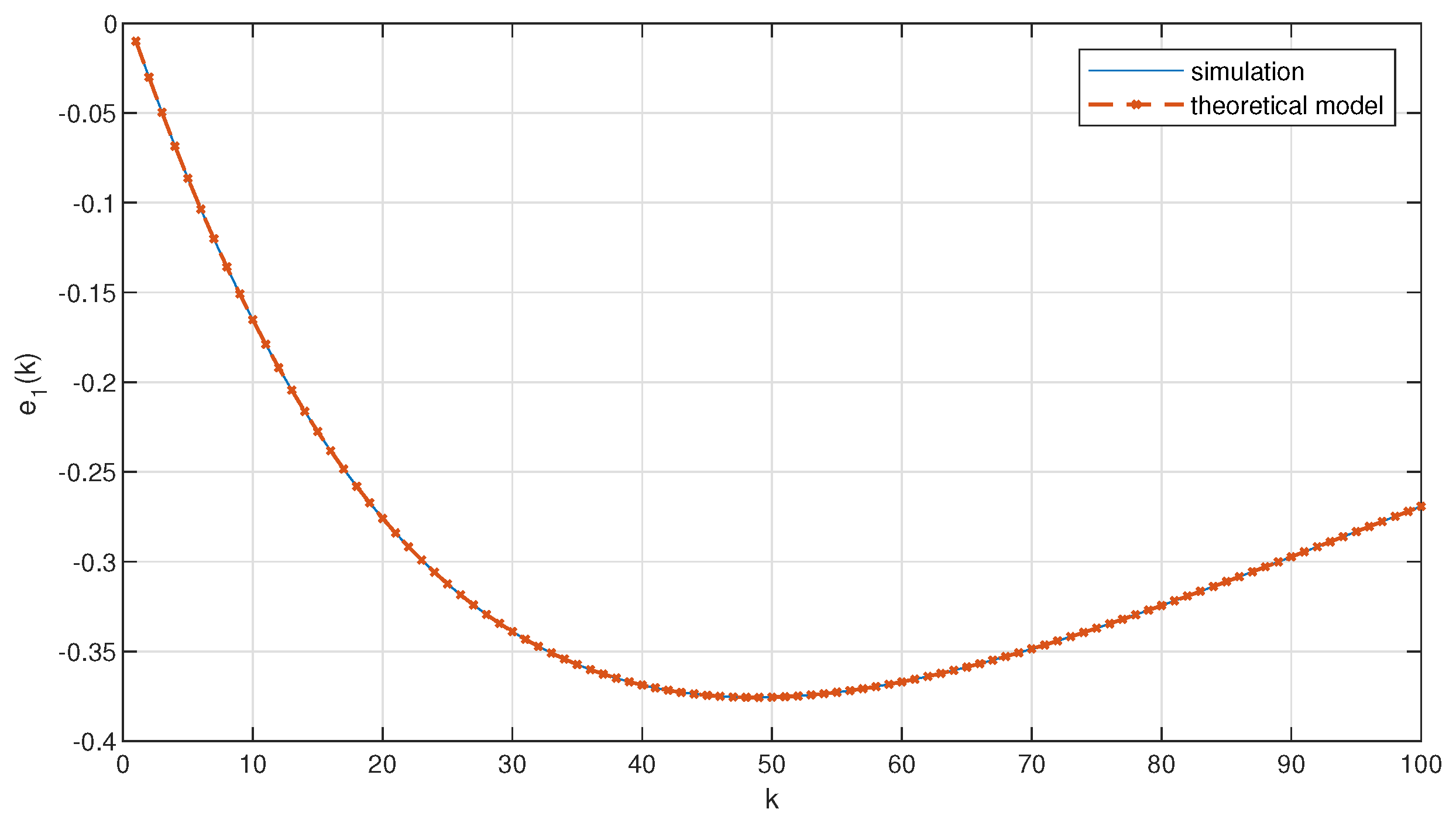
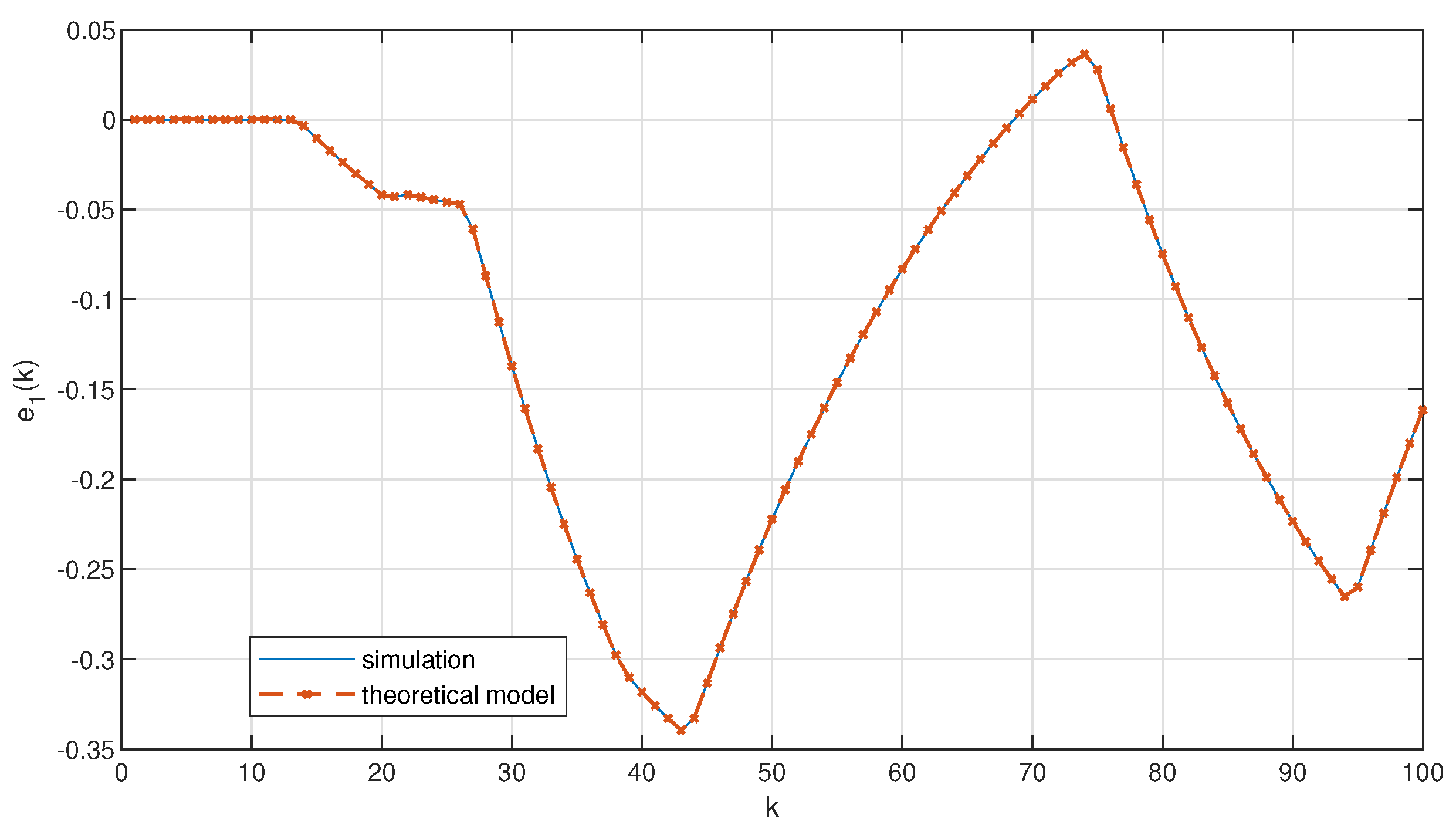
Figure 3 and
Figure 4 show the distance error calculated using the above model and simulated with the considered platoon controller for a single disturbance (
) and for random disturbances over time, respectively. The results clearly indicate the correctness of the derived model (i.e., both the curves for the simulation and the theoretical model overlap ideally).
The derivation can be continued in a similar way to obtain the distance error representations for other vehicle pairs. However, one should note that here, the relations will be more complicated, as these will account for the information received from different sources (the platoon leader and the preceding car). Hence, the impact of leader acceleration disturbance on the distance error will depend on the vehicle position in the platoon, as well as on the individual latencies when passing the information between the vehicles. One should also note that (
10) assumes a fixed and equal delay when transmitting the intra-platoon messages, which might not be the case in a real scenario. Furthermore, the problem defined in (
7) is a mixed-integer programming problem, where the constraint (
8) relies on indicator function values (
), which are discrete (in fact, Boolean). Hence, the optimal solution cannot be easily found, even when applying relaxation techniques. Therefore, in the next section, we propose a heuristic approach that is based on the iterative prediction of the distance error.
5. Heuristic Approach
As mentioned in the previous section, the optimal solution to (
7) cannot, in general, be easily found. Thus, we propose a heuristic solution based on the constraint (
8) and based on relaxing the integer problem by finding the solution {
,
} from the available values in the finite sets
and
, respectively, that maximizes the time period until the violation of the minimum distance
. We assume that each transmitting vehicle performs such a heuristic search individually, having knowledge on the information transmitted by the leader and on the motion parameters of the following vehicle. The selection process, described in Algorithm 1, relies on the prediction of the distance error
evolution for a given pair of vehicles over a predefined time span
. The distance between vehicles
and
i is calculated, assuming the update of information used in the acceleration controller for the selected values
and
. For each prediction step
, the predicted position, velocity, and acceleration of the considered vehicles are updated according to the accelerated motion law, and the distance error is calculated. The prediction is performed as long as the distance between vehicles is greater than the emergency braking threshold
. If at any prediction point such a distance constraint is violated, then the resulting time span value
t is stored for the evaluated set {
,
}. Otherwise, an infinite time span is assumed when at any point, the acceleration and velocity of the following vehicle exceeds the acceleration and velocity of the preceding vehicle, or when
is used if the distance remains above
for the whole prediction window. Finally, the solution is chosen as the pair maximizing the predicted time span.
| Algorithm 1 Exhaustive search algorithm |
- 1:
procedure Find Tx period(, , , , , , , , , , , , , ) - 2:
▹—long. position of vehicle i, —velocity of vehicle i, —acceleration of vehicle i, —target inter-vehicle distance, —minimum distance constraint, —set of possible transmission periods, —set of possible initial time offsets, —maximum prediction time span, —controller function - 3:
for each , do: - 4:
for each , do: - 5:
Calculate: - 6:
, - 7:
, , - 8:
, - 9:
, - 10:
, - 11:
while & & do: - 12:
Calculate: - 13:
, - 14:
, , - 15:
- 16:
, , - 17:
- 18:
if & & then: - 19:
- 20:
break - 21:
end if - 22:
end while - 23:
Set: - 24:
end for - 25:
Select: - 26:
Set: - 27:
Set: - 28:
end for - 29:
Select: - 30:
Set: - 31:
Set: return - 32:
end procedure
|
The approach proposed in Algorithm 1 provides a suboptimal solution, as it operates only with finite sets of and . Furthermore, it assumes accurate knowledge of the current motion parameters of the preceding and the following vehicle, as well as an error-free exchange of information. Therefore, some emergency braking distance violations can be experienced even when it is in use, as the algorithm aims only at minimizing a chance of such an event. The number of such occurrences will depend on the acceleration disturbance changes and the sets of available values and .
The approach proposed with Algorithm 1 can be further extended by applying a hysteresis-based approach, where the final values of the messaging period are selected as the minimal value out of the past values, assuming a certain memory depth of r milliseconds. The aim of the use of hysteresis is to increase the robustness of the proposed solution to sudden and frequent acceleration changes that may lead to a loss of stability when less frequent messaging is used.
6. Numerical Results
The proposed heuristic approach has been evaluated in numerical simulations using MATLAB, as it allows us to abstract the communication layer and separate it from the platoon control model. These were performed according to the model described in
Section 3. We assumed a platoon of six vehicles moving on a straight road section with an initial velocity of 20 m/s and a desired inter-vehicle spacing
of 3 m, with the leader changing its acceleration according to the disturbance process
. The acceleration disturbance
has been modeled as a random process, where the disturbance is applied with an inter-arrival time being an exponentially distributed random variable, and the amplitude of
being a uniformly distributed random variable in an interval
.
Figure 5 shows an example of the changes of a leader’s acceleration over a single simulation run duration.
Each platoon vehicle broadcasted its motion parameters (position, velocity, and acceleration) periodically, with the interval being selected according to one of the following two transmission policies:
Fixed periodic transmission—each vehicle broadcasts messages with the same pre-selected interval for the whole simulation duration.
Adaptive transmission period—the time interval between subsequent transmissions is selected dynamically according to the heuristic algorithm, with hysteresis assuming a memory size of r.
The main simulation parameters are summarized in
Table 1.
The different configurations of intra-platoon messaging have been compared in terms of the total use of resources, being understood as the average number of intra-platoon transmissions per simulation run, as well as in terms of the fraction of emergency braking distance violations observed on average per simulation run (as defined on the left-hand side of the inequality (
8)).
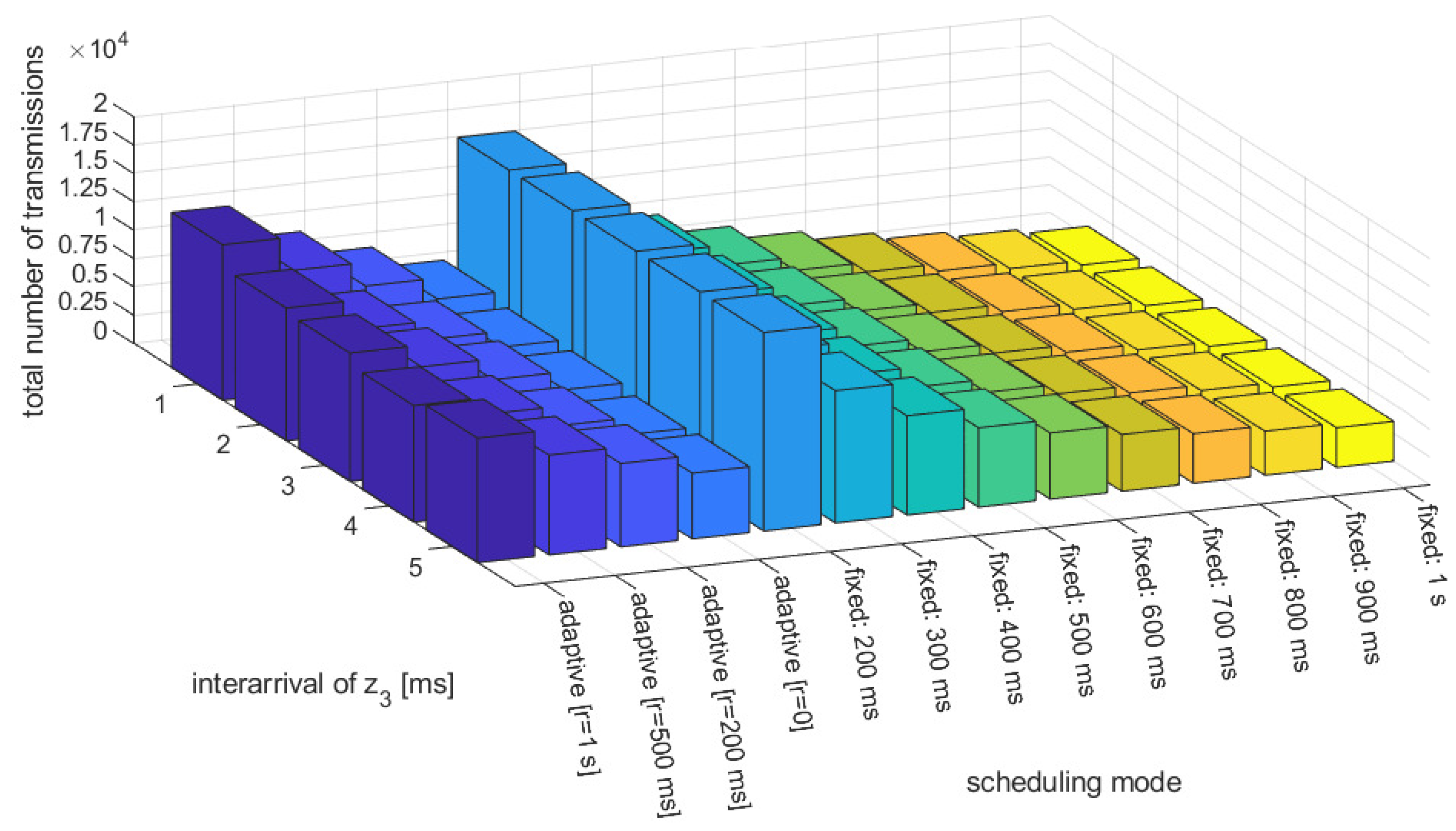
Figure 6 and
Figure 7 present the average use of resources (number of transmissions) and the fraction of emergency braking distance violations per simulation run, respectively, vs. different average inter-arrivals of the acceleration disturbance
. We have compared the proposed heuristic adaptive approach with the different memory depth used in hysteresis (
ms), and the conventional approach using fixed messaging interval, with the period ranging from 200 ms to 1 s, representing different resources consumption scenarios. As expected, the best performance in terms of the avoidance of emergency braking activation is achieved with very frequent transmissions, assuming fixed intervals of 200 or 300 ms. However, these scenarios represent a greedy approach on the resources, where over 10,000 transmissions are performed per simulation run. On the other hand, transmission with a fixed low periodicity that is close to 1 s results in frequent emergency braking activation (up to over 15% of simulation time), simply meaning that the controller fails to achieve safe platoon operation. However, when applying an adaptive approach following the proposed heuristic approach, a performance that is similar to frequent fixed interval transmission can be achieved in terms of the avoidance of emergency braking, while using far fewer resources. For the adaptive configuration without hysteresis (
) hardly any emergency braking is observed, while the use of resources is comparable with fixed interval transmission using a 600 ms period. When applying the hysteresis approach, that which is intended to provide even higher robustness, one can notice the actual fraction of emergency braking activation slightly increases compared with the approach without memory, indicating that a conservative approach, relying on selecting rather more frequent transmissions, results in a lower stability of platoon control. The reason for such an observation may be the fact that a long-term differences in periodicity used for different platoon vehicles may result in the loss of string stability, thus leading to safety degradation. Thus, there is no justification for the use of hysteresis, as it results in higher resources consumption at no improvement (or even degradation) of safety.
The observations from
Figure 7 are confirmed with the analysis of the distance error evolution in a selected single simulation run.
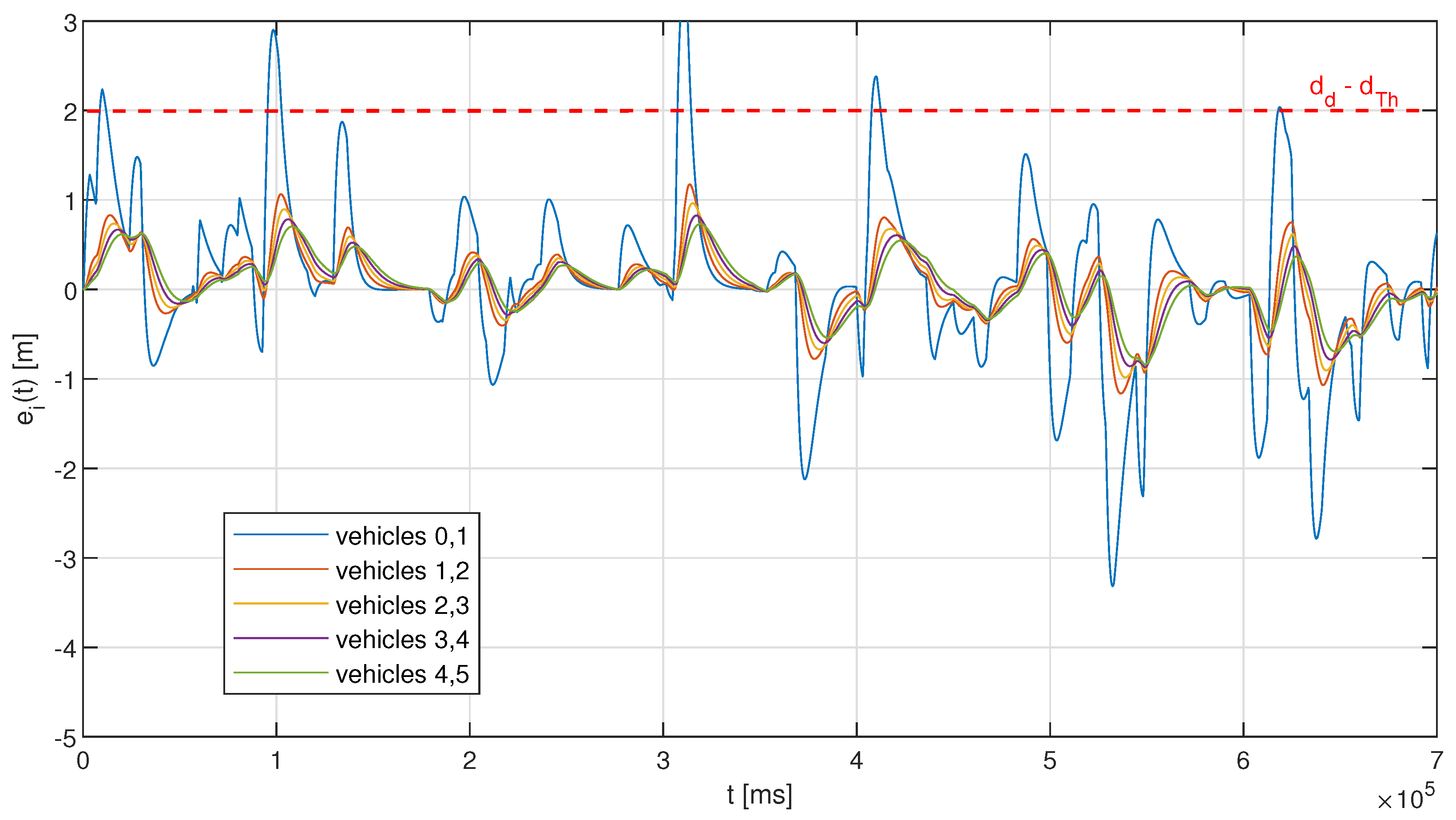
Figure 8 and
Figure 9 show examples of such an evolution for a configuration with a fixed interval of 500 ms, and for the adaptive approach with no memory (no hysteresis), respectively. One can notice in
Figure 8 that the fixed interval approach using moderate resources consumption may result in the activation of emergency braking when a series of acceleration changes occurs, leading to an increase in the distance error between the leader vehicle and the first follower over the threshold value of 2 m. In the example run presented in
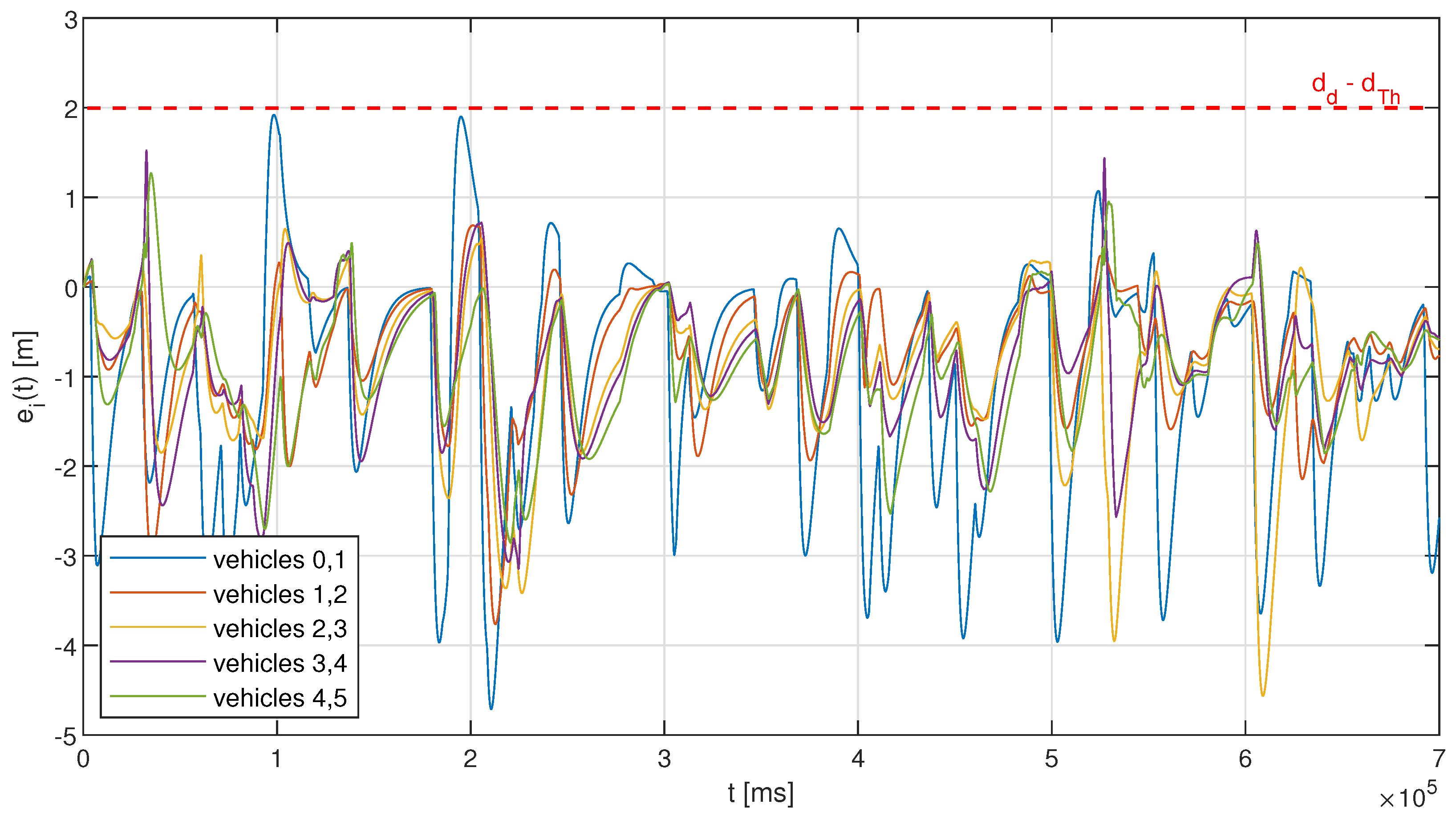
Figure 8, five such occurrences can be observed for the first platoon pair (between the leader and the first follower), corresponding to approximately 3.4% of the total simulation time. The other platoon vehicles manage to keep a much smaller distance error, with the maximum value only slightly exceeding 1 m, as with the fixed interval approach, the string stability of the platoon in ensured, and so for each next vehicles’ pair, the error is becoming smaller. The situation is slightly different when the adaptive approach is used, as shown in
Figure 9. Here we observe no distance error threshold violations, with the maximum inter-vehicle distance of approximately 1.9 m being observed for the first pair in the platoon, and so emergency braking is never activated. On the other hand, the distance error for vehicles’ pairs that are located closer to the platoon tail may actually exceed in certain situations the distance error observed for the leader–first follower pair. Such observations can be made in
Figure 9 in two time regions when accounting for the positive distance error, around 32 s and 525 s, with the maxima of approximately 1.52 m and 1.42 m being noted for the distance between vehicles 3 and 4. These distance errors result from a sudden change in the leader vehicle, from significant deceleration (approximately 2.5
) to small acceleration (up to 0.3
). The vehicles closer to the tail of the platoon adjust their accelerations already upon the reception of the leader’s message, with the parameters related to the preceding vehicle being received significantly later (even with a couple of seconds of time difference), which results in a decrease in the distance. This is due to the use of different communication intervals selected with the heuristic approach that may lead to a temporary loss of string stability. However, an important observation is that even such a temporary loss of stability does not result in the violation of the distance error threshold, indicating that the platoon is able to maintain a safe operation all of the time.
Another observation that can be made in
Figure 9 is that the adaptive algorithm introduces more significant negative distance error values, which represent a situation of an increased distance between the vehicles. Such behavior can be also considered as a negative effect, as the platooning gains diminish with the increase in inter-vehicle distances, where, with the air drag increasing, the reduction in fuel consumption (that can reach between 7% and 15%, depending on the inter-vehicle distance [
3]) will be smaller. Moreover, the reliability of V2V communications is lower at higher ranges. Depending on the wireless communication protocol used, a significant drop in the reception rate of the leader packets can be observed [
9,
31], which imposes limitations on the maximum platoon length (number of vehicles). Typically, an unacceptable reliability with DSRC can be observed already at a distance of 100 m in the case of heavy traffic, with C-V2X performing slightly better [
9]. On the other hand, the main reason for the increase in inter-vehicle distances is that in (
8), we put the constraint only on the minimum distance between the vehicles, with the aim of maintaining safety. Modifying the constraint to also account for the negative error values would mitigate this effect; however, at the cost of increased resources use.
7. Discussion
The presented numerical results clearly indicate that it is possible to find a tradeoff between the controller performance and the consumption of wireless communication resources. Depending on the road situation, more or less frequent transmissions may be required. Therefore, the adaptive selection of transmission periods for intra-platoon communications show great potential in reducing the use of wireless resources while maintaining safe platoon operation. It has been shown that the amount of used resources can be reduced by a factor of two, maintaining the same safety level (a similar fraction of emergency braking activation).
The advantage of the proposed adaptive transmission period approach is that it can be easily implemented in the state-of-the-art V2X communication systems. With DSRC, as it operates on an event-based manner, where the arrival of a new packet starts the channel access procedure, the proposed scheme can be implemented in the facilities layer, simply regulating the interval between generation of subsequent packets. Alternatively, it can be implemented in the MAC layer with selective dropping of queued packets according to the chosen messaging interval. When it comes to C-V2X and the scheduling grants mechanisms, each selection of a new messaging interval may result in the need for the negotiation of a new grant. However, in the case where the new interval is a multiple of a previous one, simply omitting th eselected transmission opportunities specified by the existing grant can be used.
The presented work, as only a heuristic approach has been proposed and evaluated, can be still further improved to achieve even higher gains, as a temporary loss of controller stability might be observed in certain situations for the current solution. Such a situation can be considered as dangerous when it comes to safety, as at some point the loss of stability may result in an uncontrollable inter-vehicle gap closing. Moreover, it may result in lower gains in terms of a reduction in fuel consumption due to an increase in air drag when the inter-vehicle distances increase. Furthermore, the unstable behavior of the controller in the vehicles closer to the platoon tail may have a significant impact on the reliability of wireless communications, as with greater distances, the number of successful receptions drops. Therefore, some measures should be taken to avoid such situations and to improve the proposed heuristic. Extending the constraint (
8) to account also for the negative distance error values (i.e., aiming at maintaining platooning efficiency) may increase the stability of the controller; however, at the cost of increased consumption of resources. With the approach imposing two-sided bounds on the distance error one can expect that any change in acceleration, no matter if an increase or decrease is observed, will result in the increased consumption of resources to notify the following vehicles of the change without excessive delays. In a scenario with frequent acceleration changes (even if these are minor), this would diminish the gains of the proposed approach, simply providing similar results to a frequent fixed-interval transmission. In such a case, gains would be observed only if a platoon moves with a constant speed for a longer period of time. On the other hand, one can consider using adaptive inter-vehicle target distance, thus increasing the range of acceptable distance errors (as it depends on the difference between the inter-vehicle target distance and the emergency braking activation distance) and providing more flexibility. Additionally, asymmetric bounds may be considered, with a larger distance error deviation being allowed for the increasing inter-vehicle distances (negative values). In such a case, the expected inter-vehicle target distance, the bounds, and the resource consumption can be jointly adapted, depending on the resources availability and the road situation. However, more detailed studies on such an adaptive approach are left for future work. Furthermore, a “less sensitive” approach to message generation can be also considered, similar to the one proposed for cooperative perception mechanism [
27], where the information update is sent only if a significant change in parameters is detected (e.g., a change in acceleration, speed, or position by more than a predefined value).
Another option to maintain stability within the platoon may be a cooperative selection of the communication intervals. In such a case, the transmission intervals could be selected jointly by a central entity (e.g., co-located with the platoon leader), and then distributed to all platoon members. However, this approach would require a knowledge of the parameters of all platoon vehicles in the central entity, as well as a very reliable information distribution mechanism. Such information could be distributed in a similar way to the cooperative perception mechanism, where each platoon member would also include in its message the information on the known other members’ parameters. Additionally, messages could be filtered before being relayed, e.g., based on their age or their relevance in the adaptation process, similarly to the approach proposed in [
32].
The proposed approach definitely requires further evaluation in a more sophisticated scenario. The considered system model assumed perfect communications between the platoon vehicles, with only some latency being introduced. In a real platooning scenario, such an assumption is certainly not valid as communication outages may occur, especially when considering the communication links between the leader and the vehicles located at the tail of the platoon. Therefore, the next step in this work should be to extend it with a more realistic communication model, accounting for packet drops and temporary communication outages. Finally, more realistic engine and acceleration models can be considered, accounting for the so-called engine lag and different vehicle acceleration capabilities, depending on its velocity (e.g., using the linear decay model).
8. Conclusions
This work investigated the aspects of the efficient use of radio resources in an autonomous platooning employing wireless communications. We considered a quasi-periodic exchange of information, where the interval between subsequent transmissions by a platoon vehicle is selected dynamically in an event-dependent way. An optimization problem focusing on the minimization of the number of wireless intra-platoon transmissions was introduced, with a simultaneous safety-based constraint on the expected number of violations of the minimum inter-vehicle distance applied. We derived a recursive formula representing the changes of distance error between the first pair of vehicles in a platoon over time, aiming at a reformulation of the constraint. As the optimal solution for the stated problem cannot be directly found, we proposed a heuristic algorithm employing the prediction of the inter-vehicle distance error evolution over a finite time window, performing an exhaustive search over the transmission intervals set to select the one securing the longest time until the predicted activation of emergency braking when the minimum distance threshold is violated. The proposed approach and the heuristic solution were then evaluated using numerical simulations, with the results showing the advantages of the adaptive transmission scheduling over fixed-interval communications. Based on the presented results, a conclusion can be drawn where it is possible to reduce the use of radio resources with the proposed adaptive approach while maintaining safe platoon operation. However, a more detailed analysis of platoon behavior is required, particularly focusing on the string stability of the platoon using adaptive transmission intervals. Furthermore, the work can be extended by considering an imperfect communication model and accounting for random drops of data packets, as well as constraints on the resource allocation mechanisms applied in V2X communications.
Author Contributions
Conceptualization, All; methodology, All; software, P.S.; validation, A.K., E.S., and T.S.; formal analysis, All; investigation, All; writing—original draft preparation, review, and editing, P.S.; visualization, P.S.; supervision, A.K., E.S., and T.S.; project administration, A.K.; funding acquisition, A.K. All authors have read and agreed to the published version of the manuscript.
Funding
The work has been realized within the NCN project 2018/29/B/ST7/01241 at the Institute of Radiocommunications, PUT.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ABS | Anti-lock Braking Systems |
| ACC | Adaptive Cruise Control |
| ASR | Anti-Slip Regulation |
| CACC | Cooperative Adaptive Cruise Control |
| CAM | Cooperative Awareness Message |
| C-V2X | Cellular Vehicle-to-Everything |
| DCC | Dynamic Congestion Control |
| DSRC | Dedicated Short-Range Communications |
| ESP | Electronic Stability Program |
| V2V | Vehicle-to-Vehicle |
| V2X | Vehicle-to-Everything |
List of Symbols
The following abbreviations are used in this manuscript:
| Symbol | Description |
| N | number of vehicles in platoon |
| t | time |
| k | time sample |
| discrete system model time step () |
| state transition matrix |
| system state vector at time instant |
| controller actions vector at time instant |
| disturbances vector at time instant |
| longitudinal position of vehicle i at time instant |
| velocity of vehicle i at time instant |
| acceleration of vehicle i at time instant |
| desired (controller-calculated) acceleration of vehicle i at time instant |
| maximum acceleration of vehicles (upper bound) |
| minimum acceleration of vehicles (lower bound) |
| autonomous controller coefficient () |
| desired inter-vehicle distance in platoon (distance gap) |
| initial latency of the first transmitted message |
| time interval between subsequent transmissions of messages by a platoon vehicle |
| transmission indicator of vehicle i at time instant |
| emergency braking activation distance threshold |
| maximum acceptable fraction of time with emergency braking activated |
| distance error between vehicles and i at time t |
| T | observation interval for emergency braking activation analysis |
| indicator function (equals 1 if condition is true, and 0 otherwise) |
| velocity difference between vehicles and i at time instant |
| recursive coefficient related to the distance error at time instant |
| recursive coefficient related to velocity difference at time instant |
| recursive coefficient related to the follower’s acceleration at time instant |
| time interval between subsequent transmissions of messages, selected in adaptation using the heuristic approach |
| initial latency of the first transmitted message selected in adaptation using the heuristic approach |
| set of possible intervals between subsequent transmissions of a message in the heuristic approach |
| set of possible initial latencies of the first transmitted message in the heuristic approach |
| prediction time span with the heuristic approach |
| controller function used with the heuristic approach |
| predicted longitudinal position of vehicle i at time instant with the heuristic approach |
| predicted velocity of vehicle i at time instant with the heuristic approach |
| predicted acceleration of vehicle i at time instant with the heuristic approach |
| r | memory depth (time span) when using the heuristic approach with hysteresis |
| leader acceleration disturbance process (continuous time representation of ) |
| minimum acceleration change |
| maximum acceleration change |
Appendix A. Derivation of the Distance Error for the First Platoon Pair
According to the well-known relations in accelerated motion and the discrete model introduced in
Section 3, the distance error at time instant
k can be calculated as:
We can assume that before any disturbance is applied (in a steady-state platoon operation)
,
, and
. Thus, assuming that
and
, the information update interval is
, and that there are no acceleration constraints (
and
), we can derive the distance error values for the first platoon pair (between the leader and the first following vehicle) as follows:
Assuming that
(following the controller constraint given in [
6]) and substituting:
and
, the equations can be rewritten as:
Denoting
,
,
,
, we can rewrite the equations as follows:
Following the approach presented above and conducting further calculations, we can obtain the general formulas for
,
, and
:
with the corresponding
coefficients calculated recursively, as follows:
where
,
,
,
,
.
The calculation can be further extended to the leader acceleration disturbances also applied in other time instants (for
k > 0), providing as a result the following general equations:
Substituting back for
and
in the above formulas, we obtain (
10).
References
- Lioris, J.; Pedarsani, R.; Tascikaraoglu, F.Y.; Varaiya, P. Doubling Throughput in Urban Roads by Platooning. Proc. IFAC Symp. Control Transp. Syst. 2016, 49, 49–54. [Google Scholar]
- Turri, V.; Besselink, B.; Johansson, K.H. Cooperative Look-Ahead Control for Fuel-Efficient and Safe Heavy-Duty Vehicle Platooning. IEEE Trans. Control Syst. Technol. 2017, 25, 12–28. [Google Scholar] [CrossRef]
- Davila, A. Report on fuel consumption. SARTRE Deliverable 4.3. 2013. [Google Scholar]
- van Arem, B.; van Driel, C.J.G.; Visser, R. The Impact of Cooperative Adaptive Cruise Control on Traffic-Flow Characteristics. IEEE Trans. Intell. Transp. Syst. 2006, 7, 429–436. [Google Scholar] [CrossRef]
- Milanés, V.; Shladover, S.E.; Spring, J.; Nowakowski, C.; Kawazoe, H.; Nakamura, M. Cooperative Adaptive Cruise Control in Real Traffic Situations. IEEE Trans. Intell. Transp. Syst. 2014, 15, 296–305. [Google Scholar] [CrossRef]
- Rajamani, R.; Tan, H.S.; Law, B.K.; Zhang, W.B. Demonstration of integrated longitudinal and lateral control for the operation of automated vehicles in platoons. IEEE Trans. Control Syst. Technol. 2000, 8, 695–708. [Google Scholar] [CrossRef]
- Lee, G.; Kim, S.; Yim, Y.; Jung, J.; Oh, S.; Kim, B. Longitudinal and lateral control system development for a platoon of vehicles. In Proceedings of the 199 IEEE/IEEJ/JSAI International Conference on Intelligent Transportation Systems (Cat. No.99TH8383), Tokyo, Japan, 5–8 October 1999; pp. 605–610. [Google Scholar] [CrossRef]
- Chen, E. Overview of the SARTRE Platooning Project: Technology Leadership Brief; SAE International: Warrendale, PA, USA, 2012; p. 4. [Google Scholar]
- Vukadinovic, V.; Bakowski, K.; Marsch, P.; Garcia, I.D.; Xu, H.; Sybis, M.; Sroka, P.; Wesolowski, K.; Lister, D.; Thibault, I. 3GPP C-V2X and IEEE 802.11p for Vehicle-to-Vehicle communications in highway platooning scenarios. Ad Hoc Netw. 2018, 74, 17–29. [Google Scholar] [CrossRef]
- Ge, X.; Xiao, S.; Han, Q.L.; Zhang, X.M.; Ding, D. Dynamic Event-Triggered Scheduling and Platooning Control Co-Design for Automated Vehicles Over Vehicular Ad-Hoc Networks. IEEE/CAA J. Autom. Sin. 2022, 9, 31–46. [Google Scholar] [CrossRef]
- Tabuada, P. Event-Triggered Real-Time Scheduling of Stabilizing Control Tasks. IEEE Trans. Autom. Control 2007, 52, 1680–1685. [Google Scholar] [CrossRef]
- Fernandes, P.; Nunes, U. Platooning With IVC-Enabled Autonomous Vehicles: Strategies to Mitigate Communication Delays, Improve Safety and Traffic Flow. IEEE Trans. Intell. Transp. Syst. 2012, 13, 91–106. [Google Scholar] [CrossRef]
- Peng, H.; Li, D.; Ye, Q.; Abboud, K.; Zhao, H.; Zhuang, W.; Shen, X.S. Resource allocation for D2D-enabled inter-vehicle communications in multiplatoons. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Han, Q.; Liu, C.; Yang, H.; Zuo, Z. Longitudinal Control-Oriented Spectrum Sharing Based on C-V2X for Vehicle Platoons. IEEE Syst. J. 2022, 1–12. [Google Scholar] [CrossRef]
- Peng, H.; Li, D.; Abboud, K.; Zhou, H.; Zhao, H.; Zhuang, W.; Shen, X. Performance Analysis of IEEE 802.11p DCF for Multiplatooning Communications With Autonomous Vehicles. IEEE Trans. Veh. Technol. 2017, 66, 2485–2498. [Google Scholar] [CrossRef]
- Öncü, S.; Ploeg, J.; van de Wouw, N.; Nijmeijer, H. Cooperative Adaptive Cruise Control: Network-Aware Analysis of String Stability. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1527–1537. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, G.; Barth, M.J. A Review on Cooperative Adaptive Cruise Control (CACC) Systems: Architectures, Controls, and Applications. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2884–2891. [Google Scholar] [CrossRef]
- Zeng, T.; Semiari, O.; Saad, W.; Bennis, M. Joint Communication and Control for Wireless Autonomous Vehicular Platoon Systems. IEEE Trans. Commun. 2019, 67, 7907–7922. [Google Scholar] [CrossRef]
- Ploeg, J.; Semsar-Kazerooni, E.; Lijster, G.; van de Wouw, N.; Nijmeijer, H. Graceful degradation of CACC performance subject to unreliable wireless communication. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, The Netherlands, 6–9 October 2013; pp. 1210–1216. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W. A Safety Reinforced Cooperative Adaptive Cruise Control Strategy Accounting for Dynamic Vehicle-to-Vehicle Communication Failure. Sensors 2021, 21, 6158. [Google Scholar] [CrossRef] [PubMed]
- Guo, G.; Wen, S. Communication Scheduling and Control of a Platoon of Vehicles in VANETs. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1551–1563. [Google Scholar] [CrossRef]
- Mei, J.; Zheng, K.; Zhao, L.; Lei, L.; Wang, X. Joint Radio Resource Allocation and Control for Vehicle Platooning in LTE-V2V Network. IEEE Trans. Veh. Technol. 2018, 67, 12218–12230. [Google Scholar] [CrossRef]
- Hong, C.; Shan, H.; Song, M.; Zhuang, W.; Xiang, Z.; Wu, Y.; Yu, X. A Joint Design of Platoon Communication and Control Based on LTE-V2V. IEEE Trans. Veh. Technol. 2020, 69, 15893–15907. [Google Scholar] [CrossRef]
- Molin, A.; Esen, H.; Johansson, K.H. Scheduling networked state estimators based on Value of Information. Automatica 2019, 110, 108578. [Google Scholar] [CrossRef]
- Xiao, S.; Ge, X.; Han, Q.L.; Zhang, Y. Resource-Efficient Platooning Control of Connected Automated Vehicles Over VANETs. IEEE Trans. Intell. Veh. 2022, 7, 579–589. [Google Scholar] [CrossRef]
- Ibrahim, A.; Goswami, D.; Li, H.; Basten, T. Delay-Aware Multi-Layer Multi-Rate Model Predictive Control for Vehicle Platooning Under Message-Rate Congestion Control. IEEE Access 2022, 10, 44583–44607. [Google Scholar] [CrossRef]
- Thandavarayan, G.; Sepulcre, M.; Gozalvez, J. Analysis of Message Generation Rules for Collective Perception in Connected and Automated Driving. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 134–139. [Google Scholar] [CrossRef]
- Filho, E.V.; Santos, P.M.; Severino, R.; Koubaa, A.; Tovar, E. Improving the Performance of Cooperative Platooning With Restricted Message Trigger Thresholds. IEEE Access 2022, 10, 45562–45575. [Google Scholar] [CrossRef]
- Sybis, M.; Vukadinovic, V.; Rodziewicz, M.; Sroka, P.; Langowski, A.; Lenarska, K.; Wesołowski, K. Communication Aspects of a Modified Cooperative Adaptive Cruise Control Algorithm. IEEE Trans. Intell. Transp. Syst. 2019, 20, 4513–4523. [Google Scholar] [CrossRef]
- Mannoni, V.; Berg, V.; Sesia, S.; Perraud, E. A Comparison of the V2X Communication Systems: ITS-G5 and C-V2X. In Proceedings of the 2019 IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 28 April–1 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Sybis, M.; Kryszkiewicz, P.; Sroka, P. On the Context-Aware, Dynamic Spectrum Access for Robust Intraplatoon Communications. Mob. Inf. Syst. 2018, 2018, 3483298. [Google Scholar] [CrossRef]
- Zhou, P.; Kortoçi, P.; Yau, Y.P.; Finley, B.; Wang, X.; Braud, T.; Lee, L.H.; Tarkoma, S.; Kangasharju, J.; Hui, P. AICP: Augmented Informative Cooperative Perception. IEEE Trans. Intell. Transp. Syst. 2022, 23, 22505–22518. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).