Comparison of Performance of Predicting the Wear Amount of Tire Tread Depending on Sensing Information
Abstract
1. Introduction
2. Related Materials
3. Methods
3.1. Development of Tire Model
Tire Modeling
3.2. Tire Model Validation
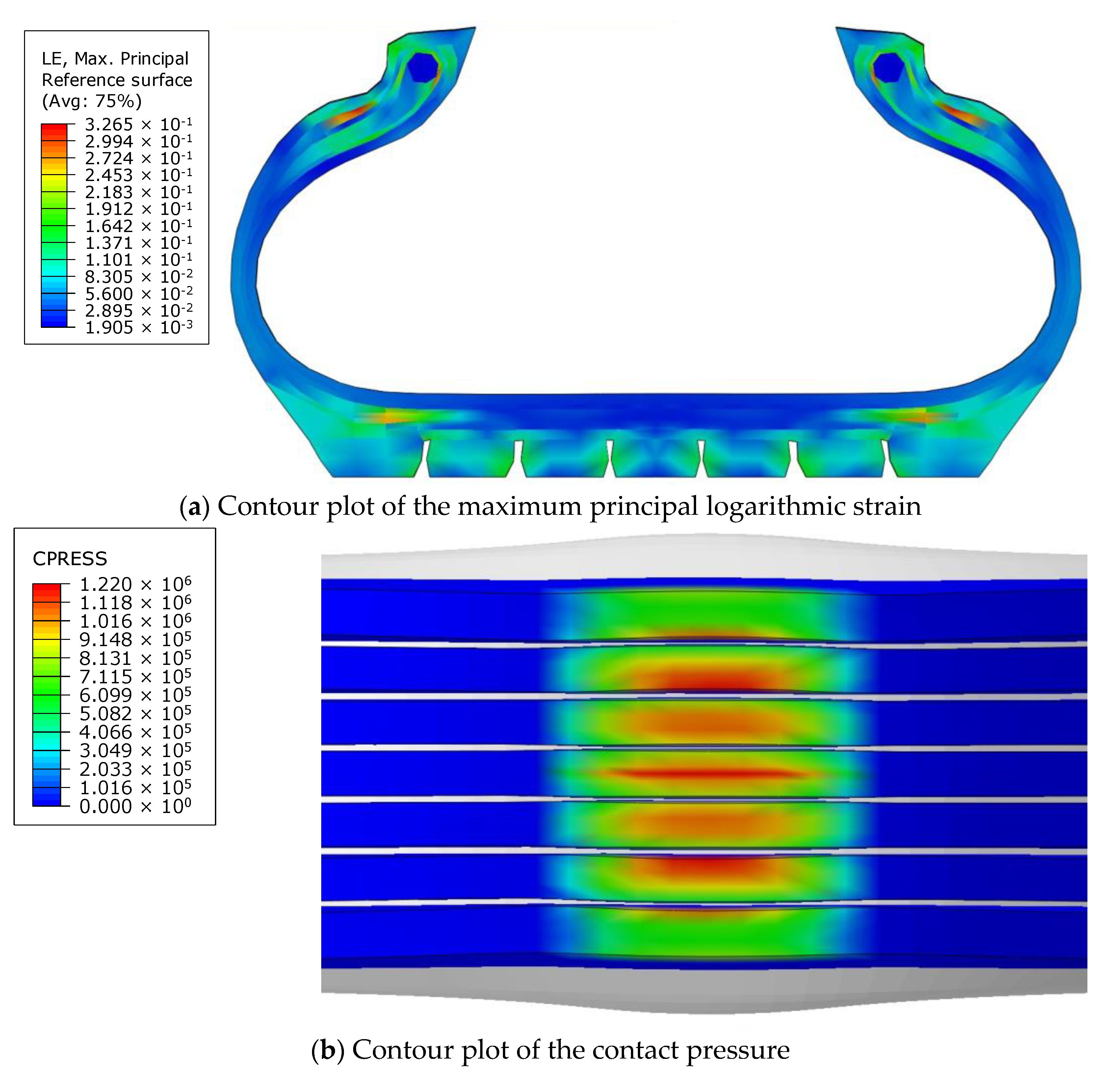
3.2.1. Validation of Rigidity
3.2.2. Validation of Modal Characteristics
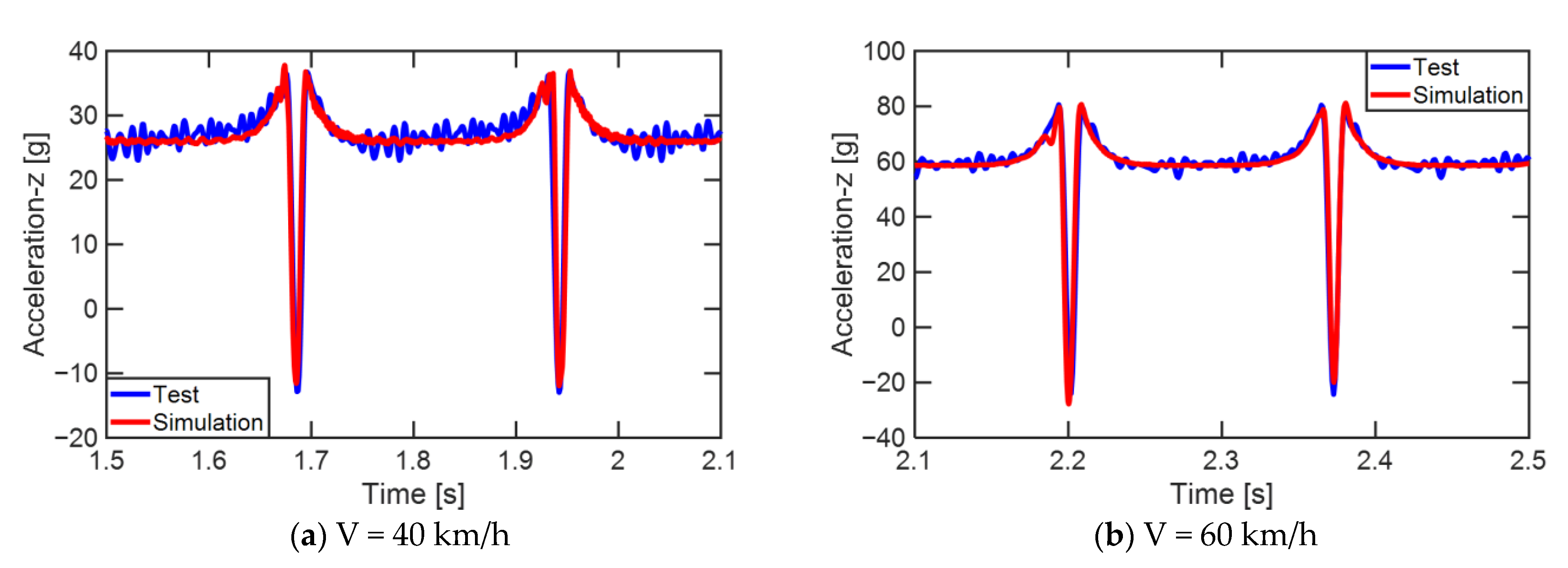
3.2.3. Validation of Internal Acceleration
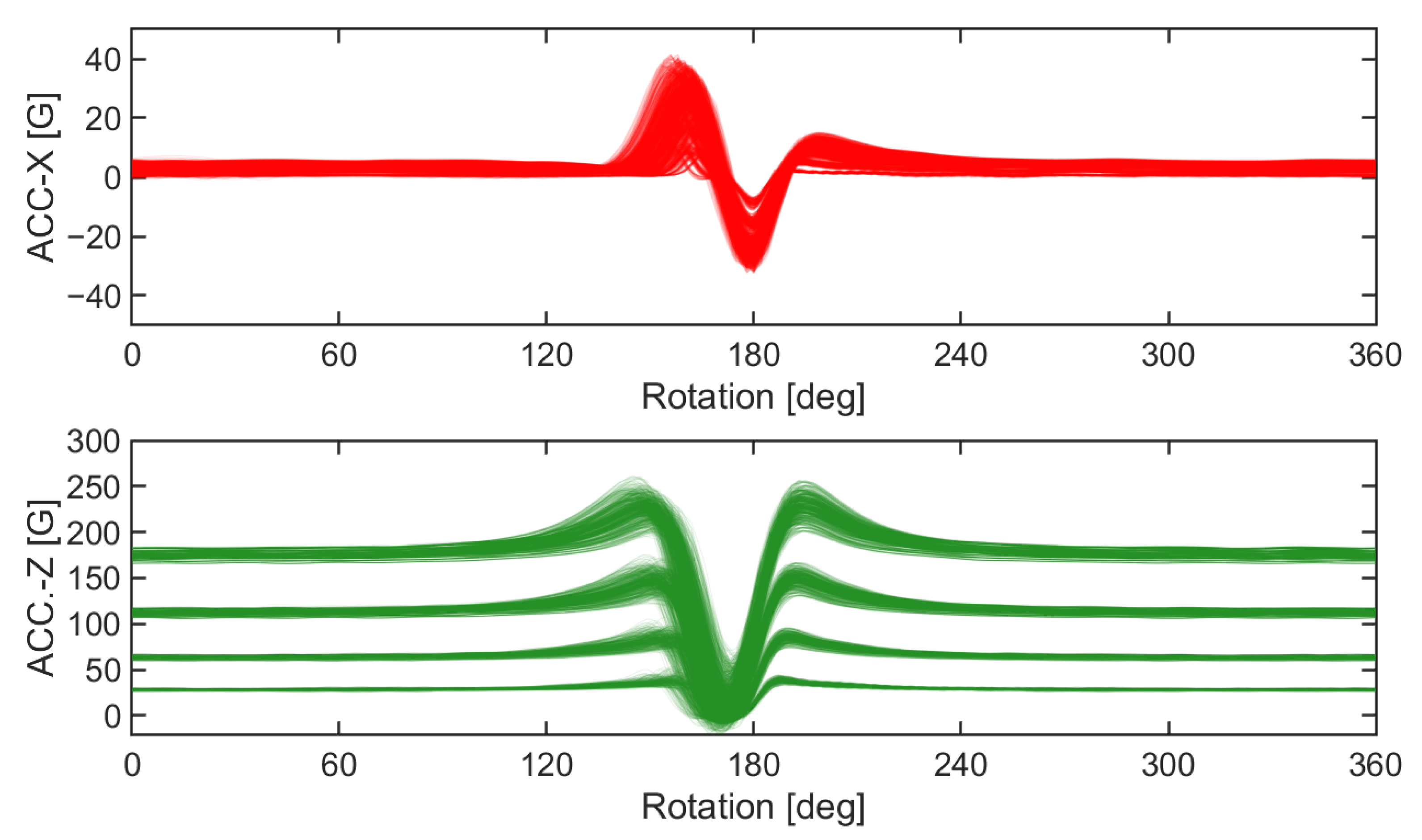
3.3. Generation of Virtual Tire Rolling Data
3.3.1. Parametric Tire Rolling Simulation
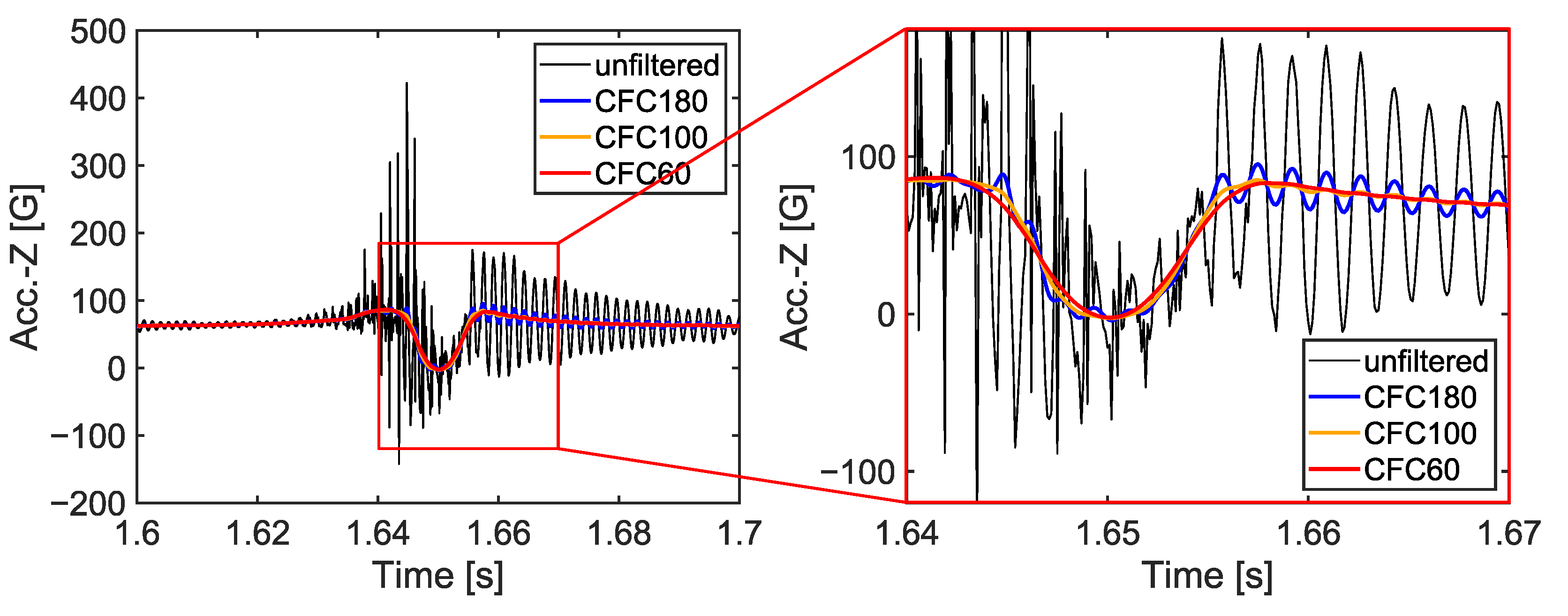
3.3.2. Processing of Acceleration Signal
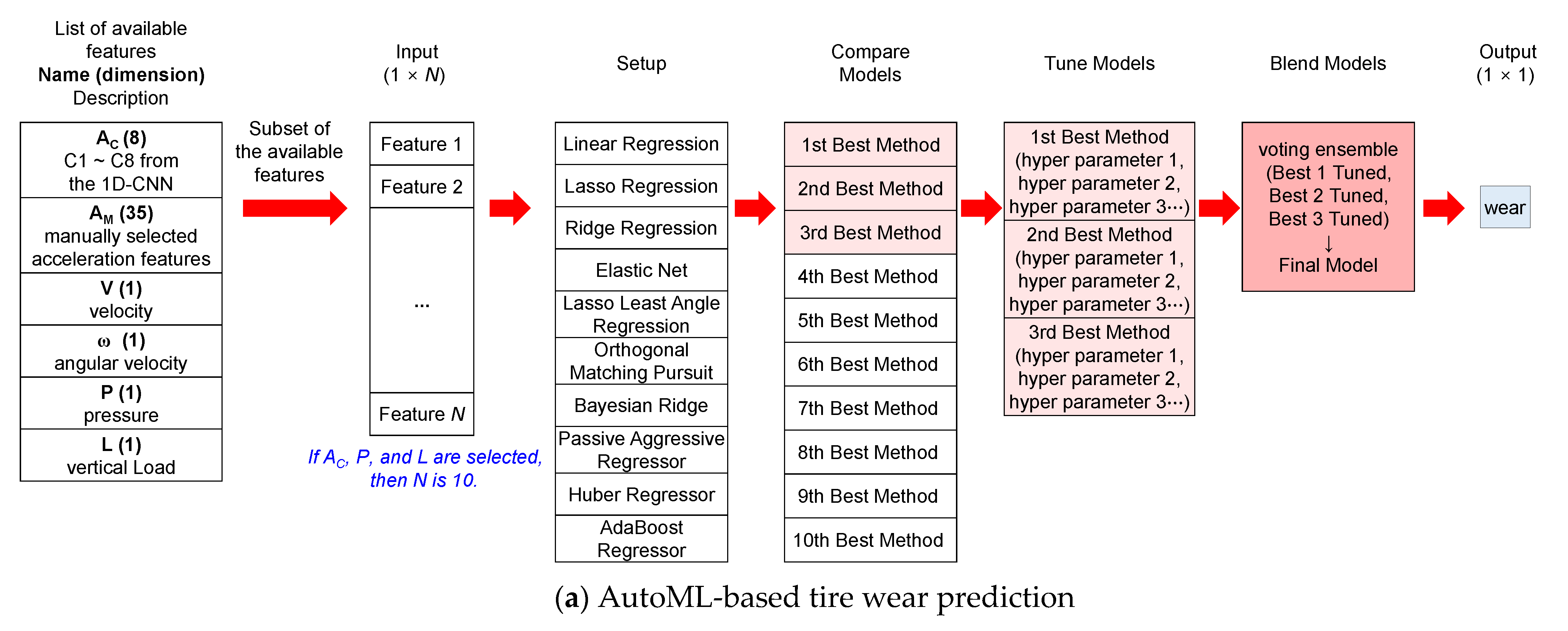
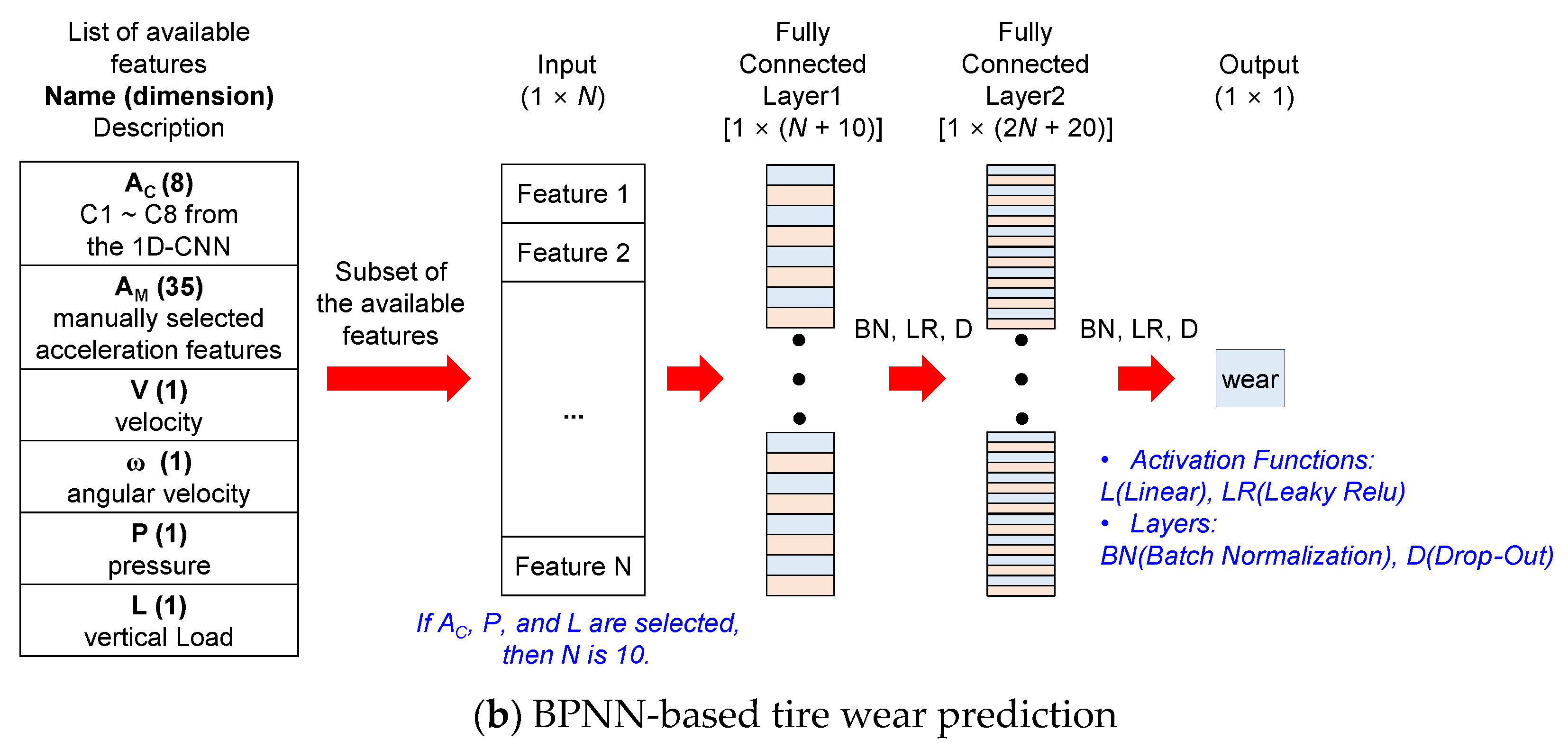
3.4. Development of Tire Wear Prediction Algorithm
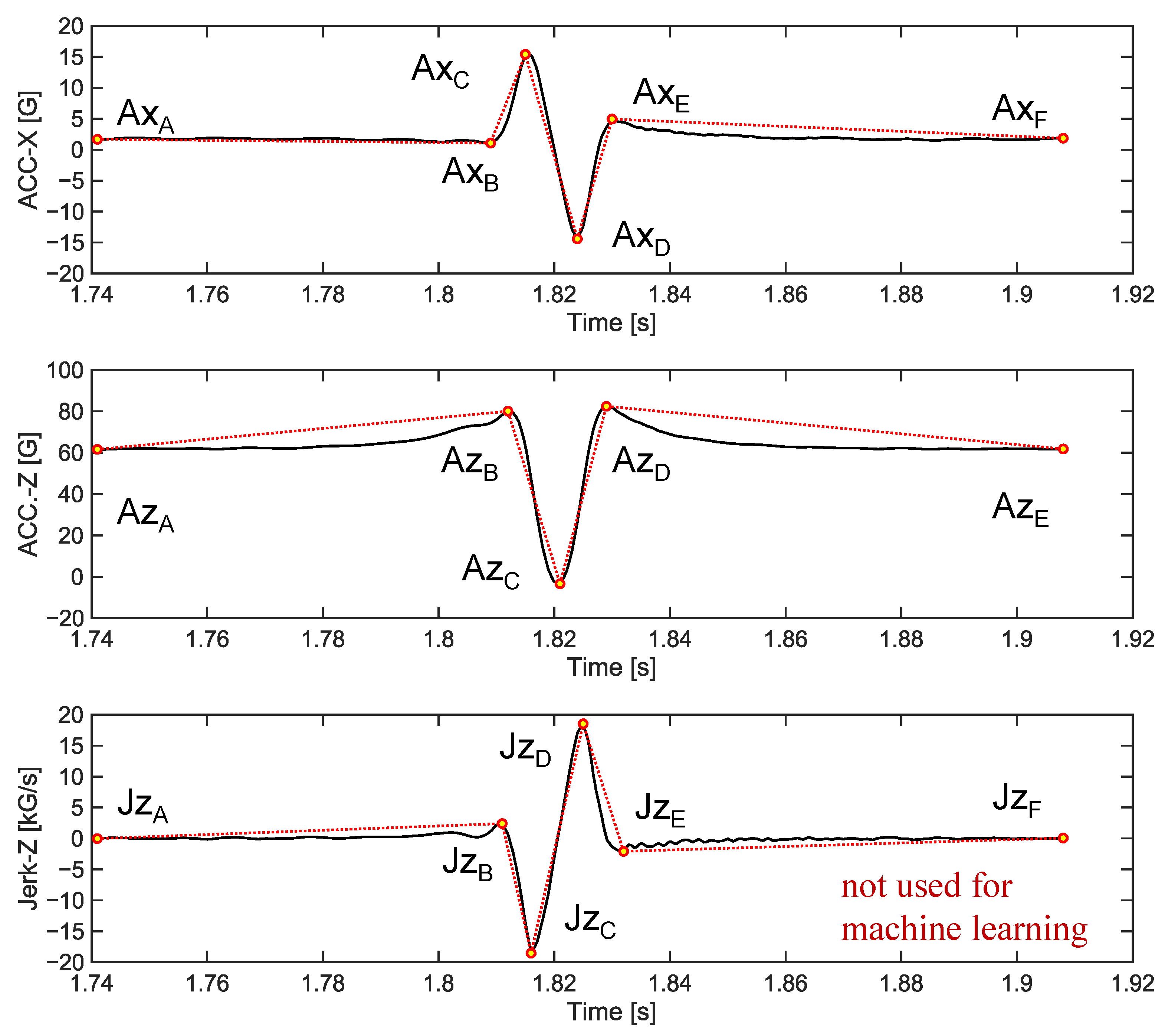
3.4.1. List of Features for Machine Learning
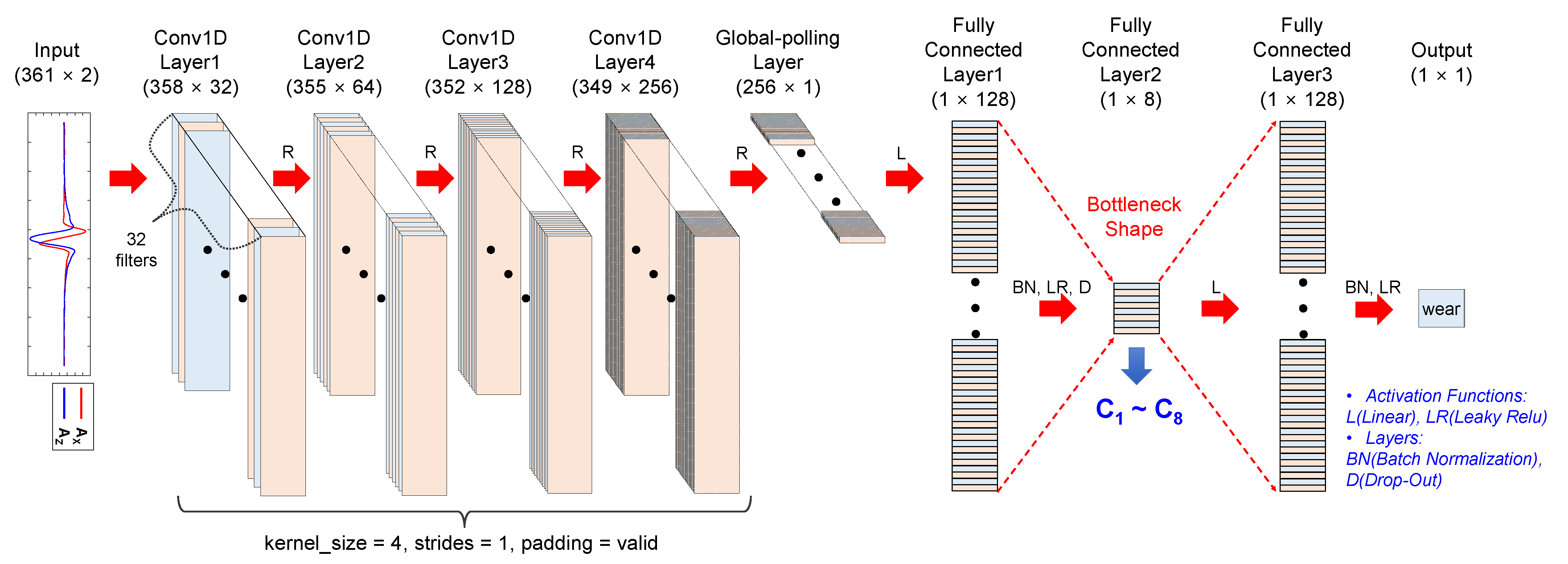
3.4.2. Estimation of Tire Wear Using Machine Learning
3.4.3. Training and Testing of Wear Prediction Algorithm
4. Results
4.1. Tire Model Validation
4.2. Tire Wear Prediction
4.2.1. Eight features from 1D-CNN
4.2.2. Prediction of Wear Amount of Tires
5. Discussion
5.1. Various Sensing Options
5.2. 1D-CNN with Bottleneck Structure
5.3. Generalization Performance
5.4. FE Tire Model for Intelligent Tire Technology
5.5. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| ID | Machine Learning Method | Default Values of Hyper Parameters |
|---|---|---|
| 1 | Linear Regression | fit_intercept = True, n_jobs = −1, normalize = False |
| 2 | Lasso Regression | alpha = 1.0, fit_intercept = True, max_iter = 1000, normalize = False, positive = False, precompute = False, random_state = 1, selection = ‘cyclic’, tol = 0.0001, warm_start = False |
| 3 | Ridge Regression | alpha = 1.0, fit_intercept = True, max_iter = None, normalize = False, random_state = 1, solver = ‘auto’, tol = 0.001 |
| 4 | Elastic Net | alpha = 1.0, fit_intercept = True, l1_ratio = 0.5, max_iter = 1000, normalize = False, positive = False, precompute = False, random_state = 1, selection = ‘cyclic’, tol = 0.0001, warm_start = False |
| 5 | Lasso Least Angle Regression | alpha = 1.0, eps = 2.220446049250313 × 10−16, fit_intercept = True, fit_path = True, jitter = None, max_iter = 500, normalize = True, positive = False, precompute = ‘auto’, random_state = 1, verbose = False |
| 6 | Orthogonal Matching Pursuit | fit_intercept = True, n_nonzero_coefs = None, normalize = True, precompute = ‘auto’, tol = None |
| 7 | Bayesian Ridge | alpha_1 = 1 × 10−6, alpha_2 = 1 × 10−6, alpha_init = None, compute_score = False, fit_intercept = True, lambda_1 = 1 × 10−6, lambda_2 = 1 × 10−6, lambda_init = None, n_iter = 300, normalize = False, tol = 0.001, verbose = False |
| 8 | Passive Aggressive Regressor | C = 1.0, average = False, early_stopping = False, epsilon = 0.1, fit_intercept = True, loss = ‘epsilon_insensitive’, max_iter = 1000, n_iter_no_change = 5, random_state = 1, shuffle = True, tol = 0.001, validation_fraction = 0.1, verbose = 0, warm_start = False |
| 9 | Huber Regressor | alpha = 0.0001, epsilon = 1.35, fit_intercept = True, max_iter = 100, tol = 1 × 10−5, warm_start = False |
| 10 | AdaBoost Regressor | base_estimator = None, learning_rate = 1.0, loss = ‘linear’, n_estimators = 50, random_state = 1 |
| ID | Description | Value |
|---|---|---|
| 1 | Session_id | 1 |
| 2 | Target | wear |
| 3 | Original Data | (1485, 723) |
| 4 | Missing Values | FALSE |
| 5 | Numeric Features | 722 |
| 6 | Categorical Features | 0 |
| 7 | Ordinal Features | FALSE |
| 8 | High Cardinality Features | FALSE |
| 9 | High Cardinality Method | None |
| 10 | Transformed Train Set | (1188, 27) |
| 11 | Transformed Test Set | (297, 27) |
| 12 | Shuffle Train-Test | TRUE |
| 13 | Stratify Train-Test | FALSE |
| 14 | Fold Generator | KFold |
| 15 | Fold Number | 10 |
| 16 | CPU Jobs | −1 |
| 17 | Use GPU | TRUE |
| 18 | Log Experiment | FALSE |
| 19 | Experiment Name | reg-default-name |
| 20 | USI | 3746 |
| 21 | Imputation Type | simple |
| 22 | Iterative Imputation Iteration | None |
| 23 | Numeric Imputer | mean |
| 24 | Iterative Imputation Numeric Model | None |
| 25 | Categorical Imputer | constant |
| 26 | Iterative Imputation Categorical Model | None |
| 27 | Unknown Categoricals Handling | least_frequent |
| 28 | Normalize | FALSE |
| 29 | Normalize Method | None |
| 30 | Transformation | FALSE |
| 31 | Transformation Method | None |
| 32 | PCA | FALSE |
| 33 | PCA Method | None |
| 34 | PCA Components | None |
| 35 | Ignore Low Variance | FALSE |
| 36 | Combine Rare Levels | FALSE |
| 37 | Rare Level Threshold | None |
| 38 | Numeric Binning | FALSE |
| 39 | Remove Outliers | FALSE |
| 40 | Outliers Threshold | None |
| 41 | Remove Multicollinearity | TRUE |
| 42 | Multicollinearity Threshold | 0.975 |
| 43 | Remove Perfect Collinearity | TRUE |
| 44 | Clustering | FALSE |
| 45 | Clustering Iteration | None |
| 46 | Polynomial Features | FALSE |
| 47 | Polynomial Degree | None |
| 48 | Trignometry Features | FALSE |
| 49 | Polynomial Threshold | None |
| 50 | Group Features | FALSE |
| 51 | Feature Selection | FALSE |
| 52 | Feature Selection Method | classic |
| 53 | Features Selection Threshold | None |
| 54 | Feature Interaction | FALSE |
| 55 | Feature Ratio | FALSE |
| 56 | Interaction Threshold | None |
| 57 | Transform Target | FALSE |
| 58 | Transform Target Method | box-cox |
References
- Fwa, T.F.; Kumar, S.S.; Anupam, K.; Ong, G.P. Effectiveness of tire-tread patterns in reducing the risk of hydroplaning. Transp. Res. Rec. 2009, 2094, 91–102. [Google Scholar] [CrossRef]
- Choi, E.H. Tire-related factors in the pre-crash phase. Report No. DOT HS 2012, 811, 617. [Google Scholar]
- Ferrero, F.; Perboli, G.; Vesco, A.; Musso, S.; Pacifici, A. Car-sharing services–part b business and service models. Tech. Rep. 2015. [Google Scholar]
- Zhang, H.; Zhang, S.; Zhang, Y.; Huang, X.; Dai, Y. Abrasion Status Prediction with BP Neural Network Based on an Intelligent Tire System. In Proceedings of the 2020 4th CAA International Conference on Vehicular Control and Intelligence (CVCI), Hangzhou, China, 18–20 December 2020; pp. 619–622. [Google Scholar]
- Kim, Y.J.; Kim, H.J.; Han, J.Y.; Lee, S. Classification of Tire Tread Wear Using Accelerometer Signals through an Artificial Neural Network. J. Korean Soc. Ind. Converg. 2020, 23, 163–171. [Google Scholar]
- Li, B.; Quan, Z.; Bei, S.; Zhang, L.; Mao, H. An estimation algorithm for tire wear using intelligent tire concept. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2712–2725. [Google Scholar] [CrossRef]
- Poloni, T.; Lu, J. An Indirect Tire Health Monitoring System Using on-Board Motion Sensors (No. 2017-01-1626); SAE Technical Paper; SAE: Warrendale, PA, USA, 2017. [Google Scholar]
- Andrews, J.B.; Cao, C.; Brooke, M.A.; Franklin, A.D. Noninvasive material thickness detection by aerosol jet printed sensors enhanced through metallic carbon nanotube ink. IEEE Sens. J. 2017, 17, 4612–4618. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, Q.; Wang, X.; Liu, Z. Vibration transfer function of in-plane rigid–elastic-coupled tire model for heavy-loaded radial tire. Adv. Mech. Eng. 2017, 9, 1687814017726917. [Google Scholar] [CrossRef]
- Braghin, F.; Brusarosco, M.; Cheli, F.; Cigada, A.; Manzoni, S.; Mancosu, F. Measurement of contact forces and patch features by means of accelerometers fixed inside the tire to improve future car active control. Veh. Syst. Dyn. 2006, 44 (Suppl. 1), 3–13. [Google Scholar] [CrossRef]
- Rosu, I.; Elias-Birembaux, H.L.; Lebon, F. Finite element modeling of an aircraft tire rolling on a steel drum: Experimental investigations and numerical simulations. Appl. Sci. 2018, 8, 593. [Google Scholar] [CrossRef]
- Behroozinia, P.; Taheri, S.; Mirzaeifar, R. Tire health monitoring using the intelligent tire concept. Struct. Health Monit. 2019, 18, 390–400. [Google Scholar] [CrossRef]
- American Society for the Testing of Materials. ASTM D 412-16; Standard Test Methods for Vulcanized Rubber and Thermoplastic Elastomers—Tension. American National Standards Institute; ASTM International: West Conshohocken, PA, USA, 2002; Volume 9, pp. 43–55.
- American Society for the Testing of Materials. ASTM D 297-15; Standard Test Methods for Rubber Products: Chemical Analysis. ASTM International: West Conshohocken, PA, USA, 2019.
- American Society for the Testing of Materials. ASTM D 2969–04; Standard Test Methods for Steel Tire Cords. ASTM International: West Conshohocken, PA, USA, 2014.
- Kim, B.S.; Chi, C.H.; Lee, T.K. A study on radial directional natural frequency and damping ratio in a vehicle tire. Appl. Acoust. 2007, 68, 538–556. [Google Scholar] [CrossRef]
- Society of Automotive Engineers. Instrumentation for Impact Test—Part 1—Electronic Instrumentation; SAE: Warrendale, PA, USA, 2007. [Google Scholar]
- Zhang, B.; Xie, L.; Yuan, Y.; Ming, H.; Huang, D.; Song, M. Deep neural network derived bottleneck features for accurate audio classification. In Proceedings of the 2016 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), Seattle, WA, USA, 11–15 July 2016; pp. 1–6. [Google Scholar]
- Ali, M. PyCaret: An Open Source, Low-Code Machine Learning Library in Python 2020, PyCaret version 2. Available online: https://pycaret.readthedocs.io/en/latest/index.html (accessed on 5 November 2022).
- Aspuru, J.; Ochoa-Brust, A.; Félix, R.A.; Mata-López, W.; Mena, L.J.; Ostos, R.; Martínez-Peláez, R. Segmentation of the ECG signal by means of a linear regression algorithm. Sensors 2019, 19, 775. [Google Scholar] [CrossRef] [PubMed]
- Erler, A.; Riebe, D.; Beitz, T.; Löhmannsröben, H.G.; Gebbers, R. Soil nutrient detection for precision agriculture using handheld laser-induced breakdown spectroscopy (LIBS) and multivariate regression methods (PLSR, Lasso and GPR). Sensors 2020, 20, 418. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Yuan, Z.; Wang, Z.; Zhao, L.; Zhang, Y.; Lu, X.; Cao, L. Hyperspectral inversion of soil organic matter content based on a combined spectral index model. Sensors 2020, 20, 2777. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Kozłowski, E.; Kłosowski, G.; Niderla, K. Logistic regression for machine learning in process tomography. Sensors 2019, 19, 3400. [Google Scholar] [CrossRef]
- Nikaein, H.; Sheikhi, A.; Gazor, S. Target detection in passive radar sensors using least angle regression. IEEE Sens. J. 2020, 21, 4533–4542. [Google Scholar] [CrossRef]
- Wang, W.; Wu, R. High resolution direction of arrival (DOA) estimation based on improved orthogonal matching pursuit (OMP) algorithm by iterative local searching. Sensors 2013, 13, 11167–11183. [Google Scholar] [CrossRef]
- Chen, X.; Yao, Y.; Li, Y.; Zhang, Y.; Jia, K.; Zhang, X.; Guo, X. ANN-Based Estimation of Low-Latitude Monthly Ocean Latent Heat Flux by Ensemble Satellite and Reanalysis Products. Sensors 2020, 20, 4773. [Google Scholar] [CrossRef]
- Kasimati, A.; Espejo-García, B.; Darra, N.; Fountas, S. Predicting Grape Sugar Content under Quality Attributes Using Normalized Difference Vegetation Index Data and Automated Machine Learning. Sensors 2022, 22, 3249. [Google Scholar] [CrossRef]
- Wang, C.; Xu, S.; Yang, J. Adaboost Algorithm in Artificial Intelligence for Optimizing the IRI Prediction Accuracy of Asphalt Concrete Pavement. Sensors 2021, 21, 5682. [Google Scholar] [CrossRef]
- Christensen, R. Analysis of Variance, Design, and Regression: Applied STATISTICAL Methods; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Ding, W.; Wang, J. Precise velocity estimation with a stand-alone GPS receiver. J. Navig. 2011, 64, 311–325. [Google Scholar] [CrossRef]
- Sabatini, S.; Formentin, S.; Panzani, G.; Jorge de-J, L.S.; Savaresi, S.M. Motorcycle tire rolling radius estimation for TPMS applications via GPS sensing. In Proceedings of the 2017 IEEE Conference on Control Technology and Applications (CCTA), Kohala Coast, HI, USA, 27–30 August 2017; pp. 1892–1897. [Google Scholar]
- Strano, S.; Terzo, M.; Tordela, C. A supervised machine learning framework for smart tires. In Proceedings of the 2021 IEEE 6th International Forum on Research and Technology for Society and Industry (RTSI), Naples, Italy, 6–9 September 2021; pp. 364–369. [Google Scholar]
- Singh, K.B.; Arat, M.A.; Taheri, S. Literature review and fundamental approaches for vehicle and tire state estimation. Veh. Syst. Dyn. 2019, 57, 1643–1665. [Google Scholar] [CrossRef]
- Singh, K.B.; Taheri, S. Accelerometer Based Method for Tire Load and Slip Angle Estimation. Vibration 2019, 2, 174–186. [Google Scholar] [CrossRef]
- Huang, J.; He, H.; Lv, R.; Zhang, G.; Zhou, Z.; Wang, X. Non-destructive detection and classification of textile fibres based on hyperspectral imaging and 1D-CNN. Anal. Chim. Acta 2022, 1224, 340238. [Google Scholar] [CrossRef] [PubMed]
- Sateesh Babu, G.; Zhao, P.; Li, X.L. Deep convolutional neural network based regression approach for estimation of remaining useful life. In Proceedings of the International conference on database systems for advanced applications, Richardson, TX, USA, 16–19 April 2016; Springer: Cham, Switzerland, 2016; pp. 214–228. [Google Scholar]
- Ku, B.H.; Kim, G.T.; Min, J.K.; Ko, H. Deep convolutional neural network with bottleneck structure using raw seismic waveform for earthquake classification. J. Korea Soc. Comput. Inf. 2019, 24, 33–39. [Google Scholar]
- Zhu, B.; Han, J.; Zhao, J. Tire-pressure identification using intelligent tire with three-axis accelerometer. Sensors 2019, 19, 2560. [Google Scholar] [CrossRef]
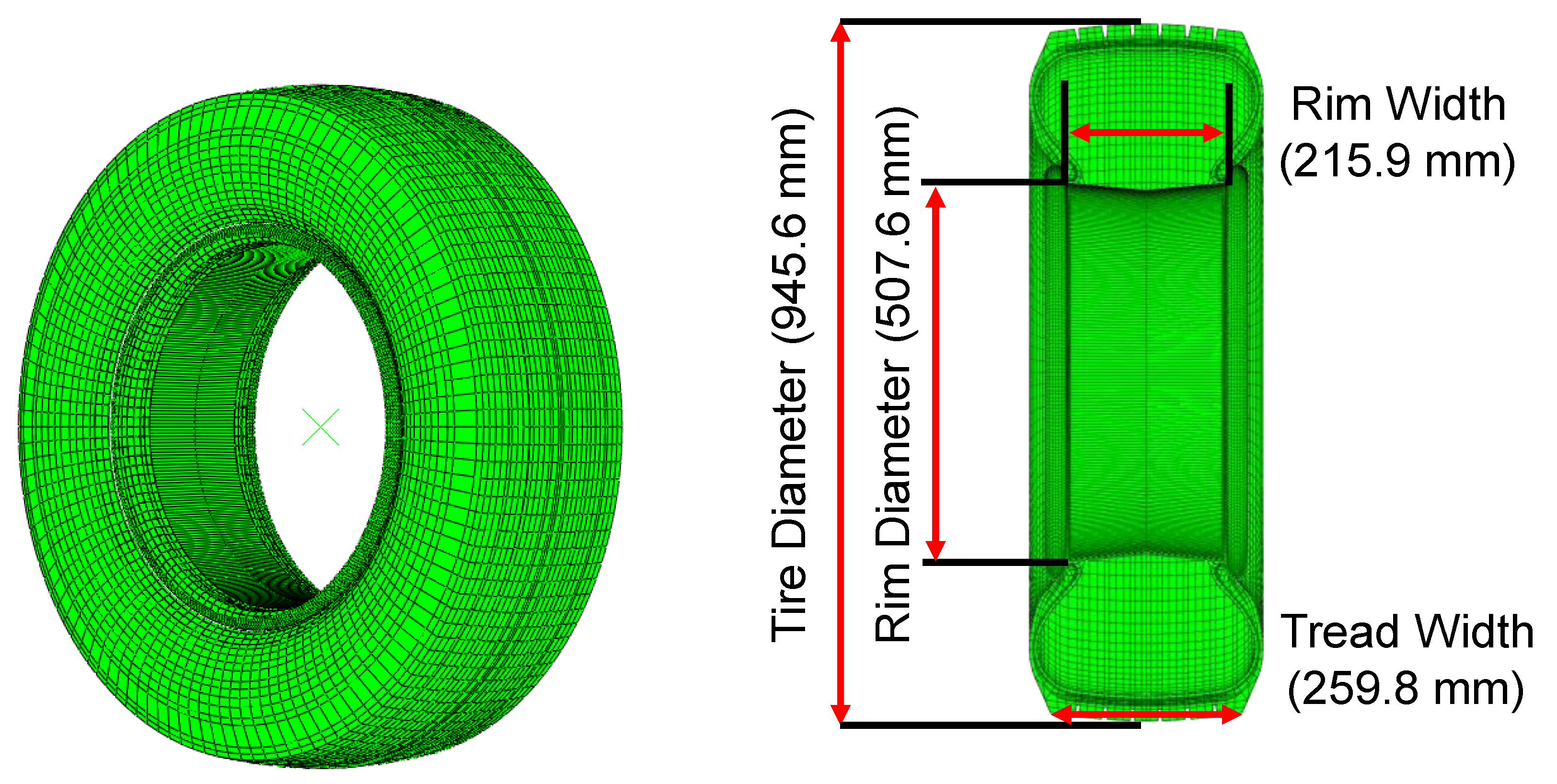


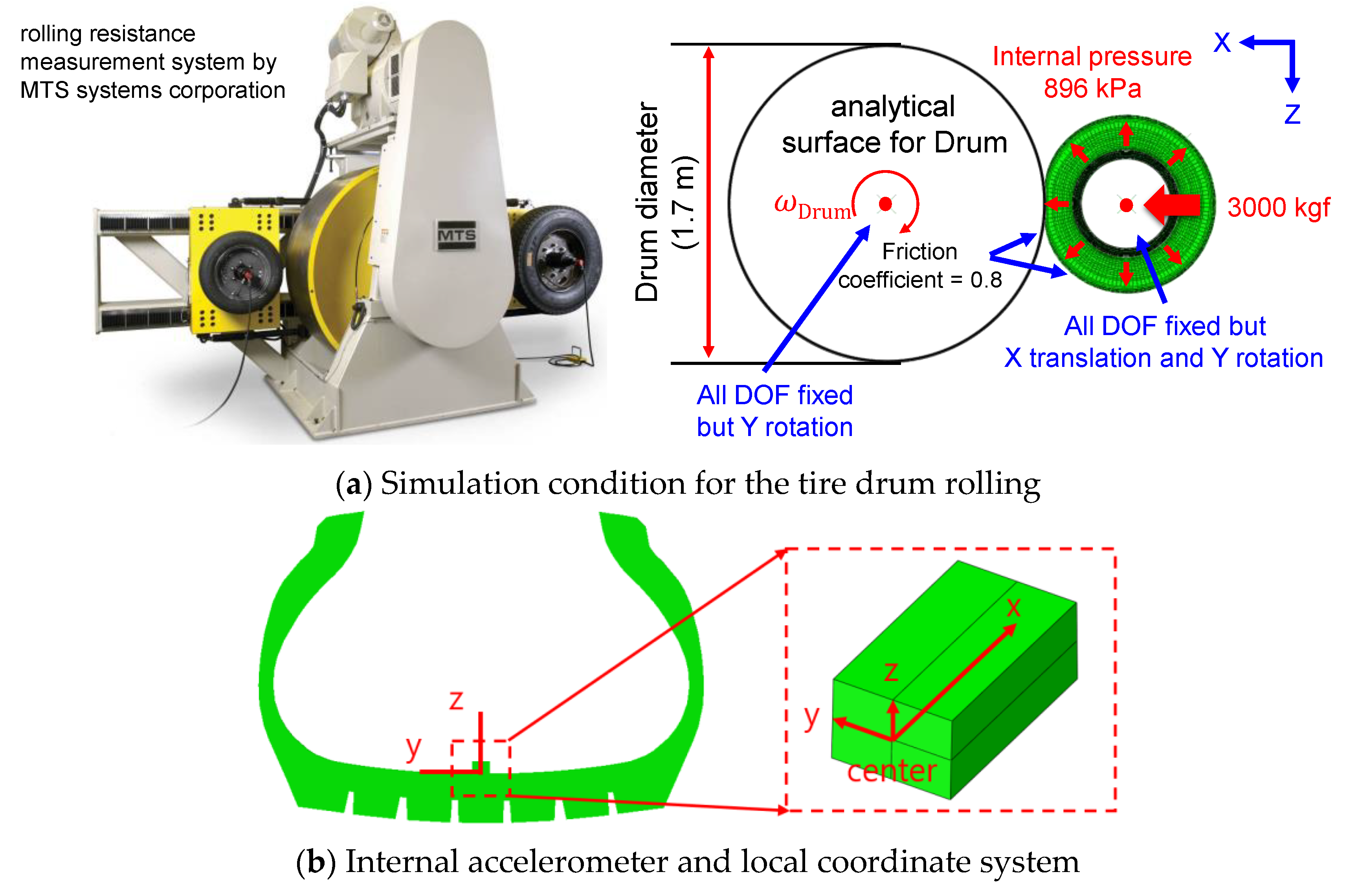
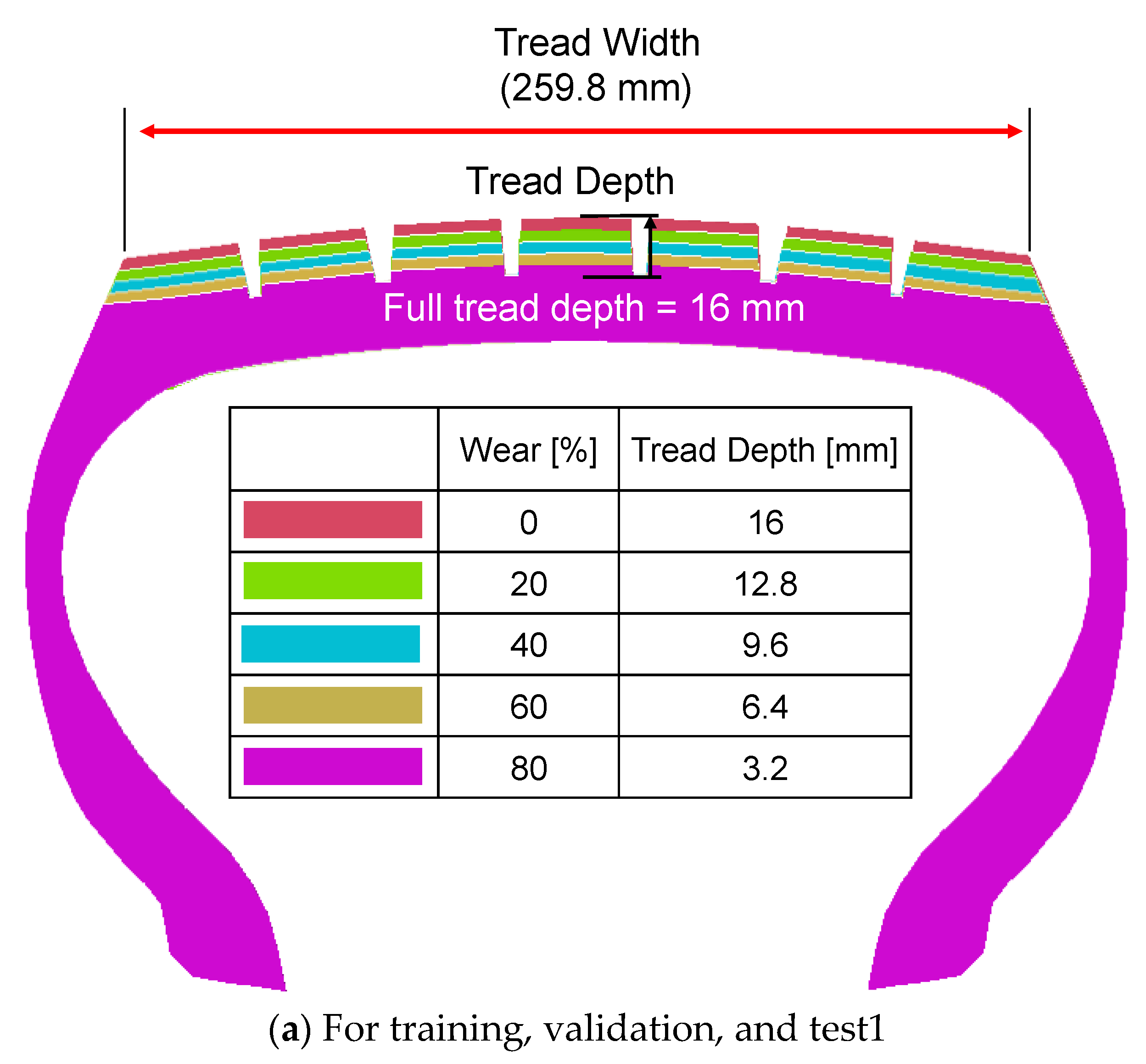
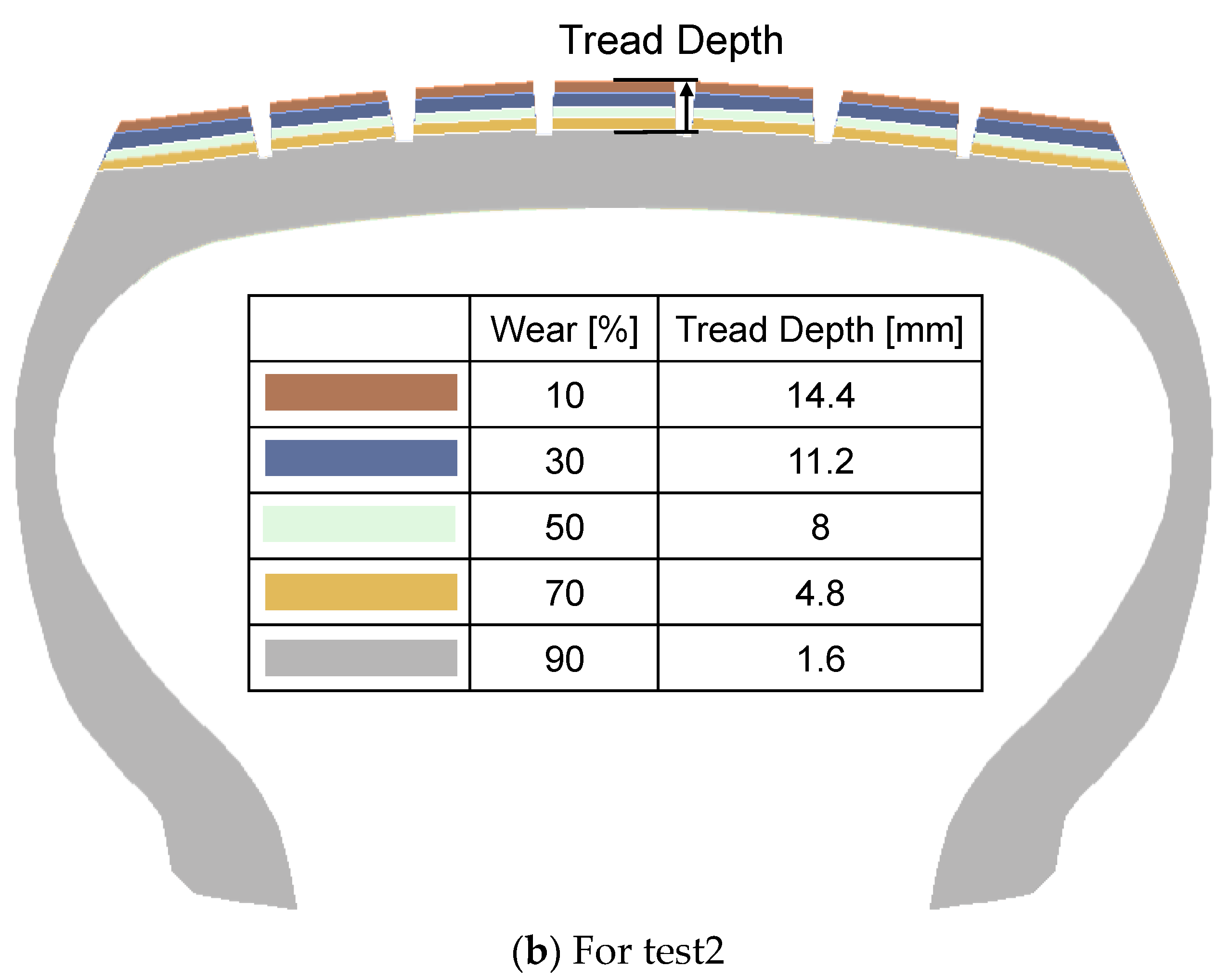




| Purpose | Parameter | Values | Number of Simulations |
|---|---|---|---|
| Training, Validation, and Test1 | Tread wear [%] (100% = 16 mm) | 0, 20, 40, 60, 80 | 180 |
| Velocity [km/h] | 40, 60, 80, 100 | ||
| Pressure [kPa] | 717, 896, 1076 | ||
| Load [kgf] | 2400, 3000, 3600 | ||
| Test2 | Tread wear [%] (100% = 16 mm) | 10, 30, 50, 70, 90 | 60 |
| Velocity [km/h] | 40, 60, 80 | ||
| Pressure [kPa] | 806, 896 | ||
| Load [kgf] | 2700, 3000 |
| Potential Source | Name | Description | |
|---|---|---|---|
| Vehicle | Wheel travel speed (V) | Travel speed at wheel center | |
| Wheel rotational speed (ω) | Wheel rotational speed | ||
| Vertical force (L) | Normal force at the contact patch | ||
| TPMS | Tire pressure (P) | Tire internal pressure | |
| Tire internal accelerometer | AM | axA | Circumferential acceleration (ax) value at the beginning of the cycle |
| axBt | Onset time for the first rise of the ax in the current cycle | ||
| axB | ax value at axBt | ||
| axCt | Time for the first local maximum ax value in the current cycle | ||
| axC | First local maximum ax value in the current cycle | ||
| axDt | Time for the first local minimum ax value in the current cycle | ||
| axD | First local minimum ax value in the current cycle | ||
| axEt | Time for the second local maximum ax value in the current cycle | ||
| axE | Second local maximum ax value in the current cycle | ||
| axdtBC | Time period between the axA and axB | ||
| axdtCD | Time period between the axC and axD | ||
| axdtDE | Time period between the axD and axE | ||
| axdyBC | Difference between axB and axC | ||
| axdyCD | Difference between axC and axD | ||
| axdyDE | Difference between axD and axE | ||
| axslBC | Rate of change between points axB and axC | ||
| axslCD | Rate of change between points axC and axD | ||
| axslDE | Rate of change between points axD and axE | ||
| azA | Radial acceleration (az) value at the beginning of a cycle | ||
| azBt | Time for the first local maximum az in the current cycle | ||
| azB | First local maximum az in the current cycle | ||
| azCt | Time for the minimum az in the current cycle | ||
| azC | Minimum az in the current cycle | ||
| azDt | Time for the second local maximum az in the current cycle | ||
| azD | Second local maximum az in the current cycle | ||
| azdtBD | Time period between the azB and azD | ||
| azdtBC | Time period between the azB and azC | ||
| azdtCD | Time period between the azC and azD | ||
| azdtDE | Time period between azD and azE | ||
| azdyBC | Difference between azB and azC | ||
| azdyCD | Difference between azC and azD | ||
| azdyDE | Difference between azD and azE | ||
| azslBC | Rate of change between points azB and azC | ||
| azslCD | Rate of change between points azC and azD | ||
| azslDE | Rate of change between points azD and azE | ||
| AC | C1~C8 | Eight features generated from 1D-CNN | |
| Step | ID | Description | Value |
|---|---|---|---|
| Setup | 1 | train_size | 0.8 |
| 2 | polynomial_features | True | |
| 3 | feature_interaction | True | |
| 4 | remove_multicollinearity | True | |
| 5 | multicollinearity_threshold | 0.975 | |
| 6 | fold | 10 | |
| Compare_models | 1 | sort | ‘RMSE’ |
| 2 | N_select | 3 | |
| 3 | include | [“lr”, “lar”, “huber”, “ada”, “omp”, “ridge”, “lasso”, “llar”, “br”, “en”, “par”] | |
| Tune_model | 1 | optimize | ‘RMSE’ |
| Blend_models | 1 | fold | 10 |
| 2 | optimize | ‘RMSE’ |
| ID | Description | Value |
|---|---|---|
| 1 | Optimizer | adam |
| 2 | Learning rate | 0.001 |
| 3 | Loss | MSE |
| 4 | epochs | 5000 |
| 5 | batch_size | 1024 |
| 6 | restore_best_weights | True |
| Vertical | Lateral | |||||
|---|---|---|---|---|---|---|
| Displacement at 4150 kgf (mm) | Stiffness (kgf/mm) | Error (%) | Displacement (mm) | Stiffness (kgf/mm) | Error (%) | |
| Test | 42.8 | 97 | - | 11 | 37 | - |
| FEM | 41.1 | 101 | 4.1 | 11 | 39 | 5.4 |
| Pressure | 1st Mode | 2nd Mode | 3rd Mode | |||
|---|---|---|---|---|---|---|
| 85% | Test | Simulation | Test | Simulation | Test | Simulation |
| Frequency (Hz) | 77 | 75 | 99 | 98 | 121 | 121 |
| Error (%) | −2.6 | −1.0 | 0.0 | |||
| Mode Shape | 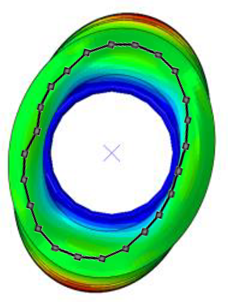 |  | 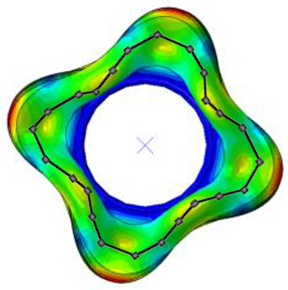 | |||
| Pressure | 1st Mode | 2nd Mode | 3rd Mode | |||
|---|---|---|---|---|---|---|
| 100% | Test | Simulation | Test | Simulation | Test | Simulation |
| Frequency (Hz) | 82 | 80 | 105 | 104 | 130 | 130 |
| Error (%) | −2.5 | −1.0 | 0.0 | |||
| Mode Shape |  | 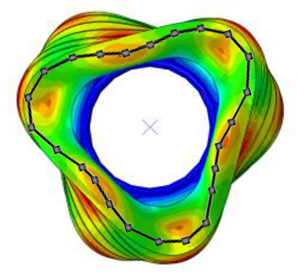 |  | |||
| Pressure | 1st Mode | 2nd Mode | 3rd Mode | |||
|---|---|---|---|---|---|---|
| 115% | Test | Simulation | Test | Simulation | Test | Simulation |
| Frequency (Hz) | 85 | 85 | 110 | 112 | 136 | 138 |
| Error (%) | 0.0 | 1.8 | 1.5 | |||
| Mode Shape |  | 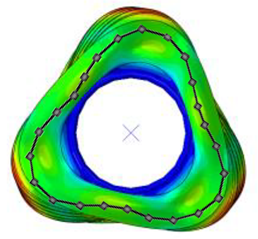 |  | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.; Park, H.; Kim, T. Comparison of Performance of Predicting the Wear Amount of Tire Tread Depending on Sensing Information. Sensors 2023, 23, 459. https://doi.org/10.3390/s23010459
Kim K, Park H, Kim T. Comparison of Performance of Predicting the Wear Amount of Tire Tread Depending on Sensing Information. Sensors. 2023; 23(1):459. https://doi.org/10.3390/s23010459
Chicago/Turabian StyleKim, Kangjun, Hyunjae Park, and Taewung Kim. 2023. "Comparison of Performance of Predicting the Wear Amount of Tire Tread Depending on Sensing Information" Sensors 23, no. 1: 459. https://doi.org/10.3390/s23010459
APA StyleKim, K., Park, H., & Kim, T. (2023). Comparison of Performance of Predicting the Wear Amount of Tire Tread Depending on Sensing Information. Sensors, 23(1), 459. https://doi.org/10.3390/s23010459






